A Weighted Random Forests Approach to Improve Predictive Performance

Abstract

Identifying genetic variants associated with complex disease in high-dimensional data is a challenging problem, and complicated etiologies such as gene-gene interactions are often ignored in analyses. The data-mining method Random Forests (RF) can handle high-dimensions; however, in high-dimensional data, RF is not an effective filter for identifying risk factors associated with the disease trait via complex genetic models such as gene-gene interactions without strong marginal components. Here we propose an extension called Weighted Random Forests (wRF), which incorporates tree-level weights to emphasize more accurate trees in prediction and calculation of variable importance. We demonstrate through simulation and application to data from a genetic study of addiction that wRF can outperform RF in high-dimensional data, although the improvements are modest and limited to situations with effect sizes that are larger than what is realistic in genetics of complex disease. Thus, the current implementation of wRF is unlikely to improve detection of relevant predictors in high-dimensional genetic data, but may be applicable in other situations where larger effect sizes are anticipated.

Introduction

In traditional genome-wide association studies, data collected at hundreds of thousands to millions of genetic variants are analyzed univariately in order to determine association with a disease. These tests of association do not account for the effects of other genetic variants, ignore complex models such as gene-gene interactions, and have low power to detect most genetic effects. Thus, identified variants account for a very small proportion of variation in complex traits [1, 2].

To circumvent these issues, data-mining and machine learning methods such as Random Forests [3] are rising in popularity for genome-wide data analysis due to their ability to handle high-dimensional data, and to consider multiple predictor variables simultaneously. Random Forests (RF) trains an ensemble of multiple classification or regression trees on many bootstrap samples of subjects, handling high-dimensional data because only random subsets of predictors are considered at each node of the tree. Predictions are aggregated, or bagged, across all trees in the forest, and the prediction model is evaluated using measures of prediction error (misclassification rate) or area under the receiver operating characteristic curve (AUC) in the out-of-bag subjects. Additionally, RF can be used to calculate variable importance measures, which assess a variable’s overall influence on prediction and can be used to rank predictors. These measures have been shown to work well in low-dimensional genetic data to capture complex effects such as interactions among predictor variables [4], and they have been proposed as filtering or screening tools in high-dimensional data [5].

However, we previously evaluated the performance of RF with increasing numbers of genetic variants, and observed that the probability of detection of the causal variants (i.e. the proportion of times the causal variants were highly ranked) decreases more rapidly for interactions than for variants with marginal effects [6]. In fact, in high-dimensional data, both the detection probability and prediction error depend primarily on the marginal effect size, suggesting little advantage over univariate methods in high-dimensional data, particularly as a filter for the detection of interacting factors. This is because as the dimension grows, interacting variants will rarely appear in a tree together (especially if those variants do not exhibit strong marginal effects), and therefore the interaction is rarely modeled. Based on this observation, we aimed to develop an improved RF-based method for capturing complex models, Weighted Random Forests (wRF). The original RF gives each tree in the forest equal weight during aggregation. However, up-weighing the class votes from the better performing trees may have the potential to improve the overall predictive performance, assuming that the better performing trees are more likely to contain the causal variables.

Previously, other weighting methods have been proposed with ensemble classification methods such as RF. For example, because the RF classifier tends to be biased towards the majority class, weights can be assigned to each class in order to deal with the issue of imbalance [7]; these class weights are applied to the node splitting criterion and the aggregation procedure in order to ensure that the minority class is weighted equally. This method is currently available in the R package ‘randomForest’. In addition to class weights, random weighting of variables/attributes within each node during the construction of decision trees has been implemented in the Random Feature Weights (RFW) method [8]. The method is similar to RF; however, rather than considering a random subset of predictors at each node, RFW considers all variables with those with higher weights being more likely to be used in tree construction. Similarly, Enriched RF alters the tree-fitting procedure by using weighted random sampling to choose the subset of variables to be considered at each node; rather than being random, variable weights are assigned based on marginal q-values [9].

Rather than weighting either classes or attributes/variables, the Weight-Adjusted Voting for Ensembles (WAVE) method uses iterative weights for both samples and trees, as an extension of both bagging and boosting for ensemble methods [10]. Trees/classifiers that perform best on the hard-to-classify instances receive the strongest weight. Other tree-weighting methods that have been incorporated into RF include an approach that weighs trees based on the average margin of similar instances in the OOB data [11]. The Tree-Weighting Random Forests (TWRF) proposed by Li et al implements weighted voting with weights based on tree accuracy in the OOB data [12]. Both of these methods construct and test their weights on the OOB data, which is expected to bias PE estimates. Additionally, different weighting schemes have not been compared and weighted measures of variable importance have not been developed.

In the current study, we introduce and describe the weighted Random Forest (wRF) method, which incorporates tree-level weights into the usual RF algorithm to emphasize more accurate trees in prediction and calculation of variable importance. We consider different tree-weights, and present simulations to compare the performance of wRF to the traditional RF algorithm both in terms of prediction accuracy and performance of variable importance measures. The simulations assess performance of wRF over a range of effect sizes and complex genetic models involving interactions. Lastly, we apply wRF to data from a gene-set from the Study of Addiction: Genetic and Environment (SAGE)[13].

Methods

Weighted Random Forests

Assume that the data consist of a binary response variable coded 0 or 1, and p predictor variables collected on N samples. The traditional Random Forests (RF) method would build an ensemble of ntree classification trees to predict the outcome from the predictors, with each tree trained on a different bootstrap sample of N subjects, and a random subset of mtry predictors considered at each node of the tree. The original implementation of RF then aggregates tree-level results equally across trees. We implement the usual RF algorithm to build the trees of the forest; however, we utilize performance-based weights for tree aggregation. In particular, we consider weighting class ‘votes’ from each tree in the forest such that better performing trees are weighted more heavily.

Because weights are performance-based, applying the weights to the same dataset from which the weights were calculated (as was done in [11, 12]) would bias prediction error assessment. To avoid this bias, we first split the data into training and testing sets, and use the training data to implement the usual RF algorithm, with trees constructed on ntree bootstrap samples. Using the out-of-bag (OOB) individuals, estimates of the predictive ability of each tree are calculated (such as tree-level prediction error), which can be used to compute weights, w_j, for each tree j=1,…,ntree. In our implementation of wRF, the training data included ¾ of the original sample (M₁ individuals); thus, for each tree, approximately ½ of the full sample was in-bag and was used to build the tree, and ¼ was out-of-bag and was used to assess tree performance and calculate tree weights.

After the tree-weights are computed in the training data, we use the ntree trees to obtain votes for the ¼ observations in the independent test data, and aggregate the votes (predicted classifications) across trees by applying the weights w_j to the votes. Let v_test,ij be the vote for tree j for subject i in the independent test data, where i=1,…, M₂=N/4. Then the weighted prediction for subject i based on all trees is:

$$w{P}_i=\sum _{j=1}^{ntree}{w}_j\cdot v_{test,ij}$$ (1)

Using the weighted predictions in (1), we can compute performance measures of the weighting procedure in the independent test set, such as the prediction error (PE_wRF) and AUC (AUC_wRF) of the Weighted Random Forest. If y_i is the true class of subject i, then the prediction error PE_wRF can be computed based on the weighted classifications wC_i:

$$\begin{array}{cc}\hfill & w{C}_i=I(w{P}_i\ge 0.5)\hfill \\ \hfill & P{E}_{wRF}=\frac{1}{M_2}\sum _{i=1}^{M_2}\mid w{C}_i-y_i\mid \hfill \end{array}$$ (2)

Similarly, we can use the weighted predictions wP_i (Equation 1) to calculate the weighted AUC (AUC_wRF).

Note that setting w_j=1/ntree gives the usual aggregate prediction in the traditional implementation of RF, and then PE_wRF is equivalent to the usual estimate of PE computed on the test set.

In addition to prediction and PE assessment, the usual RF algorithm can be used to estimate the importance of each variable used in construction of the classifier. The most commonly-used estimate of variable importance is permutation importance, or mean decrease in accuracy (MDA)—the increase in prediction error (or reduction in prediction accuracy) after the data for the variable of interest are permuted across all individuals within each tree [14]. Based on (1), we can also compute a weighted version of the MDA variable importance:

$$V{I}_{wRF}=\frac{1}{M_2}\sum _{i=1}^{M_2}\mid w{P}_i^{\ast }-y_i\mid -\mid w{P}_i-y_i\mid$$ (3)

If w_j=1/ntree, VI_wRF is equivalent to the usual MDA variable importance.

Choice of Weights

To up-weigh better performing trees, weights w_j should be chosen based on some measure of predictive ability at the tree-level. Intuitively, weights inversely related to tree-level prediction error in the OOB training data are appropriate. In the OOB training data, define v_train,ij as the vote for subject i in tree j and let oob_ij be an indicator for the out-of-bag status of subject i in tree j. We define tree-level prediction error for tree j as:

$$tP{E}_j=\frac{1}{\sum _{i=1}^{M_1}oo{b}_{ij}}\sum _{i=1}^{M_1}\mid v_{train,ij}-y_i\mid \cdot oo{b}_{ij}$$ (5)

In our proposed wRF implementation, we utilize weights of the form $w_j=x_j∕{\sum }_{j=1}^{ntre}{x}_j$, such that ${\sum }_{j=1}^{ntree}{w}_j=1$. To implement the usual RF aggregation, let x_j = 1; however, weights such as x_j = 1 − tPE_j or $x_j=\frac{1}{tP{E}_j}$ will allow for a higher weight for more accurate trees. Additionally, we may wish to further up-weigh the best performing trees by utilizing weights with a right skewed distribution, such as $x_j=\text{exp}\left(\frac{1}{tP{E}_j}\right)$ or $x_j={\left(\frac{1}{tP{E}_j}\right)}^{\lambda }$ for some λ. In fact, this strategy is supported by previous work [8], which showed that skewed weights improved performance. Alternatively, it may be advantageous to increase variability across weights by considering weights with a uniform distribution, such as $x_j=rank\left(\frac{1}{tP{E}_j}\right)$.

In addition to weights based on tPE_j, other measures of tree-level performance could be used. For instance, to capture the correlation between tree-level predictions and observed responses, we consider regression-based weights constructed from the estimated regression coefficient ${\widehat{\beta }}_j$ from the following linear model fit to the OOB subjects from tree j:

$$y_i={\alpha }_j+{\beta }_j{v}_{train,ij}+\epsilon$$ (6)

Intuitively, ${\widehat{\beta }}_j$ will be larger if the predicted votes for tree j are close to the true responses, and close to 0 or less than 0 if the predicted votes are either uncorrelated or negatively correlated with the true responses. This suggests a weight such as $x_j={\widehat{\beta }}_j+\text{min}\mid {\widehat{\beta }}_j\mid$, shifted such that all x_j>0.

Simulation Study

In order to compare the predictive performance of wRF to RF with equal tree-weights and to evaluate various choices of tree-weights, we conducted a simulation study. Because the goal of this work was to explore the potential improvement of wRF over RF for the analysis of high-dimensional genetic data, we simulated datasets consisting of p=1000 predictors representing genotypes at single nucleotide polymorphisms (SNPs), with the genotypes (predictors) coded as (0,1,2) representing the number of copies of the variant allele that a person carries at the SNP. Datasets were designed to reflect a case/control study with N=1000 subjects, including 500 cases and 500 controls. For simplicity, SNP genotypes were generated assuming a fixed minor allele frequency of 0.3 and independence across predictor variables, in order to avoid confounding effects of varying predictor frequencies or correlation among predictors. Conditional on the genetic variants, an intermediate quantitative response variable Q was generated to reflect an underlying quantitative trait, caused by a series of m causal pairs of SNPs with possible pairwise interactions. We assumed that Q is actually unobserved, and instead we observe the binary manifestation Y. Q was simulated under the following Gaussian model:

$$Q={\beta }_0+\sum _{k=1}^m({\beta }_1{X}_{1,k}+{\beta }_2{X}_{2,k}+{\beta }_3{X}_{1,k}{X}_{2,k})+\epsilon$$ (7)

where ε ~ N(0, σ) and X_i,k refers to the genotype (0,1,2) for ith SNP of the kth SNP pair. Our model for Q represents a flexible class of models, where the number of causal pairs, effect sizes, and strength or presence of interactions can vary to reflect different genetic scenarios depending on parameter choices. In our simulations, m=2 or 10 causal SNP pairs, yielding 2m causal predictor variables and p-2m variants that are not associated with the underlying quantitative trait Q. The binary response Y, representing disease status, was generated based on a threshold model, where Y=I(Q > median(Q)).

The parameter β=[β₁, β₂, β₃] controls the effect sizes for the genetic model, and was chosen to achieve a desired total broad sense heritability (H²), the proportion of trait variation that can be explained by genetic variation [6, 15]. Broad sense heritability (H²) was utilized to quantify the overall effect size of a particular genetic model and the contribution of a variable due to both marginal and interaction components. Suppose a binary disease trait is controlled by two genetic variants A and B. Then the total heritability due to the two variants (H²_AB) can be partitioned into the marginal effect of each variable (H²_M,A, H²_M,B) and the interaction effect (H²_I,AB), representing the deviation from additivity:

$$H_{AB}^2=H_{M,A}^2+H_{M,B}^2+H_{I,AB}^2$$

In this study, β was chosen such that H² ranged from 0 to 20%, with equal effects H²/m per pair of causal variants, and the ratio between the marginal effects (H²_M) and the interaction effects (H²_I) of each pair of causal variants was 0.5, 1, or 2. As a baseline comparison, we also simulated data with only marginal effects (i.e. H²_I,AB=0 and β₃=0) for the scenarios with m=10 causal loci. Specific values of β and H² are shown in Tables 1 and 2, giving the range of simulated scenarios for the class of models investigated in this study.

Table 1.

Simulated effect sizes for m=2 causal pairs.

H2	H2pair	H2M / H2I	H2M	H2I	β 1	β 2	β 3
0.5	0.25	2	0.167	0.083	0.495	0.495	0.395
		1	0.125	0.125	0.520	0.520	0.490
		0.5	0.083	0.167	0.505	0.505	0.545
1.0	0.50	2	0.333	0.167	0.710	0.710	0.570
		1	0.250	0.250	0.720	0.720	0.680
		0.5	0.167	0.333	0.720	0.720	0.780
2.5	1.25	2	0.833	0.417	1.102	1.102	0.885
		1	0.625	0.625	1.113	1.113	1.071
		0.5	0.417	0.833	1.151	1.151	1.250
5.0	2.50	2	1.667	0.833	1.583	1.583	1.276
		1	1.250	1.250	1.652	1.652	1.562
		0.5	0.833	1.667	1.662	1.662	1.802
10.0	5.00	2	3.333	1.667	2.342	2.342	1.899
		1	2.500	2.500	2.447	2.447	2.317
		0.5	1.667	3.333	2.467	2.467	2.682
15.0	7.50	2	5.000	2.500	3.022	3.022	2.468
		1	3.750	3.750	3.180	3.180	3.016
		0.5	2.500	5.000	3.198	3.198	3.484

Table 2.

Simulated effect sizes for m=10 causal pairs.

H2	H2pair	H2M / H2I	H2M	H2I	β 1	β 2	β 3
5.0	0.5	Inf	0.5	0	0.307	0.307	0
		2	0.333	0.167	0.482	0.482	0.386
		1	0.250	0.250	0.502	0.502	0.474
		0.5	0.167	0.333	0.506	0.506	0.548
10.0	1.0	Inf	1.0	0	0.436	0.436	0
		2	0.667	0.333	0.686	0.686	0.550
		1	0.500	0.500	0.714	0.714	0.673
		0.5	0.333	0.667	0.718	0.718	0.777
15.0	1.5	Inf	1.5	0	0.536	0.536	0
		2	1.000	0.500	0.842	0.842	0.675
		1	0.750	0.750	0.876	0.876	0.827
		0.5	0.500	1.000	0.883	0.883	0.956
20.0	2.0	Inf	2.0	0	0.622	0.622	0
		2	1.333	0.667	0.978	0.978	0.785
		1	1.000	1.000	1.016	1.016	0.960
		0.5	0.667	1.333	1.024	1.024	1.109

For each combination of m, H² and ratio H²_M/H²_I (resulting in 34 simulation scenarios), 100 datasets were generated and analyzed using wRF with ntree=5000 and mtry=sqrt(p), the default value for the number of predictor variables to be considered at each node. Each dataset was analyzed with the previously described weights:

• x_j=1 (which yields the original RF without weighting),

• 1 − tPE_j,

• $\text{exp}\left(\frac{1}{tP{E}_j}\right)$,

• ${\left(\frac{1}{tP{E}_j}\right)}^{\lambda }$, where λ=1,2,3,4,5

• $rank\left(\frac{1}{tP{E}_j}\right)$,

• ${\widehat{\beta }}_j+\text{min}\mid {\widehat{\beta }}_j\mid$, based on Equation 6.

For each simulation replicate, M₁=750 of the 1000 subjects made up the training set, and M₂=250 made up the test set. Rather than using the usual OOB predictions to assess unweighted PE from the standard RF approach, weights x_j=1 were used to represent RF analysis without weighting, so that all results were obtained from the same forest and evaluated on the same test set under the wRF framework, making the weighted and unweighted results more comparable. Performance was measured in terms of PE_wRF, AUC_wRF, and ranks based on VI_wRF of the causal variants. All analyses were performed in R statistical software.

Real Data Application

To assess the performance of wRF in a real dataset, we applied both the traditional RF method along with wRF to a candidate gene-set from a genome-wide association study of alcoholism, the Study of Addiction: Genetic and Environment (SAGE)[13], available on Database of Genotypes and Phenotypes (dbGaP)[16]. We investigated associations with SNPs from the NMDA-dependent AMPA trafficking cascade pathway. Previously, using traditional regression-based methods, we showed that this gene-set was significantly associated with alcohol dependence (p<0.01) [17]. Because RF requires complete data, we utilized an imputed dataset, and excluded SNPs from the X chromosome to avoid confounding with sex. Thus, after quality control, the analyzed dataset consisted of genotypes of 1149 cases and 1357 controls at 711 SNPs in 8 genes, including: GRIN1, GRIN2A, GRIN2B, CAMK2A, CAMK2B, GRIA1, GRIA2, and GRIA4.

We ran wRF with all weights discussed here, including equal weights (equivalent to traditional RF with an independent test set used for evaluation of prediction). Data were split 75% for training and 25% for testing, as in our simulations. We present results for a single data-split, as well as 4-fold cross-validation results to assess the sensitivity of the weighted analysis to a particular random split. For comparability, we assess analysis with wRF with and without the use of equal tree-weights. We also conducted a traditional RF analysis (using the usual OOB estimates) and compare the results to wRF, although it should be noted that the usual OOB prediction estimate is biased [18, 19].

Results

Simulation Study

For the simulation study with two causal pairs of SNPs, performance in terms of both PE_wRF and AUC_wRF improved as H² (i.e. overall genetic effect size) increased. Results are plotted in Figure 1A and B for the weights x_j=1,(1/tPE_j)², (1/tPE_j)⁵, and rank(1/tPE_j); results for the other weights followed a similar pattern and can be seen in Supporting Information (Supporting File 1). For low H², performance was poor with PE_wRF and AUC_wRF both near 0.5, and all weighting methods were nearly identical. As H² increased, PE_wRF decreased and the various types of weights displayed more variation in performance. For high heritability and for all ratios of marginal to interacting effects (H²_M/H²_I), equal tree-weights yielded the largest PE_wRF estimates, while the lowest estimates of PE_wRF were observed for the most extreme tree-weights, such as $x_j=rank\left(\frac{1}{tP{E}_j}\right)$ and $x_j={\left(\frac{1}{tP{E}_j}\right)}^5$. However, the advantage was not substantial; the largest improvement was observed in the case of stronger interaction effects (H²_M/H²_I=0.5) for H²=15%, where there was approximately a 2.5% improvement in PE_wRF by use of $x_j={\left(\frac{1}{tP{E}_j}\right)}^5$ compared to equal tree-weights (Figure 1A). When AUC_wRF was used to measure performance, a similar pattern was observed as H² increased (Figure 1B).

Figure 1.

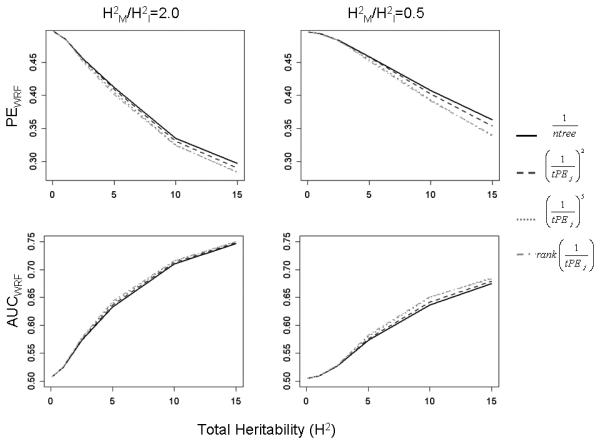
Simulation Results (wPE and wAUC), m=2 causal pairs.

Weighted Prediction Error (top row) and AUC (bottom row) plotted against total heritability for models with 2 causal interacting pairs. Results are only displayed for a subset of weights and for H²_M/H²_I = 0.5, 2.0; for the full results, see Supporting Information. The results for weights that are not plotted are similar and in the same range.

For the simulations involving 10 causal interacting SNP pairs, we observed similar results, although because the same total effect size is dispersed across more pairs of SNPs, the predictive ability was generally lower. Results are plotted in Figure 2A and B for weights x_j=1,(1/tPE_j)², (1/tPE_j)⁵, and rank(1/tPE_j); results for the other weights were in the same range and are shown in the Supporting Information (Supporting File 2). When H²=5%, performance with PE_wRF and AUC_wRF was nearly identical for all weighting methods. Performance became more differentiated as H² increased (Figure 2A and B), with the estimated PE_wRF being consistently highest for x_j=1, although the difference between results with different weights was very small. For scenarios with high total heritability (and all values of H²_M/H²_I, including scenarios with H²_I=0), the lowest PE_wRF estimates were observed for the uniformly-distributed tree-weights, $x_j=rank\left(\frac{1}{tP{E}_j}\right)$, although the largest gain over the currently implemented equal weighting was only about 0.5% (Figure 2A). Results in terms of AUC_wRF were consistent with those of PE_wRF; an improvement observed via weighting was very small (Figure 2B). Furthermore, the ratio of marginal to interacting effect sizes (H²_M/H²_I) seemed to have little impact on performance; the pattern of results was similar for scenarios with only marginal effects (H²_I=0) as for scenarios with stronger interactions (H²_M/H²_I=0.5); see Supporting Information, Supporting File 2. Rather, the total genetic effect size (H²), as well as the per SNP effect size, seemed to be the driving factor on performance of wRF.

Figure 2.

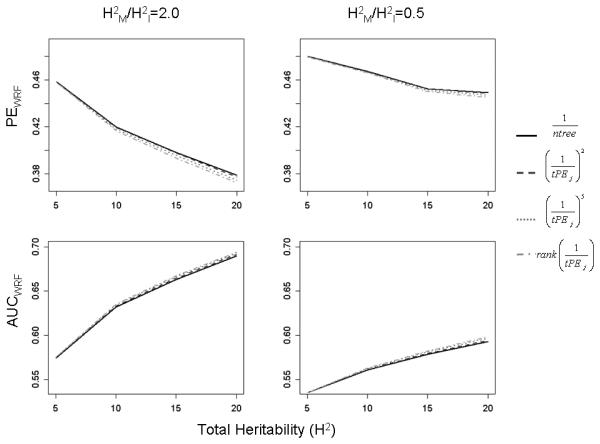
Simulation Results (wPE and wAUC), m=10 causal pairs.

Weighted Prediction Error (top row) and AUC (bottom row) plotted against total heritability for models with 10 causal interacting pairs. Results are only displayed for a subset of weights and for H²_M/H²_I = 0.5, 2.0; for the full results, see Supporting Information. The results for weights that are not plotted are similar and in the same range.

For both sets of simulation studies with either m=2 or 10 causal pairs of SNPs, there was very little change amongst weighted variable importance measures for the causal factors (Supporting Information, Supporting Files 1 and 2). Variable importance measures are typically used to rank variables, therefore we expected that the causal SNPs would rank highly out of all p=1000 predictor variables. To compare VI_wRF measures across all causal SNPs, we computed the average ranks across all 2*m causal variants. For each scenario, average ranks were almost indistinguishable across choice of weights, with the exception of the uniform-weights which produced slightly lower VI_wRF average ranks, as can be seen in Supporting Information. Median ranks demonstrated similar results.

Real Data Application

Weighted RF was fit to the 711 SNPs in the NMDA-dependent AMPA trafficking cascade pathway, with the same set of weights that were investigated in the simulation study, including x_j=1 representing an unweighted RF. Overall, the SNPs were not highly predictive of alcohol dependence; PE ranged from 0.476-0.483 and AUC ranged from 0.503-0.521. Results of the traditional analysis using RF with the OOB estimates yielded PE and AUC very similar to those seen with all of the weights. Variable importance measures differed slightly between the different methods, with rs980272 near CAMK2A and rs2267779 and rs2267780 in GRIN2A consistently ranking near the top of the results in the wRF analyses; rs1421109 and rs12322168 in GRIN2B ranked at the top of the traditional RF analyses. Results for wRF were similar between the single split of the data and cross-validation for PE/AUC, although some differences are observed for VI_wRF; however, estimates of variable importance are known to be unstable[20]. Results are shown for weights x_j=1,(1/tPE_j)², (1/tPE_j)⁵, and rank(1/tPE_j) (Table 3; Figure 3; Supporting Information, Supporting File 3).

Table 3.

Real data analysis of the NMDA-dependent AMPA trafficking cascade pathway, PE and AUC

	RF OOB	x=1	x=(1/tPE)2	x=(1/tPE)5	x=rank(1/tPE)
PE, 1 split	0.472	0.467	0.470	0.475	0.483
PE, CV	0.479	0.467	0.468	0.467	0.465
AUC, 1 split	0.505	0.507	0.506	0.505	0.503
AUC, CV	0.512	0.521	0.521	0.522	0.520

Figure 3.

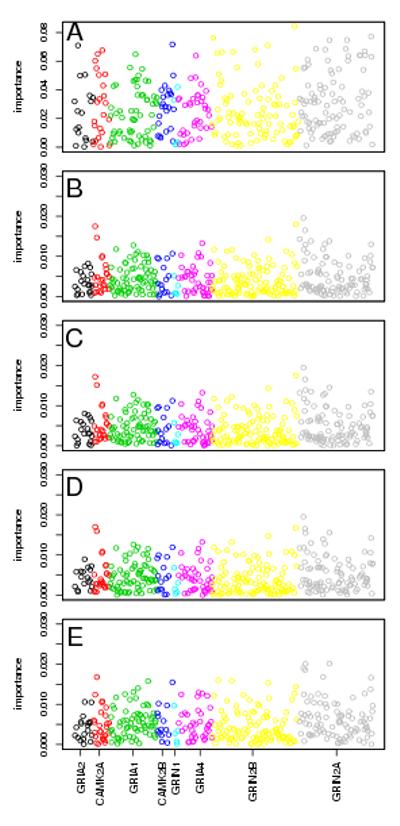
Variable importance results from real data analysis of the NMDA-dependent AMPA trafficking cascade pathway.

Importance is plotted for each SNP by chromosomal location for A: traditional RF using OOB estimates, and wRF with cross-validation and weights of B: x=1, C: x=(1/tPE)², D: x=(1/tPE)⁵, and E: x=rank(1/tPE). Colors indicate gene membership, as specified on the x-axis. Only SNPs with importance > 0 are plotted.

Importance is plotted for each SNP by chromosomal location for A: traditional RF using OOB estimates, and wRF with a single data split and weights of B: x=1, C: x=(1/tPE)², D: x=(1/tPE)⁵, and E: x=rank(1/tPE). Colors indicate gene membership, as specified on the x-axis. Only SNPs with importance > 0 are plotted.

Discussion

In this study, we proposed Weighted Random Forests, an extension of Random Forests motivated by the poor performance of RF to detect interactions in high-dimensional genetic data. The wRF method weighs better performing trees more heavily during aggregation. Our simulation studies demonstrated that the performance of wRF (as measured by PE_wRF and AUC_wRF) is at least as good as RF with equal tree-weights, and in some situations the predictive capability is slightly improved. For instance, when the effect size of the causal variants is large (i.e. high H² per causal SNP pair) then wRF has lower prediction error. The improvement in prediction is greater for the strongest weights with the greatest variability (i.e. $x_j=rank\left(\frac{1}{tP{E}_j}\right)$ and $x_j={\left(\frac{1}{tP{E}_j}\right)}^5$). This is in agreement with previous results showing that skewed weights of the form w^λ improved performance [8].

However, the gain in predictive ability is quite modest, particularly for data with strong interactions among predictor effects. We only observe meaningful improvements in prediction accuracy when effect sizes are large (i.e. H²>15%)—sizes that are rarely observed in genetic epidemiologic studies. In scenarios with weak effects, the results of wRF are essentially the same as RF; aggregation with equal weighting across trees produces similar results as aggregation with weights with a high degree of variability (such as highly skewed weights or weights with a uniform distribution). Although performance of wRF is slightly better in situations where the interaction effects are stronger than the marginal effects (H²_M/H²_I<1), the gain in predictive accuracy is small in these situations. Overall, the wRF method performs similarly to the traditional RF method, and there is little advantage given the added complexity of introducing performance-based weights.

We applied the wRF method to a real genetic dataset similar in size to those evaluated in the simulation studies. The performance of wRF on this dataset is consistent with the results of the simulation studies. Generally, the analyzed SNPs were not highly predictive of alcohol dependence, generating high PE estimates. In this situation, analysis with wRF with and without equal weights produces similar predictive performance; likewise, the traditional analysis using RF with the usual OOB did not yield better predictions. On the other hand, variable importance measures differ across methods. The wRF method identified rs980272 in CAMK2A as being one of the most important SNPs, which is consistent with previously published results [17]. Top ranking SNPs based on the traditional RF analysis were not consistent with the previously reported single SNP results.

Given our intuitive motivation for the method, it may seem surprising that we do not observe a greater improvement with wRF. In genetic association studies, the expected effect sizes are modest, as complex genetic traits are influenced by a large number of causal variants with very small effect (i.e. H²<1% per variant). Because the effect sizes are very small, even the most predictive trees within the forest are still not very accurate, and variation in predictive performance from tree to tree is low. However, the performance of wRF may be improved for other applications outside of genetics, where larger effect sizes that induce greater tree variability can be expected.

The advantages of wRF are possibly limited by the need to split the sample to avoid biased estimates of PE and variable importance. In particular, splitting the full sample into independent training and testing sets may be disadvantageous due to the reduction in sample size used for tree-building. This is of particular concern for small datasets, which will be sensitive to the particular split into training and testing sets. To circumvent this limitation, other internal validation techniques could be considered. One possibility is k-fold cross-validation, where wRF is fit to k subsets of the data. We implemented this strategy in the analysis of the addiction dataset; our real dataset, like our simulated datasets, was large with 711 variables on 2506 subjects. The use of cross-validation yielded similar results to a single split in this case, although this is not likely to be true for a small dataset.

To evaluate the effect on RF and wRF performance due to the reduced sample size used for training, for a subset of our simulation scenarios we compared the results of wRF trained on 750 samples to RF trained on 1000 samples, with prediction evaluated on the same independent set of 250 individuals. The use of 1000 (as opposed to 750) samples for training improved PE and AUC estimates by about 1%. In traditional RF analysis OOB error estimates are usually used for assessment of PE, rather than an independent test set. However, OOB estimates of PE are biased in classification problems [18, 19], which complicates a direct comparison of wRF to the traditional RF implementation. Our simulations showed that this bias is conservative (~2-3% worsening of PE) and is largest for datasets with higher predictive accuracy, which is also when we see the largest improvement with the use of weighting. Although an extremely important issue, further examination of this bias is beyond the scope of this study.

Our results are consistent with those observed in the comparison of RF to the WAVE algorithm [10], which applies weights to both tree classifiers and hard-to-classify individuals, and was shown to have similar performance to Random Forest. On the other hand, the weighted voting method that computes tree-weights based on margin of similar instances [11] and the TWRF method [12] showed improved performance over traditional RF with the use of weighting. However, both of these methods were tested on low dimensional real datasets with high RF prediction accuracy, rather than high-dimensional data. Furthermore, both methods computed and tested the weights on OOB data; therefore the observed improvement was likely (at least partly) due to bias from over-fitting. We eliminated this bias from our assessment of wRF by reserving an independent test set for predictive evaluation.

The current study was designed to compare wRF with the traditional RF implementation under scenarios that reflect genetic association data with multiple, and possibly interacting, causal variants. Although beyond the scope of this study, a direct comparison with other weighting methods (such as WAVE, TWRF, etc.) would be useful. While wRF did not yield improved predictions for the weights examined here, other weighting schemes may improve performance of wRF. An important consideration in any RF analysis is the optimization of the parameters mtry and ntree. Because the focus of this study was on a comparison of the same RF algorithm under different weighting schemes, the values of mtry=sqrt(p) and ntree=5000 were used for each run to aid in comparability. Adaptively tuning these parameters to each dataset, may lead to improved predictive ability of wRF.

In summary, the wRF method, which incorporates tree-level weights, does not dramatically improve predictive ability in high-dimensional genetic data, but it may improve performance in other domains that exhibit stronger effects.

Supplementary Material

Figure S1

Supporting File 1: Full simulation results for m=2 causal pairs.

Table S1

Supporting File 2: Full simulation results for m=10 causal pairs.

Table S2

Supporting File 3: Variable importance results from real data analysis of the NMDAdependent AMPA trafficking cascade pathway.

Importance is plotted for each SNP by chromosomal location for A: traditional RF using OOB estimates, and wRF with a single data split and weights of B: x=1, C: x=(1/tPE)², D: x=(1/tPE)⁵, and E: x=rank(1/tPE). Colors indicate gene membership, as specified on the x-axis. Only SNPs with importance > 0 are plotted.