Roadmaps through free energy landscapes calculated using the multi-dimensional vFEP approach

Abstract

The variational free energy profile (vFEP) method is extended to two dimensions and tested with molecular simulation applications. The proposed 2D-vFEP approach effectively addresses the two major obstacles to constructing free energy profiles from simulation data using traditional methods: the need for overlap in the re-weighting procedure and the problem of data representation. This is especially evident as these problems are shown to be more severe in two dimensions. The vFEP method is demonstrated to be highly robust and able to provide stable, analytic free energy profiles with only a paucity of sampled data. The analytic profiles can be analyzed with conventional search methods to easily identify stationary points (e.g. minima and first-order saddle points) as well as the pathways that connect these points. These “roadmaps” through the free energy surface are useful not only as a post-processing tool to characterize mechanisms, but can also serve as a basis from which to direct more focused “on-the-fly” sampling or adaptive force biasing. Test cases demonstrate that 2D-vFEP outperforms other methods in terms of the amount and sparsity of the data needed to construct stable, converged analytic free energy profiles. In a classic test case, the two dimensional free energy profile of the backbone torsion angles of alanine dipeptide, 2D-vFEP needs less than 1% of the original data set to reach a sampling accuracy of 0.5 kcal/mol in free energy shifts between windows. A new software tool for performing one and two dimensional vFEP calculations is herein described and made publicly available.

Introduction

Free energy is a key concept in modern physical science and offers a wealth of insights into complex molecular problems.¹ One dimensional free energy profiles are routinely employed to study various molecular systems with respect to a certain variable/coordinate and many enhanced sampling methods for accurately accomplishing this task have been developed in the past decades.² Some of the most widespread include multistage/stratified sampling,³ statically^4–6 and adaptively^7–9 biased sampling, self-guided dynamics,¹⁰ constrained dynamics,^11,12 as well as multicanonical^13,14 and replica exchange¹⁵ algorithms. In addition, a number of simulation protocols based on non-equilibrium sampling^16–19 have also been recently proposed as well as hybrid algorithms.^20,21

One of the most widely used methods for determining free energy surfaces for chemical reactions, where often there are geometric coordinates that are known to be aligned with the overall reaction coordinate, is the “umbrella sampling” technique.^5,22 Combining stratification with equilibrium and statically biased sampling, umbrella sampling is particularly amenable to parallel execution, especially in high performance distributed environments,^23–25 as well as extension or combination with replica exchange^26,27 and alchemical simulation techniques.²⁸

There are numerous well-developed and widely used methods for constructing one dimensional free energy profiles from umbrella sampling simulations, such as the weighted histogram analysis method,^29,30 umbrella integration (UI),³¹ the multistate Bennett acceptance ratio method (MBAR,^32,33 which can be seen as a binless extension of WHAM³⁴), and others.^35–38 However, publicly available implementations/programs for two dimensional cases are still very limited. Most notably, both WHAM³⁹ and MBAR³³ implementations have been made available, while two dimensional UI⁴⁰ and GAMUS^37,41 implementations have been reported but are not publicly available. Nevertheless, due to the two key difficulties in umbrella sampling methods, the problem of “data re-weighting” and of “data representation”, the cost and complexity of such calculations can still be quite prohibitive. Here we briefly review these two major problems.

The need of overlap in data re-weighting

Re-weighting from one sampled distribution to another can, in principle, be solved exactly by the free energy perturbation/Zwanzig relation and the related expression for mechanical observables.^5,42,43 However, WHAM and MBAR based methods to construct free energy profiles were developed with the understanding that this is not true in practice, since the overlap between distributions must be high in order to obtain reliable results.^29,33 An alternative approach is to assume smoothness of the free energy profile between nearby windows. Kästner’s UI approach uses a Gaussian distribution to model the un-weighted probability density for each umbrella window (or, equivalently, quadratic functions for the free energy profile), from which the analytic derivatives are calculated and integrated in order to recover the global probability density.^40,44,45 Hence, no explicit re-weighting is necessary. This approach is equivalent to assuming continuous first derivatives of the free energy profile between windows. Instead of quadratic functions centered on data-based parameters, the 1D-vFEP method⁴⁶ utilizes cubic spline functions to model the free energy profile, equivalent to assuming continuous first and second derivatives of the free energy profile between windows. It has been demonstrated in one dimensional cases that UI and 1D-vFEP require less of a degree of overlap between windows compared to WHAM and a histogram-based MBAR estimator.⁴⁶

Data representation

In order to extract a distribution function from a set of data, it is often necessary to employ a certain type of representation of that function. This is commonly formulated as the density estimation problem.^47,48 Perhaps the simplest method of data representation is to use a histogram estimator of the probability density.^28,29,49 However, this approach is frequently not numerically stable, especially when the data is too sparse such that the width of histogram bins cannot be made sufficiently small. A useful alternative approach can be to apply a more robust kernel density estimator, but this too will fail with extremely sparse data sets. A completely different type of approach is to fit the overall density distribution through a pre-defined model^37,44,50 by optimizing the model parameters according to a merit function. Maragakis, et al. suggested a maximum likelihood approach utilizing the Gaussian-Mixture Model on umbrella sampling (GAMUS) for the global probability density based on the re-weighted data.^37,51 Similarly, Basner and Jarzynski proposed a binless estimator based upon the optimal correction to an arbitrary reference distribution.⁵² UI^40,44,45 uses Gaussian models for the un-weighted probability densities and has also recently been extended to higher order densities (i.e. skewed Gaussians).⁵³ It is well known that such parametric approaches lead to a significant reduction in the number of data points needed to obtain a converged result. However this often comes at the expense of increased bias depending on the inherent accuracy of the parameteric form. For example, the approximations/assumptions of UI require near-quadratic (or near quartic) behavior of the local free energy surface for individual windows and this has been demonstrated to be inaccurate in simulations with weak biasing potentials.⁴⁶ This problem may be reduced by imposing stronger harmonic biasing potentials but this often leads to lower overlap between windows and hence the same kind of failures associated with sparsely populated histogram estimators.²² GAMUS has also been shown not to be ideal for quantitatively describing details of the free energy surface.³⁷

The vFEP implementation⁴⁶ for one-dimensional free energy profiles was demonstrated to be able to effectively address the above difficulties and outperform other methods in terms of the amount and sparsity of the data needed to construct the overall free energy profiles. The vFEP method uses higher-order (beyond quadratic) locally-compact functions to accurately model the free energy profile within each window. At the same time, it exploits the presumed smoothness of the profile in the interstitial regions that connect nearby windows. Nevertheless, its advantage is not greatly impressive since, in most cases, significant computational resources are not required when constructing one dimensional free energy profiles, even with large numbers of windows and data points. On the other hand, many more windows are needed to construct free energy profiles in two dimensions than in one. Furthermore, for each window, many more data points are required to represent the local two dimensional density distribution. This problem can effectively limit the practical applications of two dimensional umbrella sampling simulations.

In the present work we report the two dimensional extension of the vFEP method. Test cases demonstrate that vFEP is able to produce converged two dimensional free energy profiles in a more robust fashion (fewer and more sparse data points) than several other methods in common use. In addition, the resulting analytic form of free energy profiles allow the facile identification of stationary points and pathways that can be used for analysis, focused sampling, or adaptive biasing.

Theory

The theory of the maximum likelihood method utilized in vFEP has been already described in detail elsewhere.⁴⁶ Since the formulation is virtually identical in any number of dimensions, the key points are outlined here specifically for the two dimensional case. The maximum likelihood method, or maximum likelihood estimation (MLE),^54,55 is a procedure for finding the optimal set of model parameters that maximize the likelihood of a probability distribution function used to represent a given set of observed data.

Here we consider the two dimensional probability density, p(x, y), for observing a molecular system near a particular point with a generalized coordinates (x, y). This probability density is given by

$$p(x,y)=\frac{e^{-F(x,y)}}{\int \int e^{-F(x^{\prime },y^{\prime })}\mathrm{d}{x}^{\prime }\mathrm{d}{y}^{\prime }},$$ (1)

where F(x, y) ≡ F(x, y)/(k_BT) is the unitless scaled free energy profile, F(x, y) is the free energy profile, k_B is the Boltzmann constant and T is the absolute temperature. Considering a set of umbrella sampling simulations in which a biasing potential W^α(x, y) is applied in the αth window, the probability of finding the system near a certain coordinate value (x, y) is:

$$\begin{array}{l}{p}^{\alpha }(x,y)=\frac{1}{Z^{\alpha }}exp\{-[F(x,y)+W^{\alpha }(x,y)]\}\\ Z^{\alpha }\equiv \int \int exp\{-[F(x,y)+W^{\alpha }(x,y)]\}\mathrm{d}x\mathrm{d}y\end{array}$$ (2)

Suppose that, for the simulation of the αth window, there are N^α points observed with coordinate values {( $x_i^{\alpha },y_i^{\alpha }$)}. Since they are observed points, the probability of each point is equal with value 1/N^α. The likelihood of the whole system with an overall free energy profile F(x, y) can be expressed as the combination of the likelihood of individual windows as:⁴⁶

$$\widehat{\ell }(F)\equiv -\sum _{\alpha }^{\text{windows}}\left\{ln{Z}^{\alpha }+\frac{1}{N^{\alpha }}\sum _{i=1}^{N^{\alpha }}[F(x_i^{\alpha },y_i^{\alpha })+W^{\alpha }(x_i^{\alpha },y_i^{\alpha })]\right\}$$ (3)

Note that in the above equation the term $W^{\alpha }(x_i^{\alpha },y_i^{\alpha })$ is constant with respect to F and does not need to be evaluated if the goal is to maximize ℓ̂(F). It is also worth noting that the term −lnZ^α is equivalent to the relative free energies between windows in other re-weighting schemes. In the present vFEP approach, the “re-weighting” procedure is implicitly accomplished through the normalization against the global trial function F.

The search for the optimal trial F can be implemented in different ways. The present work utilizes two dimensional cubic spline functions to model F and searches for the optimal spline coefficients that maximize the likelihood function ℓ̂(F). Using two dimensional cubic splines is equivalent to assuming that the free energy profile varies slower than a cubic polynomial between windows or that the first and second derivatives of the free energy profile are continuous between windows for both of the coordinates.

Results

Implementation

The vFEP program has been modified and extended to two dimensions. However, due to the constraints of spline functions in the AlgLib package (v3.7, http://www.alglib.net), only two dimensional regular cubic spline (bicubic spline) functions are employed. Consequently, in addition to the interpolation algorithms originally utilized for 1D-vFEP,^56,57 one and two dimensional regular cubic spline algorithms were added. The vFEP program was written completely in C++ and compiled and tested with Microsoft Visual C++ 2008 on Window 7 and CMake 2.8.10.2 with Gnu C/C++ 4.7.2 on Fedora 16 and 18.

The main computationally intensive work is the numerical evaluation of Equation (3), which consists of two parts: 1) the integration of the exponential of the trial free energy profile and the biasing potential for each window; 2) the calculation of the trial free energy profile on all sampling points. The Gauss-Hermite quadrature rules are utilized to perform the integration of Equation (3) with the exponential of the biasing potential, a Gaussian function, as the background weighting function. For each window, a set of Gauss-Hermite quadrature rules (N=48) are set up for each dimension and those rules with positions outside the sampling data range are ignored, resulting, on average, in 15–20 rules remaining in each dimension for each window.

For large data sets, the evaluation of the trial free energy function on all sample points would be extremely time consuming if done directly in each optimization iteration. Since the free energy profile is modeled by a bicubic spline, in a rectangular region enclosed by four spline nodes the free energy profile can be described as products of third order polynomials of two dimensions. Hence, the second part of Equation (3), the summation of all function values over all sampling points, can be re-arranged and calculated as follows: In a region enclosed by four nearby spline nodes, summations of all 16 possible polynomial products over all sampling points can be pre-calculated when sampling data are read-in. The second term of Equation (3) can thus be calculated from the summation of all products of the spline coefficients and the pre-calculated terms from each regions. Since there is no need to do any calculations involving the sample data points except in the initial stage, the cost to evaluate Equation (3) is independent of the sample data size.

Four different methods are compared in analyzing free energy profiles: 1) the WHAM-2d approach, 2) the MBAR approach with a Gaussian kernel density estimator (gKDE), 3) the MBAR approach with a histogram estimator, and 4) the present 2D-vFEP approach. The results of WHAM were calculated by the wham-2d program from Grossfield³⁹ (v2.0.6, http://membrane.urmc.rochester.edu/content/wham). The results of MBAR were calculated using the pymbar library of Shirts and Chodera³³ (v2.0b, http://simtk.org/home/pymbar) with an in-house implementation of multi-dimensional kernel density estimation. Histogram calculations employed a fixed bin width and boundaries inferred from the data range, while gKDE calculations used bandwidths obtained with the multivariate form of the method of Silverman,⁵⁸ with the covariance matrices taken from each window. Where indicated, these bandwidths were uniformly scaled by a multiplicative constant. The MBAR library does not currently provide results when any histogram bins contain no data points. Due to this limitation, the MBAR approach with histogram analysis failed in all cases reported here, except in the case of alanine dipeptide with 576 windows, 10,000 data points per window, and 180 bins per dimension. In our implementation, this MBAR/histogram case accepted by the MBAR library requires more memory than any local workstations posses and cannot be performed. Hence no results from MBAR/histogram could be reported and all MBAR results in the subsequent sections refer to MBAR/gKDE.

All calculations were performed on a Linux (Fedora 16) workstation with an Intel i7 970 3.2GHz CPU (6-core) and 24 GB memory. WHAM-2d and 2D-vFEP did not utilize any multiple-core ability while the MBAR implementation utilized some multiple-thread functionality in the MBAR library. The results from WHAM-2d, MBAR/gKDE, and 2D-vFEP are reported in the following sections.

Alanine Dipeptide

The classic test case of a two dimensional free energy profile, the (φ, ψ) torsion free energy map of terminally blocked alanine peptide (sequence Ace-Ala-Nme) in explicit solvent, is treated as the benchmark system. The system is relatively simple and has been extensively studied.^59–64 A model Ace-Ala-Nme sequence peptide was generated by the tleap utility in the Amber12 package⁶⁵ and subsequently put in a 30 Å cube of TIP3P⁶⁶ water (540 molecules). A biasing potential of 0.02 kcal/mol-deg.² was applied to both dimensions for each window. The NAMD package (v 2.9)⁶⁷ was used with the Amber FF99SB-IDLN force field⁶⁸ under periodic boundary conditions in the NpT ensemble at 300 K and 1 atm (NAMD uses a modified Nosé-Hoover method^69,70 in which Langevin dynamics is used to control fluctuations in the barostat). Each window was simulated for 0.5 ns equilibration and 1 ns of data collection with sampling frequency of 100 fs (10,000 data points per window).

The peptide backbone torsion angles, φ and ψ, are defined as the relevant coordinates. Umbrella sampling simulations were performed by placing biasing potentials at evenly-spaced coordinates. Both φ and ψ were scanned from −180° to 180° with a step size of 15°, resulting in a set of 24×24 (576) umbrella sampling windows. Sets of 4×4 window data and 8×8 window data were extracted from the original 24×24 window data set using larger spacing (90° spacing for the 4×4 window set and 45° spacing for the 8×8 window set).

Variation in number of umbrella windows

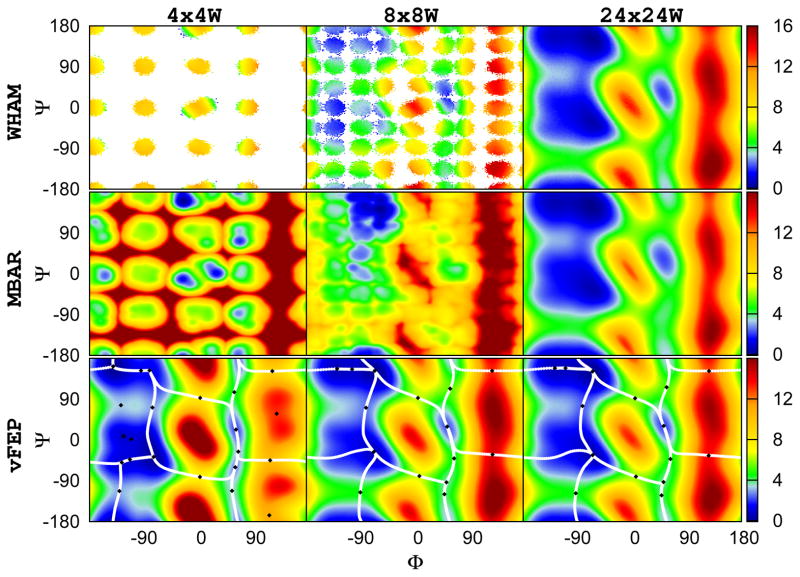
The (φ, ψ) free energy profiles of alanine dipeptide from different numbers of windows (4×4 (16), 8×8 (64), and 24×24 (576)) are first calculated and compared. Figure 1 shows the results using the same data sets with different methods: WHAM (upper row), MBAR/gKDE (middle row), and the vFEP (bottom row). The figure suggests that WHAM and MBAR/gKDE need 576 windows to deliver reasonable results while vFEP can give a rough estimation of the free energy profile with only 16 windows. In addition, the fact that, with 16 or 64 windows, WHAM cannot converge in a large number of areas (the white space/spots) and MBAR/gKDE cannot produce qualitatively correct results, demonstrates the strong requirement of overlapping between windows in the traditional approaches such as WHAM and MBAR.

Figure 1.

The 2D (φ, ψ) free energy profile of alanine dipeptide calculated from different methods using the same data sets: WHAM, MBAR/gKDE, and vFEP results are shown in the upper, middle, and bottom rows respectively. Results obtained from 4×4 (16), 8×8 (64), and 24×24 (576) windows are shown in the left, middle, and right columns respectively. All figures show results with 10,000 points per simulation window, except for the case of MBAR/gKDE with 576 windows where our current implementation only can handle 1,000 points per simulation window. White space in the WHAM results indicate empty histogram bins. WHAM and MBAR/gKDE need 576 windows to deliver reasonalbe results while vFEP can give a rough estimate of the profile with only 16 windows. All angles are in degrees. The color scheme of the free energy profile is shown at the right side color bar with units in kcal/mol. The black diamonds and the white lines shown in the vFEP contour maps are the saddle/minimum points and the possible paths found by the NEB method, respectively.

Variation in the number of sampling points per window

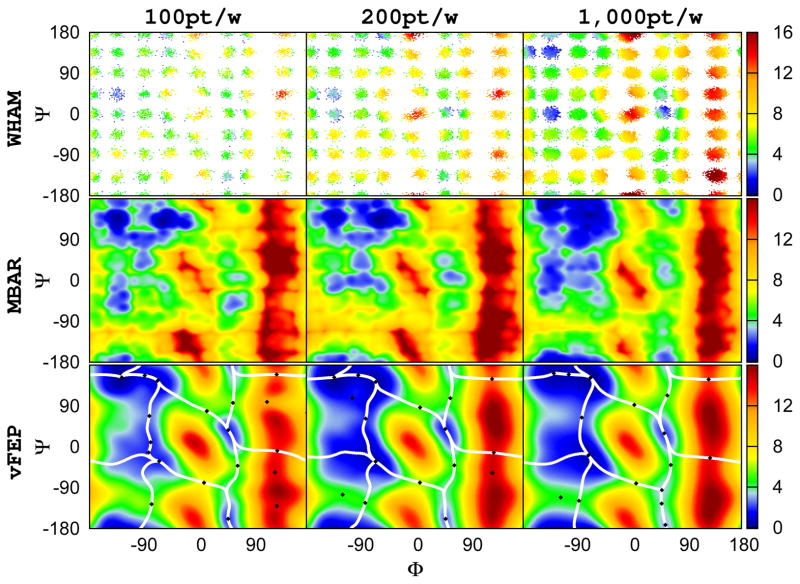
As previously mentioned, parametric approaches such as Gaussian kernel density estimation methods, compared to the histogram approaches, much reduce the number of data points required to construct the free energy profile. Figure 2 clearly shows such advantage. The original data sets (10,000 points per window) were stripped randomly to 100, 200, 1000 points per window. The results from those reduced data sets using WHAM are not able to deliver meaningful results with only 64 windows. Nevertheless better results are shown with more data points. On the other hand, although MBAR/gKDE cannot deliver good results with 64 windows, Figure 2 demonstrates the advantage of using smooth functions to represent sampling data distribution over the histogram approach utilized in WHAM: only 200 points per window are sufficient to deliver correct results compared to results from 10,000 points per window (Figure 1). 2D-vFEP not only is able to give good results with 64 windows but also only needs 200 points per window to reach more or less the same accuracy.

Figure 2.

The 2D (φ, ψ) free energy profile of alanine dipeptide calculated from different methods using 8×8 (64) windows: WHAM, MBAR/gKDE, and vFEP results are shown in the upper, middle, and bottom rows respectively. Results obtained from different 100, 200, and 1000 points per window are shown in the left, middle, and right columns respectively. White space in the WHAM results indicate empty histogram bins. WHAM and MBAR/gKDE do not produce clearly meaningful results with any number of points, although the advantage of gKDE over histograms is evident. Conversely, the 2D-vFEP results with 200 and 1000 points are essentially the same. All angles are in degrees. The color scheme of the free energy profile is shown at the right side color bar with units in kcal/mol. The black diamonds and the white lines shown in the vFEP contour maps are the saddle/minimum points and the possible paths found by the NEB method, respectively.

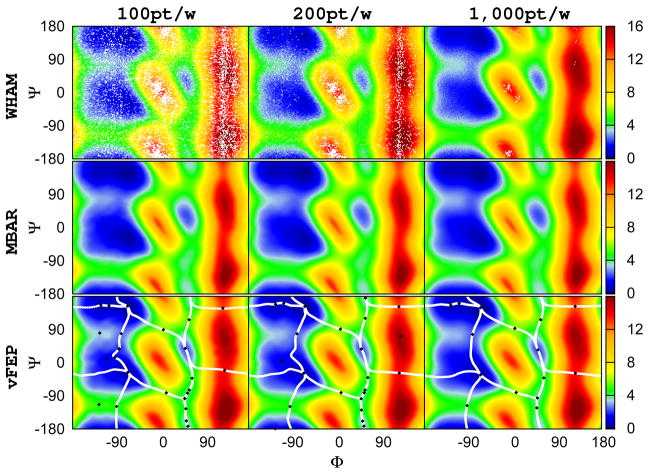
With large numbers of windows, WHAM and MBAR do not suffer from the overlap problem. Figure 3 shows the simulation results with 576 windows but reduced data sets similar to Figure 2. Results obtained from different numbers of data points per window are shown and suggest that, with 576 windows, MBAR/gKDE is able to deliver good results while WHAM still has difficulty to converge in every region even with 1,000 points per window. 2D-vFEP only needs 100 to 200 points per window to deliver qualitatively correct results.

Figure 3.

The 2D (φ, ψ) free energy profile of alanine dipeptide calculated from different methods using 24×24 (576) windows: WHAM, MBAR/gKDE, and vFEP results are shown in the upper, middle, and bottom rows respectively. Results obtained from different 100, 200, and 1000 points per window are shown in the left, middle, and right columns respectively. White space in the WHAM results indicate empty histogram bins. MBAR/gKDE is able to deliver good results while WHAM still cannot converge in all regions, even with 1000 points per window. The 2D-vFEP results with 200 and 1000 points are essentially the same, and the results with 100 points per window extremely similar in qualitative terms. All angles are in degrees. The color scheme of the free energy profile is shown at the right side color bar with units in kcal/mol. The black diamonds and the white lines shown in the vFEP contour maps are the saddle/minimum points and the possible paths found by the NEB method, respectively.

Identification of stationary points and pathways through the analytic free energy surface

In the current vFEP implementation bicubic spline functions are used to represent the model free energy profile. Such a representation provides a simple and easy way to locate stationary points, since, given a certain value of one dimension, the zero gradient points of the other dimension can be calculated analytically along with the analytic first and second gradients of both dimensions at the zero gradient points of the second dimension. Hence, by searching all zero gradient points of each dimension and calculating the analytic first and second gradients (i.e. the Hessian) of the other dimension, the extrema and saddle points can be located.

The minimum and saddle points identified by vFEP and Nudged Elastic Band^71,72 (NEB) paths are shown in the bottom rows of Figures 1 to 3. NEB calculations were performed with the DL-FIND library.⁷³ The results agree well and all of the NEB paths pass through minima and saddle points identified by vFEP, even though the initial points for the NEB calculations were not from vFEP results. In the cases with very few data points and windows, where WHAM and MBAR cannot deliver appropriate free energy profiles (Figures 1 and 2, left columns), vFEP is still able to identify reasonable minimum and saddle points, although more false positive points are found due to a higher level of noise.

A model QM/MM phosphoryl transfer reaction

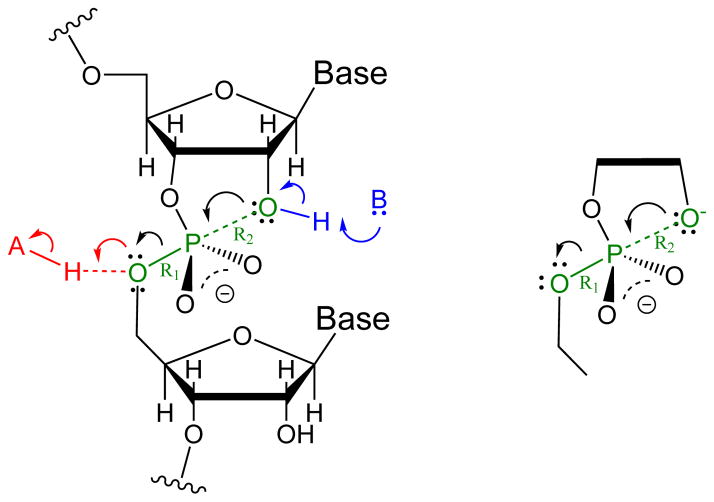
Using the AMBER12 simulation package,⁶⁵ hybrid quantum mechanical/molecular mechanical (QM/MM) umbrella sampling simulations were performed for 2-hydroxy ethyl ethyl phosphate (HEEP, see Figure 4), a model compound for RNA 2′-O-transesterification. The system was modeled in the same way as in a recent study of this system,⁷⁴ except that the periodic box was a 35.7 Å cube of TIP3P rigid water molecules⁶⁶ and the QM region Lennard-Jones parameters were taken from the AMBER FF10 force field.⁷⁵

Figure 4.

Left: Reaction scheme for RNA phosphoryl transfer reaction. Right: The HEEP model system used in the present work.

Two dimensional umbrella sampling was performed using the phosphorus to leaving group (bond breaking) distance (R₁) and nucleophile to phosphorus (bond forming) distance (R₂) (Figure 4). A total of 192 short simulations (400 ps with 50 ps equilibration) were performed with a harmonic biasing potential,

$$U_{\text{bias}}(R_1,R_2)=\frac{1}{2}k[{(R_1-R_{1,0})}^2+{(R_2-R_{2,0})}^2]$$ (4)

where k = 100 kcal/mol-Ų and the values of the bias centers, R_1,0 and R_2,0, spanned a grid of values at 0.25 Šintervals from 1.50 to 4.25 and 1.50 to 5.25, respectively.

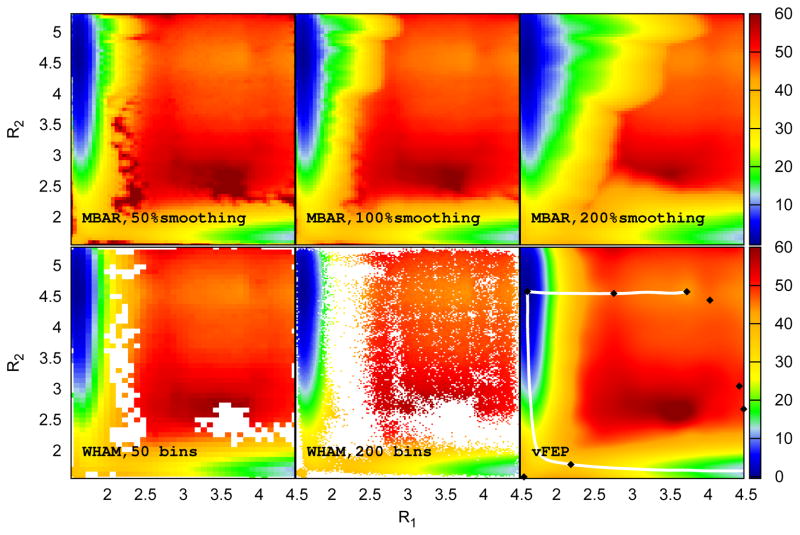
The free energy profile results obtained from WHAM, MBAR/gKDE, and vFEP, are shown in Figure 5. Due to the relatively thin set of data, histrogramming does not produce a complete surface, even when the number of bins along each axis is reduced considerably from 200 to 50. In the latter case the largest bin width is 0.075 Å, approaching a point where the results are dubiously quantiative. This problem can be somewhat mitigated by using a kernel density estimate to smooth out the regions between areas of low sampling. Using a simple, data-based choice of smoothing parameter in each window,⁵⁸ a complete surface can be generated (Figure 5, upper middle panel), but at the expense of spurious features in the reactant basin (top left of the surface). This problem is exaggerated further by scaling the smoothing parameters by a factor of two, a practice previously recommended in one dimensional cases in order to mitigate the appearance of spurious minima and maxima⁷⁴ (Figure 5, upper right panel). Unfortunately, decreasing the extent of smoothing leads to the same kinds of empty regions observed in the WHAM result (Figure 5, dark red spots in the upper left panel). Although one might reasonably expect that some combination of smoothing parameters will lead to a more balanced result, it is not at all clear what this combination will be or what kind of automatic and deterministic procedure could be followed to obtain it. Once again, however, vFEP provides a single, unique solution for the surface that maintains all of the features, both coarse and detailed, observed with the other methods.

Figure 5.

2D QM/MM free energy profiles of the HEEP system (Figure 4) calculated from different methods. Upper row: MBAR results with kernel density smoothing schemes with different scaled Silverman bandwidth settings: Left: scaled by 0.5 (under-smoothed), Middle: no scaling (normal smoothing), and Right: scaled by 2.0 (over-smoothed). Lower row: WHAM results with 50 bins (left) and 200 bins along each axis (middle), and the vFEP result (right). Coordinate values are in Å and energies are in kcal/mol. The black diamonds and the white lines shown in the vFEP contour maps are the saddle/minimum points and the possible paths found by the NEB method, respectively.

As with alanine dipeptide above, the vFEP minimum and saddle points and the NEB paths were calculated (Figure 5, bottom right). The results again suggest that the vFEP minima and saddle points agree well with the NEB paths. The “extra” path found moving right from the reactant basin is especially interesting as it suggests the possibility of an alternative, albeit extremely high energy, pathway towards the products (note that the products here are two solvated anions and thus no proper product basin will be resolved without introducing periodic boundary artifacts). It is not clear whether or not this extra basin is an artifact of vFEP, although WHAM and MBAR indicate a similar region (Figure 5). Nonetheless, the automatic search for zero-gradient points made possible by vFEP provides a simple mechanism to broadly survey the free energy profile, at least making the user aware of the additional minima and thus able to assess it on the grounds of chemical intuition.

QM/MM simulations of HHR

We have previously reported a set of large scale (921 windows) QM/MM umbrella sampling simulations to explore metal-assisted phosphoryl transfer and general acid catalysis in the extended hammerhead ribozyme (HHR).⁷⁶ Free energy profiles were constructed with two reaction coordinates: Z₁, the reaction coordinate of the phosphoryl transfer, and Z₄, the Mg²⁺ binding distance. For each window, data was collected every 1 fs for a total of 10 ps, resulting in 10,000 data points per window, in order to provide sufficient data points for the WHAM analysis.

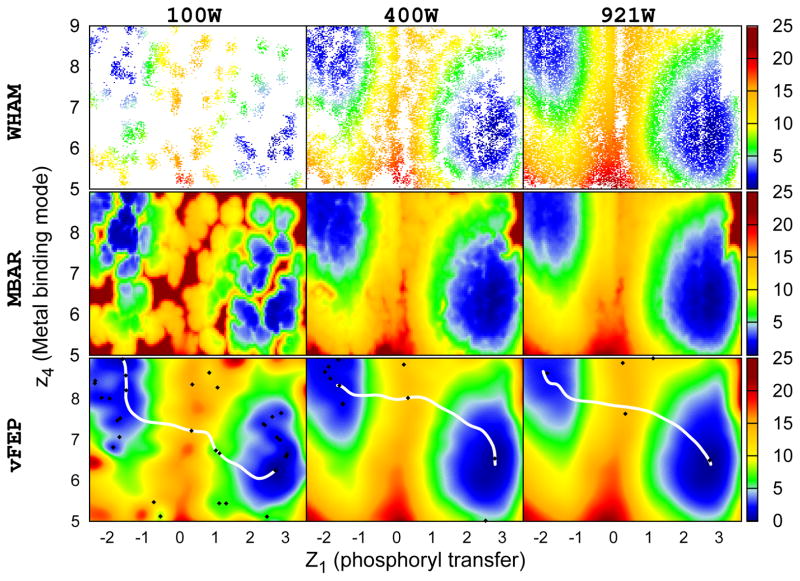
Here, selected data from this set of simulations were used as a realistic test of the performance of the proposed 2D-vFEP method. WHAM, MBAR/gKDE, and vFEP were applied to either the full 921 windows or else 100 or 400 windows selected randomly. Tests were performed with 50, 500, and 5000 data points per window. Since WHAM cannot converge with fewer than 5000 data points per window and both MBAR and vFEP deliver similar results with different numbers of data points per window, only the case of 50 data points per window is shown here (Figure 6). WHAM and MBAR/gKDE need 400 windows to deliver reasonable results, but some regions are still poorly converged. Conversely, vFEP can give a rough, but smooth, estimate of the free energy profile with only 100 windows and 50 data points per window.

Figure 6.

The 2D free energy profile of HHR ribozyme (see Wong et al. ⁷⁶ for reaction coordinate definitions). WHAM, MBAR/gKDE, and vFEP results are shown in the upper, middle, and bottom rows respectively. Results obtained from 100, 400, and 921 windows are shown in the left, middle, and right columns respectively. For each window data was collected every 100 fs for a total of 5 ps, resulting in 50 data points per window. Calculations with 100 and 400 windows used randomly selections from the original 921 windows. White space in the WHAM results indicate empty histogram bins. WHAM gives noticeably sparser results compared to the original data set. Conversely, 2D-vFEP gives a rough, but smooth, estimation of the free energy profile with only 100 windows. The two coordinates are in Å. The color scheme of the free energy profile is shown at the right side color bar with units in kcal/mol. The black diamonds and the white lines shown in the vFEP contour maps are the saddle/minimum points and the possible paths found by the NEB method, respectively.

With both 400 and 921 windows, the vFEP minima and saddle points agree well with the NEB paths (Figure 6, bottom row). This is not as clearly true with 100 windows, where the points and path are qualitatively different. Nonetheless, the basin locations from the two calculations are in rough agreement and mostly qualitatively accurate in comparison to the 400 and 921 window cases.

Lastly, in the original work,⁷⁶ WHAM was employed and hence 921 windows along with a large number of data points in each window were necessary in order to construct a reasonable free energy profile useful for mechanistic inference. Use of vFEP not only improves the calculation with the original data set, but can get essentially identical results with less than half the windows, providing a significant reduction in the necessary computational resources.

Sampling errors in free energy shifts

While the 2D-vFEP method involves no explicit re-weighting procedure, the −lnZ^α terms are equivalent to the relative free energy shifts, Δf^α, defined in MBAR and WHAM. In vFEP they are obtained implicitly through global optimization of the free energy profile, while in the MBAR and WHAM approaches they are calculated as the results of the re-weighting procedure. Simple bootstrapping schemes⁷⁷ were utilized to estimate the statistical sampling errors in free energy shifts. The errors were estimated by calculating the standard deviation between randomly chosen data sets with the same data size.

The calculated bootstrapping errors of the free energy shifts with different numbers of windows and data points are listed in Table 1. With 8×8 windows and 200 data points, 2D-vFEP is able to deliver an accuracy of 0.5 kcal.mol when only 0.22% of the original data is used (24×24 windows; 10,000 points per window).

Table 1.

Estimated bootstrap errors (50 and 100 calculations with random data sets) of free energy shifts calculated by the vFEP method. The system is an alanine dipeptide in a TIP3P water box with 8×8 and 24×24 umbrella windows.

		100pt/w		200pt/w		1,000pt/w
8×8 windows		N=50	N=100	N=50	N=100	N=50	N=100
	min	0.503	0.481	0.319	0.308	0.095	0.091
	max	3.822	4.212	0.712	0.662	0.282	0.288
	ave	0.822	0.819	0.453	0.446	0.194	0.192

		100pt/w		200pt/w		1,000pt/w
24×24 windows		N=50	N=100	N=50	N=100	N=50	N=100
	min	0.082	0.088	0.052	0.059	0.021	0.021
	max	0.185	0.188	0.119	0.114	0.058	0.053
	ave	0.115	0.115	0.079	0.079	0.032	0.032

The numbers here are derived from a set of 24×24 (576)-window umbrella sampling simulation on an alanine dipeptide in a TIP3P water box with a biasing potential of 0.02 kcal/mol-deg.² for each window, and the same results from a set of 8×8 (64)-window umbrella sampling data created by strapping from the 576 window data set (see Results). The results are estimated by performing bootstrapping type error analysis on the free energy shift term, −lnZ^α, with the same calculations performed on 50 or 100 randomly chosen data sets of the same size out from the original data set, e.g., for “100pt/w”, 100 random points were selected from the original 10,000 data points for each window. The bootstrapping standard deviation of each window among the data sets was calculated. The minimal (min) and maximal (max) bootstrapping standard deviation values for all windows, along with their averages (ave) are listed. All values are in units of kcal/mol.

Timing

To assess the practical usability of the current 2D-vFEP implementation, the time needed to perform 2D-vFEP of the alanine dipeptide system in a TIP3P water box was measured with different settings. Measurements were done with a set of 24×24 (576)-window umbrella sampling simulation and a set of 8×8 (64)-window umbrella sampling data created by strapping from the 576 window data set, the same procedure as mentioned in the previous sections. Results with WHAM and MBAR/gKDE were also measured. These programs were written in different languages (vFEP is written in C++, WHAM in C, MBAR in mixed C and Python), with different levels of optimization, and different implementations of underlining theories/algorithms; hence the timing results should not be compared directly. Rather, our purpose here is to demonstrate the usability of the 2D-vFEP program for realistic two dimensional free energy profile problems.

Table 2 lists the time needed to complete free energy profiles for alanine dipeptide system. The setting notations (8×8, 24×24 windows; 100 pt/w, 200 pt/w, etc.) are the same as used in the previous sections. The MBAR run with 576 windows and 10⁴ data points failed to allocate enough memory on a 24GB workstation. The results confirm that the computational cost of 2D-vFEP is more or less independent of the number of data points and is proportional to the number of windows.

Table 2.

Results of timing of different methods on an alanine dipeptide in a TIP3P water box with 8×8 and 24×24 umbrella windows and different numbers of data points in each window (in seconds).

		100 pt/w	200 pt/w	1,000 pt/w	10,000 pt/w
8×8 windows	WHAM	3,264.3	4,325.1	7,419.2	7,748.9
	MBAR	10.5	25.0	631.1	42,832.2
	vFEP	36.4	31.2	39.8	47.3

		100 pt/w	200 pt/w	1,000 pt/w	10,000 pt/w
24×24 windows	WHAM	16,689.0	16,723.5	16,111.8	16,191.7
	MBAR	157.1	249.0	4,682.3	failed
	vFEP	378.2	396.4	507.1	674.4

The numbers here are derived from a set of 24×24 (576)-window umbrella sampling simulation on an alanine dipeptide in a TIP3P water box with a biasing potential oef 0.02 kcal/mol/degree² for each window, and the same results from a set of 8×8 (64)-window umbrella sampling data created by strapping from the 576 window data set (see the Results section). The results were obtained from the UNIX command “time”. vFEP is written in C++, WHAM in C, MBAR in mixed C and Python. The numbers should be considered as for reference only, rather than performance tests on those methods since different implementations of WHAM and MBAR could lead to significantly different results. The convergence criteria was set to 10⁻³ for WHAM (the largest free energy shift change), 10⁻⁹ for MBAR (the maximum relative change in the free energy shifts). Different size of data sets are strapped out from the original data set, e.g., for “100 pt/w”, one data point was selected in every 100 points, resulting 100 points out of the original 10,000 data points for each window. The MBAR run with 576 windows and 10⁴ data points failed to allocate enough memory. All timing results were performed on a Linux (Fedora 16) workstation with an Intel i7 970 3.2GHz CPU (6-core) and 24 GB memory. WHAM and vFEP did not utilize any multiple-core ability while MBAR utilized some multiple-thread functionality in the MBAR library. All values are in seconds.

Discussion

There are various strategies to generate free energy profiles from umbrella sampling simulation data. WHAM and MBAR first model the free energy profiles of individual windows and then merge them into a global profile through re-weighting. Such an approach inevitably needs significant overlap between windows so that the combined free energy profile is sensible.

The approach taken by UI, GAMUS, and the present work is to assume smoothness of the free energy profile between windows and construct the global free energy profile by finding the most likely trial profile. However these approaches are different in the way they define the “best” global free energy profile. The original UI approach assumed that the free energy profile can be approximated as a combination of quadratic functions centered at umbrella sampling window centers^40,44,45 (this has now been extended to cubic and quartic functions⁵³). GAMUS utilizes a Gaussian Mixture Model to model the density distribution with Gaussians with optimal centers and widths, while vFEP approximates the global free energy profile with local cubic spline functions. Such approaches do not strictly require significant overlap of data between nearby windows and hence are capable of modeling free energy profiles with many fewer umbrella simulation windows.

Certain data fitting procedures need to be performed when constructing free energy profiles from umbrella sampling data. It is well-known that using parametric analytic functions to represent the observed data leads to faster and stable convergence at the expense of potential bias. Hence one would expect more stable results if smooth functions are used to model the local density distributions or free energy profiles, instead of deriving from non-parametric functions such as histograms. This is clearly demonstrated in the test cases in this work. However, there is no well-accepted way to choose suitable functions to represent the local density distributions or free energy profiles. Using quadratic functions for free energy profiles or Gaussians for density distributions requires a theoretically sound procedure to define the centers and widths of the corresponding Gaussians. Furthermore, these second order approximations may not be sufficiently accurate to describe the local windows well. Using third or higher order functions to model the local free energy profiles may encounter numerical instability before combining them into global free energy profiles, as well as increased bias in the parameters. On the other hand, in vFEP, the continuous and piece-wise third-order approximation of the global free energy profiles in vFEP achieves both reduction of data points needed and numerical stability. The fact that this mathematical assumption is also physically sound means that it should lead to a minimal bias. That is, it is greatly expected that the surface and its first two derivatives are piece-wise smooth and therefore it should not introduce considerable error to impose this from the start.

Kernel density smoothing is a popular way to reduce the noise in non-parametric density estimation.⁵⁸ However, the results from kernel density smoothing are critically dependent on the selection of the optimal smoothing bandwidth. While a complete discussion of this topic is beyond the scope of this paper, the QM/MM results shown in Figure 5 clearly demonstrate that kernel density smoothing methods need to be used with caution. Reasonable results may only be obtained when different bandwidths are used in different regions and there are, to our knowledge, no obvious methods for accomplishing this in a simple and general fashion.

The proposed vFEP approach, in both one and two dimensional cases, requires less overlap between windows compared to WHAM and MBAR and is more accurate compared to UI and GAMUS. Hence the vFEP approach successfully addresses the two major problems in constructing free energy profiles from umbrella sampling simulations and significantly reduces the number of data points needed. The following potential advantages of vFEP could significantly advance current free energy estimation techniques:

Fast estimate of rough free energy profiles and biasing potentials

In recent years there has been much effort to enhance sampling in MD simulations to more efficiently construct free energy profiles and/or to extend the effective time scale of simulations.^{6–9,78–90} The vFEP method may be integrated with these methods to potentially enhance their performance in following ways:

To adaptively and iteratively refine free energy profiles, often it is necessary to have a reasonable initial guess of free energy profile as the starting point. For two or higher dimensions, it is frequently prohibitively expensive to obtain even an initial rough guess of a free energy profile using methods such as WHAM, especially when the overall shape of the surface is unknown. In contrast, vFEP only requires very small amount and sparse data to deliver a semi-quantitative free energy profile that can serve as an initial rough guess to direct further simulations to collect data in the most important regions of the free energy landscape and refile the profile.

As vFEP only requires distribution data derived from simulations that may use any type of well-behaved biasing potential, or even without biasing potential (Equations (2) and (3)), it can also be utilized as a robust free energy profile estimator for distribution data from various types of MD simulations, with or without biasing potentials. Such a strategy would involve using the unbiased distribution data from accelerated MD simulations as input to vFEP in order to create an analytic free energy profile for the coordinates of interest. This strategy could then, in principle, be integrated into subsequent MD simulations as an added biasing potential to further flatten the free energy landscape and enhance sampling.

Paths, minimum points, and saddle points in 2D free energy profiles

When using any analytic form of a free energy profile, it is trivial to calculate first and second derivatives with respect to the relevant reaction coordinates. Although this advantage is not outstanding compared to other methods for the one dimensional case, the results for two dimensions demonstrate that vFEP could be significantly beneficial. To our knowledge, there is no other method capable of calculating the first and second derivatives analytically and easily. This advantage quickly leads to the efficient identification of the local minima and saddle points, as well as all zero gradient points, which can serve as candidates for possible reaction paths.

Conclusion

Here we report the extension of the variational free energy profile (vFEP) method to two dimensions. vFEP utilizes the maximum likelihood principle and bicubic spline functions to construct global free energy profiles. Test cases show that the vFEP approach efficiently addresses the major obstacles to constructing free energy profiles encounted by traditional methods: the need for overlap in the re-weighting procedure and the problem of data representation. As a result, 2D-vFEP outperforms other methods in terms of the amount and sparsity of the data needed to construct the overall free energy profile. In the case of alanine dipeptide, 2D-vFEP only needs 8×8 (64) windows and 200 data points per window, roughly 0.22% of the original data set (576 windows and 10,000 data points per window), to reach a sampling accuracy of 0.5 kcal/mol in free energy shifts between windows. Additionally, free energy stationary points, including minimum and saddle points, can be identified analytically and easily from the 2D-vFEP approach. Overall, the vFEP method is demonstrated to be highly robust, even with a paucity of sampled windows and data points, and offers a promising new tool for the construction and analysis of free energy profiles that can be used to interpret mechanisms and potentially as the foundation for new methods for adaptive biasing and enhanced sampling.