Phase coding by grid cells in unconstrained environments: Two-dimensional (2D) phase precession

Abstract

Action potential timing is thought to play a critical role in neural representation. For example, theta phase precession is a robust phenomenon exhibited by spatial cells of the rat entorhinal-hippocampal circuit. In phase precession, the time a neuron fires relative to the phase of theta rhythm (6-10Hz) oscillations in the local field potential reduces uncertainty about the position of the animal. This relationship between neural firing and behavior has made precession an important constraint for hypothetical mechanisms of temporal coding. However, challenges exist in identifying what regulates the spike timing of these cells. We have developed novel analytical techniques for mapping between behavior and neural firing that provide sufficient sensitivity to examine features of grid cell phase coding in open environments. Here, we show robust, omnidirectional phase precession by entorhinal grid cells in openfield enclosures. We present evidence that full phase precession persists regardless of how close the animal comes to the center of a firing field. We found many conjunctive grid cells, previously thought to be phase locked, also exhibit phase coding. However, we were unable to detect directional or field specific phase coding predicted by some variants of models. Finally, we present data that suggests bursting of layer II grid cells contributes to the bimodality of phase precession. We discuss implications of these observations for models of temporal coding and propose the utility of these techniques in other domains where behavior is aligned to neural spiking.

Introduction

Spike timing is thought to play an important role in neural representation (Gerstner et al., 1997). Phase coding, or firing relative to local field potential (LFP) oscillations, contributes information to the neural code (Jensen & Lisman, 2000; Kayser et al., 2009), however, identifying regressors of the temporal code is technically challenging. Throughout the hippocampal formation, theta oscillations (6-10 Hz) are a prominent component of the LFP (Green & Arduini, 1954; Vanderwolf, 1969; Buzsáki et al., 1983; Stewart & Fox, 1991; Buzsáki, 2002). Spatially tuned cells of the rodent hippocampal formation are an extensively studied class of neurons with clear behavioral correlates. Hippocampal place cells fire predominantly when an animal is in one location in an environment (O’Keefe & Dostrovsky, 1971; O’Keefe, 1976). In a phenomenon called theta phase precession, place cells fire at progressively earlier phases relative to hippocampal theta oscillations as the animal moves through the firing field on linear tracks (O’Keefe & Recce, 1993; Skaggs et al., 1996) and in open spaces (Burgess et al., 1994; Skaggs et al., 1996; Huxter et al., 2008). This temporal code has functional influences on the efficacy of communication and plasticity in the hippocampus, and is thus thought to play a major role in memory formation (Hasselmo et al., 2002; Mehta et al., 2002; Hyman et al., 2003; Jensen & Lisman, 2005; Kunec et al., 2005).

The discovery of entorhinal grid cells, which fire when the rat visits an array of locations falling on the vertices of packed equilateral triangles (Figure 4, Fyhn et al., 2004; Hafting et al., 2005), led to the insight that place cells may not derive the spatial code themselves, but instead may reflect a filtered output of entorhinal spatial tuning. Analyses in linear track environments have led to the clear demonstration that layer II and V grid cells precess (Hafting et al., 2008), and many models have been proposed which can generate grid cell precession in linear environments in hippocampal place cells (O’Keefe & Recce, 1993; Tsodyks et al., 1996; Wallenstein & Hasselmo, 1997a; Lengyel et al., 2003; Yamaguchi, 2003; Norman et al., 2006) or entorhinal grid cells (O’Keefe & Burgess, 2005; Burgess, 2008; Navratilova et al., 2012). Uncovering mechanisms driving entorhinal precession may provide insight into factors contributing to temporal coding, however, many differential predictions made by models require analysis of grid phase coding in open spaces.

Fig. 4.

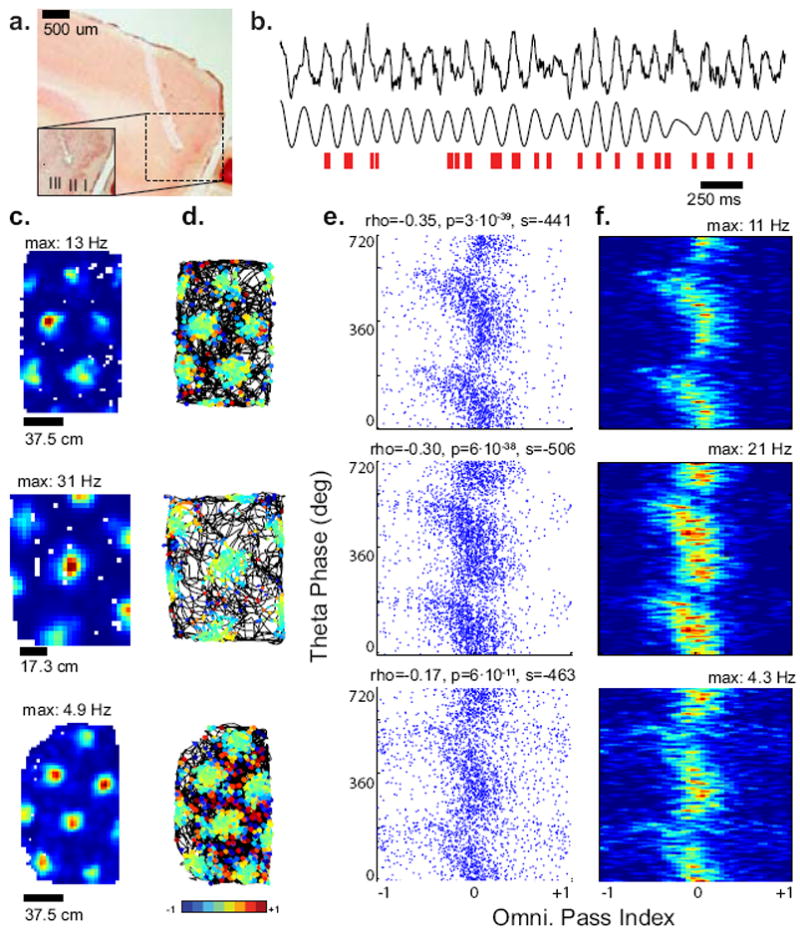
Experimental examples of precession using the omnidirectional pass index. (A) Example histology showing tetrode tracks targeted at medial entorhinal cortex. (B) Local field potential data recorded in our lab is shown in black. Top is the unfiltered trace, bottom is filtered (6–10 Hz). Red tick marks indicate the firing of a single grid cell as the animal moves in and out of grid fields. (C–F) Example plots from three precessing grid cells from our experimental data (linear–circular correlation, P < 0.05). (C) Rate maps, (D) Trajectories with spikes colored by the pass index at each spike. (E) Scatter plot of the LFP theta phase vs. the pass index. Correlation coefficients (rho), significance (P) and slopes (s, in degrees per pass) are indicated. (F) Occupancy-normalized rate maps of the scatter plots in E.

Here, we used established models of grid cells to generate specific predictions about their phase coding behaviors in open spaces, and developed methods for analyzing the relationship of recorded data to these predictions. We found that omnidirectional phase precession occurred robustly in openfield environments independent of how close it came to the center of the firing field. We describe the precession of layer III conjunctive head-direction-by-grid cells, in contrast to earlier findings on the linear track. We were unable to detect direction specific or field specific phase coding in grid cells, predicted by some models. Finally, we found evidence that bursting of layer II grid cells contributes to the characteristic bimodality of phase precession. The framework described here is not limited to examining spatial cells, and thus may be applied to phase coding in cells that have other behavioral correlates.

Methodology

Data acquisition

All procedures involving rats were carried out in accordance with the Boston University Charles River Campus Institution for Animal Care and Use Committee approved protocol and National Institute of Health guidelines. Five male Long Evans rats (350-400 g) were used in this study. Prior to surgery, animals were individually housed in Plexiglas cages with water and food ad libitum and were maintained on a 24/hour light/dark cycle. Testing always occurred during the light cycle. Prior to surgical implantation of recording electrodes, the animals were habituated to experimenter interaction and the testing arena. Animals were trained to forage for pieces of chocolate cereal (Cocoa Pebbles, Post Holdings Inc., Battle Creek, MI) in openfield environments with a variety of dimensions.

Surgery

After habituation, surgical implantation of recording electrodes was performed. Each rat was given Atropine (0.04 ml/kg) fifteen minutes prior to Isoflurane induction and anesthesia. Anesthesia was maintained using a combination of Isoflurane and a Ketamine cocktail (Ketamine 12.92 mg/ml, Acepromazine 0.1 mg/ml, Xylazine 1.31 mg/ml). Following placement in a stereotaxic holder, skin and periosteum were cleared from the skull, and anchor screws were inserted along the periphery of the dorsal surface of the skull. One screw was positioned above the cerebellum in contact with the dura, wired to the implant, and used as a recording ground. Recording drives were single bundle microdrives (Axona Ltd., St. Albans, Hertfordshire, United Kingdom), and housed four recording tetrodes (four 12.7-micron nichrome wires (Kanthal Palm Coast, Palm Coast, FL) twisted together) that could be moved as a group. At surgery, a craniotomy was performed starting 4.5 mm lateral from bregma just posterior to the fissure between the parietal and postparietal skull bone. Bone was removed in the posterior direction until the anterior edge of the transverse sinus was clearly visible. Dura was removed 4.5 mm lateral of bregma and 0.35 mm anterior of the anterior edge of the transverse sinus. The electrodes were lowered at this point ~1.5 mm from the dorsal surface into the brain. The tetrodes were angled at ~12 degrees in the anterior direction. Alternatively, entorhinal cortex was targeted in line with the ear bars, angled at ~12 degrees in the posterior direction, and lowered 1.5 mm into the brain. A guide cannula was brought down into contact with the brain and was secured in place using Kwik-Sil (World Precision Instruments, Shanghai PRC) and dental acrylic. Animals were allowed seven days to recover from surgery. When possible, at the end of experimentation animals were perfused with 0.9% saline, followed by formalin. Brains were extracted and tetrode locations were verified by either a cresyl violet or neutral red Nissl stain. Images were taken at 2 and 4X magnification, and stacks were aligned by hand and overlaid using Photoshop’s pin-light blending (Figure 4a). In most cases, the tetrodes were restricted to layer II/III. However, the error between the length of the tetrode tracks and the estimated final depth of the tetrodes from turn counts was wider than the cortical layers in all cases, preventing layer specific identification of recording sites in our data. Analysis of layer specific effects was therefore performed on a separate data set of the Moser laboratory.

Neural Recordings

Screening for grid cells using criteria based on previous studies (Fyhn et al., 2004; Hafting et al., 2005, 2008) as animals foraged in 1 m × 1.5 m, 1 m × 0.75 m, or 0.75 m × 0.75 m openfield environments was performed daily in our laboratory. Recordings were also tested for conjunctive grid-by-head-direction cells (Sargolini et al., 2006; Boccara et al., 2010) and head direction cells (Taube et al., 1990; Sargolini et al., 2006) using criteria based on previous studies. Once theta oscillations and theta rhythmic firing were prevalent in our recordings, tetrodes were turned a maximum of 50 microns per day (Hafting et al., 2005; Sargolini et al., 2006). Neural signals were preamplified by unity-gain operational amplifiers located on the headstage, near the animal’s head. Signals were then amplified (4,000-10,000×) and band pass filtered (600-6000 Hz). When the signal crossed a threshold, all four channels of the tetrode were digitized at 48 kHz and recorded. Position and head direction data were calculated from the positions of a large (anterior) and small (posterior) infrared diode lights mounted on the headstage, sampled at 50 Hz. Head direction was calculated as the angle between these positions. Position was determined as 1.9 cm anterior of the centroid of these positions to maximize the standard deviation of the rate maps and minimize the size of recorded grid cell firing fields similar to previous studies (Huxter et al., 2008). LFP traces recorded at a 250 Hz sampling rate from the MEC were referenced to the animal ground. These LFP traces contained theta rhythm oscillations that were used to compute the theta phase of spikes.

Data Analysis Methods

Cluster cutting and alignment across recording sessions

Single-units were isolated from each session “offline” manually using graphical cluster cutting software (Tint, Axona Ltd.). Units were separated based on the peak amplitude of the waveforms, as well as the voltage at time points measured relative to the peak, particularly late in the after-hyperpolarization. Evaluation of the presence of biologically realistic inter-spike intervals (≥2 ms), temporal autocorrelations, and cross correlations was used to confirm single unit isolation. The waveforms of units recorded at the same depth in the same animal were compared visually across sessions and grouped based on similarity between mean waveforms, with the pairs with highest Pearson correlation between the waveforms compared first. Only one session was used from each grouping for further analysis. Data used recorded in our laboratory is available at http://mind4.bu.edu/data/phasecoding/.

Theta Phase

For all grid cells recorded in our lab, the LFP was recorded from one of the electrodes on the same tetrode as the cell. This LFP signal was band pass filtered between 6 and 10 Hz, and the phase of the theta cycle was calculated from the LFP as the argument of the complex analytic signal produced by the hilbert function in MATLAB (MathWorks, Natick, MA). The phase was then calculated at the time of each spike to calculate the spike theta phase (Skaggs et al., 1996; Hafting et al., 2008; Huxter et al., 2008; Jeewajee et al., 2008). Note that the use of the Hilbert transform to calculate the spike theta phase differs from the use of the Hilbert transform to calculate the pass index (see “Omnidirectional Pass Index” and “Directional Pass Index” sections).

Rate Maps

Rate maps of grid cell firing were used to visualize grid cells and in the classification of grid cells. They were constructed by calculating the occupancy-normalized firing rate for the spike numbers within 3 cm × 3 cm bins of position data. Data were smoothed by a two-dimensional convolution with a pseudo-Gaussian kernel with a one pixel (3 cm) standard deviation.

To visualize the head direction tuning of the animal, we calculated the occupancy-normalized firing rate using spike numbers in 6° bins of head direction data. Head direction rate maps were not smoothed.

Classification of Grid cells

We used the modified gridness score as modified in previous studies (Langston et al., 2010; Brandon et al., 2011) We calculated an autocorrelation of the smoothed spatial rate map and extracted a ring that encased the six peaks closest to the center peak, but excluded the central peak (Sargolini et al., 2006). The radius of the inner circle was half of the mean distance to the peaks closest to the center (max six), where none of the peaks was 1.5 times farther than the first. The largest outer radius was defined as the distance to the farthest detected peak plus the radius of the central circle. We then calculated a rotational autocorrelation of the ring and observed the periodicity in the correlations. We measured the difference between the lowest correlation observed at 60 or 120 degrees of rotation and the highest observed at 30, 90, or 150 degrees of rotation. To correct for elliptical distortions, a modified version of this analysis has been developed (Langston et al., 2010) in which rotational autocorrelations and scores were computed for all possible outer radii starting from the center circle and expanding to the closest autocorrelogram edge. Gridness is reported here as the maximum score computed from these rings. Cells were labeled as grid cells if the gridness score exceeded 0.34 (Boccara et al., 2010).

To separate non-conjunctive grid cells from conjunctive head-direction-by-grid cells, we used Watson’s U² score for circularly distributed data of the neurons’ spikes across the head direction of the animal at the time of the spike (Johnson et al., 2005; Sargolini et al., 2006). We categorized grids as non-conjunctive if they exhibited a score below 3, and conjunctive if they had a score above 4, which provides a clear separation in the tuning of conjunctive and non-conjunctive cells. 21 grid cells with scores between 3 and 4 were excluded from further analysis to prevent ambiguous grouping. To determine the preferred firing direction for conjunctive cells, we calculated the weighted angular mean from the polar rate map.

Behavioral analysis

To analyze the head direction behavior of the animal, we first found the angular difference between the animal’s movement and the head direction. To estimate speed at which the animal oscillates its head, we used the mean frequency from the multitaper spectrogram of this signal. We estimate the average angular speed of the animal’s head by taking the angular mean of the absolute value of radial speed of the animals head direction movements. This analysis was performed on 134 sessions run by four rats. Note that the behavior shows a mismatch between head direction and movement direction, but all existing models of grid cells assume that the head directions code the movement direction of the animal as if always matched with the movement direction.

Phasor Model

Predictions from previously generated (Burgess et al., 2007; Burgess, 2008; Hasselmo, 2008) variants of the oscillatory interference model (OIM) using phasors provided the basis for our phase coding analysis (Figures 1-3). In these models, the phase of a velocity controlled oscillator (VCO) is controlled by

$$\psi (t)={\omega }_{0}t+\beta \stackrel{\rightharpoonup }{s}(t)·\stackrel{\rightharpoonup }{d}+\varphi$$ (1)

Fig. 1.

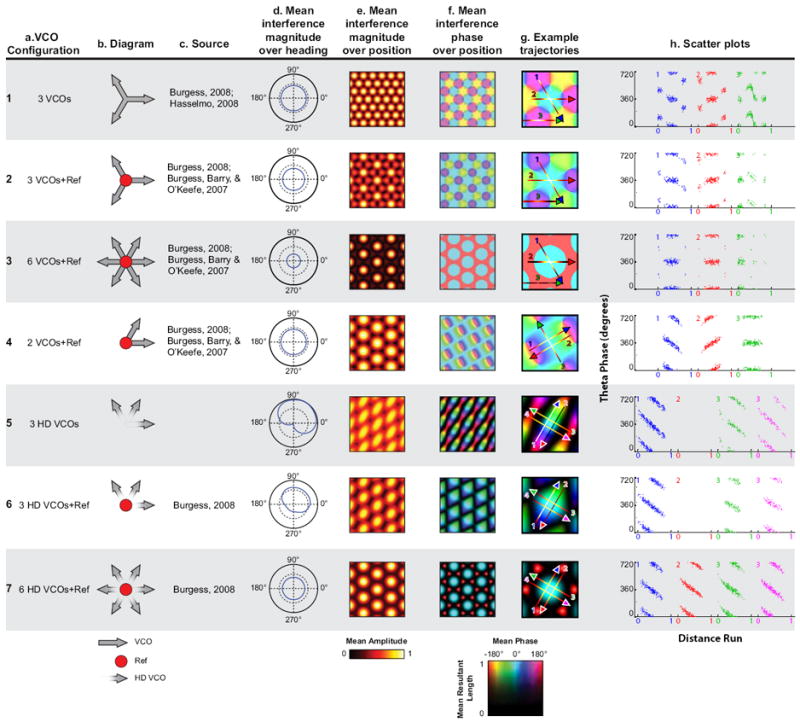
Models of grid cell firing and predictions of openfield phase coding. (A, B) Configuration of models. The diagrams indicate the component oscillator inputs to the grid cells. Velocity-controlled oscillators are indicated by an arrow pointing in their preferred direction, and HD-weighted VCOs are indicated by a fading arrow pointing in their preferred direction. A reference oscillation is indicated by a red dot, and is an oscillator with no phase change due to movement. The phase of the interference is relative to such an oscillation, even when the oscillation does not participate in the interference itself. (C) Sources using models with the specified configuration. (D) Normalized interference amplitude, averaged across all positions at each head direction. (E) Normalized interference amplitude, averaged across all head directions at each position. (F) Interference phase averaged across all head directions at each position. The color hue shows the phase, whereas the brightness shows the mean resultant length. Darker areas show a more variable phase across head direction at the same position. (G) The central field of the phase map is cropped. The arrows indicate trajectories; the color of the line indicates the interference amplitude along the trajectory. (H) Scatter plots showing predicted spiking phase of the grid cell along repeated runs of the trajectories shown in G.

Fig. 3.

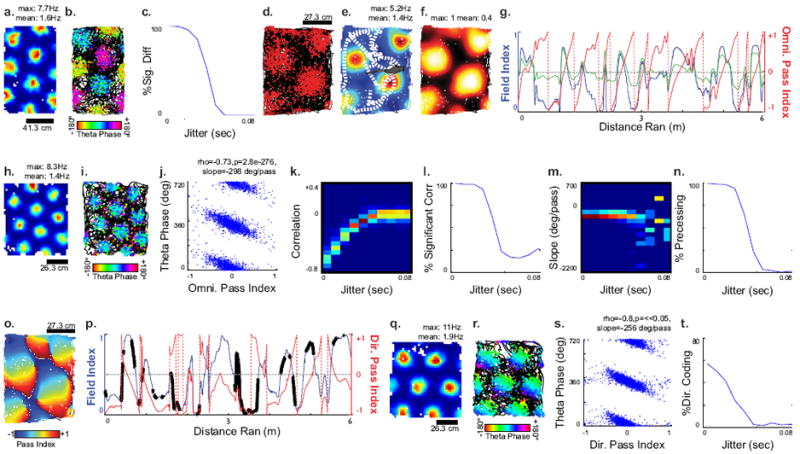
Models inform techniques for examining phase coding in the open field. (A) Rate map for simulated grid cell using the three VCOs configuration with 4 ms of temporal jitter. (B) Theta phase of each spike for simulated cell shown in a. (C) Percentage of simulated cells showing a significant phase difference between all groupings as the temporal jitter is increased (n = 250 at each jitter). (D) Trajectory of a rat (black) with spikes of a grid cell recorded in vivo in our lab shown in red. (E) Occupancy-normalized rate map with Gaussian smoothing of the grid cell shown in d and e. A sample of the trajectory of the animal is indicated by the dashed line, ending in the cartoon rat. (F) The field index is the percentile rank of the rates in each bins in the rate map in e (see Methods). This map was used to look up the field index along the trajectory of the animal. (G) Field index of the animal along its trajectory from cartoon in e is shown in blue. The omnidirectional pass index (red) is derived from the phase of the Hilbert transform of the field index filtered between 0.9 and 26.7 per m (green, on the same scale as the pass index). (H) Rate map for simulated grid cell using the 6HD-VCOs+Ref configuration with 4 ms of temporal jitter. (I) Theta phase of each spike for simulated cell shown in a. (J) Scatterplot of omnidirectional pass index vs. theta phase for the model in h and i, showing precession. (K) Histogram of correlations showing decrease in magnitude of correlation as jitter is increased. The colorscale indicates the percentage of simulated neurons. (L) Percentage of simulated cells showing a significant correlation between theta phase and pass index (P < 0.05, n = 250 at each jitter). (M) Distribution of slopes of significantly correlated cells at each temporal jitter. The colorscale indicates percentage of simulated neurons. (N) Percentage of simulated labeled precessing (significant correlation and slope between À22° and À1440° per pass). (O) The directional pass index was found by making trajectories along a single direction through the field index map (F) padded by its autocorrelogram, and finding the Hilbert phase at each point. (P) The field index and directional pass index along an animal’s trajectory, different from the one in e. The thick black lines indicate when the animal was running opposed to the test direction. (Q) Rate map for simulated grid cell using the 2VCOs+Ref configuration with 4 ms of temporal jitter. (R) Theta phase of each spike for simulated cell shown in Q. (S) Scatter-plot of directional pass index vs. theta phase for the model in Q and R, showing precession. (T) Percentage of simulated cells showing precession in at least one direction, and a significant sinusoid score.

Where ψ(t) is the phase at time t, ω₀ is some baseline frequency, β is a non-negative constant, $\stackrel{\rightharpoonup }{s}(t)$ is the position of the animal at time t, $\stackrel{\rightharpoonup }{d}$ is a unit vector indicating the preferred direction of the VCO, and · is the dot product operator. Thus, the phase offset of the VCO is the projection of the displacement of the animal onto an axis in the preferred direction. A reference or baseline oscillator maintains a constant relative phase despite the movement of the animal and would be represented by the special case when β=0. We can imagine an oscillation m cos(ψ(t)), with frequency ω₀, magnitude m, and phase $\beta \stackrel{\rightharpoonup }{s}(t)·\stackrel{\rightharpoonup }{d}+\varphi$. All oscillations with the same baseline frequency ω₀ can be represented in terms of complex exponentials that can add as phasors. This allows us to represent the activity of a VCO only in terms of the phase offset from the baseline $(\beta \stackrel{\rightharpoonup }{s}(t)·\stackrel{\rightharpoonup }{d}+\varphi )$ and magnitude as determined by Euler’s relation to generate grid cell patterns (Welday et al., 2011). That is, the activity of the VCO a can be transformed into phasor space (→) as:

$$a(t)=\mathrm{Re}\left\{m{e}^{\mathit{i}(\beta \stackrel{\rightharpoonup }{s}(t)·\stackrel{\rightharpoonup }{d}+\varphi )}{e}^{\mathit{i}{\omega }_{0}t}\right\}\to m\angle (\beta \stackrel{\rightharpoonup }{s}(t)·\stackrel{\rightharpoonup }{d}+\varphi )$$ (2)

Where $\mathit{i}=\sqrt{-1}$. The magnitude (M) of the resulting interference between a group of n oscillators will be:

$$M(t)=\sqrt{{\left({\sum }_{k=1}^n{m}_k\cos \left({\beta }_k\stackrel{\rightharpoonup }{s}(t)·{\stackrel{\rightharpoonup }{d}}_k+{\varphi }_k\right)\right)}^2+{\left({\sum }_{k=1}^n{m}_k\sin \left({\beta }_k\stackrel{\rightharpoonup }{s}(t)·{\stackrel{\rightharpoonup }{d}}_k+{\varphi }_k\right)\right)}^2}$$ (3)

And its phase (Θ) will be:

$$\mathrm{\Theta }(t)=\mathrm{atan}\left(\frac{{\sum }_{k=1}^n{m}_k\sin \left({\beta }_k\stackrel{\rightharpoonup }{s}(t)·{\stackrel{\rightharpoonup }{d}}_k+{\varphi }_k\right)}{{\sum }_{k=1}^n{m}_k\cos \left({\beta }_k\stackrel{\rightharpoonup }{s}(t)·{\stackrel{\rightharpoonup }{d}}_k+{\varphi }_k\right)}\right)$$ (4)

For some models, the magnitude of the VCO is not constant, rather, it is weighted by the heading of the animal (Burgess, 2008). In our adaptations, the modulation is:

$$m_k(t)=(\cos (h|{\theta }_d-{\theta }_h|)+1)\mathrm{H}\left(\cos \left(\frac{h}{2}|{\theta }_d-{\theta }_h|\right)\right)$$ (5)

Where H is the Heaviside function (H(k) = 0 | k < 0, H(k) = 1|k ≥ 0), θ_d is the preferred direction of the VCO, and θ_h is the heading of the animal, and h is a scalar greater than or equal to one. We refer to these head direction modulated VCOs as HD-VCOs.

If h is too small, the weighting of the HD-VCOs is not sufficiently eliminated in the reverse-precessing direction, and caused brief periods of reverse-precession (data not shown). However, the noise in our theta phase and pass index measures makes it difficult to generate concrete predictions of the behavior of in vivo, and thus we limited our predictions to models using h=1.5.

To simulate the types of spiking data we may see by neurons following these models along trajectories, we constructed probability density functions from the interference magnitude along the trajectory of the animal by normalizing between the median and maximum spatial magnitude. We determined the number of spikes as 300 times the area under this curve. The curve was then transformed into a cumulative density function, and the positions of spikes were randomly pulled from this distribution. The phase was determined via the models as above, and jittered by Gaussian noise with a standard deviation of 20°.

To validate the effectiveness of our techniques in observing the types of phase precession exhibited by these models, we simulated the spiking of grid cells generated by the models with 3 VCOs, 2 VCOs+Ref, and 6 HD VCOs+Ref configurations. To generate this spiking data, we randomly chose from a uniform distribution the orientation, as well as values for β (Equation 1) which corresponded to spacings ranging between 30 cm (near the smallest spacing of grid cells reported by Hafting et al. (2005)) and the largest spacing we can observe in a 100 cm enclosure, 1.7 m. A mean firing frequency, f, was randomly selected from a normal distribution with mean 1.78 Hz and standard deviation 1.41 Hz. These values were based on all grid cell recordings analyzed. f was reselected if it was ≤0 Hz. A field sharpness exponent, j, was chosen from a uniform distribution between 0.75 and 6. One of 83 random sessions with the associated LFP with highest theta power was then randomly selected to provide real behavioral and LFP data, and the magnitude M and firing phase Θ were generated as described above (Equations 3-4). An impulse train was generated such that an impulse was placed at every sample where the theta phase of the local field potential was the simulated firing phase (Θ), with a sampling frequency of 50 Hz. This was then convolved with a gaussian with a standard deviation t_std, which we refer to as the temporal jitter of the simulation, and represents noise between the theta phase and the timing of firing. This signal was modulated by the sharpened, simulated magnitude M^j, and scaled such that if each value represented the probability of a spike occurring in that sample, the total expected mean firing rate would be f. Spikes were then generated using Matlab’s poissrnd function. For each configuration of the model, we generated 250 grid cells for 20 values of temporal jitter ranging from 4 ms – 1/8 sec, resulting in a total of 5,000 simulated grid cells for each of the three configuration of the model.

Field index

Calculation of a measure of how in field the animal was, or the “field index,” started by calculating the occupancy-normalized firing rate for 1cm × 1cm bins of position data. Data were then smoothed by a two-dimensional convolution with a pseudo-Gaussian kernel with a five pixel (5 cm) standard deviation (Figure 3e). The value at each bin was then percentile normalized between 0 and 1, and this was called the field index map (Figure 3f). Then, the trajectory of the animal was sampled evenly along the arc-length of the trajectory at as many points as there were position tracking samples (50 Hz). The nearest bins were then found by minimizing the difference between the x and y positions and the center of the bins via the MATLAB function: bsxfun (Figure 3g, blue). The smoothing and small bin size contributed to a more continuous estimation of the field index.

Field Extraction

To compute the difference in median spike theta phases between fields, the field index map was first computed as above. Noise was further removed from the map. First, occupancy holes were filled with the average field index of the surrounding bins. Then, an initial estimate of the field centers was generated by the regions with field index greater than 0.8. Using the centroids calculated from Matlab’s regionprops function, we generated a tessellation of the field centers using the Delaunay method with the Matlab function DelaunayTri. The reciprocal of the median length of the sides of the triangles was then used as the center frequency for 2d Butterworth bandpass filter, which passed frequencies within 10% of the center. The gradient was then taken of this filtered map. Fields were regions of the filtered map where the field index was over 0.25, the rate was over 0.1 Hz, the field index was under 0.7 and the magnitude of the gradient was more than 0.15 per pixel, and the field index was under 0.8 and the directions of gradient the surrounding pixels were not opposing. If all the pixels surrounding a region satisfied these constraints, they were also labelled as fields. These fields were then analyzed using Matlab’s regionprops function. Fields with area less than 5 pixels or a perimeter to equivalent diameter ratio over 6 were rejected, to reject small fields or fields that were too far from circular. Finally, fields within this set with an area less than 1/5^th of the largest field in this set were rejected. The adjacency of fields was determined using DelaunayTri, and fields were grouped into three groups such that no adjacent field was in the same group. If three groups were established with at least 25 spikes occurring in fields of each group, they were compared using the common median multi-sample test from the CircStat toolbox (Berens, 2009).

Omnidirectional Pass Index

To compute the omnidirectional pass index, the field index along the trajectory was first band pass filtered to include frequencies between twice the largest spacing of grid cells we can observe in a 100 cm enclosure (1.7 m^-1) and one eighth of the smallest spacing of grid cells reported by Hafting et al. (2005, 26.7 m^-1) using a zero phase shift Butterworth filter (Figure 3g, green). The phase of this signal was then calculated by finding the argument of the complex analytic signal produced by the hilbert function in MATLAB, and normalized to -1 to 1 so that -1 represents the beginning of a pass, 0 represents the center, and +1 represents the end. This signal was then sampled back into the video frequency of sampling using the MATLAB’s interp1 nearest neighbor interpolation (Figure 3g, red).

Directional Pass Index

To mimic the behavior of some models, we wanted to compute the distance through a field along a particular (test) direction. To do this, we constructed imaginary paths through each point along the test direction and computed the Hilbert phase of the field index along this path at the point which crossed the animals trajectory. Because the Hilbert transform is sensitive to edge effects, we first padded the field index map with its 2D spatial autocorrelation. This extended the grid pattern on the field index map beyond the positions visited by the animal. Thus, the rate map was placed on the 2D spatial autocorrelogram at the offset determined by the peak in the cross correlation of the autocorrelogram with the original rate map closest to the origin. Then, for each point along the trajectory, a line along the test direction was constructed which passed through the point, was as long as the diagonal of the autocorrelogram, with points every 1 cm. This line was intersected with the padded field index map using Matlab’s interp2 linear interpolation. Points outside of the padded autocorrelogram or where the autocorrelogram used fewer than 20 pixels were set to 0. These hypothetical trajectories through the infieldness map was then treated as above to calculate the directional pass index at the points at which they crossed the real trajectory (Figure 3o-p).

As discussed in the results section, directionally phase coding models predict a cosine shape to the slope of precession over the test directions. Thus, to test for this cosine tuning we examined directional phase coding by calculating the linear-circular regression and correlation (See “Linear-Circular Regression and Correlation” section) between directional pass index and theta phase for 16 cardinal test directions. To examine how well the slopes could be fit by a sinusoid, we used Fourier series decomposition. Note that this is distinct from, but related to, the more commonly used Fourier transform. Fourier series decomposition assumes that the signal in question is periodic with the number of samples (N = 16), and the periodicity of the signal is referred to as the fundamental frequency $\left({\omega }_0=\frac{\pi }{8}\frac{\mathit{radians}}{\mathit{sample}}\right)$ of the periodic signal. We can decompose the signal into N complex exponential components, with the k^th component (a_k) determined by the formula:

$$a_k==\frac{1}{N}\sum _{n=<N>}s[n]e^{-\mathit{ik}{\omega }_{0}n}=\frac{1}{16}\sum _{n=0}^{16}s[n]e^{-\mathit{i}k\left(\frac{\pi }{8}\right)n}$$ (6)

Where s is the slope across the n^th direction and $\mathit{i}=\sqrt{-\mathbf{1}}$.

The first (a₁) and last (a₁₅ = a₋₁) represent the components of the signal that have the same frequency as fundamental frequency of the periodic signal (ω₀). The zeroth frequency component (a₀) is the mean value of the signal. Each other frequency component represents a harmonic of the fundamental frequency, and adds structure to the signal that doesn’t match with a sine curve of the fundamental frequency. Thus, to test how well a signal matches a sine curve, we found the ratio between the power in the first and last frequency components and the nonzero frequency components, which we refer to as the sinusoid score.

$$\frac{{|a_1|}^2+{|a_{15}|}^2}{{\sum }_{k=1}^{15}{|a_k|}^2}$$ (7)

To determine a significance cutoff for the sinusoid score, we generated 10,000 random values uniformly sampled from -1 to 1. Because the slope of the directional pass index versus in that in it’s opposite direction is it’s negative, we concatenated these 8 values with their negatives, and calculated the sinusoid score for these 100,000 curves. 95% of these scores were less than 0.67, thus, we used 0.67 as a significance cutoff for directional precession.

Linear-Circular Regression & Correlation

The significance and slope of phase precession was quantified using the slope of the circular-linear regression and the circular-linear correlation used in previous studies of phase precession (Jammalamadaka & Sengupta, 2001; Schmidt et al., 2009; Kempter et al., 2012; Reifenstein, Kempter, et al., 2012). The slope results from fitting the data to the model θ = s(x − x₀), and maximizing:

$$R=\sqrt{{\left(\frac{1}{n}\sum _{j=1}^n\cos ({\theta }_j-s{x}_j)\right)}^2+{\left(\frac{1}{n}\sum _{j=1}^n\sin ({\theta }_j-s{x}_j)\right)}^2}$$ (8)

The circular-linear correlation coefficient is then:

$$r=\frac{{\sum }_j\sin ({\theta }_j-\overline{\theta })\sin ({\varphi }_j-\overline{\varphi })}{\sqrt{{\sum }_j{\sin }^2({\theta }_i-\overline{\theta }){\sum }_k{\sin }^2({\varphi }_k-\overline{\varphi })}}$$ (9)

Where θ_j denotes the theta phase of the j-th spike, ϕ_j = sP_j mod 2π is derived from the pass index at the time of the spike P_j, and ϕ̄ and θ̄ are the circular sample mean values (Jammalamadaka & Sengupta, 2001), defined for the group of angles ζ as $\overline{\zeta }=\arg \left(\frac{1}{n}{\sum }_{j=1}^n{e}^{\mathit{i}{\zeta }_j}\right)$. For our analysis, we ensured that the sign of r always matched the sign of the slope, and used the magnitude as a Pearson correlation for estimating statistical significance.

Linear Track Fields

We also analyzed a separate set of data recorded in the Moser laboratory during running on a linear track. We identified fields and position within field on linear track data as done previously (Hafting et al., 2008). Briefly, we identified possible fields as 3 consecutive bins on the linearized rate map using 5 cm bins where the rate was above 10% of the maximum firing rate on the map. Then, each field was extended until a bin was reached that either increased in rate or was below 1% of the maximum firing rate. Fields that included the distal 5% of the track, had fewer than 50 spikes, or had a mean amplitude of the Pearson’s correlation between consecutive bins less than 0.7 were discarded. The directions on the track were analyzed separately, and epochs where the animal ran under 10 cm/second were discarded. Position was determined as percentage through the bounds of the fields identified this way.

Results

To identify possible phase-coding behaviors of grid cells in the openfield, we examined the phase coding properties of a variety of oscillatory interference models (OIMs) of grid cell activity. From these predictions, we developed techniques for estimating scores that we predicted to correlate with theta phase, which we called the “pass index.” We applied this technique to data from 177 grid cells recorded in our laboratory. We found strong, omnidirectional precession in many grid cells. To examine the validity of this technique, we also applied our techniques to 102 grid cells recorded by Sargolini et al. (2006). From all the data, we examined strongly precessing cells on passes that came to different distances from the center of the field and found that grid cells show precession on shallow passes through grid fields. As predicted by OIMs, but not previously seen (Hafting et al., 2008), we found that many of the conjunctive head-direction-by-grid cells also exhibit precession. We were unable to find evidence that phase coding exists in grid cells along particular directional axes of movement or that cells have a different median phase in each firing field. Finally, we found evidence which suggests that bursting may contribute to the distinct bimodal shape of entorhinal phase precession.

Established Models of Precession Provide Insights for Techniques

In many models of grid cells, the phase code of position is generated by oscillators changing frequency with the velocity of the animal, typically referred to as velocity-controlled oscillators (VCOs) (O’Keefe and Recce, 1993; O’Keefe and Burgess, 2005; Burgess et al., 2007; Burgess, 2008; Hasselmo, 2008). The velocity-dependent shift in frequency shifts the phase of each VCO relative to some “baseline” oscillator that does not change phase or frequency with movement and is thought to be phase locked to LFP theta oscillations. Although OIMs were first proposed as a means for generating phase coding on linear tracks by place cells (O’Keefe & Recce, 1993), they predicted multiple firing fields. The discovery of the multiple firing fields of entorhinal grid cells (Fyhn et al., 2004; Hafting et al., 2005) quickly inspired the expansion of OIMs to generate grid cell firing patterns (O’Keefe and Burgess, 2005; Burgess et al., 2007; Burgess, 2008; Hasselmo, 2008), however, these models only precess when specific conditions are satisfied (Burgess, 2008; Welday et al., 2011). The underlying mechanism of all OIMs is the deterministic relationship between the phase of oscillations of the same frequency and the phase and magnitude of the interference between them. By using phasor arithmetic to generate mathematical abstractions of these models, we can examine their phase coding properties in the absence of confounding factors, such as simulated noisy biophysical factors.

Simple models of phase coding generate phase coding processes that do not always mimic results seen in vivo on the linear track. Figure 1 a1-h1 shows one of these models (3 VCOs, used in Burgess (2008) and Hasselmo (2008)) that uses three VCOs to generate a grid pattern with a 60° difference in phase of interference generated on the center adjacent fields (Figure 1 g1-h1). Addition of a baseline oscillation (3 VCOs+Ref, Figure 1, a2-f2, used in Burgess et al (2007) and Burgess (2008)) reduces the contribution of VCOs that are not in phase with the baseline, thus, the resulting interference is primarily phase locked to this baseline (Figure 1 g2-h2,). Addition of more VCOs (e.g., 6 VCOs+Ref, Figure 1 a3-f4, used in Burgess et. al. (2007) and Burgess (2008)) enhances this canceling effect, where all non-zero magnitude activity is in phase with the baseline (Figure 1, g3, h3). This models the phase locking behavior of layer III grid cells (Hafting et al., 2008).

The simplest phase coding OIM uses two VCOs with a 60° angle difference and a reference (2 VCOs+Ref, Figure 1 a4, used in Burgess et al. (2007) and Burgess (2008)) satisfies the conditions outlined by Welday et al. (2011) for precession when the animal moves in a particular direction. Welday et al. (2011) derived the slope of phase precession $(\frac{d\mathrm{\Theta }}{\mathit{dt}})$ for any OIM:

$$\frac{d\mathrm{\Theta }}{\mathit{dt}}=\frac{\stackrel{\rightharpoonup }{\nu }(t)·{\sum }_{k=1}^n{m}_k\stackrel{\rightharpoonup }{d_k}}{{\sum }_{k=1}^n{m}_k}$$ (10)

Where n is the number of VCOs, $\stackrel{\rightharpoonup }{\nu }(t)$ is the velocity vector for the heading of the animal at time t, m_k is the magnitude and $\stackrel{\rightharpoonup }{d_k}$ is a unit vector in the preferred direction of the k^th VCO, A model precesses when $(\frac{d\mathrm{\Theta }}{\mathit{dt}})>0$ (Welday et al., 2011). Thus, for the 2 VCOs+Ref model:

$$\frac{d\mathrm{\Theta }}{\mathit{dt}}=\frac{\stackrel{\rightharpoonup }{\nu }(t)·\stackrel{\rightharpoonup }{d_1}+\stackrel{\rightharpoonup }{\nu }(t)·\stackrel{\rightharpoonup }{d_2}}{2}=\frac{\Vert \stackrel{\rightharpoonup }{\nu }(t)\Vert (m\cos ({\theta }_h)+m\cos (60°-{\mathrm{\theta }}_{\mathrm{h}}))}{2}=\frac{\Vert \stackrel{\rightharpoonup }{\nu }(t)\Vert \sqrt{3}}{2}\cos (30°-{\theta }_h)$$ (11)

We can therefore see that this model predicts a slope of precession that follows a cosine tuning to the angle between the preferred directions of the VCOs. As the animal moves along this direction, the slopes of the speed modulation are always positive, and the slopes are all negative when the animal moves against that direction, causing reverse phase precession (Figure 1, g4-h4, trajectories 1 and 2). When moving perpendicular to this direction, the phase will stay constant (Figure 1, g4-h4, trajectory 3). In the openfield, the phase of the interference is a function of the position of the animal along an axis in the preferred direction and the position within the field the animal is in (Figure 1, f4-h4). Thus, the 2 VCOs+Ref model predicts phase precession when the animal is going with the preferred direction, and reverse phase precession when the animal is going in the opposite direction, as can be seen through the output of the model when it is given the input of real behavioral data (Figure 2, a1-e1).

Fig. 2.

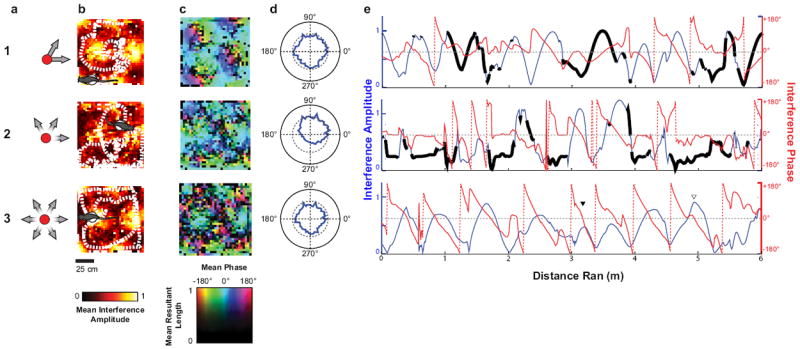
Models reveal phase structure relative to distance run. (A–E) Results of giving the model input of a trajectory of a real rat while foraging to some of the models shown in Fig. 1. (A) Configuration of VCOs. (B) Mean interference amplitude for 3-cm bins across all head directions in that bin. (C) Mean interference phase for 3-cm bins across all head directions in that bin. The color hue shows the phase, whereas the brightness shows the mean resultant length. Darker areas show a more variable phase across head direction in the same bin. (D) Mean interference amplitude for 6° bins of heading across all times in that heading. (E) Interference phase and magnitude along trajectory run, indicated by the cartoon in B. For rows 1 and 2, the dark black lines indicate when the animal was running opposed to the preferred direction. In row 3, examples of shallow (filled triangle) and close to the center (open triangle) passes are indicated.

Burgess (2008) found that the directional phase coding of simple models such as the 2 VCOs+Ref could be exploited to create omnidirectional phase coding. By weighting the VCOs via the head direction of the animal (HD-VCOs), the reverse-precessing parts of the interference results are removed by changing the output weight of each HD-VCO to 0 when the slope of its speed modulation would be negative (3 HD-VCOs, 3 HD-VCOs+Ref; Figure 1, a5h5,a6-h6). The resulting interference patterns have head-direction conjunctive tuning (Figure 1, d5,6), and exhibit precession on all passes when the activity is nonzero (Figure 1 g6,h6). Thus, the cell shows theta phase precession when the rat runs in the preferred direction of the conjunctive cell (note that all the models assume that head direction matches the movement direction). Although this model of conjunctive cells generates elongated fields, they may be rounder in vivo due to a high threshold for spiking. Here, we focus on analyzing spiking phase rather than analyzing the shape of firing fields.

Combining several of these patterns (Burgess, 2008) ensures that the slopes of the speed modulation will always be all positive, and thus the conditions set by Welday et al. (2011) will always be fulfilled (6 HD-VCOs+Ref, Figure 1, a7-h7). The 6 HD-VCOs+Ref model produces 360° of precession regardless of the heading of the animal (Figure 1, h7-h7) and on every pass through the field, including passes that cross the edges (Figure 2, e3, filled triangle) and center (Figure 2, e3, open triangle) of the firing fields.

If we consider the magnitude of summed VCOs at different positions in the field, then the increase and decrease in this magnitude as an animal runs through each field can be considered as if it were a single cycle of an oscillation (Figure 2e). The position within this single cycle can be considered as a temporal phase. In the model, the phase of the summed VCOs relative to a baseline oscillation pattern decreases with the pass phase of the magnitude, even on shallow passes. Thus, if we assume that the theta phase correlates with a reference phase, the omnidirectionally phase coding model (6 HD-VCOs+Ref, Figure a7-h7) predicts that the theta phase of firing should negatively correlate to the temporal phase of a measure that increases and decreases as the rat runs through the firing field.

Tools for Examining Open Field Phase Coding

We developed techniques for testing the modes of precession described above in experimental data. To estimate how far an animal had progressed through an individual pass of a firing field, we first measured the increase and decrease of how “in field” the animal was along its trajectory in and out of the field. To measure this, we took the occupancy-normalized rate map of grid cell firing fields in our data and found the percentile normalization of each bin, that is, its relative rank within the full set of firing rates of bins. We called this estimation of how in field the animal was the “field index” (Figure 3d-g). This normalized the falloff from the center of each field across different grid cells, and reduced small differences across different peaks on the rate map.

To examine omnidirectional phase coding, we calculated the field index along the trajectory of the animal (Figure 3g, blue). The resulting signal contains many irrelevant frequency components. Therefore, we band-pass filtered to include frequencies between twice the largest spatial frequency of grid cells we can observe in a 100 cm enclosure (1.7 m^-1) and one eighth of the smallest spatial frequency of grid cells reported by Hafting et al. (2005, 26.7 m^-1, Figure 3g, green). The phase of this field index signal was then found using the Hilbert transform, and normalized between -1 and 1, so that -1 indicates the beginning of a pass, 0 indicated the center, and +1 indicates the end (Figure 3g, red). This treats each pass through the field as if it were one cycle of an oscillation, so that the increase and decrease of firing rate on that cycle gives a measure of phase. The resulting phase signal from the Hilbert transform was an estimate of how far an animal had progressed along each pass through a grid cell firing field. We called this phase signal the “omnidirectional pass index”. Note that this measure of phase calculates a normalized distance through the field, and differs from the use of phase as a measure of spike time relative to the LFP theta rhythm (See methods). We call this the omnidirectional pass index because the analysis does not rely on or use the animal’s heading.

To test the validity of this technique, we simulated the firing of grid cells in the model with the 6 HD VCOs+Ref configuration using real behavioral trajectories and LFP data recorded in our laboratory (Figure 3h-n, See methods). The varying parameter of the model is the amount of temporal jitter, that is, the standard deviation of the spike times around the point where the model predicts a spike should occur. As this deviation approaches the duration of a theta cycle (1/12 seconds), the models lose temporal structure, but retain spatial periodicity. For each of three model configurations, we generated 250 grid cells for 20 temporal jitters ranging from 1/250 to 1/8 seconds. At relatively low amounts of temporal jitter (jitter<1/24 sec), there was a strong correlation between the omnidirectional pass index and the theta phase for simulated spikes (linear-circular correlation mean -0.29 ± 0.006 SEM, p<0.05 for 92%, Figure 3l). However, there was still a high amount of false positives at higher amounts of jitter (jitter>1/12 sec, 36%), where no temporal structure exists, likely due to oversampling. Examination of the slopes of significantly fit regressions showed that temporally unstructured simulations exhibited a wide range of slopes (Figure 3m), with very large slopes corresponding to a nearly vertical fit and very small slopes corresponding with phase locking. Thus, we called a cell omnidirectionally precessing if it exhibited a significant correlation and the slope fell between -22 and -1440 degrees/pass. This restricted range of slopes resulted in a much lower false positive rate (jitter>1/12 sec, 0.76%, Figure 3n).

To examine directional phase coding, we computed a directional pass index. We padded the outside of the field index map with its autocorrelation. For each point along the animals trajectory, we created a linear path along test directions that ran through the position of the animal. We found the field index at each point along these trajectories, and the Hilbert phase of the intersected curve at the animal’s position, normalized between -1 and 1. For conjunctive cells, we examined theta phase coding along the preferred direction of the cell, and for non-conjunctive grids we used 16 cardinal directions. The resulting directional pass index estimated the position of the animal in each field along a particular direction (Figure 3o) and correlates with running in that direction (Figure 3p).

To test the validity of the directional pass index for testing the model, we simulated the firing of grid cells as above using the model with the 2 VCOs+ref configuration (Figure 3q-t). At low amounts of temporal jitter, the spiking theta phase of the model correlates to a specific running direction of the animal (Figure 3r), and correlates with the directional pass index along a particular direction (Figure 3s). If the model correlated significantly along a specified direction (Linear-circular correlation with Bonferroni correction, p<0.0031) and the slope fell between a magnitude of 22 to 1440 degrees per slope, we further examined the slopes in the 16 directions. If the simulated cell exhibited directional phase coding, we would expect the slope of the precession to follow a cosine tuning to the test direction for the directional pass index. To examine this, we found the relative power in the first and negative first Fourier components and all nonzero Fourier components, which we will refer to as the sinusoid score (See methods). A cell was considered directionally coding if the score exceeded 0.67. A substantial amount of model cells with relatively low jitter exhibited strong precession (jitter<1/24 sec, 37%) with a low false positive rate (jitter>1/12 sec, 4.8%). The relatively high false negative rate is likely due to the lower chance of the cardinal directions lining up with the precessing direction.

It should be noted here that omnidirectional phase precession and directional phase coding are usually not both observed in the simulated data for low jitter (jitter<1/24 sec). Only 6.2% of omnidirectionally precessing grids also exhibited directional coding, and only 14% of directionally coding grids also exhibited strong omnidirectional precession.

Finally, to examine if adjacent fields are phase locked to different median theta phases, we extracted fields from the field index map and grouped them so that no adjacent field fell in the same group. If at least 25 spikes fell within the fields of each of these groups, the phases of the spikes within these fields were compared using the common median-multi sample test (Berens, 2009). Cells were considered significantly differing if all three groups had significantly different median phases (p<0.05). To test the validity of this technique, we simulated the firing of grid cell models as above with the 3 VCOs configuration (Figure 3a-c). Fields were successfully compared in 85% of the simulated cells. For low amounts of temporal jitter, most simulated cells using this model configuration exhibited a different median phase of adjacent fields (p<0.05, jitter<1/24 sec, 75%), with a false positive rate approaching zero (jitter>1/12 sec).

The simulated jitter in some of our examples (Figure 3a-b,h-j,q-s) is 4 ms, the lowest amount of temporal jitter. The resulting levels of noise arising from the simulation is substantially less than in the real data, but noise is still clearly present. A 4 ms jitter mean that, on average, each spike is offset from the model by 3.2 ms. This roughly corresponds to a 9 degree phase noise on a 8 Hz theta wave. Low jitters (<1/24 sec) include jitters up to 41 ms, which corresponds with an average of 33 ms of offset and 96 degrees of phase noise. Our success rates are reported up to 80 ms (Figure 3c, 3n, and 3t). It is worth noting that 1/24 of a second is approximately one half of a theta cycle at the upper range of theta frequencies (12 Hz), and thus we would expect a priori that a portion of the spikes at this jitter will be moved from the correct theta cycle altogether. Thus, at 1/24 of a second of jitter, we expect to see a loss of temporal structure regardless of the efficacy of our observation techniques. It is possible that phase noise of spiking relative to local field potential in awake, behaving animals is higher than this; thus, the success rates of observing these behaviors with these techniques may be lower in real data.

Grid Cells Show Robust Omnidirectional Precession

We examined the omnidirectional pass index and the phase of spikes relative to theta rhythm oscillations for 177 grid cells recorded during foraging in an openfield by five rats in our laboratory (see methods). Of these, 54 showed a significant correlation between omnidirectional pass index and theta phase (linear-circular correlation, p<0.05). Grid cells with a significant correlation between omnidirectional pass index and theta phase were much more likely to exhibit a negative slope than positive (Binomial test, p=0.005). Based on the model analysis that prevented false positives,, we categorized precessing cells as those with slopes as determined by linear-circular regression between -22 and -1440 degrees/pass (1/16 – 4.0 cycles/pass), leaving 34 strongly precessing cells for further analysis (Figure 4c-f). These cells showed strong bimodal phase precession with a shallow leading edge and a steep mode near the pass center, as has been seen previously on the linear track (Figure 4e-f, Hafting et al., 2008).

In previous studies on the linear track grid cells in layer II show precession, but notably few layer III grid cells do (Hafting et al., 2008). As a confirmation of the validity of our technique, we examined phase precession in a different set of experimental data of layer specific recordings of 102 grid cells during open field behavior made by Sargolini et al. (2006, available at http://www.ntnu.no/cbm/moser/gridcell, Figure 5). There was a significant effect of layer on the linear-circular correlation coefficient (Figure 5e, Kruskal-Wallis, ${\chi }_{3,102}^2=12.28$, p=0.007). Post-hoc tests revealed that layer II had a significantly more negative correlation than layer III (Tukey’s Post-Hoc, p<0.05). Of the layer II grid cells, 58% had a significant correlation between omnidirectional pass index and theta phase (p<0.05), as opposed to layer III (20%), layer V (63%) and layer VI (38%). Significantly correlated grid cells from layers II and VI, but not III or V, were significantly more likely to have negative correlations than positive (Binomial test with Bonferonni correction, p<0.0125). Using the same criteria as above we included 37 precessing cells from this additional data set for further analysis.

Fig. 5.

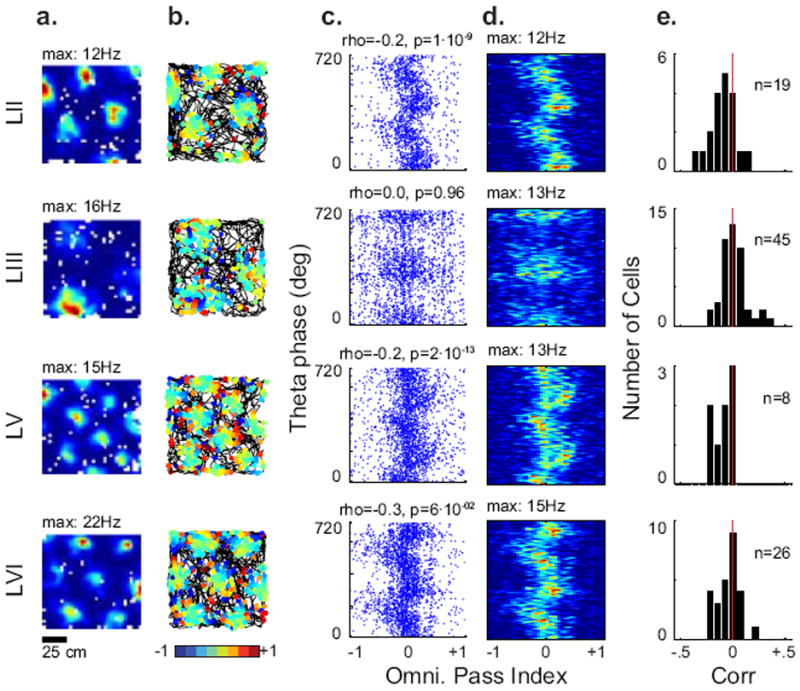
Phase precession by the omnidirectional pass index is layer specific. Precession measures from previously published layer-specific recordings (Sargolini et al., 2006). (A) Rate map. (B) Trajectory with pass index. (C) Scatter plot of the LFP theta phase vs. the pass index. (D) Occupancy-normalized rate maps of the plots in c for example grid cells from layers II, III, V and VI of the medial entorhinal cortex. (E) Linear–circular correlations between the theta phase and pass index at the time of spikes from each layer.

Precession Persists on Field Edges

The correlation between omnidrectional pass index and theta phase could arise from phase precession only on the passes through the center of the field, which have the highest spike rate. To test whether this was the case, we examined the precession of 71 precessing grid cells pooled from our recordings and those published by Sargolini et al. (2006) on passes whose peak field index fell in the top three tenths of the possible field indexes (Figure 6). These passes came close enough to the center of the field to cause spiking, but varied as to how close they came to the center of the field, as can be seen in three representative examples in Figure 6a. We grouped these passes into three selections, with peaks between 0.7 and 0.8 or 0.8 and 0.9 or 0.9 and 1 respectively (Figure 6c). We compared the 51 grid cells from which there were at least 50 total spikes altogether in their shallowest passes. We found that even shallow passes show precession (Figure 6d). Moreover, there was no significant effect of the binned depth of the pass through the field (i.e. how close it came to the center) based on the linear-circular correlation (Friedman’s Test across selection controlling for cell, ${\chi }_{3,51}^2=2.17$, p=0.34) or on the slopes of the selections which remained significantly correlated (circular-linear correlation p<0.05; Kruskal-Wallis across selection, ${\chi }_{3,24,}^2=1.59$, p=0.45). The correlations in all three selections remained significantly different from zero (3 T-tests with Bonferroni correction, T=-3.62,-3.54,-4.47; p<0.0167). The distance that the animal spent in the field (field index>0.5) strongly correlates with the peak field index (Figure 6b, Pearson’s correlation, p<0.05) suggesting that, in terms of distance, the cells precessed faster on the shallow passes to cover the full range of theta.

Fig. 6.

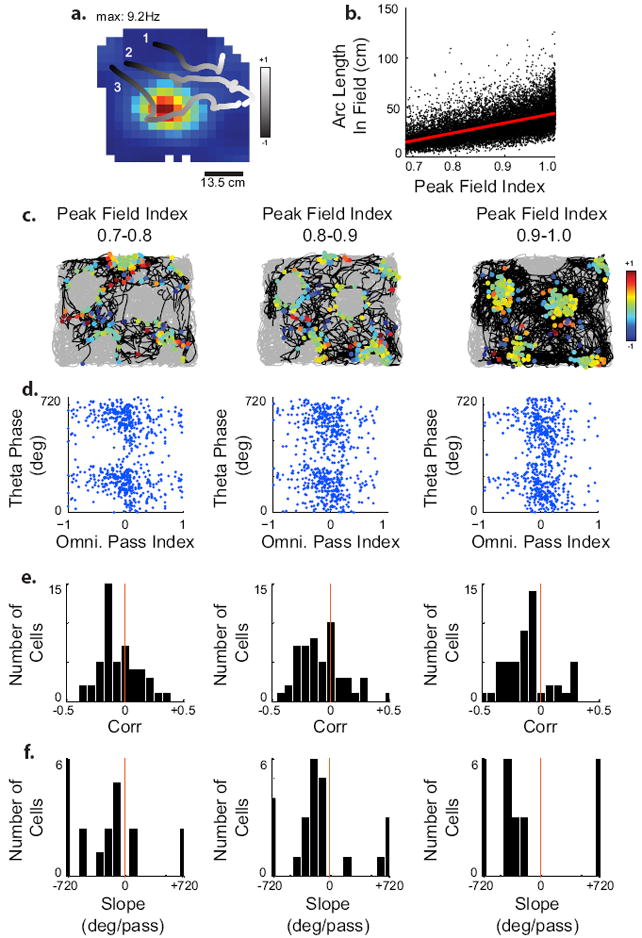
Grid cells precess on shallow passes. (A) Examples of trajectories through a grid field, with the pass index shown as a gradient between black and white. The selected passes are differentially distanced from the center of the field: with a peak field index in the 0.7–0.8 range (1), 0.8–0.9 range (2) or 0.9–1.0 range (3). (B) Scatter plot of the peak field index vs. the arc length of the pass, showing a very strong, linear correlation between the peak field index and the length of the pass (P < 0.05). (C–F) Each column represents only those passes in each cell in our experimental data with a peak field index in the indicated range. The numbers of spikes were randomly sampled so that each selection of a single cell contained the same number of spikes. (C) Representative behavioral example showing selection of trajectories from a single grid cell in black. Grey shows trajectory segments not included in the selection. The selected spikes are shown, and the color of these spikes reflects the omnidirection pass index at the time of spiking. (D) Theta phase vs. the pass index for these spikes from the examples shown in c. (E) Linear–circular correlation coefficients of these selections made from 78 precessing cells. (F) The slopes of the significantly precessing selections.

Conjunctive Grid Cells Exhibit Omnidirectional Phase Precession

One way VCOs could be combined to create omnidirectional phase coding could be the combination of omnidirectionally precessing conjunctive cells, which are predicted by HD-VCO containing OIMs (Burgess 2008, 3 HD VCOs, 3 HD VCOs+Ref, Figure 1 a5-h5, a6-h6). To examine this type of behavior in conjunctive grid cells, we examined phase coding in 76 conjunctive grid cells (gridness>0.34, Watson’s U²>4; Figure 7a-f) pooled from our (n=21) and the Sargolini et al. (2006) dataset (n=55) (Figure 7a-f). Of the 76 cells, 27 (36%) exhibited a significant correlation between the omnidirectional pass index and theta phase (Linear-circular correlation, p<0.05), and 21 (28%) exhibited precession with a slope between -22 and -1440 degrees/pass. For the population, the correlation coefficients were significantly different from zero (Students T-Test, T=-5.68, p=3.4*10^-7) and were significantly more likely to be negative than positive (Binomial test, p=7.0*10^-7).

Fig. 7.

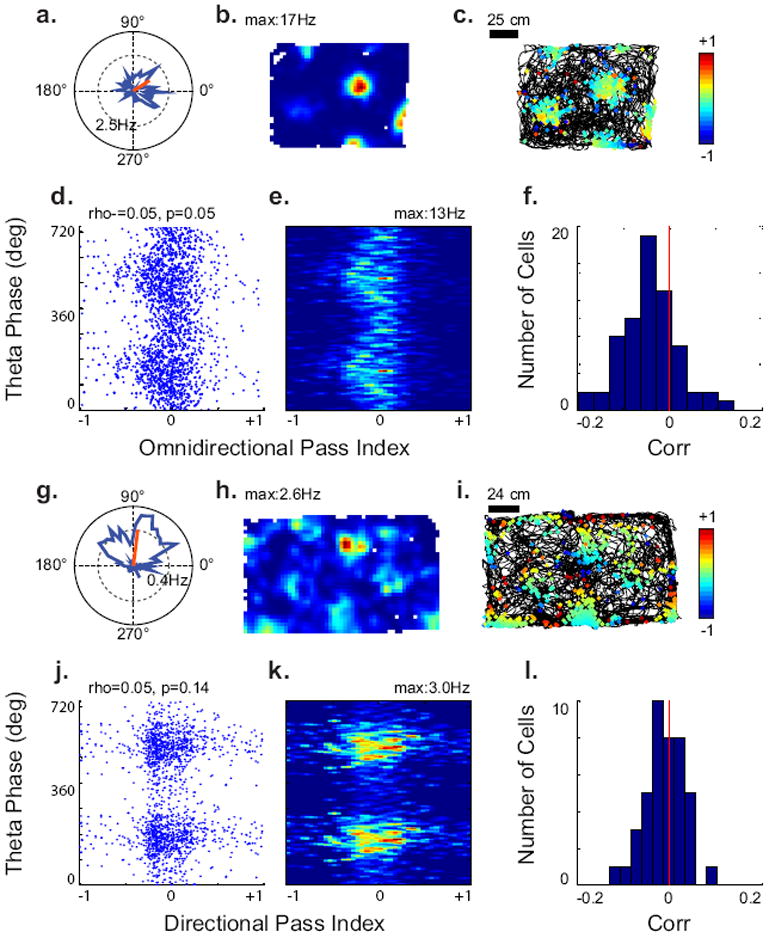
Conjunctive cells exhibit omnidirectional precession. (A–E) Examples of omnidirectional phase coding analysis of a conjunctive cell. (A) Polar, and (B) spatial rate map for the conjunctive grid cell. (C) Trajectory with spike omnidirectional pass indices. (D) Scatter plot, and (E). occupancy-normalized rate map of spike omnidirectional pass index vs. theta phase, showing correlation. (F) Histogram showing distribution of correlation coefficients between omnidirectional pass index and theta phase for conjunctive grid cells. (G–K) Examples of absence of directional phase coding in a conjunctive cell. (G) Polar, and (H). spatial rate maps for the conjunctive grid cell. (I) Trajectory with directional pass index, using the preferred direction of the conjunctive cell as the test direction. (J) Scatter plot, and (K) occupancy-normalized rate map of spike directional pass index vs. theta phase, showing little correlation. (L) Histogram showing distribution of correlation coefficients between directional pass index and theta phase for conjunctive grid cells.

Because the firing of conjunctive grid cells correlates with a particular heading of the animal, it is possible that these cells show phase coding along its particular direction as opposed to omnidirectionally. This suggests that we could generate a better correlation with the directional pass index using the test direction than the omnidirectional pass index. Thus, we examined directional phase coding in these 76 cells, and compared the results to the omnidirectional pass index (Figure 7, g-l). Of the 76 cells, 21 (28%) exhibited a significant correlation between directional pass index and theta phase (Linear-circular correlation, p<0.05), and 10 (13%) exhibited precession with a slope between -22 and -1440 degrees/pass. For the population, the correlation coefficients were not significantly different from zero (T=-0.65, p=0.52), and the correlation coefficients were significantly stronger for the omnidirectional pass index (Students T-Test, T=-2.99, p=0.004). Thus, conjunctive cells more commonly exhibited omnidirectional phase precession than directional phase coding.

The majority of the analyzed conjunctive grids with known locations from the Moser dataset were recorded in layer III (42/55, 76%), and layer III conjunctive grids exhibited a significantly stronger linear-circular precession correlation than layer III non-conjunctive grid cells (Figure 5e vs. Figure 7a, Kolmogorov-Smirnov test, D_42,42=0.36, p=0.007). However, the slopes of precession in significantly correlated layer III conjunctive cells were substantially smaller than the non-conjunctive, omnidirectionally precessing grid cells (Medians -41 and -115 degrees/pass respectively, D_21,110=0.36, p=0.002).

Grid Cells and Other Forms of Phase Coding

To examine if grid cells exhibit field specific median phase coding as in Figure 2a-c, we extracted the individual fields of 279 grids from the pooled dataset and grouped the spikes within them such that no adjacent field was in the same group (Figure 8a-d). Grouping resulted in at least 25 spikes in each group in 190 of the cells. The theta phase of spikes in each group was then tested if different for all three groups using the common median multi-sample test (Berens, 2009). The theta phase of spiking in neighboring fields was only significantly different in 2 of the 190 grids (using p<0.05).

Fig. 8.

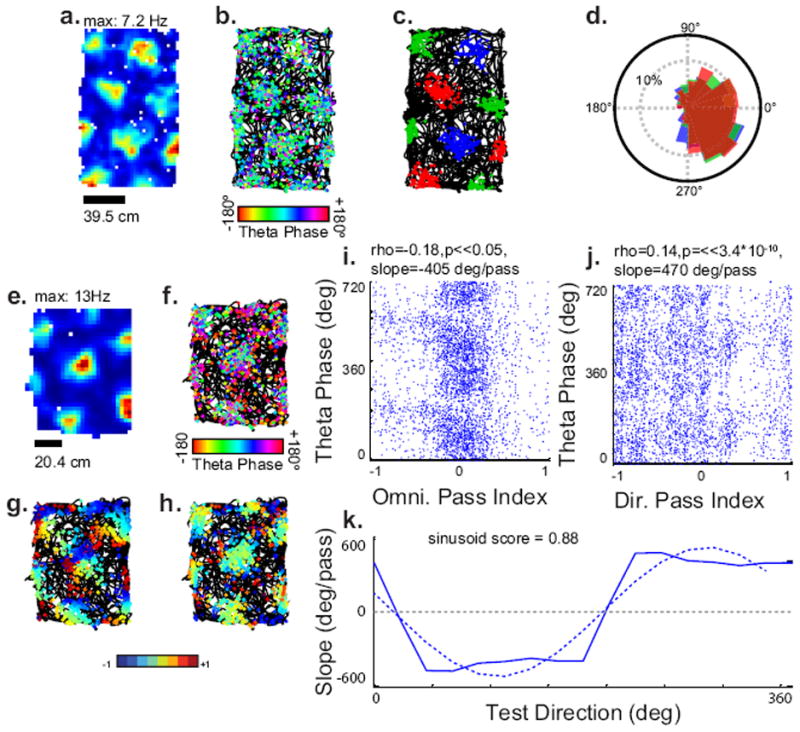
Other forms of predicted phase coding. (A–D) field-specific coding. (A) Rate map, and (B) Trajectory with spikes colored by theta phase for an example cell. (C) Grouping of spikes such that no spike within two adjacent fields is in the same group. Three groups are shown in red, green and blue. (D) Overlapping histograms of the theta phase of the spikes in the three groups, showing that they probably come from the same distribution of phases. (E) Rate map, and (F) trajectory with spikes colored by theta phase for an example cell which omnidirectionally precesses and shows significant directional coding. (G) Trajectory with spikes colored by their directional pass index. (H) Trajectory with spikes colored by their omnidirectional pass index. (I) Scatter plot of omnidirectional pass index vs. theta phase, showing precession. (J) Weak, positively sloped phase coding in the test direction indicated in G. (K) Sinusoid score analysis of the slopes across 16 test directions. The dotted line indicates the amplitude and phase of the first and last Fourier components.

To examine if non-conjunctive grid cells exhibit directional phase coding, we applied the directional pass index in 16 directions to 279 grids from the pooled dataset (Figure 7 a-e). Of the cells, 94 (33%) exhibited significant correlation between the directional pass index and theta phase in at least one direction (Linear-circular correlation with Bonferroni correction, p<0.0031). Of these, 47 (17% of total, 50% of correlated) had slopes which fell between 22 and 1440 degrees/pass.

If this portion of cells exhibited directional phase coding, we would expect the slope of the precession to follow a cosine tuning to the test direction for the directional pass index. To examine this, we found the relative power in the first and negative first Fourier components and all nonzero Fourier components, which we will refer to as the sinusoid score (Figure 8k, see methods). A directionally precessing cell was labeled significantly cosine tuned if the sinusoid score was at least 0.67. 21 (44% of candidates, 7.7% of total) exhibited significant directional coding. 11 of these cells also exhibited omnidirectional precession (52% of directionally coding, 15% of omnidirectionally precession, 4.0% of total), and may represent a directional bias to the omnidirectional precession or a directional bias in the behavior of the animals. There was no significant difference between the magnitude of the correlation between omnidirectional pass index and theta phase and the magnitude of the correlation in the best direction (T-test, p=0.24), and no correlation between these values (Pearsons correlation, rho=0.18, p=0.59), however, visual inspection of the plots showed much less structure in the directionally coded analysis. Together, only 10 (3.7%) of the non-omnidirectionally precessing cells exhibited directional phase coding in the same manner as the model in Figure 3q-t.

Bursting may contribute to the bimodality of phase precession

OIMs by themselves do not explain the striking bimodality of phase precession seen on the linear track (Hafting et al., 2008). To examine if intrinsic factors may contribute to the bimodality of phase precession, we examined bimodal phase coding as demonstrated in 162 fields of 47 layer II grid cells recorded by Hafting et al (2008) as the animal ran on the linear track where the bimodility of phase precession is more consistent, likely due to more stereotyped behavior (Figure 9a). We separated spikes out as either leading spikes (spikes with a previous inter-spike interval (ISI) greater than 1/12 second) or in-burst spikes (spike with a previous inter-spike interval less than 1/12 second) (Figure 9 b-d). Bursting spikes were much more likley to occur later in the pass (T-test, p≪0.05). Separating spikes in this way strongly divided the precession along each of the two modes. The leading spikes demonstrated a significantly more negative correlation between percentage through field and theta phase than the in-burst spikes (Medians -0.20 and 0.05 respectively, Kolmogorov-Smirnov test, D_162,162=0.35, p=2*10^-9) and the slopes of the significantly correlated fields (Medians -216 and +184 degrees/pass respectively, Kolmogorov-Smirnov test, D_102,108=0.36, p=1*10^-6). Similar results were obtained using a threshold for whether a spike is in a burst or a leading spike as strict as 50 ms (Data not shown).

Fig. 9.

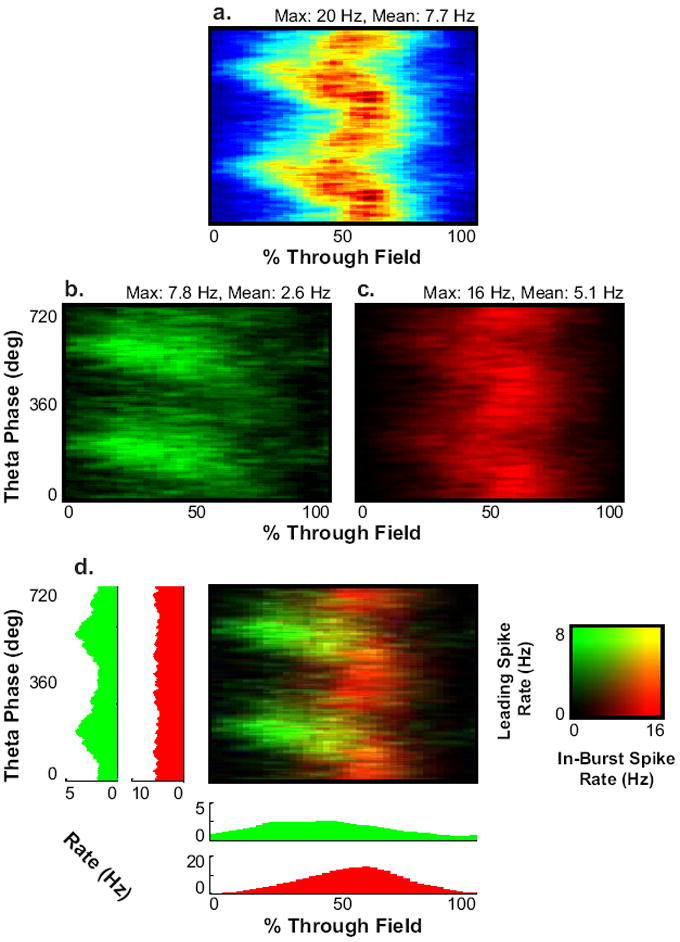
Bursting may contribute to the bimodality of phase precession in grid cells. (A) Grand mean of rate maps from layer II recordings while the animal ran through fields on a linear track (Hafting et al., 2008) (B-C) Rate maps of individual spikes and the first spike of bursts (B) and of within-burst spikes (C). (D) Merge between B and C. Histograms indicate firing rate of the spike selections over the phase and distance axis.

Discussion

We generated predictions from established models of phase coding by grid cells (Figure 1-3). From these, we generated metrics that the models predicted would correlate with the phase of spiking (Figure 3). In the experimental data, we found robust, omnidirectional theta phase precession by grid cells in openfield environments (Figure 4a-d). Only 20% of our grids met stringent criteria for strong phase precession, likely due to a greater sampling of cells in layer III. Consistent with this, we replicated the preference of precession for layer II versus layer III cells (Figure 5). Precession in the openfield occurred when the animal passed across the edge of the field (Figure 6). One specific model (6HD-VCOs+Ref, Equation 5, Figure 1a7-h7, Figure 2a3-e3, Burgess, 2008) predicts omnidirectional phase coding in conjunctive grid cells, which we identified (Figure 7). We did not find strong evidence for directional or field specific phase coding (Figure 8). We found that leading spikes and in burst spikes separate the two modes of precession, and may contribute to the bimodal shape of the phemonenon (Figure 9).

Phase precession has been reported on linear tracks for place cells (O’Keefe & Recce, 1993) and grid cells (Hafting et al., 2008). Place cells precess in openfield environments (Burgess et al., 1994; Huxter et al., 2008). The number and relatively small size of grid fields have made techniques used for measuring precession in place cells impractical. Here, we provide a novel approach to analyzing precession on unconstrained trajectories.

In openfields during foraging behaviors, a rat’s trajectory measured by head-mounted diodes rarely follows a straight line. Rather, the animal’s head moves from side to side at an average angular speed of 50.5°/second, crossing the animal’s already tortuous trajectory at 4.6 Hz. Despite this variability, we found robust, omnidirectional precession by grids in openfield environments (Figure 4a-d). Furthermore, passes that clip the outside of grid fields show full phase precession (Figure 6). This normalizes distance through the field, thus, precession across field edges covers the full theta cycle in a smaller distance (Figure 6b), consistent with recent single-pass analysis of grid cells (Reifenstein, Herz, et al., 2012).

Phase coding is thought to be a critical way grid cells represent spatial information (Solstad et al., 2006), and constrains models that generate grid cell firing (Blair et al., 2008; Burgess, 2008; Hasselmo, 2008; Zilli and Hasselmo, 2010; Welday et al., 2011; Navratilova et al., 2012). Omnidirectional phase precession and precession on field edges has implications for these models. Oscillatory interference models (OIMs) show striking similarities to the in vivo data. Many configurations of OIMs generate phase locking behaviors (e.g. 3VCOs+Ref, 6VCOs+Ref; Figure 1a2-g3) which mimic the behaviors exhibited by grid cells found in entorhinal cortex layer III (Figure 4, Hafting et al., 2008).

One OIM variant (6HD-VCOs+Ref) always satisfies the conditions for precession (Welday et al., 2011) by weighting VCOs based on the heading of the animal (6HD-VCOs+Ref, Equation 5, Figure 1a7-h7, Figure 2a3-e3, Burgess, 2008). This predicts the observed openfield precession (Figure 3-4) and full precession by grids on field edges (Figure 5; Reifenstein et al., 2012a).

Phase coding conjunctive cells may converge to create omnidirectional precession and are directly predicted by HD-VCO configurations of the OIM (Figure 1a5-f6). We found that many of our conjunctive grid cells exhibited strong phase precession (Figure 7a-f). In contrast, phase coding did not occur along the preferred firing direction of the cell, as predicted by one model of conjunctive cells (Figure 1-5, 3HD VCOs, Figure 7j-l). This implies that the non-directionality of precession on passes offset from the preferred direction provides much of the phase structure of the spiking. Interestingly, 17 of 21 strongly precessing conjunctive cells were recorded in layer III, representing 41% of the layer III conjunctive cells. Conjunctive cells were much more likely to exhibit precession than non-conjunctive grids in layer III (Figure 5e, Figure 8f). On linear tracks, layer III grid cells have been thought to exhibit little or no precession (Hafting et al., 2006), however, the head direction specificity of these cells or the lower magnitude slopes of precession may have limited the observation of precession on the linear track. Because layer III cells project primarily to area CA1 of the hippocampus (Canto et al., 2008), it is possible that these precessing conjunctive grid cells contribute to the hippocampal temporal code. Although deep layer conjunctive grids could converge on cells in layer II (Canto et al., 2008), to generate omnidirectionally precessing grids (Figure 1), few (10/55) of the analyzed conjunctive cells were recorded there.

OIMs also predict other forms of phase coding, which we were not able to observe using our techniques. OIMs using a configuration of 3 VCOs without a reference would be locked to a phase dependant on which grid field the animal was in (Figure 1 a1-h1, Figure 3a-c). However, when tested for a significant differenct in spikes where enough fields and spikes were present to be robustly divided, only 2 of 190 (1.1%) of grid cells were significant. OIMs using a simple configuration will phase precess only along one direction (Figure 1 a4-f4). These models predict that bidirectional phase coding exists on the linear track due to a contextual reset of the VCO preferred direction. Such a contextual reset could underlie the behavior of grid cells on the hairpin maze (Burgess et al., 2007; Hasselmo, 2008; Derdikman et al., 2009). However, these models predict directional phase coding in the open field, where no reset is present, and a cosine modulation of the slope of precession (Equation 11, Figure 8e-k). Relatively few (21, 7.7%) of the cells showed directional phase coding with our analysis. More than half (11, 4.0% of total) of these cells were also categorized as omnidirectionally precessing, which may indicate a subtle directional component to the omnidirectional phase precession which is not explained by our models. However, because the remaining cells represented so little of the total population (10, 3.7%) we do not feel that we found strong evidence for phase coding along a particular directional axis.

Although we were not able to detect these forms of temporal coding in relation to theta, temporal coding in these ways may still exist and be observable only relative to the timing of a subset of the neural circuit, such as the precise timing of specific neurons firing, rather than the phase of local field potential theta oscillations that reflect the larger scale network dynamics. In addition, our techniques’ ability to detect these behaviors in models are restricted to relatively small amounts of temporal jitter (Figure 3c,n and t). Particularly where our detection rates in models are relatively low as with directional phase coding, greater amounts of phase noise in experimental data prevents us from ruling out that these forms of phase coding exist. Directional coding may be more apparent using very long sessions and selecting passes based on their directionality through the field. However, as such a selection would also depend on the passes being relatively straight, and would thus require very long sessions such as those used for examining directional rhythmicity properties of theta-rhythmic neurons to prevent undersampling (Welday et al., 2011).

Although OIMs can explain many of the features of phase precession, they predict that precession should occur in a linear manner, in contrast to the bimodality we see in layer II grid cells (Hafting et al., 2008; Figure 9a). However, rat entorhinal layer II stellate cells (putatively grid cells) have been shown in vitro to exhibit theta-frequency bursting at sufficient levels of depolarization (Alonso & Klink, 1993). Addition of spikes lagging behind a correctly timed leading spike could provide a mechanism by which a second modality of precession is introduced later in the pass. In support of this hypothesis, we found that we could separate a precessing-modality from a broadly tuned modality of precession by the previous interspike interval (Figure 9b-d).

Continuous attractor models have used widening and narrowing of the attractor “bump” for phase modulation (Samsonovich & McNaughton, 1997; Conklin & Eliasmith, 2005); however, this predicts a nearly constant phase on shallow passes. Other attractor models use “look ahead” by synaptic weights (Jensen and Lisman, 1996; Tsodyks et al., 1996; Wallenstein and Hasselmo, 1997b) or conjunctive cell inputs (Navratilova et al., 2012) to push activity with the heading of the animal. Similarly, oscillatory-inhibition mediated learning models of theta phase coding (Norman et al., 2005, 2006) imply that phase precession results from activation of spatially tuned cells in order of their proximity to the animal. On each theta cycle, proximal cues activate cells coding for the most proximal positions. Spreading activation drives cells in a cascade such that the last cells firing within a cycle represent farthest positions from the animal. Inhibition silences the activation, and the cycle repeats. These models predict overshooting the actual trajectory of the animal during the frequent, sharp turns in the openfield, and may not function in open environments. Furthermore, cells on the lateral edge of the path of the attractor bump will enter it later and leave it earlier than more central cells, limiting the range of precession on shallow passes.

Ramp depolarization models (Harris et al., 2002; Mehta et al., 2002) use asymmetric excitation of neurons to drive firing earlier in the falloff of rhythmic inhibition. These models predict that limited excitation on field edges, where the spike rate is lower, corresponds to a limited phase distribution and little to no precession.

In contrast, population oscillation models do not describe the temporal coding mechanism (Geisler et al., 2010). Rather, temporally coding neurons generate population rhythms slower than the rhythmic firing of individual cells as an animal moves at a constant velocity through firing fields. Since grid cells are consistently oriented (Sargolini et al., 2006; Barry et al., 2007; Doeller et al., 2010), trajectories parallel to the “main axes” of the grid pattern are more likely to pass through grid field centers (Doeller et al., 2010). Given that we have found that phase precession occurs faster on the shorter, field edge passes (Reifenstein et al., 2012a, Figure 6b), these models predict higher frequency network and LFP theta oscillations during trajectories divergent from the main axes.

It has been claimed that scarce LFP theta oscillations and low rhythmicity in the spike time autocorrelogram as measured by the theta index of grid cells in bat MEC causally disproves all OIMs (Yartsev et al., 2011). OIMs do not require rhythmicity; they require that neurons can maintain a periodic temporal code relative to each other, such as phase coding. In OIMs, LFP theta correlates to some baseline, relative to which temporally coding neurons can interfere in a predictable way. However, there is little evidence that the LFP itself influences the behavior of neurons, rather, it likely correlates to bouts of temporally guided firing (Buzsáki, 2010). When theta was present in bat LFP, it modulated the spiking of grid cells (Yartsev et al., 2011). Therefore, a coordinator of temporal firing in bat entorhinal cortex may exist, but be poorly represented by LFP recordings. It may be more parsimonious to describe these models as temporal interference models (Zilli, 2012). There are many cases where the relative timing of neuronal spiking can be modulated by behavioral factors (e.g., Jensen & Lisman, 2000; Kayser et al., 2009). Position in sequences of timed spiking has important implications to the downstream integration in the generation of rate codes, including the sequence of the downstream spikes, and these implications can be described by OIMs. Thus, rhythmic input from the medial septum can be required for grid cell spatial coding, as shown in rats (Brandon et al., 2011; Koenig et al., 2011), by coordinating bouts of temporally coded firing, without necessarily producing rhythmicity in the LFP or significant rhythmicity as seen by the theta index, as observed in bats (Yartsev et al., 2011). We have found evidence that the temporal properties of grid cells match predictions from OIMs, but the evidence presented here does not disprove other mechanisms for generating the spatial rate code. Temporal interferance may interact with other mechanisms, such as attractor dynamics, to generate a stable path integration system. Indeed, such a mechanism may underlie recently observed results from intracellular grid cell recordings: as animals traversed the grid field, sub-threshold oscillation precessed (as predicted by OIMs) and were accompanied by a slow depolarization (as predicted by attractor dynamics) (Domnisoru et al., 2013; Schmidt-Hieber & Häusser, 2013).

We described novel techniques for examining openfield phase precession and examined phase coding in grid cells during the myriad of behaviors seen during openfield foraging. This allows us to examine the phase coding of grid cells in the context of open spaces. The techniques we describe here rely on the rate map and not the shape of the fields in 2D space. We can extend the idea of a pass index for fields in any modality to examine phase coding of cells that code non-spatial information. Since phase coding is not unique to the hippocampal formation (Jones & Wilson, 2005; Siegel et al., 2009), examining the relationship of other phase coding phenomena to precession may provide insights into mechanisms that generate temporal coding in other structures.

Abbreviations

Deg

Degrees

HD-VCO

Head Direction weighted Velocity Controlled Oscillator

LFP

Local field potential

OIM

Oscillatory interference model

Ref

Reference oscillation

VCO

Velocity Controlled Oscillator