A Positive Stable Frailty Model for Clustered Failure Time Data with Covariate-Dependent Frailty

Summary

In this article, we propose a positive stable shared frailty Cox model for clustered failure time data where the frailty distribution varies with cluster-level covariates. The proposed model accounts for covariate-dependent intracluster correlation and permits both conditional and marginal inferences. We obtain marginal inference directly from a marginal model, then use a stratified Cox-type pseudo-partial likelihood approach to estimate the regression coefficient for the frailty parameter. The proposed estimators are consistent and asymptotically normal and a consistent estimator of the covariance matrix is provided. Simulation studies show that the proposed estimation procedure is appropriate for practical use with a realistic number of clusters. Finally, we present an application of the proposed method to kidney transplantation data from the Scientific Registry of Transplant Recipients.

1. Introduction

Clustered failure time data are frequently observed in biomedical studies. For example, in the kidney transplantation setting, transplant failure times are of interest and can be taken as clustered failure times with transplant facilities as clusters. In family disease studies, time to disease onset is of interest and families are natural clusters. Subjects within cluster are correlated, with the intracluster dependence possibly due to sharing similar environmental and/or genetic conditions.

Several methods have been proposed for clustered failure time data. In general, these can be categorized into two broad strategies. In marginal models, the cluster structure is usually ignored when estimating the population-averaged covariate effect, but is used to derive valid standard error estimates. Marginal models can be used when the comparison of lifetimes across clusters is of interest. Examples include Wei, Lin, and Weissfeld (1989); Lee, Wei, and Amato (1992); and Spiekerman and Lin (1998). These authors used generalized estimating equations with an independence working assumption and the intracluster correlation structure left unspecified. As a result, some efficiency loss may occur, potentially affecting the significance of estimated covariate effects.

When the comparison of lifetimes within the same cluster is of interest, frailty models may be more appropriate. In this case, the correlation structure is specified by incorporating a random effect (frailty) that is common to subjects within the same cluster. The covariate effect is then interpreted as being conditional on the frailties and is cluster specific. One can also obtain marginal covariate effects by making additional assumptions about the frailty distribution as was done by Glidden and Self (1999) and Pipper and Martinussen (2003) under the Clayton-Oakes model. In frailty models, it is usually assumed that the frailty variables follow the same distribution across clusters, which implies equal intracluster dependence as well as between-cluster heterogeneity. This assumption may be violated in practice.

In studies comparing U.S. kidney transplant centers to the national average, the ratio of observed to expected deaths, known as the standardized mortality ratio (SMR), is used, with the expected deaths obtained from a marginal Cox model. An SMR > 1 indicates a mortality rate above the national average. In the shared frailty model, this statistic is actually a nonparametric Poisson-type estimator (Glidden and Vittinghoff, 2004) for the corresponding frailty, given the observed data in the center. An investigation of the SMRs suggests that there may be greater heterogeneity for smaller facilities, since SMRs for smaller centers are more frequently seen at either the top or at the bottom of the ordered list. Although this is partly due to sampling variance of the SMR estimator, it is also possible that an unequal degree of heterogeneity across centers results from varying cluster characteristics. This suggests a shared frailty model, but with the frailty distribution allowed to depend on cluster size. Other cluster-level covariates may also have an effect on the frailty distribution. For example, urban transplant facilities may exhibit more uniform practices than rural transplant hospitals, corresponding to less heterogeneity (smaller variance) for frailties of urban centers. In these examples of clustered failure time data, the population averaged effect is of primary interest. At the same time, however, the incorporation of cluster-level covariate effects on the frailty distribution is of practical interest and should be considered.

Similar situations exist for other types of clustered data. Prentice (1986) proposed a regression model for clustered binary data, in which the correlation between pairs of binary observation within clusters was assumed to depend on cluster-level covariates. Lin, Raz, and Harlow (1997) proposed a linear mixed model with heterogeneous within-cluster variances, where the within-cluster errors were assumed to follow a normal distribution with cluster-specific covariance matrix. Specifically, the variance of the measurement error was assumed to follow an inverse gamma distribution, where the mean depends on some linear combination of cluster-level covariates through a log link. Heagerty (1999) proposed a marginally specified logistic-normal model for longitudinal binary data in which the marginal mean, rather than the conditional mean, was regressed on covariates. In addition, a conditional model on a Gaussian latent variable is specified, where the random effect additively influences the logit of the conditional mean. Wang and Louis (2004) further extended this method to clustered binary data, allowing the distribution parameters of the random effect to depend on some cluster-level covariates. Their approach used a “bridge” distribution previously identified by Wang and Louis (2003) for the random effect to unify the form of the marginal and the conditional models. As a result, the conditional regression parameters can be expressed as functions of the marginal regression parameters and a parameter in the bridge distribution. Under this model, the regression parameter estimates have a direct marginal interpretation, while the conditional regression parameter estimates can easily be obtained. Moreover, the influence of the cluster-level covariates on the random effect can be estimated.

The positive stable distribution (Hougaard, 1986) serves as a bridge distribution for clustered failure time data under a Cox proportional hazards shared frailty model in the same sense as Wang and Louis (2003) since the resulting marginal regression parameter is a product of the conditional regression parameters and the frailty parameter. This relationship allows both marginal and conditional inference, while accounting for intracluster dependence. The shared positive stable frailty model has attracted renewed attention recently (e.g., Fine, Glidden, and Lee, 2003; Martinussen and Pipper, 2005).

In this article, we propose a covariate-dependent positive stable shared frailty model. The bridge-type frailties are allowed to depend on cluster-level covariates and so to follow different distributions across clusters. Under this unified framework, the marginal regression parameters and the covariate effects on the frailty distribution can be consistently estimated. The major contributions of this paper are the methods proposed for modeling the effects of the cluster-level covariates on the frailty distribution and the corresponding estimation of the marginal regression effects.

The remainder of this article is organized as follows. In Section 2, we introduce the proposed covariate-dependent frailty model and describe the estimation procedures. We obtain the large sample properties of the model parameter estimators in Section 3 and Section 4 presents simulation studies. The proposed method is then applied to kidney transplant data from the Scientific Registry of Transplant Recipients (SRTR) in Section 5. In Section 6, we provide some concluding remarks and discussion. Proofs of the results are provided in the Appendix.

2. Model Specification and Estimation

2.1 The Positive Stable Shared Frailty Cox Proportional Hazards Model with Covariate-Dependent Frailty

In this section, we specify a positive stable shared frailty Cox model, with the frailty distribution depending on cluster-level covariates and the corresponding marginal hazard having a proportional hazards form. Our ultimate purpose is to estimate cluster-level covariate effects on the frailty distribution, as well as the correlation within clusters and heterogeneity between clusters. We first define the Cox-type conditional and marginal hazard functions through the “bridge” property of the positive stable distribution. The relationship between the conditional hazard parameters, marginal hazard parameters, and frailty distribution parameter can be obtained accordingly. Cluster-level covariates are related to the frailty distribution parameter through a link function. Finally, we derive the individual intensity process given the observed history of all the individuals with the parameters of interest. We begin this section by establishing the requisite notation.

Suppose we have measurements from subjects in K clusters and that the cluster sizes n_k (k = 1, 2, …, K) are independent and identically distributed bounded random variables. Given n_k, let D_ik and C_ik be the failure and censoring times for the ith individual (i = 1, …, n_k) in the kth cluster; let T_ik = D_ik ∧ C_ik be the follow-up time and Δ_ik = I (D_ik ≤ C_ik) the observed death indicator. Let W_k denote the positive stable distributed frailty with dependence parameter α_k for the kth cluster that we use to describe within-cluster dependence possibly due to unobserved covariate information. Let Z_ik be a p-vector of time-independent covariates measured on individual (i, k). In addition, let X_k be a q-vector of time-independent cluster-level covariates that may influence α_k. Let D_k = (D_1k, …, D_nkk), with C_k and Z_k defined similarly. We assume that (D_k, C_k, Z_k, X_k, n_k, W_k) are independent and identically distributed for k = 1, …, K. Define the at-risk process Y_ik (t) = I (T_ik ≥ t) and the individual counting process N_ik (t) = Δ_ik I (T_ik ≤ t). We define the filtrations

$${ℱ}_t=\sigma \{N_{ik}(s),Y_{ik}(s),Z_{ik},X_k,n_k:k=1,\dots ,K,i=1,\dots ,n_k,0\le s\le t\}$$

and

$${\mathscr{H}}_t=\sigma \{N_{ik}(s),Y_{ik}(s),Z_{ik},X_k,n_k,W_k:k=1,\dots ,K,i=1,\dots ,n_k,0\le s\le t\}.$$

Similar to Martinussen and Pipper (2005), we term ℱ_t the observed filtration and ℋ_t the conditional filtration.

We assume that W_k follows a positive stable distribution with shape parameter α_k (0 < α_k ≤ 1). The positive stable distribution has been used by Hougaard (1986) for multivariate failure time data; its density function and Laplace transform are given by

$$f_{{\alpha }_k}(w)=-\frac{1}{\pi w}\sum _{i=1}^{\infty }\frac{\mathrm{\Gamma }(i{\alpha }_k+1)}{i!}{(-w^{-{\alpha }_k})}^{i}sin({\alpha }_{k}i\pi ),$$

and

$$L(s)=\epsilon \{exp(-s{W}_k)\}=exp(-s^{{\alpha }_k})(s\ge 0),$$

respectively.

Given (Z_k, X_k, W_k, n_k), the failure time D_ik, i = 1, …, n_k are assumed to be independent with hazard function

$$\underset{h\to 0^{+}}{lim}P(t\le D_{ik}\le t+h|D_{ik}\ge t,Z_k,X_k,n_k,W_k)/h=W_k{\lambda }_{0k}(t)e^{{\beta }_k^T{Z}_{ik}},$$ (1)

where λ_0k (t)(k = 1, …, K) are unknown cluster-specific baseline hazard functions and β_k (k = 1, …, K) are p-vectors of unknown cluster-specific regression parameters, all of which rely on α_k through the derived marginal hazard function below.

Since W_k has the positive stable distribution, the marginal hazard function of D_ik is given by

$$\underset{h\to 0^{+}}{lim}P(t\le D_{ik}\le t+h|D_{ik}\ge t,Z_k,X_k,n_k)/h=h_0(t)e^{{\gamma }^T{Z}_{ik}},$$ (2)

where h₀ (t) is an unspecified baseline hazard and γ is a p-vector of unknown marginal regression parameters. In this, we have assumed a constant marginal log hazard ratio γ, which, given (1) and (2), imposes the restriction γ = α_kβ_k , k = 1, …, K. Note also that ${\mathrm{\Lambda }}_{0k}(t)=H_0{(t)}^{{\alpha }_k^{-1}}$, where ${\mathrm{\Lambda }}_{0k}(t)={\int }_0^t{\lambda }_{0k}(s)\mathit{\text{ds}}$ and $H_0(t)={\int }_0^t{h}_0(s)\mathit{\text{ds}}$.

We further relate X_k and α_k through a link function α_k = g̃ (η; X_k) and let ${\alpha }_k^{-1}=g(\eta ;X_k)$, where η is a (q + 1)-vector of unknown parameters. Here, we assume that g (·) is monotone and twice differentiable with respect to η. Since α_k ∈ (0, 1], a natural choice for g̃ is the logit link function and we set

$$g(\eta ;X_k)=1+e^{-{\eta }^T{\stackrel{\sim }{X}}_k},$$ (3)

with ${\stackrel{\sim }{X}}_k={(1,X_k^T)}^T$ and $\eta ={({\eta }_1,{\eta }_2^T)}^T$ where η₁ is a scalar intercept and η₂ is a q-vector of regression parameters.

In addition, we assume that the D_ik and C_ik are independent given Z_ik for i = 1, …, n_k. Under this conditional independent censoring assumption, model (1) implies that the individual intensity process with respect to the conditional filtration ℋ_t is

$${\lambda }_{ik}(t|{\mathscr{H}}_{t^{-}})=Y_{ik}(t)W_k{\lambda }_{0k}(t)e^{{\beta }_k^T{Z}_{ik}}.$$ (4)

By applying the innovation theorem (Andersen et al., 1993) to (4) and inserting the link function (3), the individual intensity process with respect to the observed filtration ℱ_t is

$${\lambda }_{ik}(t|{ℱ}_{t^{-}})=Y_{ik}(t)f_k(t){\lambda }_{0k}(t)e^{g(\eta ;X_k){\gamma }^T{Z}_{ik}},$$ (5)

Where f_k (t) = E (W_k | ℱ_t⁻) has the explicit form

$$f_k(t)=\frac{E_{W_k}\left[W_k^{N_{.k}(t^{-})+1}{e}^{-W_k}{\sum }_{i=1}^{n_k}{\int }_0^{t^{-}}{Y}_{ik}(t)e^{g(\eta ;X_k){\gamma }^T{Z}_{ik}}d{H}_0^{g(\eta ;X_k)}(s)\right]}{E_{W_k}\left[W_k^{N_{.k}(t^{-})}{e}^{-W_k}{\sum }_{i=1}^{n_k}{\int }_0^{t^{-}}{Y}_{ik}(t)e^{g(\eta ;X_k){\gamma }^T{Z}_{ik}}d{H}_0^{g(\eta ;X_k)}(s)\right]},$$ (6)

with “.” denoting summation over a subscript.

2.2 Estimation

Model (4) differs from the existing positive stable shared frailty Cox proportional model in that it allows the frailty distribution parameter α_k to depend on cluster-level covariates, which induces the cluster-specific conditional regression parameter ${\beta }_k={\alpha }_k^{-1}\gamma$ and the cluster-specific conditional baseline hazard λ_0k (t). It can be easily seen that when η₂ = 0, α_k is a constant and the proposed model reduces to the common positive stable shared frailty model for which several estimation procedures have been developed. For example, Wang, Klein, and Moeschberger (1995) applied the E-M algorithm for parameter estimation. Fine et al. (2003) presented a simple estimation procedure that fitted a marginal model and stratified model separately and utilized the relationship α = γ/β. Martinussen and Pipper (2005) proposed a likelihood-based estimation procedure based on the individual intensity process with respect to an observed filtration similar to (5), but with α_k = α and β_k = β. However, we are not able to extend these estimation procedures in the proposed model, since the regression parameter β_k in the conditional hazard is cluster specific.

As can be seen in the existing literature, simulations and applications of the positive stable shared frailty model are usually based on small clusters, such as twin or family studies, especially when the estimation of frailties is needed. In order to apply the positive stable frailty model to studies with large clusters, it is useful to avoid the estimation of f_k (t) in (6). We notice that model (5) can be written as

$${\lambda }_{ik}(t|{ℱ}_{t^{-}})=Y_{ik}(t){\stackrel{\sim }{\lambda }}_{0k}(t)e^{g(\eta ;X_k){\gamma }^T{Z}_{ik}},$$

where λ̃_0k (t) = λ_0k (t)f_k (t), which is actually a stratified Cox model, except that the covariate effect is cluster specific and depends on a function of cluster-level covariates. The stratified partial likelihood approach (Cox, 1975; Kalbfleisch and Prentice, 2002) can be directly applied here. Due to the loss of information in f_k (t) and the multiplicative relationship between g and γ, we cannot estimate the intercept term η₁ and the remaining parameters simultaneously. Therefore, our estimation procedure is actually based on two results from models (2) and (5), respectively.

Before proceeding, it is convenient to introduce the following two sets of notation for k = 1. …, K and r = 0, 1, 2,

$$\begin{array}{lll}\hfill S^{(r)}(\gamma ,t)& =\hfill & K^{-1}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^{n_k}}{Y}_{ik}(t)e^{{\gamma }^T{Z}_{ik}}{Z}_{ik}^{\otimes r},\hfill \\ \hfill E(\gamma ,t)& =\hfill & S^{(1)}(\gamma ,t)/S^{(0)}(\gamma ,t),\hfill \\ \hfill V(\gamma ,t)& =\hfill & S^{(2)}(\gamma ,t)/S^{(0)}(\gamma ,t)-{\{E(\gamma ,t)\}}^{\otimes 2},\hfill \end{array}$$

Where a^⊗0 = 1, a^⊗1 = a, and a^⊗2 = aa^T, and

$$\begin{array}{lll}\hfill S_k^{(r)}(\eta ;\gamma ,t)& =\hfill & {\displaystyle \sum _{i=1}^{n_k}}{Y}_{ik}(t)e^{g(\eta ;X_k){\gamma }^T{Z}_{ik}}{\left\{g_1(\eta ;X_k){\gamma }^T{Z}_{ik}\right\}}^{\otimes r},\hfill \\ \hfill S_k^{(3)}(\eta ;\gamma ,t)& =\hfill & {\displaystyle \sum _{i=1}^{n_k}}{Y}_{ik}(t)e^{g(\eta ;X_k){\gamma }^T{Z}_{ik}}{g}_2(\eta ;X_k){\gamma }^T{Z}_{ik},\hfill \\ \hfill S_k^{(4)}(\eta ;\gamma ,t)& =\hfill & {\displaystyle \sum _{i=1}^{n_k}}{Y}_{ik}(t)e^{g(\eta ;X_k){\gamma }^T{Z}_{ik}}{g}_1(\eta ;X_k)Z_{ik}^T,\hfill \\ \hfill S_k^{(5)}(\eta ;\gamma ,t)& =\hfill & {\displaystyle \sum _{i=1}^{n_k}}{Y}_{ik}(t)e^{g(\eta ;X_k){\gamma }^T{Z}_{ik}}g(\eta ;X_k)Z_{ik}^T,\hfill \\ \hfill S_k^{(6)}(\eta ;\gamma ,t)& =\hfill & {\displaystyle \sum _{i=1}^{n_k}}{Y}_{ik}(t)e^{g(\eta ;X_k){\gamma }^T{Z}_{ik}}{g}_1(\eta ;X_k){\gamma }^T{Z}_{ik}^{\otimes 2}g(\eta ;X_k),\hfill \\ \hfill E_k^1(\eta ;\gamma ,t)& =\hfill & S_k^{(1)}(\eta ;\gamma ,t)/S_k^{(0)}(\eta ;\gamma ,t),\hfill \\ \hfill E_k^3(\eta ;\gamma ,t)& =\hfill & S_k^{(3)}(\eta ;\gamma ,t)/S_k^{(0)}(\eta ;\gamma ,t),\hfill \\ \hfill E_k^4(\eta ;\gamma ,t)& =\hfill & S_k^{(4)}(\eta ;\gamma ,t)/S_k^{(0)}(\eta ;\gamma ,t),\hfill \\ \hfill E_k^5(\eta ;\gamma ,t)& =\hfill & S_k^{(5)}(\eta ;\gamma ,t)/S_k^{(0)}(\eta ;\gamma ,t),\hfill \\ \hfill V_k^1(\eta ;\gamma ,t)& =\hfill & S_k^{(2)}(\eta ;\gamma ,t)/S_k^{(0)}(\eta ;\gamma ,t)-{\left\{E_k^1(\eta ;\gamma ,t)\right\}}^{\otimes 2},\hfill \\ \hfill V_k^2(\eta ;\gamma ,t)& =\hfill & S_k^{(6)}(\eta ;\gamma ,t)/S_k^{(0)}(\eta ;\gamma ,t)-E_k^1(\eta ;\gamma ,t)E_k^5(\eta ;\gamma ,t),\hfill \\ \hfill g_1(\eta ;X)& =\hfill & \partial g(\eta ;X)/\partial \eta ,g_2(\eta ;X)=\partial g_1(\eta ;X)/\partial {\eta }^T.\hfill \end{array}$$

We first estimate γ from model (2) by maximizing the pseudo partial log-likelihood

$${\ell }_1(\gamma )=\sum _{k=1}^K\sum _{i=1}^{n_k}{\int }_0^{\tau }\left\{{\gamma }^T{Z}_{ik}-log{S}^{(0)}(\gamma ,t)\right\}d{N}_{ik}(t)$$

under the working independence assumption (Wei et al., 1989). The corresponding estimating equation can be written as

$$U_1(\gamma )=\sum _{k=1}^K\sum _{i=1}^{n_k}{\int }_0^{\tau }\{Z_{ik}-E(\gamma ,t)\}d{N}_{ik}(t).$$

Given an estimator γ̂ of γ from model (2), we estimate η from model (5) by maximizing the pseudo-stratified partial log-likelihood

$${\ell }_2(\eta ;\widehat{\gamma })=\sum _{k=1}^K\sum _{i=1}^{n_k}{\int }_0^{\tau }\left\{g(\eta ;X_k){\widehat{\gamma }}^T{Z}_{ik}-log{S}_k^{(0)}(\eta ;\widehat{\gamma },t)\right\}d{N}_{ik}(t),$$

with corresponding score function,

$$U_2(\eta ;\widehat{\gamma })=\sum _{k=1}^K\sum _{i=1}^{n_k}{\int }_0^{\tau }\left\{g_1(\eta ;X_k){\widehat{\gamma }}^T{Z}_{ik}-E_k^1(\eta ;\widehat{\gamma },t)\right\}d{N}_{ik}(t).$$

Solving U₂ (η; γ̂) = 0, we can obtain the estimator η̂ for η.

3. Asymptotic Properties

Denote γ₀ and η₀ as the true values of the parameters γ and η, respectively. In this section, we emphasize the large sample results for η̂. We begin by restating a previously derived result. We list the assumed conditions, state a previously derived result, and then state the theorems for our estimators. Proofs are provided in the Appendix.

The following conditions are assumed throughout this article, where for all k = 1, …, K and some constant τ > 0:

1. (D_k, C_k, Z_k, X_k, n_k, W_k) are independent and identically distributed;

2. P {Y_ik (τ) = 1} > 0 for i = 1, …, n_k ;

3. |Z_ikl | < B_Z < ∞ and |X_kj | < B_X < ∞ for all l = 1, …, p and j = 1, …, q and some constants B_Z and B_X ;

4. g (·) is twice continuously differentiable with respect to η;

5. γ₀ and η₀ are interior to the parameter space.

6. The following matrices are positive definite,

   $$\begin{array}{lll}{A}_1\hfill & =\hfill & \epsilon \left\{{\int }_0^{\tau }V({\gamma }_0,t)S^{(0)}({\gamma }_0,t)d{H}_0(t)\right\},\hfill \\ A_2\hfill & =\hfill & \epsilon \left\{{\int }_0^{\tau }{V}_k^1({\eta }_0;{\gamma }_0,t)S_k^{(0)}({\eta }_0;{\gamma }_0,t)f_k(t)d{\mathrm{\Lambda }}_{0k}(t)\right\}.\hfill \end{array}$$

Large sample results for γ̂ have been provided by Lee et al. (1992), who showed that K^1/2 (γ̂ − γ₀) is asymptotically mean zero normal with variance ${\sum }_1=A_1^{-1}{B}_1{A}_1^{-1}$, where A₁ and B₁ can be consistently estimated by Â₁ = K⁻¹Î and ${\widehat{B}}_1=K^{-1}{{\sum }_{k=1}^K\widehat{\psi }}_k^{\otimes 2}$, with

$$\begin{array}{lll}\hfill \widehat{I}& =\hfill & {\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^{n_k}}{\int }_0^{\tau }V(\widehat{\gamma },t)d{N}_{ik}(t),\hfill \\ \hfill {\widehat{\psi }}_k& =\hfill & {\displaystyle \sum _{i=1}^{n_k}}{\int }_0^{\tau }\{Z_{ik}-E(\widehat{\gamma },t)\}\times \left\{d{N}_{ik}-Y_{ik}(t)e^{{\widehat{\gamma }}^T{Z}_{ik}}d{\widehat{H}}_0(t)\right\},\hfill \end{array}$$

where

$${\widehat{H}}_0(t)=\sum _{k=1}^K\sum _{i=1}^{n_k}{\int }_0^{t}d{N}_{ik}(u)/S^{(0)}(\widehat{\gamma },u).$$

Theorem 1

Under conditions (a)−(f), η̂ is unique and converges almost surely to η₀ as K → ∞.

The proof of the consistency of η̂ is similar to that of Prentice and Self (1983) and Lemma 3.1 in Andersen and Gill (1982).

Theorem 2

Under conditions (a)−(f), the random vector K^1/2 (η̂ − η₀) converges weakly to a (q + 1)-variate normal vector with mean 0 and covariance matrix

$${\sum }_2=A_2^{-1}\left(A_2+B_2{\sum }_1{B}_2^T-2C{B}_2^T\right)A_2^{-1},$$

where A₂ is defined in condition (f) and

$$\begin{array}{lll}\hfill B_2& =\hfill & \epsilon \left\{{\int }_0^{\tau }{V}_k^2({\eta }_0;{\gamma }_0,t)S_k^{(0)}({\eta }_0;{\gamma }_0,t)f_k(t)d{\mathrm{\Lambda }}_{0k}(t)\right\},\hfill \\ \hfill C& =\hfill & \epsilon \left\{u_k{\psi }_k^T\right\}{A}_1^{-1},\hfill \end{array}$$

with

$$\begin{array}{lll}\hfill u_k& =\hfill & {\displaystyle \sum _{i=1}^{n_k}}{\int }_0^{\tau }\left\{g_1({\eta }_0;X_k){\gamma }_0^T{Z}_{ik}-E_k^1({\eta }_0;{\gamma }_0,t)\right\}d{N}_{ik}(t),\hfill \\ \hfill {\psi }_k& =\hfill & {\displaystyle \sum _{i=1}^{n_k}}{\int }_0^{\tau }\{Z_{ik}-e({\gamma }_0,t)\}\left\{d{N}_{ik}-Y_{ik}(t)e^{{\gamma }_0^T{Z}_{ik}}d{H}_0(t)\right\},\hfill \end{array}$$

where

$$e(\gamma ,t)=\frac{\epsilon \{S^{(1)}(\gamma ,t)\}}{\epsilon \{S^{(0)}(\gamma ,t)\}}.$$

Using the proof of Theorems 1 and 2, together with the results from Lee et al. (1992), we can show that Σ₂ can be consistently estimated by

$${\widehat{\sum }}_2={\widehat{A}}_2^{-1}\left({\widehat{A}}_2+{\widehat{B}}_2{\widehat{\sum }}_1{\widehat{B}}_2^T-2\widehat{C}{\widehat{B}}_2^T\right){\widehat{A}}_2^{-1}$$

with

$$\begin{array}{lll}{\widehat{A}}_2\hfill & =\hfill & -K^{-1}\partial U_2(\eta ;\gamma )/\partial {\eta }^T{|}_{\eta =\widehat{\eta },\gamma =\widehat{\gamma }}\hfill \\ \hfill & =\hfill & K^{-1}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^{n_k}}{\int }_0^{\tau }\left\{V_k^1(\widehat{\eta };\widehat{\gamma },t)-g_2(\widehat{\eta };X_k){\widehat{\gamma }}^T{Z}_{ik}+E_k^3(\widehat{\eta };\widehat{\gamma },t)\right\}d{N}_{ik}(t),\hfill \\ {\widehat{B}}_2\hfill & =\hfill & -K^{-1}\partial U_2(\eta ;\gamma )/\partial {\gamma }^T{|}_{\eta =\widehat{\eta },\gamma =\widehat{\gamma }}\hfill \\ \hfill & =\hfill & K^{-1}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^{n_k}}{\int }_0^{\tau }\left\{V_k^2(\widehat{\eta };\widehat{\gamma },t)-g_1(\widehat{\eta };X_k)Z_{ik}^T-E_k^4(\widehat{\eta };\widehat{\gamma },t)\right\}d{N}_{ik}(t),\hfill \\ \widehat{C}\hfill & =\hfill & K^{-1}{\displaystyle \sum _{k=1}^K}{\widehat{u}}_k{\widehat{\psi }}_k^T{\widehat{A}}_1^{-1},\hfill \end{array}$$

where

$${\widehat{u}}_k=\sum _{i=1}^{n_k}{\int }_0^{\tau }\left\{g_1(\widehat{\eta };X_k){\widehat{\gamma }}^T{Z}_{ik}-E_k^1(\widehat{\eta };\widehat{\gamma },t)\right\}d{N}_{ik}(t).$$

4. Numerical Studies

Simulation studies were conducted to assess the finite sample behavior of η̂. We also compare our method to that of Fine et al. (2003) under the special case where α_k is common among clusters.

In the first simulation study, clustered failure time data were simulated from models (3) and (4) with K = 50, 100; H₀ (t) = t; γ = (0.5, 1)^T; η₁ = −0.5, −0.25, 0, 0.25, 0.5; and η₂ = 0.5. Cluster sizes were simulated from a discrete uniform distribution in the following four intervals [5, 20], [21, 50], [51, 100], and [101, 200] with approximately equal number of clusters in each interval. The cluster-level covariate X_k was the cluster size measured in units of 100 subjects. The positive stable frailties, W_k, were simulated following the method in Chambers, Mallows, and Stuck (1976),

$$W_k=\frac{sin({\alpha }_k{W}_{1k})}{sin{(W_{1k})}^{1/{\alpha }_k}}{\left[\frac{sin\{(1-{\alpha }_k)W_{1k}\}}{W_{2k}}\right]}^{(1-{\alpha }_k)/{\alpha }_k},$$

where W_1k and W_2k are independent, with W_1k following a uniform distribution U (0, π) and W_2k following an exponential distribution with mean 1. The individual-level covariate Z_ik = (Z_ik1, Z_ik2)^T was independently generated, with Z_ik1 from a Bernoulli distribution with p = 0.5 and Z_ik2 from N (0, 1) distribution. The censoring times were simulated from the uniform distribution, U (0.25, 1), yielding censoring probabilities of approximately 46%. For each scenario, 1000 replicates were carried out.

The results are summarized in Table 1. We report bias of the sampling mean of the estimators (BIAS), the mean of the standard error estimators (ASE), empirical standard deviation of the estimators (ESD), and the 95% empirical coverage probability (CP). In the last column, we present the approximate range of α_k for the simulated data. We also present the results for γ̂. We can see that the estimator η̂ is nearly unbiased. The (ASE) is generally fairly close to the ESD and, correspondingly, 95% empirical coverage probabilities are generally close to the nominal values. As the number of clusters increases from K = 50 to K = 100, the coverage probability is generally closer to the nominal value. In addition, as the value of α_k decreases, the coverage probability becomes lower. This may partly be due to the fact that, for a fixed sample size, the amount of independent information decreases as α_k decreases; that is, smaller value of α_k corresponds to stronger association within clusters.

Table 1. Summary of results for the first simulation study with η₂ = 0.5, γ₁ = 0.5, and γ₂ = 1 based on 1000 replicates.

	η̂						γ̂
K	Parameter	True	BIAS	ASE	ESD	CP	Parameter	BIAS	ASE	ESD	CP	Range of αk
50	η1	0.5	0.01	0.27	0.27	0.96	γ1	0.01	0.06	0.06	0.92	0.63–0.82
	η2		0.03	0.22	0.23	0.94	γ2	0.00	0.08	0.08	0.90
	η1	0.25	0.02	0.24	0.24	0.96	γ1	0.01	0.06	0.06	0.91	0.57–0.78
	η2		0.01	0.18	0.19	0.94	γ2	0.00	0.08	0.09	0.90
	η1	0	0.03	0.22	0.23	0.94	γ1	0.01	0.06	0.07	0.92	0.51–0.73
	η2		0.00	0.15	0.16	0.93	γ2	0.00	0.09	0.10	0.91
	η1	−0.25	0.04	0.21	0.22	0.93	γ1	0.01	0.07	0.07	0.91	0.44–0.68
	η2		−0.01	0.12	0.13	0.92	γ2	0.00	0.10	0.11	0.91
	η1	−0.5	0.07	0.20	0.22	0.91	γ1	0.01	0.07	0.07	0.92	0.38–0.62
	η2		−0.04	0.10	0.12	0.87	γ2	0.01	0.11	0.11	0.91
100	η1	0.5	0.01	0.20	0.19	0.95	γ1	0.01	0.04	0.04	0.94	0.63–0.82
	η2		0.02	0.15	0.15	0.95	γ2	0.00	0.06	0.06	0.92
	η1	0.25	0.02	0.17	0.18	0.95	γ1	0.01	0.05	0.05	0.93	0.57–0.78
	η2		0.00	0.13	0.12	0.95	γ2	0.00	0.06	0.06	0.93
	η1	0	0.02	0.16	0.16	0.93	γ1	0.01	0.05	0.05	0.93	0.51–0.73
	η2		0.00	0.10	0.10	0.94	γ2	0.00	0.07	0.07	0.93
	η1	−0.25	0.03	0.15	0.16	0.93	γ1	0.01	0.05	0.05	0.93	0.44–0.68
	η2		−0.02	0.09	0.09	0.92	γ2	0.00	0.07	0.07	0.94
	η1	−0.5	0.04	0.14	0.15	0.91	γ1	0.01	0.05	0.05	0.94	0.38–0.62
	η2		−0.03	0.07	0.08	0.87	γ2	0.00	0.08	0.08	0.93

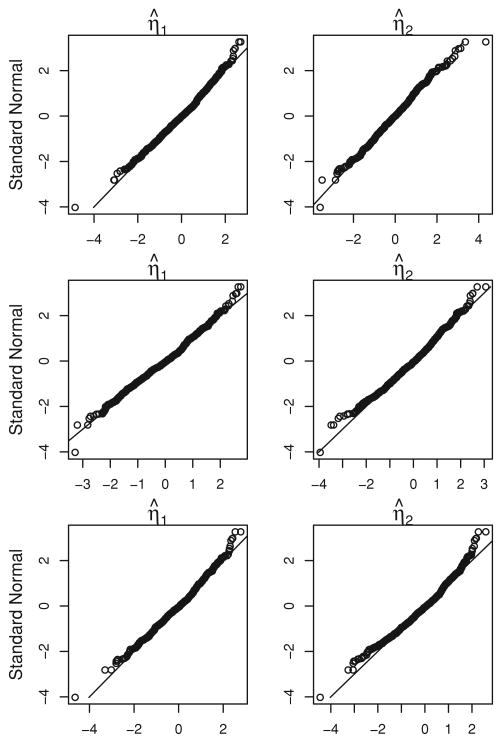
To assess the asymptotic normality of the regression parameter estimates, we study the quantile-quantile (Q-Q) plots of η̂ after being standardized against standard normal variable. In Figure 1, we show the Q-Q plots of η̂₁ and η̂₂ when K = 100 and η₁ = −0.5, 0, and 0.5. All six plots exhibit diagonal lines, which suggests that the asymptotic normal approximation is reasonable.

Figure 1.

Q-Q plots for η̂₁ and η̂₂ when K = 100 and η₁ = −0.5, 0, and 0.5.

In the second simulation study, we compare the proposed method (LKS) with Fine et al. (2003) (FGL) when α_k is fixed for all clusters. We keep the same setting for H₀, γ, and K. The individual-level covariates and the censoring variable follow the same distribution as the first study. We fix α_k = 0.5 or α_k = 0.75 for all clusters. When using our method, we let η₂ = 0 and estimate η₁ only. For the FGL method, α is estimated by averaging the truncated ratio of the marginal and conditional regression parameter estimators. The results are displayed in Table 2, In order to facilitate the comparison, we show the results for α̂ rather than η̂.

Table 2. Summary of results for the second simulation study comparing the proposed method (LKS) with FGL (see Fine et al., 2003) in the special case of constant α_k = α, k = 1, …, K with γ₁ = 0.5, γ₂ = 1, and 1000 replicates.

			LKS				FGL
K	Parameter	True	BIAS	ASE	ESD	CP	BIAS	ASE	ESD	CP
50	α	0.5	0.01	0.06	0.06	0.92	0.01	0.06	0.06	0.91
	γ1		0.01	0.07	0.08	0.92
	γ2		0.01	0.11	0.12	0.91
	α	0.75	0.01	0.06	0.06	0.91	0.01	0.06	0.06	0.87
	γ1		0.02	0.06	0.06	0.91
	γ2		0.01	0.08	0.09	0.88
100	α	0.5	0.00	0.04	0.04	0.94	0.00	0.04	0.05	0.94
	γ1		0.01	0.05	0.05	0.94
	γ2		0.00	0.08	0.09	0.94
	α	0.75	0.00	0.05	0.05	0.93	0.00	0.04	0.05	0.90
	γ1		0.01	0.04	0.04	0.94
	γ2		0.00	0.06	0.06	0.92

Both methods give an almost unbiased estimator for α, and the estimated standard error and coverage probability are reasonable. Similar to the results in Table 1, when the number of clusters increases from 50 to 100, the asymptotic standard errors of the estimators decrease and the coverage probability tends to be closer to the nominal value. The asymptotic standard error estimators from the two methods are very close. The LKS method gives somewhat better coverage probability than FGL.

Simulations have been done under covariate-dependent frailty and common frailty settings. Since there is no existing method to compare with under the covariate-dependent frailty setting, we only make comparison under the common frailty setting. For this, three methods are available. Both the traditional EM method (Wang et al., 1995) and the Martinussen and Pipper (2005) method (MP) involve estimation of the frailties as missing data, which is computationally very slow when large number of deaths are observed for some clusters and does not yield standard error easily. On the other hand, FGL does not involve the estimation of the frailties as is the case with the LKS method. Since our primary application of interest has clusters with large number of observed deaths, we have compared our method to FGL only.

5. Application

We applied the proposed methods to data on deceased donor kidney transplants performed between 2000 and 2004 in the United States. Data were obtained from the SRTR. Failure time (recorded in days) was defined as the time from transplantation to graft failure, retransplantation, or death, whichever occurred first. There were 224 facilities and a total of 23,027 transplants included in the study. The facility size varied from 1 to 708. We fitted the proposed covariate-dependent frailty model to the data with the logit link function for the dependence parameter α_k. A total of 12 patient-level covariates and four cluster-level covariates are considered in the proportional hazards model. The same cluster-level covariates are included in the link function for α_k. Patient-level covariates included age at transplantation (by decade), race (African-American, Other), gender, time on dialysis (2 dummy variables), body mass index (BMI; 3 dummy variables) and primary cause of renal disease (4 dummy variables). Cluster-level covariates included percentage of female patients, percentage of African-American patients, percentage of patients caused by diabetes, and center size (per 100 patients) in a center.

We expect that any covariate that is associated with the between-cluster variability may also be related to within-cluster variation. Moreover, it is easier to interpret a covariate's effect on the frailty variance after adjusting for its effect on the hazard function itself. Therefore, as a modeling strategy, covariates included in the logit link function should also be represented in the marginal hazards model. Naturally, such cluster-level covariates will not be used in the second stage of the estimation procedures, due to the stratification.

Results of our analysis are shown in Table 3. Percentage of female patients has a significant effect (p = 0.0063) on the frailty parameter. It is found that facilities with fewer female patients tend to have a smaller value of α_k, which corresponds to greater heterogeneity in facility performance. The percentage of female patients also influences the hazards significantly. Upon examining the point estimates, one could interpret these results as being in the same direction, as higher percent female implies lower graft failure hazard and lower variation; both desirable outcomes.

Table 3. Analysis of SRTR kidney transplant data.

Covariates	Estimates	SE	p-value
γ (Patient Level)
Age (in decades)	0.1541	0.0104	<.0001
African-American	0.2738	0.0293	<.0001
Female	−0.0957	0.0254	0.0002
Time on Dialysis (in years)
≤1	−0.1379	0.0372	0.0002
>3	0.1153	0.0277	<.0001
Recipient BMI
<20	0.0732	0.0502	0.1450
[25, 30)	0.0391	0.0298	0.1904
≥30	0.1369	0.0320	<.0001
Cause of ESRD
Diabetes	0.2970	0.0359	<.0001
Hypertension	0.1646	0.0375	<.0001
Polycystic	−0.3106	0.0571	<.0001
Other	0.1156	0.0392	0.0032
γ (Cluster level)
Percent of female (pct)	−0.0063	0.0022	0.0035
Percent of African-American (pct)	0.0039	0.0007	<.0001
Percent of diabetes (pct)	0.0084	0.0017	<.0001
Center size (in 100 patients)	0.0097	0.0068	0.1548
η
Intercept	−2.3192	2.0945	0.2682
Percent of female (pct)	0.1046	0.0382	0.0063
Percent of African-American (pct)	0.0389	0.0325	0.2316
Percent of diabetes (pct)	0.0298	0.0531	0.5745
Center size (in 100 patients)	−0.2288	0.2705	0.3977

6. Discussion

Covariate-dependent frailty models for clustered failure time data have rarely been studied previously. Wassell and Moeschberger (1993) proposed a bivariate survival model with the gamma frailty parameter depending on a pairwise covariate. Their approach only considered paired survival times in each cluster and cannot be applied to studies with larger cluster sizes. Wassell, Kulczycki, and Moyer (1995) also pointed out the increasing complexity of the application of a frailty model to clustered failure time data with larger group sizes. The model proposed in this article enables one to adjust for covariate effects on the frailty distribution and permits both marginal and conditional inference for clustered failure time data regardless of the group size. Further consideration of the proposed method reveals two additional advantages. First, model (5), on which we make inference, allows for covariate-by-cluster interaction. The covariate effect is multiplicatively influenced by clusters through the cluster-level covariate-dependent frailty parameter α_k. Second, with the rapid development of various methods for frailty models, researchers have begun to consider more carefully issues of ease of implementation and computation time (e.g., Fine et al., 2003; Liu and Huang, 2007). The proposed method performs well in both aspects. The method can be implemented using SAS IML. When we evaluated the computation time in the simulation study, it took approximately 4 hours for 1000 runs, with approximately one-third of the time spent on the PROC PHREG call.

Recalling that ${\mathrm{\Lambda }}_{0k}(t)=H_0{(t)}^{{\alpha }_k^{-1}}$, we can estimate Λ_0k with Ĥ₀(t)^g(η̂;X_k), k = 1, …, K, where the estimator Ĥ₀ (t) of H₀ (t) can be estimated from model (2) (see Spiekerman and Lin, 1998). Since the joint distribution of Ĥ₀ (t) and η̂ is complicated, we have not been able to obtain the asymptotic distribution of the Λ_0k's.

We noted that when a cluster-level covariate is included in the conditional proportional hazard model, its effect is nearly nonidentifiable and does not interfere with the estimation of other covariate effects. This is due to the use of the stratified partial likelihood approach in the estimation. Since the motivation of the proposed method is to model cluster-level covariate effects on between-cluster heterogeneity and within-cluster association, the inclusion of a cluster-level covariate in the conditional hazard is not needed. On the other hand, one is able to obtain the marginal effect of a cluster-level covariate due to the proportional hazard in the marginal model.

For ease of computation and to avoid the estimation of the f_k (t) (which is difficult for studies with large clusters), we first attempted using a stratified partial likelihood approach based on model (5) only. We found that this approach does not lead to useful estimators for the parameter η₁. As an alternative, we estimate γ from model (2), then use the estimator γ̂ in model (5) to obtain a consistent estimator for η. The proposed estimation procedure is actually a two-step procedure. Such approach has been employed previously in the context of maximum likelihood by, for example, Gong and Samaniego (1981) and for the Clayton-Oakes model with a proportional hazards model for the margins by Glidden (2000). It should be noted that some efficiency is lost under the stratified partial likelihood approach in the second stage, as exemplified by the fact that the same estimation would be obtained if we let f_k (t) = 1.

Several areas of future research are possible. The proposed method relies on the specification of a link function, and model checking on this function is of potential interest. Future research on this method may also include the extension to other frailty distributions.

Appendix.

Proof of Theorem 1

The individual counting process martingale for the observed filtration is

$$M_{ik}(t)=N_{ik}(t)-{\int }_0^t{Y}_{ik}(s)f_k(s)e^{g({\eta }_0;X_k){\gamma }_0^T{Z}_{ik}}d{\mathrm{\Lambda }}_{0k}(s).$$

The proof of the consistency of η̂ considers the following two processes,

$$\begin{array}{lll}G(\eta ,\widehat{\gamma })\hfill & =\hfill & K^{-1}\{l_2(\eta ,\widehat{\gamma },t)-l_2({\eta }_0,{\gamma }_0,t)\}\hfill \\ \hfill & =\hfill & K^{-1}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^{n_k}}{\int }_0^{\tau }\left[\left\{g(\eta ;X_k){\widehat{\gamma }}^T-g({\eta }_0;X_k){\gamma }_0^T\right\}{Z}_{ik}-log\frac{S_k^{(0)}(\eta ,\widehat{\gamma },t)}{S_k^{(0)}({\eta }_0,{\gamma }_0,t)}\right]d{N}_{ik}(t),\hfill \end{array}$$

and

$$\mathrm{\Xi }(\eta )=K^{-1}\sum _{k=1}^K\sum _{i=1}^{n_k}{\int }_0^{\tau }\left[\left\{g(\eta ;X_k){\gamma }_0^T-g({\eta }_0;X_k){\gamma }_0^T\right\}{Z}_{ik}-log\frac{S_k^{(0)}(\eta ,{\gamma }_0,t)}{S_k^{(0)}({\eta }_0,{\gamma }_0,t)}\right]Y_{ik}(t)f_k(t)e^{g({\eta }_0;X_k){\gamma }_0^T{Z}_{ik}}d{\mathrm{\Lambda }}_{0k}(t).$$

The difference between them can be decomposed into two parts,

$$\begin{array}{lll}G(\eta ,\widehat{\gamma })-\mathrm{\Xi }(\eta )\hfill & =\hfill & \{G(\eta ,\widehat{\gamma })-G(\eta ,{\gamma }_0)\}+\{G(\eta ,{\gamma }_0)-\mathrm{\Xi }(\eta )\}\hfill \\ \hfill & =\hfill & K^{-1}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^{n_k}}{\int }_0^{\tau }\left\{g(\eta ;X_k)Z_{ik}(\widehat{\gamma }-{\gamma }_0)-log\frac{S_k^{(0)}(\eta ,\widehat{\gamma },t)}{S_k^{(0)}(\eta ,{\gamma }_0,t)}\right\}d{N}_{ik}(t)+K^{-1}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^{n_k}}{\int }_0^{\tau }\left[\{g(\eta ;X_k)-g({\eta }_0;X_k)\}\times {\gamma }_0^T{Z}_{ik}-log\frac{S_k^{(0)}(\eta ,{\gamma }_0,t)}{S_k^{(0)}({\eta }_0,{\gamma }_0,t)}\right]d{M}_{ik}(t).\hfill \end{array}$$

For each η, the first term on the right-hand side of the equation converges almost surely to zero due to the consistency of γ̂ and under conditions (a) to (f), the second term is a summation of K independent and identical distributed zero mean random variables. By the Strong Law of Large Numbers (SLLN), as K → ∞, G (η, γ̂) converges almost surely to the same limiting function of η as Ξ(η).

By the conditions (d) to (f), we can evaluate the first and the second derivatives of this limiting function by taking the partial derivatives inside the integral of Ξ(η). The first derivative is thus

$$\epsilon \left[\sum _{i=1}^{n_k}{\int }_0^{\tau }\left\{g_1(\eta ;X_k){\gamma }_0^T{Z}_{ik}-E_k^1(\eta ;{\gamma }_0,t)\right\}{Y}_{ik}(t)f_k(t)\times e^{g({\eta }_0;X_k){\gamma }_0^T{Z}_{ik}}d{\mathrm{\Lambda }}_{0k}(t)\right].$$

It is 0 at η = η₀. The second derivative

$$\epsilon \left[-\sum _{i=1}^{n_k}{\int }_0^{\tau }{V}_k^1(\eta ;{\gamma }_0,t)S_k^{(0)}(\eta ;{\gamma }_0,t)f_k(t)d{\mathrm{\Lambda }}_{0k}(t)\right]$$

is minus a positive definite matrix at η = η₀ by condition (f). Therefore, G (η, γ̂) converges almost surely to a concave function of η with a unique maximum at η = η₀. Since η̂ maximizes G (η, γ̂), it follows that $\widehat{\eta }\stackrel{\mathit{\text{a.s.}}}{\to }{\eta }_0$ as K → ∞.

Proof of Theorem 2

The first-order Taylor series expansion of K^−1/2U₂ (η̂, γ̂) about η = η₀ and γ = γ₀ gives

$$K^{-1/2}{U}_2(\widehat{\eta };\widehat{\gamma })=K^{-1/2}{U}_2({\eta }_0;{\gamma }_0)-{\widehat{B}}_2({\eta }_0;{\gamma }^{\ast })K^{1/2}(\widehat{\gamma }-{\gamma }_0)-{\widehat{A}}_2({\eta }^{\ast };\widehat{\gamma })K^{1/2}(\widehat{\eta }-{\eta }_0),$$

where η* is on the line segment between η̂ and η₀ and γ* is on the line segment between γ̂ and γ₀. Thus, we have

$$K^{1/2}(\widehat{\eta }-{\eta }_0)={\widehat{A}}_2^{-1}({\eta }^{\ast };\widehat{\gamma })\left\{K^{-1/2}{U}_2({\eta }_0;{\gamma }_0)-{\widehat{B}}_2({\eta }_0;{\gamma }^{\ast })K^{1/2}(\widehat{\gamma }-{\gamma }_0)\right\}.$$

With the consistency of η̂ and γ̂ and the SLLN, we can show that ${\widehat{A}}_2({\eta }^{\ast };\widehat{\gamma })\stackrel{p}{\to }{A}_2$, and ${\widehat{B}}_2({\eta }_0;{\gamma }^{\ast })\stackrel{p}{\to }{B}_2$ and that A₂ and B₂ can be consistently estimated by Â₂ and B̂₂, respectively.

It has been noted in Section 3 that K^1/2 (γ̂ − γ₀) converges in distribution to N (0, Σ₁). We will prove that K^−1/2U₂ (η₀; γ₀) converges in distribution to N (0, A₂). It can be easily seen that the process K^−1/2U₂ (η₀; γ₀, t) can be written as a sum of orthogonal martingales,

$$K^{-1/2}{U}_2({\eta }_0;{\gamma }_0,t)=K^{-1/2}\sum _{k=1}^K\sum _{i=1}^{n_k}{\int }_0^t\left\{g_1({\eta }_0;X_k){\gamma }_0^T{Z}_{ik}-E_k^1({\eta }_0;{\gamma }_0,s)\right\}d{M}_{ik}(s),$$

with predictable variation process

$$\begin{array}{lll}\langle K^{-1/2}{U}_2({\eta }_0;{\gamma }_0)\rangle (t)\hfill & =\hfill & K^{-1}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^{n_k}}{\int }_0^t{\left\{g_1({\eta }_0;X_k){\gamma }_0^T{Z}_{ik}-E_k^1({\eta }_0;{\gamma }_0,s)\right\}}^{\otimes 2}\times Y_{ik}(s)f_k(s)e^{g({\eta }_0;X_k){\gamma }_0^T{Z}_{ik}(s)}d{\mathrm{\Lambda }}_{0k}(s)\hfill \\ \hfill & =\hfill & K^{-1}{\displaystyle \sum _{k=1}^K}{\int }_0^t{V}_k^1({\eta }_0;{\gamma }_0,s)S_k^{(0)}({\eta }_0;{\gamma }_0,s)f_k(s)d{\mathrm{\Lambda }}_{0k}(s).\hfill \end{array}$$

From Rebolledo's Theorem, the Weak Law of Large Numbers (WLLN) and condition (f), we can easily show that K^−1/2U₂ (η₀; γ₀, τ) converges in distribution to a zero mean Gaussian vector with covariance matrix

$$\underset{K=\infty }{lim}\langle K^{-1/2}{U}_2({\eta }_0;{\gamma }_0)\rangle (\tau )=A_2.$$

Finally, we need to obtain the asymptotic covariance matrix of K^−1/2U₂ (η₀; γ₀) and K^1/2 (γ̂ − γ₀). We can see that both items can be written as a summation of K i.i.d. zero mean random vectors,

$$\begin{array}{lll}\hfill K^{-1/2}{U}_2({\eta }_0;{\gamma }_0)& =\hfill & K^{-1/2}{\displaystyle \sum _{k=1}^K}{u}_k,\hfill \\ \hfill K^{1/2}(\widehat{\gamma }-{\gamma }_0)& =\hfill & K^{-1/2}{\widehat{A}}_1{({\gamma }^{\ast })}^{-1}{\displaystyle \sum _{k=1}^K}{\psi }_k+o_p(1),\hfill \end{array}$$

with

$$u_k({\eta }_0;{\gamma }_0)=\sum _{i=1}^{n_k}{\int }_0^{\tau }\left\{g_1({\eta }_0;X_k){\gamma }_0^T{Z}_{ik}-E_k^1({\eta }_0;{\gamma }_0,t)\right\}d{N}_{ik}(t),$$

and

$${\psi }_k({\gamma }_0,H_0)=\sum _{i=1}^{n_k}{\int }_0^{\tau }\{Z_{ik}-e({\gamma }_0,t)\}\times \left\{d{N}_{ik}-Y_{ik}(t)e^{{\gamma }_0^T{Z}_{ik}}d{H}_0(t)\right\}.$$

With the consistency of γ̂ and the WLLN, the asymptotic covariance matrix of K^−1/2U₂ (η₀; γ₀) and K^1/2 (γ̂ − γ₀) is $C=\epsilon \left\{u_k{\psi }_k^T\right\}{A}_1^{-1}$.

In summary, K^1/2 (η̂ − η₀) converges in distribution to a N (0, Σ₂), where

$${\sum }_2=A_2^{-1}\left(A_2+B_2{\sum }_1{B}_2^T-2C{B}_2^T\right)A_2^{-1},$$

which can be consistently estimated by replacing each quantity with its corresponding estimator.