Abstract
Regulation of cell growth and cell division plays fundamental roles in tissue morphogenesis. However, the mechanisms of regulating tissue elongation through cell growth and cell division are still not well understood. The wing imaginal disc of Drosophila provides a model system that has been widely used to study tissue morphogenesis. Here we use a recently developed two-dimensional cellular model to study the mechanisms of regulating tissue elongation in Drosophila wing. We simulate the effects of directional cues on tissue elongation. We also computationally analyze the role of reduced cell size. Our simulation results indicate that oriented cell divisions, oriented mechanical forces, and reduced cell size can all mediate tissue elongation, but they function differently. We show that oriented cell divisions and oriented mechanical forces act as directional cues during tissue elongation. Between these two directional cues, oriented mechanical forces have a stronger influence than oriented cell divisions. In addition, we raise the novel hypothesis that reduced cell size may significantly promote tissue elongation. We find that reduced cell size alone cannot drive tissue elongation. However, when combined with directional cues, such as oriented cell divisions or oriented mechanical forces, reduced cell size can significantly enhance tissue elongation in Drosophila wing. Furthermore, our simulation results suggest that reduced cell size has a short-term effect on cell topology by decreasing the frequency of hexagonal cells, which is consistent with experimental observations. Our simulation results suggest that cell divisions without cell growth play essential roles in tissue elongation.
Introduction
Regulation of cell growth and cell division plays fundamental roles in tissue morphogenesis [1]–[4]. Studies based on model systems such as epithelial cells can help to elucidate mechanisms of controlling tissue formation, organ development, and cancer progression [5]–[8]. Drosophila wing imaginal disc, an epithelial sheet of about 50,000 cells that originated from 30 cells within the anlage [9]–[11], is a commonly used model system for studying tissue morphogenesis [12]–[16]. During development, cells in the wing imaginal disc proliferate, forming an elongated tissue shape along its proximal-distal (PD) axis [3], [17], [18]. Although the molecular mechanisms of regulating tissue elongation in Drosophila wing have been the subject of extensive studies [19]–[23], the cellular mechanism that dictates this tissue structure is not yet fully understood.
One determinant of tissue elongation is the orientation of cell divisions. Oriented cell divisions can regulate tissue growth along a specific direction in a variety of tissues [2], [3], [17], [18]. A number of molecular players affecting the orientation of cell divisions have been identified. Dachs is a molecule known to mediate the orientation of cell divisions in the developing Drosophila wing [18]. When dachs is mutated (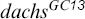 ), the orientation of mitotic spindles is disrupted, and the division plane is altered, resulting in an adult wing with reduced length along the PD-axis [18]. Theoretical studies suggest that Dachs may indirectly orient the mitotic spindle as a result of the elongated cell shape due to the polarized apical cell junctions [18]. In addition to Dachs, microtubules are another class of molecules that influence the orientation of mitotic spindles during cell divisions [24]–[27]. Microtubules in the cells in Drosophila wing align with the PD-axis [28]–[31]. Dachsous (Ds), an atypical cadherin, has also been shown in mutant studies to regulate microtubule organization, as microtubules are less aligned with the PD-axis in ds mutants [31]. The orientation of cell divisions is also less focused along the PD-axis in ds mutants than in wild-type [17].
), the orientation of mitotic spindles is disrupted, and the division plane is altered, resulting in an adult wing with reduced length along the PD-axis [18]. Theoretical studies suggest that Dachs may indirectly orient the mitotic spindle as a result of the elongated cell shape due to the polarized apical cell junctions [18]. In addition to Dachs, microtubules are another class of molecules that influence the orientation of mitotic spindles during cell divisions [24]–[27]. Microtubules in the cells in Drosophila wing align with the PD-axis [28]–[31]. Dachsous (Ds), an atypical cadherin, has also been shown in mutant studies to regulate microtubule organization, as microtubules are less aligned with the PD-axis in ds mutants [31]. The orientation of cell divisions is also less focused along the PD-axis in ds mutants than in wild-type [17].
Oriented mechanical forces are another determinant of tissue elongation in both plants and animals [4], [32], [33]. A contractile force is exerted by Dachs on apical cell junctions at the distal end of each cell and the proximal end of its neighbor [18]. Cell-cell junctions experience more tension along the PD-axis than in the other directions [18]. In addition, external forces generated by the contraction of the wing hinge are sufficient to induce tissue elongation [17]. The theoretical study further suggests that shear forces are sufficient to drive the PD-axis elongation [17].
Cell size reduction may also contribute to tissue elongation. Between 15 and 24 hour after puparium formation, cells in Drosophila wing have reduced cell size after one or two rounds of oriented cell divisions during pupal development. While the wing-blade area remains constant, the shape of the wing becomes elongated along the PD-axis and narrowed along the AP-axis [17].
Although prior studies have demonstrated the sufficiency of either oriented cell divisions or oriented mechanical forces in driving tissue elongation independently [3], [17], [18], less is known about their quantitative effects and their relative contributions. Given the now well established facts that cell proliferation does not equal cell growth, and increased cell proliferation can result in reduced cell size [34], [35], how cell size reduction affects tissue elongation is largely unknown. In addition, understanding how these factors are integrated and collectively determine tissue elongation remains a challenging problem.
Here we use a recently developed two-dimensional cellular model to study the mechanisms of regulating tissue elongation in Drosophila wing [36]–[38]. We examine the effects of oriented cell divisions, oriented mechanical forces, as well as reduced cell size on tissue elongation. Our simulation results show that oriented cell divisions and oriented mechanical forces act as directional cues during tissue elongation. Between these two directional cues, oriented mechanical forces have a stronger influence. Our simulation results also reveal a novel mechanism of reduced cell size in promoting tissue elongation. We find that reduced cell size alone cannot drive tissue elongation, as it does not have directional information. However, when combined with directional cues such as that from oriented cell divisions or oriented mechanical forces, reduced cell size can greatly enhance tissue elongation in Drosophila wing. Furthermore, our simulation results show that reduced cell size has a short term effect on cell topology. We hypothesize that cell divisions without cell growth play essential roles during tissue elongation in Drosophila wing.
Methods
Geometry and Mechanics of Cellular Model
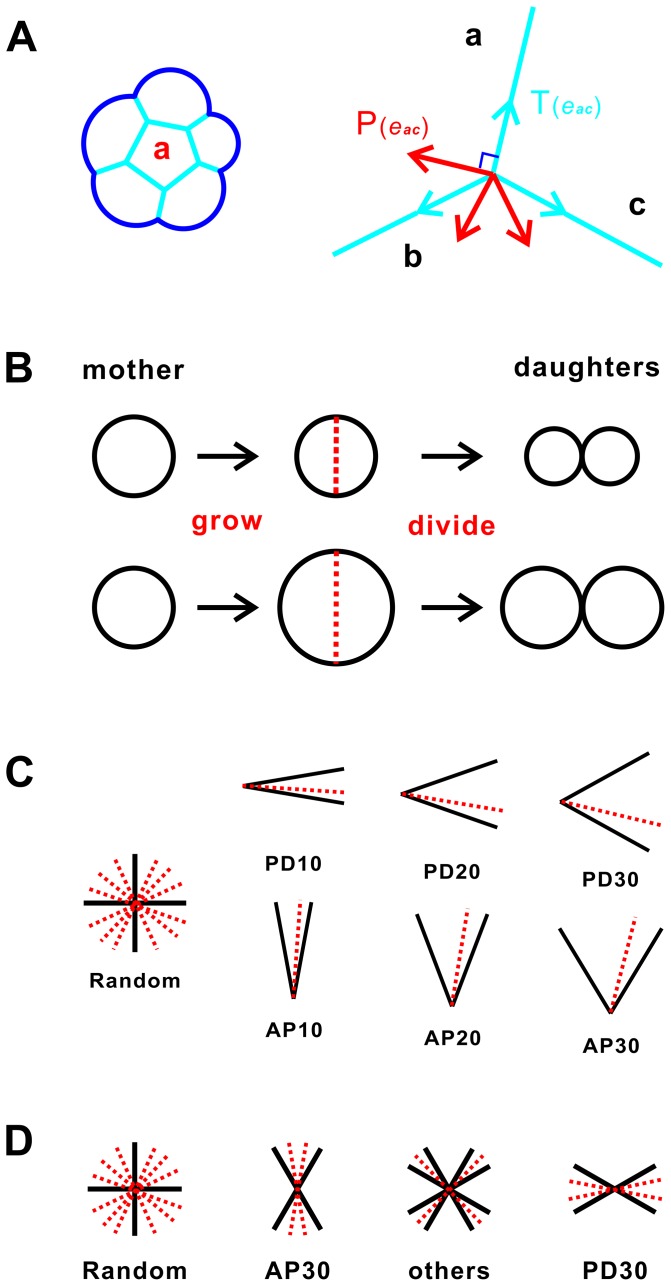
We use a recently developed cellular model [38] to study the mechanisms of regulating tissue elongation in Drosophila wing. This model captures both geometric properties of cells, including area, length, and internal angles (Fig. 1A), and key cellular mechanical forces.
Figure 1. Simulation methodology of cellular model.
(A) Left, cells are presented by geometric elements of cell, edge, and vertex. Right, mechanical forces are modeled as tension (blue) and pressure (red). (B) Growth model of reduced cell size (RCS) and non-RCS. In the RCS model, cells proliferate but do not grow. In the non-RCS model, cells grow and proliferate. (C) Division model of oriented cell divisions (OCD) and non-OCD. In the OCD model, the division plane is chosen from uniform distributions of angles in [−10°, 10°], [−20°, 20°], and [−30°, 30°], with respect to the PD-axis and the AP-axis, respectively. (D) Models for oriented mechanical forces (OMF) and non-OMF. In OMF models, tension coefficient η is set to 0.75, 1.0, and 1.5, when a cell edge is within [0°, 30°] (PD30), [30°, 60°] (others), and [60°, 90°] (AP30) with respect to the PD-axis, respectively.
We provide a brief summary of the cellular model below (details can be found in [38]). An epithelial cell is represented by an  -sided polygon when surrounded by
-sided polygon when surrounded by  neighboring cells, and has circular free boundaries when not in contact with other cells [36]–[38]. The mechanical forces in a cell are represented as tension and pressure (Fig. 1A): Tension represents compression forces acting on a cell. It originates from cytoskeletal microfilaments [39]–[41], intermediate filaments [42], and cell membrane [43]. In addition, there exists adhesion [44]–[46] or alternatively repulsion force [47] between cells. These forces can be summed up and modeled as a tension force that exerts along the direction
neighboring cells, and has circular free boundaries when not in contact with other cells [36]–[38]. The mechanical forces in a cell are represented as tension and pressure (Fig. 1A): Tension represents compression forces acting on a cell. It originates from cytoskeletal microfilaments [39]–[41], intermediate filaments [42], and cell membrane [43]. In addition, there exists adhesion [44]–[46] or alternatively repulsion force [47] between cells. These forces can be summed up and modeled as a tension force that exerts along the direction 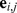 of an inner edge (interior cell boundary represented as a straight line segment), or along the tangent direction of an outer edge
of an inner edge (interior cell boundary represented as a straight line segment), or along the tangent direction of an outer edge
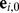 (free cell boundary represented as an arc or a circle). Pressure represents the expansion forces. It arises mostly from microtubules [40], [41], [48], [49] and extracellular matrix [43], [50].
(free cell boundary represented as an arc or a circle). Pressure represents the expansion forces. It arises mostly from microtubules [40], [41], [48], [49] and extracellular matrix [43], [50].
For an edge 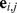 , which can be either an inner edge or an outer edge, the tension force is always tangential to the edge
, which can be either an inner edge or an outer edge, the tension force is always tangential to the edge 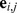 :
:
where 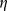 is the tension coefficient, which may depend on the cell types, and
is the tension coefficient, which may depend on the cell types, and 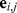 is the unit vector in the direction of shortening
is the unit vector in the direction of shortening 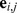 . When
. When 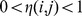 , there is a strong adhesion force. When
, there is a strong adhesion force. When 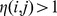 , the adhesion force is weak.
, the adhesion force is weak.
For an inner edge 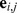 between cells
between cells  and
and 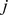 , the net pressure force is proportional to the difference in pressure in cell i and j. It is in the direction normal to the edge
, the net pressure force is proportional to the difference in pressure in cell i and j. It is in the direction normal to the edge 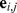 , from the cell with higher pressure to the cell with lower pressure. For an outer edge
, from the cell with higher pressure to the cell with lower pressure. For an outer edge 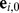 of cell
of cell  , the value of the pressure inside cell
, the value of the pressure inside cell  is determined by the curvature of the edge.
is determined by the curvature of the edge.
Model for Reduced Cell Size
We simulate the effect of reduced cell size (RCS) between 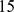 and
and 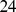 hour after puparium formation during pupal development following reference [17]. A previous study suggests that cell growth disturbs cell shapes in a random fashion such that the atypical myosin Dachs at times is unable to orient every cell to elongate and divide along the PD-axis [18]. To study this effect, we examine two different schemes of cell growth: non-RCS and RCS (Fig. 1B).
hour after puparium formation during pupal development following reference [17]. A previous study suggests that cell growth disturbs cell shapes in a random fashion such that the atypical myosin Dachs at times is unable to orient every cell to elongate and divide along the PD-axis [18]. To study this effect, we examine two different schemes of cell growth: non-RCS and RCS (Fig. 1B).
non-RCS
Cells grow during cell proliferation. When cells reach the predefined preferred cell size, they become mitotic cells. Each daughter cell after cell division inherits approximately half of the size of the mother cell. This scenario is a typical computational approximation to mimic normal growing cells, which is widely used in cellular models [17], [51]–[54].
RCS
Cells do not grow during cell proliferation. Individual cells are randomly chosen as mitotic cells. Each daughter cell inherits approximately half of the size of the mother cell. This scenario is used to model the effects of reduced cell size observed between 15 and 24 hour after puparium formation during pupal development [17].
Model for Cell Division Plane
We also simulate the effect of oriented cell divisions (OCD), which has been observed between 15 and 24 hour after puparium formation during pupal development [17]. We examine tissue elongation under different schemes of cell divisions (Fig. 1C).
non-OCD
The angle of the division plane is randomly chosen from a uniform distribution of all angles. This scheme models the scenario that the effect of the orientation of division plane is insignificant for tissue elongation.
OCD
The division plane is chosen from uniform distributions of angles in three different intervals of [−10°, 10°], [−20°, 20°], and [−30°, 30°], with respect to the PD-axis and the AP-axis, respectively. This scheme models the scenarios that division planes orient at specific angles and may influence tissue elongation.
Model for Oriented Mechanical Forces
To simulate the effect of the oriented mechanical forces (OMF) observed between 15 and 24 hour after puparium formation during pupal development [17], we examine different schemes of mechanical forces exerting on cell edges.
non-OMF
Mechanical forces on all edges are of the same magnitude. Tension coefficients 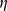 on all edges are set to 1.
on all edges are set to 1.
OMF
Mechanical forces are different according to the angles of cell edge. Tension coefficients 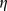 are set to 0.75, 1.0, and 1.5, respectively, when the angles of cell edge are distributed within the range of [0°, 30°] (PD30), [30°, 60°] (others), and [60°, 90°] (AP30) with respect to the PD-axis. This mimics the experimental observations that mechanical forces are doubled on cell boundaries lying at angles close to the AP-axis compared to those on cell boundaries lying at angles close to the PD-axis [18].
are set to 0.75, 1.0, and 1.5, respectively, when the angles of cell edge are distributed within the range of [0°, 30°] (PD30), [30°, 60°] (others), and [60°, 90°] (AP30) with respect to the PD-axis. This mimics the experimental observations that mechanical forces are doubled on cell boundaries lying at angles close to the AP-axis compared to those on cell boundaries lying at angles close to the PD-axis [18].
Quantification of Tissue Shape and Tissue Elongation
We approximate the PD-axis and AP-axis in Drosophila wing with the direction of  -axis and
-axis and 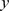 -axis, respectively. We define the tissue shape index
-axis, respectively. We define the tissue shape index
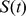 at time
at time  based on the lengths of the tissue along the PD-axis and the AP-axis:
based on the lengths of the tissue along the PD-axis and the AP-axis:
where 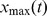 and
and 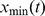 are the maximal and minimal coordinates of the tissue along the
are the maximal and minimal coordinates of the tissue along the  -axis (the PD-axis), respectively, and
-axis (the PD-axis), respectively, and 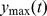 and
and  are the maximal and minimal coordinates of the tissue along the
are the maximal and minimal coordinates of the tissue along the 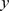 -axis (the AP-axis), respectively.
-axis (the AP-axis), respectively.
We define the tissue elongation index
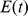 along the PD-axis at time
along the PD-axis at time  based on the ratio of tissue shape index
based on the ratio of tissue shape index 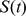 :
:
where 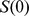 and
and 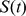 are the tissue shape indices at the beginning and at time
are the tissue shape indices at the beginning and at time  of the simulations, respectively.
of the simulations, respectively.
Simulation Methodology
Generating samples of initial tissue
Our initial condition is a single cell. Cells grow with time and divide until the tissue contains about 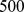 cells. Mitotic cells are chosen as cells whose volume exceed a threshold, and are divided into two daughter cells with approximately equal volume. When cells divide, the largest cell side is chosen for placement of the division plane. This division scheme can produce topological distributions of cells as observed in Drosophila wing [36], [38]. We repeat our simulations 30 times, each resulting in an initial random sample of about 500 cells. The resulting tissues of about 500 cells are isotropic and are not elongated.
cells. Mitotic cells are chosen as cells whose volume exceed a threshold, and are divided into two daughter cells with approximately equal volume. When cells divide, the largest cell side is chosen for placement of the division plane. This division scheme can produce topological distributions of cells as observed in Drosophila wing [36], [38]. We repeat our simulations 30 times, each resulting in an initial random sample of about 500 cells. The resulting tissues of about 500 cells are isotropic and are not elongated.
Tissue elongation
We found that tissue elongation index is independent of the shape of initial tissue samples (Figures S1, S2 in File S1). For clarity, we therefore discuss studies of tissue elongation using a tissue of about 500 cells obtained from the initial random sample simulation. We divide cells for  to
to  generations (as found in [17]), until the tissue reaches about
generations (as found in [17]), until the tissue reaches about 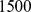 cells, which mimics the pupal development between
cells, which mimics the pupal development between 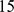 and
and 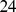 hour after puparium formation. Tissue elongation is simulated with combinations of different growth models, division models, and force models as described in Section 2.2–2.4. We examine the tissue elongation index
hour after puparium formation. Tissue elongation is simulated with combinations of different growth models, division models, and force models as described in Section 2.2–2.4. We examine the tissue elongation index 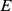 during development. For each combination of different model choices, we run simulations for
during development. For each combination of different model choices, we run simulations for 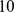 times and take the average as our results.
times and take the average as our results.
Our model is implemented in C++. Simulations were performed with 64-bit Linux cluster.
Results
Oriented Cell Divisions Drive Tissue Elongation to a Limited Extent
We first computationally studied the effect of oriented cell divisions (OCD) with our cellular model to mimic the pupal development between 15 and 24 hour after puparium formation in Drosophila wing, without considering the effects of reduced cell size and oriented mechanical forces. The orientation of division plane is chosen from three uniform distributions, with orientation angles with respect to the PD-axis and the AP-axis (e.g., PD10) in intervals of [−10°, 10°], [−20°, 20°], and [−30°, 30°], respectively. Results are compared with those obtained using random division choice.
We found that without oriented cell divisions, tissue elongation is absent throughout the simulation. The tissue elongation index 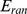 at the end of the simulation is
at the end of the simulation is 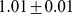 when random division is chosen (Fig. 2A), reflecting the fact that tissue shapes at the beginning and the end of the simulation are similar.
when random division is chosen (Fig. 2A), reflecting the fact that tissue shapes at the beginning and the end of the simulation are similar.
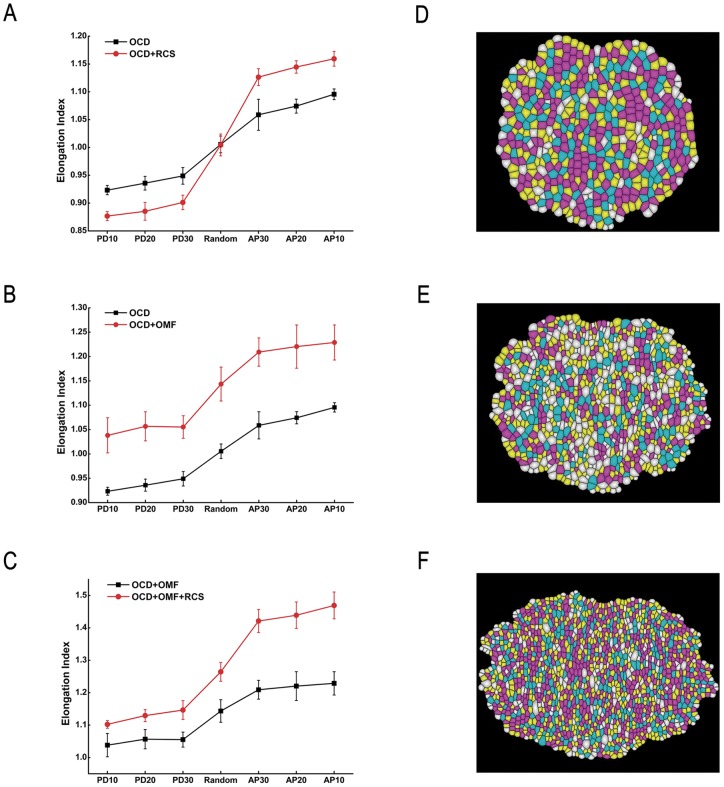
Figure 2. Simulation results of tissue elongation.
The elongation index is plotted against orientation angle for different cell models. (A) Oriented cell divisions drive tissue elongation, but only to a limited extent (black). Reduced cell size, when combined with oriented cell divisions, enhances tissue elongation (red). (B) Oriented mechanical forces produce significant tissue elongation along PD-axis. (C) Reduced cell size significantly enhances tissue elongation when both directional cues are present. (D–F) Morphology at the beginning, midpoint, and the end of the simulation with oriented cell division (AP10), oriented mechanical forces, and reduced cell size.
In contrast, with oriented cell divisions, we can generate elongated tissue shapes along different directions, although only to a modest extent. Specifically, if cells are divided along AP-axis, tissue will elongate along PD-axis (Fig. 3A). The tissue elongation index 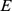 with division choices along AP-axis are
with division choices along AP-axis are 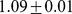 ,
, 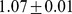 , and
, and 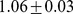 , when the orientation angles fall into the intervals of AP10, AP20, and AP30, respectively (Fig. 2A). Similarly, if cells divide along PD-axis, tissue will elongate along AP-axis, and will shorten along PD-axis (Fig. 3A). The tissue elongation index
, when the orientation angles fall into the intervals of AP10, AP20, and AP30, respectively (Fig. 2A). Similarly, if cells divide along PD-axis, tissue will elongate along AP-axis, and will shorten along PD-axis (Fig. 3A). The tissue elongation index 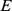 when divisions are along PD-axis with angles falling into the intervals of PD10, PD20, and PD30 are
when divisions are along PD-axis with angles falling into the intervals of PD10, PD20, and PD30 are 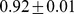 ,
, 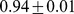 , and
, and 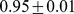 , respectively (Fig. 2A).
, respectively (Fig. 2A).
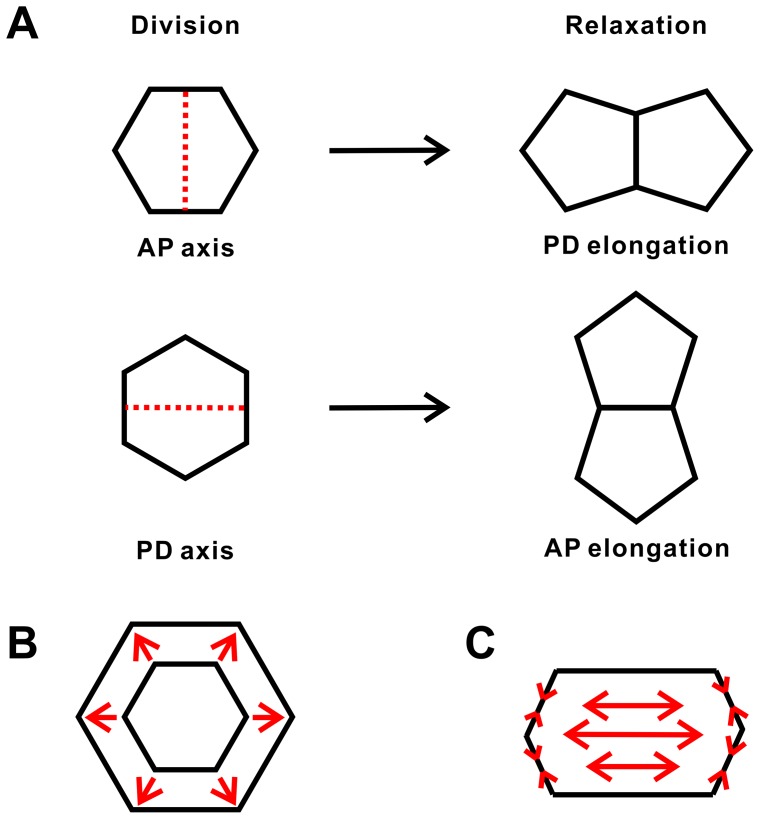
Figure 3. Physical illustrations of different simulation choices.
(A) AP-axis division leads cells to elongate in PD-axis (upper), and PD-axis division leads cells to elongate in AP-axis (lower). (B) Isotropic cell growth makes cells grow and move in all directions, and reduced cell size constraint cells to move in the direction of tissue elongation. (C) Oriented mechanical forces lead the shape of cells to change in oriented directions.
Oriented cell divisions can only drive tissue elongation to a limited extent, as the elongation index is still small, e.g., 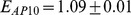 . We found that the degree of tissue elongation is influenced by the intervals of the angles from which the division plane is chosen. The smaller the interval around the AP or PD axis, the higher the degree of tissue elongation is. With oriented cell divisions alone, we cannot reproduce the elongated tissue shape to the extent observed in observed in experiments between 15 to 24 hour after puparium formation [17], indicating that other factors also influence tissue elongation during pupal development. Overall, our simulation results suggest that oriented cell divisions serve as directional cues to tissue elongation and they do not work alone.
. We found that the degree of tissue elongation is influenced by the intervals of the angles from which the division plane is chosen. The smaller the interval around the AP or PD axis, the higher the degree of tissue elongation is. With oriented cell divisions alone, we cannot reproduce the elongated tissue shape to the extent observed in observed in experiments between 15 to 24 hour after puparium formation [17], indicating that other factors also influence tissue elongation during pupal development. Overall, our simulation results suggest that oriented cell divisions serve as directional cues to tissue elongation and they do not work alone.
Reduced Cell Size Enhances Tissue Elongation in Combination with Oriented Cell Divisions
In this section, we simulate the effect of reduced cell size (RCS) on tissue elongation in conjunction with oriented cell divisions. Here we do not take into consideration the effects of oriented mechanical forces. This section of our simulation reflects the fact that cells between 15 and 24 hour after puparium formation do not grow during pupal development [17].
We found that reduced cell size alone does not affect tissue shape when cell division planes are randomly oriented. Tissue elongation index with reduced cell size 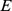 (
(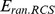 ) is
) is 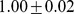 , non-distinguishable from that without reduced cell size (
, non-distinguishable from that without reduced cell size ( ) (Fig. 2A). Our simulation results indicate that reduced cell size itself does not provide directional cues for tissue elongation. It has no effect on the change of tissue shape without other directional cues.
) (Fig. 2A). Our simulation results indicate that reduced cell size itself does not provide directional cues for tissue elongation. It has no effect on the change of tissue shape without other directional cues.
However, reduced cell size can significantly amplify the effect of directional cues provided by oriented cell divisions in changing tissue shape. With non-RCS growth, tissue elongation index 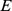 with division plane oriented along the AP-axis are
with division plane oriented along the AP-axis are 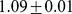 ,
, 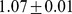 , and
, and 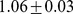 , respectively, when the orientation angle falls into the intervals of AP10, AP20, and AP30, respectively. With reduced cell size, tissue elongation index
, respectively, when the orientation angle falls into the intervals of AP10, AP20, and AP30, respectively. With reduced cell size, tissue elongation index 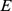 increases significantly to
increases significantly to 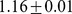 ,
, 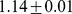 , and
, and 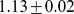 , respectively (Fig. 2A). Similarly, with non-RCS growth, tissue elongation index
, respectively (Fig. 2A). Similarly, with non-RCS growth, tissue elongation index 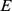 with division plane oriented along the PD-axis are
with division plane oriented along the PD-axis are 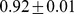 ,
, 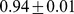 , and
, and 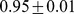 , respectively, when the orientation angle falls into the intervals of PD10, PD20, and PD30, respectively. With reduced cell size, tissue elongation index
, respectively, when the orientation angle falls into the intervals of PD10, PD20, and PD30, respectively. With reduced cell size, tissue elongation index 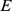 decreases to
decreases to 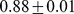 ,
, 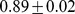 , and
, and 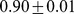 , respectively (Fig. 2A). This demonstrates that reduced cell size can significantly enhance tissue elongation when directional cues are provided by oriented cell divisions.
, respectively (Fig. 2A). This demonstrates that reduced cell size can significantly enhance tissue elongation when directional cues are provided by oriented cell divisions.
In summary, our simulation results show that reduced cell size has no direct effect on tissue elongation when the orientation of cell division is random. However, division with reduced cell size can promote tissue elongation with the presence of directional cues. While cell growth and cell division both may occur during cell proliferation, isotropic cell growth only results in proliferating cells moving randomly in all directions, with the tissue taking a round shape (Fig. 3B). Cell divisions without cell growth may act to counter the effects of isotropic cell growth and constrain tissue to elongate following the directional cues.
Oriented Mechanical Forces Significantly Influence Tissue Elongation
Although a combination of oriented cell divisions and reduced cell size can generate elongated tissue shape (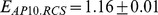 ), the elongation effect is not as pronounced as observed in experiments between 15 to 24 hour after puparium formation (E = ca. 1.4) [17]. Oriented mechanical forces (OMF) can also influence tissue elongation. To simulate the effects of oriented mechanical forces, we set the tension coefficients
), the elongation effect is not as pronounced as observed in experiments between 15 to 24 hour after puparium formation (E = ca. 1.4) [17]. Oriented mechanical forces (OMF) can also influence tissue elongation. To simulate the effects of oriented mechanical forces, we set the tension coefficients 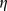 to 0.75, 1.0, and 1.5, respectively, when the angles of cell edge are distributed within the range of [0°, 30°], [30°, 60°], and [60°, 90°] with respect to the PD-axis.
to 0.75, 1.0, and 1.5, respectively, when the angles of cell edge are distributed within the range of [0°, 30°], [30°, 60°], and [60°, 90°] with respect to the PD-axis.
Our simulation results suggest that oriented mechanical forces can generate tissue elongation even with random division orientation. The tissue elongation index with oriented mechanical forces (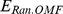 ) is
) is 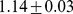 (Fig. 2B). Clearly, oriented mechanical forces can provide directional cues for tissue elongation. It is also interesting to note that oriented mechanical forces have more influence on tissue elongation than oriented cell divisions (
(Fig. 2B). Clearly, oriented mechanical forces can provide directional cues for tissue elongation. It is also interesting to note that oriented mechanical forces have more influence on tissue elongation than oriented cell divisions (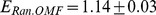 vs
vs 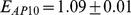 ).
).
We then combined both the directional cues, i.e., oriented cell divisions and oriented mechanical forces, under two different scenarios. First, both directional cues influence tissue elongation in the same direction. Second, two directional cues influence tissue elongation in the opposite directions. In the first scenario, tissue elongation index (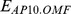 ) is
) is 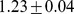 (Fig. 2B), significantly elevated compared to the tissue elongation index
(Fig. 2B), significantly elevated compared to the tissue elongation index 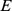 with either of the directional cues (
with either of the directional cues (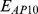 =
= 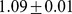 and
and 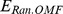 =
= 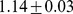 ). Our simulation results show that oriented mechanical forces and AP-axis cell division work collectively to drive more efficient tissue elongation. In the second scenario, tissue elongation index
). Our simulation results show that oriented mechanical forces and AP-axis cell division work collectively to drive more efficient tissue elongation. In the second scenario, tissue elongation index 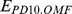 is
is 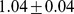 (Fig. 2B). The elongation effect is diminished compared to elongation index (
(Fig. 2B). The elongation effect is diminished compared to elongation index (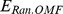 =
= 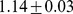 ) with oriented mechanical forces alone. However, tissue still elongated along PD-axis, the same direction as it was influenced by that of the oriented mechanical forces. We note that the PD-axis cell division drives tissue elongation in the opposite direction (
) with oriented mechanical forces alone. However, tissue still elongated along PD-axis, the same direction as it was influenced by that of the oriented mechanical forces. We note that the PD-axis cell division drives tissue elongation in the opposite direction (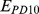 =
= 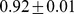 ). Our simulation results show that oriented mechanical forces are the dominant driving force and can overcome the effect of PD-axis cell division. That is, oriented mechanical forces have stronger influence on tissue elongation than oriented cell divisions.
). Our simulation results show that oriented mechanical forces are the dominant driving force and can overcome the effect of PD-axis cell division. That is, oriented mechanical forces have stronger influence on tissue elongation than oriented cell divisions.
Enhancement of Tissue Elongation by Reduced Cell Size Is Determined by Each Directional Cue
We now simulate the effect of reduced cell size in conjunction of both directional cues. We found that reduced cell size can enhance tissue elongation when compared to models with regular cell growth (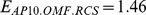 vs
vs 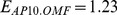 , and
, and 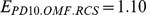 vs
vs 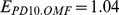 ) (Fig. 2C). The enhancements of tissue elongation by reduced cell size are different under different conditions as described in Section 3.3. For illustration, we use the ratio of elongation index
) (Fig. 2C). The enhancements of tissue elongation by reduced cell size are different under different conditions as described in Section 3.3. For illustration, we use the ratio of elongation index 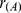 to describe the enhancement of tissue elongation due to reduced cell size in conjunction of different directional cues.
to describe the enhancement of tissue elongation due to reduced cell size in conjunction of different directional cues. 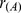 is defined as:
is defined as:
Here 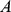 is the directional cue.
is the directional cue. 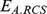 and
and 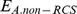 are the elongation index under
are the elongation index under 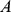 with reduced cell size, and under
with reduced cell size, and under 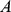 without reduced cell size, respectively.
without reduced cell size, respectively.
The enhancement of tissue elongation under oriented mechanical forces by reduced cell size 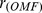 is 1.11 (>1) (Table. 1). In the first case where division planes are along the AP axis, the enhancement on all AP-axis cell divisions is about 1.06 (>1). This indicates the enhancement of reduced cell size on both oriented mechanical forces and AP-axis cell divisions are in the same direction (PD-axis). The enhancement of reduced cell size to the combined cues of AP-axis cell divisions orientation and oriented mechanical forces is
is 1.11 (>1) (Table. 1). In the first case where division planes are along the AP axis, the enhancement on all AP-axis cell divisions is about 1.06 (>1). This indicates the enhancement of reduced cell size on both oriented mechanical forces and AP-axis cell divisions are in the same direction (PD-axis). The enhancement of reduced cell size to the combined cues of AP-axis cell divisions orientation and oriented mechanical forces is 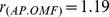 (Table. 1). It is similar to the multiplication of the enhancement to each directional cue (
(Table. 1). It is similar to the multiplication of the enhancement to each directional cue (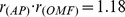 ) (Table. 1). In the second case where division planes are along the PD axis, the enhancement on all PD-axis cell divisions is about 0.96 (<1). This indicates the enhancement of reduced cell size on oriented mechanical forces and PD-axis cell divisions are in the opposite directions (PD-axis vs AP-axis). Similarly, the enhancement on the combination of oriented mechanical forces and PD-axis cell divisions is similar to the multiplication of the enhancement on each directional cue (Table. 1). Our simulation results suggest that the enhancement of tissue elongation by reduced cell size on combined directional cues is determined by the enhancement on each directional cue.
) (Table. 1). In the second case where division planes are along the PD axis, the enhancement on all PD-axis cell divisions is about 0.96 (<1). This indicates the enhancement of reduced cell size on oriented mechanical forces and PD-axis cell divisions are in the opposite directions (PD-axis vs AP-axis). Similarly, the enhancement on the combination of oriented mechanical forces and PD-axis cell divisions is similar to the multiplication of the enhancement on each directional cue (Table. 1). Our simulation results suggest that the enhancement of tissue elongation by reduced cell size on combined directional cues is determined by the enhancement on each directional cue.
Table 1. Enhancement of tissue elongation by reduced cell size.
| OMF | AP divisions + OMF | PD divisions + OMF | |||
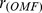
|
1.11 |
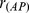
|
1.06 |
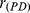
|
0.96 |
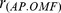
|
1.19 |
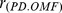
|
1.06 | ||
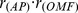
|
1.18 |
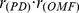
|
1.06 | ||
Comparison to Experimental Observations
Our simulation results show that oriented cell divisions and oriented mechanical forces both serve as directional cues to drive tissue elongation. Reduced cell size can significantly enhance tissue elongation when combined with these directional cues. We hypothesize that oriented cell divisions, oriented mechanical forces, and reduced cell size work collectively to regulate tissue elongation in Drosophila wing between 15 to 24 hour after puparium formation.
We compared our simulation results with the experimental work in reference [17]. We examined the change of tissue shape exactly between 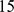 and
and 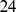 hour after puparium formation during pupal development. Tissue elongation index
hour after puparium formation during pupal development. Tissue elongation index 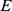 from
from 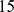 to
to 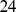 hour after puparium formation was approximately 1.40 in reference [17]. Simulation results in our model showed that
hour after puparium formation was approximately 1.40 in reference [17]. Simulation results in our model showed that 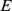 is greater than 1.40 only when we combined the choices of oriented cell divisions, oriented mechanical forces, and reduced cell size (1.42, 1,44, and 1.46 respectively with AP30, AP 20, and AP10 division choices). Morphology at the beginning, midpoint, and the end of the simulation with combined choices of oriented cell division (AP10), reduced cell size, and oriented mechanical forces are shown in (Fig. 2D–F). Other combinations of growth choice, force choice, and division choice can only generate a tissue elongation index
is greater than 1.40 only when we combined the choices of oriented cell divisions, oriented mechanical forces, and reduced cell size (1.42, 1,44, and 1.46 respectively with AP30, AP 20, and AP10 division choices). Morphology at the beginning, midpoint, and the end of the simulation with combined choices of oriented cell division (AP10), reduced cell size, and oriented mechanical forces are shown in (Fig. 2D–F). Other combinations of growth choice, force choice, and division choice can only generate a tissue elongation index 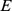 of 1.26 or less. Our simulation results suggest that oriented cell divisions, oriented mechanical forces, and reduced cell size can all mediate tissue elongation, although they are functionally different.
of 1.26 or less. Our simulation results suggest that oriented cell divisions, oriented mechanical forces, and reduced cell size can all mediate tissue elongation, although they are functionally different.
Discussion
Effect of Oriented Cell Divisions
Our simulation results show that oriented cell divisions can drive tissue elongation. Molecules such as Ds influence the orientation of planar cell polarity during development in Drosophila wing. It is possible that oriented cell divisions help to maintain some of the initial polarity pattern when forming new cell boundaries. After oriented cell divisions, cells relax, and the tissue elongates in a specific direction (Fig. 3A). However, oriented cell divisions alone are not sufficient to reproduce the experimental observations. Oriented cell divisions likely work together with other directional cues, such as oriented mechanical forces, to drive tissue elongation. In the work by Mao et al., isometric tension with oriented cell division produced more elongated and PD aligned tissue than in vivo clones [18]. The difference between their model and ours may be due to the different model parameters. In Mao et al., the division plane was always exactly perpendicular to the PD-axis. However, their experimental results showed that the orientation of cell divisions was imperfectly correlated with the PD-axis in Drosophila wing disc in culture [18]. The division plane in our simulation is set in a specific range around PD-axis according to experimental observations [17]. Moreover, the simulations by Mao et al. were run for around 4 to 5 generations (48 hours) [18], while in our simulations, cells are divided only for 1 to 2 generations, which tracks more realistically the pupal development between 15 to 24 hour after puparium formation [17].
Our simulation results also suggest oriented cell divisions alone have limited effects on tissue elongation. Oriented cell divisions may contribute to tissue elongation via two distinct mechanisms: (1) tissue elongates by oriented cell divisions while cell growth is isotropic; (2) cell growth is anisotropic, and cell divisions with orientation along the longest axis reduce the stress exerting on cell boundaries so that regular cell shape forms [55]. With oriented cell divisions alone, we cannot reproduce the elongated tissue shape observed in experiments. However, with combined oriented cell divisions, oriented mechanical forces, and reduced cell size, we are able to reproduce tissue elongation observed in Drosophila wing qualitatively [17]. Oriented mechanical forces in our model can have an equivalent effect as that of anisotropic cell growth.
Effect of Oriented Mechanical Forces
Our simulation results show that oriented mechanical forces have stronger effects on tissue elongation than the oriented cell divisions. Our simulation results also suggest that oriented mechanical forces, oriented cell divisions, and reduced cell size might work collectively to influence tissue elongation in Drosophila wing between 15 to 24 hour after puparium formation. In the work by Mao et al., oriented tension and division along the long axis were sufficient to drive tissue elongation [18]. Their results agree with ours to a certain extent, although there is no consideration of the effects of reduced cell size. Dachs, producing oriented mechanical forces at the apical junctions, can indirectly orient cell divisions. Oriented mechanical forces result in cell shape elongated along the PD-axis prior to cell divisions, which then orient the mitotic spindles. At the same time, mitotic spindles always align along the long axis of cells in mammalia [56]. Thus the strategy of oriented tension and division along the long axis in Mao's study seems to be equivalent to combining oriented mechanical forces and oriented cell divisions in our model. Mao et al. did not take into consideration of reduced cell size in their model, because in their study, they were modeling a different development stage. Altogether, the stronger influence of oriented mechanical forces on tissue elongation vs oriented cell divisions is demonstrated.
In addition to the Dachs myosin, two large and atypical cadherins, Ds and Fat, are involved in planar cell polarity (PCP) pathways of Drosophila wing [3], [57]. Mediating cell-cell interactions through adhesion is an important function of cadherin [57]. Mechanical forces by atypical cadherins with polarized properties can help to maintain cell polarity and regulate cell proliferation so that they contribute to different aspects of tissue morphogenesis such as shape and size.
Effect of Reduced Cell Size
Our simulation results show that reduced cell size alone cannot drive tissue elongation. However, when combined with directional cues such as oriented cell divisions or oriented mechanical forces, reduced cell size can significantly enhance tissue elongation in Drosophila wing. We suggest that tissue shapes are not affected by isotropic cell growth as cells are moving randomly, and cell divisions without cell growth may act to counter the effects of isotropic cell growth and constrain tissue to elongate following the directional cues. Reduced cell size can affect tissue elongation through differences in mechanical forces. It was shown recently that “mechanical relaxation” has significant effects in tissue pattern formation during tissue growth [58]. Variation in mechanical relaxation ultimately affects tissue structure and tissue shape. Our previous study also showed that growing cells reach the mechanical equilibrium and equilibrium tissue structure only after certain time duration [36]. In the current study, cell proliferation without growth, namely, reduced cell size, may constrain “mechanical relaxation” when cells divide without growing, which may lead to more elongated tissue shape. Our hypothesis can be verified experimentally by treating the tissue with inhibitor of cell division, such as Y-27632 [59]. According to findings of this study, we predict that there will be less tissue elongation after such treatment, as there will be more time for mechanical relaxation.
The overall interplay of cell size, cell division, tissue shape, and tissue structure has been a long standing problem in developmental biology [60]. The effect of cell size on proliferation and organ size has been recently observed [61]. In that study, the authors identified a gene fo that would change the number of cells and the size of each cell in the petal of Antirrhinum upon mutation. The number of cells was significantly increased, while the size of each cell was significantly decreased. These results suggested a compensatory mechanism between cell size and the number of cells for maintaining wild-type organ size. Our simulation results suggest that the cell size may also play an important role in maintaining wild-type organ shape. It is well known that morphogen gradients such as Dpp maintain tissue shape through oriented cell divisions, which result in anisotropic growth [62]. It is possible that by reducing their size, cells sense a different morphogen gradient and this can affect oriented cell divisions. It would be interesting to quantify such effect in future simulation studies, where the oriented cell divisions can be linked to morphogen gradients. Overall, it is likely that cell division without cell growth may play important roles in affecting cell mechanics and in influencing how cells sense and respond to morphogen gradient, therefore affecting formation of specific tissue and organ shape.
Cell Topology during Tissue Elongation
Our previous studies suggest that the orientation of division plane and mechanical forces play important roles on regulating cell topology [36]–[38]. It is likely that oriented cell divisions, oriented mechanical forces, and reduced cell size may also affect cell topology during tissue elongation. To address this issue, we examined hexagonal frequencies with different combinations of growth choices, division choices, and force choices.
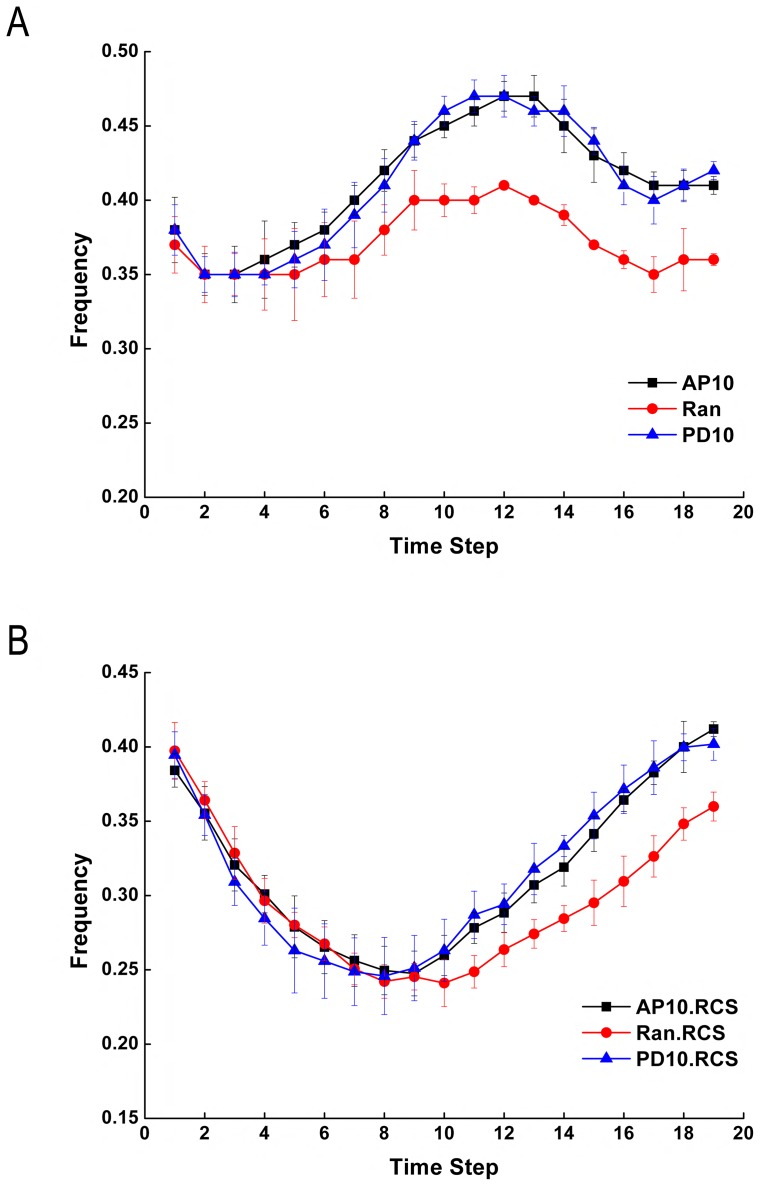
Effect of oriented cell divisions and oriented mechanical forces
We found that oriented cell divisions produced more hexagonal cells compared with the random division choice. Without the consideration of oriented mechanical forces and reduced cell size, the hexagonal frequencies were the same for all three scenarios (Ran, AP10, and PD10) at the beginning of the simulation. After certain time steps, oriented cell divisions (AP10 and PD10) generated higher hexagonal frequencies (by about 0.05) compared with the random division choice, and this higher hexagonal frequency is maintained afterwards (Fig. 4A). Higher hexagonal frequency by oriented cell divisions was also shown in other scenarios when the oriented mechanical forces and reduced cell size were taken into consideration (Figures S3–S6 in File S1). This suggests that oriented cell divisions can increase the amount of hexagonal cells and can generate more structured tissue pattern compared with the random division choice. Our simulation results also showed that hexagonal frequencies were not affected using the oriented mechanical forces (Figures S4, S6 in File S1). This suggests that oriented mechanical forces have little influence on cell topology during tissue elongation.
Figure 4. Hexagonal frequencies during tissue elongation by different simulation choices.
(A) Oriented cell divisions increase the hexagonal frequencies compared with the random division choice. (B) Reduced cell size has a short term effect of decreasing the hexagonal frequencies.
Effect of reduced cell size
We then took the reduced cell size into consideration. We found that the hexagonal frequencies decreased at the beginning, but increased afterwards (Fig. 4B). The average of hexagonal frequencies over all time steps are different between the two scenarios (RCS vs non-RCS). With RCS, much less hexagonal cells are produced compared with that when non-RCS models are used (Table. 2). However, at the end of the simulation, both scenarios generated similar hexagonal frequencies (Table. 2). This suggests that reduced cell size has a short term effect on cell topology by decreasing the hexagonal frequency. After the tissue relaxes, the effect of decreased hexagonal frequency is lost.
Table 2. Comparison of hexagonal frequencies between RCS and non-RCS growth choices.
| AP10 | Random | PD10 | ||||
| Hexagonal frequency | RCS | Non-RCS | RCS | Non-RCS | RCS | Non-RCS |
| Last time step | 0.41 | 0.41 | 0.36 | 0.36 | 0.40 | 0.42 |
| Average of all steps | 0.32 | 0.41 | 0.30 | 0.37 | 0.32 | 0.41 |
We compared our simulation results with the experimental work in reference [17]. It was observed that the hexagonal frequency decreased first, and then increased after a certain period in the experiments [17]. This is consistent with our simulation results, despite the difference in initial hexagonal frequency. This difference might be a result of different tissue size. Specifically, our simulation starts from about 500 cells, at which the hexagonal frequency is less than that is observed in the experiments. Overall, our simulation results suggest that reduced cell size affects cell topology during tissue elongation.
Future Applications
Cell divisions and mechanical forces in diseases and cancer
We have previously shown that the orientation of division plane and mechanical forces have significant impacts on regulating cell topology during epithelial proliferation with isotropic growth [38]. Here we found that oriented cell divisions and oriented mechanical forces play important roles in tissue elongation in Drosophila wing with anisotropic growth. These directional cues are correlated with molecules such as Dachs and Ds involved in PCP pathways [17], [18], [63], [64]. It would be interesting to study the effects of cell divisions and mechanical forces and their relationship with PCP pathways in epithelial diseases [65], [66], especially in cancer progression [67], [68]. In addition, mechanical forces are tightly correlated in cancer invasion and metastasis [69]–[71]. Cell-cell and cell-matrix interactions are shown to alter significantly during cancer progression both theoretically and experimentally [72]–[74]. Fully understanding the underlying mechanisms that are regulated by cell divisions and mechanical forces may possibly provide potential targets for cancer therapy.
Long range morphogen gradient
Dachs is essential for oriented mechanical forces and oriented cell divisions, which can affect tissue elongation. It is suggested that planar polarization of Dachs is ultimately oriented by long-range gradients of secreted morphogens from compartment boundaries [18]. It will be interesting to study the fundamental mechanisms of controlling tissue pattern, size and shape by these secreted molecules.
Symmetric and asymmetric cell divisions
In this study, we have examined tissues with symmetric cell divisions, where one cell gives rise to two identical daughter cells. It was shown that in the developing organism, asymmetric cell divisions, in which two daughter cells were generated with different cell sizes and cell fates, played a central role [55], [75], [76]. This is an intrinsic property of stem cells [76]–[78], and defects in asymmetric cell divisions can lead to cancer [76], [79], [80]. It is still puzzling to understand many biological phenomena associated with asymmetric cell divisions. How the relative proportions of cell population each with different fates are achieved? How does stochasticity influence cell division and cell differentiation? It will be interesting to use our model to quantitatively study the fundamental mechanisms to coordinate asymmetric cell divisions with other factors such as cell fates and cell positions during development. A preliminary study into the population dynamics of stem cells using our model has generated important insights [81].
Conclusions
We have used a recently developed two-dimensional cellular model to study the mechanisms of regulating tissue elongation in Drosophila wing between 15 to 24 hour after puparium formation. We simulated the effects of directional cues, including oriented cell divisions and oriented mechanical forces, on tissue elongation. We also computationally analyzed the role of reduced cell size. Our simulation results suggest that tissue elongation in Drosophila wing is influenced collectively by oriented cell divisions, oriented mechanical forces, and reduced cell size. We show that oriented cell divisions and oriented mechanical forces act as directional cues during tissue elongation. Between them, we find that oriented mechanical forces have a stronger influence compared to oriented cell divisions. In addition, our simulation results reveal a novel mechanism of reduced cell size in promoting tissue elongation. We find that reduced cell size alone cannot drive tissue elongation, as it does not have directional information. However, when combined with directional cues such as oriented cell divisions and oriented mechanical forces, reduced cell size can significantly enhance tissue elongation in Drosophila wing between 15 to 24 hour after puparium formation. Furthermore, our simulation results show that reduced cell size affects cell topology during tissue elongation. Overall, our simulation results suggest that cell division without growth is essential for tissue elongation in Drosophila wing.
Supporting Information
Combined Supporting Information. Figure S1 shows the changes in tissue shape index of samples with different initial shapes; Figure S2 shows tissue elongation index is independent of the shape of initial samples; Figure S3–S6 show the comparison of hexagonal frequencies between different strategies during tissue elongation.
(PDF)
Acknowledgments
We thank Dr. Ping Ao for useful discussions.
Funding Statement
This work is supported by National Institutes of Health Grants GM079804 and GM086145 (http://www.nih.gov), National Science Foundation Grant DBI-1062328 and DMS-0800257 (http://www.nsf.gov), the Chicago Biomedical Consortium with support from the Searle Funds at The Chicago Community Trust, National Basic Research Program of China 2010CB834300, Research Fund of Science and Technology Commission of Shanghai Municipality 11DZ2211001, and 985 Project from Shanghai Jiao Tong University. YL was supported by the China Scholarship Council. HN was supported by the Fulbright Fellowship, the Higher Education Commission of Pakistan, the Chinese Academy of Sciences Fellowship for Young International Scientists 2012Y1SB0006, and the China National Natural Science Foundation 31250110524. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. O'Brochta D, Bryant P (1985) A zone of non-proliferating cells at a lineage restriction boundary in drosophila. Nature 313: 138–141. [DOI] [PubMed] [Google Scholar]
- 2. Gong Y, Mo C, Fraser S (2004) Planar cell polarity signalling controls cell division orientation during zebrafish gastrulation. Nature 430: 689–693. [DOI] [PubMed] [Google Scholar]
- 3. Baena-Lopez L, Baonza A, Garcia-Bellido A (2005) The orientation of cell divisions determines the shape of drosophila organs. Curr Biol 15: 1640–1644. [DOI] [PubMed] [Google Scholar]
- 4. Lecuit T, Lenne P (2007) Cell surface mechanics and the control of cell shape, tissue patterns and morphogenesis. Nat Rev Mol Cell Biol 8: 633–644. [DOI] [PubMed] [Google Scholar]
- 5. Shraiman B (2005) Mechanical feedback as a possible regulator of tissue growth. Proc Natl Acad Sci U S A 102: 3318–3323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Hanahan D, Weinberg R (2000) The hallmarks of cancer. Cell 100: 57–70. [DOI] [PubMed] [Google Scholar]
- 7. Bhowmick N, Neilson E, Moses H (2004) Stromal fibroblasts in cancer initiation and progression. Nature 432: 332–337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Hanahan D, Weinberg R (2011) Hallmarks of cancer: the next generation. Cell 144: 646–674. [DOI] [PubMed] [Google Scholar]
- 9. Gibson M, Patel A, Nagpal R, Perrimon N (2006) The emergence of geometric order in proliferating metazoan epithelia. Nature 442: 1038–1041. [DOI] [PubMed] [Google Scholar]
- 10. Milan M, Campuzano S, Garcia-Bellido A (1996) Cell cycling and patterned cell proliferation in the wing primordium of drosophila. Proc Natl Acad Sci U S A 93: 640–645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Garcia-Bellido A, de Celis J (1992) Developmental genetics of the venation pattern of drosophila. Annu Rev Genet 26: 277–304. [DOI] [PubMed] [Google Scholar]
- 12. Tree D, Ma D, Axelrod J (2002) A three-tiered mechanism for regulation of planar cell polarity. Semin Cell Dev Biol 13: 217–224. [DOI] [PubMed] [Google Scholar]
- 13. Sagner A, Merkel M, Aigouy B, Gaebel J, Brankatschk M, et al. (2012) Establishment of global patterns of planar polarity during growth of the drosophila wing epithelium. Curr Biol 22: 1296–1301. [DOI] [PubMed] [Google Scholar]
- 14. Canela-Xandri O, Sagues F, Casademunt J, Buceta J (2011) Dynamics and mechanical stability of the developing dorsoventral organizer of the wing imaginal disc. PLoS Comput Biol 7: e1002153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Rauzi M, Lenne P (2011) Cortical forces in cell shape changes and tissue morphogenesis. Curr Top Dev Biol 95: 93–144. [DOI] [PubMed] [Google Scholar]
- 16. Aegerter-Wilmsen T, Heimlicher M, Smith A, de Reuille P, Smith R, et al. (2012) Integrating force-sensing and signaling pathways in a model for the regulation of wing imaginal disc size. Development 139: 3221–3231. [DOI] [PubMed] [Google Scholar]
- 17. Aigouy B, Farhadifar R, Staple D, Sagner A, Roper J, et al. (2010) Cell flow reorients the axis of planar polarity in the wing epithelium of drosophila. Cell 142: 773–786. [DOI] [PubMed] [Google Scholar]
- 18. Mao Y, Tournier A, Bates P, Gale J, Tapon N, et al. (2011) Planar polarization of the atypical myosin dachs orients cell divisions in drosophila. Genes Dev 25: 131–136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Matakatsu H, Blair S (2004) Interactions between fat and dachsous and the regulation of planar cell polarity in the drosophila wing. Development 131: 3785–3794. [DOI] [PubMed] [Google Scholar]
- 20. Simon M (2004) Planar cell polarity in the drosophila eye is directed by graded four-jointed and dachsous expression. Development 131: 6175–6184. [DOI] [PubMed] [Google Scholar]
- 21. Cho E, Irvine K (2004) Action of fat, four-jointed, dachsous and dachs in distal-to-proximal wing signaling. Development 131: 4489–4500. [DOI] [PubMed] [Google Scholar]
- 22. Lawrence P, Casal J, Struhl G (2004) Cell interactions and planar polarity in the abdominal epidermis of drosophila. Development 131: 4651–4664. [DOI] [PubMed] [Google Scholar]
- 23. Matakatsu H, Blair S (2006) Separating the adhesive and signaling functions of the fat and dachsous protocadherins. Development 133: 2315–2324. [DOI] [PubMed] [Google Scholar]
- 24. Wittmann T, Hyman A, Desai A (2001) The spindle: a dynamic assembly of microtubules and motors. Nat Cell Biol 3: E28–34. [DOI] [PubMed] [Google Scholar]
- 25. Walczak C, Heald R (2008) Mechanisms of mitotic spindle assembly and function. Int Rev Cytol 265: 111–158. [DOI] [PubMed] [Google Scholar]
- 26. Gatlin J, Bloom K (2010) Microtubule motors in eukaryotic spindle assembly and maintenance. Semin Cell Dev Biol 21: 248–254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Stevermann L, Liakopoulos D (2012) Molecular mechanisms in spindle positioning: structures and new concepts. Curr Opin Cell Biol. [DOI] [PubMed]
- 28. Eaton S, Wepf R, Simons K (1996) Roles for rac1 and cdc42 in planar polarization and hair outgrowth in the wing of drosophila. J Cell Biol 135: 1277–1289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Turner C, Adler P (1998) Distinct roles for the actin and microtubule cytoskeletons in the morphogenesis of epidermal hairs during wing development in drosophila. Mech Dev 70: 181–192. [DOI] [PubMed] [Google Scholar]
- 30. Shimada Y, Yonemura S, Ohkura H, Strutt D, Uemura T (2006) Polarized transport of frizzled along the planar microtubule arrays in drosophila wing epithelium. Dev Cell 10: 209–222. [DOI] [PubMed] [Google Scholar]
- 31. Harumoto T, Ito M, Shimada Y, Kobayashi T, Ueda H, et al. (2010) Atypical cadherins dachsous and fat control dynamics of noncentrosomal microtubules in planar cell polarity. Dev Cell 19: 389–401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Baskin T (2005) Anisotropic expansion of the plant cell wall. Annu Rev Cell Dev Biol 21: 203–222. [DOI] [PubMed] [Google Scholar]
- 33. Dumais J (2007) Can mechanics control pattern formation in plants? Curr Opin Plant Biol 10: 58–62. [DOI] [PubMed] [Google Scholar]
- 34. Neufeld T, de la Cruz A, Johnston L, Edgar B (1998) Coordination of growth and cell division in the drosophila wing. Cell 93: 1183–1193. [DOI] [PubMed] [Google Scholar]
- 35. Su T, O'Farrell P (1998) Size control: cell proliferation does not equal growth. Curr Biol 8: R687–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Li Y, Naveed H, Kachalo S, Xu L, Liang J (2011) Mechanical forces mediate localized topological change in epithelia. Conf Proc IEEE Eng Med Biol Soc 2011: 178–181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Li Y, Naveed H, Kachalo S, Xu L, Liang J (2012) Mechanisms of regulating cell topology in proliferating epithelia: impact of division plane, mechanical forces, and cell memory. PLoS One 7: e43108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Mizushima-Sugano J, Maeda T, Miki-Noumura T (1983) Flexural rigidity of singlet microtubules estimated from statistical analysis of their contour lengths and end-to-end distances. Biochim Biophys Acta 755: 257–262. [DOI] [PubMed] [Google Scholar]
- 40. Burnside B (1971) Microtubules and microfilaments in newt neuralation. Dev Biol 26: 416–441. [DOI] [PubMed] [Google Scholar]
- 41. Madreperla S, Adler R (1989) Opposing microtubule- and actin-dependent forces in the development and maintenance of structural polarity in retinal photoreceptors. Dev Biol 131: 149–160. [DOI] [PubMed] [Google Scholar]
- 42. Brown M, Hallam J, Colucci-Guyon E, Shaw S (2001) Rigidity of circulating lymphocytes is primarily conferred by vimentin intermediate filaments. J Immunol 166: 6640–6646. [DOI] [PubMed] [Google Scholar]
- 43. Ingber D (2003) Tensegrity i. cell structure and hierarchical systems biology. J Cell Sci 116: 1157–1173. [DOI] [PubMed] [Google Scholar]
- 44. Chen C, Posy S, Ben-Shaul A, Shapiro L, Honig B (2005) Specificity of cell-cell adhesion by classical cadherins: Critical role for low-affinity dimerization through beta-strand swapping. Proc Natl Acad Sci U S A 102: 8531–8536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Patel S, Ciatto C, Chen C, Bahna F, Rajebhosale M, et al. (2006) Type II cadherin ectodomain structures: implications for classical cadherin specificity. Cell 124: 1255–1268. [DOI] [PubMed] [Google Scholar]
- 46. Shimoyama Y, Tsujimoto G, Kitajima M, Natori M (2000) Identification of three human type-II classic cadherins and frequent heterophilic interactions between different subclasses of type-II classic cadherins. Biochem J 349: 159–167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Evans A, Turner M, Sens P (2003) Interactions between proteins bound to biomembranes. Phys Rev E Stat Nonlin Soft Matter Phys 67: 041907. [DOI] [PubMed] [Google Scholar]
- 48. Hotani H, Miyamoto H (1990) Dynamic features of microtubules as visualized by dark-field microscopy. Adv Biophys 26: 135–156. [DOI] [PubMed] [Google Scholar]
- 49. Domnina L, Rovensky J, Vasiliev J, Gelfand I (1985) Effect of microtubule-destroying drugs on the spreading and shape of cultured epithelial cells. J Cell Sci 74: 267–282. [DOI] [PubMed] [Google Scholar]
- 50. Harris A, Wild P, Stopak D (1980) Silicone rubber substrata: a new wrinkle in the study of cell locomotion. Science 208: 177–179. [DOI] [PubMed] [Google Scholar]
- 51. Hufnagel L, Teleman A, Rouault H, Cohen S, Shraiman B (2007) On the mechanism of wing size determination in fly development. Proc Natl Acad Sci U S A 104: 3835–3840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Farhadifar R, Roper J, Aigouy B, Eaton S, Julicher F (2007) The influence of cell mechanics, cell-cell interactions, and proliferation on epithelial packing. Curr Biol 17: 2095–2104. [DOI] [PubMed] [Google Scholar]
- 53. Aegerter-Wilmsen T, Aegerter C, Hafen E, Basler K (2007) Model for the regulation of size in the wing imaginal disc of drosophila. Mech Dev 124: 318–326. [DOI] [PubMed] [Google Scholar]
- 54. Aegerter-Wilmsen T, Smith A, Christen A, Aegerter C, Hafen E, et al. (2010) Exploring the effects of mechanical feedback on epithelial topology. Development 137: 499–506. [DOI] [PubMed] [Google Scholar]
- 55. Morin X, Bellaiche Y (2011) Mitotic spindle orientation in asymmetric and symmetric cell divisions during animal development. Dev Cell 21: 102–119. [DOI] [PubMed] [Google Scholar]
- 56. Minc N, Burgess D, Chang F (2011) Influence of cell geometry on division-plane positioning. Cell 144: 414–426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Halbleib J, Nelson W (2006) Cadherins in development: cell adhesion, sorting, and tissue morphogenesis. Genes Dev 20: 3199–3214. [DOI] [PubMed] [Google Scholar]
- 58. Cerruti B, Puliafito A, Shewan A, Yu W, Combes A, et al. (2013) Polarity, cell division, and out-of-equilibrium dynamics control the growth of epithelial structures. J Cell Biol 203: 359–372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Ishizaki T, Uehata M, Tamechika I, Keel J, Nonomura K, et al. (2000) Pharmacological properties of y-27632, a specific inhibitor of rho-associated kinases. Mol Pharmacol 57: 976–983. [PubMed] [Google Scholar]
- 60. Fankhauser G (1945) Maintenance of normal structure in heteroploid salamander larvae, through compensation of changes in cell size by adjustment of cell number and cell shape. J Exp Zool 100: 445–455. [DOI] [PubMed] [Google Scholar]
- 61. Delgado-Benarroch L, Causier B, Weiss J, Egea-Cortines M (2009) FORMOSA controls cell division and expansion during floral development in antirrhinum majus. Planta 229: 1219–1229. [DOI] [PubMed] [Google Scholar]
- 62. Bittig T, Wartlick O, Gonzalez-Gaitan M, Julicher F (2009) Quantification of growth asymmetries in developing epithelia. Eur Phys J E Soft Matter 30: 93–99. [DOI] [PubMed] [Google Scholar]
- 63. Segalen M, Bellaiche Y (2009) Cell division orientation and planar cell polarity pathways. Semin Cell Dev Biol 20: 972–977. [DOI] [PubMed] [Google Scholar]
- 64. Vladar E, Antic D, Axelrod J (2009) Planar cell polarity signaling: the developing cell's compass. Cold Spring Harb Perspect Biol 1: a002964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Fischer E, Legue E, Doyen A, Nato F, Nicolas J, et al. (2006) Defective planar cell polarity in polycystic kidney disease. Nat Genet 38: 21–23. [DOI] [PubMed] [Google Scholar]
- 66. Saburi S, Hester I, Fischer E, Pontoglio M, Eremina V, et al. (2008) Loss of fat4 disrupts PCP signaling and oriented cell division and leads to cystic kidney disease. Nat Genet 40: 1010–1015. [DOI] [PubMed] [Google Scholar]
- 67. Wang Y (2009) Wnt/planar cell polarity signaling: a new paradigm for cancer therapy. Mol Cancer Ther 8: 2103–2109. [DOI] [PubMed] [Google Scholar]
- 68. Jessen J (2009) Noncanonical wnt signaling in tumor progression and metastasis. Zebrafish 6: 21–28. [DOI] [PubMed] [Google Scholar]
- 69. Cavallaro U, Schaffhauser B, Christofori G (2002) Cadherins and the tumour progression: is it all in a switch? Cancer Lett 176: 123–128. [DOI] [PubMed] [Google Scholar]
- 70. Cavallaro U, Christofori G (2004) Cell adhesion and signalling by cadherins and ig-CAMs in cancer. Nat Rev Cancer 4: 118–132. [DOI] [PubMed] [Google Scholar]
- 71. Kumar S, Weaver V (2009) Mechanics, malignancy, and metastasis: the force journey of a tumor cell. Cancer Metastasis Rev 28: 113–127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72. Turner S, Sherratt J (2002) Intercellular adhesion and cancer invasion: a discrete simulation using the extended potts model. J Theor Biol 216: 85–100. [DOI] [PubMed] [Google Scholar]
- 73. Anderson A (2005) A hybrid mathematical model of solid tumour invasion: the importance of cell adhesion. Math Med Biol 22: 163–186. [DOI] [PubMed] [Google Scholar]
- 74. Takeichi M (1993) Cadherins in cancer: implications for invasion and metastasis. Curr Opin Cell Biol 5: 806–811. [DOI] [PubMed] [Google Scholar]
- 75. Yamashita Y, Fuller M (2008) Asymmetric centrosome behavior and the mechanisms of stem cell division. J Cell Biol 180: 261–266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76. Neumuller R, Knoblich J (2009) Dividing cellular asymmetry: asymmetric cell division and its implications for stem cells and cancer. Genes Dev 23: 2675–2699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77. Lechler T, Fuchs E (2005) Asymmetric cell divisions promote stratification and differentiation of mammalian skin. Nature 437: 275–280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78. Shinin V, Gayraud-Morel B, Gomes D, Tajbakhsh S (2006) Asymmetric division and cosegregation of template DNA strands in adult muscle satellite cells. Nat Cell Biol 8: 677–687. [DOI] [PubMed] [Google Scholar]
- 79. Cicalese A, Bonizzi G, Pasi C, Faretta M, Ronzoni S, et al. (2009) The tumor suppressor p53 regulates polarity of self-renewing divisions in mammary stem cells. Cell 138: 1083–1095. [DOI] [PubMed] [Google Scholar]
- 80. Knoblich J (2010) Asymmetric cell division: recent developments and their implications for tumour biology. Nat Rev Mol Cell Biol 11: 849–860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81. Cao Y, Liang C, Naveed H, Li Y, Chen M, et al. (2012) Modeling spatial population dynamics of stem cell lineage in tissue growth. Conf Proc IEEE Eng Med Biol Soc 2012: 5502–5505. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Combined Supporting Information. Figure S1 shows the changes in tissue shape index of samples with different initial shapes; Figure S2 shows tissue elongation index is independent of the shape of initial samples; Figure S3–S6 show the comparison of hexagonal frequencies between different strategies during tissue elongation.
(PDF)