Hippocampal “Time Cells”: Time versus Path Integration

SUMMARY

Recent studies have reported the existence of hippocampal “time cells,” neurons that fire at particular moments during periods when behavior and location are relatively constant. However, an alternative explanation of apparent time coding is that hippocampal neurons “path integrate” to encode the distance an animal has traveled. Here, we examined hippocampal neuronal firing patterns as rats ran in place on a treadmill, thus “clamping” behavior and location, while we varied the treadmill speed to distinguish time elapsed from distance traveled. Hippocampal neurons were strongly influenced by time and distance, and less so by minor variations in location. Furthermore, the activity of different neurons reflected integration over time and distance to varying extents, with most neurons strongly influenced by both factors and some significantly influenced by only time or distance. Thus, hippocampal neuronal networks captured both the organization of time and distance in a situation where these dimensions dominated an ongoing experience.

INTRODUCTION

Numerous studies have shown that the hippocampus plays a crucial role in episodic memory in both humans and animals, and a fundamental characteristic of episodic memory is the temporal organization of sequential events that compose a particular experience. Recent research has suggested that sequential organization of episodic memories may be supported by “time cells,” temporally tuned patterns of neuronal activity in the hippocampus (Gill et al., 2011; MacDonald et al., 2011; Manns et al., 2007; Pastalkova et al., 2008). However, it remains unclear what mechanisms are driving the apparent temporal tuning of hippocampal neurons. In experiments where time cells have been observed, the animals either run continuously in place (in a running wheel) (Pastalkova et al., 2008) or can move on a small platform (Gill et al., 2011) or in a chamber (MacDonald et al., 2011), allowing movement to play a substantial role in accounting for variations in firing rate (Hasselmo, 2009, 2012). Even when statistical models have extracted a temporal modulation from influences of location and speed (Lepage et al., 2012; MacDonald et al., 2011), it remains possible that temporal tuning occurs only when the animal is moving. In addition, in previous studies when animals remained in a relatively constant location, elapsed time was confounded with the distance the animal traveled (the number of steps taken), allowing for the possibility that variations in firing rate reflect an integration of distance along an egocentrically defined path. Indeed, several theoretical conceptions have proposed that path integration is the primary function of hippocampal networks (Etienne and Jeffery, 2004; McNaughton et al., 1991, 1996, 2006; O’Keefe and Burgess, 2005; Samsonovich and McNaughton, 1997). To fully understand the extent to which time and distance, as well as location, govern hippocampal neuronal firing patterns, it is critical to disentangle these parameters.

Here, we distinguished influences of location, time, and distance by recording from multiple hippocampal neurons as rats ran continuously in place at different speeds on a treadmill placed in the stem of a figure-eight maze (Figure 1). On each trial, the rats entered the central stem of the maze from one of two directions (left or right), and then walked onto the treadmill where they received a small water reward. After a short delay, the treadmill accelerated to a speed randomly chosen from within a predetermined range, and the rats ran in place until the treadmill stopped automatically and another small water reward was delivered. Subsequently the animals finished the trial by turning in the direction opposite from their entry to the stem (spatial alternation) to arrive at a water port at the end of a goal arm. Our strategy in distinguishing behavior, location, time, and distance was to “clamp” the behavior and location of the animal on the maze, and vary the treadmill speed to decouple the distance the rat traveled from the time spent on the treadmill. Multiple analyses showed that the activity of most hippocampal neurons that were active when the rat was on the treadmill could not be attributed to residual variations in location, but were heavily influenced by time and distance. Most neurons were influenced to differing extents by both time and distance, but some were best characterized as representing time but not distance and others as representing distance and not time.

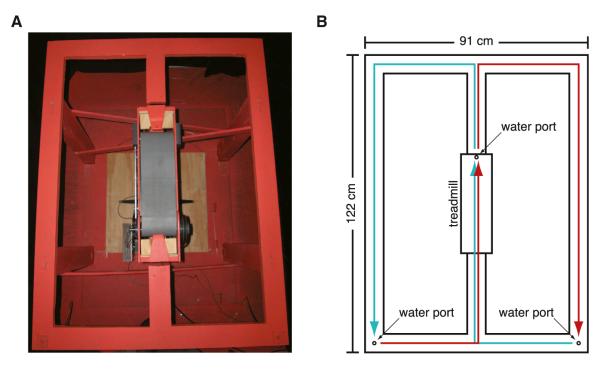
Figure 1. Figure-Eight Maze with Treadmill.

(A) Picture of the figure-eight maze with treadmill (gray belt) located in the center stem.

(B) Diagram of the figure-eight maze indicating the dimensions and location of the water ports and treadmill. Cyan line indicates right-to-left alternation; red line indicates left-to-right alternation.

See also Movie S1.

RESULTS AND DISCUSSION

Behavior and Location

During treadmill running, the rats’ heads were consistently facing forward, and 75% of the time spent on the treadmill could be accounted for by an area with a radius of approximately 3.3 cm (average area: 35 cm²; standard deviation: 15.9 cm²; range: 12 to 59 cm²). This indicates that the location of the rats’ heads were generally consistent despite fluctuations in position due to side-to-side, forward, and backward shifts on the treadmill. Thus, our “clamping” of behavior and location was largely successful, although minor variations persisted, and were taken into account in subsequent analyses. The variation in head and body location during treadmill running can be visualized in the supplemental movie (see Movie S1 available online). We refer to the area accounting for 75% of the time spent on the treadmill in a particular session as A₇₅.

Neuronal Population

The following analysis focuses on 18 recording sessions from 6 rats, containing a total of 927 putative pyramidal cells (average: 52 per session; standard deviation: 25; range: 15 to 102). Units with an average firing rate over the entire session of greater than 8 Hz were considered putative interneurons and were excluded from further analysis. Of the total population of putative pyramidal cells, 400 (43%) had an average firing rate of at least 0.2 Hz and peak firing rate of at least 1 Hz during periods when the treadmill was moving (average: 22 per session; standard deviation: 10; range: 9 to 50), while 625 (67%) had an average firing rate of at least 0.2 Hz and peak firing rate of at least 1 Hz during the remainder of the session (average: 35 per session; standard deviation: 16; range: 9 to 65). The overlap of these populations consisted of 312 (34%) cells that were active on both the treadmill and the remainder of the maze (average: 17 per session; standard deviation: 8; range: 6 to 37). These results are similar to those found by Pastalkova et al. (2008) and show that significantly more neurons were active on the treadmill than would be expected if they were simply hippocampal place cells with place fields on the treadmill.

The remaining analysis focuses on the time between the start and stop signal sent to the treadmill on each run and includes only those neurons that were active during those periods on the treadmill, unless stated otherwise. The center water port was activated (producing an audible click) simultaneously with the stop signal, so although the treadmill did not stop instantaneously, spikes occurring after the stop signal, during the deceleration of the treadmill, were not included in our analysis.

Hippocampal Neurons Fire in Sequences during Treadmill Running

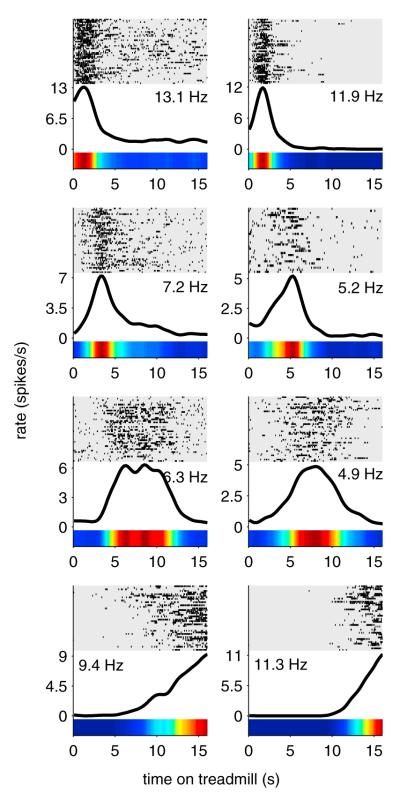
Similar to previous reports (Gill et al., 2011; MacDonald et al., 2011; Pastalkova et al., 2008), the majority of neurons active on the treadmill fired transiently at specific moments during running, rather than firing continuously the entire time the treadmill was active. Figure 2 shows representative firing patterns from eight different neurons during treadmill running. As an ensemble, these firing fields spanned the entire time on the treadmill (Figure 3). Therefore, at any one point during treadmill running a subset of hippocampal neurons were firing, and the subset of neurons changed in a regular sequence that repeated every treadmill run. Examples of three neurons, recorded concurrently, are provided in Movie S1.

Figure 2. Treadmill Firing Fields.

Firing patterns from eight different neurons active on the treadmill during “time-fixed” sessions. Each row on the raster plots represents one run on the treadmill, aligned to the time the treadmill started. Rows are sorted with the slowest treadmill speed on top and fastest speed on bottom. Black lines and color bars represent average firing rates over all runs. Numbers indicate peak firing rates in spikes per second (Hz). See also Movie S1.

Figure 3. Ensemble Activity Spans Entire Treadmill Run.

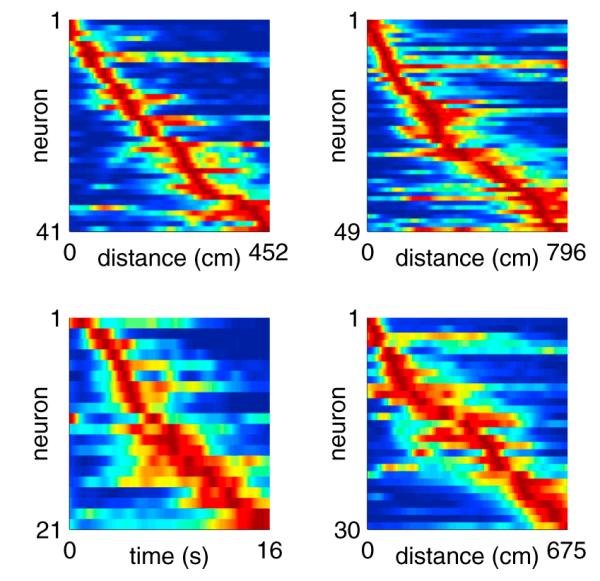
Each panel includes data from a single session. Each row represents the normalized firing rate of one neuron, sorted by the peak firing time. Neurons were included if they fired ≥0.2 Hz averaged across the entire treadmill run, with peak firing ≥1 Hz. The top two panels and bottom right panel are from “distance-fixed” sessions. The bottom left panel is from a “time-fixed” session. In each row, blue represents no firing (zero spikes per second), and red represents peak firing for that particular neuron.

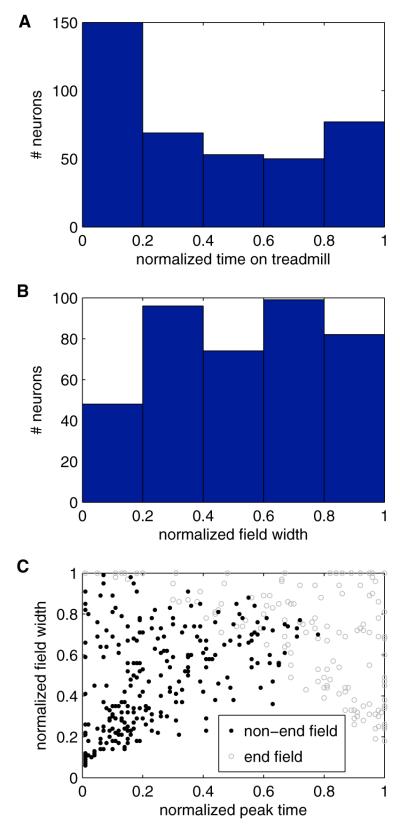
Across the entire population, the normalized peak firing time (time of peak firing divided by the duration of each lap, see caption for Figure 4) for each neuron occurred in the first, second, third, fourth, and last 1/5 of the treadmill run in 38%, 17%, 13%, 13%, and 19% of the neurons, respectively (Figure 4A). Normalized firing field widths (duration of firing field divided by the duration of each lap) ranged from 0.06 to 1 (6% to 100% of the treadmill run) (Figure 4B). When considering only the 256 neurons whose firing fields ended before the treadmill stopped, the normalized peak firing time and firing field width for each neuron were linearly correlated (Pearson’s linear correlation coefficient: 0.50; p = 2 × 10⁻¹⁷) (Figure 4C) with larger field widths for fields occurring closer to the end of the treadmill run.

Figure 4. Firing Fields Span the Entire Time on Treadmill.

(A) Histogram showing the distribution of the normalized peak firing times. A normalized time value of 1 indicates the moment the stop signal was sent to the treadmill. In this figure, and the corresponding analysis, time was normalized by dividing time by the duration of each individual lap, such that data from “distance-fixed” session was normalized based on distance traveled, while data from “time-fixed” sessions was normalized based on time elapsed.

(B) Histogram showing the distribution of normalized field widths (defined as the extent of firing at least 20% of the peak rate). A field width of 1 indicates the field extended across the entire treadmill run.

(C) The normalized field widths plotted against the normalized peak firing time. The neurons are subdivided based on whether their firing fields ended before the treadmill stopped (black dots) or whether the edge of the field reached the end of the treadmill runs (gray circles). Peak time and field width were correlated among the fields that did not reach the end of the treadmill run (Pearson’s linear correlation coefficient: 0.50; p = 2 × 10⁻¹⁷). The distinct pattern seen among the fields observed at the end of the treadmill run is a result of many of those fields being truncated when the treadmill abruptly stopped, such as in the bottom two examples in Figure 2.

Hippocampal Activity during Treadmill Running Cannot be Explained by Spatial Position

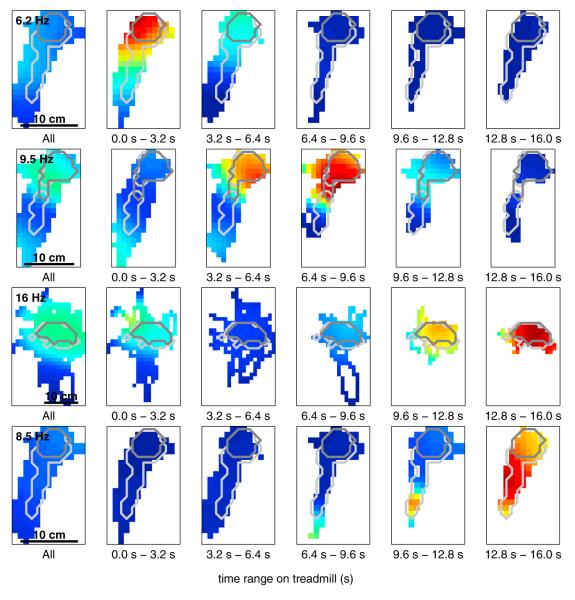
To visualize the space occupied by the rats as a function of time on the treadmill, and to determine whether the spatial firing patterns of a single neuron changed as time progressed on the treadmill, we generated occupancy-normalized firing rate maps (which we also refer to as spatial tuning curves) for each neuron, both for the overall session on the treadmill, and again for five evenly divided bins of time spent on the treadmill (Figures 5 and S1). The colored pixels in the image denote firing rates within 1 cm² spatial bins that were visited at least once during treadmill running overall (first panel) or within one of the time bins during treadmill running (remaining panels). We defined an area—referred to as A_AT (“AT” stands for “all time-bins”) to distinguish it from A₇₅ defined earlier—containing all spatial bins that were visited at least once in each time bin across the entire treadmill run. The average size of A_AT was 52 cm² (standard deviation: 22.1 cm²; min: 20 cm²; max: 106 cm²), and the rats spent on average 74% of their time on the treadmill within this area (standard deviation: 10%; min: 55%; max: 89%). A_AT contained, on average, 82% of A₇₅ (standard deviation: 14%; min: 57%; max: 100%) indicating that the rats’ positions were relatively stable throughout the time spent on the treadmill, and each rat spent a majority of their time in the same area throughout this period.

Figure 5. Spatial Distribution of Firing Rates on the Treadmill Depends on Time.

Each row represents the spatial distribution of firing rates for a single neuron during treadmill running. The left-most panel on each row shows the overall firing rate map (spatial tuning curve) for the entire time on the treadmill. The remaining five panels show the firing rate map for each of five evenly divided bins of time spent on the treadmill. The light gray and dark gray outlines indicate the extent of A_AT and A₇₅ (respectively) for that session. Both outlines are duplicated across panels to aid comparison. In each rate map: white represents areas that were not visited by the rat during that period of time; blue represents no firing (zero spikes per second) in a visited location; red represents peak firing for that particular neuron. The number in the upper-left corner of the first panel indicates peak firing rate in spikes per second (Hz). The color scale is consistent across panels within a row to allow for comparison across panels. See Figure S1 for additional examples.

The light gray outlines indicate the extent of A_AT, and the dark gray outlines indicate the extent of A₇₅ for that session. Despite some changes in spatial location across time bins, in each of the neurons shown in Figure 5 the firing rate can be seen to vary from one time bin to the next within A_AT. A two-factor ANOVA of both position and time indicated that 92% of neurons active on the treadmill (366/400) significantly changed their firing rate across time bins (significant main effect of time; p ≤ 0.05), indicating that the activity of these neurons was significantly influenced by time (MacDonald et al., 2011).

To quantitatively evaluate the extent to which the observed firing patterns could be explained based on location alone, we used the spatial firing rate map of each neuron as a look-up table to generate predicted firing rates for that neuron based on the rat’s position at each moment in time (see Experimental Procedures). We next generated two temporal tuning curves showing the firing rate of that neuron as a function of time spent on the treadmill for both the actual firing (the empirical temporal tuning curve) and the firing predictions based solely on the spatial firing rate map (the model temporal tuning curve) (Figure 6) (see Experimental Procedures). If location is sufficient to explain the observed firing patterns of each neuron, then the two tuning curves for that neuron should match. Alternatively, if the rat was perfectly stationary while on the treadmill, or if the firing of that neuron was completely uncorrelated with location, the model temporal tuning curve should be perfectly flat.

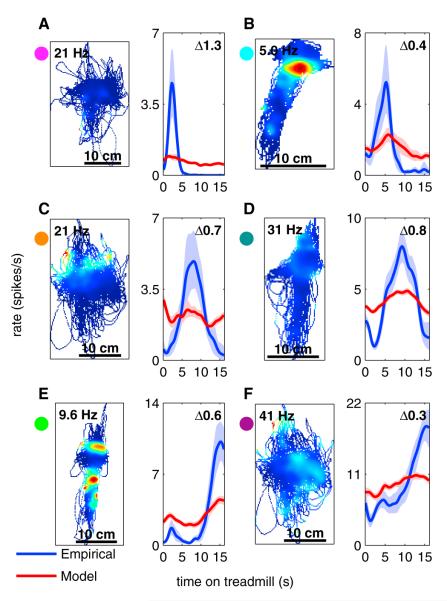
Figure 6. Spatial Activity Cannot Account for Temporal Activity.

The letters (A) through (F) indicate individual neurons recorded from different recording sessions. For each neuron there are two panels. The left panel is a spatial firing rate map, while the right panel includes two temporal tuning curves. The blue curve is the observed (empirical) temporal tuning curve of a single neuron, calculated based on the actual firing of that neuron. The red curve is the model-predicted temporal tuning curve based on the spatial firing-rate map given in the left panel of each pair. Shaded region denotes 95% confidence bounds on firing rate calculated using a bootstrap method. A bin size of 1 pixel × 1 pixel with a standard deviation of 3 pixels was used for this analysis (see Experimental Procedures). See Figure S5B for a comparison of the results from this analysis to the results from the GLM. The difference score calculated for each neuron is indicated in the upper-right corner of the right panels and in Figure S5B. The colored circles next to each neuron correspond to the colored circles in Figure S5B.

A bootstrap method was used to generate confidence intervals around each temporal tuning curve and to identify regions where the two curves were significantly different (see Experimental Procedures). Although nearly all neurons showed some degree of spatial tuning (indicated by a nonflat model tuning curve), in each example shown in Figure 6, and in the majority of hippocampal neurons, there was a region of significant difference between the empirical and model tuning curves, indicating that information about location was not sufficient to explain the firing activity seen on the treadmill.

Each neuron was assigned a “difference score” ranging from 0 (identical) to 2 (nonoverlapping), quantifying the difference between their empirical and model tuning curves (see Experimental Procedures). This difference score was compared to the results from the generalized linear model discussed below (Figure S5).

Hippocampal Activity during Treadmill Running Is Influenced by Both Distance and Time

On each trial, the treadmill speed was randomly selected from within a predetermined range over which the rat’s behavior was consistent (typically 35 to 49 cm/s). By randomizing the treadmill speed, we were able to decouple the distance the rat traveled on the treadmill from the time spent on the treadmill, and evaluate the effects of each variable on firing patterns. Figure 7 shows raster plots for four different neurons (one neuron per row) plotted as a function of both the time since the treadmill started (left panels) and distance traveled since the treadmill started (right panels). Although the speeds were randomly presented during the recording session, the rows in the raster plots represent treadmill runs sorted in order of slowest speed (top row) to fastest speed (bottom row) to highlight the effects of varying speed on firing patterns. Within an individual session, either the time spent on the treadmill (“time-fixed” sessions) or the distance traveled on the treadmill (“distance-fixed” sessions) was held fixed for each run. All examples shown in Figures 2, 5, 6, and S1 were recording during time-fixed sessions, but statistics in the text and Figures 3 and 4 included both time-fixed and distance-fixed sessions. It is important to note that it is impossible to completely separate time and distance as long as the rat is still running on the treadmill. Moreover, the effects of varying speed becomes more pronounced as time elapses, making the effect of aligning to time versus distance more easily visualized at the end of the treadmill run than the beginning. For this reason, the most visually distinct examples among those included in Figures 7 and S2 typically fire at the end of the treadmill run.

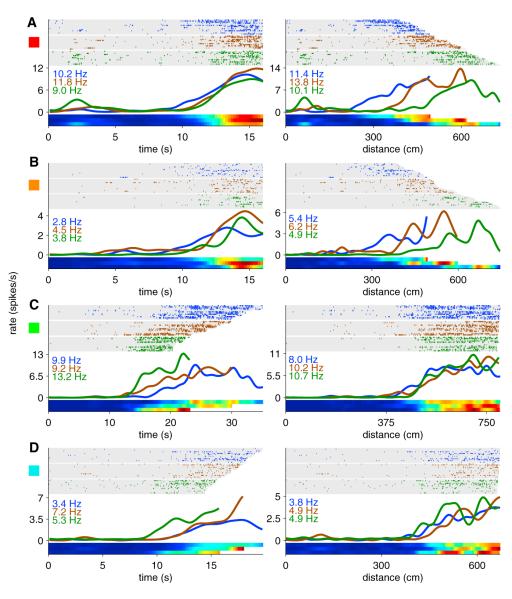
Figure 7. Hippocampal Coding for Time and Distance.

Examples of two cells that were more strongly influenced by time (A and B) and two cells that were more strongly influenced by distance (C and D). For each neuron, the same firing activity is plotted both as a function of time since the treadmill started (left panels) and distance traveled on the treadmill (right panels). Blue, brown, and green ticks (and tuning curves) represent the slowest 1/3 of runs, middle 1/3 of runs, and fastest 1/3 of runs, respectively. Numbers in blue, brown, and green indicate the peak firing rate in spikes per second (Hz) of the corresponding group of runs. The rows in the raster plots represent treadmill runs sorted in order of slowest speed (on top) to fastest speed (on bottom). Colored squares to the left edge of each neuron correspond to colored squares in Figures 8A and S3. See Figure S2 for additional examples. The activity of these neurons on the remainder of the maze can be seen in Figure S3.

Figures 7A and 7B show two example neurons whose firing is best accounted for as occurring at the same time regardless of the treadmill speed. Although the firing fields were aligned with each other when plotted as a function of time (left panels), when the same data were plotted as a function of distance (right panels) the fields shifted toward longer distances as the speed increased, suggesting that these neurons were more accurately encoding time. Figures 7C and 7D show two neurons whose firing is best accounted for as occurring at the same distance, regardless of the time it took the rat to travel that distance. Note that when the firing fields were plotted as a function of time the fields shifted toward shorter times as the speed increased, suggesting that these neurons were more accurately encoding distance.

If a neuron is more accurately reflecting time than distance, the temporal tuning curve for slow runs should align with the temporal tuning curve for fast runs (Figures 7A and 7B). However, the same tuning curves plotted as a function of distance should be shifted toward longer distances on fast runs when compared to slow runs (i.e., if the treadmill is moving faster, the rat travels farther in the same amount of time). However, if the neuron is more accurately reflecting distance than time, the temporal tuning curve for fast runs should be shifted toward shorter times when compared to slow runs (i.e., if the treadmill is moving faster, it takes less time to travel the same distance) (Figures 7C and 7D). Additional examples are included in Figure S2.

These results demonstrate the existence of both hippocampal cells that more accurately encode the time the rat has spent on the treadmill and hippocampal cells that more accurately encode the distance the rat has run on the treadmill. The firing activity of these cells during periods when the rat was traversing the maze, excluding periods of treadmill running, can be seen in Figure S3. Of note, neurons identified as responding more accurately to time or more accurately to distance based on their activity during treadmill running often expressed standard place fields in other regions of the maze when the treadmill was off.

Hippocampal Neuronal Activity Reflects Location, Time, and Distance

While the results from the previous section indicated whether neurons were more accurately representing time or distance, this method did not take into account possible influences of spatial location. To simultaneously and quantitatively examine the extent to which each neuron was influenced by location, time, and distance, we fit the spiking of each neuron to a generalized linear model (GLM) that included treadmill time, treadmill distance, spatial position (x and y room coordinates), treadmill speed, and spike history as covariates (see Experimental Procedures) (Lepage et al., 2012; MacDonald et al., 2011). We then refit the data using six nested models (Figure S4A). Each nested model removed one or more categories of covariates (time, distance, or space) from the full model. The first three nested models (space and time [“S+T”], time and distance [“T+D”], and space and distance [“S+D”]; middle row, Figure S4A) removed only one category of covariates (distance, space, and time, respectively). The remaining three nested models (time [“T”], space [“S”], and distance [“D”]; bottom row, Figure S4A) removed two categories of covariates. The deviance of each nested model compared to the full model quantified the effect of removing that category of covariates on the quality of the model fit. Covariates related to treadmill speed and spike history were included in all nested models.

We first tested the space (“S”) nested model, which included covariates from space (as well as speed and spike history), but excluded time and distance covariates. The deviance of the “S” model from the full model quantified the effect of removing both time and distance covariates from the full model, while accounting for any influence due to spatial movement. Thus, comparing the “S” model to the full “S+T+D” model measured the combined importance of distance and time in the model. The results from this model indicated that for 380/400 neurons, combined information about time and distance on the treadmill significantly improved the model fit (95%; χ²₁₀ > 18.3; p ≤ 0.05) (Figure S4B). A similar comparison of the time and distance (“T+D”) nested model to the full model indicated that 371/400 neurons showed spatial modulation (93%; χ²₅ > 11.1; p ≤ 0.05) in addition to the modulation due to time and distance (Figure S4C). These results are consistent with the results above (Figure 5), and show that although many neurons did demonstrate spatial tuning as a result of minor residual variations in location, the majority of neurons demonstrated time and distance tuning in addition to spatial tuning.

Like the tuning curve method used earlier to show that hippocampal activity during treadmill running cannot be explained by spatial position (Figure 6), the “S” GLM used only spatial covariates to account for the firing properties of each neuron. The difference score from the earlier turning curve method measured how different the model prediction (using only space) was from the actual firing, and larger values indicated a larger role of time and distance in driving firing. Similarly, the deviance of the “S” GLM (using only space) from the full model (including time and distance) measured the importance of time and distance in the quality of the model fit (Figure S4B). These two distinct approaches model the firing of neurons using very different assumptions. The tuning curve method is a nonparametric method that builds a spatial firing rate map without making assumptions about the shape of that map (Figure 6). The GLM, however, attempts to fit the spatial firing rate map of the neuron to a function with five parameters (see Experimental Procedures, Equation 4). We found a strong correlation between the difference score and the deviance of the “S” model from the full model (Pearson’s linear correlation coefficient: 0.49; p = 2 × 10⁻²⁴) (Figure S5B) indicating that the results from these two methods agree with one another, and the finding that hippocampal activity during treadmill running cannot be explained by spatial position does not depend upon the assumptions made by either model.

As noted previously, it is impossible to completely separate time and distance as long as the rat is running on the treadmill, and the results from analyzing the “S” model refer to the combined influences of time and distance. However, the randomized treadmill speed did allow us to also consider the components of time and distance that were independent from one another. The space and time (“S+T”) and space and distance (“S+D”) nested models allowed us to determine the influence on the model fit of adding information about distance to a model that already included time (“S+T” versus “S+T+D”) or adding time to a model that already included distance (“S+D” versus “S+T+D”) to show the independent effects of each variable. This analysis indicated that distance (in addition to time and space) was informative in 314/400 neurons (79%, χ²₅ > 11.1, p ≤ 0.05), while time (in addition to distance and space) was informative in 326/400 neurons (82%, χ²₅ > 11.1, p ≤ 0.05) (Figure 8A). Both distance and time were independently informative in 284 neurons (70%), while neither distance nor time were independently informative in 44 neurons (11%). Of particular note are 42 neurons (11%) that showed distance but not time as informative, and 30 neurons (8%) that showed time but not distance as informative (Figure 8A). These results demonstrate that while the majority of neurons were influenced by both time and distance, individual neurons varied in their degree of tuning to either time or distance. At the extremes of this distribution, some neurons exclusively signaled time and other neurons exclusively signaled distance.

Figure 8. GLM Comparison of Time versus Distance.

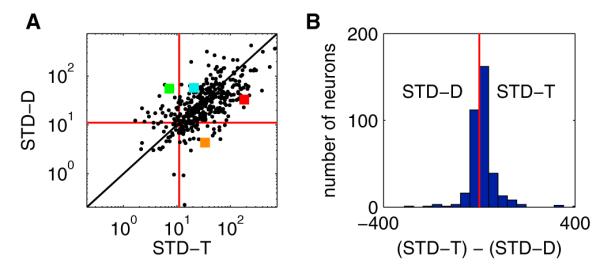
(A) x values are the deviances of the space and distance (“S+D”) model from the full (“S+T+D”) model (the result of removing time from the full model, hence the label “STD-T”). A larger x value indicates a more significant contribution from time. y values are the deviances of the space and time (“S+T”) model from the full (“S+T+D”) model (the result of removing distance from the full model, hence the label “STD-D”). A larger y value indicates a more significant contribution from distance. Each point represents a single neuron. The red lines indicate the minimum thresholds for significance. Points in the upper-right quadrant had a significant influence of both distance and time. Points in the upper-left quadrant had a significant influence of just distance. Points in the lower-right quadrant had a significant influence of just time. Points in the lower-left quadrant were not significantly influenced by either time or distance. Points along the diagonal have an equal contribution from distance and time. Colored squares correspond to the examples shown in Figure 7.

(B) Histogram of the y values from (A) subtracted from the x values from (A). More positive values indicate a larger contribution from time; more negative values indicate a larger contribution from distance. Red line is at 0 (equal contribution of time and distance, the diagonal line in (A)). This figure shows that while the majority of neurons were influenced by both time and distance, individual neurons varied in their degree of tuning to either time or distance, with some neurons responding exclusively to time and other neurons responding exclusively to distance.

See Figure S4 for additional results from the GLM. See Figure S5B for a comparison of the results from the GLM to the results from Figure 6.

For all 356 neurons that showed a significant contribution of either time or distance, we subtracted the deviance of the “S+T” model from the deviance of the “S+D” model to obtain a measure of the tuning of each neuron for either time or distance. Values greater than zero indicate a stronger tuning to time whereas values less than zero indicate a stronger tuning for distance. Using this metric, 220/356 neurons (62%) were more tuned to time and the remaining 136 neurons (38%) were more tuned to distance (Figure 8B). We used a similar analysis to compare the effects of space to time and space to distance (Figures S4D–S4G), showing that 240/380 neurons (63%) were more heavily influenced by time than space, while 236/380 neurons (62%) were more heavily influenced by distance than space.

To determine whether time and distance were being represented concurrently or whether the hippocampus was switching between separate representations of time and distance (Jezek et al., 2011), we examined whether neurons at opposite extremes of the distribution seen in Figure 8 were active together within the same theta cycles (see Supplemental Experimental Procedures). We found that even neurons only responding significantly to time (distance not informative in the GLM analysis described above) fired within the same theta cycle as neurons only responding significantly to distance (time not informative), suggesting that the hippocampus is representing both time and distance simultaneously (Figure S6).

Overall, these results demonstrate that hippocampal neurons are capable of encoding a range of contextual variables—including time and distance as well as spatial location—and that each individual neuron is influenced to a different degree by each of these variables. However, in this behavioral paradigm, where spatial location was held relatively fixed, time and distance played a larger role in driving hippocampal firing.

Time versus Path Integration in Hippocampal Neurons

In 1987, Muller and colleagues introduced the “random foraging” task, in which rats search continuously in all directions and locations to find food scattered throughout their environment (Muller et al., 1987). Their aim was to “clamp” behavior (as foraging) and vary direction randomly to determine whether a spatial signal would emerge in hippocampal neuronal firing patterns. This strategy was highly successful in that hippocampal place fields were readily identified. Notably, in this situation where head and movement direction were unsystematic and irrelevant to the task, the firing patterns of hippocampal neurons were not influenced by head or movement direction. However, when direction becomes meaningful, such as in the radial maze (McNaughton et al., 1983), the linear track (Huxter et al., 2003), or in open fields as animals run specific trajectories (Markus et al., 1995; Wiener et al., 1989), direction begins to influence these firing patterns. Furthermore, across many experimental paradigms, hippocampal neuronal activity reflects the relevant stimulus and behavioral regularities that characterize the task at hand (e.g., Ranck, 1973; Eichenbaum et al., 1990; Lenck-Santini et al., 2008; reviewed by Eichenbaum et al., 1999). In a task where rats were required to remember odors across multiple locations in an open field, hippocampal firing patterns reflected to an equivalent extent the odors and locations, and most cells were tuned variably to both parameters (Wood et al., 1999).

During the treadmill running described in the present experiment, we held behavior and location relatively constant while systematically varying time and distance. We found that hippocampal neurons fired transiently at specific moments during treadmill running, and that this firing could not be explained by residual variations in location.

As with previous experiments that examined hippocampal firing during task delays (Gill et al., 2011; MacDonald et al., 2011; Pastalkova et al., 2008), at any one point during treadmill running, a subset of hippocampal neurons were firing and the subset of neurons changed in a regular sequence that repeated during every treadmill run. This sequential firing could underlie the ability of the hippocampus to encode temporal aspects of episodic memory, by serving as a time-based template upon which new memories are stored and later recalled. This is important for disambiguating memories that share spatial locations (Hasselmo, 2009, 2012).

By systematically varying time and distance, we were also able to separate the influences of time and distance on firing and measure the extent to which each variable influenced firing. Our main finding is the prevalent observation of both cells that more accurately encoded the distance the rat has run on the treadmill and cells that more accurately encoded the time the rat has spent on the treadmill. The observation of distance coding in this task indicates that hippocampal neurons can integrate the length of a path even in the absence of visual cues usually associated with movement through space. Also, the presence of cells that signal distance indicates that these neurons are not driven entirely by network dynamics without the influence of either idiothetic or allothetic cues, as suggested by Pastalkova et al. (2008) (see also Itskov et al., 2011), as the neurons must be responding to the treadmill speed, or self-motion cues influenced by the treadmill speed, in order to encode distance. In addition, the observation of cells whose activity was significantly influenced by only time indicates that these neurons are also not exclusively driven by path integration (Etienne and Jeffery, 2004; McNaughton et al., 1996, 2006). Rather, in the present study where both of these dimensions are prominent, our results show that the hippocampus represents both the distance traveled and time elapsed simultaneously. Furthermore, a large fraction of hippocampal neurons combine information about these dimensions to varying extents, such that different neurons largely reflected distance or time and others equivalently reflected the combination of these dimensions.

Due to the residual correlation between time elapsed and distance traveled, we cannot say with certainty whether those neurons that were influenced by both time elapsed and distance traveled were encoding both time and distance simultaneously or whether the hippocampus was shifting between types of representations (such as was demonstrated in Jezek et al., 2011). However, we found that cells significantly influenced by only time and those significantly influenced by only distance regularly fired together (Figure S6), showing that both time and distance are being represented simultaneously in the hippocampus, and strongly suggesting that the remaining cells are conjunctively encoding both time and distance at all times.

In this experiment, when behavior and location were held relatively constant, time and distance predominated in their influence over the firing patterns of hippocampal neurons. However, other neurons, and many of the same neurons that were active on the treadmill, had place fields elsewhere on the maze (see Movie S1 and Figure S3), indicating that during other components of the task, where locations on the maze were important to task success, space was a strong influence over firing patterns of even the same neurons. These observations support the view that hippocampal neuronal activity reflects both the temporal and spatial regularities, along with other salient features of experience, all of which are reflected in our capacity for episodic memory.

EXPERIMENTAL PROCEDURES

Subjects and Behavioral and Electrophysiological Procedures

Subjects were six male Long-Evans rats kept on food and water restriction and monitored closely to maintain good health and a minimum of 85% free-feeding weight. All animal procedures were approved by the Boston University Institutional Animal Care and Use Committee.

On the first day of training rats were allowed to wander freely around a figure-eight maze consisting of a 122 cm × 91 cm (48” × 36”) rectangular track bisected lengthwise by a 122 cm (48”) long central stem (Figure 1). A 41 cm (16”) segment of the center stem was removed and replaced with a treadmill adapted from a commercially available treadmill (Columbus Instruments). Two ports for delivering water reward were located in the corners of the maze closest to the start of the central stem, and a third water port was located at the end of the treadmill. The water ports produced an audible click when they were activated.

For clarity, the term “session” is used to refer to an entire training or testing session (typically 40–60 min), “trial” is used to refer to one full lap on the maze (starting and ending at either the left or right water port), and “run” is used to refer to one period during which the treadmill was moving (from the moment the treadmill starts to the moment the stop command is sent to the treadmill). Beginning on the second day of training, rats started each session by being placed at the start of the central stem. Throughout training the rats were prevented from turning around. Once the rats progressed forward so their hind legs were on the treadmill they were given a small water reward and allowed ~2 s to drink. The treadmill was then turned on at a low speed (5–10 cm/s). The rat was blocked from running forward off the treadmill while the treadmill was moving. The treadmill run was manually aborted (and the treadmill stopped immediately) if the rat either turned around or if his hind legs reached the back edge of the treadmill. The treadmill run was restarted (using the same settings but restarting the elapsed time) once the rat returned to the treadmill facing forward. Aborted runs occurring during recording sessions were ignored in subsequent analyses. The rat was rewarded with another small water reward for running continuously until the treadmill stopped automatically. This reward typically caused the animal to spend the majority of its time on the treadmill with its mouth positioned close to the water port. The rat was then allowed to either remain on the treadmill, or to exit the treadmill and finish the lap. If the rat remained on the treadmill, the treadmill was started again using the same rules as before. When the rat exited the treadmill, he was forced to turn either left or right and rewarded for reaching the water port in the corner of the maze. Another trial was started when the rat reached the center stem.

During the first few trials, each run lasted only 5–10 s. As the rat grew accustomed to the treadmill, both the treadmill speed and the time required to receive a reward were gradually increased until the rat was consistently running 49 cm/s (maximum speed) for greater than 16 s. The rats took between 6 and 15 training sessions to reach this criterion. At this point, the protocol was changed to either a “distance-fixed” or a “time-fixed” protocol, and the rat was required to complete one trial for each run on the treadmill. In both protocols the speed on each lap was randomly selected from within a predetermined range. The treadmill speed was held constant throughout each full treadmill run, and a new speed was randomly selected at the start of each treadmill run. In the “distance-fixed” protocol, the duration of each run was adjusted so that the distance traveled was constant regardless of the treadmill speed. In the “time-fixed” protocol, the duration of each run was kept constant regardless of the speed. The minimum speed was chosen based on the lowest speed in which the individual rat ran smoothly on the treadmill. If the treadmill runs too slowly, the rat stops running smoothly and instead repeatedly runs forward then rides the treadmill back. The maximum speed was limited by the endurance of the rat, and the need to run enough laps to fully sample the range of available speeds.

Once the rat was comfortable with the randomly varying speeds, the rats were trained to alternate from the left reward arm to the right reward arm until they consistently met criterion of steady running on the treadmill through the range of speeds used, for at least 40 trials per session, with at least 75% accurate alternation. The rats took between 2 and 7 training sessions to reach 75% accuracy, and as the addition of alternation often slowed down the animals, between 3 and 15 sessions to reach the combined requirement of 40 trials with 75% accuracy.

Following training, rats were implanted with microdrives containing 24 independently drivable tetrodes aimed bilaterally at the pyramidal cell layer of dorsal hippocampal CA1 (anterior-posterior [AP] = −3.2 mm; medial-lateral [ML] = ± 1.9 mm). Each tetrode consisted of four strands of 0.0005” (12.7 μm) Stablohm 800 wire (California Fine Wire Company, Grover Beach, CA) gold-plated to reduce impedance to between 180 and 220 kΩ at 1 kHz. At the end of surgery, each tetrode was lowered ~1 mm into tissue. Rats were allowed at least one week recovery before training resumed and the tetrodes were lowered into the CA1 layer. The amplitude and phase of theta waves, the amplitude and sign of sharp-wave events, and the presence of theta modulated complex spiking cells were used to localize CA1. After recordings were concluded, 40 μA of current were passed through each electrode for 30 s before perfusion and histological confirmation of tetrode placement.

Once any tetrode reached CA1, rats were tested for 40–60 min, including at least 40 laps per recording session. Electrical recordings were made using a 96 channel Multichannel Acquisition Processor (MAP) (Plexon Inc.). Each channel was amplified and band-pass-filtered for both high-frequency spiking activity (154 Hz–8.8 kHz) and low-frequency local field potentials (1.5 Hz–400 kHz). One local field potential per tetrode was continuously digitized at 1 kHz. Spike channels were referenced to another ipsilateral electrode to remove movement related artifacts. Action potentials were detected by threshold crossing and digitized at 40 kHz. Following recordings, action potentials belonging to single neurons were isolated (“cluster cutting”) using Offline Sorter (Plexon Inc).

Each day, 5 min of data were acquired while the rat rested on a stool prior to recording, and the peak value of each waveform on each electrode was plotted against the peak value of the waveform on other electrodes within the same tetrode. The decision to record on that day was based on whether a visual inspection of the clusters identified units that had not been previously recorded. To reduce the likelihood of analyzing the same neuron across multiple recording sessions, the data analyzed in this paper do not include any sessions recorded less than three days apart.

For three of the six rats, recordings were made during both “distance-fixed” and “time-fixed” sessions. With these rats, the initial recordings were made using the same protocol used during the final stage of training (either “distance-fixed” or “time-fixed”). After several recordings with the initial protocol, the protocol was switched from “distance-fixed” to “time-fixed” (or vice versa). The protocol was never changed mid-session, and the recording from the first full session with the new protocol was not included in the analysis for this paper. For the remaining three rats the same protocol was used throughout the life of the animal (for training and recording sessions).

Analysis Methods

Following cluster cutting, all data analysis was performed using custom scripts for MATLAB. Tuning curves indicating the average firing rate of a single unit as a function of spatial position, time spent on the treadmill, or distance traveled on the treadmill (Figures 2, 3, 5, 6, 7, S1, S2, and S3), were calculated by first binning the respective variable, and counting the spikes occurring and the amount of time spent in each bin. The spike counts and occupancy times in each bin were independently smoothed by convolving with a Gaussian smoothing kernel, then the spike counts were divided by the occupancy times to calculate the average firing rate. For spatial tuning curves (also referred to as spatial firing rate maps) in Figures 5 and S1, we used 1 cm × 1 cm bins and a circularly symmetrical Gaussian kernel with a standard deviation of 3 cm. For spatial tuning curves in Figure 6 and corresponding analysis we used 1 camera pixel square bins (approximately 0.2 cm × 0.2 cm) with a standard deviation of 3 pixels. For spatial tuning curves in Figure S3 we used 2 cm × 2 cm bins with a standard deviation of 6 cm. For temporal tuning curves (time spent on the treadmill, Figures 2, 3, 6, 7, and S2), we used 200 ms bins and a Gaussian kernel with a standard deviation of 600 ms. For distance (traveled on the treadmill) tuning curves (Figures 3, 7, and S2), we used 5 cm bins and a Gaussian kernel with a standard deviation of 15 cm.

In the ensemble temporal tuning curves presented in Figure 3, each row represents the temporal tuning curve for a single neuron, normalized by dividing by the peak firing rate of that neuron. For distance-fixed sessions, activity was plotted in units of distance, and for time-fixed sessions activity was plotted in units of time. All neurons active on the treadmill during a single session were included, sorted by their peaking firing time or distance.

To quantify a rat’s movement through physical space during treadmill running, we divided the space occupied during treadmill running into 1 cm × 1 cm bins and counted the number of video frames the rat spent in each spatial bin. We then ranked the bins in order of decreasing time and counted the number of bins required to reach 75% of the total time spent on the treadmill. This number was then multiplied by the area of each bin (1 cm²) to get the area that accounted for 75% of the time spent on the treadmill. We refer to this area as A₇₅, and the smaller the value of A₇₅, the less the rat moved through space while on the treadmill.

We next quantified the degree to which the rat’s location systematically varied as a function of the time spent on the treadmill. To do this, we took either the distance (for distance-fixed sessions) or the time (for time-fixed sessions) spent on the treadmill and divided it into five evenly divided “time” bins. We then counted the number of spatial bins that were occupied at least once in each “time” bin and multiplied that number by 1 cm² to get the area that was visited consistently across the entire treadmill run. We refer to this area as A_AT (“AT” stands for “all time bins”) to distinguish it from A₇₅. If the rat’s position systematically changed over the time spent on the treadmill, then A_AT would be much smaller than A₇₅. However, if the rat’s movements were small and uncorrelated with time, then both A₇₅ and A_AT would be small and would largely overlap one another (Figures 5 and S1).

To determine whether the spatial tuning curve of a single neuron changed as time progressed on the treadmill, we used a two-factor ANOVA with spatial bin and “temporal” bin as two factors (MacDonald et al., 2011). We included only those spatial bins that were occupied at least once in each “time” bin (bins located within A_AT) in the ANOVA. We considered a neuron as having a significant change in firing rate as a function of time when the ANOVA produced a main effect of time (p ≤ 0.05).

To test the theory that the observed temporally-modulated firing patterns could be entirely explained by the movement of the rat through space (i.e., place fields), we used the spatial tuning curve for each individual neuron to predict the firing rate of that neuron at each point in time. We started by using the rat’s actual spatial position (x and y room coordinates) and spike counts (sampled at 30 Hz) to generate a traditional occupancy normalized spatial tuning curve based on the firing of each neuron as described above (using 1 camera pixel square bins [approximately 0.2 cm × 0.2 cm] and a standard deviation of 3 pixels). Then we used the spatial tuning curve as a look-up table: for each video frame we looked up the rat’s actual spatial coordinates in the spatial tuning curve to predict the firing rate of the neuron in that video frame. The result is two vectors for each neuron: one containing the actual spike counts for each video frame and another containing the predicted firing rate based purely on the spatial tuning curve and the rat’s trajectory. We then divided the time spent on the treadmill into 200 ms bins and generated two occupancy-normalized temporal tuning curves for each neuron: (1) an empirical temporal tuning curve which gave the actual average firing rate of the neuron for each time bin and (2) a model temporal tuning curve which used the predicted firing rates to calculate the average firing rate for each time bin. We then used a bootstrap method to generate confidence intervals around each temporal tuning curve. We generated N (N = 1,000) bootstrap samples by randomly sampling (with replacement) a subset of all the treadmill runs. For each bootstrap sample, we calculated a temporal tuning curve for both the actual (empirical) firing rates and predicted (model) firing rates, and then calculated the difference between these two tuning curves for each time bin. The result was N empirical tuning curves, N model tuning curves, and N difference curves which were used to generate 95% confidence bounds on each temporal tuning curve and the difference curve (Figure 6).

We considered significant any time bins in which zero fell outside the confidence bounds of the difference curve, and we considered the empirical and model curves different if they were significantly different in at least one time bin. To quantify the difference between the empirical and model tuning curves for each neuron, both curves were normalized so the area under each curve was 1, then the area between the curves was calculated to assign each neuron a “difference score” ranging from 0 (identical) to 2 (nonoverlapping) (Figure S5).

Generalized Linear Model (GLM)

A GLM framework was used to quantify the effects of time, distance, and position on neural activity (Dobson, 2002; Lepage et al., 2012; MacDonald et al., 2011; McCullagh and Nelder, 1989; Truccolo et al., 2005). For this analysis the spiking activity was modeled as an inhomogeneous Poisson process with the firing rate a function of various covariates that modulate spiking activity (Lepage et al., 2012; MacDonald et al., 2011). During treadmill running, the spiking activity was modeled as

$${\lambda }_{\mathrm{S}+\mathrm{T}+\mathrm{D}}\left(\mathrm{t}\right)={\lambda }_{\text{time}}\left(\mathrm{t}\right)\cdot {\lambda }_{\text{distance}}\left(t\right)\cdot {\lambda }_{\text{space}}\left(\mathrm{t}\right)\cdot {\lambda }_{\text{speed}}\left(\mathrm{t}\right)\cdot {\lambda }_{\text{history}}\left(\mathrm{t}\right)$$ (Equation 1)

Here λ_{s + t + d}(t) is the probability of a spike within each 1 ms time bin (“S,” “T,” and “D,” stand for “space,” “time,” and “distance,” respectively). ln(λ_time(t)) is a fifth-order polynomial of time relative to the start of each treadmill run (Equation 2), ln(λ_distance(t)) is a fifth-order polynomial of the distance the belt moved since the start of each treadmill run (Equation 3), λ_space(t) is a Gaussian shaped place field composed of five parameters (Equation 4) ln(λ_speed(t)) is a first-order polynomial of the treadmill speed (Equation 5), and λ_history(t) contains the spiking history of the neuron (Equation 6).

$${\lambda }_{\text{time}}\left(\mathrm{t}\right)={\mathrm{e}}^{{\sum }_{\mathrm{i}=1}^5{\alpha }_{\mathrm{i}}\tau {\left(\mathrm{t}\right)}^i}$$ (Equation 2)

$${\lambda }_{\text{distance}}\left(\mathrm{t}\right)={\mathrm{e}}^{{\sum }_{\mathrm{i}=1}^5{\beta }_{\mathrm{i}}\mathrm{d}{\left(\mathrm{t}\right)}^i}$$ (Equation 3)

$${\lambda }_{\text{space}}\left(\mathrm{t}\right)={\mathrm{e}}^{{\gamma }_1\times \left(\mathrm{t}\right)+{\gamma }_2\times {\left(\mathrm{t}\right)}^2+{\gamma }_3\mathrm{y}\left(\mathrm{t}\right)+{\gamma }_4\mathrm{y}{\left(\mathrm{t}\right)}^2+{\gamma }_5\times \left(\mathrm{t}\right)\mathrm{y}\left(\mathrm{t}\right)}$$ (Equation 4)

$${\lambda }_{\text{speed}}\left(\mathrm{t}\right)={\mathrm{e}}^{{\delta }_1+{\delta }_2\mathrm{s}\left(\mathrm{t}\right)}$$ (Equation 5)

$${\lambda }_{\text{history}}\left(\mathrm{t}\right)={\mathrm{e}}^{{\sum }_{\mathrm{i}=1}^5{\theta }_{\mathrm{i}}\mathrm{n}(\mathrm{t}-(\mathrm{i})\mathrm{ms},\mathrm{t}-(\mathrm{i}-1\left)\mathrm{ms}\right)+{\sum }_{\mathrm{i}=6}^{11}{\theta }_{\mathrm{i}}\mathrm{n}(\mathrm{t}-(25\mathrm{i}-120)\mathrm{ms},\mathrm{t}-(25\mathrm{i}-145\left)\mathrm{ms}\right)}$$ (Equation 6)

In Equation 2, τ(t) refers to the time since the treadmill last started, and the five α’s are parameters that control the degree to which the spike rate is modulated by time. In Equation 3, d(t) refers to the distance the treadmill belt has moved since the start of each treadmill run, and the five β’s are parameters that specify the influence of this distance on spike rate. In Equation 4, x(t) and y(t) refer to the spatial position (x and y room coordinates) of the rat at time t and five γ’s specify the influence of space on spike rate. In Equation 5, δ₁ is a constant representing the mean firing rate, s(t) refers to the treadmill speed at time t, and δ₂ specifies the influence of speed on spike rate. In Equation 6, n(t₁, t₂) is the number of spikes that occurred between times t₁ and t₂. The eleven history terms represent five 1 ms bins going back 5 ms (0–1 ms, 1–2 ms, 2–3 ms, 3–4 ms, 4–5 ms) and six 25 ms bins going back an additional 150 ms (5–30 ms, 30–55 ms, 55–80 ms, 80–105 ms, 105–130 ms, 130–155 ms). Each history term is modulated by one θ parameter.

Equation 1 represents the full model encompassing the influence of space, time, and distance on spiking activity (“S+T+D” model). We similarly defined six nested models (Figure S4A):

$${\lambda }_{\mathrm{S}+\mathrm{T}}\left(\mathrm{t}\right)={\lambda }_{\text{time}}\left(\mathrm{t}\right)\cdot {\lambda }_{\text{space}}\left(\mathrm{t}\right)\cdot {\lambda }_{\text{speed}}\left(\mathrm{t}\right)\cdot {\lambda }_{\text{history}}\left(\mathrm{t}\right)$$ (Equation 7)

$${\lambda }_{\mathrm{T}+\mathrm{D}}\left(\mathrm{t}\right)={\lambda }_{\text{time}}\left(\mathrm{t}\right)\cdot {\lambda }_{\text{distance}}\left(\mathrm{t}\right)\cdot {\lambda }_{\text{speed}}\left(\mathrm{t}\right)\cdot {\lambda }_{\text{history}}\left(\mathrm{t}\right)$$ (Equation 8)

$${\lambda }_{\mathrm{S}+\mathrm{D}}\left(\mathrm{t}\right)={\lambda }_{\text{distance}}\left(\mathrm{t}\right)\cdot {\lambda }_{\text{space}}\left(\mathrm{t}\right)\cdot {\lambda }_{\text{speed}}\left(\mathrm{t}\right)\cdot {\lambda }_{\text{history}}\left(\mathrm{t}\right)$$ (Equation 9)

$${\lambda }_{\mathrm{D}}\left(\mathrm{t}\right)={\lambda }_{\text{distance}}\left(\mathrm{t}\right)\cdot {\lambda }_{\text{speed}}\left(\mathrm{t}\right)\cdot {\lambda }_{\text{history}}\left(\mathrm{t}\right)$$ (Equation 10)

$${\lambda }_{\mathrm{S}}\left(\mathrm{t}\right)={\lambda }_{\text{space}}\left(\mathrm{t}\right)\cdot {\lambda }_{\text{speed}}\left(\mathrm{t}\right)\cdot {\lambda }_{\text{history}}\left(\mathrm{t}\right)$$ (Equation 11)

$${\lambda }_{\mathrm{T}}\left(\mathrm{t}\right)={\lambda }_{\text{time}}\left(\mathrm{t}\right)\cdot {\lambda }_{\text{speed}}\left(\mathrm{t}\right)\cdot {\lambda }_{\text{history}}\left(\mathrm{t}\right)$$ (Equation 12)

Equation 7 defines the space and time (“S+T”) model, Equation 8 defines the time and distance (“T+D”) model, Equation 9 defines the space and distance (“S+D”) model, Equation 10 defines the distance (“D”) model, Equation 11 defines the space (“S”) model, and Equation 12 defines the time (“T”) model.

The parameters for each model were estimated using an iterative Newton-Raphson method to maximize the likelihood function, as described in Lepage et al. (2012). The resulting maximum likelihoods (Γ_i) for each model (λ_i) were then used in likelihood ratio tests to compare each nested model to the full model to determine whether the additional covariates provided significant information about spiking.

$${\mathrm{D}}_{(\mathrm{S}+\mathrm{T}+\mathrm{D})-\mathrm{S}}=2\left(\ln \right({\Gamma }_{\mathrm{S}+\mathrm{T}+\mathrm{D}})-\ln ({\Gamma }_{\mathrm{T}+\mathrm{D}}\left)\right)$$ (Equation 13)

$${\mathrm{D}}_{(\mathrm{S}+\mathrm{T}+\mathrm{D})-(\mathrm{T}+\mathrm{D})}=2\left(\ln \right({\Gamma }_{\mathrm{S}+\mathrm{T}+\mathrm{D}})-\ln ({\Gamma }_{\mathrm{S}}\left)\right)$$ (Equation 14)

$${\mathrm{D}}_{(\mathrm{S}+\mathrm{T}+\mathrm{D})-\mathrm{T}}=2\left(\ln \right({\Gamma }_{\mathrm{S}+\mathrm{T}+\mathrm{D}})-\ln ({\Gamma }_{\mathrm{S}+\mathrm{D}}\left)\right)$$ (Equation 15)

$${\mathrm{D}}_{(\mathrm{S}+\mathrm{T}+\mathrm{D})-\mathrm{D}}=2\left(\ln \right({\Gamma }_{\mathrm{S}+\mathrm{T}+\mathrm{D}})-\ln ({\Gamma }_{\mathrm{S}+\mathrm{T}}\left)\right)$$ (Equation 16)

Equations 13 and 14 calculate the deviance of the “T+D” model and “S” model respectively from the full model due to the removal of the covariates missing from the nested model. The results are shown in Figures S4B and S4C. Note that D_{(S + T + D)−S} is calculated using Γ_{T + D} (the likelihood of the model with time and distance, but without space), such that the larger the value of D_{(S + T + D)−S}, the larger the influence of space on spiking activity. Under the null hypothesis, that the addition of space to the nested model containing time and distance does not provide more information about spiking activity, the test statistic D_{(S + T + D)−S} has a χ²-distribution with 5 degrees of freedom. Similarly, under the null hypothesis that the combination of time and distance do not provide more information about spiking activity to the nested model already containing space, the test statistic D_{t + d}D_{(S + T + D)–(T + D)} has a χ²-distribution with 10 degrees of freedom (as time and distance encompass 10 covariates in the full model). The test statistics D_{(S + T + D)–T} and D_{(S + T + D)–D} (Equations 15 and 16) indicate whether time (in addition to distance) or distance (in addition to time) provided more information about spiking activity, and under the null hypothesis both have a χ²-distribution with 5 degrees of freedom. Figure 8A plots the value of D_{(S + T + D)–D} against the value of D_{(S + T + D)–T}. We next subtracted D_{(S + T + D)–D} from D_{(S + T + D)–T} to obtain a measure of the influence of time compared to the influence of distance (Lepage et al., 2012; MacDonald et al., 2011; Figure 8B).

$$\begin{array}{c}\hfill \Delta {\mathrm{D}}_{\mathrm{T}-\mathrm{D}}={\mathrm{D}}_{(\mathrm{S}+\mathrm{T}+\mathrm{D})-\mathrm{T}}-{\mathrm{D}}_{(\mathrm{S}+\mathrm{T}+\mathrm{D})-\mathrm{D}}\hfill \\ \hfill \Delta {\mathrm{D}}_{\mathrm{T}-\mathrm{D}}=2\left(\ln \right({\Gamma }_{\mathrm{S}+\mathrm{T}+\mathrm{D}})-\ln ({\Gamma }_{\mathrm{D}}\left)\right)-2\left(\ln \right({\Gamma }_{\mathrm{S}+\mathrm{T}+\mathrm{D}})-\ln ({\Gamma }_{\mathrm{T}}\left)\right)\hfill \\ \hfill \Delta {\mathrm{D}}_{\mathrm{T}-\mathrm{D}}=2\left(\ln \right({\Gamma }_{\mathrm{T}})-\ln ({\Gamma }_{\mathrm{D}}\left)\right)\hfill \end{array}$$ (Equation 17)

The value of ΔD_T–D will be negative if D_{(S + T + D)–D}>D_{(S + T + D)–T}, indicating a stronger influence of distance than time on the spiking activity. Similarly, ΔD_T–D will be positive if D_{(S + T + D)–T}>D_{(S + T + D)–D}, indicating a stronger influence of time on the spiking activity (Figure 8B).

As the subtraction in Equation 17 is only valid when both nested models have the same number of degrees of freedom, to directly compare space with just time, or space with just distance, we calculated the deviance of the “S” and “T” models from the “S+T” model and the deviance of the “S” and “D” models from the “S+D” model, as shown in Equations 18, 19, 20, 21,22, and 23.

$${\mathrm{D}}_{(\mathrm{S}+\mathrm{T})-\mathrm{T}}=2\left(\ln \right({\Gamma }_{\mathrm{S}+\mathrm{T}})-\ln ({\Gamma }_{\mathrm{S}}\left)\right)$$ (Equation 18)

$${\mathrm{D}}_{(\mathrm{S}+\mathrm{T})-\mathrm{S}}=2\left(\ln \right({\Gamma }_{\mathrm{S}+\mathrm{T}})-\ln ({\Gamma }_{\mathrm{T}}\left)\right)$$ (Equation 19)

$${\mathrm{D}}_{(\mathrm{S}+\mathrm{D})-\mathrm{D}}=2\left(\ln \right({\Gamma }_{\mathrm{S}+\mathrm{D}})-\ln ({\Gamma }_{\mathrm{S}}\left)\right)$$ (Equation 20)

$${\mathrm{D}}_{(\mathrm{S}+\mathrm{D})-\mathrm{S}}=2\left(\ln \right({\Gamma }_{\mathrm{S}+\mathrm{D}})-\ln ({\Gamma }_{\mathrm{D}}\left)\right)$$ (Equation 21)

$$\Delta {\mathrm{D}}_{\mathrm{S}-\mathrm{T}}={\mathrm{D}}_{(\mathrm{S}+\mathrm{T})-\mathrm{S}}-{\mathrm{D}}_{(\mathrm{S}+\mathrm{T})-\mathrm{T}}$$ (Equation 22)

$$\Delta {\mathrm{D}}_{\mathrm{S}-\mathrm{D}}={\mathrm{D}}_{(\mathrm{S}+\mathrm{D})-\mathrm{S}}-{\mathrm{D}}_{(\mathrm{S}+\mathrm{D})-\mathrm{D}}$$ (Equation 23)

Figures S4D and S4F plot the value of D_{(S + T)–T} against the value of D_{(S + T)–S} and the value of D_{(S + D)–D} against the value of D_{(S + D)–S}, respectively. Figures S4E and S4G show a histogram of the resulting values of ΔD_S−T and ΔD_S−D, respectively.

The GLM analysis was performed twice, first on the data from the entire time the treadmill was running and then again using only data from spatial bins located within A₇₅. The second version of the analysis was conducted to eliminate the influence of the times when the rat’s behavior violated our assumption of constant and steady running (by momentarily shifting outside A₇₅). The results of both analyses were qualitatively the same. The data presented in the text and figures are from the second version of the analysis.