AUTOMATED SKIN SEGMENTATION IN ULTRASONIC EVALUATION OF SKIN TOXICITY IN BREAST CANCER RADIOTHERAPY

Abstract

Skin toxicity is the most common side effect of breast cancer radiotherapy and impairs the quality of life of many breast cancer survivors. We, along with other researchers, have recently found quantitative ultrasound to be effective as a skin toxicity assessment tool. Although more reliable than standard clinical evaluations (visual observation and palpation), the current procedure for ultrasound-based skin toxicity measurements requires manual delineation of the skin layers (i.e., epidermis-dermis and dermis-hypodermis interfaces) on each ultrasound B-mode image. Manual skin segmentation is time consuming and subjective. Moreover, radiation-induced skin injury may decrease image contrast between the dermis and hypodermis, which increases the difficulty of delineation. Therefore, we have developed an automatic skin segmentation tool (ASST) based on the active contour model with two significant modifications: (i) The proposed algorithm introduces a novel dual-curve scheme for the double skin layer extraction, as opposed to the original single active contour method. (ii) The proposed algorithm is based on a geometric contour framework as opposed to the previous parametric algorithm. This ASST algorithm was tested on a breast cancer image database of 730 ultrasound breast images (73 ultrasound studies of 23 patients). We compared skin segmentation results obtained with the ASST with manual contours performed by two physicians. The average percentage differences in skin thickness between the ASST measurement and that of each physician were less than 5% (4.8 ± 17.8% and −3.8 ± 21.1%, respectively). In summary, we have developed an automatic skin segmentation method that ensures objective assessment of radiation-induced changes in skin thickness. Our ultrasound technology offers a unique opportunity to quantify tissue injury in a more meaningful and reproducible manner than the subjective assessments currently employed in the clinic.

INTRODUCTION

Radiation-induced toxic effects on skin, including skin thickening, swelling and hardening, are the most common, debilitating, short-term and long-term side effects of breast cancer radiotherapy (Small and Woloschak 2006). Although recognized for decades, the assessment of skin toxicity is carried out subjectively by physicians through visual evaluation and palpation. We, along with other researchers (Huang et al. 2007; Liu et al. 2010; Warszawski et al. 1998; Zhou et al. 2009), have recently reported that ultrasound can be used to quantitatively assess skin toxicity after radiotherapy for breast cancer. In particular, skin thickening was observed in almost all post-radiotherapy patients (Huang et al. 2007; Liu et al. 2010), making it an important parameter in ultrasonic evaluation of skin toxicity.

The major challenge in ultrasonic skin evaluation is accurate skin segmentation (delineation) on B-mode images. Human skin has two layers: the epidermis and the dermis. The tissue below the dermal layer is the hypodermis (subcutaneous tissue) (Fig. 1). On the 10-MHz-frequency ultrasound B-mode images (Fig. 2a), the normal epidermis and dermis have bright, well-defined boundaries; whereas the relatively thin epidermis appears as a single echo band. However, after breast radiotherapy, radiation-induced damage to the basal layers of dermal cells (Archambeau et al. 1995; Fajardo et al. 2001) can often result in decreased contrast at the hypodermis interface, as shown in Figure 2b. Identification of this interface is a demanding task even for experienced physicians. In our previous skin toxicity studies, the skin was manually delineated, and inter-observer reliability was determined (Yoshida et al. 2012). Nevertheless, manual segmentation is time consuming. In addition, such extensive human interaction inevitably induces subjectivity into the process.

Fig. 1.

Schematic diagram of the skin. Skin comprises two layers: epidermis and dermis. The hypodermis lies under the dermis.

Fig. 2.

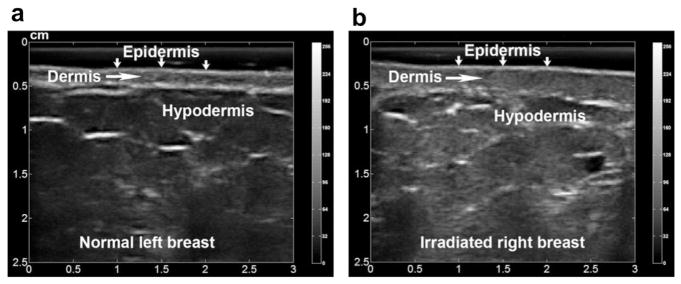
Ultrasound B-mode images of an (a) untreated (normal) breast and (b) irradiated breast. The two layers of the skin, epidermis and dermis, can be seen in both images. Radiation-induced skin injury is evidenced by the skin thickening and segmented dermis-hypodermis interface on the B-mode images.

In this article, we report the development of an automatic skin segmentation tool (ASST) based on the active contour method with two major modifications. The active contour (snake) method has had a large audience in the image segmentation community since its proposal by Kass et al. (1988). To deal with skin segmentation, one major modification introduces a dual-curve evolution technique that is used to detect the epidermis-dermis and dermis-hypodermis interfaces. The other modification is that the proposed algorithm uses a geometric active contour framework as opposed to the previous parametric algorithm (Lagarde et al. 2005), which requires parameter input before segmentation. The main advantage of the proposed ASST algorithm is that it fully automates skin delineations on ultrasound breast images. Furthermore, we found that the ASST could accurately segment both normal skin and radiotherapy-damaged skin.

The remainder of the article is structured as follows. In the next section, Methods, we introduce our ASST algorithm and emphasize the modifications made to the active contour methods. In the Results section, we describe the findings of our clinical study of ASST using 73 breast ultrasound examinations (730 B-mode images), including 365 normal breast images and 365 post-radiotherapy breast images. The ASST results were compared with physicians’ manual contours of the skin layers, and statistical analyses were conducted to evaluate the performance of the ASST. In the Discussion, we highlight the strength of the proposed automatic segmentation algorithm.

METHODS

Theory behind the automatic skin segmentation tool

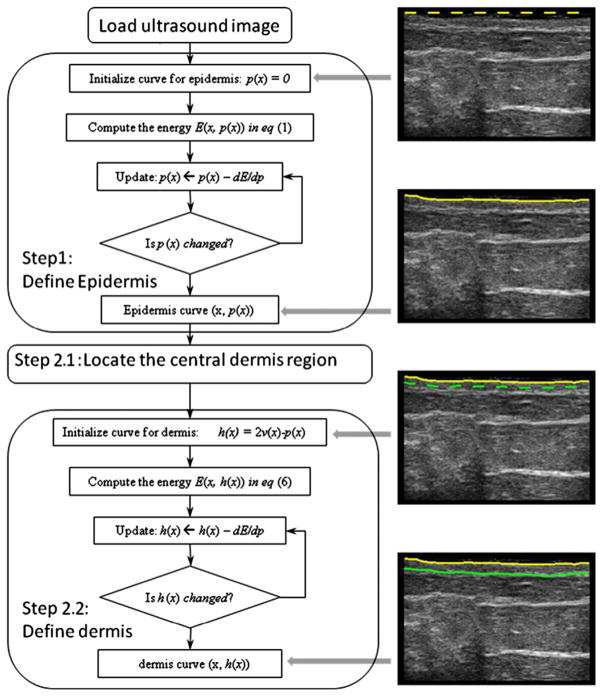
The proposed skin segmentation algorithm, illustrated in Figure 3, consists of two major components. First, a Riemannian metric (Caselles et al. 1997; Kichenassamy et al. 1996; Siddiqi et al. 1998) is derived from the image information, and the curve is evoled by minimizing its length under the Riemannian metric, in order to converge to the desired epidermis-dermis interface. Next the dermis-hypodermis interface is identified through a two-step optimization process. The “center line” of the dermis is determined in the first step; the dermis-hypodermis interface is located in the second step.

Fig. 3.

Flowchart for the proposed method for automatic skin segmentation of ultrasound B-mode images. The block diagram on the left summarizes the two main steps of the skin segmentation algorithm. On the right are the intermediate segmentation curve positions corresponding to the block diagram.

Epidermis-dermis interface segmentation

In this section, we describe the method used to identify the interface between the epidermal and dermal layers. The intensity of the ultrasound image to be segmented is denoted as I(x, y), where x indicates the horizontal axis with a range of [0, X], and y indicates the vertical axis with a range of [0, Y]. Because the breast skin does not fold, to preserve this condition, we wrote the curve of the skin layers as a graph (x, p(x)) of function p: [0, X] → [0, Y]. The location of the epidermis-dermis interface usually corresponds to image regions with drastic intensity changes, which results in a high image gradient magnitude. Therefore, we expected the curve (x, p(x)) to pass through those high gradient locations. This is achieved within the framework of curve evolution under the Riemannian metric. Specifically, first, using the image intensity information, we define a Riemannian metric f(x, y) as

$$f(x,y):=\frac{1}{1+{(S\ast G_{\sigma }(x,y)\ast I(x,y))}^2}$$ (1)

where G_s(x, y) is Gaussian kernel with standard deviation σ. In this application, σ is fixed at 3 to balance between image blurring and noise removal. It is also noted that the purpose of Gaussian filtering is to remove some non-smoothness in the segmentation cost function, rather than to improve the visual appearance of the ultrasound images, which, on its own, is an active research field (Hao et al. 1999; Michailovich and Tannenbaum 2006; Yu and Acton 2002). S is the Sobel edge operator, S = (1, 2, 1; 0, 0, 0; −1, −2, −1), and the operator * denotes 2-D convolution. The design of the discrete operator should take the sampling rate into consideration. This includes adjusting the size of the discrete operator and the values within the kernel for the given sample frequency and edge size. On the other hand, the prior Gaussian filtering is able to construct a nesting of scale space that is able to accommodate the original sampling frequency. Therefore, we can fix the Sobel operator and adjust the Gaussian filtering for the given image and target. Therefore, the Sobel operator is fixed to its canonical form. The metric f(x, y) is a positive function on the same domain as the original image. Wherever a high gradient edge region exists, the f(x, y) value decreases. In Euclidean geometry, the infinitesimal curve length of the parametric curve (x, p(x)) at position x is [1 + (p′(x))²]^1/2 (Hamming 2004). However, under this new Riemannian metric f(x, y), the infinitesimal curve length at position x is f(x, p(x))g[1 + (p′ (x))²]^1/2. If the curve covers the skin regions, the total curve length would be small due to the effect of f(x, y). Therefore, we modeled the epidermis-dermis interface curve as the function that minimizes the energy (Riemannian curve length):

$$\begin{array}{l}p(x)=\text{argmin}E(x,p(x))\\ E(x,p(x)):=\underset{0}{\overset{X}{\int }}f(x,p(x))\sqrt{1+{(p^{\prime }(x))}^2}dx\end{array}$$ (2)

Next, to solve for the optimal epidermis-dermis interface curve, the Euler-Lagrange equation of E(x, p(x)) in eqn (2) is computed. Denoting the Lagrangian as L, the Euler-Lagrange equation is computed as

$$\frac{\partial L}{\partial p}-\frac{d}{dx}\frac{\partial L}{\partial p^{\prime }}=f_y\sqrt{1+{(p^{\prime }(x))}^2}-f_x\frac{p^{\prime }(x)}{\sqrt{1+{(p^{\prime }(x))}^2}}-f\frac{p^{″}(x)}{\sqrt{1+{(p^{\prime }(x))}^2}}-f_y\frac{{(p^{\prime }(x))}^2}{\sqrt{1+{(p^{\prime }(x))}^2}}+f\frac{p^{″}(x){(p^{\prime }(x))}^2}{{\left(\sqrt{1+{(p^{\prime }(x))}^2}\right)}^3}$$ (3)

We augment the curve p(x) with an artificial time variable t, and the optimal curve can then be found by solving the initial-boundary-value problem:

$$\begin{array}{l}\frac{\partial p}{\partial t}=\frac{\partial }{\partial x}\frac{\partial L}{\partial p^{\prime }}-\frac{\partial L}{\partial p}\\ {\frac{\partial p}{\partial x}|}_{x=0}={\frac{\partial p}{\partial x}|}_{x=X}=0\\ p(x,0)=0\end{array}$$ (4)

At convergence, the curve would locate the expected epidermis-dermis interface corresponding to a minimal Riemannian length/energy.

Dermis-hypodermis interface segmentation

Compared with the epidermal-dermis interface, extracting the dermis-hypodermis interface poses a bigger challenge because of the contrast at the dermis-hypodermis interface. Moreover, for radiation-damaged skin, multiple fragments often appear on the dermis-hypodermis interface. Overall, the dermis-hypodermis interface should correspond to a minimal energy state under the same Riemannian metric created for the epidermis.

The energy defined in eqn (2) has at least two local minimal configurations. One corresponds to the epidermis-dermis interface and the other to the dermis-hypodermis interface. The curve in the center of the dermis has a high energy state. In solving eqn (2), we have already identified one energy minimization configuration for the epidermis-dermis interface; the finding of the dermis-hypodermis interface is modeled as a process that skips the epidermis-dermis interface and converges to the dermis-hypodermis interface. As one step toward that goal, previous researchers assumed a certain width for the dermis (Lagarde et al. 2005). Consequently, they initiated the dermis-hypodermis interface by moving a distance p(x) and then fine-tuned the curve by minimizing the energy. However, two issues are associated with using this scheme in our skin toxicity assessment scenario. First, dermis thickness varies significantly in irradiated and non-irradiated patients. This creates technical difficulties in determining a pre-defined “jump distance.” Second, and more fundamentally, dermis thickness is a key parameter in measuring toxicity, but the pre-defined “jump distance” is an estimate for that value; hence, the estimate strongly biases the final results.

In this work, we propose a robust two-step scheme to identify the dermis-hypodermis interface, without the aforementioned assumptions and limitations.

In the first step, the optimization problem needs to be solved to find the center curve of the dermis:

$$\begin{array}{l}v(x)=\text{argmin}E(x,v(x))\\ E(x,v(x)):=\underset{0}{\overset{X}{\int }}\frac{1}{f(x,v(x))}\sqrt{1+{(v^{\prime }(x))}^2}dx\end{array}$$ (5)

Here the initial position of v(x) is v(x) = p(x) + ε, and ε is a small positive value like 0.1 pixel that moves the epidermis curve down a short distance; the optimization then drives the curve further to the center position in the dermal layer. Essentially, the metric image f(x, y) is placed in the denominator, and the energy function is effectively flipped: what used to be minimizer now becomes a maximizer, and vice versa. Previously (when f(x, y) was in the numerator, as in eqn [2]), the two skin layer interfaces corresponded to a low-energy state, and the center curve of the dermis to a high-energy state. Now (as in eqn [5]), the center curve of the dermis has a low energy state and will be extracted by solving eqn (5). The reason for using the reciprocal, instead of negation, is that the reciprocal gives another metric that satisfies the positive definite requirement of being a Riemannian metric. However, by negation, such requirements would be violated and numerical instability would occur. The choice of the ε value would not bias the thickness computation. In the second step, with the center curve located, the dermis-hypodermis interface curve is computed by solving

$$\begin{array}{l}h(x)=\text{argmin}E(x,h(x))\\ E(x,h(x)):=\underset{0}{\overset{X}{\int }}f(x,h(x))\sqrt{1+{(h^{\prime }(x))}^2}dx\end{array}$$ (6)

with the initial position of h(x) h(x)at h(x) = 2v(x) − p(x). Equation (6) is structurally similar to eqn (2), but the initial condition differs. As a result, at convergence, the final position of h(x) is located on the dermis-hypodermis interface.

Validation and reliability study

The ASST was tested and validated using our breast cancer radiotherapy ultrasound imaging database. Our study was conducted under institutional review board approval, and written, informed consent was obtained from all participants. Twenty-three patients with breast cancer who underwent breast conservation surgery (lumpectomy) and breast irradiation for early-stage breast cancer were included in this study (Liu et al. 2010). The median age was 56 (range: 44–74), and the median time elapsed between completion of radiotherapy and ultrasound examination was 22 mo (range: 6–92 mo). All patients received 50.0–50.4 Gy to the whole breast (1.8- or 2.0-Gy fractions); an electron boost of 10.0–16.0 Gy at the lumpectomy site followed. Doses were delivered using parallel and opposed 6-MV tangential fields. Beams were modulated using wedges to ensure dose homogeneity according to standard International Commissions on Radiation Units and Measurements 50 (ICRU-50) guidelines (ICRU 1993). Eighteen patients underwent one ultrasound exam, and the other 5 underwent multiple exams over a 1-y period. Overall, 73 ultrasound exams and 730 ultrasound images (365 normal breast images and 365 post-radiotherapy breast images) were analyzed in this study, and these gray-scale images have an intensity range of [0, 255]. (The ultrasound image is stored in a matrix of bytes. Each byte represents an 8-bit unsigned integer with 256 levels ranging from 0 to 255.) Ultrasound data acquisition has been reported previously and is briefly summarized here (Liu et al. 2010). Patients were scanned with a clinical ultrasound scanner in the supine position. Five ultrasound scans of each breast were obtained: left breast-upper (12:00), lateral (3:00), lower (6:00), medial (9:00) and tumor bed, and right breast-upper (12:00), medial (3:00), lower (6:00), lateral (9:00) and tumor bed. As a baseline measurement, we also scanned the same areas on the untreated (contralateral) breast. Ultrasound studies were performed using a clinical scanner (Sonix RP, Ultrasonix, Richmond, BC, Canada) with a linear array transducer (L14-5/38 probe, 128 elements). All ultrasound data were acquired with the same settings: 10-MHz frequency, 1-cm focal length, 4-cm depth, 72% gain, 26 frames/s and 80-dB dynamic range. Ultrasonic B-mode images were acquired from the treated and contralateral normal breast.

The reliability study was conducted in two ways. First, we tested our skin segmentation algorithm by measuring skin thickness. Two observers were asked to independently contour the two skin layer interfaces on all 730 images. Observer 1 is an ultrasound expert, and observer 2 is a radiation oncologist. The skin thickness results obtained with our segmentation algorithm were compared with the manual contour results. Linear regressions were performed and correlation coefficients were calculated for assessment of consistency between the ASST and the observers. Furthermore, the accuracy of the segmentation of the two skin layers was evaluated using the absolute curve difference (ACD). For the two curves c₁(x) and c₂(x) with x ε[0, X], the absolute curve difference D_1,2(x) between them is defined as

$$D_{1,2}(x):=\mid c_1(x)-c_2(x)\mid$$ (7)

The ACD was computed between the ASST results and each observer’s results and also between the two observers’ results.

RESULTS

Skin segmentation with the ASST was performed on all 730 breast images, and the overall computation time was less than 5 min. Figure 4 is an example of a post-radiotherapy breast image, in which the skin was delineated by the ASST program and two physicians. This ultrasound image was obtained 1 y after treatment of a 55-y-old breast cancer patient with a radiation dose of 60.4 Gy. According to the physician’s assessment, based on Radiation Therapy Oncology Group (RTOG) Late Morbidity Scoring Scheme, the patient developed mild (grade 1) late skin toxicity. On the ultrasound image, such radiation-induced skin damage was evidenced by the low contrast and segmented interface between the dermis and hypodermis. On visual inspection, the ASST skin segmentation is similar to the manual contours performed by the two experts.

Fig. 4.

Ultrasound breast images and skin segmentation. (a) Original ultrasound B-mode image. (b) Skin layers manually delineated by observer 1. (c) Skin layers manually contoured by observer 2. (d) Skin layers segmented by the proposed automatic skin segmentation algorithm (ASST).

Overall, the ASST skin segmentation results were close to the manual segmentation results, which are currently the gold standard in the clinic. For all 730 ultrasound images, percentage differences between skin thickness measurements made using the ASST algorithm and measurements by the two observers are summarized in Table 1. For the skin thickness, with similar variances, the average percentage differences between the ASST and observers 1 and 2 were 4.8% and −3.8%, whereas the average percentage difference between the two observers was −9.9%. Figure 5 illustrates the linear regression of skin measurements between the ASST and each observer. The correlation coefficients, R², were 0.74 for observer 1 and 0.70 for observer 2, demonstrating the accuracy of ASST skin segmentation.

Table 1.

Percentage differences in skin thickness measurements made with the proposed automatic skin segmentation tool (ASST) and two observers’ manual segmentations

Comparison	Difference
ASST versus observer1	4.8 ± 17.8%
ASST versus observer 2	−3.8 ± 21.1%
ASST versus obsever 3	−9.9 ± 20.1%

Fig. 5.

Linear regressions comparing automatic skin segmentation tool (ASST)-computed skin thickness with human observer-delineated skin thickness. (a) ASST skin thickness versus observer 1. (b) ASST skin thickness versus observer 2.

Performance of the ASST was also evaluated separately for the normal breast and the treated breast. As seen in Figure 6, the differences between the ASST algorithm and each observer were larger for irradiated breasts than for normal breasts. The reason for this is that radiation injury increases the difficulty of skin segmentation. In addition, the ACDs were larger for the dermis than for the epidermis, not only for the ASST algorithm, but also for the two observers.

Fig. 6.

Absolute curve differences in skin segmentation between results for the automatic skin segmentation method and manual results for the two observers. (a) Epidermis segmentation. (b) Dermis segmentations. Comparisons are made for normal and irradiated breasts.

DISCUSSION

We developed an ASST algorithm that automates skin segmentation on breast ultrasound images. The ability of the ASST to delineate normal as well as radiation-damaged skin was explored with a database of 730 ultrasound images, among which 365 were of normal (untreated) breasts and 365 were of radiation-treated breasts. In current clinical practice, skin contours on breast ultrasound images are performed manually by physicians. The proposed ASST method is more accurate and faster, compared with manual skin segmentations. Specifically, the average percentage differences between skin thickness measurements made using the ASST and measurements made by manual segmentation were less than 5%. Moreover, the two physicians each spent approximately 700 to 800 min to contour the skin layers for the 730 ultrasound images, whereas the ASST completed all segmentations within 5 min. Figure 7 illustrates three representative cases: normal breast, irradiated breast in a patient without toxicity and irradiated breast in a patient with toxicity. For all three cases, ASST skin segmentation results are similar to physicians’ manual contours.

Fig. 7.

Three representative data sets on the different cases observed: (a) normal breast image with (b) skin layers manually contoured by physician and (c) skin layers contoured with the automatic skin segmentation method. (d) Post-irradiation patient without toxicity with (e) skin layers manually contoured by physician and (f) skin layers contoured with the automatic skin segmentation method. (g) Post-irradiation patient with toxicity with (h) skin layers manually contoured by physician and (i) skin layers contoured with the automatic skin segmentation method.

In 2005, Lagarde et al. proposed using the original active contour method to segment skin in various regions, including the arm, thigh, forehead and neck. A parametric model was used to represent the contour and its evolution with the local image gradient. Comparison of their automatic segmentation results with physicians’ contours yielded R² values ranging from 0.01 to 0.61. In this study of breast skin segmentation, comparison of our automatic segmentation results with manual results for one physician yielded an R² value of 0.76, and for the other physician, 0.74, representing a significant improvement in consistency with the physicians’ manual contours.

Although segmentation for ultrasound images has been studied extensively in organs (Noble and Boukerroui 2006) such as the heart (Mitchell et al. 2002) and prostate (Ladak et al. 2000; Zhan and Shen 2006), investigations on skin segmentation are limited (Lagarde et al. 2005). To the best of our knowledge, this is the first segmentation study on breast skin after radiation treatment. To extract the two skin layers from the ultrasound image, we extended the well-known active contour method and designed an open-ended, dual-curve evolution technique. During skin layer extraction, our ASST method considers both the information from the ultrasound image information and skin properties, such as smoothness. More explicitly, a set of partial differential equations (PDEs) is derived for the position of the curve, so that the curve will be passing through the locations where the greatest change in image intensity occurs, which is the expected location of the skin layer. Although such a technique accurately locates the epidermis, because of the decreased contrast and possible radiation damage, extraction of the dermis is often more challenging.

The other significant modification of the proposed ASST method was fully automatic detection of the dermis under the Riemannian geometry framework. Previous researchers usually extracted the dermis with a parametric algorithm (Lagarde et al. 2005). In the parametric method, on one hand, the curves are represented by spline nodes, which is numerically less stable. On the other hand, after the first curve (epidermis-dermis boundary) is located, an initial guess of a uniform shift (“jump distance”) f is required to locate the second curve (dermis-hypodermis interface). Then, this shift is fine-tuned within a limited range from the initial position to capture the second boundary. Therefore, the final accuracy is strongly affected by the initial shift. The skin thickness measurement is also affected by the value of f, which implicitly induces subjectivity. In contrast, our ASST is a geometric-based method, where one set of PDEs moves the epidermis curve to the center of the dermis area. Then, another set of PDEs finally moves the center-of-dermis curve to the position of the dermis-hypodermis interface. The entire process is automatic, and more importantly, by using PDEs, we remove the subjectivity induced by the user-given parameter f.

We realize that other than the active contour framework employed in the present work, many other techniques may be able to solve skin the segmentation problem. Noticeably, the mean shift algorithm proposed by Comaniciu and Meer (2002) gives a robust estimation of the centers of the modes among random samples in the feature space. The level-set algorithm seeks a contour to separate an image into two parts (Chan and Vese 2001). Although those algorithms tend to extract “blob”-shaped targets in the images, instead of curve-shaped objects, as needed for the skin, future studies will investigate how such algorithms could be used for a more accurate, more robust and faster algorithm for the clinical task.

In dermatology, skin is frequently imaged with 20-MHz high-frequency ultrasound, greatly improving the contrast between different layers of the skin (Foster et al. 2000; Harland et al. 2006; Hoffmann et al. 1991; Ritter et al. 2002; Vogt and Ermert 2005). In high-frequency ultrasound, the epidermis appears as a layer of certain width, as compared with our study in which the epidermis-dermis interface appeared fused as a single echo band. We used a frequency of 10 MHz to image the breast, because both skin and deeper glandular tissue are evaluated for radiation-induced damage.

In breast cancer radiotherapy, radiation toxicity is very common and routinely assessed through physical examinations. The drawbacks of physical examinations are subjectivity and imprecision. There is significant inconsistency in clinical assessments. We have conducted a series of studies to introduce an ultrasound imaging tool into the diagnosis of post-irradiation breast tissue toxicity. This research tool would be useful in comparing skin toxicity after various treatment strategies, such as altered fractionation and external beam radiation versus brachytherapy, for example, Mammosite. The motivation is to develop an automatic, non-invasive and quantitative tool to measure normal tissue toxicity that has the potential to overcome the limitations of the current assessment tools in the clinic. In other words, our ultrasound tool may help distinguish good treatments from bad treatments, with respect to skin toxicity, and determine the effects of different types of treatment schemes in breast radiation. Toward this goal, the proposed ASST helps us move one step further—it will free physicians from tedious segmentation work and mitigate the subjectivity in skin delineation.

CONCLUSIONS

A fully automated skin segmentation algorithm based on the active contour method is described. The proposed ASST makes two contributions to the development of a non-invasive and quantitative imaging tool to assess radiation-induced tissue toxicity. First, the ASST program reduces physicians’ manual work in skin delineation. More importantly, this program further reduces the subjectivity in radiation toxicity evaluation and provides more objective measurements of normal tissue injury in breast cancer radiotherapy. Although first clinically applied in breast cancer radiotherapy, our ASST program can also be used for other treatment sites, such as the head and neck.