Outline of a General Theory of Behavior and Brain Coordination

Abstract

Much evidence suggests that dynamic laws of neurobehavioral coordination are sui generis: they deal with collective properties that are repeatable from one system to another and emerge from microscopic dynamics but may not (even in principle) be deducible from them. Nevertheless, it is useful to try to understand the relationship between different levels while all the time respecting the autonomy of each. We report a program of research that uses the theoretical concepts of coordination dynamics and quantitative measurements of simple, well-defined experimental model systems to explicitly relate neural and behavioral levels of description in human beings. Our approach is both top-down and bottom-up and aims at ending up in the same place: top-down to derive behavioral patterns from neural fields, and bottom-up to generate neural field patterns from bidirectional coupling between astrocytes and neurons. Much progress can be made by recognizing that the two approaches —reductionism and emergentism— are complementary. A key to understanding is to couch the coordination of very different things —from molecules to thoughts— in the common language of coordination dynamics.

I. The neural choreography challenge

New information about the brain is accruing at an astonishing rate at every level—from the molecular to the social. Though tremendous progress has been made, conspicuously lacking is a broad framework of ideas with which to interpret and integrate findings from so many different scales and levels of observation. We are confronted, as a former President of the Society for Neuroscience remarked in recent testimony to the US Congress, with the grand challenge of elucidating “neural choreography” (see also Akil, Martone & van Essen, 2011). No single focused level of analysis suffices to understand the brain and its disorders. We need to identify the dancers¹, capture the essence of the dance and uncover how disease disrupts it. The task is daunting: the ‘functions’ of the brain and of brains interacting with each other, are manifold and nearly countless. Sift through, for example, typical issues of Neural Networks or The Journal of Neuroscience. The deep problem that won’t go away is the relationship between brains and minds, whether individual or collective. Much progress has been made, not least by the efforts of scientists and engineers in the field of neural networks, but an integrative picture is still lacking. The gap between the language of molecules and cellular machinery (genetics, neuroscience) and the language of mind and its various disorders (cognitive science, neurology and psychiatry) seems very large indeed and is fast widening. There is a belief that things will work out in the end, but at the moment it remains just that—a belief.

Might we take a different tack on the problem? Our intent here is to outline a conceptual and empirical framework (‘a general theory’) that aims to provide insight into how different levels of organization across multiple space and timescales are connected. Though it certainly relies upon them, on offer here is not a detailed model of neurons and neural machinery supporting hypothesized processes involved in cognition and behavior. The central idea is that all such processes –regardless of level of description— depend on coordination and the different forms it takes. Our approach is to identify the dynamic laws of coordination and reveal their mechanistic realizations level by level, using both a top-down and a bottom-up approach. By ascribing physiological meaning to the parameters and mathematical expressions in a (computationally implemented) phenomenological theory we aim to bridge the gap between behavioral phenomena and their neural underpinnings.

II. Connecting the micro- and the macro-

Twenty-five years ago, around the time that the journal Neural Networks was being founded, we reported empirical and theoretical results demonstrating that coordinated patterns of human behavior could be explained using the concepts of self-organization in open, nonequilibrium systems, particularly synergetics (Haken, 1983) and the mathematical tools of nonlinear dynamics (Schöner & Kelso, 1988, for review). We intimated then that similar principles are likely to be present also in elementary neural circuits called central pattern generators. In the intervening period, the evidence for mulitifunctionality in neural circuitry viewed as multistable dynamical systems is overwhelming (Briggman & Kristan, 2008; Prinz et al., 2004; see also Grillner & Graybiel, 2006). Moreover, in the last 30 years principles of self-organization have been shown to govern patterns of coordination (a) within a moving limb and between moving limbs; (b) between the articulators during speech production; (c) between limb movements and tactile, visual and auditory stimuli; (d) between people interacting with each other spontaneously or intentionally; (e) between humans and avatars; (f) between humans and other species, as in riding a horse; and (g) within and between the neural substrates that underlie the coupled behavior of human beings as measured using MEG, EEG and fMRI (Fuchs & Jirsa, 2006; Kelso, 1995; 2009, for reviews). How might these phenomena be understood?

There are strong hints that laws of coordination in neurobehavioral systems are generic and deal with collective properties that emerge from microscopic dynamics, but how to understand such emergent phenomena has proven difficult in the extreme. An argument can be made that such laws are truly sui generis and that it may not be possible, even in principle, to deduce higher level descriptions from lower level ones (Laughlin & Pines, 2000). The present approach is entirely conventional with respect to the history of science. Fundamentally, it begins with the identification of the macroscopic behavior of a system and attempts to derive it from a level below. Even for physical systems, however, the derivation of the ‘macro’ from the ‘micro’ is nontrivial. Only in the 70′s, for example, was it possible to derive the behavior of ferromagnets (as described by Landau’s mean field theory) from more fundamental grounds using the so-called renormalization group method that earned Kenneth Wilson the Nobel Prize in 1982. Thus, only some 70 years after atoms were discovered did it become possible to derive macroscopic properties of certain materials from a more microscopic basis, and only then using rather sophisticated and somewhat cumbersome mathematical techniques (cf. Laughlin & Pines, 2000).

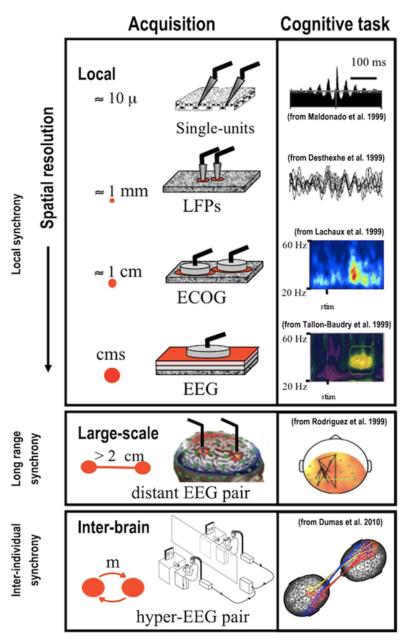
One lesson to be learned from such successes in connecting the micro- and the macro- is that it is crucial to first have a precise description of the macroscopic behavior of a system in order to know what to derive. Without the phenomenological theory of phase transitions, for instance, with their critical exponents and so forth, microscopic approaches would be meaningless. Another lesson is that even in a system whose microscopic constituents are homogeneous (unlike, say the neurons, glia and neurotransmitters of the brain) special methods are needed to handle events and interactions that are occurring on many spatial and temporal scales. In an apparently heterogeneous, hierarchically organized system like the nervous system, it is necessary to proceed in a trans-level fashion with as intimate an interplay between theory and experiment as possible using multiple observables in line with what the existing technology allows—and keeping an eye out for new techniques that may open up additional levels of description. Figure 1 conveys some of the scales and methods we will consider here, along with examples of how they have been employed in various cognitive tasks.

Figure 1.

Multiple scales of the nervous system using synchrony as an example of neural coordination. Notice the right column corresponds to effects that are observed in various task settings. The ‘local scale’ has three levels of analysis: single units, local field potentials (LFP) and ECOG/EEG. At larger scales, long range synchrony may be observed between distant brain regions. At the inter-individual scale, neural synchronization emerges between different brains through reciprocal social interaction (adapted from Varela et al. 2001).

III. Finding relevant variables

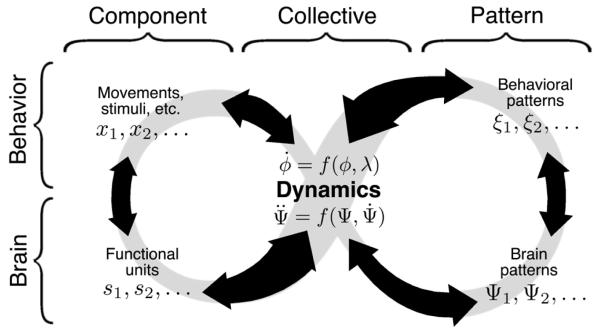
Our strategy for traversing levels is shown in Figure 2.

Figure 2.

Level-crossing strategy (both horizontal and vertical) connecting components, behavioral and brain patterns and their dynamics (see text for details). Notice the strategy reflects a strictly operational approach.

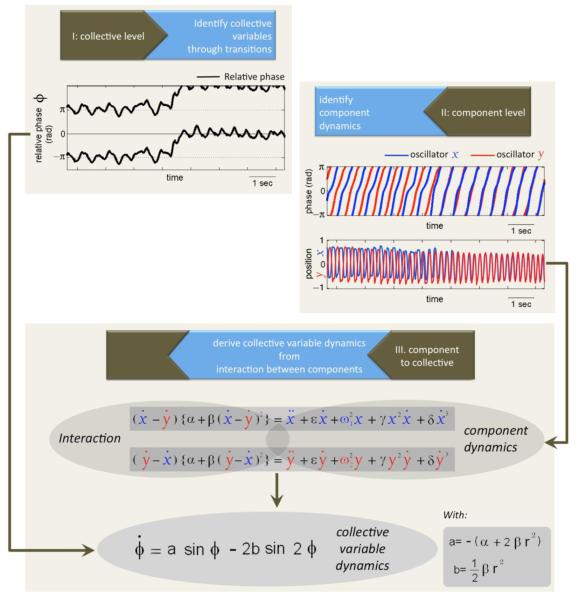
The basic idea is to identify relevant variables characterizing coordinated or collective states of the system and the collective variable’s dynamics (i.e. equations of motion for collective variables). Note that in most neurobehavioral systems these are not known in advance, but have to be found. The experimental method uses transition points or instabilities to clearly distinguish different coordinated behaviors. In coordination dynamics, phase transitions are exploited both as a dynamical mechanism for effecting change (‘switching’, decision-making’) and as a methodology to identify key collective variables and their dynamics. The reason is that in complex systems very many features can be measured but not all are relevant; coordination dynamics assumes that the variable that changes qualitatively is the most important one for system function (and, incidentally, for the scientist trying to understand it). It is these collective variables that are mapped on to a dynamical system. Further experiments are necessary to identify the component dynamics and further theory is needed to derive the collective variable dynamics from nonlinear interactions among components. Rhythmic coordination, an example of which is synchronization (cf.Fig.1) —with its long history in biology and behavior—proves to be an excellent starting point for developing a multi-level understanding of coordination. Experiments show, for example that the rhythmic motion of a single finger, which exhibits dynamic properties such as transient behavior and amplitude dependence on movement rate can be modeled as a Van der Pol-Rayleigh oscillator. Once the finger motion is coupled to other signals, e.g. the other hand starts to move or an external periodic stimulus is present--or even a virtual moving finger is present as in the human dynamic clamp or virtual partner interaction paradigm (Kelso, et al., 2009) -- then the relative phase between finger motion and the additional signal becomes a meaningful descriptor of coordination. However, not every relative phase will be selected. The coupling establishes a symmetry breaking by constraining the number of existing phase states. Moreover, not every existing relative phase is actually stable: an unstable state or repellor may separate stable states. When control parameters such as the movement rate are manipulated, coordination states may become unstable and the system may exhibit a transition from one state to another. In the vicinity of phase transitions, complex, open systems become low dimensional. Thus, in this picture, phase transitions are the core of self-organization. Since their original discovery in experiments and consequent theoretical modeling (Kelso, 1981; 1984; Haken, Kelso & Bunz, 1985; Kelso, Delcolle & Schöner, 1990; Schöner, Haken & Kelso, 1986), phase transitions and related dynamical phenomena have been observed in many different systems ranging from bimanual and sensorimotor coordination and their neural correlates, to interpersonal and interbrain coordination (for reviews, Fuchs & Kelso, 2009; Kelso, 1995; 2009; 2010; Tognoli, 2008; Kelso et al., 2009; Oullier & Kelso, 2009; Dumas, et al., 2010). A specific example of our strategic approach is provided in Figure 3.

Figure 3.

A specific example of deriving the collective variable, relative phase dynamics from the (nonlinear) components and their (nonlinear) interaction.

IV. Phase transitions in coupled neural populations

To find generic mechanisms of dynamical systems is a powerful way to classify behavior on any level of description, but on its own makes no explicit connection to the underlying neural substrate and its dynamics. The key idea is to follow the same conceptual approach as on the behavioral level, namely to identify functionally relevant neural components (‘our dancers’) that must be coupled together to accomplish the coordination involved in cognitive processing. For such coordination, information flow is seldom of the sender-receiver, input-output unidirectional kind (Tognoli & Kelso, in press). On the contrary, the bidirectional nature of the coupling proves to be a crucial aspect of dynamic coordination, regardless of whether two hands, two people and two brains are interacting for social functions (Banerjee, et al., 2012; Dumas, et al., 2010; Tognoli, et al., 2007; Naeem, et al., 2012) or astrocytes and neurons are interacting for normal synaptic transmission (Wade et al., 2011).

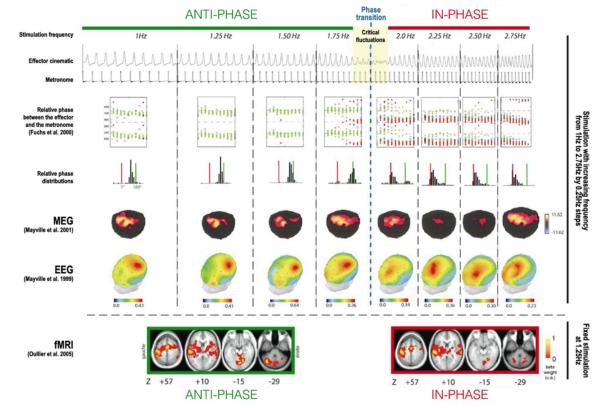
The answer to the question of neuronal mechanisms depends again on the chosen level of description. Experimentally accessible observables are provided by non-invasive techniques such as electroencephalography (EEG), magnetoencephalography (MEG) and structural and functional magnetic resonance imaging (MRI, fMRI). The first two techniques, EEG and MEG, are direct measures of the functional organization of neuronal populations. EEG measures the electric potential on the skull surface; MEG usually measures the gradient of the magnetic field over the radial direction above the surface of the skull. Both signals are generated by the simultaneous neuroelectric activity of hundreds of thousands of neurons located mainly in neocortex. The spatial resolution of EEG and MEG is on the order of cm., its temporal resolution is msec. Structural MRI provides three-dimensional coordinates of neuronal tissue on the scale of mm. fMRI measures the metabolic activity of the brain, hence providing an indirect measure of neuronal activation on the spatial scale of mm and temporal scale of sec. In short, EEG and MEG provide measures of neuronal correlates on the same (or even faster) time scale as human behavior, but are confined to the skull surface, whereas fMRI is three-dimensional and spatially precise, but remains an indirect measure and a bit too slow to capture human behavior in real time. Taken together, these techniques measure complementary facets of the same neuronal processes. For illustrative purposes, we turn to Figure 4 where the same phase transition paradigm (Kelso, 1990) is carried out on behavioral, EEG, MEG and fMRI levels, albeit in different experiments. Not shown is recent work that focuses on the transition itself, for instance Jantzen, et al.’s (2009) study of BOLD changes in specific neural regions as a control parameter drives the system toward instabilities; remarkable work by Meyer-Lindenberg et al., (2002) which uses TMS as a perturbation to provoke instabilities in both brain recordings and behavior²; and Banerjee et al.’s (2012) research which captures transient recruitment of neural assemblies at the transition from antiphase to inphase.

Figure 4.

Observations of phase transitions and their neural correlates: behavior (top three panels), MEG, EEG and fMRI (adapted from Oullier et al. 2006). The approach emphasizes garnering experimental evidence at multiple levels using multiple technologies.

V. Connecting behavioral and neural dynamics

Following the same strategy as the behavioral level, with the foregoing techniques it is possible to define an isolated spatiotemporal event such as a rhythmic finger movement, with the goal of identifying its neuronal correlates. Simple sensory and motor events are well represented in EEG and MEG signals and hence well-suited to investigating the neural dynamics. Obviously there is a relation between the spatiotemporal pattern in the EEG and MEG and the underlying neuronal generators. For present purposes, we bypass the so-called inverse problem (but see Murzin, et al., 2011) and seek to identify the dynamics of the patterns in the EEG and MEG. In the case of sensorimotor coordination, MEG experiments (Kelso, et al., 1998) showed that to get the finger to the right place at the right time, the velocity of movement is a key parameter that is highly correlated with the spatiotemporal pattern of the MEG. To model this simple but tight relationship, Fuchs et al (2000) were able to express the finger movement r(t) as a convolution of a memory function G(t – τ) with its neuronal signal Ψ(x, τ) over past times, τ. This expression was projected on a spatial template pattern β(x) which represents the spatial distribution of the neuronal areas involved in the behavioral task. Both, the memory function and the template can be identified from the experimental reconstructed the data. Then Fuchs et al (2000) reconstructed the finger movement r(t) as:

$$r\left(t\right)={\int }_{\Gamma }\mathit{dx}\beta \left(x\right){\int }_{\Gamma }d\tau G(t-\tau )\Psi (x,\tau )$$

The linear relationship between the neuronal activation Ψ(x,t) and the finger movement r(t) is due to the rhythmic nature of the movement task. Experimentally, it also turns out that the memory function is an exponential function and the spatial template involves mainly contralateral primary motor areas and some minor contributions from ipsilateral cortex. Equivalently, the above relationship says that the finger movement is an oscillator that is driven by neuronal activity. Given experimental information about the memory function and the spatial template, finger movement can be “read out” directly from the neuronal activity Ψ(x,t) . In the case of bimanual coordination, the neuronal patterns Ψ₁(t) and Ψ₂(t) corresponding to the two finger motions, r₁ (t) and r₂ (t) have to interact. These patterns are obtained as projections ${\Psi }_i\left(t\right)={\int }_{\Gamma }{\beta }_i\left(x\right)\Psi (x,t)\mathit{dx}$ of the neuronal activity onto the individual spatial templates β_i(x)i,=1,2 Jirsa et al. (1998) applied a simple transformation Ψ₊(t)=Ψ₁(t)+Ψ₂(t) and Ψ₋(t)=Ψ₁(t)-Ψ₂(t) that expressed the neuronal pattern dynamics in terms of the patterns of behavioral coordination observed in the original Kelso experiments. At the critical frequency, this predicts that the neuronal pattern for antiphase behavior, Ψ₋(t) becomes unstable and leads to the emergence of a new spatiotemporal organization, the in-phase pattern Ψ₊(t). Experimental data from full-head MEG measurements supported this prediction, analysis revealing that a change in the symmetry of the brain pattern occurred across the behavioral transition (Jirsa, et al., 1998; see also, Banerjee, et al., 2012 for a different approach using EEG). The dynamical mechanism for both neuronal and behavioral levels proves to be of the same generic type, a Pitchfork bifurcation.

VI. Deriving behavioral and brain patterns from neural ensemble dynamics

How close are we to our goal of connecting neuronal dynamics to underlying biological mechanisms? According to the present strategy, in order to move beyond this still phenomenological level and identify underlying neural processes one has to go at least to the level of neural ensembles. Models of neural ensembles have a long history and differ in terms of connectivity and inclusion of physiological detail (see, for example, Amari, 1977; Ermentrout, 1998; Nunez, 1974; 1995; Robinson, et al., 1997; Wilson & Cowan, 1972; 1973; Wright & Liley, 1995). For our purposes, a good candidate is Jirsa and Haken’s (1996; 1997) neuronal field model which uses so-called ‘conversion operations’ (see Freeman, 1992 for review) to define mathematical relations between firing rates and local field potentials (cf. Fig.1). This is important because: a) Freeman’s and others’ experiments on a variety of cortical areas reveal a well-defined relation between neuronal firing rates and the local field potential; and b) it allows a connection to observable quantities in the EEG and MEG. Dendritic currents generated by active synapses are responsible for the extracellular local field potential measured in the former, and likewise intracellular dendritic currents are thought to generate the MEG signal. The wave-to-spike conversion from the local field potential is sigmoidal within a neuronal ensemble; the inverse spike-to-wave conversion from firing rate to the local field is also sigmoidal but is constrained to a small signal linear change³. Both short range intracortical fibers (excitatory and inhibitory) and long range corticocortical fibers (excitatory only) constitute the connectivity required to capture the relatively large spatial and temporal scales of EEG and MEG. Propagation along long range fibers may cause propagation delays up to 200 msec., consistent with the timescale of most behavior. In the neuronal field model, the notion of a functional unit--a spatiotemporal mapping relating external events to neuronal events-- is central (cf. Fig.2). For the specific case of bimanual coordination, the cortical sheet is divided into left and right hemispheric areas representing pre- and postcentral cortices containing the primary motor and sensorimotor areas of the left and right fingers. Localization of these areas obeys a reflection symmetry with respect to the plane between the two hemispheres. Sensorimotor units receive proprioceptive and kinesthetic information from the respective finger movements and motor areas may be thought of as driving the fingers. The spatiotemporal details of how the motor areas drive the finger oscillation is given by the functional mapping described above (Kelso, et al., 1999; Fuchs, et al., 2000). Mathematical analysis of these equations by Jirsa et al. (1998; 1999) predicts that the neuronal activity will show a spatially antisymmetric organization in the antiphase condition, but then undergo a transition to a symmetric organization simultaneously with the behavioral transition to in-phase. Numerical simulations of the neuronal ensemble dynamics confirm the mathematical predictions.

VII. Combining dynamical modeling with anatomical structure

In contrast to a purely phenomenological theory, notice that it is now possible to make statements about the relationship between behavioral dynamics and biological mechanisms. Phenomenological parameters on the behavioral level are now expressed in terms of the physiological and anatomical parameters in the neuronal field model. Callosal projections of motor and sensorimotor areas between the hemispheres are spatially symmetric with respect to the reflection at the plane separating the hemispheres. These connections couple the motor systems on both hemispheres directly; thus they strongly contribute to the neuronal dynamics during bimanual coordination in particular, because they contribute to the spatial overlap of functional units (see also Banerjee & Jirsa, 2007; Banerjee, et al., 2008; Daffertshofer, et al., 2005; Tuller & Kelso, 1989). The spatial overlap hypothesis was tested in the experimental MEG data and found to be consistent with neuronal field theory (see Jirsa et al., 1998). More recently, Banerjee and colleagues (2012) tracked spatiotemporal reorganization of the brain through the transition from antiphase to inphase bimanual coordination. Brain networks participating in unimanual movements were found to reorganize themselves during bimanual coordination patterns; recruitment of additional brain areas was mostly confined to the period surrounding the behavioral phase transition. The story told in the previous segments is a testament to the strategy of connecting levels using as tight a connection between experiment and theory as possible. Much more of course can be (and has been) done. Obviously, the level of anatomical and physiological detail can always be enhanced. For example, the geometry of the cortex can be defined in three dimensions to enable stronger experimental testing. The neuronal field model has to be elaborated to include functionally relevant subsystems, including subcortical components, so that their role in brain coordination can be addressed. The connectivity should contain additional structure. For instance, the density of connections of axonal fiber systems is not translationally invariant, i.e., is not everywhere the same. Intracortically speaking, the description of the cortex by a densely connected mesh is attractive and justifiable. However, the myelinated extracortical fiber system is sparse and selective. One would expect this aspect to have some functional significance for the spatial and temporal scales measured in EEG and MEG.

All of these aspects and more have been elaborated in further work by Jirsa and colleagues (Jirsa, et al., 2001; 2002). Neuronal field dynamics on the sphere along with the mapping of functional units onto the folded cortex and forward solutions (aided by fMRI) for EEG and MEG provide a platform for the further development of a multi-level model of human brain and behavioral function (see also Jirsa et al., 2010). Interconnected neural ensembles with homogeneous connections represent a neural level, while a network or systems level is defined by the interaction between heterogeneously connected cortical regions. The complementarity of structure and dynamics is at play here: while the anatomical structure constrains the dynamics, the dynamics simultaneously shapes the structure.The former relationship has been specifically approached through the study of how anatomical connectivity influences resting state activity and more specifically the so-called Default Mode Network (DMN) (Honey et al. 2009, Cabral et al. 2011). In coordination tasks, heterogeneous fiber tracts connect the cortical, subcortical and spinal subsystems involved. These pathways couple the subsystems and thus add to their cross-talk and the resulting coordination dynamics. Without getting overly technical, heterogeneities introduce additional entries in the connectivity matrix of the neural field (Assisi, et al., 2005; Jirsa & Kelso, 2000; Qubbaj & Jirsa, 2007) carrying information on distance and strength of coupling between areas. Developing technologies, such as diffusion tensor weighted imaging (DTI), provide information regarding the integrity of white matter tracts in the connectivity matrix of individual subjects (for an interesting application, see Jing, et al., 2011). The present approach thus allows for the integration of neurophysiological and anatomical facts regarding the coupling among neural ensembles for various behavioral functions, setting the stage on which non-invasive brain imaging, theory, experiment, modeling and data analysis can play out—a true TEAM approach (Theory, Experiment, Analysis and Modeling). From the perspective of coordination dynamics, the conceptual and methodological framework presented here allows for the development of a theoretical model of human brain function and behavior that operates at multiple levels of description. Laws of behavioral coordination may be connected to laws of neuronal pattern generation at the level of neuronal ensembles. Via the TEAM approach of coordination dynamics, it is now possible to link dynamical mechanisms and physiological quantities.

VIII. Down to the level of neural masses

It is obviously possible to continue the strategy of traversing scales further and further downward to levels that the field of neuroscience and neurocomputation consider quite basic for information processing, namely the level of spiking neurons (Fig.1). This is a place where the mathematical formalisms of neural networks and their applications have been quite successful. For example, in the field of fault tolerant computing, neural networks offer a fine-grained distributed computing architecture that enables fault tolerance to be realized at very low levels of granularity; computations may be mapped across many neuron clusters permitting a “scattering” of faults without significantly degrading computation (Harkin, et al., 2009). Interesting and challenging though such applications are, the goal here is slightly different. Above we reviewed evidence and theory indicating that ordinary behavioral coordination can be connected explicitly to neural fields: might it now be possible to reverse direction, as it were, and derive neural field descriptions from the bottom up? On the theoretical side, one of the bridges one has to cross is that large parameter spaces are involved: the interacting elements are differentiated and so numerous that combinatoric explosion is a humongous problem. Once again we are faced with the problem of preserving biophysical relevance at the same time as handling the large number of degrees of freedom involved. One way to decrease the complexity of models is by reducing the number of different types of neurons, synaptic connections and states. Such an approach simplifies simulations of large heterogeneous neural networks by mapping the collective state of similar types of neuron onto a probabilistic density distribution in the phase space (for an excellent review see Deco et al. 2008). Then, the dynamics of each class can be summarized in a single set of differential equations. These Fokker-Planck equations describe the temporal evolution of the probability density distributions over the state-space, representing the distribution of the ensemble of trajectories of all neurons within one class. Although a systematic exploration of the parameter space is still computationally expensive, two approximations are commonly used: the first consists of focusing only on the stationary solutions of the Fokker-Planck equations; the second consists in replacing the probability density distributions by their mass-center which provides a single number that represents the average activity of the population. The resulting model is then called a ‘neural mass’. Neural masses have already proven useful in modeling electrophysiological recordings such as EEG and MEG: ‘dynamic causal modeling’ uses them as a heuristic to infer the coupling among brain regions from experimental data (Friston et al. 2003; Marreiros et al. 2010). Despite fairly realistic results, neural mass models are a work in progress: further efforts are needed in order to accommodate the joint and often conflicting demands of biological realism and computational tractability. One technique is to subdivide neuronal populations according to their types (e.g. excitatory/inhibitory) and reduce complexity using mode decomposition techniques (Stefanescu and Jirsa, 2008). This gives access to a vaster range of complex dynamics observed in real data yet still employs a low dimensional description, thereby greatly easing computational costs. Figure 5 provides an image of the neural mass, an hypothesized unit of neurocomputation (Izhikevich and Edelman, 2008). Other recent developments introduce spatial constraints (Pinotsis and Friston 2011). Such spatial priors allow one to recover the dynamics of cortical activity even in the absence of explicit spatial information in experimental data (Pinotsis et al. 2012): they also can accommodate dynamic behaviors such as pattern formation and traveling waves (Coombes 2008). Even though the relation between neural masses (as nodes in a network) and neural fields seems conceptually clear, it is fair to say that the distance between neural masses, neural fields and human cognition and behavior still needs shortened. Nevertheless, the path advocated here to understand how neural fields arise from both cellular and behavioral constraints seems open.

Figure 5.

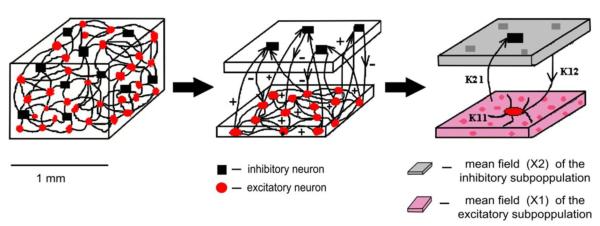
Schematic of the neural field method (adapted from Stefanescu & Jirsa, 2008). A small cortical volume with mixed populations of excitatory (red) and inhibitory (black) neurons is synthesized in two mean fields: X1 representing the excitatory subpopulation (pink) drives every neuron, and X2 representing the inhibitory subpopulation (gray) affects only the excitatory neurons.

IX. Bidirectional coupling: from neuro-glial masses to social interaction

The importance of bidirectional coupling in a general theory of neural and behavioral coordination can hardly be overemphasized. At the level of individual cells—the last rung in the ladder, at least for present purposes, bidirectional coupling is manifest in the tripartite synapse. The usual pre-post synaptic communication involves one-way (sender-receiver, Shannonian-like) chemical transmission. As is now well-known, in the tripartite synapse an astrocyte process connects with the axon and dendrite of both the pre- and post-synaptic neurons and is sensitive to neurotransmitters within the extracellular fluid in the synaptic cleft. When neurotransmitter, e.g. glutamate, is released into the synaptic cleft by the presynaptic terminal, some of it interacts with glutamate receptors on the astrocyte. This then initiates the release of so-called IP3 into the astrocytic cytoplasm. IP3 subsequently binds to IP3 receptors on the Endoplasmic Reticulum (ER), a long network of tubes and vesicles used to store calcium within the cell. The binding of IP3 with IP3 receptors opens channels that allow the release of Ca2+ from the ER into the cytoplasm (Ca2+ puff). While individual Ca2+ puffs are incapable of propagating intracellularly, several puffs can raise Ca2+ levels in the cytoplasm beyond a threshold and an oscillating Calcium Induced Calcium Release (CICR) propagation is observed. The increase in cytosolic Ca2+ then causes the release of neurotransmitter, more commonly called gliotransmitter, back into the synaptic cleft. The end result of all this is that the astrocyte can modulate synaptic transmission between pre- and post-synaptic neurons based on the previous activity of the synapse and the type of transmitter released--bidirectional neuronal~astrocyte coupling.

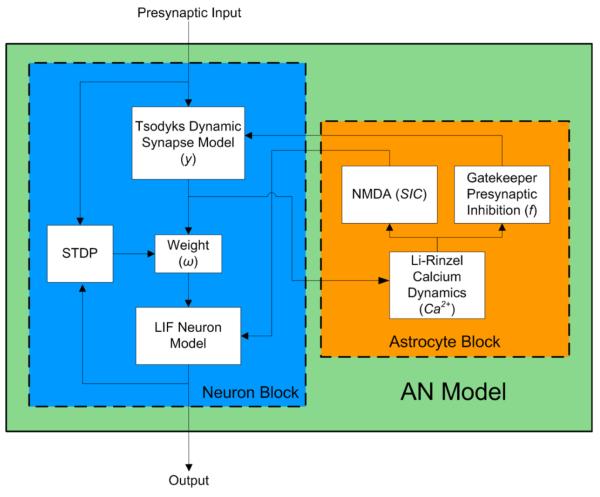
At this level of description the strategy is to construct biophysically realistic models of essential cellular processes such as calcium transport, presynaptic inhibition, etc. and ‘synergize’ them –just like Nature herself--to produce emergent coordinative effects such as synchronization and phase-locking, learning (Spike Timing Dependent Plasticity), repair, and so forth. This has already been demonstrated in the astrocyte-neuronal (AN) model of Wade et al (2011a,b) illustrated in Figure 6. The intriguing possibility (perhaps even more than that) is that these elementary models can be scaled up to the level of neuro-glial masses, that scale up to the level of neural fields composed of networks that produce patterns of neural activity in distributed cortical and subcortical areas of the brain, that (when exposed to external stimuli and internal influences such as neuromodulators) lead to the coordinated patterns of behavior involved in perceiving, attending, decision-making, learning, remembering, selecting and controlling movements—all the functions of mind-- and ultimately to the coordination between brains and people.

Figure 6.

The astrocyte~neuron (AN) model block diagram showing interactions between an astrocyte and neuron (from Wade et al. 2011a). The AN model itself is constructed from empirically verified biophysical models which are combined in realistic ways to produce emergent coordinative effects

X. The brain: A geography of rhythms

The general theory of behavioral and brain coordination uses instabilities in behavior as an entry point and proceeds downward to the level of neural masses and (if Providence permits) back up again from the level of astrocyte-neuronal interactions. An approach entirely consistent with the theory has explored variability (1/f fluctuations) at behavioral and neural levels demonstrating the existence of similar scaling laws in psychophysical studies and neural data (Palva & Palva, 2011; see also Chen, et al., 1997; Chialvo, 2010; Ding, et al., 2002; Plenz & Thiagarian, 2007). Such work is highly suggestive that common dynamics are at play at multiple scales--without necessarily providing a picture about their local underpinnings (Beggs & Timme, 2012). In this respect, neuroscience has made considerable progress in the theorization of brain dynamics noticeably with the study of oscillatory activity. Interestingly, the collective effort of the computational neuroscience community toward the creation of a “virtual brain” (Jirsa et al. 2010) has also demonstrated the pervasive nature of such mesoscopic dynamical patterns. At this scale, the brain is indeed dominated by rhythmic activity covering frequencies from approximately near DC to several hundred Hertz, with specific frequency bands hypothesized to act as independent channels of communication and coordination (Roopun et al. 2008). Since even single neurons are also endowed with the capacity to express multiple frequencies, it has been proposed to view neural oscillations as the “critical middle ground” connecting neurons to behavior (Buzsaki and Draguhn, 2004). Understanding of neural oscillations and synchrony has progressively evolved from the early correlative observations with EEG to more functional accounts (Uhlhaas, et al., 2009). This shift has been accelerated in the 90′s when an international buzz appeared around gamma oscillations and their potential link with consciousness. Even if a bit hyped, this produced a number of insightful results and extended our knowledge of neurodynamics. Observations span across multiple scales in both space and time, from the percept-related modulation of gamma oscillations in neuronal microcircuits (e.g., Bressler and Freeman, 1980) to motor-related modulations of beta oscillations at scalp level (e.g., Boonstra et al., 2007; Houweling et al., 2010). In short, neural synchronization has been under the spotlight ever since it was proposed as a potential mechanism for the integration of information among distant brain regions (Varela et al., 2001; Fries, 2005).

A mathematical account of both oscillation and synchronization phenomena can be carried out with networks of oscillators, very much along the lines of the general theory proposed here. Whereas such a model may appear biophysically far from the individual neurons compared to neural masses, it fits the mesoscopic scale dominated by oscillatory activity. Though an idealization as far as the brain is concerned, the Kuramoto model of weakly phase-coupled oscillators is the most commonly used. As long as the coupling is weak and the subsystems nearly identical, this model has been demonstrated to approximate the long-term behavior of any ensemble of interacting oscillatory systems (Kuramoto, 1975; Acebron, et al., 2005). It has already been proposed for unifying brain oscillations and their relationship to basic computational processes including multistability, criticality, and information capacity (for review see Breakspear et al. 2010). Combined with ‘realistic’ connectivity, the Kuramoto model has shown similar efficiency to neural mass models for simulating the dynamical consequences of cortical lesions (Honey and Sporns 2008). Recent studies have also demonstrated how resting-state neural dynamics can originate from the interplay between the local neural dynamics and the large-scale structure of the brain (Honey et al. 2009; Cabral et al. 2011). Most of the studies thus far have focused on the isolated brain. Yet the Kuramoto model has been applied to complex systems in physics, biology, and social science, and is a useful tool for traversing multiple scales of brain and behavior. The inter-individual level has been approached recently through the modeling of perception-action coupling between two virtual brains using Kuramoto oscillators combined with realistic anatomical structure (Dumas et al. 2012). This study follows directly the experimental demonstration that behavioral synchrony correlates with the emergence of inter-brain synchronization (Dumas et al. 2010; cf Fig.1). Simulations describe how the anatomical structure affects both intra- and inter-individual neural dynamics: at the intra-individual level by favoring dynamical modes such as the alpha rhythm; at the inter-individual level, by facilitating inter-brain synchronization and thus partly accounting for our propensity to generate self-other dynamical couplings. By directly linking intra- and inter-brain synchronization, the work opens a way to draw a connection between neural, behavioral and social scales and thereby extend the general theory.

XI. From synchronization to metastability

As an hypothesized mechanism for integration in the brain, synchronization has captured by far the most attention among neuroscientists (see, e.g. the many contributions in von der Malsburg, et al., 2010). We all like to see order in our data and synchronization-- as a highly ordered form of phase- and frequency-locked coordination— not only catches the eye but is accessible through an armamentarium of analysis methods (cf. Fig.1). But the brain and the mind are always in constant flux, ensembles of neurons being assembled and annihilated continuously. Whereas synchronization (usually in-phase) naturally arises in Kuramoto-like models, it is viewed as only one regime of brain coordination dynamics. Elsewhere we have discussed in some detail also the metastable regime which arises when the system exhibits both an integrative tendency, i.e. a tendency to synchronize, and a tendency for the components to maintain their autonomy (e.g. Bressler & Kelso, 2001; Kelso, 1991; 1995; 2001; 2008; 2012; Kelso & Tognoli, 2007; Tognoli & Kelso, 2009). Metastability consists of a more subtle dwell and escape dynamic in which the brain is never quite stable and merely expresses a joint tendency or disposition for neural areas to synchronize together and to oscillate independently. In the general theory, metastability (with its slow-fast, dwell-escape dynamic) is the way the brain constantly creates and destroys neural assemblies. Measuring metastability in neurophysiological (and behavioral) data represents a methodological challenge since this dynamical phenomenon is more complex than phase locking (for possible metrics, see Kelso, 2008). The two main issues are to first determine if a system is metastable (in whole, in parts and at times); and then to quantify its properties to assess the kind of coordination dynamics that exists between the parts (for instance, the degree of integration~segregation, the particular phase relationships between transient subensembles, their spatial and temporal endurance, the temporal positioning of escape behaviors, and all other properties that contribute to the specifics of the system’s function). The former issue, determination of metastability, may be addressed with perturbation paradigms applied to properly prepared systems (Massimini et al. 2009; Stamoulis et al. 2011; Kitajo et al. 2011). As for the latter issue (what kind of metastability one is dealing with), a promising method would be model fitting performed on collective variables, with special emphasis on the location of dwells and escapes and their spread. When there are two tendencies, the most common metastability case, it is possible to relate empirically observed features (e.g. histograms of the relative phase) with the parameters of the extended-HKB model (Kelso et al., 1990). Importantly, such an approach combines both dwell and escape phenomena rather than treating them separately as instances of coordination behavior resembling states and transition (see also Kelso & Tognoli, 2007). Nevertheless, metastability could be associated with multistable or monostable regimes of coordination by alternation in time and co-existence in space as in dynamical chimera (Kelso & Tognoli, 2007; Shanahan, 2010; Kelso, 2012). Metastability emphasizes the transient nature of the ongoing coordination dynamics and is linked to intermittency (Pomeau & Manneville, 1980) and chaotic itinerancy (Tsuda et al. 1987; Tsuda, 2001). These aspects can been approached quantitatively with tools such as the entropy derived from the spectral density (Friston 1997) or connectivity indicators and metrics computed on brain functional networks (Sporns & Tononi, 2002; Sporns, 2004). Furthermore, as metastability is characterized by a stationary transient regime, its presence may also be associated with self-organized criticality (Bak et al. 1988). This last phenomenon is traditionally assessed through the discovery of power-laws and scale-free quantities (Chen, et al., 1997; Kitzbichler et al. 2009; Chialvo, 2010). At this point, it is important to notice how metastability is a phenomenon in its own right not just a sequence of transitions between multiple states (Kelso & Tognoli, 2007; Kelso, 2012).

Viewed as a generative dynamical mechanism, metastability is in line with observations that ensembles of neurons of various sizes come together and disband incessantly (Beggs & Timme, 2012; Plenz & Thiagarian, 2007). According to the present theory, the normal brain realizes its complexity at all scales not in its most ordered form (integration qua synchronization) or disordered form (segregation qua desynchronization), but in a subtle blend of both tendencies (see also Tononi, et al., 1994). The logic of the brain is not only either/or, but both~and. Dual tendencies for integration and segregation constitute a complementary pair (Kelso & Engstrøm, 2006) very much along the lines proposed by Stephen Grossberg, one of the pioneers of the field of Neural Networks: the brain is organized to obey principles of complementarity (Grossberg, 2000). Metastable coordination dynamics rationalizes William James (1890) beautiful metaphor of the stream of consciousness as the flight of a bird whose life journey consists of ‘perchings’ (phase gathering, integrative tendencies) and ‘flights’ (phase scattering, segregative tendencies). Both tendencies appear to be crucial: the former to summon and create thoughts; the latter to release individual brain areas to participate in other acts of cognition, emotion and action. Of course, the hypothesis of metastable coordination dynamics in all its manifestations as the organizing principle of brain and cognitive function--as the essence of ‘neural choreography’-- is the testbed of the general theory. If the brain does not work according to metastable coordination dynamics, and if brains working together do not work according to metastable coordination dynamics, and if metastable coordination does not break down in diseases of the brain, such as Parkinson’s and schizophrenia, the theory is wrong.

XII. Conclusion

In 1979, Francis Crick in a special issue of Scientific American on the brain said the following: “If a breakthrough in the study of the brain does come, it is perhaps likely to be at the level of the overall control of the system. If the system were as chaotic as it appears to be, it would not enable us to perform even the simplest tasks satisfactorily. To invent a possible, although unlikely example, the discovery that the brain was run phasically by some kind of periodic clock, as a computer is would probably constitute a major brakthrough” (p .137). According to the general theory outlined here, the brain is a self-organized, pattern forming dynamical system living in the metastable regime where fluctations play a key role. This is definitely not the way computers, at least as we know them, are organized. Nevertheless, on the basis of much research in coordination dynamics, Crick’s intuition has a ring of truth about it. Though the brain is not a clock, it is run phasically: coordination dynamics shows that relative phase is a key quantity that couples diverse regions of the brain whose neurons exhibit tendencies to oscillate. The primitives of the brain do appear to take the form of oscillations and the natural language of the brain is the way these oscillatory ensembles are coupled. The two “forces” that constitute the general theory deal fundamentally with (mostly bidirectional) information exchange. One force is the strength of coupling between the elements; this allows information to be distributed to all participating elements and is a key to integrative, collective action. The other is the ability of individual elements to express their autonomy, and thereby minimize the influence of others. Self-organization in the metastable regime is the interplay of both⁴. This brings us to a final point, perhaps more on the philosophical side but with quite cogent scientific consequences. Your neural network and my neural network are not the same. The nodes are different, the connections too; individual differences exist at all levels of structure and function. You walk differently than me, you think differently than me, you feel differently than me, you respond to the environment differently than me, you structure your world differently than me. A general theory, then, is not (or not only) about the contents of mind and emotions and their neural correlates. Rather it is about the dynamical processes of forming, breaking, uniting, dissolving, and harmonizing patterns of activity that occur at all levels. A general theory of behavioral and brain coordination applies just as much to the mind-world of ideas as it does to the brain-world of cells.

Highlights.

• An account of brain and behavioral function that encompasses multiple levels in a coherent manner without reifying one level or another

• Uses instabilities as an experimental window to identify behavioral and neural dynamics

• General theory employs both a top-down and bottom-up approach to connect phenomenological models to physiology and biophysics

Highlights.

• A theory of brain and behavior is proposed based on the principles of coordination dynamics

• The theory connects multiple levels of description

• Instabilities are used experimentally to identify relevant quantities and their dynamics

• Bidirectional coupling is emphasized at all levels, both within and across brains

Figure 7.

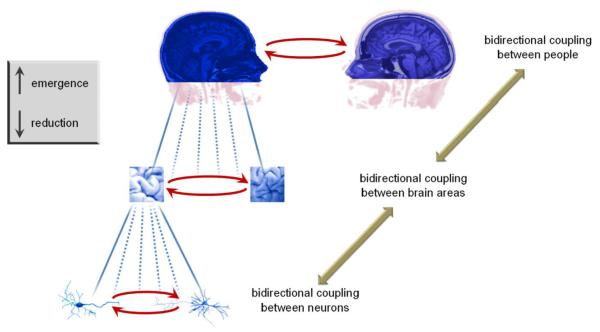
The complementary nature of reduction and emergence in the general theory emphasizes bidirectional coupling at all levels, both within and across brains.