QSAR study on maximal inhibition (I_max) of quaternary ammonium antagonists for S-(−)-nicotine-evoked dopamine release from dopaminergic nerve terminals in rat striatum

Abstract

Maximal inhibition (I_max) of the agonist effect is an important pharmacological property of inhibitors that interact with multiple receptor subtypes that are activated by the same agonist and which elicit the same functional response. This report represents the first QSAR study on a set of 66 mono- and bis-quaternary ammonium salts that act as antagonists at neuronal nicotinic acetylcholine receptors mediating nicotine-evoked dopamine release, conducted using multi-linear regression (MLR) and neural network (NN) analysis with the maximal inhibition (I_max) values of the antagonists as target values. The statistical results for the generated MLR model were: r² = 0.89, rmsd = 9.01, q² = 0.83 and loormsd = 11.1; the statistical results for the generated NN model were: r² = 0.89, rmsd = 8.98, q² = 0.83 and loormsd = 11.2. The maximal inhibition values of the compounds exhibited a good correlation with the predictions made by the QSAR models developed, which provide a basis for rationalizing selection of compounds for synthesis in the discovery of effective and selective second generation inhibitors of nAChRs mediating nicotine-evoked dopamine release.

1. Introduction

Tobacco smoking is a leading health problem accounting for more illnesses and deaths in the US than any other single factor.¹ Several drugs are currently marketed for smoking cessation, including nicotine (as a replacement therapy) and bupropion (an antidepressant agent with nicotinic receptor antagonist properties), ² as well as the newest non-nicotine prescription drug, varenicline. ^3,4 Unfortunately, relapse rates are high with these agents, indicating that novel medications are still needed.^2–5

Previous research^6–13 in our laboratories has led to the discovery of a new class of neuronal nicotinic acetylcholine receptor (nAChR) antagonist resulting from N-n-alkylation of the pyridine moiety of either the nicotine molecule or structural analogs of nicotine. These novel quaternary ammonium compounds exhibit potent and selective inhibition of nAChR subtype(s) that mediate nicotine-evoked dopamine (DA) release from dopaminergic nerve terminals in striatum.^6,7 Such antagonists may have potential as novel smoking cessation agents, and are of considerable interest, due to their selective antagonist activity at nAChR subtypes, and their ability to penetrate the blood–brain barrier (BBB) via active transport by the BBB choline transporter.¹⁴ We have previously reported structure-based studies on the molecular interaction of some typical agonists and antagonists with nAChRs.^15–18 In addition, the structure activity/function relationships of the novel quaternary ammonium nAChR antagonists have been studied previously using various QSAR modeling approaches.^19–21

In the nicotine-evoked DA release assay, two parameters are measured to define antagonist interaction with nAChRs mediating this effect, that is, IC₅₀ and I_max values. IC₅₀ is defined as the concentration of antagonist that inhibits the agonist effect by 50% of the maximal effect, and is related to the affinity of the antagonist for the receptor site, but takes into account that a functional assay is employed. Thus, the direct affinity (K_i value) of the antagonist for the receptor is not measured in the nicotine-evoked DA release assay, since it is several steps removed from the ligand–receptor protein interaction. The I_max value is defined as the concentration of antagonist producing maximal inhibition of the agonist effect.

A number of different nAChRs subtypes have been reported to mediate nicotine-evoked DA release from the striatum. Thus, α4β2, α6β2, α4α5β2, α6β2β3, α4α6β2 and α4α6β2β3 nAChRs play an important role in nicotine-evoked DA release in mouse striatum, whereas deletion of β4 and α7 subunits do not appear to play a role in nAChR-mediated DA release from this brain region. ^22,23 The α4α6β2β3 subtype constitutes about 50% of α6-containing nAChRs on DA terminals of wild-type mice and has the highest sensitivity to nicotine of any native nAChR, strongly implicating this subtype in nicotine-evoked DA release.^24,25 The nonselective nAChR antagonist, mecamylamine, was shown to nearly completely inhibit (I_max = 91%) nicotine-evoked DA release,²⁶ while the snail toxin α-conotoxin MII (α-CtxMII) is a selective, high-potency antagonist at a subset of nAChR subtypes containing α6 (I_max = 62%).^27–29 We have reported recently on the nAChR antagonist properties of a series of small molecules that are quaternary ammonium salts which inhibit nicotine-evoked DA release from rat striatum and appear to interact with the same α6β2-containing subtypes with which α-CtxMII interacts.³⁰ The lead compound in this series was N,N′-dodecane-1,12-yl-bis-3-picolinium dibromide (bPiDDB), which exhibited an IC₅₀ of 2 nM and an I_max of 78%.

The I_max values of a series of quaternary ammonium analogs synthesized in our laboratory ranged from 0% to 100%, and many of them, such as the N,N′-alkane-diyl-bis-3-picolinium analogs with C₆–C₁₂ methylene linkers, exhibited I_max values of 54–64% of nicotine-evoked DA release from rat striatal slices, suggesting that they selectively inhibit some, but not all nAChR subtypes mediating nicotine-evoked DA release in this brain tissue.³⁰ Further research has demonstrated that quaternization of the pyridine nitrogen of the nicotine molecule with a lipophilic N-alkyl substituent to afford N-alkylnicotinium analogs and/or various quaternary ammonium moieties interconnected with a lipophilic linker to afford N,N′-bis-analogs, generates subtype-selective nAChR antagonists.^6,7 Discovery of antagonists that can selectively inhibit nAChR subtypes is important, since such compounds may be advantageous as potential compounds for the treatment of nicotine addiction because they would be predicted to have minimal side effects in comparison to nonspecific nAChR antagonists such as mecamylamine.

In this study, the I_max values of a series of quaternary ammonium analogs were taken as target values on which to build QSAR models using multi-linear regression procedures and back-propagation neural network approaches. To our knowledge, this is the first QSAR study that utilizes I_max values as target values. The experimentally measured I_max values generally have a smaller data range (0%–100%) and relatively larger experimental errors (20%), thus introducing some difficulty for mathematical modeling. Based on currently available I_max values for 66 mono- and bis-quaternary ammonium salts identified as antagonists at nAChR subtypes that mediate nicotine-evoked dopamine release, descriptors selected by stepwise regression from various molecular properties were used to train and validate multiple linear regression and neural network QSAR models. The maximal inhibition of the synthesized antagonists was evaluated. The results demonstrate that the performance of the generated QSAR is satisfactory, and consistent with expectations, based on the validation measurements.

2. Results and discussion

The experimental I_max values for 72 molecules are provided in Table 1, and vary from 0% to 100%. MLR analysis was initially applied to the complete data set of molecules utilizing 1497 descriptors and a single empirical I_max value. The preliminary analysis of I_max values produced a squared correlation coefficient (r²) of 0.74 and a predictive q² of 0.64 for leave-one-out cross validation. The residual variance plot from the MLR regression revealed that compounds BCDD, NBuPI, NHpPI, NOPI, bPiHxI, and bIQNB were outliers. Removing these compounds from the model significantly improved the correlation (r² of 0.88 and q² of 0.83). These compounds were thus excluded from further analysis. Constant and near constant descriptors and the highly inter-correlated (>0.90) descriptors were discarded to obtain a reduced set of 250 descriptors.

Table 1.

Structures, experimentally determined I_max values (in %) from nicotine-evoked DA release assays for 72 molecules, and I_max values (in %) calculated by the MLR model and the NN11-1-1 model, as well as their leave-one-out validation results for 66 quaternary ammonium salts^a

No.	Compd name	R	Imax% (Expt.)	Imax% (calcd)		Imax% (LOO)
				MLR	NN	MLR	NN
N-Alkylnicotinium salts
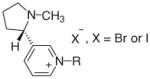
1	NMNI	CH3	0	−2	5	−3	5
2	NPNI	CH2CH2CH3	58	66	67	68	71
3	NnBNI	(CH2)3CH3	80	63	67	61	65
4	NHxNI	(CH2)5CH3	80	86	83	87	83
5	NHpNI	(CH2)6CH3	75	72	75	72	75
6	NONI	(CH2)7CH3	88	90	84	90	84
7	NNNI	(CH2)8CH3	100	93	85	92	84
8	NDDNI	(CH2)11CH3	95	89	83	88	82
9	NBzNB	CH2C6H5	0	−6	3	−8	2
10	NANI	CH2CH=CH2	0	17	12	19	14
11	NONB-3c	cis-(CH2)2CH=CH(CH2)3CH3	83	70	73	68	70
12	NONB-3t	trans-(CH2)2CH=CH(CH2)3CH3	79	80	80	81	80
13	NONB-7e	(CH2)6CH=CH2	87	70	71	68	69
14	NONB-3y	(CH2)2C≡C(CH2)3CH3	47	47	48	47	49
15	NDNB-4t	trans-(CH2)3CH=CH(CH2)4CH3	85	81	80	81	80
16	NDNB-9e	(CH2)8CH=CH2	72	81	80	82	80
17	NDNB-3y	(CH2)2CC(CH2)5CH3	29	29	28	29	27
18	NUNB-10e	(CH2)9CH=CH2	87	87	82	87	82
Bis-N,N′-alkylnicotinium salts
19	bNDDB	(CH2)12	38	52	49	56	57
Conformationally restricted N-alkylnicotinium salts (syn conformation)
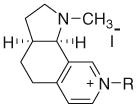
20	ACO	(CH2)7CH3	60	59	59	59	59
21	ACN	(CH2)8CH3	56	57	54	57	54
22	ACD	(CH2)9CH3	67	61	61	60	60
23	ACU	(CH2)10CH3	72	69	68	68	68
24	ACDD	(CH2)11CH3	62	72	71	74	72
Conformationally restricted N-alkylnicotinium salts (anti comformation)
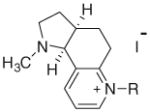
25	BCO	(CH2)7CH3	88	81	83	80	82
26	BCN	(CH2)8CH3	86	83	83	83	83
27	BCD	(CH2)9CH3	93	81	82	79	82
28	BCU	(CH2)10CH3	79	81	82	81	82
29	BCDD	(CH2)11CH3	25
N-Alkylpyridinium salts
30	NMPI	CH3	0	−10	1	−29	1
31	NEPI	CH2CH3	0	3	7	6	9
32	NPrPI	CH2CH2CH3	22	34	25	36	27
33	NBuPI	(CH2)3CH3	2
34	NPePI	(CH2)4CH3	44	39	33	39	29
35	NHxPI	(CH2)5CH3	21	29	21	29	21
36	NHpPI	(CH2)6CH3	0
37	NOPI	(CH2)7CH3	0
38	NPeDPI	(CH2)14CH3	58	56	60	56	60
39	NecPB	(CH2)19CH3	60	53	58	51	56
N-Alkyl-3-picolinium salts
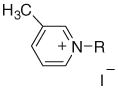
40	NOPiI	(CH2)3CH3	49	62	65	64	69
41	NDPiI	(CH2)9CH3	73	70	72	69	72
42	NDDPiI	(CH2)11CH3	63	79	78	82	80
Bis-N,N′-alkylpyridinium salts
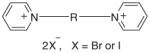
43	bPPeI	(CH2)5	0	16	13	21	17
44	bPOI	(CH2)8	0	−1	4	−5	5
45	bPNB	(CH2)9	28	25	19	25	16
46	bPDI	(CH2)10	27	35	28	36	28
47	bPDDB	(CH2)12	91	90	83	87	75
Bis-N,N′-Alkyl-3-picolinium salts
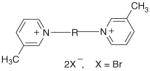
48	bPiHxI	(CH2)6	7
49	bPiHpB	(CH2)7	54	48	50	47	50
50	bPiOI	(CH2)8	53	60	63	60	64
51	bPiNB	(CH2)9	63	54	58	54	57
52	bPiDI	(CH2)10	63	58	59	58	59
53	bPiUB	(CH2)11	68	61	64	61	64
54	bPiDDB	(CH2)12	78	71	72	70	71
Bis-N,N′-alkylquinolinium salts
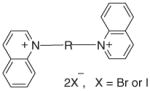
55	bQHxI	(CH2)6	55	61	66	62	68
56	bQOI	(CH2)8	71	65	69	65	68
57	bQNB	(CH2)9	58	55	58	55	58
58	bQDI	(CH2)10	76	72	74	71	73
59	bQUB	(CH2)11	91	95	85	95	84
60	BQDDB	(CH2)12	52	61	60	63	64
Bis-N,N′-alkylisoquinolinium
61	bIQHxI	(CH2)6	47	44	44	43	42
62	bIQOI	(CH2)8	74	56	58	52	52
63	bIQNB	(CH2)9	0
64	biQDI	(CH2)10	65	68	70	68	71
65	bIQUB	(CH2)11	55	64	69	66	72
66	biQDDB	(CH2)12	53	70	72	73	74
6-Aza-4-aminotetralin salts
67	ASP	H, H	56	59	63	59	65
68	ASSC	H, CH3	57	76	80	80	82
69	AST	CH3, CH3	68	43	42	40	32
5-Aza-1-aminotetralin salts
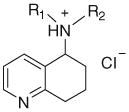
70	BSP	H, H	69	69	74	69	75
71	BSS	H, CH3	87	91	86	96	86
72	BST	CH3, CH3	53	56	63	57	65

^aAll compounds and experimental data in this table were generated in the laboratories of Drs. Peter A. Crooks and Linda P. Dwoskin.

2.1. Determination of the number of descriptors for building the multi-linear regression model

To build the most reasonable linear model, the forward-selection and backward-elimination stepwise regression procedure was used to select descriptors from the reduced set of 250 descriptors. Single descriptors were gradually added to build the MLR model. The ‘break point’ technique³¹ was used to control the model expansion in the improvement of the statistical quality of the model. The ‘break point’ was found by analyzing the relationship of the number of descriptors involved in a generated model versus the value of the correlation coefficient r² corresponding to the model. The optimum number of descriptors for the MLR model was determined as the number of descriptors corresponding to the ‘break point’. If the difference between r² of the two consequent regression equations was less than or equal to 0.02 after obtaining a certain number of descriptors selected for the model (the ‘break point’), then no statistical improvement of the regression model was demonstrated.

Five MLR models were generated. The first MLR model was initiated from a descriptor which is most correlated to the target values. Accordingly, the other four MLR models started with a descriptor in which the Pearson correlation coefficient with the target values ranked as the second, the third, the fourth, or the fifth, in a descending order among the 250 utilized descriptors. The five QSAR models obtained and their statistical characteristics are shown in Table 2. Results in Table 2 indicate that the ‘break point’ occurred when the number of the descriptors used to generate the MLR models was between 10 and 12. In other words, although the linear models were generated by utilizing initially five different descriptors, the number of descriptors used to build the most reasonable MLR models does not change significantly. The training r², training root mean square derivation (rmsd), q² and leave-one-out root mean square derivation (loormsd) of the five linear models are similar, and give rise to average values of 0.87, 9.60, 0.81, and 11.8, respectively. The data in Table 2 indicate that the number of descriptors used to build the most reasonable MLR model to fit the observed I_max values is 11 on average.

Table 2.

Determination of the number of descriptors used to generate the MLR model

Starting descriptor	Na	r2	rmsd	q2	Loormsd
1	12	0.87	9.67	0.80	12.08
2	11	0.89	9.01	0.83	11.06
3	11	0.86	10.18	0.78	12.47
4	12	0.87	9.69	0.80	12.08
5	10	0.88	9.44	0.82	11.42
Average	11	0.87	9.60	0.81	11.82

^aNumber of descriptors corresponding to the ‘break point’ used in each model.³¹

2.2. Quality of the generated MLR model

Although the five linear models created in Table 2 have similar quality, the best model was entry 2. The linear model with 11 descriptors is given in Eq. 1:

$$\begin{array}{l}{I}_{max}=3150.467-2628.961\ast \text{MATS}4\text{m}+218.213\ast \text{MATS}3\text{e}\\ -1599.952\ast \text{PW}5-435.168\ast \text{Du}-1.185\ast \text{DISPv}\\ -375.838\ast \text{G}3\text{v}+332.321\ast \text{G}2\text{m}-19.016\ast (\text{n}\#\text{CR})\\ -120.800\ast \text{AROM}+3.322\ast \text{RDF}070\text{m}-3.154\\ \ast \text{RDF}045\text{m}\end{array}$$ (1)

where MATS4m and MATS3e are among the 2D autocorrelations; PW5 is among the topological descriptors; Du, G3v and G2m are among the WHIM descriptors; DISPv is among the geometrical descriptors; n#CR is among the functional groups; AROM is among the aromaticity indices; and the RDF070m and RDF045m are among the RDF descriptors calculated by DRAGON software.³² Brief definitions of the descriptors used in the linear regression relationship are provided in Table 3. The Pearson correlation coefficient R between the 11 descriptors is listed in Table 4. All the non-diagonal elements were less than 0.70, indicating that the co-linear situation between different descriptors and redundant information included in the set of descriptors are low. The statistical analysis for the multi-linear regression indicated that the correlation coefficient r² and rmsd between the observed and the fitted I_max values was 0.89 and 9.01, respectively (Table 2). The leave-one-out validation q² was 0.83, and the loormsd (the root mean square derivation from the leave-one-out validation) was 11.1 (Table 2). The Fischer statistic F was 38.43. Figure 1 shows the relationships of the trained and LOO-predicted I_max values versus the experimental I_max values for the MLR model. The calculated I_max values for the 66 molecules from the MLR model (Eq. 1), as well as the LOO validation results, are provided in Table 1.

Table 3.

Brief definitions of the descriptors used in the linear regression relationship

No.	Descriptor	Definition
1	MATS4m	Moran autocorrelation—lag 4/weighted by atomic masses
2	MATS3e	Moran autocorrelation—lag 3/weighted by atomic Sanderson Electronegativities
3	PW5	Path/walk 5—Randic shape index
4	Du	D total accessibility index/unweighted
5	DISPv	d COMMA2 value/weighted by atomic van der Waals volumes
6	G3v	3rd component symmetry directional WHIM index/weighted by atomic Van der Waals volumes
7	G2m	2nd component symmetry directional WHIM index/weighted by atomic masses
8	n#CR	Number of non-terminal C(sp)
9	AROM	Aromaticity
10	RDF070m	Radial distribution function—7.0/weighted by atomic masses
11	RDF045m	Radial distribution function—4.5/weighted by atomic masses

Table 4.

Pearson correlation coefficient R between the descriptors used in the MLR model

No.	1	2	3	4	5	6	7	8	9	10	11
1	1.00	−0.58	−0.57	−0.01	−0.29	0.53	0.63	−0.12	0.29	0.07	−0.24
2		1.00	0.49	0.00	0.23	−0.59	−0.57	−0.08	−0.34	0.15	0.13
3			1.00	−0.30	−0.15	−0.30	−0.30	−0.12	−0.53	−0.12	0.07
4				1.00	−0.03	−0.24	−0.30	0.20	0.24	0.44	0.44
5					1.00	−0.07	−0.10	0.06	0.08	−0.45	−0.22
6						1.00	0.67	−0.08	0.08	−0.31	−0.38
7							1.00	−0.06	0.11	−0.36	−0.39
8								1.00	−0.03	0.10	0.11
9									1.00	0.17	0.20
10										1.00	0.68
11											1.00

Figure 1.

The calculated versus the experimentally determined I_max values from the DA release assay for the trained (shown in blue squares) and leave-one-out cross-validation (shown in red triangles) for the best MLR QSAR model. The solid line represents a perfect correlation. The dotted lines represent ±20% difference from a perfect fit.

2.3. Evaluation of the generated MLR model by leave-n-out validation

To test the ability of the model for predicting I_max values of a set of molecules, the leave-n-out cross validation was performed. For the 66 quaternary ammonium salts studied, the 66 observed I_max values were ranked in ascending order. Six subsets were constructed by collecting the 1st, 7th, 13th, etc. data points into the first subset; and the 2nd, 8th, 14th, etc. data points into the second subset. The other four subsets were constructed accordingly. Six training sets were prepared as combinations of any five subsets. The remaining subset was used as a test set. Thus, every time 55 molecules (83.3%) out of the 66 data set of molecules were used to train the model, a subset of 11 molecules (16.7%) out of the 66 molecules was used to test the model. For each training set, a correlation equation was derived with the same 11 descriptors listed in Table 3. New regression coefficients were obtained. Then, the generated new regression equation was used to predict the I_max values for the molecules from the corresponding test set. The quality of the QSAR models was demonstrated by the statistical results provided in Table 5. The average correlation coefficients of the training r², rmsd, leave-n-out predictive $r_{\text{test}}^2$ and root-mean square derivation (testrmsd) are 0.89, 8.79, 0.80 and 11.6, respectively, which is close to the statistical results (0.89, 9.01, 0.83, and 11.1, respectively) obtained from training and LOO validation of the MLR model (Eq. 1). These results indicate that the MLR QSAR model has stable predictive power within the current experimental data set.

Table 5.

Evaluation for the MLR model prediction of the test set

Set	r2	rmsd	$r_{\text{test}}^2$	Testrmsd
1	0.89	9.06	0.88	9.30
2	0.89	8.87	0.84	10.47
3	0.92	7.77	0.62	15.99
4	0.90	8.70	0.76	12.72
5	0.88	9.29	0.90	8.49
6	0.88	9.05	0.81	12.79
Average	0.89	8.79	0.80	11.63

2.4. Neural network analysis

A limitation of the results calculated by the generated MLR models in Table 2 is that for some compounds where the experimental I_max values are zero, the theoretical prediction for these compounds gives rise to negative values. Similarly, the model could over-predict the I_max value of a compound to provide a value over 100%, when the compound has a large experimental I_max value (e.g., 95%–100%). This is the common feature of a linear model when dealing with the boundary points within a data range. However, I_max values should never be less than 0% or larger than 100%.

The artificial neural network technique has been demonstrated to be an effective tool for data mining, and has been used in many QSAR studies.^{19–21,33–38} This artificial system emulates brain function, in which a very high number of information-processing neurons are interconnected and are known for their ability to model a wide set of functions, including linear and non-linear functions, without knowing the analytic forms in advance. Being different from a linear model, neural network prediction can be expected in a pre-specified data range. With the 11 descriptors used in the MLR model (Equation 1, descriptors listed in Table 3), the back propagation neural network model with architecture NN11-h-1 (h = 1–3) was trained and leave-one-out validated, in which 11 is the number of input neurons corresponding to the 11 descriptors, and h represents the number of hidden neurons. The neural network models have one output neuron corresponding to the I_max value.

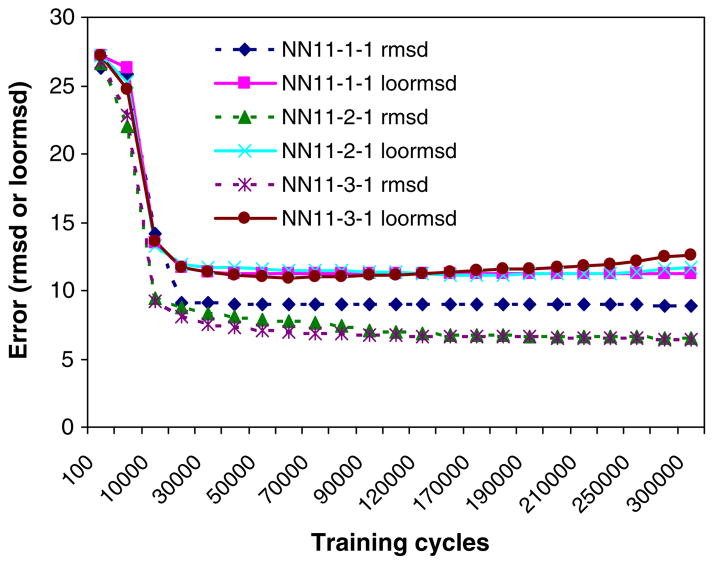
Figure 2 shows the training and leave-one-out errors (rmsd and loormsd) as functions of the number of training cycles for the NN11-1-1, NN11-2-1 and NN11-3-1 models. From the data, increasing the number of hidden nodes (h = 2 or 3) does not apparently decrease loormsd in the validation. However, the training errors decrease for models NN11-2-1 and NN11-3-1 compared with the results from model NN11-1-1. For model NN11-1-1, the training and validation errors do not change after the training cycles are over 30000. To avoid overtraining the model, the model NN11-1-1 was considered to be optimal.

Figure 2.

The training and leave-one-out errors (rmsd and loormsd) as functions of the number of training cycles of the NN11-1-1, NN11-2-1 and NN11-3-1 models.

The statistical results for the NN11-1-1 model with errors converged versus training cycles are as follows: r² = 0.89, rmsd = 8.98, q² = 0.83 and loormsd = 11.2, which are close to the statistical results for the generated MLR model (r² = 0.89, rmsd = 9.01, q² = 0.83 and loormsd = 11.1). Thus, both MLR and NN models afford similar predicted values. I_max values calculated by the NN11-1-1 model, as well as its leave-one-out validation results for the 66 quaternary ammonium salts, are provided in Table 1. Comparing the I_max values with those calculated by the MLR model (Eq. 1), many of the values are equal to or close to each other, except for those boundary points between 0% and 100%. The linear feature of the I_max values versus the 11 variables was sufficiently reflected by the nearly linear model NN11-1-1. However, the I_max value of a compound was never predicted to be negative or larger than 100% by the NN11-1-1 model. Figure 3 shows the relationships of the trained and LOO-predicted I_max values versus the experimental I_max values for the NN11-1-1 model.

Figure 3.

The calculated versus the experimentally determined I_max values from the DA release assay for the trained (shown in blue squares) and leave-one-out cross-validation (shown in red triangles) for the NN11-1-1 QSAR model. The solid line represents a perfect correlation. The dotted lines represent ±20% difference from a perfect fit.

Leave-n-out cross-validation was also performed for the NN11-1-1 model to test its ability to predict an external compound set. Six subsets were constructed from the dataset of 66 quaternary ammonium salts in the same way as those created for the leave-n-out validation of the MLR model (Eq. 1). Similarly, six training sets were generated as combinations of any five subsets. The remaining one was used as a test set. Six neural networks (11-1-1 architecture) with 11 descriptors (listed in Table 3) as inputs were trained, based on each of the six newly generated training sets, and the prediction was made for their corresponding test set. The results are listed in Table 6. As seen from Table 6, the statistical average of the training r², rmsd, leave-n-out predictive $r_{\text{test}}^2$ and root-mean square derivation (testrmsd) for the six groups examined are 0.89, 8.73, 0.79 and 11.7, respectively, which is similar to the statistical average obtained from the leave-n-out validation of the MLR model (i.e., 0.89, 8.79, 0.80 and 11.6, respectively), and is close to the statistical results (0.89, 8.89, 0.83, and 11.2, respectively) obtained from the training and LOO validation of the NN11-1-1 model with the 66 molecule set. These results indicate that the NN11-1-1 model has stable predictive power on a set of compounds like the MLR model (Eq. 1).

Table 6.

Leave-n-out cross-validation of the NN11-1-1 model

Set	r2	rmsd	$r_{\text{test}}^2$	Testrmsd
1	0.89	9.03	0.87	9.69
2	0.90	8.62	0.81	11.50
3	0.92	7.53	0.45	19.28
4	0.89	8.74	0.82	11.22
5	0.89	9.12	0.84	10.52
6	0.87	9.37	0.93	7.97
Average	0.89	8.73	0.79	11.70

An interesting phenomenon shown in Table 6 is that compared to other entries, entry 3 has better training r² (0.92) with a smaller root-mean square derivation (7.53), but worse $r_{\text{test}}^2$ (0.45) with a larger root-mean square derivation (19.28). Data analysis reveals that the reason for this is that the two molecules (AST and bIQOI in Table 1) with exceptionally large training and LOO validation errors in Figure 3 (the two points outside the dash line boundaries) are both allocated to the test set of entry 3. The same fact holds for the leave-n-out validation of the MLR model, as shown in Table 5.

2.5. Descriptor contribution analysis

The 11 descriptors used in the generated MLR model (Eq. 1) and the neural network model NN11-1-1 can be classified as follows: (i) 1D descriptor: n#CR. (ii) 2D descriptors: PW5, MATS4m, and MATS3e. (iii) 3D descriptors: Du, DISPv, G3v, G2m, AROM, RDF070m, and RDF045m. Based on a previously described procedure, ^19,34 the relative contribution of each descriptor in the MLR model (Eq. 1) and the NN11-1-1 model were determined, and are provided in Table 7. The significance of the descriptors involved in the MLR model decreases in the following order: MATS4m > PW5 > G3v > MATS3e > n#CR > G2m > RDF070m > DU > RDF045m > AROM > DISPv. The significance of the descriptors involved in the NN11-1-1 model decreases in the order: MATS4m > PW5 > n#CR > RDF070m> RDF045m > DU > G2m > G3v > MATS3e > DISPv > AROM. The two most significant descriptors in both the MLR and NN11-1-1 models are identical, that is, 2D descriptors MATS4m and PW5. MATS4m is a 2D autocorrelations descriptor calculated from molecular graph by summing the products of atom weights of the terminal atoms of all the paths of the considered path length (the lag). MATS4m represents Moran autocorrelation, that is, lag 4/weighted by atomic masses. The MATS4m descriptor itself correlated relatively high (R = 0.604) with the target experimental I_max values. The positive Pearson correlation coefficient for MATS4m indicated that the compounds with larger values for this descriptor would have larger I_max values. Thus, this descriptor could be an indicator for inhibitors that have a large I_max value. PW5 is a topological descriptor related to molecular shape, and has a smaller Pearson correlation coefficient with the experimental I_max values (R = 0.218). Although the order of the relative contribution from the other nine descriptors is different from each other in the two models, the individual contribution from all of these descriptors is very close (i.e., from 7.76 to 8.78 for the MLR model and from 7.75 to 9.46 for the NN11-1-1 model). Thus, the contribution from these descriptors to both models can be regarded as similar.

Table 7.

Relative contributions of the 11 descriptors to the structure–activity relationship in the MLR model and the NN11-1-1 model

Descriptor	MATS4m	MATS3e	PW5	DU
MLR Ci (%)	13.79	8.81	11.49	7.91
NN Ci (%)	10.33	8.52	10.72	8.96
Descriptor	DISPv	G3v	G2m	n#CR
MLR Ci (%)	7.76	8.87	8.56	8.78
NN Ci (%)	8.15	8.76	8.91	9.46
Descriptor	AROM	RDF070m	RDF045m
MLR Ci (%)	7.68	8.43	7.91
NN Ci (%)	7.75	9.28	9.16

It should be noted from Table 7 that the difference in descriptor contribution between any two descriptors used in the models is not significant, indicating that all descriptors are indispensable in generating the predictive models. Eleven descriptors were needed in the QSAR models from a 66 molecule dataset, showing that the analyzed dataset is quiet ‘noisy’ within a small data range (0%– 100%), although it is not against the rule of thumb for building a linear model, that is, at least five data point (molecules) per descriptor must exist in the model.

3. Conclusion

In the current study, MLR and NN approaches have been used to build QSAR models to predict I_max values of quaternary ammonium salts which are antagonists at nAChRs mediating nicotine-evoked DA release from dopaminergic nerve terminals in striatum. This work is the first report of a QSAR technique being applied to the prediction of I_max values for a series of nAChRs antagonists. The statistical results for the generated MLR model are: r² = 0.89, rmsd = 9.01, q² = 0.83 and loormsd = 11.1; The statistical results for the generated NN model are: r² = 0.89, rmsd = 8.98, q² = 0.83 and loormsd = 11.2. The I_max values correlated well with the predicted values generated by the two models developed in the present study, which provide a basis for rationalizing selection of compounds for synthesis in the discovery of effective and selective second generation inhibitors of nAChRs mediating nicotine-evoked DA release.

4. Methods

4.1. Generation of the molecular database

Seventy-two molecules listed in Table 1 constituted a database for the structure-activity correlation analysis. Molecular modeling was carried out with the aid of the SYBYL discovery software package. ^39a This software was used to construct the initial molecular structures used in the geometry optimization (energy minimization) for all molecules involved in this study. In construction of the initial molecular structures, a formal charge of +1 was assigned to each positively charged nitrogen atom in the structures of these compounds, and the alkyl chain connecting the head group(s) was kept in its fully extended conformation.^19,21 The geometry optimization was first performed using the molecular mechanics (MM) method with the Tripos force field and the default convergence criterion, which was then followed by a semi-empirical molecular orbital (MO) energy calculation at the PM3 level.³⁹

4.2. Generation of molecular descriptors

The optimized three-dimensional conformations were used for generation of molecular descriptors. A total number of 1497 descriptors consisting of zero-dimensional (constitutional), one-dimensional (functional groups, atom-centered fragments, empirical descriptors, properties), two-dimensional (topological descriptors, molecular walk counts, BCUT descriptors, Galvez topological charge indices, and 2D autocorrelations), as well as three-dimensional descriptors (charge descriptors, aromaticity indices, Randic molecular profiles, geometrical descriptors, RDF descriptors, 3D-MoRSE descriptors, WHIM descriptors, and GETAWAY descriptors) were created by the DRAGON program for each compound. ³² Most of the descriptors from the DRAGON program have been reviewed in the textbook by Todeschini and Consonni.⁴⁰ A reduced descriptor set of 250 was obtained after the constant and near constant descriptors and the highly inter-correlated (>0.90) descriptors were discarded.

4.3. Stepwise descriptor selection by multiple linear regressions

The descriptor selection and the MLR analyses were performed using the SYBYL discovery software package³⁹ and an in-house FORTRAN 77 program.^19,21 Starting from the entire set of descriptors, variable selection by a forward and reverse stepwise regression procedure was performed, in which forward selection was followed by backward elimination of variables, resulting in an equation in which only variables that significantly increased the predictability of the dependent variable were included.

4.4. Neural network QSAR modeling

Feed-forward, back-propagation-of-error networks were developed using a neural network C program.^19,21,34 Network weights (W_ji(s)) for a neuron ‘j’ receiving output from neuron ‘i’ in the layer ‘s’ were initially assigned random values between −0.5 and +0.5. The sigmoidal function was chosen as the transfer function that generates the output of a neuron from the weighted sum of inputs from the preceding layer of units. Consecutive layers were fully interconnected; there were no connections within a layer or between the input and the output. A bias unit with a constant activation of unity was connected to each unit in the hidden and output layers.

The input vector was the set of descriptors for each molecule in the series, as generated by the previous steps. All descriptors and targets were normalized to the [0,1] interval utilizing Eq. 2

$$X_{ij}^{\prime }=\frac{X_{ij}-X_{j,min}}{X_{i,max}-X_{j,min}}$$ (2)

where X_ij and $X_{ij}^{\prime }$ represents the original value and the normalized value of the jth (j = 1, …, k) descriptor for compound i (i = 1, …, n), and X_min and X_max represent the minimum and maximum values for the jth descriptor. The network was configured with one or more hidden layers. During the neural network learning process, each compound in the training set was iteratively presented to the network. That is, the input vector of the chosen descriptors in normalized form for each compound was fed to the input units, and the network’s output was compared with the experimental ‘target’ value. During one ‘epoch’, all compounds in the training set were presented, and weights in the network were then adjusted on the basis of the discrepancy between network outputs and observed I_max values by back-propagation using the generalized delta rule.

4.5. Target properties

Experimental I_max values for the synthesized compounds were measured according to the procedure described by Dwoskin et al.^7,30 The I_max values (in percent) were used as the target property to derive the QSARs.

4.6. Model validation

Models were cross-validated using the ‘leave-one-out (LOO)’ and ‘leave-n-out (n = 11)’ approaches.

4.7. Evaluation of the QSAR models

The overall quality of the models is indicated by the Pearson correlation coefficient r², the root-mean squared deviation (rmsd), the Fischer statistic (F), predictive q² or $r_{\text{test}}^2$, and the leave-one-out/leave-n-out root-mean squared deviation loormsd/testrmsd. The predictive q² or $r_{\text{test}}^2$ are defined in Eq. 3 below:

$$q^2(\text{or}{r}_{\text{test}}^2)=\frac{SD-\mathit{PRESS}}{SD}$$ (3)

where SD is the sum of squared deviations of each measured I_max value from its mean, and PRESS is the predictive sum of squared differences between actual and predicted values.