Abstract
Respiration-induced organ motion is one of the major uncertainties in lung cancer radiotherapy and is crucial to be able to accurately model the lung motion. Most work so far has focused on the study of the motion of a single point (usually the tumor center of mass), and much less work has been done to model the motion of the entire lung. Inspired by the work of Zhang et al (2007 Med. Phys. 34 4772–81), we believe that the spatiotemporal relationship of the entire lung motion can be accurately modeled based on principle component analysis (PCA) and then a sparse subset of the entire lung, such as an implanted marker, can be used to drive the motion of the entire lung (including the tumor). The goal of this work is twofold. First, we aim to understand the underlying reason why PCA is effective for modeling lung motion and find the optimal number of PCA coefficients for accurate lung motion modeling. We attempt to address the above important problems both in a theoretical framework and in the context of real clinical data. Second, we propose a new method to derive the entire lung motion using a single internal marker based on the PCA model. The main results of this work are as follows. We derived an important property which reveals the implicit regularization imposed by the PCA model. We then studied the model using two mathematical respiratory phantoms and 11 clinical 4DCT scans for eight lung cancer patients. For the mathematical phantoms with cosine and an even power (2n) of cosine motion, we proved that 2 and 2n PCA coefficients and eigenvectors will completely represent the lung motion, respectively. Moreover, for the cosine phantom, we derived the equivalence conditions for the PCA motion model and the physiological 5D lung motion model (Low et al 2005 Int. J. Radiat. Oncol. Biol. Phys. 63 921–9). For the clinical 4DCT data, we demonstrated the modeling power and generalization performance of the PCA model. The average 3D modeling error using PCA was within 1 mm (0.7 ± 0.1 mm). When a single artificial internal marker was used to derive the lung motion, the average 3D error was found to be within 2 mm (1.8 ± 0.3 mm) through comprehensive statistical analysis. The optimal number of PCA coefficients needs to be determined on a patient-by-patient basis and two PCA coefficients seem to be sufficient for accurate modeling of the lung motion for most patients. In conclusion, we have presented thorough theoretical analysis and clinical validation of the PCA lung motion model. The feasibility of deriving the entire lung motion using a single marker has also been demonstrated on clinical data using a simulation approach.
1. Introduction
Respiration-induced organ motion is one of the major uncertainties in lung cancer radiotherapy, which may cause clinically significant targeting errors and greatly degrade the effectiveness of conformal radiotherapy. It is therefore crucial to be able to accurately model the respiratory motion. Among the vast literature on respiratory motion models, we distinguish between two main categories: one that devotes solely to the study of the motion of a single point (usually the tumor center of mass), and the other one that attempts to model the motion of the entire lung by employing the spatial relations among different regions of the lung.
Most work in the literature is of the first category. Some early work relies on the assumption that the breathing pattern is periodic as a function of time. Lujan et al (1999) and Seppenwoolde et al (2002) modeled breathing as an even power of a cosine function with adjustable period and amplitude. However, it is well known that under free breathing conditions, many patients have irregular breathing patterns such that a periodic function is inadequate to characterize respiratory motion (Neicu et al 2003, Vedam et al 2003, Nehmeh et al 2004). In light of this fact, researchers have resorted to more sophisticated respiratory models, mostly in the framework of motion prediction, such as (Murphy and Dieterich 2006, Ruan et al 2007, 2009, Sharp et al 2004, Wu et al 2004, Vedam et al 2004, Murphy et al 2002, Kakar et al 2005, McCall and Jeraj 2007, Ren et al 2007).
While it is essential to study the motion of a single point of interest, one does not have the luxury of having a complete knowledge of the motion for the entire lung, which may be important for some applications. Another drawback with single-point motion study is that it ignores the fact that different parts of the lung are not independent and their motion is often quite correlated. The goal is to exploit the spatial relations in the motion data and come up with a coherent spatiotemporal model such that one can use partial or even sparse information to derive the motion for the entire lung. These fall into second category of respiratory models. There have been relatively fewer works in this respect. McClelland et al (2006) proposed a continuous 4D motion model by fitting B-spline functions to point motion over an ‘average’ respiratory cycle. In estimating 3D motion from cone-beam projection images, Zeng et al (2007) assumed synthetic periodic respiratory motion and used an aperiodicity penalty term to regularize the solutions. Zhang et al (2008) developed a geometry-based respiratory model using concatenated cosine functions for organ motion. These models still rely more or less on the assumption of regular breathing (at least for model construction) and can yield suboptimal solutions if irregular breathing occurs.
As far as we know, there exist two spatiotemporal models which do not assume regular breathing patterns and thus are more suitable to characterize respiratory motion under free breathing conditions. Low et al (2005) described a 5D lung motion model parameterized by tidal volume and airflow measured with spirometry, which allows characterization of hysteresis and irregular breathing patterns. The model was recently tested on a large number of patients (Zhao et al 2009). Basically, the position of a voxel is derived by superimposing two displacement vectors induced by tidal volume and airflow on top of its reference position at zero tidal volume and airflow. There are five independent parameters in the model (hence the name 5D lung motion model). The five parameters are tidal volume, airflow, and the 3D reference position. More recently, Zhang et al (2007) applied principal component analysis (PCA) to the 3D deformation field derived from a deformable image registration (DIR) between a reference phase and other phases in a four-dimensional computed tomography (4DCT) data set. They found that two principal components are adequate to accurately describe respiratory motion in 4DCT of four patients. Some clarification about the term ‘PCA lung motion modeling’ is appropriate here. In the following, by ‘PCA lung motion modeling’, we mean the eigen-decomposition of the lung motion data only. Any data processing after that is not part of the ‘PCA lung motion modeling’ and in fact can be application dependent. Although the PCA motion model proposed by Zhang et al (2007) seems promising based on the results for a small number of patients, there is still a need to understand the underlying reason why it works and whether there is any deeper connection between the two lung motion models besides their superficial similarity in mathematical forms.
Low’s 5D lung motion model is based on lung anatomy and motion dynamics and thus is a physiological model. On the other hand, the PCA motion model is based on a multivariate data analysis technique and is more mathematically flavored. But, these two seemingly different models are both a decomposition of the lung motion into spatial and temporal components and they both fall under the general model: , where x(t) is a vector function of time representing the lung motion at each voxel, ai and si (t) are the spatial and temporal components, respectively. This is a linear generative model, which describes how lung motion may be generated from a number of (hopefully a few) components. In the case of 5D lung motion model, K equals to 2; s0(t) is a constant function and s1(t), s2(t) are tidal volume and airflow respectively; ai can be fitted from x(t) and spirometry measurements. In the case of PCA lung motion model, K is user-specified; s0(t) is a constant function and s1(t), s2(t), … are the PCA coefficients; a0 is the sample mean of x(t) along the time dimension and a1, a2, … are eigenvectors obtained from PCA.
The primary goal of this work is not to compare the two existing lung motion models mentioned above. Instead, we seek to have a clear understanding and gain some insight about the effectiveness of PCA to model the complex spatiotemporal relationships of the entire lung motion. Given such a model, we can then use a sparse subset of the lung, such as an implanted marker (as proposed in this work), the diaphragm, or the chest surface, to drive the lung motion model and thus to derive the tumor motion. From this perspective, the purpose and scope of this work is different from, and much more general than, that of Zhang et al (2007). The main contributions of this work, and also what distinguish it from the previous work, are in the following aspects. First, we present a deep and detailed analysis of the PCA-based lung motion model in a theoretical framework. We provide the theoretical justification of the effectiveness of PCA in modeling lung motion. We shall see that it is closely related to Low’s physiological 5D lung motion model and that under certain conditions, these two models are actually equivalent. In Zhang et al (2007), the use of two principal components is based on observations of the eigenvalues and is somewhat heuristic. In this work, we attempt to address the important question of how many principal components are necessary in order to model the lung motion in a statistical framework. Another distinction from the previous work is in the way the PCA motion model is applied to predict lung motion after it is constructed. In Zhang et al (2007), the current diaphragm position and its previous value are used as surrogates to predict the lung motion. In this work, we will propose an alternative method to predict the lung motion with the PCA model and demonstrate the feasibility of using the measurement of a single fiducial marker to derive the entire lung motion.
The organization of the paper is as follows. In section 2, we first briefly describe the construction of the PCA lung motion model and then present some nice properties of the model. Section 3 introduces two mathematical respiratory motion phantoms and the clinical data, to which the PCA motion model will be applied. In section 4, we first derive some theoretical results when PCA model is applied to the two respiratory motion phantoms. We then present the results on clinical data and evaluate its performance. Section 5 summarizes the paper and discusses some possible future applications of the PCA motion model.
2. Methods
2.1. Construction of the PCA lung motion model
We first briefly describe how PCA may be used to construct a lung motion model. The description follows that of Zhang et al (2007), with a slight modification for clarity. Interested readers are also referred to Sohn et al (2005) for a more detailed mathematical description of PCA applied to displacement vectors, although their study is about interfractional organ deformation in male pelvis.
We form a matrix X, where each row represents the displacement vectors (which may be obtained from a DIR between a reference CT scan and all the other scans in a 4DCT data set) of a certain voxel in the lung along one of the three coordinates in space at all time points. So the number of rows in the matrix is the number of voxels in the lung times 3, and the number of columns is the number of sampling points in time. Let X̃ be the motion matrix where the sample mean has been removed from each row. PCA essentially performs singular value decomposition (SVD) of the motion matrix X̃:
| (1) |
where r is the rank of X̃. PCA gives two sets of eigenvectors u1, u2, … and v1, v2, …, corresponding to a set of non-negative and decreasing eigenvalues λ1, λ2, …. It can be easily seen that the eigenvectors u1, u2, … are defined in space, while v1, v2, … are defined in time. Intuitively, each eigenvalue represents how much variation or variance in the data is captured by the corresponding eigenvector. In practice, the eigenvalue usually decreases very fast (Zhang et al 2007). Therefore, we hypothesize that every possible lung motion state can be approximated by a linear combination of the eigenvectors corresponding to the largest eigenvalues:
| (2) |
or in the continuous domain:
| (3) |
where the scalars wk (t) are called PCA coefficients. K is a user-specified parameter and is usually chosen to be a small integer. It is worth mentioning that the eigenvectors are fixed after PCA and it is the temporal evolution of the PCA coefficients that drives the dynamic lung motion in real time. The solution for the PCA coefficients wk (t) will be discussed in greater detail later.
2.2. Properties of the PCA lung motion model
An important property of PCA is that it provides the best linear representation of the data in the least mean-square-error (LMSE) sense (Jolliffe 2002). Specifically, of all the K-dimensional linear approximation of the deformation vector fields (DVFs), the mean square error is minimized by summing the time-averaged DVFs and a linear combination of the first K eigenvectors (with the K largest eigenvalues) weighted by the corresponding principal components given by PCA.
Another property is concerned with the implicit regularization imposed by the PCA motion model. Let X̃ be the motion matrix where the sample mean has been removed from each row, and Ỹ = UΛVT be a low-rank approximation to the DVFs, where Λ is a K by K diagonal matrix containing the first K largest eigenvalues (K ≤ r), U, V are unitary matrices with size N by K and M by K, where each column is the corresponding left and right eigenvector, respectively. If we look at one particular row ỹi = qi ΛVT, it is the motion of the corresponding voxel along one direction over time. (Note that: qi is a row vector in the matrix U; it is not an eigenvector.) We can rewrite that as qi = ỹi VΛ−1. If we look at the difference between any two rows (i.e. motion of two voxels along one direction), we can see that,
| (4) |
where vi are the column vectors of V and ||vk|| = 1. The last inequality holds due to Cauchy–Schwartz inequality.
Since , (where the corresponding elements are from the full SVD of X̃) and ,
| (5) |
From equations (4) and (5), we have
| (6) |
Equation (6) basically tells us that if the difference between two rows in the motion matrix or ||Δx̃||2 is sufficiently small, then the difference between the corresponding two rows in the matrix U will also be sufficiently small. The implication is that if two voxels move similarly along one direction, then their motion represented by the PCA motion model in equation (3) will also be similar, provided that the principal components kept in the model do not have vanishing eigenvalues associated with them. We can also learn from equation (6) that this property begins to break down if any eigenvalue approaches to zero. In this case, the magnitude of the difference between two eigenvectors is not limited by the corresponding difference between the real motion and can be arbitrarily large, then the motion of two voxels reconstructed by equation (3) can be wildly different, even if they move very similarly, which is not desirable. Therefore, in order to get a well-behaved PCA motion model, we should not use more principal components than necessary.
2.3. Using a single marker to derive the entire lung motion
Suppose we have measured the 3D position of a certain voxel at a new time point, namely rt. We wish to derive the new lung motion xt using x̄ and ui. In this case, we only have access to rt, which consists of only three entries in xt, which is a huge-dimensional vector in reality. (Notice that here we have ignored measurement noise compared with reality.) If we were to do ordinary least squares (OLS), the errors we got are usually large and blow up for more PCA coefficients. The problem with this approach is that since now we have very sparse data to solve for wit, OLS does not take into the account the fact that the magnitude of wit decreases very fast with i.
Here, we consider the problem in the framework of Bayesian estimation, where the parameters wt have some probabilistic distribution associated with it. The goal is to find the distribution of wt (called posterior) after we have seen the data. In appendix E, we derived the maximum a posterior (MAP) estimator:
| (7) |
3. Materials
In this section, we first introduce two mathematical respiratory motion phantoms based on simple and yet realistic assumptions and then describe the clinical data, to which the PCA motion model will be applied.
3.1. Respiratory phantom with cos (t) motion
The main feature of respiration is that it is somewhat (though not perfectly) periodic. The simplest function that captures this feature is a cosine function. In the cosine respiratory phantom, the motion of each voxel along each of three coordinates in space is in the form of cosine functions. We allow arbitrary amplitude and arbitrary phase for each cosine function. In matrix form
| (8) |
where X is an N by M matrix; N is the number of voxels in the lung times 3, and M is the number of samples in time. A1, …, AN and φ1, …, φN are amplitude and phase; θ is the time interval between successive samples.
It may seem to be an idealistic respiratory phantom at first. However, notice that any three rows in the above matrix is exactly the parametric form of an ellipse in 3D, so the 3D trajectory of each voxel follows an ellipse, and since we allow arbitrary amplitude and phase for each spatial coordinate, this ellipse (i.e. the 3D trajectory of a voxel) can have arbitrary shape, size and orientation in space. Therefore, this respiratory phantom can be seen as a coarse approximation to regular breathing.
3.2. Respiratory phantom with cos2n (t) motion
In this respiratory phantom, we replace the cosine functions in the above phantom with even power of cosine functions, i.e. X(t) = A cos2n(t + Φ). We still allow arbitrary amplitude and arbitrary phase for each function. This formula has been used by Lujan et al (1999) and Seppenwoolde et al (2002) to model lung motion. The bias term in this function does not matter for PCA because of centering and is set to zero without loss of generality. One can see that for the special case where n equals 1, the respiratory phantom essentially reduces to the cosine phantom. The reason why we separate the special case of cosine phantom will be clear later.
3.3. Clinical data
Currently, 11 image datasets from eight patients have been acquired and analyzed in this study. The scanner was a Philips 64-slice Brilliance CT scanner operating in ciné mode with resolution of 0.625 mm craniocaudally and 0.97 mm laterally and anteroposteriorly. Each scan covered 40 mm of the lung craniocaudally and 25 scans were acquired before the patient was moved to the next couch position. Six or seven couch positions were usually sufficient to cover the entire lung. A spirometer was used to measure the tidal volume during the acquisition. Drifting of tidal volumes up to 100% of its average amplitude was observed due to accumulated measurement errors received from the inertia of the fan in the spirometer at the transition between inhalation and exhalation. The drift was corrected by placing a pneumatic belt around a patient’s abdomen. The expansion and contraction of abdomen, which is assumed to be synchronized with and proportional to the tidal volume both in time and magnitude, was recorded and converted into electrical signal. While this signal does not exhibit baseline drift, it can be affected by sensor placement and patient positioning. The drift of the spirometry signal was compensated for by combining spirometry and bellows systems. Correlations between the belt signals and the tidal volumes were obtained along the time axis, converting the belt signals into un-drifted tidal volumes (Werner et al 2010).
The ciné CT data were sorted by the amplitude sorting method (Lu et al 2006) and eight phases were constructed for each patient. Figure 1 shows the coronal slices at the end of exhale and the end of inhale phases in the 4DCT of patient 1. In order to get the DVF for each voxel in the lung, we performed DIR using a TV-L1 (total variation with L1 norm in the data fidelity term) optical flow method (Zach et al 2007) between a reference phase defined at the end of exhalation and all other phases by registering the whole thoracic cavities including rib cages. Studies (Yang and Klette 2010, Baker et al 2011) have shown that TV-L1 based registration methods generally perform over most L2 based methods in term of accuracy. Additional advantages of TV-L1 include the robustness in handling discontinuities in the displacement field and outliers in the data (Heinrich et al 2010). Pock et al (2007) demonstrated that the TV-L1 optical flow method was able to achieve an average 3D error of less than 2 mm and superior robustness than Demons method for thoracic 4DCT images. In this study, all registrations were performed on an Intel system with Core™2 Duo processor running at 2.2 GHz and 8 GB RAM. The regularization parameter λ and the relaxation parameter θ (Zach et al 2007) were set empirically at 70 and 0.25 respectively in this study. Registration between two typical CT datasets of 2563 voxels took approximately 25 min. Seven DVFs were obtained in total for each patient.
Figure 1.
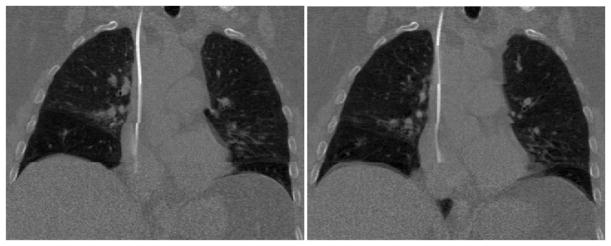
Coronal slices in 4DCT of patient 1. Left: end of exhale phase; right: end of inhale phase.
4. Results
4.1. Applications to the respiratory phantom with cos (t) motion
There are two main theoretical results when PCA is applied to the cosine respiratory phantom. First, the motion matrix has a rank of 2, which implies that 2 PCA coefficients and eigenvectors will completely represent the lung motion. Second, regardless of the distribution of the amplitude and phase, the PCA coefficients as a function of time (i.e. PCA eigenfunctions) are sinusoids, which are simply a phase-shifted version of the voxel motion. In addition, the second eigenfunction is always the time derivative of the first one, indicating a close relationship between the 5D and PCA model. In this section, we will also derive the equivalence condition between 5D and PCA models for the cosine respiratory phantom.
First we show that the motion matrix X has a rank of 2. We can express X as a summation of two rank-1 matrices, each being an outer product of a column vector and a row vector:
| (9) |
Since rank(A + B) ≤ rank(A) + rank(B) for two matrices of the same size, we know that rank(X) ≤ 2. However, the column vectors are linearly dependent only under very special conditions, e.g., φ1 = φ2 + kπ, k ∈ Z; this happens with probability 0. (If it does happen, then rank(X) = 1·) So rank(X) = 2 with probability 1.
PCA deals with the covariance matrix, i.e. the sample mean needs to be subtracted in each variable (this procedure is also called centering). Here we treat each row (i.e. the time evolution of each coordinate of one voxel) as one variable and subtract the mean from each row. Denote X̃ as the centered motion matrix. Then rank(X̃) ≤ rank(X) = 2. With the same reason as above, we can also see that rank(X̃) = 2 with probability 1. The physical meaning of this result is that using two PCA coefficients and eigenvectors will completely represent the lung motion.
Appendix A derives the functional form of the PCA eigenfunctions (there are two in this case) as sinusoids, and thus the eigenfunctions are simply a phase-shifted version of the voxel motion. Appendix A also shows that regardless of the distribution of amplitude and phase, the second eigenfunction is always the time derivative of the first eigenfunction, for any distribution of amplitude and phase. This implies a close relationship between the PCA and 5D model.
In fact, under certain circumstances, the PCA and 5D motion models (Low 2005) are equivalent for the cosine respiratory phantom. Appendix B finds a necessary and sufficient condition: E[A2 sin(2Φ)] = 0, where Φ is a random variable representing the phase shift between tidal volume and voxel motion along each coordinate. If A, Φ are uncorrelated random variables, the equivalence condition becomes E[sin(2Φ)] = 0. There are many situations where this condition is satisfied. For instance, any distribution of Φ that is symmetric about 0, or ±π /2, or ±π will satisfy the condition and yields equivalent PCA and 5D lung motion models.
4.2. Applications to the respiratory phantom with cos2n (t) motion
In parallel to 4.1, there are also two main theoretical results when PCA is applied to the respiratory phantom with cos2n (t) motion. First, the centered motion matrix has a rank of 2n, which implies that using 2n PCA coefficients and eigenvectors will completely represent the lung motion. Second, PCA eigenfunctions are not sinusoids any more, but a linear combination of cosine and sine functions at even multiples (up to 2n) of the fundamental frequency.
We first show that in the discrete case, rank(X) = 2n + 1. First notice that , where ck are known constants. They can be solved using Euler’s formula
Then the motion matrix can be written as
| (10) |
We can see that matrix X is a summation of 2n + 1 rank-1 matrices, each being an outer product of a column vector and a row vector. Notice that all column vectors and row vectors are linearly independent, with probability 1. So rank(X) = 2n + 1.
In appendix C, we show that the rank of X̃ (centered matrix) is actually reduced by 1, i.e. 2n. So a full representation of X only requires at most 2n PCA coefficients and eigenvectors. It is worth mentioning that, even if each voxel moves differently, as long as they follow the same general cosine model but with different powers, we can see that rank(X̃) is 2nmax, which is the maximum power of the cosine functions.
Regarding the eigenfunctions, there are 2n of them in this case. Appendix D shows that the eigenfunctions are a linear combination of cosine and sine functions at even multiples (up to 2n) of the fundamental frequency. In general, the actual forms of the eigenfunctions depend on the distributions of the amplitude and phase for all the voxels and are not phase-shifted version of the voxel motion. This is in contrast to the 5D model, where the ‘eigenfunctions’ are external surrogates (tidal volume and air flow) and do not depend on internal lung motion.
4.3. Applications to clinical data
In the following sections, we will validate the PCA lung motion model in two respects: its modeling power (how well it represents the training data) and its generalization performance (how well it generalizes to data it has never seen before).
4.3.1. Modeling power
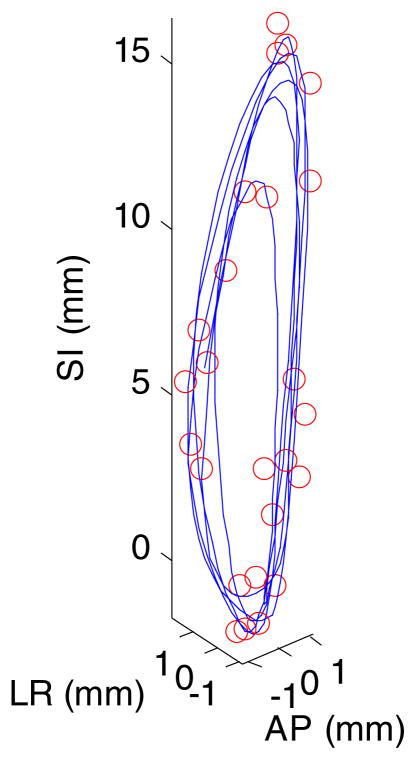
For this part, we used all the deformation vectors (seven in total) derived from DIR between 4DCT phases as training data for PCA. We measure the modeling power by the average 3D error for all voxels in the lung at all time points. Compared with 4DCT, a cine CT scan has the advantage of incorporating irregular breathing patterns over several breathing cycles, but with a limited longitudinal coverage of the patient. Figure 2 shows the 3D positions of a particular voxel for 25 cine CT scans over 18.2 s at one couch position for a patient as well as the interpolated 3D trajectory from PCA model output using two coefficients and eigenvectors. (Note that the cine CT data were used to generate figure 2 for illustration purposes only; it was not used anywhere else in the study.) We can see that the PCA model is able to capture the hysteresis component of the motion. Table 1 lists the average 3D error for all voxels for the PCA lung motion model for all eight patients. For the PCA model, the modeling error decreases with the number of coefficients. But here we used two coefficients and eigenvectors to calculate the error. The small error of PCA model is expected because of the way it is constructed (cf section 2.2).
Figure 2.
3D positions of a particular voxel for 25 cine CT scans in a patient (shown in circles) as well as the interpolated 3D trajectory from PCA model output using two coefficients and eigenvectors. SI: superior–inferior; AP: anterior–posterior; LR: left–right. The average 3D error for this voxel is 0.4 mm.
Table 1.
Average 3D modeling error of the PCA model for all eight patients.
| Patient (scan) index | PCA model error (mm) with two coefficients | Average motion magnitude (mm) |
|---|---|---|
| 1 | 0.6 | 6.9 |
| 2(1) | 0.6 | 14.6 |
| 2(2) | 0.6 | 11.1 |
| 3(1) | 0.8 | 11.2 |
| 3(2) | 0.7 | 8.5 |
| 4 | 0.5 | 3.9 |
| 5(1) | 0.7 | 14.5 |
| 5(2) | 0.7 | 13.3 |
| 6 | 0.9 | 18.4 |
| 7 | 0.7 | 18.0 |
| 8 | 0.7 | 17.4 |
| Mean ± Std | 0.7 ± 0.1 | 12.5 ± 4.7 |
Table 2 lists the correlation between PCA and 5D model parameters for all eight patients. We can see that there is a high correlation between the first PCA coefficient and tidal volume as well as the first eigenvector and α. Except for a few patients (1 and 4) with small motion, the model parameters are almost identical. On the other hand, the correlation between the second PCA coefficient and airflow as well as the second eigenvector and β is more variable. For some patients (e.g., 2, 7, and 8), the correlation is quite high, while for others, the correlation is very low.
Table 2.
Correlation between PCA and 5D model parameters for all eight patients.
| Patient (scan) index | First PCA coefficient and tidal volume | Second PCA coefficient and airflow | x̄ and x0 | First eigenvector and α | Second eigenvector and β |
|---|---|---|---|---|---|
| 1 | 0.99 | 0.29 | 0.06 | 0.79 | 0.90 |
| 2(1) | 0.98 | 0.89 | 0.76 | 1.00 | 0.70 |
| 2(2) | 0.99 | 0.80 | 0.16 | 1.00 | 0.84 |
| 3(1) | 0.99 | 0.85 | 0.75 | 1.00 | 0.95 |
| 3(2) | 0.97 | 0.21 | 0.23 | 0.98 | 0.20 |
| 4 | 0.83 | 0.62 | 0.03 | 0.88 | 0.60 |
| 5(1) | 0.99 | 0.06 | 0.76 | 1.00 | 0.04 |
| 5(2) | 0.92 | 0.87 | 0.28 | 1.00 | 0.56 |
| 6 | 0.99 | 0.19 | 0.99 | 1.00 | 0.29 |
| 7 | 0.99 | 0.82 | 0.79 | 0.98 | 0.96 |
| 8 | 1.00 | 0.62 | 0.96 | 1.00 | 0.89 |
| Mean ± Std | 0.97 ± 0.05 | 0.57 ± 0.32 | 0.52 ± 0.38 | 0.97 ± 0.07 | 0.63 ± 0.32 |
4.3.2. Generalization performance
In this section, we test how the PCA model performs on new lung motion data which it is not trained on. We will look at two scenarios: the ideal case, where we know exactly how all voxels move in 3D space; the more realistic case, where we know exactly how one voxel moves in 3D space. The second case is to simulate the clinical practice where one or more internal markers are sometimes implanted near the tumor. For simplicity, we only look at 1-marker case.
The evaluation metric that we choose is leave-one-out cross validation (LOOCV). Cross validation is a well-established statistical technique which is used to estimate generalization error of a given model. LOOCV is a useful evaluation tool with severe under-sampling of training data (Duda et al 2001). In this work, since we have seven DVFs, we train a PCA model on six DVFs and test its performance on the remaining one DVF. This procedure is repeated seven times until every DVF has been tested. The final performance is then the average from the seven tests.
The ideal case
Suppose that we have obtained the sample mean x̄ and a set of eigenvectors ui from the PCA model trained on six DVFs and that we now have a new motion state xt that we wish to approximate using x̄ and ui. This can be done via the following optimization procedure:
| (11) |
where wt = [w1t, …, wkt]T and k is the number of PCA coefficients.
Using the fact that , this can be easily solved:
| (12) |
So the model output then is
| (13) |
If we plug back into equation (11), one can show that the residual fitting error has the following expression:
| (14) |
where zt = xt − x̄.
We can see that the residual error is monotonically decreasing as a function of k, i.e. the more PCA coefficients we use, the less error we will get.
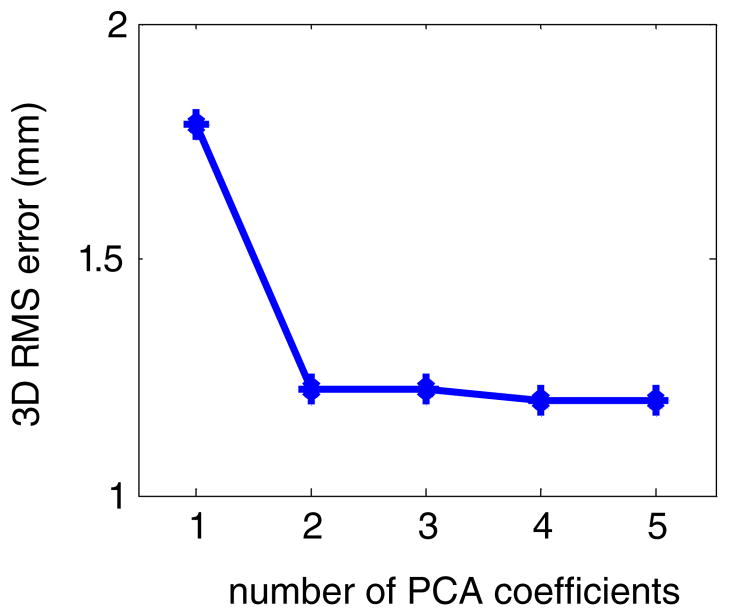
Figure 3 shows the average 3D error as a function of the number of PCA coefficients for patient 1 obtained from LOOCV in the ideal case. Note that the curve is monotonically decreasing as the number of PCA coefficients k increases. This is expected because the LOOCV curve is a simple average of equation (14) over t.
Figure 3.
LOOCV of the PCA model in the ideal case: the average 3D error as a function of the number of PCA coefficients for patient 1.
The LOOCV curve in the ideal case is theoretically interesting. Notice that equation (12) gives the LMSE solution for the PCA coefficients given the motion vector for all the voxels and the PCA motion model in equation (3). Therefore, for a fixed number of PCA coefficients, no matter how they are determined (either from single or multiple marker measurements or other types of imaging methods), the average residual error cannot be smaller than that in figure 3. In other words, it defines the lower bound of LOOCV error for the PCA motion model.
1-marker case
Hypothetically, the marker can be implanted anywhere in the lung. In order to get some meaningful estimation of its performance, we generated a Cartesian grid with a grid size of 2 × 2 × 2 cm3. We put an artificial marker at each grid point and only look at those markers with motion magnitude greater than 1 cm (except for patients 1 and 4, where a threshold of 5 mm was used since the mean lung motion magnitude was relatively small). For each artificial marker, we calculated the LOOCV error using equation (7) as the solution for the PCA coefficients. In this way, we ended up with hundreds of (between 200 and 600) LOOCV curves for each patient. We then averaged LOOCV curves for all the artificial markers, given different numbers of PCA coefficients.
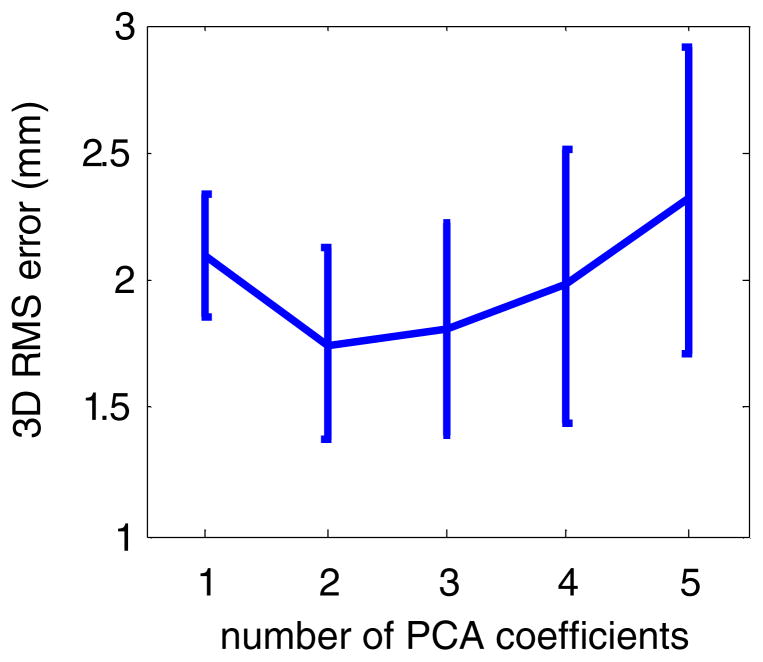
Figure 4 shows the mean and standard deviation of the 3D error as a function of the number of PCA coefficients for patient 1. Table 3 shows the 3D error for the PCA model for all eight patients obtained from LOOCV. Overall, using two PCA coefficients gave the smallest average 3D error. This is true in the majority of cases (7 out of 11 scans), while in the other cases, using one PCA coefficient gave the smallest average 3D error, although the error is marginally smaller (about 0.1 mm) than that using two PCA coefficients. Due to the sparse nature and high multicollinearity of the input data (three coordinates of an internal marker), using more than two PCA coefficients could lead to the overfitting problem and therefore gives larger errors.
Figure 4.
LOOCV of the PCA model in the 1-marker case: mean and standard deviation of the 3D error as a function of the number of PCA coefficients for patient 1. Note the standard deviation is computed with respect to the grid points.
Table 3.
LOOCV: 3D error (mm) for the PCA model for all eight patients.
| Patient (scan) index | Number of PCA coefficients
|
||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 2.1 ± 0.2 | 1.7 ± 0.4 | 1.8 ± 0.4 | 2.0 ± 0.5 | 2.3 ± 0.6 |
| 2(1) | 1.7 ± 0.3 | 1.5 ± 0.4 | 1.6 ± 0.5 | 1.7 ± 0.5 | 3.9 ± 1.1 |
| 2(2) | 1.9 ± 0.2 | 1.8 ± 0.3 | 1.9 ± 0.4 | 2.1 ± 0.5 | 3.0 ± 0.8 |
| 3(1) | 2.2 ± 0.2 | 2.1 ± 0.3 | 2.2 ± 0.3 | 2.3 ± 0.4 | 3.6 ± 0.8 |
| 3(2) | 1.7 ± 0.2 | 1.8 ± 0.2 | 1.9 ± 0.3 | 2.1 ± 0.5 | 2.8 ± 0.7 |
| 4 | 1.1 ± 0.1 | 1.1 ± 0.2 | 1.2 ± 0.2 | 1.3 ± 0.2 | 1.6 ± 0.4 |
| 5(1) | 1.7 ± 0.3 | 1.8 ± 0.3 | 1.8 ± 0.4 | 2.0 ± 0.4 | 3.7 ± 1.0 |
| 5(2) | 2.2 ± 0.3 | 1.8 ± 0.5 | 1.9 ± 0.5 | 2.0 ± 0.6 | 3.5 ± 0.8 |
| 6 | 2.1 ± 0.4 | 2.1 ± 0.4 | 2.3 ± 0.5 | 2.5 ± 0.7 | 5.1 ± 1.3 |
| 7 | 2.7 ± 0.5 | 2.2 ± 0.6 | 2.3 ± 0.7 | 2.6 ± 0.8 | 4.2 ± 1.1 |
| 8 | 2.0 ± 0.6 | 1.9 ± 0.4 | 2.0 ± 0.5 | 2.1 ± 0.6 | 4.7 ± 1.5 |
| Mean ± Std | 1.9 ± 0.4 | 1.8 ± 0.3 | 1.9 ± 0.3 | 2.1 ± 0.4 | 3.5 ± 1.0 |
5. Discussions and conclusions
We have presented a detailed analysis and clinical validation of a lung motion model based on PCA. Based on simple and yet realistic assumptions, we introduced two mathematical respiratory phantoms with cos (t) and cos2n (t) motion. For the cosine respiratory phantom, we found that the motion matrix has a rank of 2 and thus using two PCA coefficients and eigenvectors can fully represent lung motion. The eigenfunctions are simply a phase-shifted version of voxel motion, and under certain circumstances, the PCA model is equivalent to 5D model. Similarly, for the cos2n (t) motion phantom, the centered motion matrix has a rank of 2n and thus a full representation of lung motion requires 2n PCA coefficients and eigenvectors. The eigenfunctions, however, are not a phase-shifted version of voxel motion and depend on the phase and amplitude distribution of the voxel motion. The clinical implications of these findings are two folds: (1) the fact that two principle components can completely represent the lung motion in the cosine motion phantom demonstrates the effectiveness of the PCA lung motion model. This result is true no matter how many voxels and time points there are in the lung motion data, and regardless of the motion amplitude and phase of any voxel. Since the cosine motion phantom is a good approximation of regular breathing, it is conceivable that two principle components will approximate the real lung motion quite well in such a case, though not perfectly. (2) The fact that 2 and 2n principle components are required to represent the lung motion in the two motion phantoms implies that depending on the specific spatiotemporal lung motion patterns, the optimal number of principle components to model lung motion is patient dependent and should be determined for each specific patient.
We applied the PCA motion model to clinical data and tested its modeling power and generalization performance. We have demonstrated the feasibility of using the measurement of a single marker to derive the entire lung motion once the PCA model is constructed. The optimal number of PCA coefficients has to be determined on a patient-by-patient basis. We used the LOOCV technique to evaluate the generalization performance of the PCA motion model. As long as the DVFs are given, the PCA modeling and LOOCV tests can be completed within a few minutes in MATLAB running on a desktop with a 2.8 GHz CPU and 4 GB memory. So this procedure is computationally practical in a clinical setting. It was found that two PCA coefficients seem to be sufficient for accurate modeling of lung motion. It is worth mentioning that, from the LOOCV of the ideal case and 1-marker case, we conclude that the optimal number of PCA coefficients also depends on the amount of useful information about lung motion, given the same motion pattern for the same patient. Consequently, if we had used multiple markers or other imaging modalities to derive lung motion, the optimal number of PCA coefficients could be different from that determined in this study.
The purpose of the single marker in this study, if it is implanted inside or very close to the tumor, is not for tumor tracking per se. Rather, it is the entire lung motion that we are trying to reconstruct. As we have demonstrated in this study, it is feasible to do so using such sparse information as a single marker measurement. It is also worth noting that the tumor is not always easily accessible via a safe marker implantation procedure. For instance, percutaneous implantation involves the risk of pneumothorax and other serious side effects (Arslan et al 2002, Geraghty et al 2003), and thus its clinical applicability is severely limited. In cases where the implanted marker is not in close proximity of the tumor and thus cannot be directly used for tumor tracking purposes, the PCA lung motion model is still useful, as it is able to derive the entire lung motion, including the tumor itself, from a single marker measurement. In testing the generalization performance of the PCA model, we have only looked at the 1-marker case for the sake of simplicity. For the multiple-marker case, if the markers are close to each other, it is expected that we would get similar results, since nearby soft tissues move similarly. If the markers are relatively far away from each other, it is conceivable that the performance should be more robust because of the extra information, as long as registration is reasonably accurate.
In validating the PCA lung motion model, we have used 4DCT data for the entire thoracic region. Alternatively, the validation could have been done on the deformation fields of the unsorted cine CT data. In this case, its ability to model respiratory motion can be tested on irregular breathing patterns (baseline drift, period and amplitude changes, etc). The cine CT data do not contain the artifacts often seen between adjacent couch positions in 4DCT although image registration becomes more challenging. However, clinically it is essential to build the PCA model based on 4DCT if the entire lung motion is of interest. It is also important if the tumor move between adjacent couch positions in 4DCT or radiographic imaging is to be used as surrogate signals. The 256-slice CT scanner from Toshiba with a longitudinal coverage of 16 cm is ideal for this type of analysis.
In this study, the PCA lung motion model is built from a single session 4DCT scan from the same patient. As such, our PCA model is patient-specific. Alternatively, the PCA lung motion model may also be built from 4DCT data from multiple patients (Ehrhardt et al 2011) or from multiple 4DCT scans of the same patient (Klinder et al 2009). Ehrhardt et al built a 4D mean motion model by first estimating the subject-specific motion for each 4DCT scan, building an average shape and intensity atlas of the lung for a reference breathing state, and finally registering all subject-specific motion models to the lung atlas (Ehrhardt et al 2011). However, establishing correspondence among different subjects remains a challenging task, especially among lung cancer patient with tumor heterogeneities in a radiotherapy environment. Klinder et al built both intra- and inter-subject respiratory motion models from multiple 4DCT scans and evaluated the performance using LOOCV tests (Klinder et al 2009). There are three important differences between this work and that of Klinder et al (2009): (1) the LOOCV was performed with respect to each voxel in the lung in our study, while Klinder et al did the evaluation with respect to each 4DCT scan. (2) We used an implanted marker as the surrogate, while Klinder et al used the current position of the lung surfaces at the diaphragm dome as the surrogate. (3) In estimating the PCA model parameters, we used the MAP estimation method in a Bayesian framework, while Klinder et al used the maximum likelihood estimator with a single regularization parameter.
We would like to point out several important differences of our work from Zhang et al (2007), although both are based on the concept of parameterizing lung motion using PCA. First, in Zhang et al (2007), it was observed that two principal components appear to be sufficient to model lung motion and thus PCA model is connected with 5D lung motion model. In this work, we theoretically justify this connection based on a mathematical respiratory motion phantom under certain circumstances and demonstrated their relations using clinical data from eight patients. In this respect, our work can be seen as an extension of Zhang et al (2007). Second, our work differs from theirs in that we used simulated concurrent marker position to derive the PCA coefficients. On the other hand, Zhang et al (2007) used the current diaphragm position and its prior position approximately one third of a respiratory period as surrogate signals. This complicates matters because patients’ breathing is not reproducible (particularly, breathing period can change both intra- and inter-fractionally). Therefore, care must be taken to ensure that the regression model between diaphragm positions and PCA coefficients built during simulation is still valid during treatment. Last but not least, in solving for PCA coefficients, Zhang et al (2007) used OLS, and thus the number of PCA coefficients is limited by the number of surrogates. On the other hand, we used Bayesian estimation, which has no such limitation and is clearly more robust with few measurements.
We maintain that, in this work, there is no temporal constraint whatsoever (e.g., periodicity) on the PCA coefficients, so the model output need not be regular breathing either. On the other hand, it might be beneficial to include some form of temporal constraint in the model so that it captures the gross breathing patterns. For instance, one can combine the PCA model with linear prediction by including time-lagged information: . This is a truly spatiotemporal motion model and will be the topic of future work.
The PCA model can handle certain types of irregular breathing, but not all. It is important to distinguish between two kinds of irregular breathing patterns: (1) the temporal pattern of the voxel motion can change but the relative spatial relation among voxel motion remains constant; (2) the spatial configuration of organ motion can change. Because the PCA motion model grants full flexibility to the PCA coefficients, it is immune to the first kind of irregular breathing patterns as long as the lung motion can be represented by a linear combination of the PCA eigenvectors. However, since in the current PCA model the sample mean vector and eigenvectors are fixed after model construction, there are some situations that may be difficult to model. For instance, there may be baseline changes of the diaphragm due to stomach filling; or the relations between motion of different lung tissues can change between treatment fractions. It remains an open question if or how well the PCA model handles such situations. We plan to acquire serial 4DCT scans to investigate this question.
It is worth mentioning that the accuracy of the PCA lung motion model depends on the accuracy of 4DCT and subsequent deformable registration. Both image and motion artifacts in 4DCT are likely to degrade the quality of deformable registration. Although PCA is able to remove small independent noise in the DVFs generated by deformable registration, it will not remove large errors in the deformation. Therefore, the PCA lung motion model can benefit from careful quality assurance of 4DCT as well as a good deformable registration algorithm. Although the evaluation of the registration algorithm is not the focus of this study, it does affect the input (displacement vector fields) to the PCA lung motion model. Therefore, we have done an initial evaluation using 20 manually identified landmark points (10 in left lung, 10 in right lung) in three patients with the largest motion (patient index: 6, 7, and 8). Results showed that the 3D average error of the registration algorithm is ~1–2 mm when evaluated against the manually identified landmark points. Future studies will involve a systematic evaluation using more landmark points, which could also be used to evaluate the PCA lung motion models directly.
The clinical applications of the PCA motion model are not limited to derive the entire lung motion using single-marker measurements. Other tracking or imaging techniques may be used too. For instance, if skins are included in the deformable registration, then a PCA ‘body motion model’ may be constructed. Real-time surface imaging can then be used to derive the entire body (including lung) motion. In principle, spirometry can also be used because once we derive the entire lung motion, we can then calculate the lung volume change and this would closely mimic the spirometry measurements. In the case of a pressure belt, if the relevant abdominal anatomy is included in 4DCT, and relationship between the belt circumference and pressure measurement is calibrated, the PCA motion model would still be applicable, as long as the abdominal anatomy is included in the deformation registration. Of course, such an application may not be possible in general. A notable clinical application of the PCA motion model is the volumetric image reconstruction and 3D tumor localization from a single x-ray projection image acquired by the on-board imaging system (Li et al 2010, 2011). By deforming a reference CT image with the deformation fields parameterized by PCA coefficients and matching its projection with the x-ray image, one can obtain the entire lung motion as well as reconstruct the dynamic patient anatomy in real time, without implanted fiducial markers. This is potentially useful for many clinical applications, e.g., noninvasive 3D tumor tracking from a single x-ray imager, accurate dose reconstruction, on-line replanning, etc.
Acknowledgments
This work was partially supported by Master Research Agreement from Varian Medical Systems. We wish to thank the anonymous reviewers who gave valuable comments and suggestions and helped improve this paper.
Appendix A
For analysis purpose, it is cumbersome to work in the discrete domain. Instead we will work out the results in the continuous domain. PCA in this limiting case becomes Karhunen–Loeve (KL) expansion (Loeve 1978), which is a generalization of PCA to infinite dimensions. Eigenvectors then become eigenfunctions.
If we consider the values Ai, φi in each row as realizations of random variables A, Φ, as θ → 0 and Mθ → T, the motion matrix X can be represented by a random process: X(t) = Acos(t + Φ), where 0 ≤ t < T. Without loss of generality, we assume that the motion period T is 2π.
Karhunen–Loeve theorem states that a centered random process {X(t)}t∈[0,T ] can be represented by a linear combination of an infinite number of orthonormal deterministic functions with random coefficients which are uncorrelated with each other, i.e.
| (A.1) |
The basis functions ϕk(t) (also called eigenfunctions) must satisfy the integral equation:
| (A.2) |
where
| (A.3) |
is the covariance function.
The random coefficients are determined by
| (A.4) |
Note that correlation function is also a positive semidefinite kernel and by Mercer’s theorem it admits the expansion of the same form (Mercer 1909). We wish to point out here that because of the way we remove the sample mean in the discrete case, in order to get the correct limiting results, we should do KL expansion on the random process X(t)−X̄, where . So instead of subtracting the mean function μ(t) and expanding the covariance function of X(t), we will expand the correlation function of X(t) − X̄. Consequently, the random coefficients Zk do not have zero mean in general; instead, every eigenfunction will integrate to 0 between 0 and T.
It is easy to see that X̄ = 0. We can compute the correlation function as (it is understood that all expectations are with respect to the joint pdf of A, Φ):
| (A.5) |
where , γ1 = E[A2 cos2 Φ], γ2 = E[A2 sin2 Φ]. They are known constants given the joint pdf of A, Φ.
We express the eigenfunction in [0, T] in its Fourier expansion:
| (A.6) |
Plugging the correlation function and eigenfunction into equation (A.2) and equating the sinusoidal terms at different frequencies, we can see that the constant and all high frequency terms in the eigenfunction vanish except at fundamental frequency and therefore:
| (A.7) |
The eigenvalues and Fourier coefficients must satisfy the following set of equations:
| (A.8) |
Reorganizing the first two equations, we have
| (A.9) |
where .
Since a1, b1 cannot be 0 at the same time, we have det C (λ) = 0.
The eigenvalues and the corresponding eigenfunctions can then be solved accordingly. The eigenvalue equation has two nonnegative solutions if and only if γ1γ2 ≥ ξ2. This is guaranteed by Cauchy–Schwartz inequality:
| (A.10) |
So far, we have shown that for the cosine respiratory phantom there are two eigenfunctions in the form of sinusoids. Next, we will show that the second eigenfunction is always the time derivative of the first eigenfunction, for any distribution of amplitude and phase. Suppose the first and second eigenfunctions are ϕ1(t) = a1 cos(t) + b1 sin(t) and , respectively. Since all eigenfunctions are orthonormal, we have
| (A.11) |
This condition leads to the following set of equations:
| (A.12) |
Solving this, we get, and . It is easy to see that the second eigenfunction is indeed the time derivative of the first eigenfunction (except for a negative sign for the other solution).
Appendix B
Here, we derive the necessary and sufficient condition under which the PCA and 5D motion models are equivalent for the cosine respiratory phantom.
Proof
The 5D lung motion model (Low et al 2005) has the following expression:
| (B.1) |
where v(t) is the tidal volume and f (t) is the airflow, which is defined to be the time derivative of the tidal volume.
Suppose tidal volume is v(t) = A0 cos t. Then air flow is f (t) = −A0 sin t. Given the cosine respiratory motion phantom, it is easy to see that 5D motion model is
| (B.2) |
Sufficiency
If ξ = 0, then the two eigenvalues are λ1 = πγ1, λ2 = πγ2. Solve for a1, b1 from equation (A.8) and plug them into equation (A.7), and we get the corresponding eigenfunctions:
| (B.3) |
Then KL expansion gives us
| (B.4) |
where .
We can see that except for a scaling factor, tidal volume and air flow are exactly the first and second eigenfunctions, and the last two parameters in 5D motion model are the corresponding PCA coefficients.
Necessity
If X(t) can be represented by equation (B.2), then KL theorem states that E[Z1Z2] = 0, i.e.
| (B.5) |
In reality, tidal volume is positive. Then there will be a constant shift in the initial position. Everything else is the same.
Appendix C
Proof
The centering operation in PCA is equivalent to a projection:
| (C.1) |
such that X̃ = X · CM, where 1 is an M by 1 vector consisting of all ones. This projection projects vectors onto the (M − 1)-dimensional subspace that is orthogonal to the nullspace 1. It follows that if the nullspace 1 lies in the span of the N row vectors of X, then the rank of centered matrix will be reduced by 1, i.e. rank(X̃) = 2n.
Next, we show that the nullspace 1 does lie in the span of the N row vectors of X. Let us consider a linear combination of the row vectors of X:
| (C.2) |
where the weights are given by and Z is a N by M matrix (same dimension as X) and each entry is
| (C.3) |
Notice that we have separated the constant and harmonic terms.
It is easy to see that rank(Z) = 2n (compare with X). Therefore, if N ≤ 2n or M ≤ 2n (in practice, both N and M are much larger than 2n), we have rank(X̃) ≤ 2n. Otherwise, the matrix Z is rank deficient. There exist non-zero vectors α such that αT · Z = 0. Apparently, the column vectors of Z in general cannot span the N by 1 vector 1N. This means αT · 1N ≠ 0. Take α1 + ··· + αN = 1/c0. We can see that the nullspace 1 indeed lies in the span of the row vectors of X. So the rank of X̃ is 2n.
Appendix D
In this appendix, we show that for the respiratory phantom with cos2n (t) motion, there are 2n eigen functions and they are a linear combination of cosine and sine functions at even multiples (up to 2n) of the fundamental frequency.
In the continuous case, we shall do KL expansion directly on the random process:
| (D.1) |
where . Note that the summation index starts from 1 instead of 0 due to centering. Using the same technique as in appendix A, it is straightforward (although tedious) to show that all eigenfunctions are in the following form:
| (D.2) |
From the integral equation, all the eigenvalues and Fourier coefficients in eigenfunctions must satisfy the following set of equations:
| (D.3) |
for k = 1, …, n, where gk(·), hk(·) are linear functions of the Fourier coefficients.
The first 2n equations can be reorganized as
| (D.4) |
where C(λ) is a 2n × 2n matrix. Similarly as before, the eigenvalues can be solved using det C(λ) = 0. Note that this will lead to a polynomial of λ with an order of 2n. Therefore, we will have 2n eigenvalues and corresponding eigenfunctions with centering.
Appendix E
We know a priori that wt follows a Gaussian distribution with zero mean and covariance matrix of Λ, which is exactly the diagonal matrix from diagonalization of the covariance matrix of the training data, i.e.
| (E.1) |
Assuming the model error also follows a Gaussian distribution, we get the likelihood (since it is defined for one time point only, it is also a pdf):
| (E.2) |
where Ũ is a 3×K matrix whose columns consist of entries in the eigenvectors that correspond to rt ;
is the sample mean estimated from the training set, and
 is the index set of the training data. The covariance matrix Σ is a 3 × 3 matrix with six independent entries. Since we only have six samples to estimate Σ, we constrain it to be spherical: Σ = σ2I. In this case, an unbiased estimator is
is the index set of the training data. The covariance matrix Σ is a 3 × 3 matrix with six independent entries. Since we only have six samples to estimate Σ, we constrain it to be spherical: Σ = σ2I. In this case, an unbiased estimator is
| (E.3) |
Combining equations (E.1) and (E.2), we form the posterior distribution:
| (E.4) |
The MAP estimator can then be easily calculated:
| (E.5) |
References
- Arslan S, et al. CT-guided transthoracic fine needle aspiration of pulmonary lesions: accuracy and complications in 294 patients. Med Sci Monit. 2002;8:CR493–7. [PubMed] [Google Scholar]
- Baker S, et al. A database and evaluation methodology for optical flow. Int J Comput Vision. 2011;92:1–31. [Google Scholar]
- Duda RO, Hart PE, Stork DG. Pattern Classification. 2. New York: Wiley; 2001. [Google Scholar]
- Ehrhardt J, et al. Statistical modeling of 4D respiratory lung motion using diffeomorphic image registration. IEEE Trans Med Imaging. 2011;30:251–65. doi: 10.1109/TMI.2010.2076299. [DOI] [PubMed] [Google Scholar]
- Geraghty PR, et al. CT-guided transthoracic needle aspiration biopsy of pulmonary nodules: needle size and pneumothorax rate. Radiology. 2003;229:475–81. doi: 10.1148/radiol.2291020499. [DOI] [PubMed] [Google Scholar]
- Heinrich MP, et al. Discontinuity preserving regularization for variational optical-flow registration using the modified Lp norm. MICCAI Workshop on Evaluation of Methods for Pulmonary Image Registration (EMPIRE).2010. [Google Scholar]
- Jolliffe IT. Principal Component Analysis. New York: Springer; 2002. [Google Scholar]
- Kakar M, et al. Respiratory motion prediction by using the adaptive neuro fuzzy inference system (ANFIS) Phys Med Biol. 2005;50:4721–28. doi: 10.1088/0031-9155/50/19/020. [DOI] [PubMed] [Google Scholar]
- Klinder T, Lorenz C, Ostermann J. Free-breathing intra- and intersubject respiratory motion capturing, modeling, and prediction. Proc SPIE. 2009;7259:72590T. [Google Scholar]
- Li R, et al. Real-time volumetric image reconstruction and 3Dtumor localization based on a single x-ray projection image for lung cancer radiotherapy. Med Phys. 2010;37:2822–6. doi: 10.1118/1.3426002. [DOI] [PubMed] [Google Scholar]
- Li R, et al. 3D tumor localization through real-time volumetric x-ray imaging for lung cancer radiotherapy. Med Phys. 2011;38:2783–94. doi: 10.1118/1.3582693. [DOI] [PubMed] [Google Scholar]
- Loeve M. Graduate Texts in Mathematics. 4. Vol. 2. New York: Springer; 1978. Probability theory. [Google Scholar]
- Low DA, et al. Novel breathing motion model for radiotherapy. Int J Radiat Oncol Biol Phys. 2005;63:921–9. doi: 10.1016/j.ijrobp.2005.03.070. [DOI] [PubMed] [Google Scholar]
- Lu W, et al. A comparison between amplitude sorting and phase-angle sorting using external respiratory measurement for 4D CT. Med Phys. 2006;33:2964–74. doi: 10.1118/1.2219772. [DOI] [PubMed] [Google Scholar]
- Lujan AE, et al. A method for incorporating organ motion due to breathing into 3D dose calculations. Med Phys. 1999;26:715–20. doi: 10.1118/1.598577. [DOI] [PubMed] [Google Scholar]
- McCall KC, Jeraj R. Dual-component model of respiratory motion based on the periodic autoregressive moving average (periodic ARMA) method. Phys Med Biol. 2007;52:3455–66. doi: 10.1088/0031-9155/52/12/009. [DOI] [PubMed] [Google Scholar]
- McClelland JR, et al. A continuous 4D motion model from multiple respiratory cycles for use in lung radiotherapy. Med Phys. 2006;33:3348–58. doi: 10.1118/1.2222079. [DOI] [PubMed] [Google Scholar]
- Mercer J. Functions of positive and negative type, and their connection with the theory of integral equations. Proc R Soc A. 1909;83:69–70. [Google Scholar]
- Murphy MJ, Dieterich S. Comparative performance of linear and nonlinear neural networks to predict irregular breathing. Phys Med Biol. 2006;51:5903–14. doi: 10.1088/0031-9155/51/22/012. [DOI] [PubMed] [Google Scholar]
- Murphy MJ, Jalden J, Isaksson M. Adaptive filtering to predict lung tumor breathing motion during image-guided radiation therapy. Proc. 16th Int. Conf. on Computer Assisted Radiology (CARS 2002); Paris, France. 2002. [Google Scholar]
- Nehmeh SA, et al. Quantitation of respiratory motion during 4D-PET/CT acquisition. Med Phys. 2004;31:1333–8. doi: 10.1118/1.1739671. [DOI] [PubMed] [Google Scholar]
- Neicu T, et al. Synchronized moving aperture radiation therapy (SMART): average tumour trajectory for lung patients. Phys Med Biol. 2003;48:587–98. doi: 10.1088/0031-9155/48/5/303. [DOI] [PubMed] [Google Scholar]
- Pock T, et al. A duality based algorithm for TV-L1-optical-flow image registration. Med Image Comput Comput Assist Interv. 2007;10:511–8. doi: 10.1007/978-3-540-75759-7_62. [DOI] [PubMed] [Google Scholar]
- Ren Q, et al. Adaptive prediction of respiratory motion for motion compensation radiotherapy. Phys Med Biol. 2007;52:6651–61. doi: 10.1088/0031-9155/52/22/007. [DOI] [PubMed] [Google Scholar]
- Ruan D, et al. Real-time profiling of respiratory motion: baseline drift, frequency variation and fundamental pattern change. Phys Med Biol. 2009;54:4777–92. doi: 10.1088/0031-9155/54/15/009. [DOI] [PubMed] [Google Scholar]
- Ruan D, Fessler JA, Balter JM. Real-time prediction of respiratory motion based on local regression methods. Phys Med Biol. 2007;52:7137–52. doi: 10.1088/0031-9155/52/23/024. [DOI] [PubMed] [Google Scholar]
- Seppenwoolde Y, et al. Precise and real-time measurement of 3D tumor motion in lung due to breathing and heartbeat, measured during radiotherapy. Int J Radiat Oncol Biol Phys. 2002;53:822–34. doi: 10.1016/s0360-3016(02)02803-1. [DOI] [PubMed] [Google Scholar]
- Sharp GC, et al. Prediction of respiratory tumour motion for real-time image-guided radiotherapy. Phys Med Biol. 2004;49:425–40. doi: 10.1088/0031-9155/49/3/006. [DOI] [PubMed] [Google Scholar]
- Sohn M, et al. Modelling individual geometric variation based on dominant eigenmodes of organ deformation: implementation and evaluation. Phys Med Biol. 2005;50:5893–908. doi: 10.1088/0031-9155/50/24/009. [DOI] [PubMed] [Google Scholar]
- Vedam SS, et al. Acquiring a four-dimensional computed tomography dataset using an external respiratory signal. Phys Med Biol. 2003;48:45–62. doi: 10.1088/0031-9155/48/1/304. [DOI] [PubMed] [Google Scholar]
- Vedam SS, et al. Predicting respiratory motion for four-dimensional radiotherapy. Med Phys. 2004;31:2274–83. doi: 10.1118/1.1771931. [DOI] [PubMed] [Google Scholar]
- Werner R, et al. Technical note: development of a tidal volume surrogate that replaces spirometry for physiological breathing monitoring in 4D CT. Med Phys. 2010;37:615–9. doi: 10.1118/1.3284282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu H, et al. A finite state model for respiratory motion analysis in image guided radiation therapy. Phys Med Biol. 2004;49:5357–72. doi: 10.1088/0031-9155/49/23/012. [DOI] [PubMed] [Google Scholar]
- Yang X, Klette R. Evaluation of motion analysis on synthetic and real-world image sequences; IEEE Proc IVCNZ.2010. [Google Scholar]
- Zach C, Pock T, Bischof H. A duality based approach for Realtime TV-L1 optical flow. Pattern Recognit. 2007;4713:214–23. [Google Scholar]
- Zeng R, Fessler JA, Balter JM. Estimating 3-D respiratory motion from orbiting views by tomographic image registration. IEEE Trans Med Imaging. 2007;26:153–63. doi: 10.1109/TMI.2006.889719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J, et al. Development of a geometry-based respiratory motion-simulating patient model for radiation treatment dosimetry. J Appl Clin Med Phys. 2008;9:2700. doi: 10.1120/jacmp.v9i1.2700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Q, et al. A patient-specific respiratory model of anatomical motion for radiation treatment planning. Med Phys. 2007;34:4772–81. doi: 10.1118/1.2804576. [DOI] [PubMed] [Google Scholar]
- Zhao TY, et al. Characterization of free breathing patterns with 5D lung motion model. Med Phys. 2009;36:5183–9. doi: 10.1118/1.3246348. [DOI] [PMC free article] [PubMed] [Google Scholar]