Abstract.
Evaluation of tear film is performed by an optical reflectometer system with alignment guided by a galvanometer scanner. The reflectometer system utilizes optical fibers to deliver illumination light to the tear film and collect the film reflectance as a function of wavelength. Film thickness is determined by best fitting the reflectance-wavelength curve. The spectral reflectance acquisition time is 15 ms, fast enough for detecting film thickness changes. Fast beam alignment of 1 s is achieved by the galvanometer scanner. The reflectometer was first used to evaluate artificial tear film on a model eye with and without a contact lens. The film thickness and thinning rate have been successfully quantified with the minimum measured thickness of about 0.3 μm. Tear films in human eyes, with and without a contact lens, have also been evaluated. A high-contrast spectral reflectance signal from the precontact lens tear film is clearly observed, and the thinning dynamics have been easily recorded from 3.69 to 1.31 μm with lipid layer thickness variation in the range of 41 to 67 nm. The accuracy of the measurement is better than of the film thickness at an estimated tear film refractive index error of . The fiber-based reflectometer system is compact and easy to handle.
Keywords: reflectometry, optical devices, interferometry, ophthalmology
1. Introduction
Dry eye syndrome (DES) is an ocular disease caused by a lack of tears or excessive tear loss due to evaporation.1–3 Ocular discomfort and irritation are common symptoms.3 Severe DES may result in corneal erosion and secondary infection that may lead to vision loss.4,5 However, current clinical evaluations, such as tear breakup test and Schirmer’s test, may not be sufficient for accurate diagnosis of the DES. It has been shown that the tear film thickness is thinner in dry eye patients.6,7 Furthermore, wearing contact lenses interferes with the tear system, which may cause contact lens-related dry eye.8 It is more common for contact lens wearers to develop the DES than the general population.9 It has been suggested that thinned prelens tear film or postlens tear film may be responsible for those DES symptoms in contact lens wearers.10–12 Therefore, it is important to determine the precise tear film thickness and tear thinning dynamics in an eye with or without a contact lens.
Several techniques have been proposed for tear film measurement in eyes. Mishima13 and Benedetto et al.14 first estimated tear film thickness in eyes using fluorescence technique through instilling saline-fluorescein and achieved microns resolution. But, the invasive nature of their technique adds unconvincing aspects to the experimental results, since the instillation of saline-fluorescein may disturb the tear film. In 1989, Doane15 for the first time introduced the noninvasive optical interferometry technique using a thickness dependent fringe to the in vivo tear film measurement on a contact lens and successfully evaluated tear film dynamics and break up characteristics. The method which Doane proposed has the advantage of two-dimensional recording of the tear film distribution. However, it requires dry areas for reference that are sometimes difficult to acquire or color clues that increases analysis complexity. In 1998, Fogt and King-Smith16 introduced another noninvasive interferometric technique for tear film measurement using wavelength-dependent fringe (WDF). The spectral dependent interference reflectance curves were examined and Fourier transform and least square fit calculations were performed to obtain the tear film thicknesses.17 The data processing technique is attractive because it contributes to fine thickness evaluation accuracy on tear films. But, the technique uses free space bulk optics which is complex and requires careful alignment. In 2003, Wang et al.18,19 used real-time anterior segment optical coherent tomography to quantify tear film thickness and reported human tear film thickness of about 3.3 μm, consistent with the WDF method.20 However, this method suffers from less measurement precision compared to the interferometry technique.
We report herein a compact fiber-based optical reflectometer system to add to the existing tools for tear film evaluation. Comparing to the techniques mentioned above, our system could offer fast noninvasive tear film thickness measurement with high resolution. The fiber-based system is more flexible, allowing a direct integration solution with other imaging devices. In addition, the use of a galvanometer scanner for fast measurement beam positioning makes the system easy to handle. The system we used here is developed from a reflectometry-based thin film measurement device (TF-166, New Span Opto-Technology, Miami, Florida), which is capable of measurement error or of the film thickness, whichever is larger for a coated dielectric solid film. Adapting the optical reflectometry technique to the tear film measurement provides an intrinsically accurate measurement. With the optical reflectometer system, the wavelength dependent interference fringes from the tear film reflections, which carry the film thickness information, are acquired. The tear film thicknesses are then determined by curve fitting using the nonlinear least-squares method and the spectrally dependent refractive indices of the tear films given in literatures.21,22 As a phantom study, we first tested the system with artificial tear (AT) films on a model eye, with and without contact lenses, and evaluated the AT film thicknesses and thinning rates. The AT film thicknesses in the range of 0.3 to 22.56 μm have been measured, demonstrating the system’s capability of measuring both thin and thick tear films. We further evaluated the precontact lens tear film in an eye with a contact lens as well as the precornea tear film in an eye without a contact lens to demonstrate the capability of the system for in vivo measurement. Precontact lens tear film in a human eye is examined for its thinning dynamics from 3.69 to 1.31 μm with a lipid layer thickness averaged at 54 nm. High contrast spectral reflectance from tear film on a contact lens is observed. We also measured the precornea tear film thickness in three human eyes without a contact lens. The fiber-based optical reflectometer used in the present study is compact and easy to handle.
2. Optical Reflectometry Measurement System
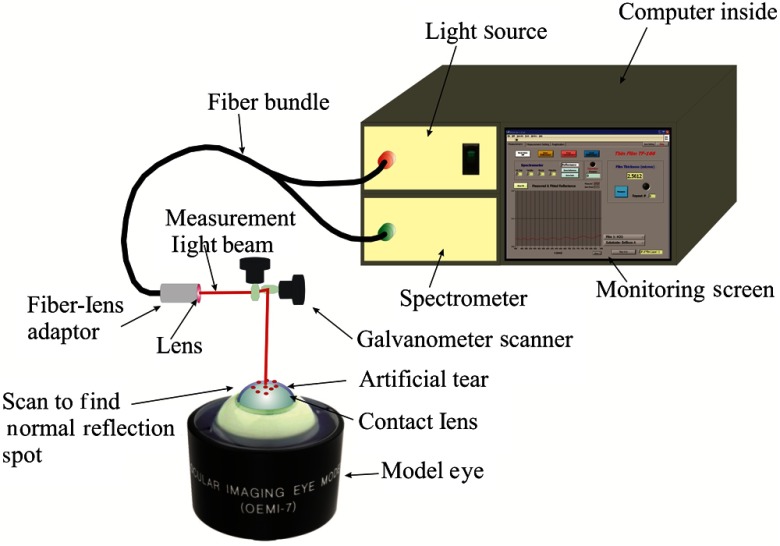
The operation principle of the fiber-based reflectometry for tear film evaluation can be briefly described as follows in Fig. 1. The light from a broadband Tungsten Halogen light source (LS-1, Ocean Optics, Dunedin, Florida) is directed into a bifurcated fiber coupler, which delivers the illumination light to the tear film. An achromatic lens is placed after the fiber to focus the illumination light on the tear film. This tear film is illuminated at near normal incidence, and the reflected light is collected by the achromatic lens and transferred by the fiber coupler to an optical spectrometer for measurement. The reflected light measured by the spectrometer, namely wavelength dependent reflectance , is then processed by the software program. By curve fitting, the film thicknesses of different layers of the tear film can be extracted based on the theory of multilayer optical reflection23–25 in white light reflectometry.
Fig. 1.
Fiber-based reflectometer measurement system with a galvanometer scanner and a model eye.
To perform the tear film thickness evaluation, the thin film measurement device has been modified in the following ways. First, a galvanometer scanner (6215H, Cambridge Technology, Bedford, Massachusetts), controlled by a data acquisition card (PCI-6259, National Instruments, Austin, Texas), is used to auto align the incident light (Fig. 1). The incident light passes through the horizontal and vertical scanning mirrors and is navigated by the scanner to search for the best incident position on the tear film that gives reflectance with the highest signal-to-noise ratio (SNR). After analyzing the reflectance from each of the different positions across the scanned area and determining the one with the highest SNR, the galvanometer is then set to fix on this measurement spot. This fast auto scan has been found to be capable of identifying the best beam measurement spot within 1 s. Next, the optical reflectometer software is custom configured to allow real time recording of the tear film thinning dynamics. The film thickness determination accomplished through curve fitting is a complex computational process that may take anywhere from a few hundred milliseconds to a few seconds. The spectrometer integration time for each spectral curve is set to be 5 ms, and the delay time due to data transfer and software program is 10 ms, giving a total time of 15 ms for each spectral reflectance acquisition, which is fast enough for detecting film changes and studying the film thinning dynamics. Thus, to analyze the tear film thinning dynamics, the optical reflectometer software is modified to allow periodic saving of the measured spectral reflectance data, and then, after recording the curve fitting thickness determination is performed to reveal the tear film thinning process as a function of time.
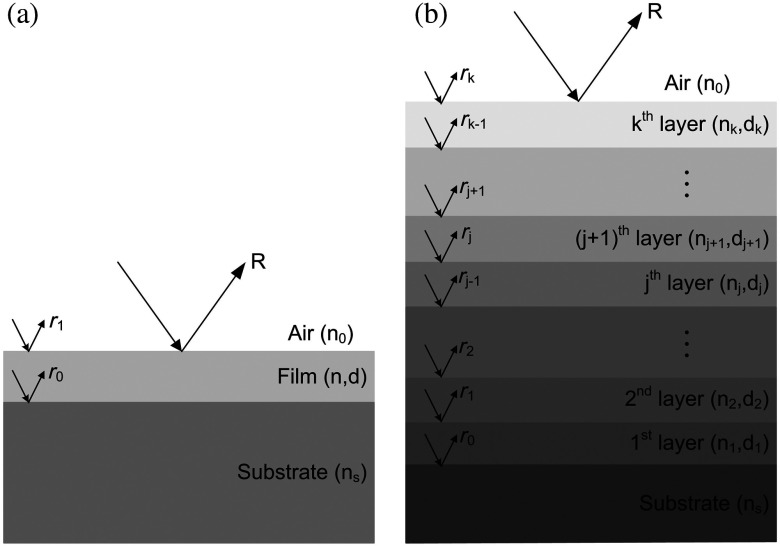
The mathematical framework of the reflectometry method23–25 can be described as follows. For a single film as shown in Fig. 2(a), the reflectance is the interference between the reflections from the air/film interface and the film/substrate interface. Assuming the film thickness, the air refractive index, the film refractive index, the substrate refractive index, the Fresnel coefficient of the film/substrate and air/film interfaces and the phase change within the thin film layer to be , , , , , , and , respectively, the theoretical reflectance can be written as
| (1) |
in which is the overall effective Fresnel coefficient for the single layer thin film. In case of normal direction incidence,
| (2) |
| (3) |
| (4) |
Fig. 2.
Schematic of optical reflection in a (a) single layer film system and (b) multilayer film system.
Figure 2(b) shows a layer film structure. and are the refractive index and the film thickness of the ’th layer. The overall effective Fresnel coefficient for films is related to previous films’ effective Fresnel coefficient by
| (5) |
For normal direction incidence,
| (6) |
| (7) |
The thickness of each film layer is related to the reflectance by the corresponding phase term [Eqs. (4) and (7)]. Given the film layer number , the theoretical reflectance of the multilayer film case is
| (8) |
It is shown in the equations above that in case of normal direction incidence would only depend on the thicknesses of different layers through phase terms if the refractive indices of are known parameters. For tear film evaluation, the light absorption in the measurable spectral range from 400 to 900 nm is negligible, and the refractive indices are real values.
By comparing the experimental reflectance with the theoretical reflectance given by Eq. (8) for a multilayer film, curve fitting computation by the nonlinear least-squares numerical method24 to determine the film thicknesses can be performed. The system first predicts a group of film thicknesses to initiate the reflectance calculation. Then, with known refractive indices of , the calculated reflectance by Eq. (8) is compared to the measured reflectance curve to determine the error. If the error is not small enough, the predicted thicknesses are adjusted for a second computation and comparison. The computation process continues to adjust the estimated thicknesses for reducing error in each subsequent computation step until a minimum error is achieved, and the calculated reflectance curve is best fitted with the measured spectral reflectance curve. At this point, the film thicknesses can be extracted. This method can also be called predictor–corrector method based on its error minimization approach. The number of film layers that can be determined is limited by the refractive index difference between adjacent layers and the optical quality of the test film sample. A small refractive index difference between adjacent layers results in a weak reflection from that film interface, which may be indistinguishable from optical noise. In this case, the two film layers may be treated as a combined single layer. For a single layer film thickness determination, the same curve fitting computation process described above is performed by using theoretical reflectance Eq. (1) and a single thickness variable . In general, the film thickness measurement by optical reflectometry technique with nonlinear least-squares curve fitting method24 as conceptually described above has been maturely developed.
The accuracy of the reflectometry system is evaluated by measuring two samples:
-
1.
A standard 200-nm thick film on a Si substrate purchased from U.S. National Institute of Standards and Technology (NIST).
-
2.
A photoresist film coated on a glass ball of similar curvature as the eye. The thickness was measured by a Tencor Alpha Step 200 surface profiler to be 1.755 μm with a measurement resolution of about 5 nm.
Measurement of the first sample using the reflectometer showed an error of , which was indicative of an excellent accuracy. Evaluation of the second sample gave a thickness of 1.764 μm, which was a 9 nm difference from that measured by the Tencor Alpha Step 200 surface profiler. The result shows that the reflectometry system still have a good accuracy on the measurement of a curved film. The system error is of the film thickness.
The thickness determination accuracy is found to be dependent on the accuracy of the refractive indices of the films as well as the system error. In Eqs. (4) and (7), . For a given reflectance, would be determined and the variation of the determined film thickness would be related to refractive index error by . Therefore, the thickness determination error by the refractive index uncertainty can be roughly estimated by . Combined with the system error mentioned above, the total film thickness determination error is better than of film thickness. The refractive index of the tear film, as given by various literature,22,26 is around 1.336 to 1.337 at a wavelength of 589 nm. The error of the refractive index is conservatively estimated to be within . Such a refractive index error will lead to a tear film thickness determination uncertainty of of the tear film thickness according to . Together with the system error, the total combined error is better than of the tear film thickness or 12 nm for a 1-μm-thick tear film. The tear film refractive index is continuously updating in literatures through improved experimentation. The tear film thickness determination accuracy may be adjusted according to above estimation equation. The overall tear film thickness determination error is small. An experimental evaluation of the uncertainties of the measured tear film thickness values due to inaccuracy of refractive indices of the tear film has also been performed on the tear film in an eye with a contact lens. We take the experimental wavelength dependent reflectance curve at in Fig. 6(a) as an example. With tear film refractive index given in Ref. 22, the tear film thickness is determined to be 1.839 μm with a lipid layer thickness of 54 nm. A conservative assumption of variation in the tear film refractive index will result in a tear film thickness of 1.838 and 1.840 μm, respectively, with a lipid layer of 54 nm. This is consistent with the theoretical estimation above that the total combined error is better than of the tear film thickness. If using the same refractive index values, the curve fitting computation for thickness determination is highly repeatable with calculation repeatability of no more than 0.1 nm.
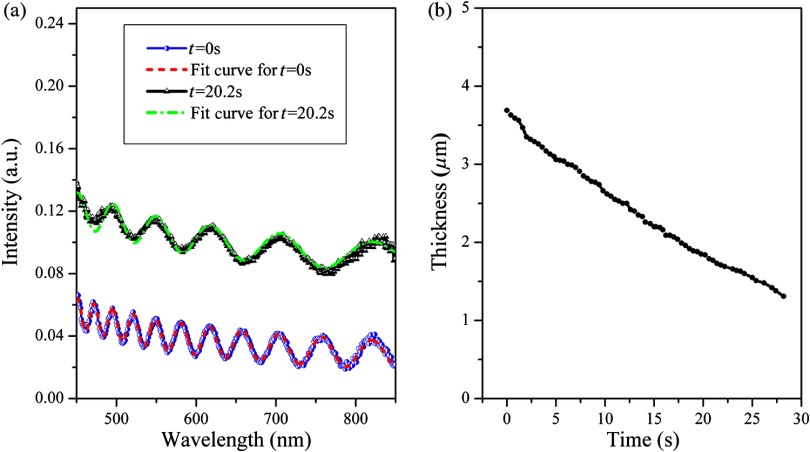
Fig. 6.
(a) Spectral reflectance from tear film in an eye with a soft contact lens at time of 0 s (bottom) and 20.2 s (top). Curves at of 0 and 20.2 s correspond to precontact lens tear film thickness of 3.69 and 1.84 μm with lipid layer of 46 and 54 nm, respectively. Two curves are vertically offset for illustration clarity. (b) Precontact lens tear film thinning with time in an eye.
3. Water Film Thickness and Thinning Process
Using the setup of the reflectometer measurement system shown in Fig. 1, tear films have been successfully evaluated on a model eye (OEM-7, Ocular Instrument, Bellevue, Washington) with or without a contact lens as well as in a human eye. The illumination light intensity is 440 μW, below the maximum permissible exposure for eye safety. The measurement beam spot size on the tear film is about 0.8 mm in diameter.
3.1. Measurements of AT Film on a Model Eye with and without a Contact Lens
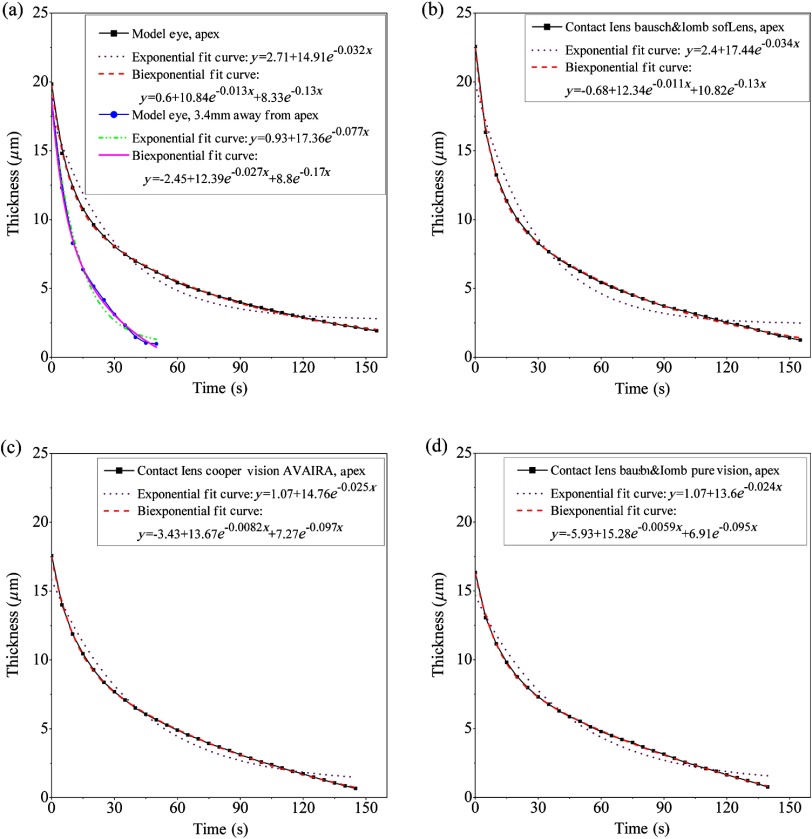
In our present study, we first evaluated AT film on the model eye with and without a soft contact lens. The AT film on a model eye with or without a contact lens can be considered as a single layer AT film on a substrate of a contact lens or a model eye. The theoretical reflectance for this case can be determined by Eq. (1). The reflection interference from the contact lens body or the model eye are ignored in the signal processing since the thickness of the contact lens or the model eye are above 100 μm, which is beyond the reflectometer measurement range. The model eye, which includes key features of the ocular structure, best simulates the human eye and is placed facing upward on a two-axis translation stage below the reflectometry system for adjustment flexibility. The AT film used was CVS brand ATs and the formulation consisted of lubricant-glycerin (0.3%), propylene glycol (1.0%) preserved with benzalkonium chloride (0.01%), and purified water. Three different brands of soft contact lens, Bausch&Lomb SofLens (Rochester, New York), Cooper Vision AVAIRA (Pleasanton, California), and Bausch&Lomb PureVision (Rochester, New York), were selected for the experiments. In each test, a drop of AT was given to the model eye and the spectral reflectance curves were recorded by the reflectometer over time. The system recorded the reflectance data at a time interval of 0.5 s while the film continuously thinned over time until the spectral dependent reflectance curve as shown in Fig. 3 was not measurable. After finishing the real time recording, the saved reflectance data series were reloaded to the reflectometry evaluation software to determine their corresponding thicknesses. The AT film thinning dynamics were then reconstructed. The data acquisition is fast enough for video demonstration of the continuous reflectance curve changing for evaluating the AT film thinning dynamics.
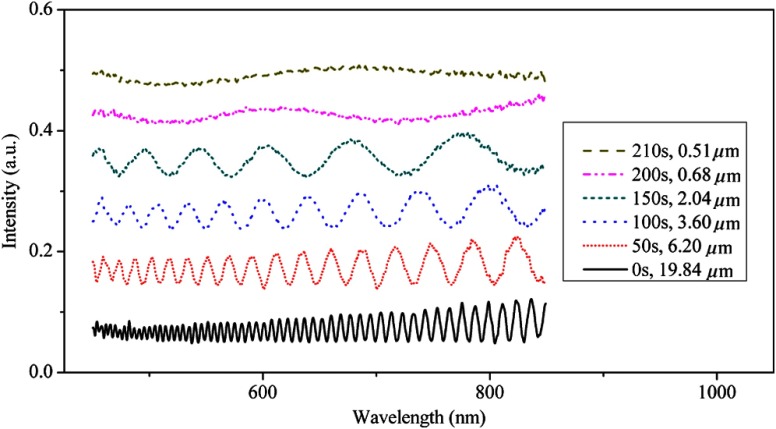
Fig. 3.
Reflectance curves from an artificial tear (AT) film on the apex of a model eye without a contact lens at different times showing the film thinning dynamics.
Figure 3 shows the reflectance curves at different times on the apex of a model eye without a contact lens as an example. The AT film experiments conducted on various other spots on the model eye or on the apex of a different contact lens demonstrated a similar reflectance curve trend. The curves’ periods increased with time at their local wavelengths with an appearance of curve motion toward shorter wavelengths, indicating the film is getting thinner. This is consistent with the reflectometry theory,23–25 in that a thinner thickness corresponds to oscillation with a larger period. It is also noticeable that the reflectance curve contrast is generally higher at longer wavelengths, which may attribute to the film thickness uniformity within the measurement spot, since shorter wavelengths are more sensitive to the local film uniformity variation.27
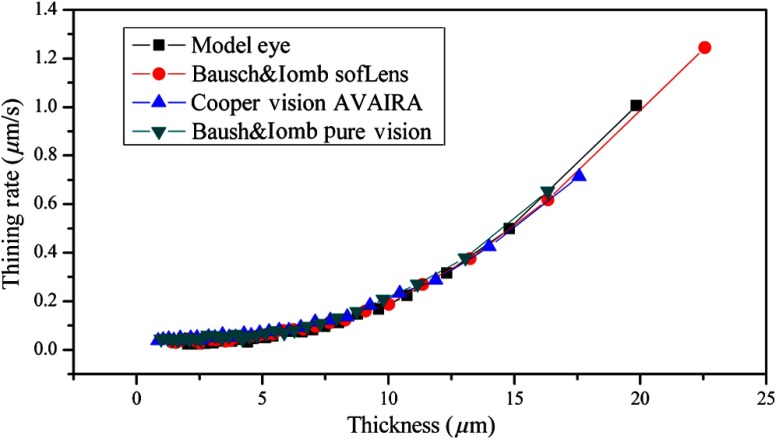
Starting from the initial film thickness just after a drop of the AT is applied to the time when film thickness is not measurable, Fig. 4 shows the AT film thinning dynamics of the horizontally positioned model eye with and without contact lenses (Bausch&Lomb SofLens, Cooper Vision AVAIRA, and Bausch&Lomb PureVision). The fitting curves and equations by exponential functions and biexponential functions are also shown in the figure. Here, the AT film thinning processes show similar characteristics, indicating the presence of similar thinning mechanisms. For all four cases, the biexponential functions fit better than the exponential functions for the experimental tear film thinning curves. The better fitted biexponential functions contain short time constants and long time constants, which should better associate with the two-type tear film thickness thinning process. Initially, the tear film thickness thins very fast but soon the thinning slows down with time. The initial thinning process should be mainly attributed to gravity-related AT film flow after the liquid has been suddenly dropped on the model eye or the contact lens surface. The later portion of the tear film thinning should be more attributed to the film evaporation. Figure 5 shows the AT film thinning rate as a function of the film thickness. The four curves correspond to the cases of an AT film on the apex of the model eye without a contact lens (black square) and with contact lenses of Bausch & Lomb SoftLens (red dot), Cooper Vision AVAIRA (blue triangle), and Bausch&Lomb PureVision (green inverted triangle) as in Fig. 4. Here, the trend of thinning rate with different thicknesses for the four cases shows almost the same results. This similarity should indicate that gravity and evaporation play a more important role in the AT film thinning process than different material properties of the model eye and the three contact lenses.
Fig. 4.
The AT film thickness thinning as a function of time on a model eye with and without a contact lens.
Fig. 5.
The AT film thinning rates as a function of the film thickness on a model eye with and without a contact lens.
The optical reflectometer has also demonstrated the capability of measurement at off-apex positions on the model eye by focusing the measurement beam on a spot of interest but one needs to ensure near radial direction incidence illumination. The blue solid line with dots in Fig. 4(a) shows measurement at a spot 3.4-mm away from the apex. Compared to the measurement on the apex of the horizontally positioned model eye, the tear film on the off-apex spot is thinning slightly faster due to gravity effect.
3.2. Measurements on a Human Eye with a Contact Lens
After verifying the measurement capability of the reflectometer system for accurate measurement of the AT film on a model eye with and without a contact lens, we extended our study to test the validity of the measurement on a human eye wearing a soft contact lens (brand of ACUVUE ADVANCE). The difference between the AT film on a model eye and tear film in a human eye is that the former has only one layer of the AT film, while the latter consists of three layers—lipid layer, aqueous layer, and mucus layer in terms of Wolff’s theory.28 The reflection from the aqueous/mucus interface is very weak since the refractive index difference between the aqueous layer and the mucus layer is much smaller than that across other interfaces (air/lipid, lipid/aqueous, mucus/contact lens, contact lens/aqueous, and mucus/cornea).17,29,30 Besides, the boundary between the aqueous layer and the mucus layer is not clear.31,32 Therefore, we ignore the difference of the aqueous layer and mucus layer and use the two-layer model [lipid layer and the layer that include the aqueous and mucus layers (A-M)] to represent the tear film. For clarification, by tear film, we mean the tear film including the lipid layer, the mucus layer, and the aqueous layer. Its thickness is defined by the distance between the air/lipid and the mucus/contact lens interfaces.
When we process the reflectance signal from tear film in an eye with a contact lens, all the reflections from the interfaces of air/lipid, lipid/A-M, A-M/contact lens, contact lens/A-M, and A-M/cornea contribute to the overall reflectance. The intensity of the reflections from each interface depends on the refractive index difference across the interface. The larger the refractive index difference, the higher the reflection signal intensity will be. The refractive indices of the tear lipid,21 aqueous layer,22 and contact lens (from manufacture specifications) were used for the thickness calculations.
Tear film measurement in an eye with a soft contact lens is performed in a time period of 28 s. Figure 6(a) shows two spectral dependent reflectance curves from the precontact lens tear film in an eye at time of 0 and 20.2 s with corresponding fitting curves in red dash line and green dotted dash line, respectively. The fitting curves represent the theoretical spectral dependent reflectance calculated under the best fit thickness values. The curves are offset in axis for easier viewing purposes. The two spectral reflectance curves shown here are clearly oscillatory with high contrast. The curve fitting calculation gives the tear film thicknesses of 3.69 and 1.84 μm and lipid layer thicknesses of 46 and 54 nm for time of 0 and 20.2 s, respectively. We only deduced the precontact lens tear film thickness from the spectral reflectance curves recorded here as shown in Fig. 6(a), since the main oscillations in the reflectance curves are assumed to be from the precontact lens tear film. This assumption is based on the fact that the oscillation contrast from the precontact lens tear film is much higher than that from the other postcontact lens layers. For the test of an eye wearing contact lens, three precontact lens interfaces are involved, which are the air/lipid layer interface, the lipid layer/A-M layer interface, and the A-M layer/contact lens interface. There are also two postcontact lens interfaces, namely the contact lens/A-M layer and the A-M layer/cornea interface. The two interface groups are separated by a relatively thick contact lens, which exceeds the reflectometer thickness measurement range and does not produce measurable spectral reflectance curves due to high fluctuation frequencies beyond the spectrometer resolving limitation. The refractive indices of air, lipid layer,21 A-M layer,22 contact lens, and cornea22 are 1, 1.48, 1.337, 1.405, and 1.376, respectively at wavelength 588 nm as an example. The Fresnel reflection coefficients of the above interfaces at this wavelength are 0.1935, 0.0508, 0.0248, 0.0248, and 0.0144, respectively. The reflections from the two postcontact lens interfaces are obviously weak as compared with those from the precontact lens interfaces. The decrease of the reflection at the cornea interface due to cornea roughness33 would further reduce the interference between the two postcontact lens interfaces making it hardly visible in the overall spectral reflectance data. The weak reflection from the cornea interface has been confirmed in the following experiment without wearing a contact lens. Thus, the weak reflection signal from the postcontact lens tear film can be treated as noise and ignored in the computation determination of precontact lens tear film.
The spectral reflectance data were recorded every 40 ms with total 68 spectral reflectance files saved. Figure 6(b) shows the precontact lens tear film thickness changing curve. The measured tear film thickness (including the lipid layer, the aqueous layer, and the mucus layer) varies from a maximum of 3.69 μm to a minimum of 1.31 μm, showing a similar thickness thinning trend as that of the AT film on a model eye. The average thinning rate is in the eye under present test. The tear film is expected to continue thinning after 28 s. However, we did not keep the eye open long to explore the minimum measurable tear film thickness, due to eye discomfort. The minimum measurable thickness has been demonstrated to be 0.3 μm in the model eye study.
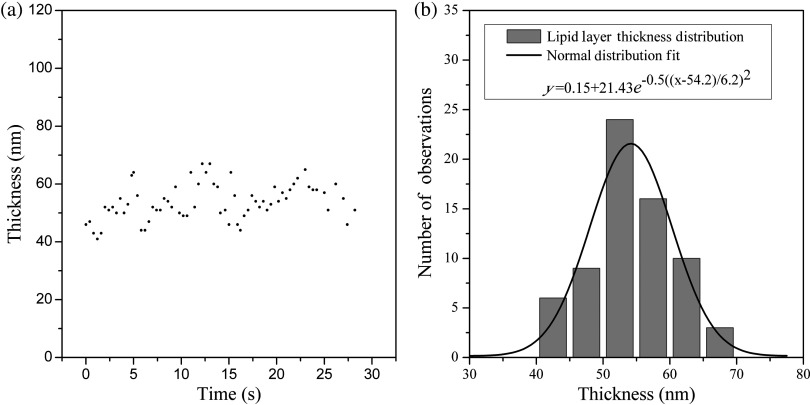
Figure 7(a) plots the lipid layer thickness change as a function of time from a subject wearing a contact lens of brand ACUVUE ADVANCE between two eye blinks. In general, the lipid layer thickness is relatively stable within the range of 41 to 67 nm and shows no reduction trend. Unlike the aqueous layer that is primarily composed of water and subject to draining and evaporation loss, the lipid layer is an oily film that is not quite evaporating and appears more stable within the range. The quality of the lipid layer controls the tear film evaporation.34 The tangential flow and redistribution of the lipid layer may contribute to the small thickness variation over time as shown in Fig. 7(a). Figure 7(b) is the histogram of the lipid layer thickness at a fixed measurement spot. From the histogram, we can see that the lipid layer thickness follows the normal distribution. The mean value of the lipid layer thickness is 54 nm.
Fig. 7.
(a) Lipid layer thickness changes with time. (b) Histogram of the lipid layer thickness.
3.3. Measurements on a Human Eye without a Contact Lens
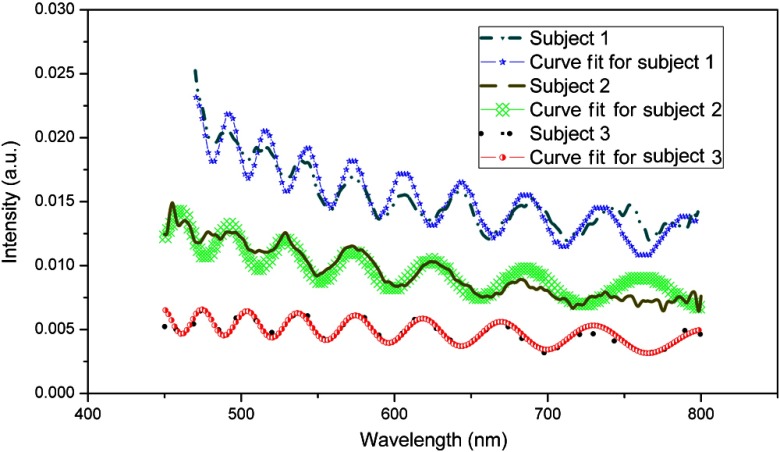
We further tested the validity of the reflectometer measurement on a human eye. Similar to the tear film on a human eye with a contact lens, tear film on a human eye without a contact lens can be considered as a two layer film system of the lipid layer and the A-M layer on the substrate of the cornea. The refractive index of the lipid layer,21 the A-M layer,22 and the cornea22 are used in the calculations. Figure 8 shows the spectral dependent reflectance curves with fitting from three different eyes without contact lenses. The curves are not as smooth as those found with a contact lens. This should be due to the roughness of the cornea surface.33 The calculated tear film thicknesses in those measurements are 3.79, 2.52, and 2.93 μm for subject 1, 2, and 3, respectively. The corresponding lipid layer thicknesses are 55, 40, and 66 nm, respectively.
Fig. 8.
Spectral dependent reflectances from a tear film in an eye without a contact lens and their fitting curves for three subjects.
4. Summary
In conclusion, a fiber-based optical reflectometer system with a galvanometer scanner for fast alignment has been introduced as a potential tool for noninvasive tear film measurement. The galvanometer scanner offers fast measurement beam positioning within 1 s. The spectral reflectance of the tear film is acquired to determine the tear film thickness by using nonlinear least-squares curve fitting method. The measurement technique is highly accurate with computation repeatability of 0.1 nm and measurement error of of film thickness or within 12 nm for a 1-μm-thick tear film in considering the tear film refractive index error of within . The AT films on a model eye with and without contact lenses have been evaluated in film thicknesses and film thinning dynamics. The minimum measured AT film thickness is 0.3 μm. Thinner AT film thickness measurement is possible if thinner film is properly maintained. We have also demonstrated the capability of the reflectometer for in vivo measurement of tear film in an eye wearing and not wearing a contact lens. Both the lipid layer and the tear film below the lipid layer (including the aqueous and mucus layers) have been measured, showing the tear thinning dynamics and relative stable lipid layer thickness. Precontact lens tear thickness is about 3.69 μm in the initial moment after a blink, and the tear film thickness in an eye without a contact lens is around 3.79, 2.52, and 2.93 μm for three subjects in our experiment. These values are consistent with measurements by King-Smith17 and Wang18 who also demonstrated that tear film thickness is . From our measurement, the lipid layer is ranging from 41 to 67 nm and averages at about 54 nm, which is similar to lipid layer thickness measurements by color look-up table (LUT) and two-wavelength methods.20 The fiber-based optical reflectometry technique is clearly capable of high accuracy evaluation of tear films in an eye with or without a contact lens and should serve as a useful tool for noninvasive evaluation of tear film in eyes.
Acknowledgments
This project was sponsored by the National Institute of Health 1R21EY019742. We express our appreciation of Guomin Jiang on helping the testing and useful discussions.
Biographies
Hui Lu received her BS degree in electrical engineering from Tianjin University, Tianjin, China, in 2007. She received her MS degree in optics from Shanghai Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, Shanghai, China, in 2010. Currently, she is pursuing a PhD degree in electrical and computer engineering at the University of Miami, Coral Gables, Florida. Her research interests are reflectometry and optical coherence tomography for noninvasive high resolution eye imaging.
Michael R. Wang received his PhD degree in electrical and computer engineering from the University of California, Irvine, in 1992. He is a full professor of electrical and computer engineering at the University of Miami. He has managed more than 50 U.S. government sponsored research projects. He has authored and coauthored more than 170 journal papers, proceedings, and conference presentations. His current research areas include photonic devices, optical interconnects, spectral imaging, and optical coherence tomography.
Jianhua Wang is currently a tenured associate professor at the Bascom Palmer Eye Institute, University of Miami. He is also a co-director of the experimental imaging laboratory. He graduated from Zhejiang Medical University, Hangzhou, China, in 1988. In 2003, he obtained his PhD in vision science from the University of Waterloo, Waterloo, Canada. His current research interests include clinical applications of ophthalmic structural and functional imaging.
Meixiao Shen is currently a researcher at the School of Optometry & Ophthalmology, Wenzhou Medical College. She got her BS degree in physics in 2001 and MS degree in optics in 2004 from Zhejiang University. She received her PhD in 2012 from Wenzhou Medical College. Now she conducts scientific and clinical studies using OCT and other devices, such as the ocular response analyzer (ORA). Her research interests include tear film, dry eye, and corneal biomechanical properties.
References
- 1.Holly F. J., Lemp M. A., “Tear physiology and dry eyes,” Surv. Ophthalmol. 22(2), 69–87 (1977). 10.1016/0039-6257(77)90087-X [DOI] [PubMed] [Google Scholar]
- 2.Mathers W. D., Daley T. E., “Tear flow and evaporation in patients with and without dry eye,” Ophthalmology 103(4), 664–669 (1996). 10.1016/S0161-6420(96)30637-4 [DOI] [PubMed] [Google Scholar]
- 3.Lemp M. A., “Epidemiology and classification of dry eye,” Adv. Exp. Med. Biol. 438, 791–803, Springer, USA: (1998). 10.1007/978-1-4615-5359-5 [DOI] [PubMed] [Google Scholar]
- 4.Lemp M. A., “Pathophysiology and diagnosis of tear film abnormalities. Surfacing abnormalities,” Int. Ophthalmol. Clin. 13(1), 191–197 (1973). 10.1097/00004397-197301310-00014 [DOI] [PubMed] [Google Scholar]
- 5.Behrens A., et al. , “Dysfunctional tear syndrome: a Delphi approach to treatment recommendations,” Cornea 25(8), 900–907 (2006). 10.1097/01.ico.0000214802.40313.fa [DOI] [PubMed] [Google Scholar]
- 6.Azartash K., et al. , “Pre-corneal tear film thickness in humans measured with a novel technique,” Mol. Vis. 17, 756–767 (2011). [PMC free article] [PubMed] [Google Scholar]
- 7.Hosaka E., et al. , “Interferometry in the evaluation of precorneal tear film thickness in dry eye,” Am. J. Ophthalmol. 151(1), 18–23 (2011). 10.1016/j.ajo.2010.07.019 [DOI] [PubMed] [Google Scholar]
- 8.Efron N., Contact Lens Complications, 3rd ed., Elsevier, Edinburgh: (2012). [Google Scholar]
- 9.Asbell P. A., Lemp M. A., Dry Eye Disease: The Clinician’s Guide to Diagnosis and Treatment, 1st ed., Thieme Medical Publishers, New York: (2006). [Google Scholar]
- 10.Chen Q., et al. , “Ultrahigh-resolution measurement by optical coherence tomography of dynamic tear film changes on contact lenses,” Invest. Ophthalmol. Vis. Sci. 51(4), 1988–1993 (2010). 10.1167/iovs.09-4389 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Young G., Efron N., “Characteristics of the pre-lens tear film during hydrogel contact lens wear,” Ophthal. Physiol. Opt. 11(1), 53–58 (1991). 10.1111/opo.1991.11.issue-1 [DOI] [PubMed] [Google Scholar]
- 12.Nichols J. J., King-Smith P. E., “The effect of eye closure on the post-lens tear film thickness during silicone hydrogel contact lens wear,” Cornea 22(6), 539–544 (2003). 10.1097/00003226-200308000-00010 [DOI] [PubMed] [Google Scholar]
- 13.Mishima S., “Some physiological aspects of the precorneal tear film,” Arch. Ophthalmol. 73(2), 233–241 (1965). 10.1001/archopht.1965.00970030235017 [DOI] [PubMed] [Google Scholar]
- 14.Benedetto D. A., Shah D. O., Kaufman H. E., “The instilled fluid dynamics and surface chemistry of polymers in the preocular tear film,” Invest. Ophthalmol. 14(12), 887–902 (1975). [PubMed] [Google Scholar]
- 15.Doane M. G., “An instrument for in vivo tear film interferometry,” Optom. Vis. Sci. 66(6), 383–388 (1989). 10.1097/00006324-198906000-00008 [DOI] [PubMed] [Google Scholar]
- 16.Fogt N., King-Smith P. E., Tuell G., “Interferometric measurement of tear film thickness by use of spectral oscillations,” J. Opt. Soc. Am. A. 15(1), 268–275 (1998). 10.1364/JOSAA.15.000268 [DOI] [PubMed] [Google Scholar]
- 17.King-Smith P. E., et al. , “The thickness of the human precorneal tear film: evidence from reflection spectra,” Invest. Ophthalmol. Vis. Sci. 41(11), 3348–3359 (2000). [PubMed] [Google Scholar]
- 18.Wang J., et al. , “Precorneal and pre- and postlens tear film thickness measured indirectly with optical coherence tomography,” Invest. Ophthalmol. Vis. Sci. 44(6), 2524–2528 (2003). 10.1167/iovs.02-0731 [DOI] [PubMed] [Google Scholar]
- 19.Wang J., et al. , “Repeated measurements of dynamic tear distribution on the ocular surface after instillation of artificial tears,” Invest. Ophthalmol. Vis. Sci. 47(8), 3325–3329 (2006). 10.1167/iovs.06-0055 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.King-Smith P. E., et al. , “The thickness of the tear film,” Curr. Eye Res. 29(4–5), 357–368 (2004). 10.1080/02713680490516099 [DOI] [PubMed] [Google Scholar]
- 21.Tiffany J. M., “Refractive index of meibomian and other lipids,” Curr. Eye Res. 5(11), 887–889 (1986). 10.3109/02713688609029242 [DOI] [PubMed] [Google Scholar]
- 22.Atchison D. A., Smith G., “Chromatic dispersion of the ocular media of human eyes,” J. Opt. Soc. Am. A. 22(1), 29–37 (2005). 10.1364/JOSAA.22.000029 [DOI] [PubMed] [Google Scholar]
- 23.Leveque G., Villachon-Renard Y., “Determination of optical constants of thin film from reflectance spectra,” Appl. Opt. 29(22), 3207–3212 (1990). 10.1364/AO.29.003207 [DOI] [PubMed] [Google Scholar]
- 24.Debnath S. K., et al. , “Determination of film thickness and surface profile using reflectometry and spectrally resolved phase shifting interferometry,” Int. J. Precis. Eng. Manuf. 10(5), 5–10 (2009). 10.1007/s12541-009-0086-0 [DOI] [Google Scholar]
- 25.Born M., Wolf E., Principles of Optics, 7th ed., Cambridge University Press, UK: (2003). [Google Scholar]
- 26.Craig J. P., et al. , “Refractive index and osmolality of human tears,” Optom. Vis. Sci. 72(10), 718–724 (1995). 10.1097/00006324-199510000-00004 [DOI] [PubMed] [Google Scholar]
- 27.King-Smith P. E., Fink B. A., Fogt N., “Three interferometric methods for measuring the thickness of layers of the tear film,” Optom. Vis. Sci. 76(1),19–32 (1999). 10.1097/00006324-199901000-00025 [DOI] [PubMed] [Google Scholar]
- 28.Wolff E., The Anatomy of the Eye and Orbit, 3rd ed., H. K. Lewis and Co., UK: (1948). [Google Scholar]
- 29.Barer R., Ross K. F. A., Tkaczyk S., “Refractometry of living cells,” Nature 171(4356), 720–724 (1953). 10.1038/171720a0 [DOI] [PubMed] [Google Scholar]
- 30.Creeth J. M., “Constituents of mucus and their separation,” Br. Med. Bull. 34(1), 17–24 (1978). [DOI] [PubMed] [Google Scholar]
- 31.Chen H. B., et al. , “Structure and composition of rat precorneal tear film: a study by an in vivo cryofixation,” Invest. Ophthalmol. Vis. Sci. 38(2), 381–387 (1997). [PubMed] [Google Scholar]
- 32.Dilly P. N., “Structure and function of the tear film,” Adv. Exp. Med. Biol. 350, 239–247 (1994). 10.1007/978-1-4615-2417-5 [DOI] [PubMed] [Google Scholar]
- 33.Nichols J. J., King-Smith P. E., “Thickness of the pre- and post-contact lens tear film measured in vivo by interferometry,” Invest. Ophthalmol. Vis. Sci. 44(1), 68–77 (2003). 10.1167/iovs.02-0377 [DOI] [PubMed] [Google Scholar]
- 34.King-Smith P. E., Hinel E. A., Nichols J. J., “Application of a novel interferometric method to investigate the relation between lipid layer thickness and tear film thinning,” Invest. Ophthalmol. Vis. Sci. 51(5), 2418–2423 (2010).http://dx.doi.org/ 10.1167/iovs.09-4387 [DOI] [PMC free article] [PubMed] [Google Scholar]