A preclinical assay for chemosensitivity in multiple myeloma

Abstract

Accurate preclinical predictions of the clinical efficacy of experimental cancer drugs are highly desired but often haphazard. Such predictions might be improved by incorporating elements of the tumor microenvironment in preclinical models by providing a more physiological setting. In generating improved xenograft models, it is generally accepted that the use of primary tumors from patients are preferable to clonal tumor cell lines. Here we describe an interdisciplinary platform to study drug response in multiple myeloma (MM), an incurable cancer of the bone marrow. This platform uses microfluidic technology to minimize the number of cells per experiment, while incorporating 3D extracellular matrix and mesenchymal cells derived from the tumor microenvironment. We used sequential imaging and a novel digital imaging analysis algorithm to quantify changes in cell viability. Computational models were used convert experimental data into dose-exposure-response "surfaces" which offered predictive utility. Using this platform, we predicted chemosensitivity to bortezomib and melphalan, two clinical MM treatments, in 3 MM cell lines and 7 patient-derived primary MM cell populations. We also demonstrated how this system could be used to investigate environment-mediated drug resistance and drug combinations that target it. This interdisciplinary preclinical assay is capable of generating quantitative data that can be used in computational models of clinical response, demonstrating its utility as a tool to contribute to personalized oncology.

Major Findings

By designing an experimental platform with the specific intent of generating experimental parameters for a computational clinical model of personalized therapy in multiple myeloma, while taking in consideration the limitations of working with patient primary cells, and the need to incorporate elements of the tumor microenvironment, we have generated patient-individualized estimations of initial response and time to relapse to chemotherapeutic agents.

Quick Guide to Equations and Assumptions

Analysis of experimental data

The default function of dose response was written as Equation 1, and the data points were the normalized viability in each ROI at a given time point and drug concentration:

$$\mathit{\text{Viability}}(\%)=100\times \frac{2^{\raisebox{1ex}{$\mathrm{\Delta }T$}\!\left/ \!\raisebox{-1ex}{$\mathrm{T}$}\right.}}{(1+{\left(\frac{Rx}{IC{50}_{Rx}}\right)}^{\mathit{\text{exp}}Rx}\times {\left(\frac{\mathrm{\Delta }T}{IC{50}_{\mathrm{\Delta }T}}\right)}^{\mathit{\text{exp}}T})}$$ (Equation 1)

The goodness of the fit was calculated from a linear regression of the points of the fit equation with the actual observed experimental points using Prism 5 (GraphPad) and quantifying the slope and R² of the regression. The complete Matlab code is available in the Supplementary Material. For each example, two hypotheses were tested: either the sample was composed of one or two sub-populations. When no significant differences were observed in R², the simplest model was used (one population).

Equation 1 is the simplest expression that describes how a homogenous population of MM cells responds to chemotherapy as a function of concentration and exposure time. A growth term was included in the numerator of Equation 1, where Τ is the doubling time, and ΔΤ is the variable representing drug exposure time. Rx represents the drug concentration to which cells are exposed, while IC50_Rx, IC50_ΔΤ, exp_Rx, and exp_T are constants that determine the drug concentration and exposure time that causes death of 50% of the MM cells, and the steepness of the slope of the viability curve, respectively.

The alkylating agent melphalan has a short half-life in media and in vivo of approximately 2h, mainly due to hydrolysis (1). We have observed, however, that in long-term experiments, cells continue to die a week after melphalan exposure (see Results). For this class of drugs, we have created a mathematical expression that encompasses drug half-life, DNA-damage, and DNA-damage-induced cell death (Equation 2).

$$\mathit{\text{Viab}}(\%)=100\times \mathit{\text{Death}}\times \mathit{\text{Growth}}\mathit{\text{Death}}=\frac{1}{1+\frac{{\mathit{\text{CumulDamage}}}^{{\text{exp}}_{IC50}}}{I{C}_{50}}}\mathit{\text{CumulDamage}}(t+dt)=\mathit{\text{CumulDamage}}(t)+{(\int Rxdt)}^{{\text{exp}}_{DMG}}\mathit{\text{Growth}}(t)=2^{\frac{t}{\mathrm{T}\times (1+\mathit{\text{CumulDamage}}(t)\times K_{\mathrm{T}})}}Rx(t)=R{x}_o\times 2^{-\frac{t}{{\mathrm{T}}_{\mathit{\text{Mel}}}}}$$ (Equation 2)

“Death” and “Growth” are the two functions that determine the changes in number of viable cells in a given drug concentration, at a certain time point. “Death” represents the probability that any given cell from a population will die as a function of accumulated DNA damage (“CumulDamage”), which in turn is proportional to the area under the curve (AUC) of drug concentration “Rx” and exposure time “dt”. “expDMG” is an empirical exponent. “Growth” quantifies cell replication, which depends on the drug-free doubling time Τ, the amount of DNA damage “CumulDamage”, and an empirical proportional constant K_T. In other words, DNA damage slows replication(2). The last expression means that the concentration of active melphalan in media, Rx, decays with a half-life Τ_Mel of 2h.

Equation 2 is an empirical expression, with the goal of interpolating the data points across time and concentration dimensions, while recapitulating known mechanisms of melphalan toxicity and degradation. It is not, however, the only possible expression possible, and it may not properly compute the viability in concentrations or exposure times significantly higher than the experimental conditions.

Computational modeling of therapy

In this computational model, one or more sub-populations are represented, each with a size, a doubling time, and a level of sensitivity to the chemotherapeutic agent tested. Carrying capacity, which is the maximum theoretical growth rate of the entire tumor burden, was estimated from the labeling index commonly observed in MM patients (~1–3%). Intra-tumoral competition was modeled by an equation that determines that bigger populations have higher chance of replicating than smaller ones (Equation 3), a dynamic similar to genetic drift.

$$N_i(t+dt)=N_i(t)\times {(1+{\left(\frac{Rx}{IC{50}_{Rxi}}\right)}^{\text{exp}RXi}\times {\left(\frac{dt}{IC{50}_{\mathrm{\Delta }Ti}}\right)}^{\exp Ti})}^{-1}\times \left\{\right[{(1+LI)}^{\frac{dt}{\mathrm{T}i}}-1]\times \frac{N_i(t)}{\sum N_j(t)}+1\}$$ (Equation 3)

Equation 3 describes how the size of a sub-population within the tumor burden (N_i) changes within an interval of time (dt) in response of drug-induced cell death induced by exposure to a drug at the concentration Rx for the interval of time dt. The surviving cells may replicate at a rate determined by their labeling index (LI), the duration of their cell cycle (Τ), and the percentage that the sub-population represents in the total tumor burden.

Bortezomib concentration in blood is characterized by a peak of ~100nM, followed by a sharp decrease, and a stable concentration of ~1–3nM between 2 and 192h post IV administration (1.3mg/m²) (3, 4). The in vitro chemosensitivity data from patients 8, 11, 12, and 13 parameterized the computational models of clinical response for each of these patients in a hypothetical single-agent bortezomib regimen, in which the bone marrow concentration would remain constant at 3nM.

As a preliminary validation of the correlation between in vitro and in vivo chemosensitivity, we have used computational models parameterized by assays with the human MM cell line NCI-H929 to estimate the response to bortezomib treatment of a sub-cutaneous mouse model, treated with 1mg/kg bortezomib bi-weekly(5). Pharmacokinetic studies have shown that such IV injections in mice cause a peak blood concentration of ~0.5nM, and ~0.4nM at 48h. For these simulations, we consider a stable 0.4nM concentration of bortezomib in the bone marrow of these mice along the treatment. NCI-H929 cells have a cell cycle of approximately 24h, and in the subcutaneous model the tumors have a doubling time of approximately 3.5 days, indicating that in this animal model, approximately 20% of H929 cells are actively replicating at a given time, which was used as labeling index in the simulations.

Introduction

The purposes of pre-clinical systems range from early identification of compounds with anti-cancer activity, estimation of patient-specific clinical response, or the discovery of novel targetable cellular mechanisms(6, 7). All available systems have strengths and limitations: in vitro assays using cell lines are scalable, reproducible and inexpensive, but cell lines are significantly different from their originating tumors(8), and the tumor microenvironment’s effects are often absent in these assays. Animal models include more realistic elements such as drug pharmacokinetics and influence of the tumor microenvironment, but they often rely on cell lines, require long-term experiments, and carry significant financial cost. Irrespective of the pre-clinical model used, the data generated cannot be directly ported into clinical estimations without the help of an adequate computational framework.

Computational modeling has long been used to study the dynamics of tumor response to therapy, as well as emergence of drug resistance(9–11). These theoretical models are powerful tools for analyzing complex interactions like the tumor-host-therapy system, and could, in a near future, become decision-support systems for oncologists, making personalized oncology a possibility(12). The Achilles’ heel of such models, however, is the reliability of the experimental data used to parameterize them. More often than not, these computational models are parameterized by data from literature, in many cases from experiments that have been performed at incompatible conditions.

We propose that pre-clinical assays, specifically designed to generate data to parameterize such computational models, would significantly advance the field. Such assays, however, should comply with minimum requirements: (a) compatibility with patient primary cancer cells; (b) recapitulate the tumor microenvironment, namely extra-cellular matrix and stroma; (c) be non-destructive, so longitudinal studies can be performed, incorporating the temporal dimension; (d) require as few cells per experimental condition as possible, so each patient sample could be tested against a panel of chemotherapeutic agents, in different environmental conditions; and (e) the data generated should result in testable clinical predictions, such as the depth of response and/or progression-free survival (PFS).

Four decades ago, Salmon and collaborators(13) proposed an in vitro method for estimation of clinical response of cancer patients based on the capacity of primary cancer cells to form colonies at physiologically reachable chemotherapy concentrations. The main limitation of these early assays, however, was the small number of patient samples that were capable of forming colonies under control conditions. With a cloning efficiency between 0.001% and 0.1%, the growth of colonies in vitro was a challenge comparable to surviving the chemotherapeutic insult itself. Consequently, these restrictions limited the number of drugs, concentrations and time points that could be studied for a single patient(14), even in more recent models(15). Finally, the outcome of these assays were often dichotomized, in other words, either a patient was “sensitive” or “resistant” to the drug, but no information was provided regarding duration of response and time to relapse. Given that in many cancers the overall survival is more dependent on the duration of the response than on its depth(16, 17), the application of these early assays as predictive biomarkers was somewhat limited.

Similar to Leonardo Da Vinci’s “aerial screw”, designed in the 15^th century, which only came to fruition as the helicopter five centuries later, we propose that Salmon’s drug sensitivity assay was hindered by technological limitations of its time, not by an inherent design fault. Building on this pioneering work, we here describe a novel approach for pre-clinical assessment of drug efficacy. We apply this method to multiple myeloma (MM), an incurable plasma cell malignancy in which cancer cells uncontrollably proliferate in the bone marrow. Adhesion to bone marrow’s extracellular matrix or stroma has been shown to confer de novo multi-drug resistance (environment mediated drug resistance, EMDR)(18, 19).

The here described system combines a microfluidic dose-response platform, for in vitro screening of drugs, and a computational model of clinical response. The in vitro component consists of a 3D reconstruction of the bone marrow microenvironment, including primary MM cells, extracellular matrix, and patient-derived stroma and growth factors. Live microscopy and digital image analysis are used to detect cell death events in different drug concentrations, which are used to generate dose-response surfaces. The in silico component is an evolutionary computational model designed to simulate how a heterogeneous population of cancer cells responds to therapy. From the in vitro data, the model identifies the size and chemosensitivity of sub-populations within the patient’s tumor burden, and simulates how the tumor would respond to the drug(s) in physiological conditions in a clinical regimen.

The main innovations of this platform are: (a) small number of cancer cells required (1,000–10,000 per experiment); (b) assessment of drug efficacy in different environmental conditions (collagen+/−patient stroma+/−patient-derived growth factors/cytokines), allowing quantification of innate and environmental drug resistance; (c) only bright field imaging is used, thus no toxicity from viability markers; (d) continuous imaging provides drug effect as a function of concentration and exposure time; and (e) the integration between in vitro and computational evolutionary models, to estimate clinical outcome: not only the initial response, but also progression-free survival (PFS), a more relevant clinical endpoint for assessment of drug efficacy(16).

In this manuscript we describe the experimental and computational platforms, the results with human myeloma cells lines, and how they compare with literature data. We also describe preliminary experiments with patient primary cells, and how these results could be used in the estimation of clinical efficacy of experimental drugs, or personalized medicine (the right drugs and the right regimen for each patient).

Materials and Methods

Cell lines

The human myeloma cell lines RPMI-8226, HS-5/GFP-labeled, NCI-H929 and 8226/LR-5 were kindly provided by Dr. William Dalton’s laboratory. The 8226/dsRed2 cell line was stably transfected with the fluorescent protein dsRed2. All cells were maintained in culture with RPMI 1640 (Gibco) media supplemented with 10% heat inactivated fetal bovine serum (Life Technologies) and 1% penicillin–streptomycin solution (Invitrogen), in incubators at 5% CO₂, 37°C. Melphalan-resistant 8226/LR-5 cells were maintained in 5µM melphalan in medium, and cultured in drug-free medium for 2 weeks prior to experiments.

Primary cancer cells

We investigated the in vitro response of cancer cells from 7 MM patients in the clinical trial MCC# 14745 conducted at the H. Lee Moffitt Cancer Center and Research Institute, as approved by the Institutional Review Board. The medical records were de-identified and only the following clinical-relevant information was reviewed: (A) treatment administered (chemotherapeutic agents, doses and schedule) prior to biopsy; (B) cytogenetics; (C) blood and urine electrophoresis results. Patients in trial MCC# 14745 received standard-of-care treatment, and consented to provide an extra sample of bone marrow aspirate during a routine biopsy. These aspirates were used in the in vitro assays further described. After informed written consent, bone marrow aspirates were obtained from multiple myeloma patients either newly diagnosed or with refractory disease. Processing of bone marrow aspirate and selection of MM cells is described in Supplementary Material. MM cells were seeded into the Ibidi µ-slide Chemotaxis 3D device under experimental culture conditions (described below) within 4 hours of each patient biopsy.

In vitro procedures

Drugs

In this work, the following chemotherapeutic agents were tested: bortezomib (acquired from Selleckchem), melphalan (from Sigma), and FAM-HYD-1 (kindly provided by Dr. Hazlehurst).

In vitro dose response assays in 3D microfluidic chambers

Commercially available 3D cell culture slides (µ-slide Chemotaxis 3D Ibitreat from Ibidi, LLC) were gas and temperature equilibrated at 37°C, 5% CO₂ overnight prior to cell seeding. Each slide is comprised of three separate chambers each with a 1mm wide, 50µm high cell-viewing chamber that holds a volume of 6µL. It is connected to two 65µL reservoirs along both sides. Linear chemical gradients form across the cell chamber via passive diffusion. Aliquots consisting of 6.67µL 10× MEM (Life Technologies), 6.67µL deionized H₂O, 3.33µL 7.5% sodium bicarbonate solution (Life Technologies), and 16.67µL 1× RPMI 1640 (Life Technologies), were premixed and stored at 4°C prior to experiments, as per manufacturer (Ibidi) instructions. 50µL of 3.1mg/mL Bovine collagen type I (Advanced BioMatrix) was added at time of seeding. 16.67µL of cells suspended in RPMI 1640 were mixed into the collagen/media mix to a final volume of 100µL in 1.5mg/mL bovine collagen I (6-fold dilution of RPMI 1640 cell suspension). 6µL of this cell/matrix mix were used to load each viewing chamber. For cell lines in single culture or mixed culture, the final concentration of cells was 3×10⁶ myeloma cells/mL. For patient primary cells, the densities were 7×10⁶ cells/mL for MM (CD138+), and 1×10⁶ cells/mL for mesenchymal cells. These cell densities were optimized to better reflect physiological cell density, and maximize the number of cells in the observation chamber, while still maintaining enough separation to allow the individual identification of cells. Cell lines were seeded at lower density to account for their larger size and faster replication. The interval between mixing collagen with cells and media, and seeding the chambers was kept below five minutes at ambient temperature to minimize collagen polymerization. After seeding, an additional 15 minutes at room temperature allowed adherent cells (HS-5 or patient stroma) to sink to the bottom of the 3D chamber and keep the same focal plane for subsequent live imaging. Slides were then incubated at 37°C, 5% CO₂ for 1 hour. Collagen polymerization was checked by visual inspection of fiber formation on an inverted phase contrast microscope with a 20× objective lens. After gelation, reservoirs on each side of the slide were filled with 65µL culture media. 16.25µL of 4× drug in culture media was dropped onto a filling port on the left reservoir and then an equal volume was immediately drawn out of the other filling port. Slides were then placed into incubator for live imaging. For each experiment, there was a control with no drug added, which was used to detect spontaneous cell death. For single culture experiments, chemotherapy was added 2–4h after cell seeding. For co-culture experiments with adherent stroma (HS-5 or patient stroma), drugs were added 24h later to ensure stroma adhesion.

Continuous versus pulsed exposure

In experiments with continuous exposure, the drug was maintained in media for the duration of the experiment. If this duration exceeded 48h, the media on both reservoirs was completely removed, and replaced by fresh media, to which drug was added as previously described (16.25µL at 4× concentration). In pulsed exposure experiments, the media on both reservoirs was completely removed, and replaced by fresh media at the end of the pulsed exposure.

Imaging

Image acquisition

Two different models of fluorescence microscopes were used for the experiments here described: the first, JULI (Digital Bio), is a portable fluorescence microscope with bright field and red fluorescence capacities (ex/em 630nm/660nm), which was maintained inside a standard incubator for the duration of the experiments. The second platform was the EVOS FL (AMG), a bench top fluorescence microscope (red channel ex/em 531nm/593nm), which required the use of a stage-top heating stage/incubator (Ibidi), which maintained the cells at 37°C, 5% CO₂, and 80% humidity. For the experiments here described, images were acquired every 5-minute intervals. In experiments where the red fluorescent 8226/dsRed2 cell line was tested, or the cell-death molecular probe ethidium homodimer-1 (EthD-1) was used, both bright field and red fluorescent channels were imaged, the first for changes in cell morphology and membrane motion, and the second for loss of innate fluorescence or activity of EthD-1, respectively.

Quantification of drug concentration over time within microfluidic device

In order to quantify the shape and stability of the drug gradient in the microfluidic device, we used a fluorophore-conjugated of the peptide HYD-1 (1.5kDa) within the dose-response assay, a 3D gel matrix consisting of 1.5mg/ml bovine collagen I with RPMI1640/MEM media was placed into the culture chamber of the Ibidi microfluidics device. After 45 minutes incubation at 37°C, reservoirs were filled with RPMI1640 media 10% heat inactivated FBS, 1% penicillin–streptomycin. FAM-HYD1 was diluted into media before replacing 1/4th of the volume in the left reservoir with fluorescent drug solution (1/10 of stock). Fluorescence within the culture chamber was imaged in an EVOS FL microscope using the GFP filter (ex/em 470nm/525nm, 5× objective) with heated stage and gas incubation (37°C, 5% CO₂). Images were acquired at 1-minute intervals for 24 hours.

Digital image analysis

With a stable drug gradient established across the main channel of the microfluidic slide, we arbitrarily divided the observation channel into five sections, or regions of interest (ROI), each with an average drug concentration of 100%, 80%, 60%, 40% and 20% of the concentration in the drug reservoir, respectively. Sectioning the channel into five areas was a compromise between a minimum number of cells in each area, and the rounding due to the averaging of the drug concentrations across each section. Dose response was quantified with a macro developed for the software ImageJ (http://rsbweb.nih.gov/ij), further described. As discussed in the Results section of this manuscript, membrane-impermeable probes for detection of cell death, such as EthD-1, present a significant variation in the time for fluorescence acquisition after death in cell lines or patient samples. To avoid this confounding effect, we have developed a novel approach that identifies cell death based of motion of the membrane, described below.

Assessment of cell viability through membrane motion detection

We have observed that, although it was not possible to clearly discern a dead from a live cell based on the morphology in the bright field of a single image, all live cells suspended within the collagen matrix had observable membrane motion or shape changes, between two images taken in a 5-minute interval. These morphological changes abruptly stopped prior to cell death, indicating that this feature could be exploited as a marker for cell death. We created a macro for the open source software ImageJ using the plugins TurboReg (20) and RunningZProjector (http://valelab.ucsf.edu/index.html). The macro quantifies the amount of cell membrane motion in the different regions of interest, and writes a file with this information for each frame, or time point. The source code of the macro is provided in the Supplementary Material. Briefly, the macro loads the stack of bright field images taken at 5-minute intervals, and aligns them using the plugin TurboReg. This action removes translational motion, such as sliding of the microfluidic chamber, as well as vibration. Next, the native ImageJ “background subtraction” function was used with parameters “rolling ball radius=1 pixel” and “sliding parabolic” (21). Background subtraction served to normalize image sequences across different experiments and/or microscopes used to image the chambers, making cells appear as bright spots against a uniform dark background. Motion and small variations in cell membranes were detected using the plugin RunningZProjector. It detects the maximum pixel intensity across a 6-frame/slice interval, corresponding to 30 minutes. The original image was then subtracted from the maximum pixel intensity projection, resulting in an image where actively moving membranes appear as bright rings. ImageJ’s “Gaussian blur” filter was used to convert these bright rings into spots that cover the entire cell, and produce the overlaid images shown in this manuscript.

Validation of motion detection algorithm through fluorescence

Different fluorescent-labeling agents for cell viability were tested as live-imaging approaches for response to chemotherapy. However, cytotoxicity, photo bleaching, intercellular variability of delay between cell death and signal detection, and incomplete representation of viable/apoptotic/necrotic cell states added noise to the assay. A multiple myeloma cell line was stably transfected with dsRed2 (8226/dsRed2), and used as a reference to visually detect the cytotoxic effect of drugs through loss of red fluorescence. RFP expression is an intrinsic marker for these cells: live cells will quickly loose fluorescence upon cell death due to membrane burst accompanied by release of cytoplasmic components, including the fluorescent protein.

Validation of motion detection algorithm through bioluminescence

NCI-H929 cells were seeded in 96-well plates in culture media or in a 3D collagen matrix with culture media added on top of the cell/collagen layer. In wells without collagen, 1.5×10⁵ cells were resuspended in 50µL of media for a final density of 3×10⁶ cells/mL. To more closely resemble microfluidic assay conditions, 1.5×10⁵ cells were suspended in 30µL of 1.5mg/mL collagen matrix and were left to polymerize at 37°C for 1 hour. 20µL of media was then added as a separate phase on top of the cell/collagen layer. Melphalan was serially diluted in 2-fold steps to a final concentration range of 100 µM to 1.56 µM in 7 rows. The same procedure was performed for bortezomib to final concentrations of 20 nM to 0.31 nM. All conditions and controls were performed in triplicate. After 24 hours of continuous drug exposure at 37°C and 5% CO₂, 50 µL CellTiterGlo was added to each well and the plates were placed on an orbital shaker at room temperature for 10 minutes. 20 minutes later, bioluminescence was measured at ambient temperature on a microplate reader. Percent cell viability was defined as luminescence normalized to controls at 24 hours.

Analysis of experimental data

The quantification of the dose response of the cells in the experiment used Matlab’s (MathWorks) function lsqcurvefit, which finds the coefficients that minimize the distance between a function and a set of data points. Details on the fitting procedure and equations used are presented in the Quick Guide to Equations and Assumptions.

Computational modeling of therapy

As a proof of principle, to exemplify the application of these in vitro chemosensitivity assays in estimating patient response to therapy, we have used a computational model, previously described(22), to simulate a hypothetical single-agent bortezomib regimen in an animal model (s.c. NCI-H929 in SCID mouse), and for four patients whose MM cells’ sensitivity to bortezomib were tested in vitro. Implementation of the computational model of therapy is presented in the Quick Guide to Equations and Assumptions.

Results

Characterization of shape and duration of drug gradient

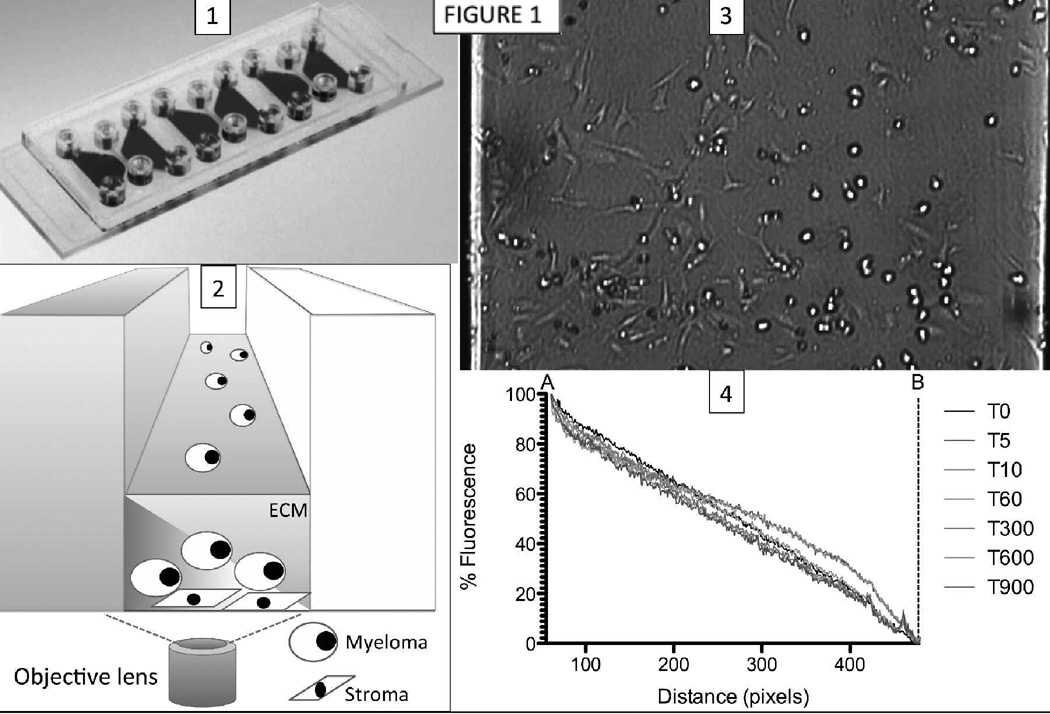
The first step of validating the in vitro platform was to determine the stability, and also the duration of any transients during the formation of the drug gradient across the observation chamber. For this purpose, we used a conjugate of the fluorescent molecule fluorescein (FAM) and the 1.5kDa peptide HYD-1, an experimental drug with direct toxicity to MM cells (23). We used live imaging to quantify the fluorescence in images taken at 1-minute intervals during 18h (Figure 1). The fluorescent signal gradient was stable for the interval of the experiment, and the transient time for its formation was shorter than the period between drug injection in the slide and start of imaging (~5–10’).

Figure 1. Schematic view of microfluidic assay used for in vitro reconstruction of bone marrow.

(1) Each microfluidic chip contains three chambers, each of them composed of two side reservoirs, and one center observation chamber. Myeloma and stromal cells are loaded in the observation chamber simultaneously, resuspended in collagen. Overnight, the matrix gellifies, and stromal cells adhere to the bottom of the chamber and stretch. (2) One of the side reservoirs is filled with medium with a chemotherapeutic agent (left), while the other is filled with standard growth medium (right). The diffusion of the chemotherapeutic agent from one reservoir to the other creates a stable gradient across the observation chamber. (3) The observation channel with the human MM cell line NCI-H929 and adherent bone marrow derived stromal cell line HS-5 is shown in bright field under a gradient of the necrosis-inducing peptide HYD-1. Note that MM cells on the left (higher drug concentration) have died and became dark spots, while cells on the right (lower drug concentration) are still alive. (4) A gradient of the fluorescent conjugated peptide FAM-HYD1 was established, and fluorescence quantified across the channel during 18h. Normalization and re-scaling to the minimum and maximum concentration within the observation channel confirm the linear stable gradient during the 18h-window of experiment.

Loss of membrane motion is a reliable maker of cell death

A novel algorithm for detection of cell membrane motion was necessary to detect cell death in patient primary cells, due to the significant variation of the delay between cell death and membrane permeabilization, and acquisition of fluorescence from molecular probes. Supplementary Figure 1 depicts the delay between the detection of cell death using the motion-detection algorithm, and loss of fluorescence in the stably transfected cell line 8226/dsRed2. Supplementary Figure 2 exemplifies the delay of acquisition of the molecular probe Ethidium homodimer-1 (EthD-1) red fluorescence in NCI-H929 cells.

Effect of the proteasome inhibitor bortezomib

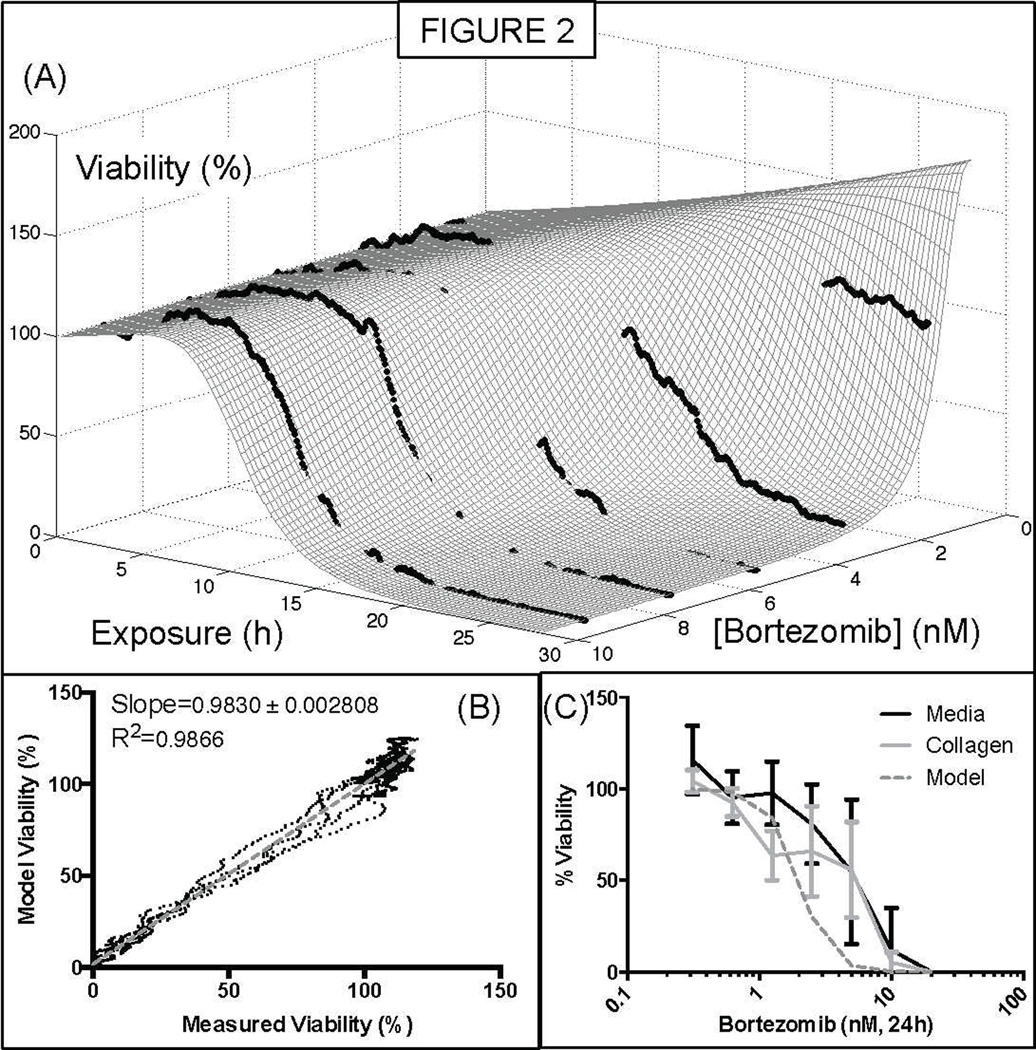
The cell line NCI-H929 was exposed to a stable gradient of bortezomib (maximum concentration 10nM) for 24h, and a dose-response surface was created (Figure 2, A). According to these results, the bortezomib concentration that would lead to a 50% reduction in the number of live cells after 24h, compared to the initial time point, was ~2.5nM. The concentration that would lead to a 50% reduction in the number of live cells, compared to the control at 24h was ~1.9nM. The same cell line was seeded in a 96-well plate, in suspension or in collagen, and cell viability was measured using the ATP-based assay CellTiter-Glo (Figure 2, C). The Pearson test produced “r” values of 0.8905 and 0.8704 (P values 0.003 and 0.0049) for the correlation between the model and suspension, and collagen results, respectively.

Figure 2. Quantification of sensitivity of the human myeloma cell line NCI-H929 to the proteasome inhibitor bortezomib.

The microfluidic assay described in this project generates a series of measurements corresponding to cell viability at combination of exposure time and drug concentration. These data points in turn are fit to the mathematical expression of dose response, Equation 1. (A) Sensitivity of the human myeloma cell line to the proteasome inhibitor bortezomib. (B) Goodness of fit of the mathematical model to the 1,670 data points. (C) Comparison of viability measurements at 24h between the mathematical model and a standard ATP-based bioluminescent assay, with NCI-H929 cells in suspension in media or in collagen, using a standard 96-well plate.

Quantification of melphalan innate resistance in cell lines in single culture

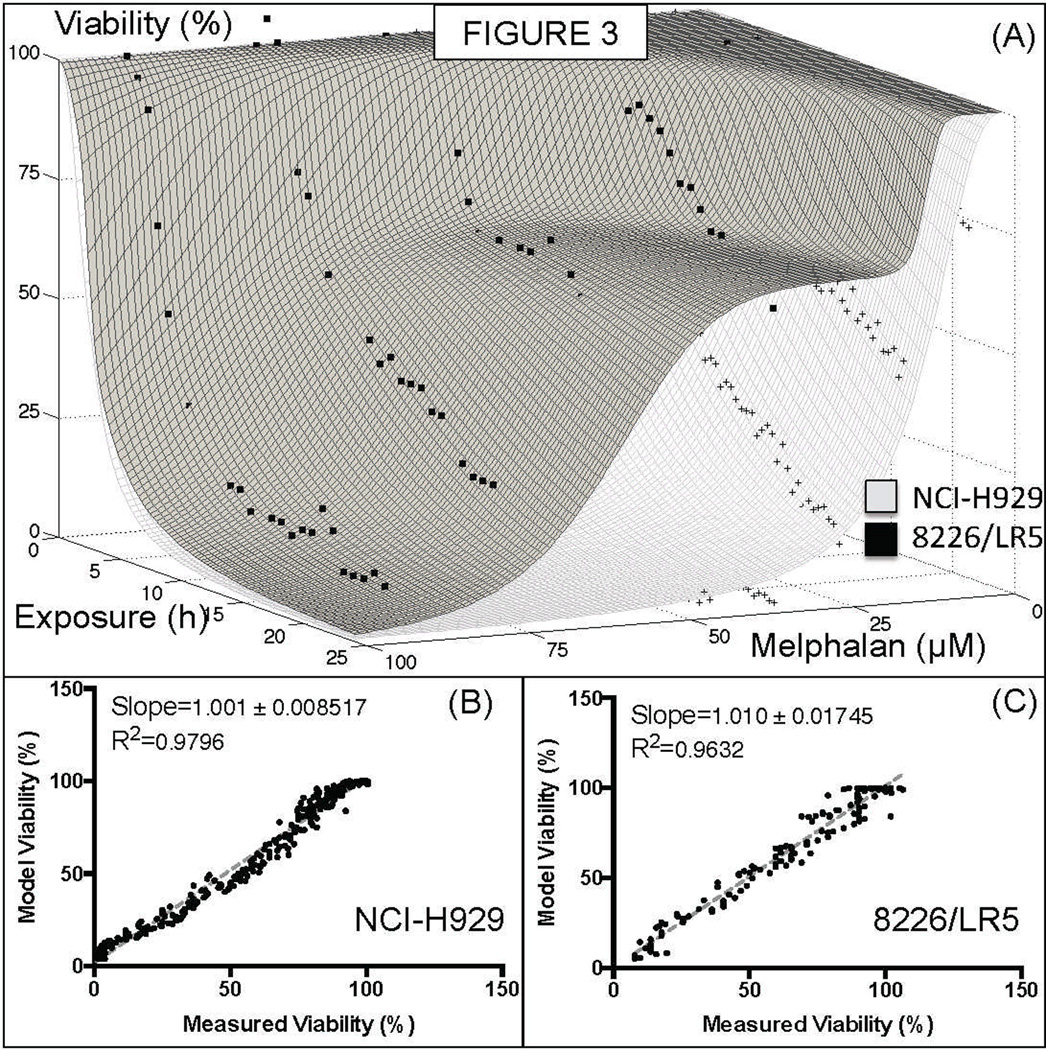
The melphalan sensitive and resistant cell lines NCI-H929 and 8226/LR5 were exposed to stable gradients of melphalan for 24h (highest concentrations of 50µM and 100µM, respectively) and chemosensitivity was quantified. The analysis of 8226/LR5 detected a sub-population of sensitive cells (~30%, Figure 3A), indicating that this cell line is actually heterogeneous, a possible explanation for the loss of resistance commonly observed when these cells are maintained in melphalan-free medium for many weeks(24). Melphalan concentration that induced 50% of death in cells (EC50) for 24h continuous exposure was ~50µM for 8226/LR5, and ~12µM for H929. Long-term exposure to lower, more physiological doses (10–20µM) of melphalan, however, indicated that, although all melphalan had been hydrolyzed in the first 24h in media, cell death continued to occur after 6 days of drug exposure (Supplementary Figure 3).

Figure 3. Intrinsic chemoresistance to melphalan.

The human MM cell lines 8226/LR5, selected by continuous exposure to melphalan, and NCI-H929 were exposed for a 24h continuous stable of gradient of melphalan in the microfluidic chamber. While the cell line NCI-H929 was fit to a single population, the 8226/LR5 cell line was better fit by a two-population curve, with approximately 70% of resistant cells and 30% of sensitive. This result indicates that the loss of chemoresistance of 8226/LR5 cells in absence of melphalan might be due to heterogeneity in this population.

Quantification environment-mediated melphalan resistance

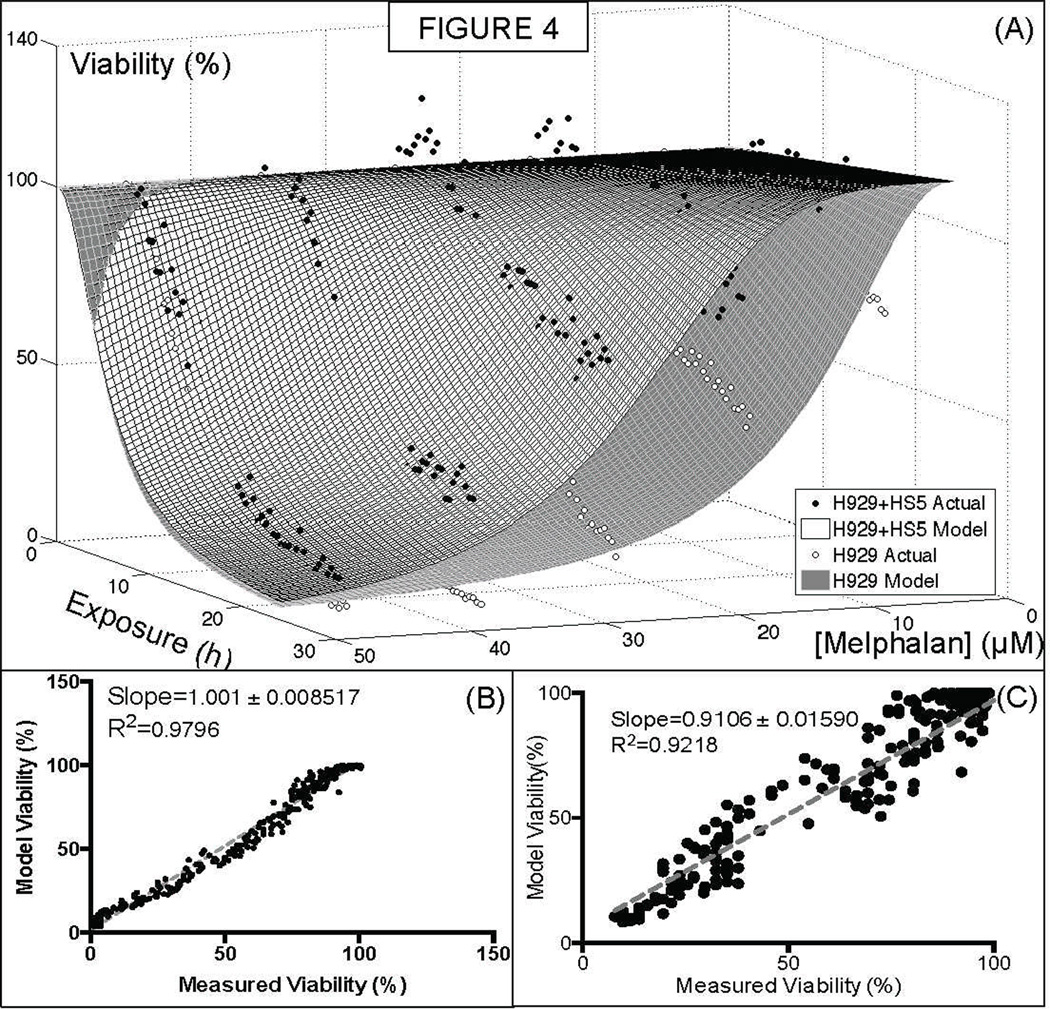
Cell adhesion mediated drug resistance (CAMDR) is believed to be a major cause of minimal residual disease in multiple myeloma (18). This mechanism is caused by direct MM-stroma cell adhesion, by paracrine loops of soluble factor secretion, or MM-extracellular matrix adhesion. In order to quantify the importance of MM-stroma adhesion under physiological conditions (high density, in presence of ECM), the MM cell line NCI-H929 was co-cultured with the bone marrow derived stromal cell line HS-5/GFP. A significant shift towards resistance was observed at later time points (~24h), and was most expressive around the concentration of 20–30µM (Figure 4).

Figure 4. Effect of Cell Adhesion Mediated Drug Resistance in the MM cell line NCI-H929 treated with melphalan.

(Top) The co-culture of the NCI-H929 human MM cell line with the human bone marrow derived stromal cell line HS-5 confers increased resistance to melphalan. Melphalan concentration and exposure required in order to reduce viability in 50% (kR and kT, respectively) increase from 28 to 40µM and 12 to 15h, respectively. (Bottom) Linear regression of fit and actual experimental points for both experiments.

Continuous versus pulsed exposure to drugs

To exemplify the study of continuous versus pulsed exposure to drugs, two chambers with NCI-H929 cells were exposed to bortezomib for 24h. In one the medium was replaced by drug-free medium, while in the other fresh medium with bortezomib was added. Being a reversible proteasome inhibitor, the results suggest that bortezomib-induced death stops upon drug withdrawal (Supplementary Figure 4), unlike melphalan (Supplemental Figure 3).

Melphalan chemosensitivity of primary MM cells in single and co-culture

From the 17 patient samples obtained so far in this protocol, the first 10 were used for development and optimization of the platform. The results of the 7 others are here described. We have exposed CD138+ sorted primary MM cells from patient 14, a newly diagnosed patient, for 48h to a stable gradient of 25µM melphalan in single and co-culture, with patient-derived stroma. As shown in Figure 5, adhesion to stroma significantly increased the survival of MM cells, shifting the 48h EC50 from 2µM in single culture to 12µM in co-culture. This effect could be circumvented by combination of a proteasome inhibitor at sub-lethal levels(25) (Figure 6 and Supplementary Video 1).

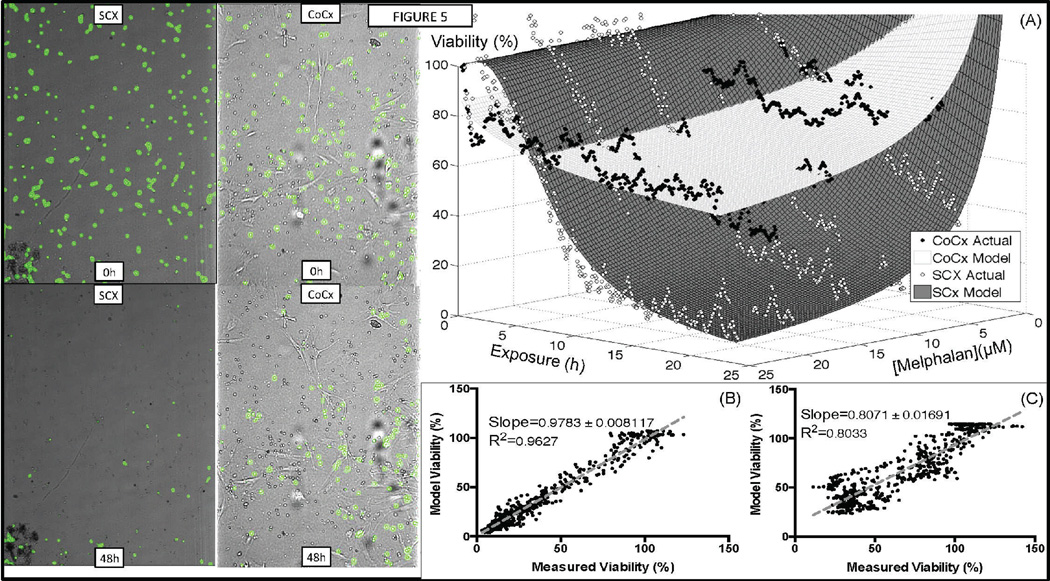
Figure 5. Primary MM cells in co-culture with patient stroma are significantly more resistant to melphalan.

Patient 14 is a newly diagnosed patient. MM cells were sorted (CD138+) from bone marrow aspirate, and seeded into microfluidic chamber in single (SCX, 0h) or co-culture with patient stromal cells (CoCx, 0h). Digital image analysis identifies live cells and pseudo-colors them as green. A stable linear gradient of melphalan was established across observation channel: 25µM on the left, 0µM on the right, and cells were imaged every 5 minutes for 48h. After 48h, almost all MM cells are dead in single culture (SCX, 48h), while a significant number of MM cells are still alive in co-culture with stroma (CoCx, 48h). (A) Dose response surfaces built using measurements of viability in single (SCX) and co-culture (CoCx). (B) Goodness of fit of dose response surfaces (model) and actual data points for single culture, and (C) co-culture.

Figure 6. Quantification of bortezomib-induced EMDR circumvention in primary MM cells.

Patient 14 is a newly diagnosed patient. MM cells were sorted (CD138+) from bone marrow aspirate, and seeded into microfluidic chamber in single and co-culture with adherent stromal cells (CD138−). (A) In single culture, MM cells are significantly more sensitive than in co-culture (B). A dose-response assay with bortezomib indicated that 1nM was the highest concentration that did not cause MM cell death (C) during the 24h-period. By combining a stable gradient of melphalan, with a uniform concentration of bortezomib, the chemosensitive phenotype is restored in co-culture (D).

Melphalan and bortezomib chemosensitivity among MM patients

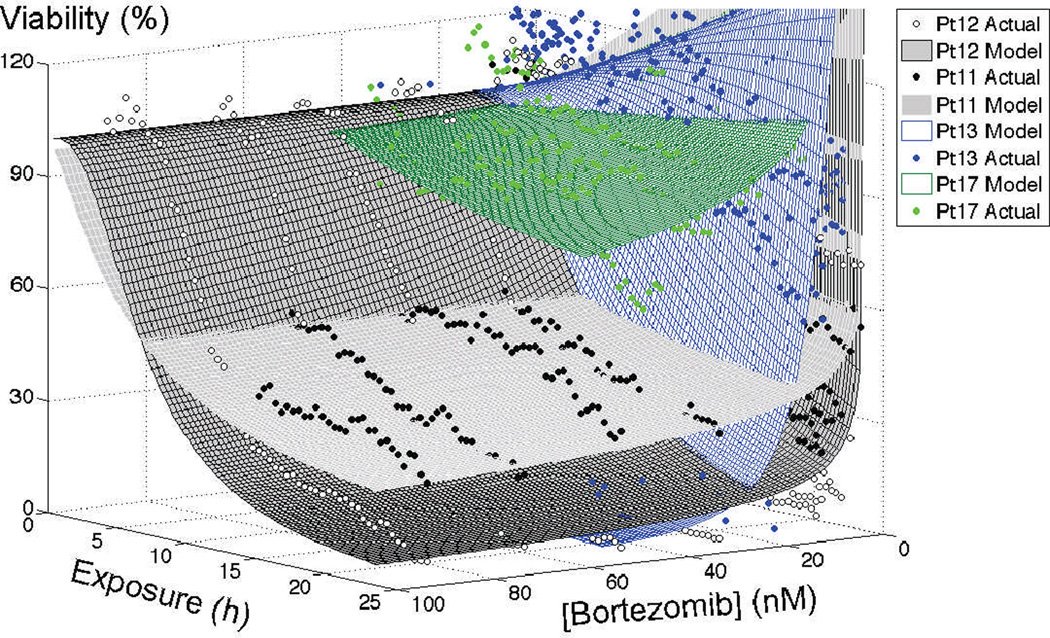
Supplementary Figure 5 depicts the in vitro chemosensitivity of three MM patients to melphalan in single culture: patient 14, patient 11 (smoldering myeloma), and patient 12 (relapsed after bone marrow transplantation). The EC50s at 24h exposure were 4µM for patients 14 and 12, and 1µM for patient 11. However, the percentage surviving cells at 20µM, a more physiological concentration of high-dose melphalan treatment, was 30% for patient 12, 11% for patient 14, and 4% for patient 11. Figure 7 represents bortezomib chemosensitivity of patients 11, 12, 13 (newly diagnosed) and 17 (smoldering myeloma). For patients 11 and 12, EC50 after 24h continuous exposure was below 2nM, however, at higher concentrations, MM cells from patient 11 were significantly more resistant: 30% live cells at 50nM bortezomib for patient 11, and ~8% for patient 12. 24h EC50 for patient 13 was ~10nM, while EC50 was not reached with the sample from patient 17.

Figure 7. In vitro response of primary MM cells to bortezomib in single culture 3D collagen matrix.

Patient 11 was a smoldering/standard-risk patient, and thus never previously treated with bortezomib. Patient 12 was a relapsed/standard-risk patient previously treated with bortezomib-based regimens, and high-dose melphalan followed by bone marrow transplantation. Patient 12’s bortezomib-based induction regimen (bortezomib/lenalidomide/dexamethasone) occurred 3 years prior to the biopsy used for this in vitro assay. Patient 13 was a newly diagnosed/high-risk patient, while patient 17 was a smoldering myeloma patient.

Extrapolation of in vitro data into in vivo and clinical response

By parameterizing Equation 3 with values obtained from fitting Equation 1 to the in vitro dose response data, it is possible to simulate how a tumor mass would respond to a therapeutic regimen. As an example, the sub-cutaneous mouse model SCID (severe combined immunodeficient), when implanted with the cell line NCI-H929, develops a tumor that grows 45-fold in 20 days (26). When treated with 1mg/kg bortezomib twice a week, the tumor growth is reduced, and tumors are 20-fold bigger at day 20 than at implantation(27). From the bortezomib in vitro chemosensitivity assay with the cell line NCI-H929 (Figure 2), the parameters from Equation 3 were: IC50_Rx=10.35nM, IC50_ΔT=10.38h, exp_RX=2.7, and exp_T=7.1. Supplementary Figure 6 depicts the computational simulation of the tumor growth under control conditions, under a bi-weekly treatment with 1mg/kg of bortezomib (which leads to a stable blood concentration of 0.4nM(28)), and a hypothetical regimen where mice received a pulsed therapy with the same AUC (area under the curve), with bi-weekly injections of bortezomib every other week (therapy holidays). The simulated tumor would have increased 53.4-fold in control conditions (Pearson r=0.9762), 18-fold in standard bortezomib treatment (Pearson r=0.9869), and 5-fold in the hypothetical pulsed regimen. The same approach was used to simulate the response of patients 11, 12, 13, and 17 to a single agent regimen of bortezomib (1.3mg/m², Supplementary Figure 7). In this regimen, plasma concentration stabilizes at ~1nM(4), and according to simulations, would achieve complete response in patients 11 an 12, relapse in patient 17, and no response in patient 13.

Discussion

In this work we have described an interdisciplinary platform to study pre-clinical drug activity in primary MM cells. First, MM cells are embedded in a microfluidic chamber that recapitulates the bone marrow microenvironment, including high cell density, extracellular matrix and patient-derived stromal cells. A linear and stable drug gradient is established across the chamber, which is then imaged sequentially in bright field. A digital image analysis algorithm detects live MM cells by the motion of cell membrane: upon death this activity ceases. The measurements of viability, at different concentrations and time points, are fit to mathematical models of chemosensitivity. These models can represent one or multiple sub-populations, and can be empirical or mechanistic. The data from these experiments can thus be used to parameterize mathematical models to simulate clinical outcome.

This platform overcomes some major limitations of pre-clinical assays using primary cancer cells. It has long been known that extracellular matrix and stroma are major components of chemoresistance in many tumors. However, the inclusion of these elements significantly increases the complexity of dose response assays, often requiring the separation between cancer and stromal cells, by matrix digestion and/or flow sorting(29). Also, viability assays are often destructive or cytotoxic, if carried for long periods of time, limiting the information acquired in the temporal dimension. In the here described assay, MM cells, stroma and matrix are never separated, and no cytotoxic agents are used to determine cell viability, thus allowing longitudinal studies of drug activity without interfering with the microenvironment.

In cancers such as MM, where a few million cells are obtainable per patient biopsy, it is important to minimize the number of cells per experimental condition, which is in the order of 1,000–10,000 cells in this assay. The poor clonal efficiency of MM cells, as well as their spontaneous death in vitro(6), suggest that experiments with these samples be performed in the first few days after the biopsy. By studying the effect of long-term exposure and drug withdrawal in human MM cell lines, we have created mechanistic theoretical models of the drug activity(2). Once a model is generated for a particular drug, the data from patient samples are used to parameterize and extrapolate the response for longer periods of time.

As shown for bortezomib-induced melphalan sensitization in co-culture (Figure 6), this system can be used to study drug interactions(30). The addition of the time dimension, instead of fixed time points, would allow the study of time-shifted drug combinations, such as, for instance, nuclear export agents and doxorubicin(31). Combination indices(30) may be obtained by adding the two drugs being studied on the same reservoir, which will induce two superimposed drug gradients.

This assay allows the observation of individual cells. Thus, it is possible to assess the heterogeneity of drug response by plotting in a histogram the area under the curve (AUC) at the moment of death of each individual cell. Further improvements in the digital image analysis algorithm could identify and track individual cells, from their original replication until their death. By combining this information with the dose response surfaces, it would be possible to determine if particular drugs and concentrations are capable of maintaining a tumor burden quiescent, or in a balance between proliferation and death(32, 33).

These preliminary results describe a framework to better understand the dynamics of interactions between tumor and stroma in response to therapeutic agents in vitro. These assays can be performed in a middle- to high-throughput manner, and significantly reduce the complexity of working with patient primary cells in reconstructions of the tumor microenvironment. Ultimately this may become a platform for personalized pre-clinical estimation of drug efficacy in cancer.

Future directions are to standardize methods to extrapolate in vitro predictions into clinical outcome. We will also explore the application of alternative therapeutic regimens of drug combinations, proposed by data extrapolated from this in vitro system, and simulated using evolutionary computational models(34, 35). We hypothesize that, patient-specific computational models, parameterized by in vitro platforms as the here described, could be combined with genomic(36) datasets to better understand the dynamics that underlie evolution of drug resistance in MM patients. Understanding these dynamics would not only allow accurate predictions of response, but also suggest the best therapeutic strategies for each patient, and continue adjusting these strategies as needed.