Tumour–stromal interactions generate emergent persistence in collective cancer cell migration

Abstract

Cancer cell collective migration is a complex behaviour leading to the invasion of cancer cells into surrounding tissue, often with the aid of stromal cells in the microenvironment, such as macrophages or fibroblasts. Although tumour–tumour and tumour–stromal intercellular signalling have been shown to contribute to cancer cell migration, we lack a fundamental theoretical understanding of how aggressive invasion emerges from the synergy between these mechanisms. We use a computational self-propelled particle model to simulate intercellular interactions between co-migrating tumour and stromal cells and study the emergence of collective movement. We find that tumour–stromal interaction increases the cohesion and persistence of migrating mixed tumour–stromal cell clusters in a noisy and unbounded environment, leading to increased cell cluster size and distance migrated by cancer cells. Although environmental constraints, such as vasculature or extracellular matrix, influence cancer migration in vivo, our model shows that cell–cell interactions are sufficient to generate cohesive and persistent movement. From our results, we conclude that inhibition of tumour–stromal intercellular signalling may present a viable therapeutic target for disrupting collective cancer cell migration.

1. Introduction

One of the most harmful features that tumour cells acquire is the ability to migrate and invade surrounding tissues, leading to deadly systemic metastases [1]. This has fuelled an active research programme to understand cancer cell migration and invasion from experimental and theoretical points of view. Novel techniques for direct visualization of tumour invasion in vivo [2] have revealed that cancer cells frequently migrate as groups of closely interacting cells [3]. The paradigm of collective cell migration has been rapidly accepted by experimentalists and it is now clear that collective migration is not exclusive to cancer but a widely used mode of cell migration [4]. However, we still lack a complete and thorough understanding of how individual cells coordinate to migrate collectively.

Ecological models may be useful in understanding cancer collective migration. Collective migration is observed in biological systems of many disparate length scales, ranging from bird flocks [5–7] to bacterial swarms [8,9]. It is an emergent phenomenon and a universality class, in which the large-scale properties of the collective result from the activities of individuals, but are to some extent independent of the specific behaviour of individuals [10,11]. Similarly, in cell biology, collective migration of groups of closely interacting cells has been implicated in such behaviours as organ morphogenesis during embryonic development or vascularization [4,12–15] and, the main motivation for our study, cell invasion during cancer progression [13,16].

One of the most successful theoretical approaches to study the emergence of collective migration from simple interactions between moving individuals are a class of models called self-propelled particles (SPPs). In the classic SPP model [17] an individual moving at a fixed speed interacts with its neighbours by aligning itself with the average direction of all individuals within a given radius. These simple rules for local interaction give rise to emergent global properties, such as a phase transition from disordered, or individual, motion to ordered, or collective, motion with a decreasing level of noise in the interaction. This model and derivations of it have been applied to numerous problems in collective migration by using the individual particle to represent real-world individuals in collectives, such as an animal in a flock [18,19], micro-organisms in a colony [20] or a cell in a tissue [21,22].

Experiments in which a homogeneous cell population displays collective migration in the absence of other cell types or external signals [22–25] are compatible with the original SPP model. However, migratory cancer cells interact with each other but also with stromal cells. For example, stromal cells such as macrophages [26,27] and fibroblasts [28] are known to assist cancer cell migration through secretion of migration-stimulating cytokines and proteinases that remodel and create permissive tracks in the extracellular matrix [1,29]. Thus, the application of the SPP model to cancer is complicated because cell migration in tumours requires synergy between diverse cell types [29–31]. The SPP paradigm has been used before to investigate cell sorting in development and regeneration [32,33]. Yet, it remains unknown how interactions between different, non-reciprocally interacting cell types affect collective cell migration.

Here, we explore what are the consequences of implementing experimentally inspired modifications to the original SPP model. More specifically, we investigate what are the consequences of the presence of a small subpopulation—representing stromal cells—with a distinct behaviour. Thus, we extend the Vicsek SPP algorithm [17] to introduce an additional particle type representing stromal cells. Tumour-associated macrophages are one of the most abundant and well-studied stromal cell types within solid tumours [27]. These macrophages are known to attract cancer cells, and this interaction is crucial for tumour invasiveness in vivo [29,34,35]. Based on these observations, we add a specific non-reciprocal attraction rule compelling cells of one type (tumour) towards nearby cells of the second type (stromal). This attraction has a relatively longer range of action, i.e. can occur between non-adjacent cells. We use our expanded model (hereafter referred to as the cancer–stromal model) to explore cell displacement and cell cluster size as metrics for quantifying the impact of stromal cells on collective cancer cell migration. Our simulations suggest that stromal cells can have profound implications for large-scale cancer cell collective migratory patterns and, consequently, for tumour aggressiveness.

It is important to stress that, although our initial motivation is to model attractive macrophage–tumour interactions described experimentally [29,34,35], our model is simplified and neglects other aspects of cancer–macrophage interaction such as angiogenesis promotion [36,37] and modulation of the inflammatory response [38]. Thus, the model is general and can be extended to any other attractive stromal cell.

2. Results

2.1. Extending self-propelled particles to model a tumour–stromal interaction

We use the homogeneous population of SPPs with one simple alignment rule as described in the original SPP model [17] as a starting point to model migrating tumour cells. To this population, we introduce a minority population of a second type of SPP, representing stromal cells. Cells of both kinds, tumour or stromal, align non-specifically to the mean polarization of cells in the neighbourhood. In addition, we add an attractive tumour–stromal interaction. This interaction is assumed to be type-specific and asymmetrical, that is, tumour cells are attracted to nearby stromal cells, but not vice versa (figure 1a). The angle of polarization θ of each cancer cell i is thus recalculated at each iteration:

2.1

where θ(t)_ral is the mean angle of polarization of all cells within distance r_al of the focal tumour cell i; a_ts is the strength of the attractive tumour–stromal interaction relative to cell–cell alignment; arg(r_ij)_rts is the mean angle of vectors from the centre of focal tumour cell i to all stromal cells j within distance r_ts of cell i; and Δθ is a random angle on the interval [−η, η], representing noise. The polarization calculation for stromal cells lacks the second term, and thus is identical to the migration rule in [17],

2.2

All length scales and cell speeds in the model are normalized as previously [17]: that is, the range of cell–cell alignment, r_al, equals 1. Local interaction mechanisms such as cell–cell adhesion and shear viscosity at high cell density [39] can account for this short-range alignment.

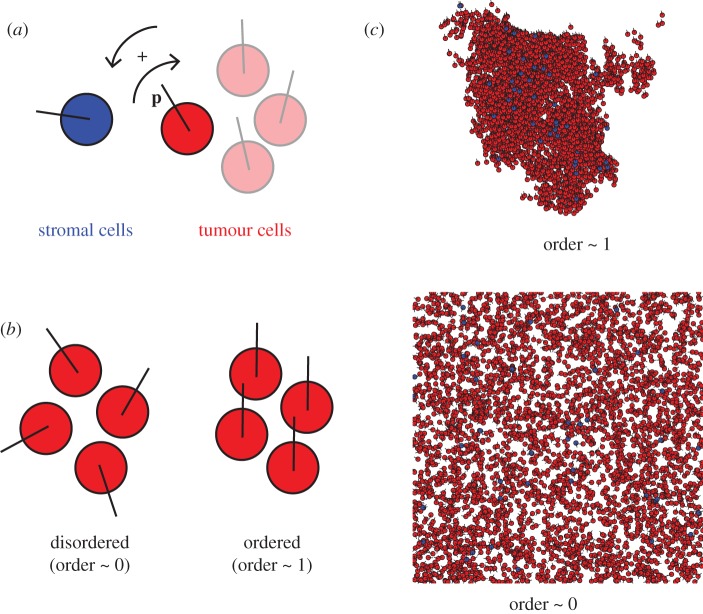
Figure 1.

(a) Cell–cell interactions in the cancer–stromal model of self-propelled particles. Cells move at fixed speed with a direction set by the polarization vector p. Stromal cells align non-specifically to the local mean direction of motion. Tumour cells align non-specifically in addition to moving towards any nearby stromal cells. (b) Order parameter quantifies the extent of cell polarization. When the global order parameter is approximately 0, cells are randomly polarized. When the global order parameter is approximately 1, cells are polarized in the same direction. (c) In a system with no tumour–stromal attraction (a_ts = 0; i.e. all cells behave as tumour cells) with low noise and cyclic boundary conditions, in the infinite-time limit, the global order parameter approaches 1: almost all cells eventually group into a single coherent cluster, in which individual polarizations deviate little from the mean polarization of the cluster. In a high-noise system, the global order parameter approaches 0, and the cells are spread throughout the available space with no discernible clustering.

Conversely, we assume that the possible mechanisms for tumour–stromal interaction, such as paracrine signalling through diffusible molecules [29,34], chemotactic motility from cancer cells towards stromal cells or forms of long-range alignment via adhesion to common collagen fibres in the extracellular matrix [1,29], have greater effective range than those contributing to cell–cell alignment adhesion to common collagen fibres in the matrix [1], and set r_ts = 2. Interaction and noise strengths are normalized to the cell–cell alignment strength; that is, cell–cell alignment strength equals 1. The noise amplitude, η, varied from 0 ≤ η ≤ 5, which is the range in which the ordered–disordered phase transition was observed previously [17], and the interaction strength, a_ts, varied from 0 ≤ a_ts ≤ 2.

All simulations were performed in two dimensions, replicating the cell density and boundary conditions, again as used previously [17]. We used a ratio of 4000 simulated tumour cells and 40 simulated stromal cells. With a_ts = 0, the stromal cells effectively behave identically to the tumour cells and the model should be equivalent to the original SPP. Our cancer–stromal model, when its additional parameters are set to 0, thus reproduces the behaviour previously observed in the original SPP study [17]. Simulation parameters are summarized in table 1.

Table 1.

Parameters used in model. Parameters not in the original SPP model [17] are given in bold. All parameters are dimensionless.

cell migration speed	0.03
size of simulation space	31.6 × 31.6
range of cell–cell alignment	1
strength of cell–cell alignment	1
noise	0 ≤ η ≤ 5
number of cancer cells	4000
number of stromal cells	40
range of tumour–stromal attraction	2
strength of tumour–stromal attraction	ats = [0, 0.2, 0.4, 0.6, 0.8, 1.0, 2.0]

2.2. Tumour–stromal interaction enhances collective migration in noisy environments

We first evaluated whether our model performed consistently by calculating the global order parameter, a key parameter in the original SPP model [17]. Briefly, the order parameter quantifies the average direction of particles, which we then compared at the pseudo-steady state (10 000 iterations) with the results in the original study. As expected, a global order parameter of approximately 0 indicates a disordered system with cells randomly polarized and distributed throughout the simulation space, while a global order parameter of approximately 1 indicates a system in which all the cells are roughly aligned and migrating as a single coherent cluster (figure 1b,c). A phase transition from ordered to disordered motion occurred as η increases. These observations confirmed that our SPP implementation corresponded to the original model [17].

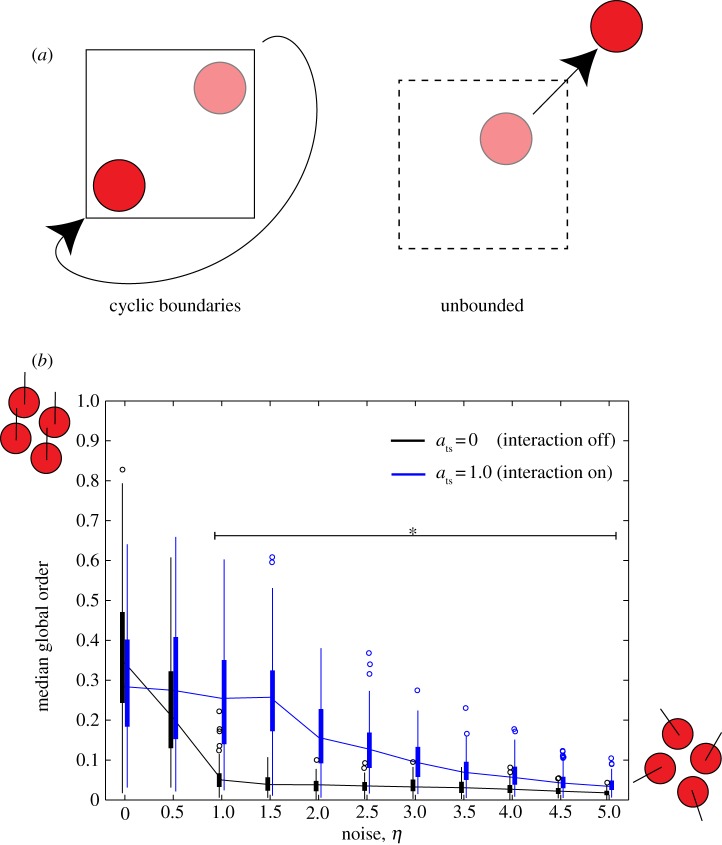
We then considered the effect of tumour–stromal attraction on the order of motion by setting a_ts to positive values. Simulations with a_ts > 0 showed notable deviations from the original SPP model [17]. We observed high variability in global order at the end of the simulation runs, but with opposite trends for low and high noise. The global order decreased compared with a_ts = 0 for low values of η (η < 2.5), and increased for high values of η (η ≥ 3; figure 2). End-simulation global order did not noticeably vary between simulations with different positive values of a_ts and the same value of η (not shown). The effect of changing cell density simultaneously with noise on the phase diagram of the order parameter is shown in the electronic supplementary material, figure 1.

Figure 2.

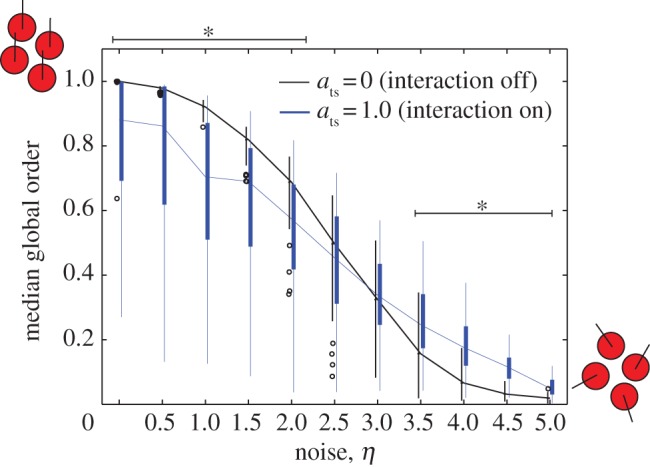
Global order parameter as a function of noise in a system with cyclic boundary conditions. Under a fixed value of a_ts, as η is increased, the system exhibits a phase transition from ordered (global order parameter approx. 1) to disordered (global order parameter approx. 0). When a_ts = 0, the phase transition occurs as in ref. [8]. When a_ts = 1.0, global order is decreased for low values of η, but increased for high values of η compared with the a_ts = 0 system. Asterisks indicate a significant difference between the a_ts = 1.0 and a_ts = 0 simulations (p < 0.001).

These results demonstrate that a simple extension to the original SPP can produce a significant change in the predicted pattern of collective migration and may have important implications for cancer. Specifically, the results suggest that tumour–stromal interaction can stabilize cancer collective migration in noisy systems.

2.3. The effect of stromal stabilization is stronger in expanding tumours

Our model so far, like the original SPP model, assumes cyclic boundary conditions [17], which confine the particles to a space of torus-like geometry and unrealistically small volume. However, cancer invasion in vivo drives cancer progression on time and length scales much larger than those of individual cell migration or even intercellular signalling within small groups of cells [40]. To extrapolate collective co-migration of cancer and stromal cells to larger length scales and longer simulation times, we implemented a second extension in our model, now using an unbounded system in which cell migration is essentially unlimited by spatial constraints (figure 3a).

Figure 3.

(a) Comparison of a system with cyclic boundary conditions with an unbounded system. Squares indicate areas of inoculation. In a system with cyclic boundary conditions, cells leaving the area of inoculation will re-enter the area at the diametrically opposite point, maintaining its polarization. In an unbounded system, the cell is not spatially constrained and may leave the area of inoculation. (b) Global order parameter as a function of noise in an unbounded system. The order of the system decreases rapidly as η increases. When a_ts = 1.0, the order increases for all positive values of η compared with simulations in which a_ts = 0. Asterisks indicate a significant difference between the a_ts = 1.0 and a_ts = 0 simulations (p < 0.001).

We carried out simulations with the unbounded system for a range of interaction strength and noise levels and we calculated the global order parameter after 10 000 time steps. As expected, with no tumour–stromal interaction (a_ts = 0), the global order decreases towards the end of simulation for all levels of noise (figure 3b). This occurs because, in unbounded systems, the decoherence effect of noise in each cell cluster is cumulative, and is unlikely to be cancelled by encounters with other cell clusters; thus, the ability of the system to sustain large coherent clusters over long time spans is decreased. Adding tumour–stromal interaction uniformly increases the end-simulation global order for all noise levels, implying that tumour–stromal interaction has much greater impact on the coherence of migrating cancer cell groups when the available space is large. Tumour–stromal interaction delays the disintegration of coherent migrating clusters, and increases the end-simulation global order (figure 3b).

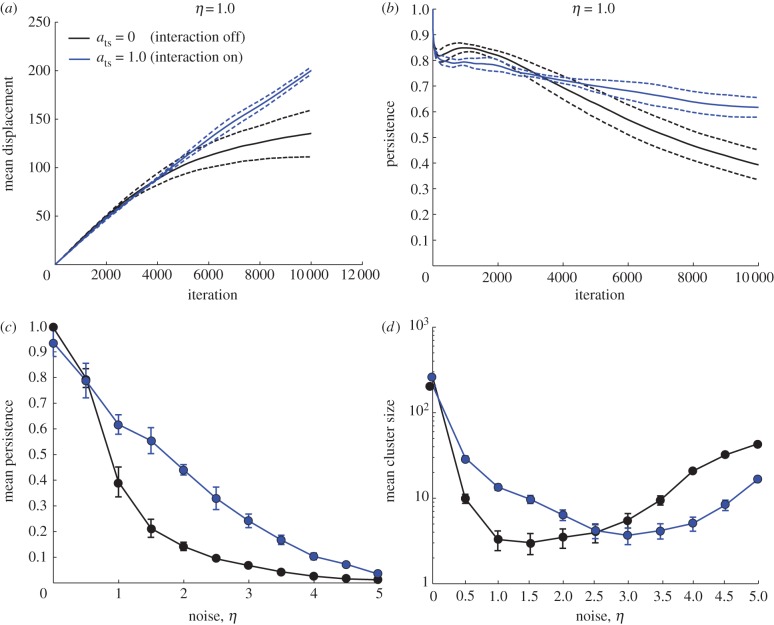
In addition to calculating the order parameter, we also examined the distance migrated by cancer cells as a measure of cancer cell invasiveness. For simulations without tumour–stromal interaction in which noise is moderate to high, the mean displacement rapidly increases initially but starts to level off within the simulation time (figure 4a). In contrast, in simulations with tumour–stromal interaction, the mean displacement increases steadily (linearly) throughout the duration of the simulation; this increase is seen to saturate within the simulation time only when noise levels are high (figure 4a). Consequently, for all positive values of η tested, tumour–stromal interaction increased the mean distance migrated by cancer cells (figure 4b). We conclude that tumour–stromal interaction increases the persistence and ultimately the performance of collective cancer cell migration, as measured by distance travelled.

Figure 4.

(a) Time course of mean displacement of cells in the system. Dashed lines indicate standard deviation across five replicates. The mean cell displacement at the end of simulation is increased for a_ts = 1.0 when compared with a_ts = 0. In the a_ts = 0 simulations, the rate of displacement increase decreases over time, whereas the effect is not observable in the a_ts = 1.0 simulations. (b) Persistence over time of the same simulation sets. The decay of persistence over larger time scales is more gradual for a_ts = 1.0. (c) Mean persistence over the time scale of the simulation as a function of noise. The mean persistence is increased for a_ts = 1.0 compared with a_ts = 0 for all values of η > 0 tested. (d) Mean cluster size at simulation end as a function of noise. The mean cluster size is increased for a_ts = 1.0 at low values of noise. At high levels of noise, tumour–stromal interaction decreases the mean cluster size, reflecting the dissolution of the cell population into small clusters.

We also considered the effect of tumour–stromal interaction on the size of collectively migrating cell clusters, as measured by the number of cells in the clusters. Clusters are defined as groups of cells within the same interaction network, i.e. cells interacting directly or indirectly via other cells. We determined the presence of cell–cell interactions by thresholding the centre–centre distance of each pair of cells with the appropriate interaction range (1 for a pair of tumour cells or a pair of stromal cells, 2 for a heterogeneous pair of 1 stromal cell and 1 tumour cell) and sorted the cells into clusters using the well-established equivalence class sorting algorithm [41]. Stromal cells were included in the statistics for stromalized clusters; however, as they constituted 1 per cent of the total population, we assumed that they did not significantly affect the overall statistics. Cells not in contact with another cell were interpreted as clusters of size 1. At low levels of noise, tumour–stromal interaction increased the global mean size of collectively migrating cell clusters compared with the control simulations. However, this trend reversed as η was increased above approximately 2.5, and for high levels of noise, tumour–stromal interactions in fact decreased the global mean cluster size (figure 4c).

2.4. Stromalized clusters are more invasive

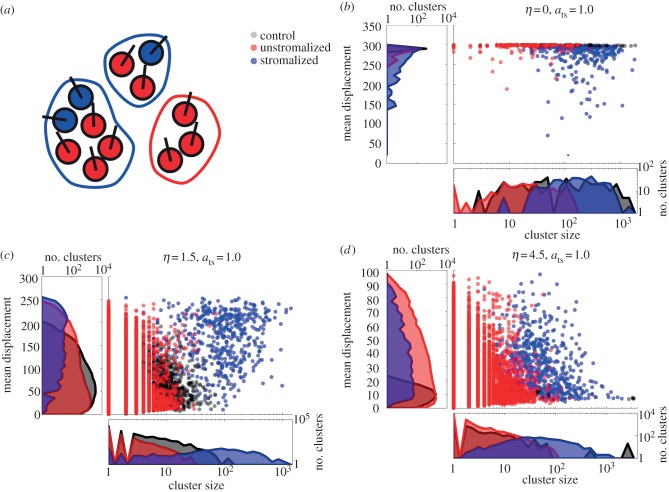
To understand this biphasic effect of tumour–stromal interaction on the sizes of migrating clusters (figure 4c), we then sorted the cell clusters into those that included at least one stromal cell (‘stromalized’ clusters) and those that did not (‘unstromalized’ clusters) (figure 5a). We estimated the distance migrated by a cluster of interacting cells by calculating the mean displacement of all cells in the cluster at the end of simulation. We then examined the relationship between the stromalized clusters, the distance migrated by a cluster and its size. In the low-noise (η ≤ 0.5) regime, both the stromalized and unstromalized clusters were smaller and displayed a smaller mean displacement than clusters in the control (a_ts = 0) simulations (figure 5b). This is caused by the same fragmentation and consequent decrease in coherence observed in the cyclic boundary simulations. In addition, the distribution of multiple stromal cells throughout the cell population at inoculation possibly creates multiple conflicting directional signals that propagate through many cancer cells, leading to wandering behaviour that contributes little to the mean displacement.

Figure 5.

(a) Clusters incorporating at least one stromal cell are considered stromalized. (b) Distributions of cluster sizes and displacements for stromalized and unstromalized clusters in five test simulations (a_ts = 1.0) versus control (a_ts = 0) for a low-noise condition. Clusters in the control simulations varied in size but are uniformly far-migrating. In the test simulations, stromalized clusters tended to be larger than unstromalized clusters, though they showed greater variance in displacement. (c) Distributions of cluster sizes and displacements for stromalized and unstromalized clusters in five test simulations (a_ts = 1.0) versus control (a_ts = 0) for a medium-noise condition. Unstromalized clusters in test simulations distributed similarly to clusters in control simulations both in terms of size and displacement. Stromalized clusters in test simulations distributed distinctively from the unstromalized and control clusters, displaying greater displacement and cluster size overall. (d) Distributions of cluster sizes and displacements for stromalized and unstromalized clusters in five test simulations (a_ts = 1.0) versus control (a_ts = 0) for a high-noise condition. Stromalized and unstromalized clusters from the test simulations distributed similarly with respect to displacement, with stromalized clusters being larger overall. Cells in the control simulations formed large, nonmotile clusters owing to being unable to significantly migrate from their points of origin. In the test simulations, tumour–stromal interactions break the cells into small, motile clusters.

For larger values of η, both the size of and distance migrated by clusters decreases noticeably for the control simulations. The stromalized clusters separate into a distinct coherent, far-migrating subpopulation (figure 5c). At very high noise levels, cluster size and distance migrated are decreased for both stromalized and unstromalized clusters in test simulations, and for all clusters in control simulations. Regardless, stromalized clusters retain a significantly larger mean cluster size than the unstromalized subpopulation (figure 5d). These results suggest that tumour–stromal interaction can increase both the motility of migrating cancer cells and the number of motile cancer cells.

Notably, control simulations saw the emergence of very large clusters, of the order of 1000 cells, with cluster displacement close to 0 (figure 5d). This is because the cells are inoculated at high enough density to constitute a single interacting cluster, and at high noise most cells are unable to ‘escape’ the inoculum cluster. Similarly to the medium-noise situation, these results suggest that, in microenvironments that present strong barriers to cancer cell migration, interaction with stromal cells can aid in the escape of motile cancer cells from the main tumour mass.

3. Discussion

In order to understand the effect of complex tumour–stromal and tumour–tumour intercellular interactions on collective cancer cell migration, we have implemented and analysed the cancer–stromal model, a minimal computational model for simulating the collective co-migration of two phenotypically distinct cell types under the SPP paradigm. We have designed the model with intended application to stromal cell-assisted cancer cell invasion, but it can theoretically be applied to any heterogeneous population in which interaction between subpopulations is orthogonal to interaction within subpopulations; for example, a symbiotic or antagonistic relationship between two animal herds of different species. We find that, given an unbounded space in which to disperse, the addition of tumour–stromal interaction increases the end displacement of cells within stromalized clusters. The presence of system-level effects in our simulations is remarkable, considering the stromal cells constitute less than 1 per cent of all cells in the system, and in an unbounded system only a slim minority of cancer cells will directly interact with stromal cells in the course of a simulation.

The effect of tumour–stromal interactions on the sizes of co-migrating cell clusters changes relative to the amount of noise in the system. At finite but low levels of noise, positive attraction between tumour and stromal cells increases the size of stromalized clusters over unstromalized clusters in the same system or clusters in systems in which tumour–stromal attraction is absent. With high levels of noise, cancer cells tend to clump in large but non-migratory clusters. Interaction with stromal cells causes cancer cells to fragment from these static clusters into smaller, but more invasive clusters, leading to the escape of cancer cells from the inoculum.

Our results suggest that the presence of a small number of stromal cells expressing an attractive signal for migrating cancer cells can lead to a population-level increase in the ability of cancer cells to migrate long distances, and that cell clusters of significant size leaving the initial tumour site will probably be aided in their migration by stromal cells. In realistic settings, increasing the coherence of migrating cancer cell clusters may increase the aggressiveness of cancer invasion by preserving other deleterious collective phenotypes, such as pooling of paracrine growth signals or matrix-remodelling proteases [1,16,28,29,35,42,43]. Tumour–stromal interactions increase the number of cells that are able to migrate coherently and maintain cell–cell signalling. Thus, they may increase the fitness of the invading cancer cell population [36,38,44].

It is now well established that collective migration can emerge within cancer even without the presence of stromal cells. This phenomenon seems to be suitably described by the 1-species SPP model [15,22]. Here, we add one degree of complexity by investigating the effect of a minority of attracting cells within a large population. While this work is inspired by reports showing that carcinoma cells are attracted to epidermal growth factor secreted by tumour-associated macrophages [34], it necessarily presents a simplified view. There are potentially many other interaction processes existing within macrophages, tumour cells and their complex microenvironment [36–38]. Such interactions represent further levels of complexity that are outside the scope of this study.

Nonetheless, our simple model already shows a dramatic effect on the behaviour of the population. Specifically, the emergence of system-level increases in migration distance in our cancer–stromal model does not require a structured environment featuring system-level signals such as chemoattractant or extracellular matrix gradients [45]. We show that increased migration efficiency and escape of tumour cells from a primary tumour mass can be achieved purely through local, pairwise cell–cell interactions; no global migration trigger or directional cue is necessary. When we investigate the spatial distribution of stromal cells in migrating cell clusters, we find that it becomes asymmetrical and correlated with the mean polarization of the stromal cells when tumour–stromal interaction is switched on (see the electronic supplementary material, figure 2b). This effect decreased with increasing noise (see the electronic supplementary material, figure 2a), suggesting that tumour–stromal interaction causes the stromal cells to emerge as leaders on the leading edge of their moving clusters. Still, on a theoretical level, our model is distinct from collective migration models in which the population is divided into ‘leaders’ that are sensitive to a global directional signal (e.g. a patchy nutrient environment) and ‘followers’ that are not [46], since in our case the stromal cells do not follow a global directional cue. On a biological level, the dynamic construction of leadership we use in the cancer–stromal model reflects the experimental observation that leadership in collective cancer cell migration can be defined not by genotype but by the spatial structure of the cell population itself and differential access to microenvironmental factors [13,47].

It is also worth noting that our cancer–stromal model makes the assumption that long-range signalling between tumour cells and stromal cells has a digital response, vanishing at distances greater than the range of tumour–stromal interaction r_ts. To determine whether our results are an artefact of this model assumption, we performed additional simulations using a function in which the strength of the tumour–stromal interactions decayed continuously away from the stromal cell as r_ij/r_ts with a maximum value of a_ts. We found that at η = 1, a_ts = 1, cancer cells moved towards the centre of mass of the stromal cells, which, given the uniform distribution of cells at inoculation, was calculated to be the centre of the simulation space. This effect is a modelling artefact owing to boundary conditions used in simulations and has no relevance to biological reality. When we started decreasing a_ts to 0.01 the artefact vanished and the simulation yielded similar results to those using equation (2.1). Given that the two methods yielded similar results, and that the continuous interaction function increased both the degrees of freedom in the model and the computation time required, we concluded that equation (2.1) was preferable for modelling tumour–stromal interactions. In addition, within the dense and heterogeneous tissue of real solid tumours, continuous decay over long distances may not accurately describe the distribution of diffusible molecular signals.

Recent studies on interactions between the tumour and its stromal microenvironment have generated interest in targeting the microenvironment for treatment, that is, ‘ecological therapy’ [48]. Our results suggest that cell–cell communication among the migrating cancer cell population may serve to amplify and increase the robustness of pro-invasive tumour–stromal interactions, propagating signals beyond the leading edge of cancer cells in direct contact with stromal cells. It may thus be necessary to consider the reinforcement of pro-tumour tumour–stromal interactions by signalling within the tumour cell population when designing and testing potential ecological therapies. A hybrid therapy targeting tumour–stromal and tumour–tumour intercellular signalling simultaneously may be required for effectiveness.

It is worth noting that the metrics we used to quantify the performance of collective migration may be applicable to both simulated and experimental cell systems such as in vitro cell tracking assays [22]. By collecting phenomenological data with sufficient resolution to track the positions and velocities of individual cells and quantifying collective migration experimentally for a specific biological system (here meaning a stromal cell type and a cancer cell type), one may parameterize or ‘tune’ a phenomenological model to reproduce the collective-level behaviour of an experimental system. Such hybrid experimental/computational studies have been performed in animal [49] and cellular [22] systems. The tuned computational model may then be modified and interrogated to make testable hypotheses for the specified system; for example, to predict the co-migration patterns of cancer cells and tumour-associated macrophages in a highly structured in vivo environment using data collected in an unstructured in vitro co-culture assay, such as a chemotaxis chamber or collagen gel. We hope that our expanded SPP model will help bridge the knowledge gap between the tractability of low-perturbation in vitro experiments and the complexity of stromal-assisted cancer cell invasion in vivo.