An empiricist's guide to theoretical predictions on the evolution of dispersal

Abstract

Dispersal, the tendency for organisms to reproduce away from their parents, influences many evolutionary and ecological processes, from speciation and extinction events, to the coexistence of genotypes within species or biological invasions. Understanding how dispersal evolves is crucial to predict how global changes might affect species persistence and geographical distribution. The factors driving the evolution of dispersal have been well characterized from a theoretical standpoint, and predictions have been made about their respective influence on, for example, dispersal polymorphism or the emergence of dispersal syndromes. However, the experimental tests of some theories remain scarce partly because a synthetic view of theoretical advances is still lacking. Here, we review the different ingredients of models of dispersal evolution, from selective pressures and types of predictions, through mathematical and ecological assumptions, to the methods used to obtain predictions. We provide perspectives as to which predictions are easiest to test, how theories could be better exploited to provide testable predictions, what theoretical developments are needed to tackle this topic, and we place the question of the evolution of dispersal within the larger interdisciplinary framework of eco-evolutionary dynamics.

1. Introduction

Understanding why organisms from all species have a tendency to disperse away from their parents is a key question in evolutionary ecology [1–5]. From a fundamental perspective, dispersal propensity is intertwined with speciation and species extinction in a complex fashion [6]. On the one hand, dispersal may help species escape local catastrophes [7]; on the other hand, dispersal of common species may endanger rarer ones by ‘stepping over’ their geographical distributions, and limited dispersal favours divergence among allopatric populations. From a more applied viewpoint, understanding why certain species or genotypes disperse more than others might help to understand shifts in species distributions because of global change [8], to understand constraints on the adaptation of species to changing environmental conditions [9], to plan conservation strategies for threatened species or communities [10,11] and to design strategies for the management of invasive species [12] that build upon our knowledge of their evolutionary histories.

Dispersal, i.e. the tendency for an organism to reproduce away from its birthplace [3] (see glossary for definitions of words in italics), has been the subject of many theoretical studies, because (i) both population geneticists and ecologists have had hypothetical answers to the question of why organisms disperse and (ii) this topic has been linked to other important discoveries and theories in both fields of research. Historically, theoreticians have tried to understand why species disperse at all [13–15]; research questions have then focused on predicting (i) the proportion of dispersed offspring or (ii) the distribution of dispersal distances. Theoretical population geneticists have long been interested in the evolution of dispersal, because it is a good example of the effect of kin competition [13,16], and because inter-population migration tends to coevolve with inbreeding and recombination [17–20]. Ecologists have also proposed arguments on the evolution of dispersal based on emergent theories in ecology. For example, perturbations have been proposed to be selective pressures acting on dispersal [7,21]. Another example is the link between the evolution of dispersal, source–sink dynamics and the ideal free distribution of organisms [14,22,23]: indeed, dispersal re-distributes individuals among patches with different growth rates.

Empirical studies on the evolution of dispersal have always lagged behind theoretical ones [5,24]. Several reasons account for this: (i) dispersal is rarely defined in an unequivocal fashion—and while this poses no problem for a self-contained theory, it impedes dialogue between theory and empirics; (ii) direct measures of dispersal, when they are possible, are difficult at best; (iii) proxies or indirect measures of dispersal—which are less costly—have received far less theoretical treatment than dispersal per se, and hence are prone to fewer empirical tests of any theory; (iv) experimental evolution studies can be lengthy and can only be applied to a restricted range of taxa; and (v) field data bring only information about correlation, not causation. As a result, empirical refutations of theories on the evolution of dispersal are scarce, despite the need to understand how and why differences in dispersal rates arise, e.g. to predict the potential invasiveness of a given species or genotype [25–27].

As theoretical approaches to the evolution of dispersal have considerably widened their scope, methods and assumptions, it is now time to lay out their various predictions and the assumptions they are based upon. Here, we review the different aspects of theories on the evolution of dispersal and propose a synthetic outlook on fruitful theoretical approaches that could lead to more easily testable predictions.

2. Selective pressures

After five decades of theoretical models, consensus among evolutionary ecologists has it that the evolution of dispersal has multiple causes [5,28–30]. This occurs because dispersal serves different functions: (i) spreading risk among offspring, through increasing variance in expected fitness among offspring; (ii) reducing competition or mating with relatives; and (iii) escaping locally bad conditions, such as crowded patches [30]. Selective pressures tending to increase dispersal thus include (i) spatio-temporal variation in local conditions, (ii) kin competition and inbreeding depression; and (iii) characteristics of population dynamics. Dispersal is, however, costly and its costs tend to reduce the propensity to disperse.

2.1. Dispersal costs

Dispersal may incur costs of different natures [31]. First, dispersal incurs an energetic cost. In animals, there is both a metabolic cost to move to a new place, and a cost to produce and maintain dispersal structures (muscles, wings, etc.). In contrast to animals, in plants the energetic cost of producing dispersal structures (fleshy fruits, pappus, samara, etc.) is borne by the mother. Second, dispersing takes time: this time is not used to feed or to mate. Third, dispersal may be risky: dispersed individuals may suffer predation. Last, dispersing means leaving a patch where reproduction was possible, to an unknown place where conditions may be worse. Dispersal costs may also arise due to imprecision of cues on patch quality in temporally variable environments [32] or be linked to the process of gaining information [33]. The propensity of organisms to disperse usually decreases as dispersal becomes more costly [31], but this link is rarely linear [13,34]. Some models have investigated the role of distance-dependent costs [35], or of asymmetric dispersal costs [36], on the evolution of dispersal strategies.

2.2. Temporal variability of the environment

Variability in environmental characteristics is predicted to select for dispersal. In particular, random, extremely severe variations (i.e. catastrophic perturbations) select for dispersal as a means to evade large-scale extinction [7,21]. The frequency [37], magnitude [34], variability in magnitude [38], spatial correlation [39] and predictability [32,34,40] of environmental changes all have a say on the strength of this selective pressure. By contrast, perturbations aimed at habitats, rather than at populations, are expected to select against dispersal [41,42].

2.3. Spatial. heterogeneity

When carrying capacities differ among patches, mean-field theory predicts that dispersal is disfavoured, because migrants will on average go from large patches with high associated fitness to smaller patches with lower fitness [14,22]. However, this prediction does not hold when demographic stochasticity, drift or other means of environmental heterogeneity are taken into account [38,41,43,44], mostly because lowering carrying capacity also means increasing kin competition, thus selecting for dispersal [41,43]. Spatial heterogeneity in population extinction rates also favours polymorphisms of dispersal rates [44].

2.4. Kin competition

When patch sizes are finite, a proportion of offspring are expected to disperse, even when dispersal costs are high, to avoid competing with local relatives [13]. The kin competition argument has been refined through focusing on spatial heterogeneity [43], conditional dispersal [45], overlapping generations [46], ploidy [47] or on maternal versus offspring control of dispersal [47,48].

2.5. Inbreeding depression and genetic incompatibilities

For sexual species, staying home means being likely to mate with relatives, which may incur a cost: inbreeding depression. Selection for dispersal depends on the balance between the costs of dispersal and of inbreeding depression [19,20,49,50]. When the cost of dispersal differs among sexes, this tendency to avoid inbreeding leads to the emergence of sexual dimorphisms in dispersal [18].

2.6. Demographic dynamics

The interplay between demographic dynamics and the evolution of dispersal has mostly been addressed through simulations. Non-equilibrium metapopulation dynamics select for some level of dispersal, possibly with various coexisting strategies [51], even when corresponding stable models predict zero dispersal [14]. This is because chaotic population dynamics generate spatio-temporal variability in population densities, which favour dispersal [15]. In turn, the evolution of dispersal sometimes tends to stabilize otherwise complex population dynamics [52] (but see [51]). Complex, non-equilibrium population dynamics can also select for condition-dependent dispersal (e.g. in predators responding to spatio-temporal variability in prey availability [53]). Stochasticity in population dynamics affects dispersal evolution in ways similar to non-equilibrium dynamics, i.e. generally selects for dispersal [54] and can drive the evolution of density-dependent dispersal [55,56].

2.7. Life cycles and the timing of dispersal

In semelparous species (reproducing once in their lifetime), dispersal is most often assumed to occur at birth or during the juvenile stage. Both iteroparity and overlapping generations lead to increased level of dispersal, because they increase local relatedness, hence kin competition and potential inbreeding [46,57]. The timing of dispersal—whether occurring at juvenile or adult stage—also leads to different selective regimes for the evolution of local adaptation [58,59], and, hence, to different predictions on the evolution of dispersal in spatio-temporally variable environments [60,61].

2.8. Reproductive system

Mating systems may promote or impede the maintenance of dispersal polymorphisms: assortative mating tends to impede their emergence [62], yet the evolution of assortative mating in turn depends on the degree of spatial structuring among populations, hence on dispersal [63]. More generally, reproductive system and dispersal tend to coevolve, because they feedback on one another, and share selective pressures [63–65]. While different variances in reproductive success between sexes does not select for sex-biased dispersal, among-site variance in reproductive success does. Thus, mating system has a strong influence on the evolution of sex-biased dispersal [66].

3. Assumptions and predictions

One of the difficulties of interpreting theoretical models on dispersal evolution lies with understanding assumptions made and predictions given. Here, we review the main assumptions and predictions as they are tackled in theoretical models.

3.1. What dispersal?

Here, we review the various characteristics defining the dispersal trait in theoretical studies. These different axes mainly refer to (i) the recurrence of dispersal; (ii) the ploidy of the dispersed life stage; (iii) the representation of dispersal; and (iv) the viewpoint on dispersal; (v) the genetic architecture (or lack thereof) underlying dispersal; and (vi) the plasticity of dispersal.

3.1.1. The recurrence of dispersal

Dispersal is defined by gene flow among populations [5], thus the temporal scale of dispersal is intrinsically linked to the recurrence of reproductive events within an organism's lifetime—as opposed to non-dispersal movements. In mobile and iteroparous organisms, dispersal can occur between birth and the first reproduction, but can also occur between two successive reproductions: natal dispersal may differ from breeding dispersal.

3.1.2. Propagule dispersal versus gamete dispersal

In most sessile organisms, both gametes and propagules disperse away (e.g. pollen and seeds in angiosperms). Thus, dispersal might be coined for both gamete and propagule dispersal. However, because of their different ploidy, gamete and propagule dispersal differ in sensitivity with respect to relatedness-based selective pressures (kin competition and inbreeding avoidance; [67]).

3.1.3. Representation of dispersal

One of the most divisive aspects of the literature on the evolution of dispersal is about whether dispersal refers to the propensity for individuals to disperse, or to parent–offspring distance. On the one hand, classic patch models focus on the propensity to disperse at a global scale (i.e. to any other patch). More sophisticated patch models can have non-global dispersal, e.g. when modelling metapopulations on graphs [68,69]. On the other hand, continuous space models characterize the distribution of dispersal distances by the statistical moments of the dispersal kernel. Continuous space representations may have trouble characterizing multiple-modes dispersal kernels based just on a few statistical moments. Dispersal propensity, although not an explicit variable, can emerge from the distributions of evolutionarily stable dispersal distances in explicit space models (e.g. [35]). Sometimes, dispersal distances and dispersal rates are explicitly modelled jointly [70].

Predictions of dispersal propensity and distance generally agree in the intuitive way, i.e. both are predicted to increase under the same conditions (e.g. compare [41] with [42]). For instance, kin competition can be thought of as increasing the propensity to disperse [13], or as increasing the average dispersal distance [71]. The only well-documented reason for a disagreement between these two measures of dispersal can be observed along a gradient of spatial autocorrelation of habitat quality [72].

While the spatial scale at which individuals disperse is meaningless in the absence of a comparative scale (figure 1), dispersal propensity—although a rough measure of dispersal—is a non-dimensional measure of dispersal, not prone to scale-related misinterpretations. In patch models, the different ecological processes (competition for resources, environmental perturbations, etc.) are assumed to be homogeneous at the scale of the patch. Dispersal propensity thus corresponds to the propensity for an individual to disperse further than the typical distance at which all of these processes can be considered homogeneous. Dispersal distance thus needs to be compared to the spatial scale of perturbation, competition and other metapopulation processes [74] (figure 1).

Figure 1.

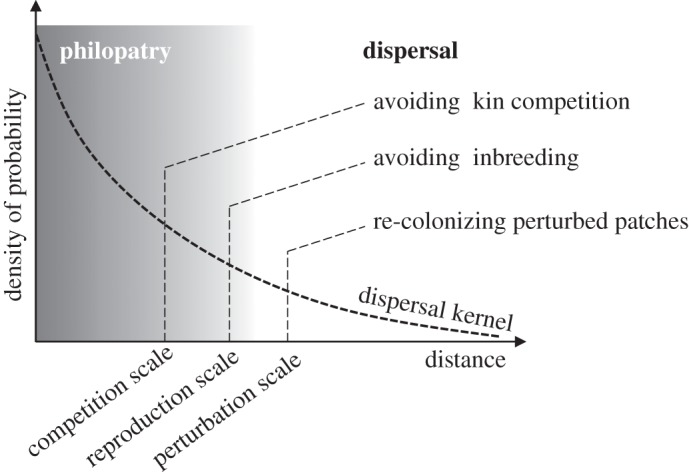
Relationship between the dispersal kernel (i.e. the probability distribution function of the dispersal distance, thick dashed line) and the typical scales of processes involved in metapopulation dynamics, here competition, reproduction and perturbation (thin dashed lines). In this example, competition is assumed to be more localized than reproduction which, in turn, is more localized than perturbation, but other hierarchies of process scales are possible. Depending on the main ‘function’ assigned to dispersal (i.e. avoiding kin competition, avoiding inbreeding or helping re-colonize perturbed patches), a propagule is said to be dispersed if it disperses farther than the typical competition, reproduction or perturbation scale, respectively. These typical scales can change due to dispersal evolution. For instance, when dispersal increases, population density is expected to become more uniform, and hence competition scale is bound to decrease (e.g. [72,73]). Similarly, gamete dispersal influences reproduction scale, and thus gamete dispersal and propagule dispersal are bound to interfere with one another [67].

3.1.4. Viewpoints on dispersal

In patch models, dispersal may be defined by dispersal propensity, d, or by two other related quantities, the population genetics migration parameter, m, and the metapopulation colonization rate, c.

Population geneticists often treat gene flow as a cause, rather than as a consequence, of evolutionary processes. Dispersal has thus been quantified by the proportion of immigrant propagules: the migration parameter m. Here m and d are naturally related given sufficient knowledge about carrying capacities and dispersal cost, e.g. in the case of death–birth models [43]; yet the evolution of m is misleading, except in very simple ecological scenarios [75], because it overlooks constraints owing to dispersal cost.

In metapopulation models [76], dispersal is considered as a rare and costly process counteracting local extinction. As such, dispersal is studied through the colonization rate, c, which integrates the propensity to disperse and the probability that a single propagule might generate a viable population. Again, given sufficient information, c can be related to d [77]. In most situations however, the link between dispersal cost and the trade-offs between extinction, colonization and takeover rates is not clear [27].

3.1.5. Genetic determinism of dispersal

Two main approaches are commonly used to describe the evolution of life-history traits such as dispersal:

• (i) Describing the dynamics of alleles at certain loci that determine the value of the trait. This corresponds to the population genetics approach to evolutionary dynamics.

• (ii) Directly describing the dynamics of the trait under study. This is what has been dubbed by Grafen [78] the ‘phenotypic gambit’: as long as it allows understanding otherwise complex phenomena, it may be preferable to abstract from the intricacies of genetic architecture.

While most models on dispersal evolution have openly embraced Grafen's phenotypic gambit, some models have treated this question using alleles at one or several loci as coding for dispersal value [79,80]. One good reason for explicitly accounting for genetic architecture is when dispersal coevolves with inbreeding depression or heterosis, so that recombination between dispersal and deleterious mutation alleles has to be accounted for [20,80]. Epistasis, dominance, genetic incompatibilities, variable ploidy are but a few potential elements that require taking genetic architecture into account because adaptive dynamics and quantitative genetics are not adapted to their modelling (but see [81]). One particular instance of genetic determinism that has garnered much attention is the question of maternal versus offspring control of dispersal [47,48,71].

3.1.6. Condition-dependent dispersal

While early models on the evolution of dispersal focused on the evolution of fixed, unconditional dispersal, more recent approaches have explored the evolution of condition-dependent dispersal—i.e. plastic dispersal, which is informed by external conditions or by the organism's internal state [82–84]. Classically, dispersal is assumed to be informed by within-patch density [55,56,85–88], carrying capacity [86], maternal age [89], body condition [90] or by expected local fitness [87,91], which can rely on the density of predators or prey [92], on the distance to inhospitable habitats [70] and/or on the distribution of local phenotypes. Age-, stage-specific [89,93] and sex-biased dispersal [18,66] have also been investigated. Theoretically, in the absence of information costs, informed dispersal evolves quite easily, e.g. when demography is stochastic [55]. Assessing how plastic dispersal evolves when information is costly or imprecise is a still poorly explored area (but see [32,33]).

3.2. Demographical assumptions and predictions

Model assumptions that are linked to the demographics of studied species mainly concern two characteristics: the timing and synchrony of life cycles, and the importance of stochasticity in demography.

3.2.1. Timing, synchrony and life cycles

Models on the evolution of dispersal treat the passing of time either as discrete [2,13] or continuous [43,44]. Discrete-time models are synchronized: reproduction, regulation and dispersal happen at the same time for all individuals. By contrast, continuous-time models consider populations where birth and death events happen at random—generally, following Poisson processes with constant rates. Because they describe life stages separately, discrete-time models often lend themselves to more detailed descriptions of the life cycle than continuous-time models.

Differences among life cycles that may impact dispersal traits include:

• (i) whether modelled organisms are semelparous or iteroparous. In the latter case, adult survival [46,57] and possibly age-structure [89,93] have to be modelled;

• (ii) the sequence of stages (reproduction, emigration, immigration and regulation) within a reproductive season [58,59,61].

3.2.2. Stochasticity and determinism

Stochastic population dynamics can affect different processes with a potential side effect on dispersal:

• (i) stochastic recruitment (or genetic drift) occurs when the numbers of offspring selected for the next generation are not equal to their expectations for each of the genotypes present, but rather represent a statistical sample drawn from a finite population. This form of stochasticity is at the heart of kin competition models on the evolution of dispersal;

• (ii) stochastic demographics arise when fecundity and mortality vary in time, leading to variable and unpredictable population sizes. Many models have looked at the effect of demographical stochasticity on the evolution of dispersal, mostly contrasting situations in which population sizes are assumed constant versus situations in which they are not [54–56]; and

• (iii) stochastic environments (where conditions cannot be predicted with 100% accuracy) usually select for dispersal. The most extreme case of environmental stochasticity is local population extinction. Environmental stochasticity can be studied independently from genetic drift and demographical stochasticity [38,64].

It is important to realize that stochastic recruitment and stochastic demographics are two separate forms of stochasticity: recruitment can be stochastic in the absence of demographic stochasticity—the reverse case is less plausible.

Well-known simple population dynamics models (such as the Lotka–Volterra equations for community dynamics) tend to use a mean-field description of the abundance of a given species, with no stochasticity in demography or in recruitment. The mean-field dynamics assumption implies that the coefficient of variation of abundance is expected to be very low, which, in turn, can be realized when mean abundance is sufficiently high (note though that this is not a strict requirement, but rather a loosely defined assumption common to most mean-field models). Hence, mean-field models implicitly have zero intra-population relatedness and, hence, do not take kin competition into account when modelling the evolution of dispersal. To capture the effect of kin competition, one can either describe population dynamics in a stochastic context (e.g. [94]), or explicitly compute the inclusive fitness version of the selection gradient and the average within-population relatedness coefficient [77].

3.2.3. Eco-evolutionary feedbacks

Exploring the feedback of the evolution of traits on population dynamics is a road seldom trodden [95,96]. Few models link dispersal traits to resulting population dynamics [51,52,97], even though this feedback naturally arises when dispersal evolves as a result of predator–prey dynamics [53]. Understanding in what instances higher dispersal triggers higher or lower complexity of population dynamics [98] is a topic worthy of interest, but still not really explored. For example, dispersal rate is expected to decrease as patches age [99]. An instance of extreme feedback of dispersal evolution on population dynamics arises when dispersal evolves in metapopulations subjected to local Allee effects and to environmental stochasticity: the evolution of higher dispersal rates then tends to increase extinction risk [100].

3.3. More sophisticated predictions

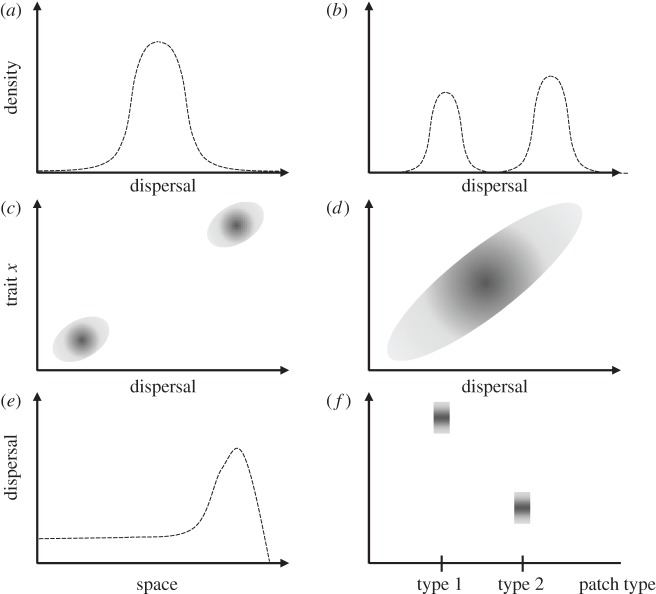
Besides predicting whether evolutionary forces select for or against dispersal, less crude predictions can be obtained (figure 2), mainly (i) whether selection is stabilizing or disruptive at evolutionary equilibria, (ii) how different traits might coevolve with dispersal; and (iii) how evolutionarily selected dispersal values become spatially structured.

Figure 2.

Classes of predictions about the evolution of dispersal. (a) The density of dispersal trait values within a metapopulation following an ESS, with residual variance corresponding to the result of mutation and local genetic drift (i.e. stochastic effects). (b) The density of dispersal trait values in a polymorphic population (here, with two modes). (c) Prediction of a positive association syndrome between dispersal and trait x. (d) Prediction of a genetic covariance between dispersal and trait x within a given population or metapopulation. (e) Spatial structure of average dispersal value along a one-dimensional space—here, dispersal is higher on the right, possibly because of an invasion wave into a new environment. (f) Structuring of dispersal trait values among two types of patches—here, dispersal is selected for in patches of type 1 and disfavoured in patches of type 2.

3.3.1. Dispersal polymorphism

One type of prediction that has garnered much attention from evolutionary ecologists is whether selection on dispersal is stabilizing or disruptive (figure 2a,b). In game theory or adaptive dynamics parlance, the former is characterized by an evolutionarily stable strategy (ESS) for dispersal [101,102]; by contrast, disruptive selection is associated with evolutionary branching [103] or with an increase in the standing variance of the trait studied. Early papers on the evolution of dispersal had difficulties in teasing apart ESS from evolutionary branching—at least analytically—because the theory of inclusive fitness focuses on the derivation of the selection gradient, not on the higher order derivatives of the mutant fitness function that are needed to evaluate evolutionary stability [16,104]. However, novel methods (and resurrection of old ones) now allow for the computation of ESS criteria, in particular, the metapopulation fitness criterion R_m [81,88,94,105,106]. The connection between predictions of polymorphism and of condition-dependence is still not clear [107], especially in the case of dispersal evolution [82]. Besides, since many models dealing with the evolution of trait polymorphisms are based on the adaptive dynamics framework, they describe only eco-evolutionary dynamics under a restricted subset of mutation distribution and frequency [108,109]. Individual-based models have also tackled and predicted the evolution of dispersal polymorphisms [72].

3.3.2. Dispersal syndromes

While a number of studies concentrate on predicting the evolution of dispersal only, others have tackled the evolution of dispersal syndromes, i.e. of the set of traits coevolving with dispersal—or of values of other traits associated with high dispersal [110] (figure 2c). Natural candidate traits that are bound to be associated with dispersal are survival to dispersal [79,111] and habitat selection [112,113]. Other less intuitive candidates include traits that determine adaptation to local conditions (local adaptation per se [114] or self-fertilization rates [34,64,65]), and traits resulting in either the same kin competition aversion (altruism and cooperation [115,116]) or in the same bet-hedging strategy as dispersal (e.g. dormancy [117–119]).

3.3.3. Spatial structure

One fruitful aspect of research on the evolution of dispersal comes from the study of the spatial structure of dispersal abilities, for example, when the environment varies along a qualitative gradient, or when the focal species is invading a novel environment [120–124] (figure 2e,f). Such studies aim at describing the spatial variation of dispersal traits along invasion waves or in response to habitat structure, and thus predict ecologically meaningful quantities such as invasion speed [125,126] or the latitudinal range of a species' distribution. In heterogeneous environments, dispersal evolution has mostly been studied through simulations while, by contrast, analytical approaches to diffusion–advection models have been used to study the evolution of dispersal in homogeneous environments or when invasion is considered at the landscape scale [113,127,128].

It is important to note that predictions of the spatial structure of dispersal will depend on the ecological scenario underlying the spatial structure of habitat. Three broad scenarios are distinguished in the literature [65]:

• (i) metapopulations in which migration among patches is bidirectional;

• (ii) mainland–island systems in which migration goes only from mainland to islands; and

• (iii) waves of advance where dispersal is expected to evolve as habitat becomes filled with more and more individuals or range shifts under changing conditions.

Between cases (i) and (ii), there is a continuum of scenarios that account for partially biased migration patterns [36]. Case (iii) can refer both to invasive species spreading onto new grounds [120,129], or to species evolving in response to environmental quality shifting in time (e.g. to mimic climate change [130–133]).

3.4. Evolutionary dynamics of dispersal

Theoretical work on the evolution of dispersal mostly proceeds through two main methods: analyses and simulations. While simulation work is bounded only by a modeller's proficiency with code writing, computer power and their ability to subsequently analyse the obtained simulations, analytical approaches are constrained by the state-of-the-art on the assessment of mutant invasibility analyses. Here, we briefly describe the different ‘roads to analytical predictions’ that have been used to understand the evolution of dispersal, with a clear articulation between how these methods handle evolutionary dynamics and spatial structure, and how their approximations impair or improve the study of certain selective pressures. This section ends with a short discussion on the pros and cons of analyses versus simulation models of the evolution of dispersal.

3.4.1. Fitness and spatial structure

When modelling the evolution of a trait-like dispersal, three elements are needed to be able to compute evolutionary trajectories and outcomes:

• (i) How is the trait under study inherited?

• (ii) How do mutant trait values arise?

• (iii) How does the trait affect individual fitness?

Regardless of the trait and of its genetic architecture, the processes of inheritance and mutation are bound to trade-off at some point—genetic transmission cannot be both perfectly accurate and innovative. How dispersal is described in terms of genetic architecture, and hence of transmission, has already been reviewed above (section ‘Genetic determinism of dispersal’). Thus, only remains the issue of describing the fitness effects of dispersal.

In well-mixed populations, mutant fitness corresponds to the growth rate of a population of initially scarce mutants [134]. What needs to be understood is that mutant invasion fitness is not a growth rate per se, but rather a criterion for the instability of the system in the absence of mutants. This can be seen when looking at populations with age- or size-structure, in which fitness is described by the dominant eigenvalue of the corresponding demographic transition matrix [135]. The idea behind this is that the typical ‘scarcity’ of an initial mutant population may be biased towards, e.g. young life stages when mortality accelerates with age. This typical scarcity is given by the eigenvector associated with the dominant eigenvalue of the demographic transition matrix, because all deviations from the structure defined by this eigenvector will inevitably decrease as they are associated with lesser eigenvalues of the matrix.

The crux of defining fitness thus resides in understanding the ‘typical scarcity’ and associated growth rate of a mutant for the dispersal trait. In patch models with global dispersal, one fruitful approach is to exploit the formulation of the metapopulation state in terms of classes of mutant abundance (with a metapopulation transition matrix between mutant abundant classes) and use the R_m criterion, derived in a fashion similar to the fitness of stage-structured population described above [88,94,105,106]. In patch models with local dispersal (i.e. graph models where nodes are patches), this approach becomes restricted to the case of regular graphs [68], as heterogeneity in node degrees will lead to correlations between local mutant abundance and patch location within the network. In diffusion–advection models, dominant eigenvalue-based methods have been developed using a decomposition of potential solutions in a series of waves with different speeds and frequencies [136]. In stochastic differential equation point-process models, the use of perturbation theory at the limit of large dispersal scale allows for the computation of a dominant eigenvalue representing the fitness of a rare mutant in a resident population at steady state [41,137]. This last method is promising as a general recipe to model the evolution of dispersal kernels, and in particular performs better than classical moment closure methods (e.g. [138]). However, the approximations underlying this approach restrict its use to the case of large-scale dispersal (i.e. when the effective degree of ‘patches’ as nodes on a graph amounts to 10 or higher).

3.4.2. Selective pressures and mathematical approximations

Because all models are wrong at least concerning one (or more) of their underlying assumptions, it is important to remember that each of the methods developed to obtain analytical results on the evolution of dispersal, described above, may be inadequate to account for certain selective pressures:

• (i) mean-field approaches (e.g. [14,22]) are particularly ill-suited to account for kin competition effects. Even worse fitted to this job are models that assume infinite population size, or continuous space models with localized competition (such as diffusion–advection models in which competition happens only between ‘individuals’ occurring at exactly the same location [139]);

• (ii) continuous-time models can hardly tackle questions about the effect of semelparity, life cycles or other characteristics linked to the precise life history of the species under study [46,57–59,61];

• (iii) as soon as competition for resources or space is introduced into the model, the calculation of fitness becomes complicated (as highlighted in the previous subsection) and gives rise to frequency-dependent or density-dependent selection. Thus, trying to ‘bluntly optimize fitness’ is not a good modelling strategy under such assumptions [65,140];

• (iv) when dispersal costs or carrying capacities are spatially heterogeneous and/or temporally variable, attempting to model the evolution of the migration parameter (measuring the proportion of immigrants among recruited offspring) is an ill-suited approach, because migration will be differentially constrained in patches with different carrying capacities or dispersal costs (e.g. [43,44]); and

• (v) when modelling the effects of environmental variability or heterogeneity on the evolution of dispersal, it is worth keeping in mind that natural settings are rarely separated in clearly different types of patches with different habitat quality. Instead, nature is more blurry. Changing the classic theoretical formulation of environmental heterogeneity from discrete to continuous would be much more useful to the empiricist.

3.4.3. Relative merits of simulations and analyses

While we have mainly discussed the different ways to obtain analytical results on the evolution of dispersal so far, using simulations has to be reckoned as a helpful exploratory approach as well. Many individual-based models on the evolution of dispersal have been able to pinpoint interesting phenomena in contexts that are too complex for analytical methods, e.g. on the link between accelerating invasion waves and selection for dispersal [141], on the evolution of dispersal during range expansion [142–145] or on the evolution of movement rules in patchy landscapes [91,146]. Simulation studies are also capable of disentangling more subtle effects of multiple selective pressures on dispersal, e.g. teasing apart the roles of kin versus individual selection in the evolution of dispersal [147].

It should be noted that both analytical and simulation approaches have their own merits and that, for sufficiently complex questions, e.g. arising from the combination of different selective pressures or in non-equilibrium conditions, striving to use both approaches is the best path to answering them. The advantage of simulation methods is that they can address complex questions ‘by brute force’, i.e. as long as the modeller is clear as to what ingredients to put in the model, simulations can be run and results can be obtained. However, the attached drawback is that simulations have intrinsically poor predictive power, insofar as one cannot extrapolate results obtained with some parameter values to other parameter values without running new simulations. Statistical analyses of large simulation data are sometimes difficult, especially when simulations run with the same parameter values show high inter-replicate variability. Analytical methods, on the other hand, are predictive by essence, i.e. results are predictable from a given equation, and hold as long as assumptions underlying that equation are not violated. However, analytical methods can be constrained by the sheer complexity of a question, and even rough approximations might not help. As a rule of thumb to empiricists, complementing analytical approximations with simulations is always a wise move, as simulations may help confirming or infirming the validity of approximations, and, hence, help question the nature of approximations that can be made to obtain predictions in different situations.

4. Perspectives

4.1. Empirical considerations

Connecting theoretical models to data in evolutionary ecology is a difficult endeavour for several reasons, mainly because experimental manipulations involving evolutionary processes are often lengthy, and because field data bring only information about correlation, not causation. Yet, models on the evolution of dispersal need empirical testing.

Experimental evolution of dispersal traits needs to design a spatially structured device, where organisms can express different dispersal abilities. Artificial selection for dispersal traits may focus on a proxy of dispersal, like mobility (e.g. using wind tunnels [148]), the proportion of winged morphs (e.g. in aphids, planthoppers, crickets, etc. [149–151]), the proportion of seeds with explicit dispersal traits (e.g. pappus [152]), etc. Dispersal among populations can also be measured through capture–mark–recapture experiments. When directly measuring dispersal, experimental studies have mainly used two-patch settings—either small patches in Petri dishes [29,153], or larger ones [154]. More complex settings have also been set up for small organisms (e.g. linear stepping-stone habitats [155,156], or a set of connected patches for beetles and their parasitoids [157]). In the past decade, large-scale experiments aiming at measuring dispersal of middle-sized organisms were set up in artificially fragmented landscapes (e.g. measures of bird dispersal at the Savannah River Site, [158]). Another example is the Metatron, a structure of 48 patches of 100 m² arranged on a grid and connected by corridors, which allows to study dispersal behaviours of small animals over months to years [159].

Field data provide weaker tests of theories than do experimental tests, since causes and consequences may not really be disentangled in the absence of manipulation, and since diverse factors may interact to select for or against dispersal. If field data cannot be used to prove a particular theory, they may help disprove it [43,160,161], provided adequate proxies of dispersal and selective pressures are available. For example, if one were to assess the selective pressures driving the evolution of dispersal in a planthopper species, one could assess the possible influence of kin competition using joint measures of population size and relatedness. However, to assess whether spatio-temporal variability in reproductive success is sufficient to drive the evolution of dispersal is a lot harder. Notably, spatial heterogeneity and temporal variability ought to be quantified on a scale related to that of the studied organism [160].

Ideally, field data-based assessment of theories on the evolution of dispersal should be based on strong statistical tools, e.g. goodness-of-fit indices like the Akaike information criterion [162]. For empiricists to be able to test among different models, theories need to move from general to precise predictions, e.g. by providing a sampling theory [163] of realized dispersal distance within landscapes. In practice, such a theory could be tested using information on local and landscape characteristics of interest (perturbation frequency, grain of spatial heterogeneity, etc.) and on dispersal of samples of individuals. Because dispersal distances might not always be readily measurable, proxies may be used, such as genetic indicators of spatial structure (measures of relatedness [164] or assignment tests [165]). When competing theories on the evolution of dispersal are able to provide unique predictions on the expected realizations of such samples, a strong test of the theory will be at hand.

In order to become testable, models on the evolution of dispersal need to derive sufficiently cleaving predictions on, e.g. trait associations, age-trait, population age-trait and spatial trait correlations, which can be used to disentangle the influence of selective pressures on the evolution of dispersal. When field data on the dispersal of species are associated with data on the co-occurrence of focal species and their natural enemies, they could be exploited to obtain weak tests for or against the effect of natural enemies as an incentive for higher dispersal rates. In short, modellers need to rethink the way they formulate predictions on the evolution of dispersal, to (i) emphasize differences with existing predictions, (ii) yield directly testable predictions.

An important effort to be made in order to connect models and data on the evolution of dispersal lies with uncovering the existing mismatches between areas which have been heavily studied on one side and very little on the other. For example, empiricists have shown great interest in testing whether and why dispersal could be sex-biased [31,166,167], condition-dependent (depending on food level [168], on the local density of conspecifics [155], on brood size [169], on parasite load [156] or on temperature [170]) or in testing whether habitat persistence [153], kin competition [155,171,172] or habitat fragmentation [154,173] actually affect the evolution of dispersal. Other related issues with potential immediate applications, e.g. the existence of accelerating invasion fronts due to the evolution of dispersal [148,174], have also been investigated more heavily from the empirical side than from the theoretical one. Yet, many theoretical predictions remain scarcely tested, e.g. those linked with dispersal as a mechanism to avoid inbreeding or outbreeding depression, or predictions linking population dynamics to the evolution of dispersal. This occurs despite some models yielding ready-to-be-tested predictions, e.g. ‘In a metapopulation in which the dispersal rate is at its evolutionary endpoint the unrelatedness approximately equals the reciprocal of the dispersal rate minus twice the characteristic return time of the local population divided by the average lifetime of a patch.’ [77, p. 2394]. Other readily testable predictions include relating carrying capacities in a metapopulation with the occurrence (or not) of polymorphisms in dispersal, and with the levels of dispersal observed in differently sized patches [43], or checking whether species submitted to strong Allee effects are less likely to evolve higher dispersal and, thus, to become invasive [175,176].

To caricature the existing imbalance between the states of theories and empirics on the evolution of dispersal, empirical studies have been quite focused on highlighting costs of dispersal and their effects on limiting the evolution of high dispersal rates, while theoretical models have explored many different selective pressures, but rarely provided precise predictions on eco-evolutionary feedbacks between population dynamics and the evolution of dispersal [97]. Few models link dispersal with population dynamics (but see [51,52,97]) or with local adaptation (but see [64,114,169]). Advancing these two avenues of theoretical research will probably bring some testable predictions that are still lacking. Moreover, these could also bridge the gap between theory on the evolution of dispersal and data on differences in range size among species with different dispersal rates [177] or different abilities to track climate change [178] and will also help in understanding differences in mobility among species at different trophic levels or in different functional groups [179,180].

4.2. Five emergent issues about the evolution of dispersal

Arguing that empirical studies need to feed on current theoretical results and vice versa is not sufficient to make a scientific field move forward. Having reviewed the literature on the question of dispersal evolution, we want to propose, as an ending to this review, a list of five key issues that might be addressed in the near future, provided that experimentalists and theorists collaborate more than they used to:

• (i) How do transient or non-equilibrium population dynamics affect the evolution of dispersal? Though some theoretical papers have tackled part of this issue [51,52], this topic has never really caught evolutionary ecologists' interest enough to be developed, both theoretically and experimentally. From what is now known about rapid evolution, especially in short-lived organisms (e.g. [181]), tackling how population cycles or the replenishment of resource pool might impact the evolution of dispersal in bacteria may be useful for disease treatments.

• (ii) What are the links between the evolution of dispersal and the ability of a species to invade a new environment? Theoretical models and empirical data seem to indicate that selection for dispersal accelerates invasion waves [8,141]. However, there is still much to be developed on this subject, in particular, regarding the different ways in which we could exploit knowledge on the evolution of dispersal to compare different schemes aimed at curbing invasions, similarly to the framework proposed to compare vaccination targets using knowledge on the evolution of virulence in pathogens [182]. Likewise, answers to this question could help predict the effects of climate change on species extinctions through the understanding of how dispersal evolution could effectively serve as ‘evolutionary rescue’ for polewards moving species. Indeed, the probability of evolutionary rescue in metapopulations strongly depends upon dispersal [183].

• (iii) Can we relate movement patterns to dispersal in animals or, more generally, how do we make a connection between micro- and macro-scale considerations on the evolution of dispersal? This is clearly an emerging topic for theoreticians [91,145,146], but it would successfully feed on tracking data collected by field ecologists on, e.g. marine birds, turtles, large mammals, etc. This question would need to delve into the costs associated with information gained about the environment [33], and the impacts of these cues and their costs on the evolution of condition-dependent dispersal.

• (iv) How do habitat spatial structure and connectivity affect the evolution of dispersal? Even though some theoretical works have been studying the effect of patchy landscape structure and spatial autocorrelation on the evolution of dispersal [41,42], we still need the equivalent of Ohtsuki and Nowak's framework [68] to study the evolution of traits affecting population structures on irregular graphs. This would allow for the identification of ‘sources’ and ‘sinks’ due to the combined effects of habitat heterogeneity and local dispersal evolution [184]. Because the new wave of experimental facilities designed to study dispersal evolution can be thought of as ‘small-size networks’ of patches (see, e.g., the Metatron facility [159]), such a theory would help in predicting and interpreting the results of experiments run in such facilities.

• (v) How can we apply knowledge on the evolution of dispersal to biological conservation issues? When models predict the emergence of a polymorphism in dispersal, high- and low-dispersal types tend to segregate across the landscapes [184], e.g. when carrying capacity varies across space, highly dispersing types tend to be associated with small patches [43]. Thus, it seems straightforward to ask whether we can make use of such models to predict the effect of landscape alterations on the polymorphism of dispersal within a given endemic species, and whether these alterations will indirectly fuel the extinction of this species or not through dispersal evolution. More generally, when human impacts on the environment affect the carrying capacity, fecundity or mortality rates of a given species, knowledge of how dispersal tends to evolve in response to these changes can help predict migrational meltdowns [185], and ways to prevent them.

Glossary

Adaptive dynamics

a mathematical framework aimed at studying the evolutionary dynamics of phenotypic traits [102]. Adaptive dynamics relies on two main assumptions: (i) mutations are rare and (ii) of weak effect. Based on these two assumptions, analyses are performed so that, at any moment, the population consists of a given number of resident strategies (initially, one) and one mutant strategy equipped with a trait value infinitesimally close to one of the residents'. Evolutionary trajectories are obtained through the computation of the mutant fitness, the ensuing selection gradient (first-order derivative of the mutant fitness with respect to mutant trait value) which determines evolutionary trajectories through the ‘canonical equation’ [186], and second-order derivatives defining the convergence and evolutionary stability of the coalition of phenotypes [103].

Colonization

a process by which a species or genotype invades a patch still devoid of the focal species or genotype. The ‘colonization rate’ has been popularized by R. Levins' metapopulation model [76] in which species are alternately present or absent from patches, following extinction and colonization processes. The metapopulation paradigm can be related to more detailed descriptions of within-patch demographics [187–189], with a natural interpretation of colonization as the result of dispersal, survival and successful build-up of a new population [77].

Dispersal

dispersal can be defined in different ways. The most commonly admitted definition of dispersal is ‘any movement of individuals or propagules with potential consequences for gene flow across space’ [5, p. 232]. On the one hand, for zoologists, dispersal involves the movement of individuals, at any life stage, between the birth place (or a former breeding site) towards a new breeding site [83]. Botanists, and zoologists interested in sessile organisms, on the other hand, tend to consider dispersal as a two-sided process, with gamete dispersal and zygote dispersal being two sides of the same coin [190,191]. While the mode of dispersal in animals is almost always straightforward (but see [36]), plants can use many different modes of gamete and zygote dispersal (see, e.g., [192] for a good glossary of terms). One difficulty linked to defining dispersal without any explicit relation to gene flow is that many animal species move all the time in search of food (foraging movements), so that definitions of dispersal based on spatial or temporal scales of movements are more difficult to formulate [74].

Iteroparity

a species is iteroparous if it can reproduce more than once in a lifetime. Botanists sometimes refer to iteroparity as polycarpy.

Kin competition

the process by which related individuals tend to compete with one another. Strong kin competition selects for dispersal following Hamilton's rule [193,194]. It should be noted that relatedness is influenced by both dispersal and local population size, so that dispersal and relatedness feedback on one another [16].

Metapopulation

a population of populations, i.e. a collection of populations subjected to the processes of colonization and extinction [76,195]. By extension, in the context of dispersal evolution, subdivided populations (i.e. collections of populations subjected to dispersal but not to extinctions) have been termed metapopulations (e.g. [43]).

Migration

in population genetics, migration is often used as an equivalent for dispersal. Migration rates specifically relate to the proportion of the next-generation gene pool that is contributed by reproduction events outside of the focal patch (e.g. [196]). As argued in the main text, substituting migration for dispersal in models of phenotypic evolution can lead to confusion because dispersal cost and differences in population sizes among patches are implicit in the migration formulation, while they are explicit in the dispersal formulation.

Quantitative genetics

a mathematical framework aimed at studying the evolutionary dynamics of traits. Quantitative genetics relies on the conceptualization of phenotypes as the sum of a genetic and an environmental effects [197, eqn. 8.11] and assume by default that all traits follow Gaussian distributions given a proper transformation (because of the assumed large number of loci underlying the trait). The central analytical tenet of quantitative genetics is the ‘breeder's equation’ which predicts the response to selection based on the value of a trait's heritability [197, eqn. 11.2].

Semelparity

a species is semelparous if it can reproduce only once in a lifetime, usually at the very end of its life. Annual plants, some fish (e.g. salmons), some arachnids, insects and squids are some of the best-known examples of semelparous organisms. Botanists sometimes refer to semelparity as monocarpy.

Syndrome

an association of values of different phenotypic traits due to selection (figure 2c). For a syndrome to exist, there should be at least one reason for divergent selection of different trait values across habitats. Syndromes should not be confused with standing genetic variances and covariances, which specify how traits co-vary (within a population or metapopulation) as a consequence of mutation (with potentially pleiotropic mutations affecting more than one trait at once), recombination (linked loci would statistically co-vary), selection, drift and migration (figure 2d). A syndrome does not emerge as a result of a trade-off either (i.e. a constraint on trait values due to physical or chemical constraints).

Funding statement

A.D. was funded by the French Agence Nationale de la Recherche (project EVORANGE ANR-09-PEXT-01102). F.M. was supported by the CNRS.