Biological information: why we need a good measure and the challenges ahead

Abstract

Evolution can be characterized as a process that shapes and maintains information across generations. It is also widely acknowledged that information may play a pivotal role in many other ecological processes. Most of the ecologically relevant information (and some important evolutionary information too) is of a very subjective and analogue kind: individuals use cues that may carry information useful only to them but not to others. This is a problem because most information theory has been developed for objective and discrete information. Can information theory be extended to this theory to incorporate multiple forms of information, each with its own (physical) carriers and dynamics? Here, I will not review all the possible roles that information can play, but rather what conditions an appropriate theory should satisfy. The most promising starting point is provided by entropy measures of conditional probabilities (using the so-called Kullback–Leibler divergence), allowing an assessment of how acquiring information can lead to an increase in fitness. It is irrelevant (to a certain extent) where the information comes from—genes, experience or culture—but it is important to realize that information is not merely subjective but its value should be evaluated in fitness terms, and it is here that evolutionary theory has an enormous potential. A number of important stumbling points remain, however; namely, the identification of whose fitness it concerns and what role the spatio-temporal dynamics plays (which is tightly linked to the nature of the physical carriers of the information and the processes that impact on it).

1. Information is a central concept

That information is a key concept in evolution is obvious, as it is well known how natural selection is continually shaping genetic information carried by DNA [1,2]. However, information plays an important role in ecology too; for instance, optimal foraging theory [3] shows how predators modify their behaviour in response to changes in their environment, while at the same time prey may change their defensive behaviour [4]. In fact, the link between ecology and evolution often involves information in one form or another. A phenotype can be seen as the ecological manifestation of genetic information. Natural selection, on a larger time scale, encodes ecological adaptation into genetic information. More and more researchers focus on information as a structuring concept in ecology and evolution, next to the classical ones of matter and energy [1,5–7]. How information plays an important role in ecology and evolution is well illustrated by the following examples.

1.1. Behaviour and phenotypic flexibility

It is well known that individuals of many species use information about their environment to modify their phenotypes. Sometimes the information is relatively easy to identify, such as predator cues inducing defensive phenotypes [8], but it is likely that in many cases we do not really know what (if anything) individuals respond to and why. Better ways to assess information use will help us to better understand the causes and consequences of phenotypic plasticity.

1.2. Dual inheritance systems

The avalanche of DNA sequence data that is descending upon us shows that some vital traits are actually not coded by DNA but are controlled by epigenetic mechanisms [9]. Because these traits are nevertheless at least partially transmitted to offspring, this implies that other forms of information are transmitted across generations next to that carried by DNA [6,10–12]. Epigenetic information, in particular, is often seen as a way that allows individuals to transmit acquired traits or information about their environment (e.g. parasites) to their descendants (often called maternal effects) although the effect may travel further down the pedigree.

1.3. Game theory

The outcome of games may fundamentally change if players are allowed to communicate. Bargaining games, for instance, may lead to higher levels of cooperation than when communication is not allowed [13,14]. What is a bit surprising, however, is that the information that is exchanged during the bargaining bout usually remains implicit [15]. Such bargaining interactions may explain the maintenance of cooperation between unrelated mutualists such as plants and their rhizosphere partners [16,17].

1.4. Non-human communication

It is obvious that many organisms communicate, but typically we do not know their language [18,19]. We may have an idea what its function is (mate attraction, coordination, threatening, etc.) but usually we can state very little about precisely what information is transferred and how it affects individual decisions [20,21].

1.5. Information-dependent dynamics

Because many organisms respond to environmental cues, their fitnesses and thus their population dynamics depend on the information that is available [5]. Ecology is often seen as the science of fluxes of matter and energy, but it is becoming clear that fluxes of information may have important consequences too. Ecosystems are effectively bathed in information—visual, auditory and chemical (Schoonhoven [22] compared the perception of the world by many insects to the highly sensitive antagonist in the novel Perfume by Süskind [23])—but how to assess its importance and the ecological consequences is not at all obvious even though it is clear that the consequences may be many and varied [24].

1.6. Adaptation

An alternative way of defining adaptation is having the necessary information to solve a given life-history problem [25]. The dual inheritance problem of assessing multiple sources of information comes back here in full force: the necessary information can be genetically or epigenetically encoded, but also maternally transmitted, acquired individually or learnt culturally. It may even be a different organism that provides the information, as is the case for many mutualistic symbioses. There is even a name for this concept: the ensemble of genetic information formed by a host and its suite of symbionts is called the ‘microbiome’ [26].

In all these cases, the pivotal interactions are non-trophic and usually even non-material. Cues produced by and responded to thus play an essential role in ecology but the information itself carried or implied by these cues often remains implicit, at least unquantified. Even in game theoretical models that do consider information exchange, the consequences are typically only inferred from contrasting the outcome with and without information transfer [27].

2. Why we need to have a biological definition of information

The concept of information is central in any theory that attempts to integrate different forms of evolution [6] or even in many attempts to generalize the concept of adaptation [25].

However, to make the role of information explicit, we need a way to quantify it, and currently we do not have a satisfactory measure for assessing how much information is created, transferred and stored in ecosystems. As I discuss below, one can quantify the information stored in DNA, but this is not enough. I discuss first, therefore, why, in a biological context, precisely those aspects need to be incorporated so that standard information theory is simplified. It is of course also possible to interpret gene frequencies as probabilities and assess how entropy measures of these probabilities evolve over time. Frank [2] shows how it is possible to quantify genetic information this way and that it increases as a consequence of natural selection, but, as I argue, a biological theory of information should be applicable to other forms of information too. Ideally, one should be able to compare genetic information with information acquired from other sources.

3. Why entropy-based measures do not suffice

Anyone interested in quantitative aspects of information ends up studying information theory and its links with entropy, such as has been developed in thermodynamics and communication theory. However, straightforward application of standard information theory to ecology and evolution is difficult.

Entropy measures were developed in the 1940s by Shannon [28] to address the very important issue in radio communications that any signal carrier will be affected to some extent by noise, so that there is a limit to the amount of information that can be transmitted. If the sender and receiver have agreed upon a common code, this amounts to the questions of how many bits the message contains and how many extra bits may have to be added to minimize corruption of the transmitted message through the noisy channel.

Given that there are four DNA bases, a basepair can be said to contain two bits of information. Using Shannon's equation, the entropy of a stretch of DNA can thus be calculated easily. Given the fact that the genetic code is redundant, one can also calculate the entropy of a transcribed stretch in terms of triplets (amino acids) but this does not fundamentally affect the discrete nature of this form of genetic information. Frank [2] has used this idea to assess the dynamics of genetically encoded information.

However, it is now clear that not all information that is transmitted from generation to generation is in the form of DNA [9,11]. For instance, the effect of some genes depends strongly on their methylation states, and these methylation states are to a certain extent heritable [29]. Many other so-called epigenetic inheritance mechanisms exist [9], and typically the epigenetic information is of a much more fuzzy (analogue) nature (methylation of genes comes often in grades rather than discrete states). So how do we measure the information content in such parallel inheritance systems? Day & Bonduriansky [11] have published a series of papers to study what happens when different inheritance systems combine. They show that through differential effects of mutation and transfer mechanisms, the interaction may have unexpected outcomes. However, their approach is less well suited to serve as a basis for quantifying information because it is based on the dynamics of average phenotypes in the population (traits) rather than in individual (epi-)genotypes.

Shannon's theory defined the bit as the binary unit of information, of fixed but arbitrary value. This concept eventually led to our capacity to digitize information and, with it, the possibility to design electronic circuitry to handle this. Assuming information can be coded as arbitrary bits was thus tremendously successful. However, it also prevents application of the theory to cases where information is not fixed and of universal value. In the biological reality (but actually the probably most important part of human life too), information has variable value, depending on who is detecting it and under what conditions. That is, information is fundamentally subjective and this subjectivity is not normally taken into account (except in conditions when shared knowledge can be used to design more efficient data compression algorithms [30]).

4. Subjectivity

The first necessary extension of information theory is thus that it needs to incorporate subjectivity, in the sense that the same cue or signal may mean different things to different receivers (in general, a cue can be anything detectable, whereas a signal is produced by a sender with a certain intention). The Shannon–Weaver theorem states that information reduces uncertainty but it is often actually unclear to whom or in respect to what [31]. Although it is asserted by many that there is a link with entropy, it is rarely pointed out that this implies that a priori knowledge plays an important role. In a largely forgotten paper, Bateson [31] developed the crucial insight that we should compare the entropies of the receiver with and without the message. Recently, it has been noted that information has a strong link with regulation, where ‘feed-forward’ information (cues) interacts with historic, or ‘feedback’, information (set points) [32].

Information is fundamentally subjective also in the sense that it depends on what a receiver can do with it [32–34]. In evolutionary terms, the question is how the perception of a cue enables an individual to increase its expected fitness. To assess the impact of information, we thus need to know (i) what the individual ‘knows’ already and (ii) how it can use the information provided by the cue to modify its phenotype or behaviour to increase its fitness.

So to start with, to understand the role of information one has to appreciate also that prior knowledge plays a crucial role. This prior knowledge can have many sources: genetically fixed thresholds, biochemical pathways, hard-wired behaviour, learnt experiences, culture, etc. But, in every case, a cue should be evaluated against this background which makes it subjective, because no individual even from the same species will have the same knowledge as any other. Bayes' theorem thus plays a central role because this is the mathematical construct one needs to assess for differential knowledge. Given what you already know, what can you infer from a given cue? However, to incorporate fitness we need to know not the actual value (if it exists) but rather the effect it has on expected fitness. This implies that we need to take the expectation impact on fitness. And when one takes the expectation, one obtains a version of the so-called Kullback–Leibler divergence, which is in essence the entropy of conditional probabilities. It may not be possible to quantify the ensemble of prior knowledge, but it should certainly be possible to assess the information content of a given cue this way.

5. Quantifying information

As an instructive example of how biologically relevant information can be quantified, consider the following: an individual of a given prey species, say a mouse, finds itself in front of a bush, behind which can be found either some food or either a fox or a cat, with absolute probabilities p = (p_food, p_fox, p_cat) = (0.8, 0.1, 0.1). Now suppose it perceives a certain smell that can only be made by a fox: this cue thus tells the prey that the probabilities are not p = (0.8, 0.1, 0.1) but in fact p′ = (0, 1, 0). By taking evasive action, it can therefore save its life and increase its fitness from 0 to 1 (it survives but consumes no food). The fitness value of the information provided is thus 1; I return to this notion below. Suppose now, however, that only a less revealing cue is available, say one that only allows the adjustment of probabilities to p′ = (0.6, 0.3, 0.1). How much information does the cue contain?

The extent to which the cue provides information is often linked to the difference between the a priori probabilities p and the adjusted probabilities p′. In standard information theory, the information gain provided by the cue is often formalized using the so-called Kullback–Leibler divergence [7,30],

5.1

which, like information entropy, is measured in bits. (Note that this quantity is only defined if all p_x > 0, that is, if the a priori probabilities do not contain certainties. It is also worth noting that Kullback–Leibler divergence is not symmetric, and that the inverse does not even always exist.)

If the cue does not provide any information, 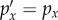for all x and hence D_KL is zero. If the cue does provide information, some outcomes will become more likely (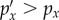), whereas others become less likely (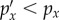). It is not intuitively obvious but can be shown that the Kullback–Leibler divergence is always positive [30].

As an example, the perfect cue in our example contains

5.2

bits of information, whereas the imperfect cue only contains

5.3

bits.

Mathematically, the Kullback–Leibler divergence allows us to assess how much arbitrary certainty is gained. But how is this gain linked to the fitness of our hypothetical prey animal? If our individual inspects the space behind the bush without any supplementary information, it will be dead with probability 0.2, but with probability 0.8 it will find some food, good for, say, R offspring. Its expected fitness is then 0.8 · (R + 1) + 0.1 · 0 + 0.1 · 0 (if by fitness we mean the expected number of surviving individuals after the inspection event). An individual that does not explore will survive but will not reproduce either, so its fitness will be unity. Thus, only if R > 0.2 (=1/0.8 − 1) does it pay for our potential prey to inspect, even if there is a lethal danger lurking.

How does the presence of a revealing cue affect the prey's decision and fitness? We have seen that the perfect cue revealing the presence of a fox allows the prey to save its life and that represents a fitness value of 1. But what if the cue is imperfect? Inspect or not? If it goes to inspect, it will now have an expected fitness of 0.6 · (F + 1) + 0.3 · 0 + 0.1 · 0 (if it stays put, it will have again an expected fitness of just 1). It should inspect only if R > 0.666 (=1/0.6 − 1): it ‘knows’ of the increased danger so the potential benefit should be larger.

6. Fitness equivalents

Using mainstream evolutionary theory as a starting point, the value of information is not necessarily its surprise value (how unlikely it is [30]) but rather how it can be used to increase fitness. A number of recent studies show how one can evaluate the value of the information in terms of fitness [32–34]. These studies show how information in the form of cues can be used to improve the match between phenotype and environmental conditions (phenotypic plasticity). A fundamental consequence is that information can only increase expected fitness: a cue that would decrease fitness is simply ignored.

Here, I will discuss how we can use these results to arrive at a means to quantify information in a way that biologically makes sense. McNamara & Dall [34] and Donaldson-Matasci et al. [33] illustrate their analyses using the example of bet-hedging as a reproductive strategy. Here, I will try to focus more on the role of the correlation between cue and environment in a more general setting.

Consider, for instance, an individual of a given species that perceives a certain cue, denoted by Q (which can attain a certain number of values 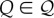). Suppose also that this individual possesses an a priori body of knowledge (K) of an unspecified origin which will allow it to achieve a certain expected lifetime reproductive success (fitness) F_K, even in the absence of extra information. For notational clarity, I drop the variable K from what follows.

Now assume that the individual has some behavioural response to cue Q, which I denote R_Q, and that this response is adaptive in that it leads to an increased expected fitness of .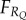

One can suppose that in a fixed, completely predictable world the individual (through natural selection) is fully adapted, and thus possesses all the necessary information (in its a priori knowledge K), so that it does not even need to respond to the cue. Things change in fluctuating environments, however, in particular when individuals are uncertain about relevant aspects of their environment. Then, the cue may provide crucial additional (typically more actual) information allowing an increase in fitness.

Following recent studies [32–34], I suppose that the environment E fluctuates unpredictably between a number of states, and that there is a positive correlation between the environment E (itself undetectable) and a detectable cue Q. The fitness associated with a response to the cue Q then depends also on the actual value of the environment, so I write 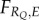. We can model the unpredictability of the environment by assuming that, at any given instant, the value of the environment and the value of the cue are given by a joint probability distribution, 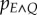with 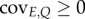(so that Q does provide information about E).

The probability that the state of the environment is E when the individual perceives cue Q is given by the conditional probability

6.1

where p_Q is the marginal distribution of Q,

6.2

(the sum is over the domain of E, denoted as ℰ).

Thus, the expected fitness increase of an individual that perceives Q (and responds to it with R_Q) is given by

6.3

where

6.4

is the fitness increase owing to the response R_Q in environment E. McNamara & Dall [34] call this the ‘reproductive value’ of the information, but I feel ‘fitness value’ [33] is a more appropriate term.

Donaldson-Matasci et al. [33] and Rivoire & Leibler [32] work out the consequences using the concept of ‘mutual information’ (which measures how much of the entropy is determined by correlation) but insight can also be gained by phrasing the problem in terms of the covariance of cue and environment. We can always write

where the covariance between E and Q is cov_E,Q (which may be constant but also depend on E and Q). Then, p_E|Q = p_E cov_E,Q, and the fitness value (6.3) can be rewritten concisely as

6.5

where the pointed brackets indicate the average over the environments (p_E). The expected fitness increase is thus linked to both the covariance between cue and environment (cov_E,Q) and the fitness increase a response permits (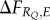). If there is no covariance, information value is zero. But, even if there is a covariance, if there is no associated fitness increment, information is zero too.

Given that the individual will perceive a range of cue values (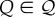) [33,34], its expected fitness increase will be

6.6

In standard information theory, the information content of a particular value of cue Q is simply its ‘surprise value’ [30],

6.7

the idea being that the rarer the cue, the more likely it is it will reveal something about an underlying process. Biological information content, on the other hand, is linked to fitness increase V_Q, which even if it can be written in simple form, as in equation (6.5), is a more complicated concept.

Now is there any way to connect the fitness value of a cue and its surprise value? Let us assume for the moment that the correlation between cue and environment is perfect, cov_E,Q = 1. Then, the value of the cue is directly related to the fitness increment it allows,

6.8

and rarity of the signal itself (i.e. whether p_Q is large or small) plays no role (rarity of the associated environment does).

Rarity may play a role here but only indirectly, via the covariance between cue and environment and the increase in fitness that a response allows. Some insight can already be obtained by inspecting the admittedly completely hypothetical example in figure 1. To start with, the example shows that the potential fitness benefit may not always be that big. It also suggests that values in the centre of the distribution are not as informative as values in the tails. This way, rarity may be important. Thus, in the hypothetical example of figure 1, only the low values of Q are rare and informative.

Figure 1.

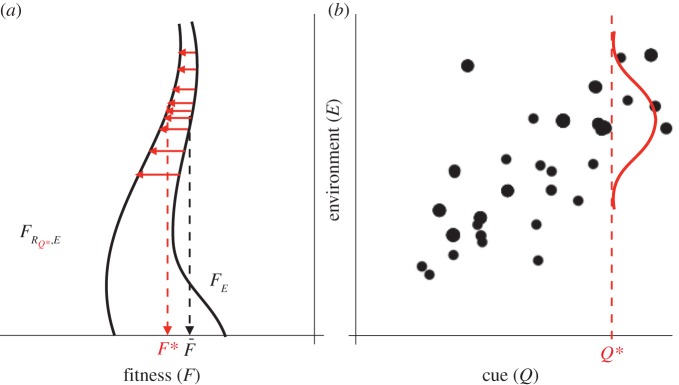
(a,b) From cue to fitness increment. An example (completely hypothetical) of how a cue (Q) may give information about the environment (E) and thus yield an increased fitness 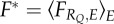, where the expected fitness of an uninformed individual is 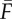. The curve drawn in (b) gives the conditional distribution of the environmental value given a cue Q*. The curves in (a) depict fitness with and without the optimum response (to Q*) to the variation in the environment. The figure illustrates that having correct information about the environment is sometimes more important (here, the difference between 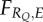and F_E is the largest for low values of E) than at other times (here, high values of E). Given the covariance, the cue therefore conveys more biological information at low values than at high values. (Online version in colour.)

Note that the curve representing the response only shows the dependency responsive and non-responsive individuals on variations in the environment given the response to the particular cue Q indicated in the graph. If the individual perceives another cue, it may respond differently, which may change the shape of the associated curve.

7. A priori knowledge

The role of a priori knowledge can be explored using a more classical approach. Suppose an individual estimates that some hypothesis H (e.g. ‘There is a predator stalking you!’) is true with probability p_H|K, where K stands again for the ensemble of a priori knowledge that an individual possesses.

If the individual's knowledge K is such that the estimate p_H|K corresponds to the true probability, no cue can improve it (D_KL is always zero). Of course in reality no individual possesses perfect knowledge but we can still state that better a priori knowledge will reduce the amount of additional information that is needed.

It is here that it may pay to combine different sources of information, to arrive at better estimates of the actual state of the environment. If there is much to be gained, natural selection may well favour increased capacities for the perception of cues, even if these are costly.

Then, it may actually pay individuals not only to use a priori knowledge to assess the value of a given cue, they may also be selected to update it. Of course an individual cannot typically modify its genetic information (with the exception of some genes important in immunological responses) but it can update other forms of stored information, from implicit to dedicated. An individual's physiological state contains a memory of past experiences (a well-fed prey individual will respond differently to a cue indicating the presence of a predator than a hungry one), but of course many animals have evolved more or less sophisticated cognitive capacities for memory management. Precisely what ecological conditions and specific lifestyles select for more sophisticated information use is a promising area of research.

8. ‘Qui bono?’

This is often asked by the investigator of a crime in old-fashioned detective novels, as who benefits from the crime is automatically an important suspect. In a similar way, we can ask who benefits (‘qui bono’) from a given adaptation, to identify the evolutionary pressures behind it. This question is nevertheless often surprisingly difficult to answer [25].

The fact that information is fundamentally subjective implies that we have to state with respect to whom it is subjective. That is, whose fitness is it that the information increases? Often, of course, it is just the individuals of a given species that use information to increase their individual fitness. Then, it is typically not so difficult, for us, to assess what an adaptation is for [35], as we can assess or estimate fitness in the sense of expected number of offspring. However, I want to stress that, in many cases, the relevant unit is not the individual, and adaptations benefit structures that are either smaller (genes) or larger than individuals, such as clones and symbioses [25,36–38].

The ability to digest grass is not an adaptation of cattle, for instance. That is, a cow alone does not have all of the necessary information to digest cellulose: this information is carried by her symbionts. The ability to subsist on grass is therefore an adaptation benefitting the complex formed by a cow and its suite of symbionts. In the context of this article, the unit of adaptation is that which (or who) benefits from having information, but what this unit is is not always so obvious. Think, for instance, of the network formed by plants and the soil microflora [39]: the exchange of nutrients clearly hints at an adaptive function, but it is very difficult to circumscribe the relevant unit. As virtually everything is formed out of subunits (we also depend on symbionts for digestion and protection), units of adaptation will often depend on information from different sources.

Quantitative genetics is an alternative and very common way to view and model evolution, which focuses on the rate of change of the mean of a given character [40]. These approaches are very useful to understand short-term, non-equilibrium responses to selection but are less suitable for identifying the appropriate unit of adaptation. Using Price's equation is one way to assess the consequences of multi-level selection on trait evolution [41–43], but it is not so obvious how to extend this approach to study multi-species complexes.

Emergent structures may function as units of adaptation even if they are not persistent. For instance, a calf needs to establish a working relationship with its microbiotic symbionts in order to be able to digest grass, but this association stops when the cow dies (and the actual partners may change during its lifetime too). Plants and rhizosphere organisms typically establish a mutualistic (but not conflict-free!) interaction when seeds germinate, which will end with the death of the plant [16,44]. A colony of social insects is typically founded by a mated queen and disintegrates when the queen dies. One can even consider a diploid organism as a temporary association of two haploid genomes.

When units of adaptation are associations of some form, it is important to be precise about what ‘fitness’ actually means. As long as what Maynard Smith & Szathmáry [37] termed a ‘major evolutionary transition’ has not occurred, the complex does not reproduce as a whole, and therefore we cannot directly assign a fitness to it. However, there exist methods to assess the invasion fitness of more loose associations, such as spatial clusters [45,46] or pairs of symbionts [47]. For such cases, the invasion fitness of members may be dominated by the success of the associations they help to form, and in this sense one can associate a fitness with the association. In line with kin selection theory, the end result may hinge on a delicate balance between the interests of different levels.

Danchin and co-workers [6,10,48] advocate a quantitative genetics approach that permits the assessment of different information flows in determining phenotype variation. This is a very promising way to study dual inheritance systems and epigenetics, provided that the units of adaptation (as in any population genetics model; see Buss [49]) are well-defined individuals. When units of adaptation are more short-lived associations, the approach is more difficult to apply, as the crucial technical notion of ‘heritability’ becomes problematic [25].

9. Information carriers

Presenting his views on Dawkin's [36] notion of genes as units of evolution, Williams [50] made the important point that we should separate the physical manifestation of genes from their information content. Evolution, Williams argued, takes place in the information domain, or the ‘codical domain’ as he called it: information gets transmitted and DNA molecules eventually perish. What I wish to argue here is that this insight not only applies to genes, but should also be extended so as to incorporate all of the evolutionarily relevant forms of information: genes but also epigenes, genes from symbionts, various forms of experience, culture and so forth. In this information-based view, individuals (units of adaptation) are merely bundles of information.

This does not mean that physical form becomes irrelevant. On the contrary, the physical aspects of an information carrier determine its dynamics, through its capacity for change, storage and transfer. Different sources and origins of information may have very different kinds of dynamics indeed: some of my genes contain very ancient information, whereas my brain contains extremely recent (and mostly ephemeral) information [6]. The physics of a given carrier may have an effect on interpretation of the information it contains.

To us, the physical support of a message contributes to its meaning because it helps us to interpret it. If we were to encounter a piece of text in an unknown script, we would tend to guess its message differently if the text were hewn in a stone monument than if it were merely scribbled on a piece of paper. In a biological context, a sequence in DNA does not mean the same as the equivalent sequence in RNA: many sequences in DNA are not transcribed and thus potentially irrelevant, whereas an RNA sequence is more likely to be relevant because it has been transcribed, and therefore linked to some particular environmental conditions. Danchin [6] calls the physical manifestation of information its ‘avatar’, which is a generalization of the concept of phenotype [51].

Genetics is characterized by high-fidelity copying over long time scales. The mechanism of neo-Darwinian natural selection ensures that genetic information is generally trustworthy, at least for solving life-history problems that do not change too quickly (are sufficiently predictable). By contrast, epigenetics is characterized by relatively low-fidelity copying [9,29], but it allows coordination/transfer of useful information among members of complex units of adaptation (clones, symbioses, etc.) about a more recent past.

Culture, as it is defined by biologists, functions as an epigenetic system, but more quickly, and it allows horizontal and oblique transfer of information even within generations [52,53]. An as yet unexplored aspect of culture (as far as I am aware) is that it leads to the creation of a collective memory (a ‘shared library’) that allows individuals to access a body of information that transcends by far their own memory capacity.

10. Memes

A few words are appropriate on the idea of memes, as this concept can be said to have started the discussion on the role of the proper dynamics of information in human culture. Dawkins [36] suggested that mental structures can have similar properties, and consequently similar evolutionary dynamics as genes. Memes mostly spread because they are useful for their carrier, but sometimes memes’ spread is even damaging to their human hosts. Notwithstanding popular appeal (to explain itself the concept did spread rapidly in the human population, and there are now probably many people who use the term without realizing that it comes from evolutionary theory), the idea that culture is just a question of memetics hurts important obstacles [54]. In spite of some claims that, in humans, memes have come to dominate genes (‘memes keep genes on a leash’ [55]), few evolutionary biologists believe in the existence of memes as envisaged by Dawkins.

The most important criticism is that, contrary to genes, as far as we know there is no universal code for memes, and consequently how they are copied is far from obvious. Claidière & Sperber [56] argued that, if one wants to follow the dynamics of information, one has to accept that the same unit of information may be embodied (‘encoded’) very differently in different brains, and actually partly loses its identity if it gets transmitted, so that one has to follow all potential manifestations across the stochastic ‘transmission chain’.

If we have a good way to identify and to quantify biological information, we also may have a means to go forward here, as it will allow us to disentangle physical embodiment (cognitive state) and information content. Whether this will allow us to track precise defined units of information (‘memes’) as they spread through a population remains to be seen, however.

11. Information from different sources

A useful method for quantifying information should be able to deal with information from different sources and transmitted by different physical carriers. If these different sources of information are concordant, there is no problem, but what to do when, as will often be the case, different sources of information conflict? The credibility of the sources should be taken into account. Genes may specify useful rules of thumb, but they do not possess information about actual environmental conditions: an individual may very well increase its fitness by ignoring genetic information (hard-wired behaviour) and rely on personal experience instead to improve its options. However, acquired information is not always as credible, in particular when it depends on the observation of other individuals (be it of the same or of other species).

The fact that individuals may rely on information from different sources may provide a new perspective on the Baldwin effect [57]. The Baldwin effect stipulates that individuals explore a set of phenotypes to find a good match with their environment rather than encode all options genetically: phenotypes result from learning rather than from phenotypic plasticity. In this former case, individuals need more information about their environment than in the latter: phenotypic plasticity needs just a good cue, learning needs more information in order to assess the potential fitness returns associated with possible phenotypes.

It can actually also shed light on what might be called the inverse Baldwin effect, genetic assimilation [58], which occurs when acquired traits such as learnt behaviours, when repeatedly acquired by successive generations, will eventually find their way into the genome. This allows individuals to avoid making costly mistakes in the learning process.

Note that both the Baldwin effect and the inverse Baldwin effect integrate genetic and environmental variation to produce a phenotype, only in different measures. Both views merely stress the fact that environmental information is important.

12. Communication

As discussed earlier, in spite of their singular aspect, individuals are often actually complex associations or ‘units of adaptation’ [25]. The mere fact that they are participants means that members have at least partially overlapping interests, so that they are likely to interpret a particular cue in a similar way. However, members of an association may also have diverging (or private) interests that are not shared by other members [47]. Then, a particular cue may incite a response that is advantageous to one but detrimental to other members of the association. In other words, cues may boost but also weaken an association. (For instance, Axelrod & Hamilton [59] note that symbiotic bacteria may turn nasty when they perceive that their host is in bad health.)

The problem thus is that the same cue may mean different things to different members of the association. This is even more pertinent when the cues are actually signals emitted by other individuals in the ecosystem, whose agendas may be suspicious. Moreover, an individual may even need to assess how other partners may respond in order to work out the relevance of the cue [60].

Insight into how information use can be affected by partially overlapping interests can be obtained by considering models for the evolution of communication [61–63]. If individuals have perfectly overlapping interests (both sender and receiver gain equally by successful communication), then natural selection can produce elaborate schemes that permit efficient communication [64], even when initial hurdles have to be overcome (for instance, encoding and decoding mechanisms have to evolve in tandem [65]).

Jansen and van Baalen [66,67] found that for intermediate levels of conflict communication systems may be unstable, leading to cycles where different cues may acquire and then lose meaning. These fluctuations result because honest information use has a rarity advantage but becomes vulnerable to exploitation by cheaters when common, which is a form of negative frequency dependence.

A consequence of these fluctuations is that signals (cues) have no universal meaning: it all depends on who receives them and where and when. The signals can mediate cooperative behaviour because population structure means that cooperators are likely to be surrounded by similar cooperators (so that to them the cues are predominantly informative). Cheaters, on the other hand, are surrounded by other cheaters, so to them the same cue carries much less information. However, even if, on average, the cue contains more information to a cooperator than to a cheater, the respective subjective information associated with the cue may fluctuate in time too [66,67]. In a situation where information users have a conflict of interest, any individual that perceives a signal therefore has to assess its usefulness or its ‘credibility’ when it implies a form of communication.

Also the producers of cues may have to take into account who is listening. Cooperators may want to convey information to other cooperators, but there are eavesdroppers that may benefit without returning favours or worse. In order to optimize fitness, broadcasters should assess evolutionary interests of all parties. These involve not only other participating individuals, but also the compound individuals (units of adaptation) they are part of, with their own evolutionary interests. Cells may be selected to communicate via hormones when the interest of the multicellular organism they are part of predominates. But also in more loose units of adaptation, such as social insect colonies and bacterial clones, members may need to communicate to coordinate actions (e.g. quorum sensing [68,69]).

13. Discussion

By reducing uncertainty, information helps an individual (or whatever the relevant unit of adaptation may be) to adapt to its environment. A simple way to quantify the information content of a given cue is to compare the unit's knowledge vector before and after perception using the so-called Kullback–Leibler divergence. However, this measures information content only in terms of bits, that is, in terms of the number of yes-or-no questions the information resolves. In biology, however, it is more relevant to measure information in terms of fitness effects, which is not the same [2,33].

Developing an adequate theory of biological information poses many challenges. As recent studies have shown [32–34], it is possible to quantify biological information with a fitness-based approach. These authors focus on how individuals should use information to improve their bet-hedging strategies. I would like to argue here that this approach is more general and applies also at both shorter (behaviour) and longer (group selection) time scales.

Assuming that evolution corrects mistakes in a species' genome, MacKay [30] confirms Maynard Smith's original idea that through natural selection an asexual species acquires one bit of information per generation. However, it is not so obvious with what such a bit corresponds. Moreover, his model does not take into account the loss of information through mutation, so this approach serves as a starting point to compare asexual and sexual reproduction but not to quantify ecologically relevant information. We can only understand why some alleles are better than others when we know what they code for and why they encode an adaptation for a given environment.

It would be nice to have some catchy word, in analogy with ‘bit’. Shannon [28] defined the bit, short for binary digit, as a neutral information measure. As biological information is linked to fitness, we can coin the term ‘fbit’ for the notion of a subjective, fitness-equivalent bit. The fbit would be the equivalent of one offspring gained in the expected fitness. How fbits are related to Maynard Smith's idea [30] that natural selection makes a species acquire one bit (in the classical sense, measured along the genome) remains to be elucidated.

Of course, technical advances are very welcome, in particular to put the notion of the fbit on a sounder theoretical foundation, but some important conceptual change is necessary too to develop a more encompassing biological theory of evolution. Two aspects are particularly important. The first is that units of adaptation do not always coincide with the preconceived notion of individual, and the second (actually related to the first aspect) is that the information needed to adapt may come from multiple sources and interact in complicated ways. The DNA-based view of evolution has tremendous explanatory power, but it may also have blinded us to the parallel information streams that are important too.