Skip to main content
PMC home page
Interface Focus logoLink to Interface Focus
. 2013 Dec 6;3(6):20130036. doi: 10.1098/rsfs.2013.0036

Evolutionary rescue can maintain an oscillating community undergoing environmental change

Gregor F Fussmann 1,✉, Andrew Gonzalez 1
PMCID: PMC3915851  PMID: 24516721

Abstract

The persistence of ecological communities is challenged by widespread and rapid environmental change. In many cases, persistence may not be assured via physiological acclimation or migration and so species must adapt rapidly in situ. This process of evolutionary rescue (ER) occurs when genetic adaptation allows a population to recover from decline initiated by environmental change that would otherwise cause extirpation. Community evolutionary rescue (CER) occurs when one or more species undergo a rapid evolutionary response to environmental change, resulting in the recovery of the ancestral community. Here, we study the dynamics of CER within a three-species community coexisting by virtue of resource oscillations brought about by nonlinear interactions between two species competing for a live resource. We allowed gradual environmental change to affect the traits that determine the strength and symmetry of the interaction among species. By allowing the component species to evolve rapidly, we found that: (i) trait evolution can allow CER and ensure the community persists by preventing competitive exclusion during environmental change, (ii) CER brings about a change in the character of the oscillations (period, amplitude) governing coexistence before and after environmental change, and (iii) CER may depend on evolutionary change that occurs simultaneously with or subsequently to environmental change. We were able to show that a change in the character of community oscillations may be a signature that a community is undergoing ER. Our study extends the theory on ER to a world of nonlinear community dynamics where—despite high-frequency changes of population abundances—adaptive evolutionary trait change can be gradual and directional, and therefore contribute to community rescue. ER may happen in real, complex communities that fluctuate owing to a mix of external and internal forces. Experiments testing this theory are now required to validate our predictions.

Keywords: eco-evolutionary dynamics, community evolutionary rescue, competitive exclusion, intrinsic population cycles

1. Introduction

The persistence of natural communities is challenged by anthropogenic environmental change. In many cases, this is because environmental change is rapid, with respect to the generation time of many organisms, and extended over large spatial scales. For example, climate change [1], human exploitation [2], heavy metal pollution [3] and the application of herbicides and pesticides [4] all impose strong selective pressures that may rapidly imbalance demographic rates (where death rates exceed birth rates) and drive populations to extinction that are unable to respond via physiological acclimation. Alternatively, species may persist in the face of environmental change by migrating away, and so shifting their spatial distribution to regions where selection is weaker and population growth is possible. Another outcome is that populations may evolve in situ and adapt quickly to redress the demographic imbalance, restore growth and escape extinction. Uncertainty about how species will respond to rapid environmental change has forced a greater theoretical focus on the dynamic links between evolution and demography, and on the evolutionary potential of declining populations.

Evolutionary rescue (ER) occurs when genetic adaptation allows a population to recover from demographic effects initiated by environmental change that would otherwise cause extirpation [5,6]. Whether evolution can rescue a population fast enough to prevent extinction depends on a number of factors, which include: the rate of environmental change [7,8], initial population size [9,10], the amount and supply of beneficial genetic variation [9–11], phenotypic plasticity [12–14] and the presence of competitors [15,16]. Many of these factors have been modelled mathematically, and the general principles governing the likelihood of rapid evolution have been identified. However, despite a few exceptions, the theory of ER has ignored the challenges created by the dynamics of multi-species communities (but see [14,17,18]). Coexistence in multi-species communities may derive from nonlinear interactions between species and involve complex dynamics that may complicate the evolutionary response to environmental change. For example, interactions between species, such as those between predators and their prey, can generate oscillations where population size may make periodic excursions to very high and low densities. Large fluctuations in species’ densities may increase the probability of extinction under environmental change, which may constrain or preclude ER.

The prevalence of cycles and large amplitude fluctuations in natural communities [19–21] suggests that it is important to extend the theory of ER to dynamic communities. Community evolutionary rescue (CER) occurs when one or more species undergo a rapid evolutionary response to environmental change, resulting in the recovery of the ancestral community. Here, we study the dynamics of CER within a three-species community coexisting by virtue of resource oscillations brought about by nonlinear interactions between two species competing for a live resource [22,23]. We allow gradual environmental change to affect the traits that determine the strength and symmetry of the interaction among species. By allowing the component species to evolve rapidly, we ask the following questions: (i) Can trait evolution allow ER, and ensure the community persists by preventing competitive exclusion during environmental change? (ii) Does ER bring about a change in the character of the oscillations (period, amplitude) governing coexistence before and after environmental change? (iii) How does evolutionary change that occurs during environmental change differ in its contribution to ER from evolutionary change that occurs after the environmental change?

2. Material and methods

Our base model is a classical system of two species competing for a common biotic resource [22]. The Armstrong–McGehee system is known to allow coexistence of the competitors through intrinsically generated stable limit cycle oscillations. We use a version with nonlinear functional responses (FRs) of both species (rather than giving one species a linear response). This makes the conditions for coexistence more restrictive [24,25] but is likely a more realistic representation of natural communities.

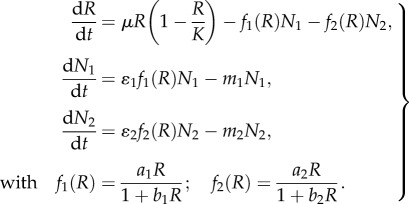2. 2.1

The system of differential equations represents the rate of change of three state variables: the two consumer species N1 and N2 competing for the logistically growing resource R (with growth rate μ and carrying capacity K). Resource uptake is described by Holling type 2 FRs fi(R) with attack rates ai, half-saturation constants 1/bi and transfer efficiencies ɛi. The competitors experience mortalities mi. We rescaled variables to reduce parameters and substituted 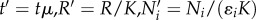Inline graphic. With the new parameters 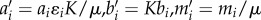Inline graphic, and the primes dropped, the system becomes

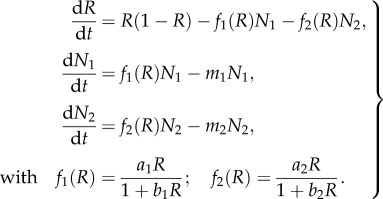2. 2.2

The parameters determining the curvature of the FR are subject to environmental change and/or evolutionary change. We implement a trade-off as b = caq (with q > 1; all simulations shown in this paper refer to qi = 2) to avoid cost-free changes to extreme resource exploitation efficiency or unrealistically high growth rates. Without trade-off, our model would describe run-away processes of trait change and only be able to document competitive superiority of the species that moves more quickly towards extreme trait values providing cost-free gain in fitness. An environmental variable T (e.g. temperature) changes linearly at rate p and alters the curvature-determining parameter a of the FR in an additive fashion. By replacing ai = αi + ziT(t), we obtain

2. 2.3

where αi is a focal trait quantity (subject to both environmental change and evolution) and parameter zi determines the susceptibility of species i to environmental change. We consider here values of −0.05 ≤ zi ≤ 0.05. With increasing environmental parameter T and positive zi, the curvature of the FR will change towards lower maximum uptake and higher uptake efficiency at low resource concentrations (as, for instance, in figure 1b). Negative zi values have the opposite effect. Our model is consistent with thermal dependence of parameters describing interaction of consumer–resource interactions, which have been theoretically and empirically established [26]. For the sake of simplicity and to keep our model applicable to environmental parameters other than temperature, we implemented a linear relationship between FR parameters and environment.

Figure 1.

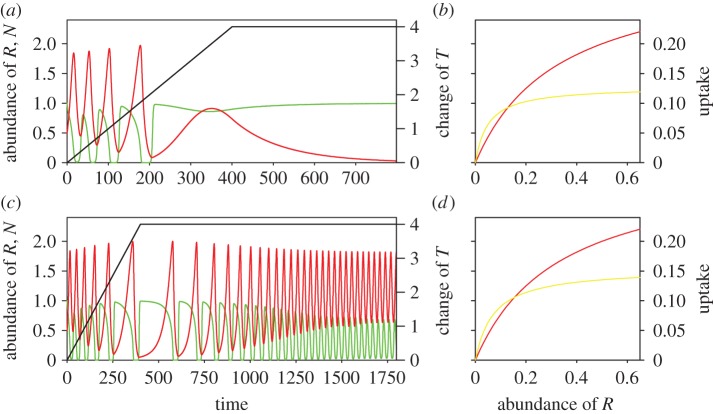
Figure 1.

Open in a new tab

Extinction and ER in a one-consumer–one-resource system. (a) Environmental change destabilizes the dynamics towards extinction following extreme oscillatory dynamics (z = 0.4; ν = 0.0). (c) Adaptive trait evolution rescues the consumer–resource community from extinction resulting from environmental change (z = 0.4; ν = 0.025). Resource, green; consumer, red; temperature change, black. (b,d) Change of FR owing to change of parameter a during dynamic scenarios (a) and (c), respectively. FR at t = 0: red; maximum change of FR: yellow.

To model evolutionary change, we assume parameter αi to be a quantitative trait of competitor Ni subject to adaptive evolution. Direction and speed of trait change are determined by the fitness landscape around the current value of αi and proportional to the change of the per capita growth rate (1/Ni)(dNi/dt) with trait change [27]. The factor of proportionality νi is a rate parameter describing the phenotypic variation of trait αi, which can be provided via standing genetic variation or be generated de novo through mutations. This approach borrowed from quantitative genetics has been used on many occasions to model the eco-evolutionary dynamics of communities structured by competitive and predator–prey interactions [28–30]. In our case, the trait dynamics are described by

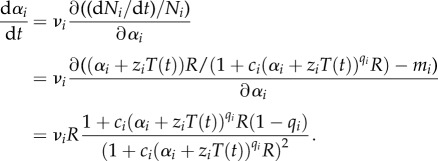2. 2.4

Evolutionary trait change depends nonlinearly on resource concentration and the current value of the evolving trait α (potentially modified by the environment), with a general tendency towards increasing α from low values and decreasing α from high values.

The full, scaled eco-evolutionary system reads

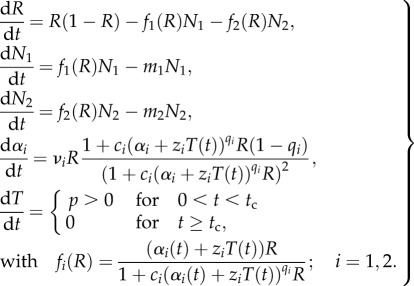2. 2.5

The piecewise definition of dT/dt reflects that we evaluated dynamics for a period of simulated environmental change lasting from t0 to tc (here equivalent to a temperature increase of 4°C) followed by a period of environmental constancy. Using numerical integration with an ordinary differential equation solver, we compared dynamics with and without environmental change as well as dynamics with and without adaptive trait evolution, and the combination of both causes of change. When trait evolution was simulated it was present during the whole simulation (except for analyses shown in figure 5), i.e. continued to operate when environmental change had ceased. We parametrized m1 = 0.07; m2 = 0.13; c1 = 3.75; c2 = 3.0; q1 = q2 = 2.0; p = 0.01 (in the case of environmental change). Initial conditions of variables were R(0) = 1.0; N1(0) = N2(0) = 0.5; α1(0) = 2.0; α2(0) = 1.0; T(0) = 0.0, i.e. parameters and initial conditions are specifically chosen so that N1 is a better competitor when R is small, whereas N2 is better when R is large. These conditions and the parameter space around them allow for coexistence of the two competitors on a stable limit cycle, while larger divergences lead to extinction of one of the competitors [25]. We found it useful to also analyse and present ER dynamics of a simplified system that only includes one consumer and the biotic resource, i.e. N1(0) = 0.0; N2(0) = 0.5. The findings of this analysis are presented in the first subsection of the Results. The values of parameters zi and νi were changed to simulate different intensities of environmental and evolutionary change. For the two-consumer case, we evaluated 25 combinations of z1 and z2 each at four different evolutionary strengths of species N2 (table 1) and present the dynamics of exemplary cases in figures 1–5. Under the current parametrization, species N1 always benefitted disproportionally from evolution (|νi| ≠ 0) and typically excluded N2 (as in figure 3a) even when the latter species was allowed to evolve at much greater evolutionary strength ν2. Because we emphasize in this study the interaction between environment and evolution, we do not show results of this very predictable outcome of coevolutionary dynamics. All numerical integrations were performed with Matlab version R2013A, using the ode45 solver. To avoid difficulties with integration around the critical time point tc of piecewise-defined ODE systems, we performed two separate numerical integration sets, one ranging from t0 to tc, the other from tc to tfinal. The final values of all state values in the first set were used as initial values in the second set. The programming language R [31] was used for wavelet analyses.

Figure 5.

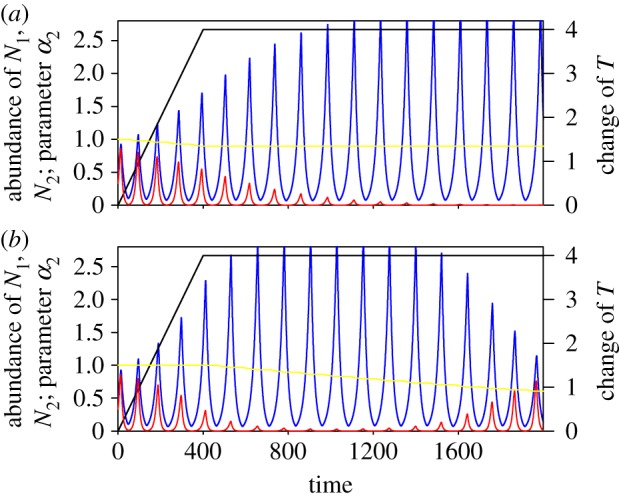
Figure 5.

Open in a new tab

Temporal decomposition of evolutionary change. ER dynamics as in figure 3e; however, with adaptive trait evolution acting only (a) during the period of environmental change (t = 0–400) or (b) after the period of environmental change (t = 400–2000). Adaptive trait change is sufficient for ER to occur under scenario (b), but not under scenario (a). Line colours as in figure 3.

Table 1.

Outcome of ER dynamics for parameter combinations representing different strengths of evolutionary change (parameters zi) and adaptive trait evolution (parameters νi). Values of z1 in rows; values of z2 in columns. N1: species N1 outcompetes species N2; Co: coexistence of species N1, N2 and resource R. Simulations were run for 20 000 time steps; species N1,2 were assumed to be extinct if abundance was less than 10−4 at any point in time during the simulation. Note: species N2 never outcompeted species N1.

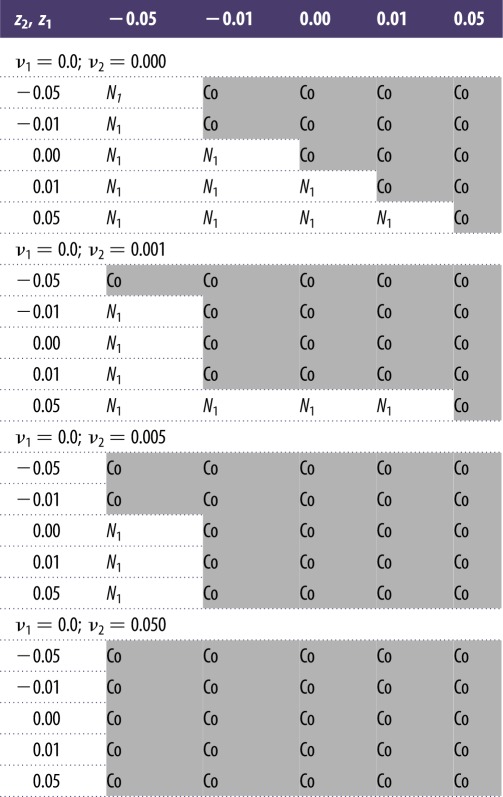graphic file with name rsfs20130036-i3.jpg
Open in a new tab

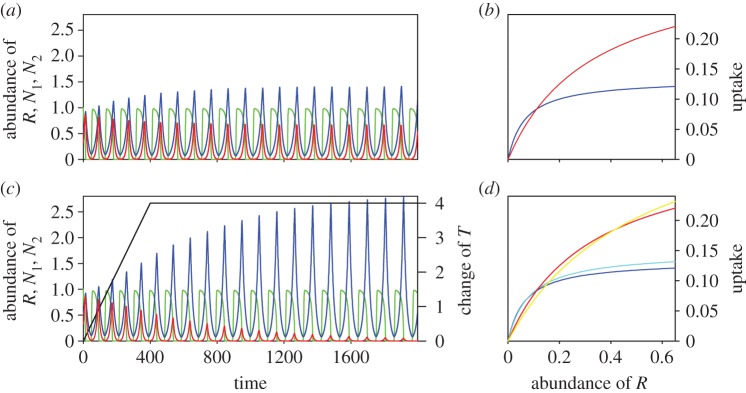
Figure 3.

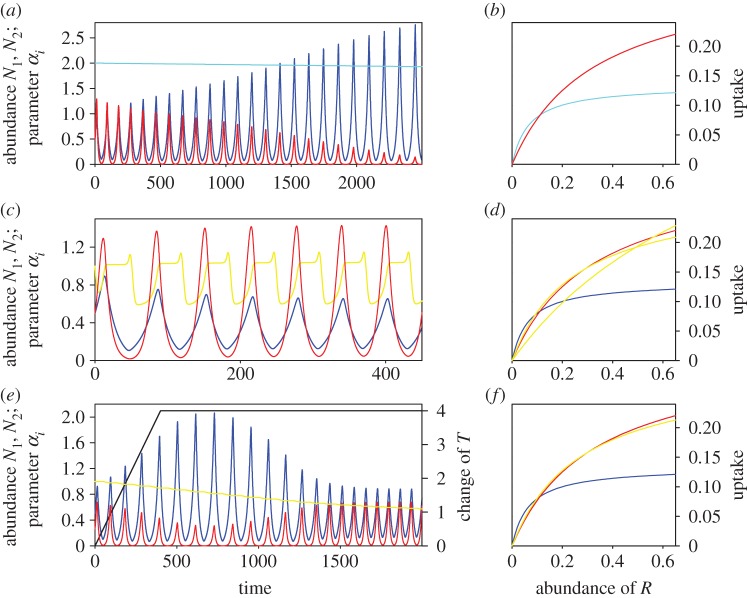
Figure 3.

Open in a new tab

Extinction, coexistence and ER in a two-consumer–one-resource system subjected to evolutionary change. (a) Minimal evolutionary change allows N1 to outcompete N2 (z1 = z2 = 0.0; ν1 = 0.001; ν2 = 0.0). (c) N1 and N2 coexist despite strong, cyclical evolutionary change of N2's FR (z1 = z2 = −0.05; ν1 = 0.0; ν2 = 1.0). (e) ER. Through adaptive trait evolution N2 can equalize the competitive advantage that N1 gains through environmental change (z1 = 0.0; z2 = 0.05; ν1 = 0.0; ν2 = 0.005). Consumer N1: blue; consumer N2: red; temperature change: black; FR parameters α1, α2: light blue, yellow; resource concentrations omitted for clarity. (b,d,f) Changes of FRs owing to change of parameters αi during dynamic scenarios (a,c,e), respectively. FR of N1 at t = 0: dark blue; maximum change of FR of N2: light blue (covers dark blue curve in (b)); FR of N2 at t = 0: red; maximum changes of FR of N2: yellow. Note that FRs fluctuate between steeper and flatter curves under scenario (c).

3. Results

3.1. One-consumer–one-resource system

Environmental change alters the specific efficiency with which the consumer takes up the resource, either favouring higher efficiency at low or high resource concentrations. This can lead to dramatic changes in the consumer–resource dynamics. When the changing environment (increasing temperatures combined with negative z-values) leads to a FR curve with increased uptake efficiency at high resource concentrations (higher half-saturation constants) the dynamics can cross a Hopf bifurcation point and switch from oscillations to stable equilibrium dynamics (results not shown). However, when environmental change leads to FRs with increased uptake efficiency at low resource concentrations (lower half-saturation constants) extended periods of extreme resource scarcity may occur that eventually lead to the extinction of the consumer (figure 1a,b).

By contrast, in the absence of environmental change (but otherwise identical conditions) even very strong adaptive trait evolution cannot change the dynamical regime of the consumer–resource oscillations (results not shown). The direction of evolution of parameter α changes at the frequency of the oscillations, so that there is no consistent long-term trend towards flatter or steeper FRs; stabilizing and destabilizing forces equalize each other. Adaptive evolution, however, has the capacity to reverse or delay trait and dynamical changes that are mediated by environmental change (figure 1c,d). We can see in figure 1c the period of the dynamics of the consumer slows down during and just after environmental change, and progressively increases over time after environmental change. Because increasing temperatures effectively increase the value of parameter a (as α + zT) the adaptive landscape has changed and favours an evolutionary decrease in this parameter that counters environmental change and its dynamical consequences.

3.2. Two-consumer–one-resource system

When two consumers compete for the same resource, environmental change typically affects the traits of the competitors asymmetrically so that the balance of coexistence (figure 2a) becomes disturbed and one consumer species is able to outcompete the other (figure 2c). For competitive exclusion to occur, it is not necessary that both species have different sensitivities to environmental change (see figure 2c, where z1 = z2 = −0.05), although this will normally accelerate the process. It is also noteworthy that coexistence is not so fragile that any trait deviation from the current state leads to extinction; indeed, almost half of the possible combinations of sensitivities to environmental change (z1–z2 combinations; table 1) result in coexistence at a somewhat altered oscillatory regime.

Figure 2.

Figure 2.

Open in a new tab

Coexistence and extinction in a two-consumer–one-resource system without evolution. (a) Coexistence of N1 and N2 through the Armstrong–McGehee mechanism (z1 = z2 = 0.0; ν1 = ν2 = 0.0). (c) N1 outcompetes N2 because environmental change leads to changes of N1's FR that increase its fitness more (z1 = z2 = −0.05; ν1 = ν2 = 0.0). Resource: green; consumer N1: blue; consumer N2: red; temperature change: black. (b,d) Changes of FRs owing to change of parameter α during dynamic scenarios (a) and (c), respectively. FR of N1 at t = 0: dark blue; maximum change of FR of N2: light blue; FR of N2 at t = 0: red; maximum change of FR of N2: yellow. Note that FRs are constant under scenario (a).

Like environmental change, trait evolution unaccompanied by environmental change can turn the dynamics from coexistence to competitive exclusion. In our example, the slightest evolvability of the FR-related trait α1 gives species N1 the edge and it wins competition independent of N2's evolutionary potential (figure 3a,b). However, in the case of evolution of species N2 even the strongest evolutionary changes of trait α2 are insufficient to let the evolving species outcompete the non-evolving one (figure 3c,d).

Adaptive evolution can change the outcome of competition under environmental change if the adaptive landscape dictates trait evolution in a direction that is opposite to the direction favoured by the environmental change. This means that the three-species community can be rescued from extinction because the consumers rendered inferior by environmental change can evolve (figure 3e,f). We can distinguish three different dynamic states of the community during the process of ER: (i) the initial state of coexistence of the community before environmental change and evolution start, (ii) the period of decline and rescue when environmental change threatens the competitively inferior species, but it survives because it evolves rapidly, and (iii) the dynamic state of the rescued community coexisting after environmental change has terminated. Wavelet analysis is able to reveal the prevailing periodicity of oscillatory dynamics across these phases of ER. For both competitors, the analysis shows a shift to longer period oscillations during the phase of decline and rescue (figure 4), which is owing to the fact that the two consumers reduce the resource to relatively low concentrations from which it takes increased periods of time to recover. Increasing the evolutionary potential of the inferior competitor (by increasing the value of ν2) leads to faster rescue of the community; in this case, rescue occurs without the initial decline of the inferior competitor and without overexploitation of the resource and markedly increased period lengths of the oscillations (results not shown). Wavelet analysis also reveals that the oscillatory state of the rescued community has changed compared with its initial state; both pre- and post-rescue communities coexist on simple cyclic dynamics but the period of oscillations has decreased (figure 4).

Figure 4.

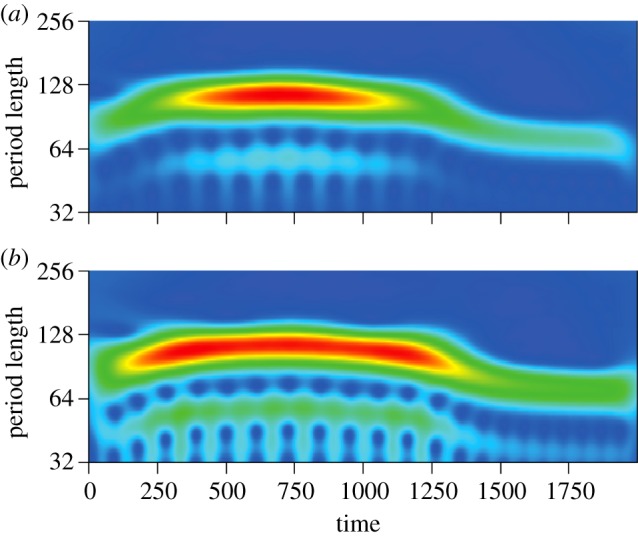
Figure 4.

Open in a new tab

Wavelet analysis of ER consumer dynamics (parametrization as in figure 3e). (a) Wavelet spectrum of consumer N1 (blue in figure 3e). (b) Wavelet spectrum of consumer N2 (red in figure 3e). Periodicity of oscillatory dynamics changes over the course of ER. Period lengths are slightly shorter after rescue (t = 1500–2000) than before (t = 0–400). Warm colours indicate high signal strength for a given period length at a given time.

Our analysis also allows us to decompose phases of the rescue process according to the contribution they make to the eventual rescue of the community. Evolutionary change needs to accomplish two elements of rescue to ensure the survival of the community. First, the inferior competitor needs to survive the period of environmental change for rescue to occur. Second, the community needs to be in a dynamical state that allows long-term coexistence once the environmental change ceases. If evolutionary change is very strong and effective, the contribution of evolution to trait change during the period of evolutionary change can be sufficient to accomplish ER. However, in our model simulation, we frequently observed that evolution happening after environmental change is critical for rescuing the community (figure 5a). In cases where the inferior competitor is only reduced in abundance but not extirpated, evolution following environmental change may be sufficient to restore community coexistence (figure 5b).

4. Discussion

We have shown that ER is capable of maintaining an oscillating community experiencing sustained environmental change. To build on previous research that has explored the consequences of trait change for the coexistence of competitive communities [16,18,32–35], we found that trait evolution, acting on the resource uptake rate, could maintain an inferior competitor and prevent competitive exclusion. As such, we identified conditions that allowed the community to undergo CER. Here, quantitative trait evolution approximates the evolutionary process, assuming the existence of additive genetic variation at the outset (determined by parameter νi) and no de novo generation of genetic variation through mutation during the evolutionary process.

In our case, CER occurred owing to rapid trait evolution in the FRs of the component species. We therefore coupled the environmental change to the mechanism of resource uptake. Environmental change acted to adjust the efficiency of resource uptake, typically favouring the superior competitor and driving the system to competitive exclusion. However, evolution countered this tendency and allowed the inferior competitor to bounce back. It is important to note that CER occurred over a wide range of evolutionary strengths (or genetic variances) and, thus, did not depend on evolution being ‘just right’ (table 1). Very strong evolution will rescue the inferior competitor more quickly, without allowing a visible decline of the ‘rescued’ population in the first place. Moderate and low rates of evolution need time to take effect, and therefore put the inferior competitor at peril initially, resulting in a U-shaped curve of decline and recovery (figure 3e) that has previously been established for non-oscillatory, single-species rescue dynamics [5,36]. In a previous theoretical study, Fox & Vasseur [18] observed qualitatively similar dynamics of decline and recovery of an inferior but evolving competitor in a two-consumer–two-resource system. There are two important differences from our study: (i) their system does not include environmental change and is primarily a study of adaptive coevolution in an intrinsically changing competitive system and (ii) equilibrium coexistence is possible in the two-resource system and dynamics are characterized by non-oscillatory trajectories of species abundances and trait change. More recently, Kremer & Klausmeier [34] analysed how the addition of evolution contributes to (or sabotages) coexistence in nonlinear ecological models. They found that rapid evolution has a negative impact on the coexistence of competitors in a two-consumer–one-resource system that is similar to ours. Contrary to our approach, they modelled a periodically changing environment that acts as an external driver of species oscillations. Species fail to coexist because they rapidly coevolve trait values that optimize their fitness over the course of the resource fluctuations, which renders them competitively neutral and, with the slightest demographic stochasticity, susceptible to exclusion. Our study, however, demonstrates that under low-to-moderate evolutionary strength adaptive evolutionary trait change can be gradual and directional—despite high-frequency changes of population abundances—and therefore contribute to community rescue. This gives the first indication that (and how) ER may happen in real, complex communities that fluctuate owing to a mix of external and internal forces.

Another novel aspect of our analysis is the hypothesis that CER may involve changes to the oscillatory dynamics governing coexistence before, during and after environmental change. Previous studies have favoured an analysis of ER in the short term, and typically in response to a single abrupt press perturbation. We were able to show that a change in the character of community oscillations may be a signature that a community is undergoing ER. The transient changes in periodicity during ER can be seen in the time series plots but are captured particularly well by wavelet analysis. In both the single- and the two-consumer cases, the period of decline prior to recovery was characterized by a slowing of the periodicity and a reduction in the amplitude of the oscillations of the species undergoing ER. In our case, both effects can be explained by the benefits that the superior competitor has owing to environmental change. With increasing temperature, it becomes more efficient in exploiting the common resource, which leads to higher amplitude cycles of the superior competitor but lower amplitude cycles of the inferior competitor. At the same time, stronger resource exploitation by the combination of the two competitors leads to increasingly lower resource minima during the cycles from which the resource takes longer times to recover, thereby decreasing the frequency of the oscillations. Finally, and perhaps most interestingly, a rescued community does not necessarily occupy the same dynamical state as pre-rescue, i.e. evolutionary and environmental trait changes do not exactly compensate one another but may lead to coexistence at a new balance of altered traits of the competitors. Future theoretical and experimental studies need to explore the generality of these interesting dynamical signatures of CER.

Finally, our simulation results also revealed the possibility that ER may not just be restricted to the period of environmental change (or stress, from the point of the inferior competitor) itself. A species that survives a period of environmental stress may or may not subsequently be rescued, and the eventual fate of the whole community can rely on ER happening after the environment has ceased to change. This observation highlights the length and intensity of the period of environmental change as a critical factor determining the possibility of ER; it is also complementary to findings emphasizing the importance of adaptation occurring prior to environmental change [9,37].

Our theoretical analyses have produced a number of hypotheses concerning rescue dynamics in real communities, some of which show similarities to previously studied single-species ER (U-shaped rescue dynamics; distinct phases of rescue), while others are specific to the competitive community situation (coexistence on cycles; change of oscillatory regime during rescue). Experiments testing these results will likely begin in laboratory microcosms with short-lived organisms for which trait evolution has been shown to occur at the time scale of community dynamics [38,39]. Experimental verification of our theoretical results—and those of others—is important because the real values of some parameters are hardly known; genetic variance or evolutionary potential (ν), for instance, can only be set to arbitrary units in our model. This being said, there is already ample experimental evidence that trait evolution can change the dynamics of experimental communities [38–40]; what is still lacking is experimentation explicitly geared to CER.

We elected to study ER in a system driven by nonlinear resource competition so that we could assemble a simple food web module founded on a single live resource. This is the first pass at the problem, but other, perhaps more general, mechanisms of coexistence could be used to explore community rescue. For example, is community rescue possible in communities coexisting owing to environmentally driven storage effects [41]? Again, we might expect changes in the fluctuations defining the community before and after environmental change. Ultimately, ER always occurs within the context of a multi-species community. Future studies might also incorporate more trophic complexity (e.g. [14]), or other types of indirect interactions. All of these will complicate the story because CER will arise from the joint effect of direct responses to abiotic environmental change, and indirect responses to environmental change as mediated by the species’ interactions. Whether CER is hindered by trophic complexity is an open question of great importance. Many more theoretical studies of this problem will be required if we are to understand the extent to which anthropogenic environmental change will erode the Earth's biodiversity.

Acknowledgements

We thank Lars Rudolf and Bernd Blasius for help with the wavelet analysis and figure 4 as well as for helpful discussions. The comments of three reviewers considerably improved the manuscript.

Funding statement

A.G. is supported by the Canada Research Chair program. G.F. and A.G. are supported by NSERC Discovery Grants.

References

  • 1.Thomas CD, et al. 2004. Extinction risk from climate change. Nature 427, 145–148. ( 10.1038/nature02121) [DOI] [PubMed] [Google Scholar]
  • 2.Handford P, Bell G, Reimchen T. 1977. A gillnet fishery considered as an experiment in artificial selection. J. Fish. Res. Board Can. 34, 954–961. ( 10.1139/f77-148) [DOI] [Google Scholar]
  • 3.Klerks PL, Weis JS. 1987. Genetic adaptation to heavy metals in aquatic organisms: a review. Environ. Pollut. 45, 173–205. ( 10.1016/0269-7491(87)90057-1) [DOI] [PubMed] [Google Scholar]
  • 4.Fox JE, Gulledge J, Engelhaupt E, Burow ME, McLachlan JA. 2007. Pesticides reduce symbiotic efficiency of nitrogen-fixing rhizobia and host plants. Proc. Natl Acad. Sci. USA 104, 10 282–10 287. ( 10.1073/pnas.0611710104) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Gomulkiewicz R, Holt RD. 1995. When does evolution by natural selection prevent extinction? Evolution 49, 201–207. ( 10.2307/2410305) [DOI] [PubMed] [Google Scholar]
  • 6.Gonzalez A, Ronce O, Ferriere R, Hochberg ME. 2013. Evolutionary rescue: an emerging focus at the intersection between ecology and evolution. Phil. Trans. R. Soc. B 368, 20120404 ( 10.1098/rstb.2012.0404) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Gienapp P, Lof M, Reed TE, McNamara J, Verhulst S, Visser ME. 2013. Predicting demographically sustainable rates of adaptation: can great tit breeding time keep pace with climate change? Phil. Trans. R. Soc. B 368, 20120289 ( 10.1098/rstb.2012.0289) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Bell G, Gonzalez A. 2011. Adaptation and evolutionary rescue in metapopulations experiencing environmental deterioration. Science 332, 1327–1330. ( 10.1126/science.1203105) [DOI] [PubMed] [Google Scholar]
  • 9.Bell G. 2013. Evolutionary rescue and the limits of adaptation. Phil. Trans. R. Soc. B 368, 20120080 ( 10.1098/rstb.2012.0080) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Ferriere R, Legendre S. 2013. Eco-evolutionary feedbacks, adaptive dynamics and evolutionary rescue theory. Phil. Trans. R. Soc. B 368, 20120081 ( 10.1098/rstb.2012.0081) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Kirkpatrick M, Peischl S. 2013. Evolutionary rescue by beneficial mutations in environments that change in space and time. Phil. Trans. R. Soc. B 368, 20120082 ( 10.1098/rstb.2012.0082) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Chevin L-M, Gallet R, Gomulkiewicz R, Holt RD, Fellous S. 2013. Phenotypic plasticity in evolutionary rescue experiments. Phil. Trans. R. Soc. B 368, 20120089 ( 10.1098/rstb.2012.0089) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Chevin LM, Lande R, Mace GM. 2010. Adaptation, plasticity, and extinction in a changing environment: towards a predictive theory. PLoS Biol. 8, e1000357 ( 10.1371/journal.pbio.1000357) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Kovach-Orr C, Fussmann GF. 2013. Evolutionary and plastic rescue in multitrophic model communities. Phil. Trans. R. Soc. B 368, 20120084 ( 10.1098/rstb.2012.0084) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Osmond MM, de Mazancourt C. 2013. How competition affects evolutionary rescue. Phil. Trans. R. Soc. B 368, 20120085 ( 10.1098/rstb.2012.0085) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Johansson J. 2008. Evolutionary responses to environmental changes: how does competition affect adaptation? Evolution 62, 421–435. ( 10.1111/j.1558-5646.2007.00301.x) [DOI] [PubMed] [Google Scholar]
  • 17.de Mazancourt C, Johnson E, Barraclough TG. 2008. Biodiversity inhibits species’ evolutionary responses to changing environments. Ecol. Lett. 11, 380–388. ( 10.1111/j.1461-0248.2008.01152.x) [DOI] [PubMed] [Google Scholar]
  • 18.Fox JW, Vasseur DA. 2008. Character convergence under competition for nutritionally essential resources. Am. Nat. 172, 667–680. ( 10.1086/591689) [DOI] [PubMed] [Google Scholar]
  • 19.Blasius B, Huppert A, Stone L. 1999. Complex dynamics and phase synchronization in spatially extended ecological systems. Nature 399, 354–359. ( 10.1038/20676) [DOI] [PubMed] [Google Scholar]
  • 20.Gilg O, Hanski I, Sittler B. 2003. Cyclic dynamics in a simple vertebrate predator-prey community. Science 302, 866–868. ( 10.1126/science.1087509) [DOI] [PubMed] [Google Scholar]
  • 21.Kendall BE, et al. 1999. Why do populations cycle? A synthesis of statistical and mechanistic modeling approaches. Ecology 80, 1789–1805. ( 10.1890/0012-9658(1999)080[1789:wdpcas]2.0.co;2) [DOI] [Google Scholar]
  • 22.Armstrong RA, McGehee R. 1980. Competitive exclusion. Am. Nat. 115, 151–170. ( 10.1086/283553) [DOI] [Google Scholar]
  • 23.Koch AL. 1974. Competitive coexistence of two predators utilizing the same prey under constant environmental conditions. J. Theor. Biol. 44, 387–395. ( 10.1016/0022-5193(74)90169-6) [DOI] [PubMed] [Google Scholar]
  • 24.Abrams PA, Holt RD. 2002. The impact of consumer-resource cycles on the coexistence of competing consumers. Theor. Popul. Biol. 62, 281–295. ( 10.1006/tpbi.2002.1614) [DOI] [PubMed] [Google Scholar]
  • 25.Xiao X, Fussmann GF. In press Armstrong–McGehee mechanism revisited: competitive exclusion and coexistence of nonlinear consumers. J. Theor. Biol. ( 10.1016/j.jtbi.2013.05.025) [DOI] [PubMed] [Google Scholar]
  • 26.Dell AI, Pawar S, Savage VM. In press Temperature dependence of trophic interactions are driven by asymmetry of species responses and foraging strategy. J. Anim. Ecol. ( 10.1111/1365-2656.12081) [DOI] [PubMed] [Google Scholar]
  • 27.Lande R. 1976. Natural selection and random genetic drift in phenotypic evolution. Evolution 30, 314–334. ( 10.2307/2407703) [DOI] [PubMed] [Google Scholar]
  • 28.Saloniemi I. 1993. A coevolutionary predator-prey model with quantitative characters. Am. Nat. 141, 880–896. ( 10.1086/285514) [DOI] [PubMed] [Google Scholar]
  • 29.Tien RJ, Ellner SP. 2012. Variable cost of prey defense and coevolution in predator–prey systems. Ecol. Monogr. 82, 491–504. ( 10.1890/11-2168.1) [DOI] [Google Scholar]
  • 30.Yamauchi A, Yamamura N. 2005. Effects of defense evolution and diet choice on population dynamics in a one-predator–two-prey system. Ecology 86, 2513–2524. ( 10.1890/04-1524) [DOI] [Google Scholar]
  • 31.Team RDC. 2013. R: a language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing; See http://www.R-project.org. [Google Scholar]
  • 32.Abrams PA. 1987. Alternative models of character displacement and niche shift. 2. Displacement when there is competition for a single resource. Am. Nat. 130, 271–282. ( 10.1086/284708) [DOI] [PubMed] [Google Scholar]
  • 33.Matthews B, et al. 2011. Toward an integration of evolutionary biology and ecosystem science. Ecol. Lett. 14, 690–701. ( 10.1111/j.1461-0248.2011.01627.x) [DOI] [PubMed] [Google Scholar]
  • 34.Kremer CT, Klausmeier CA. In press Coexistence in a variable environment: eco-evolutionary perspectives. J. Theor. Biol. ( 10.1016/j.jtbi.2013.05.005) [DOI] [PubMed] [Google Scholar]
  • 35.Norberg J, Urban MC, Vellend M, Klausmeier CA, Loeuille N. 2012. Eco-evolutionary responses of biodiversity to climate change. Nat. Clim. Change 2, 747–751. ( 10.1038/nclimate1588) [DOI] [Google Scholar]
  • 36.Bell G, Gonzalez A. 2009. Evolutionary rescue can prevent extinction following environmental change. Ecol. Lett. 12, 942–948. ( 10.1111/j.1461-0248.2009.01350.x) [DOI] [PubMed] [Google Scholar]
  • 37.Gonzalez A, Bell G. 2013. Evolutionary rescue and adaptation to abrupt environmental change depends upon the history of stress. Phil. Trans. R. Soc. B 368, 20120079 ( 10.1098/rstb.2012.0079) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Becks L, Ellner SP, Jones LE, Hairston NG., Jr 2012. The functional genomics of an eco-evolutionary feedback loop: linking gene expression, trait evolution, and community dynamics. Ecol. Lett. 15, 492–501. ( 10.1111/j.1461-0248.2012.01763.x) [DOI] [PubMed] [Google Scholar]
  • 39.Yoshida T, Jones LE, Ellner SP, Fussmann GF, Hairston NG., Jr 2003. Rapid evolution drives ecological dynamics in a predator–prey system. Nature 424, 303–306. ( 10.1038/nature01767) [DOI] [PubMed] [Google Scholar]
  • 40.Fussmann GF, Ellner SP, Hairston NG., Jr 2003. Evolution as a critical component of plankton dynamics. Proc. R. Soc. Lond. B 270, 1015–1022. ( 10.1098/rspb.2003.2335) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41.Chesson P. 2000. General theory of competitive coexistence in spatially-varying environments. Theor. Popul. Biol. 58, 211–237. ( 10.1006/tpbi.2000.1486) [DOI] [PubMed] [Google Scholar]

Articles from Interface Focus are provided here courtesy of The Royal Society

RESOURCES