Analysis of variance (ANOVA) comparing means of more than two groups

Mean values obtained from different groups with different conditions are frequently compared in clinical studies. For example, two mean bond strengths between tooth surface and resin cement may be compared using the parametric Student's t test when independent groups are subjected to the comparison under the assumptions of normal distribution and equal variances (or standard deviation). In a condition of unequal variances we may apply the Welch's t test as an adaptation of the t test. As the nature and specific shape of distributions are predetermined by the assumption, the t test compares only the locations of the distribution represented by means, which is simple and intuitive. The t statistic is the ratio of mean difference and standard errors of the mean difference.

Even when more than two groups are compared, some researchers erroneously apply the t test by implementing multiple t tests on multiple pairs of means. It is inappropriate because the repetition of the multiple tests may repeatedly add multiple chances of error, which may result in a larger α error level than the pre-set α level. When we try to compare means of three groups, A, B, and C, using the t test, we need to implement 3 pairwise tests, i.e., A vs B, A vs C, and B vs C. Similarly if comparisons are repeated k times in an experiment and the α level 0.05 was set for each comparison, an unacceptably increased total error rate of 1-(0.95)^k may be expected for the total comparison procedure in the experiment. For a comparison of more than two group means the one-way analysis of variance (ANOVA) is the appropriate method instead of the t test. As the ANOVA is based on the same assumption with the t test, the interest of ANOVA is on the locations of the distributions represented by means too. Then why is the method comparing several means the 'analysis of variance', rather than 'analysis of means' themselves? It is because that the relative location of the several group means can be more conveniently identified by variance among the group means than comparing many group means directly when number of means are large.

The ANOVA method assesses the relative size of variance among group means (between group variance) compared to the average variance within groups (within group variance). Figure 1 shows two comparative cases which have similar 'between group variances' (the same distance among three group means) but have different 'within group variances'. When the between group variances are the same, mean differences among groups seem more distinct in the distributions with smaller within group variances (a) compared to those with larger within group variances (b). Therefore the ratio of between group variance to within group variance is of the main interest in the ANOVA.

Figure 1.

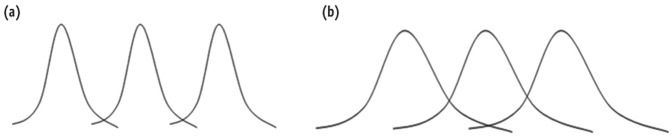
Distributions with the same between group variance. (a) smaller variance within groups; (b) larger variance within groups.

Table 1 displays an artificial data of bond strength according to different resin types and Table 2 shows the result of the one-way ANOVA. The 'SSB' represents the sum of squares between groups which is the variation of group means from the total grand mean, and the mean of squares between groups (MSB) is subsequently obtained by dividing SSB with degrees of freedom. The 'SSW' represents sum of squares within groups which is the sum of squared deviations from the group means and individual observations because the equal variances in all the groups were already assumed. The mean of square within groups (MSW) is subsequently obtained by dividing SSW with degrees of freedom, in the same way. The ratio of MSB and MSW determines the degree of how relatively greater the difference is between group means (between group variance) compared to within group variance. If the ratio is greater than expected by chance we may think not all the group means are the same which means that at least one mean is substantially different. As the result is interpreted about the whole set of groups, it is called as a global or overall test. The ratio of MSB and MSW is known to follow the F distribution. Therefore, to get a statistical conclusion we may compare the F value calculated from the observed data with the critical value at an α error level of 0.05 in the F table.

Table 1.

Measurements of bonding strength according to three different types of resin (artificial data)

Table 2.

One-way ANOVA table

Larger F value implies that means of the groups are greatly different from each other compared to the variation of the individual observations in each groups. Larger F value than the critical value supports that the differences between group means are larger than what would be expected by chance. In this example the critical F value is 3.23 in the F table when the degrees of freedom of numerator and denominator are 2 and 42 respectively at the α error level 0.05. As the observed F value 8.4 is larger than the critical value, the result in Table 2 may be interpreted as statistically significant difference among the means of the groups at the α error level 0.05. The result suggests to rejection of the null hypothesis that all the group means are the same, and coincidently supports that at least one group mean differs from other group means.

If any significant difference is detected by the 'overall F test' above, we need to examine what specific pair of group means shows difference and what pairs do not. While many different kinds of post-hoc multiple comparison procedures have been proposed, the choice needs to be made according to the specific research question. One basic method is implementing multiple pairwise t tests using the common variance as MSW and appropriately adjusting α error level to get the optimal α error level for the whole experiment. For example, the Bonferroni correction is a simple method that adjusts comparisonwise type α error level as the usual experiment-wise α error level divided by the number of comparisons, e.g., 0.05/k. However, caution is needed because in some situations the Bonferroni correction may be substantially conservative that actual experiment-wise α error level applied may be lower than 0.05. Tukey's HSD, Schaffe method, and Duncan multiple range test are more frequently preferred methods for the multiple comparison procedures. Table 3 displays the analysis results by both the ANOVA and multiple comparison procedure. We usually need to report the p-value of overall F test and the result of the post-hoc multiple comparison. Table 3 shows that 'C' resin has the highest bond strength and 'A' resin shows the lowest.

Table 3.

Comparative mean bond strength according to different types of resin (display of ANOVA results)

^*Different superscripts mean statistically different.

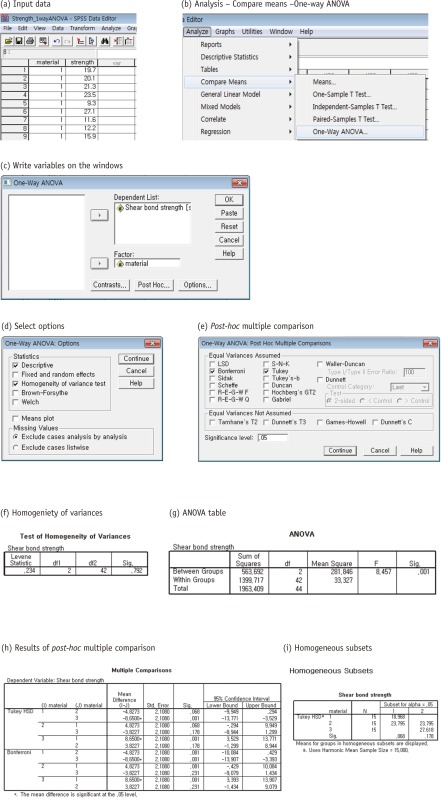
The comparison of more than two group means by ANOVA using the SPSS statistical package (SPSS Inc., Chicago, Il) according to the following procedures: