Exploring variation-aware contig graphs for (comparative) metagenomics using MaryGold

Abstract

Motivation: Although many tools are available to study variation and its impact in single genomes, there is a lack of algorithms for finding such variation in metagenomes. This hampers the interpretation of metagenomics sequencing datasets, which are increasingly acquired in research on the (human) microbiome, in environmental studies and in the study of processes in the production of foods and beverages. Existing algorithms often depend on the use of reference genomes, which pose a problem when a metagenome of a priori unknown strain composition is studied. In this article, we develop a method to perform reference-free detection and visual exploration of genomic variation, both within a single metagenome and between metagenomes.

Results: We present the MaryGold algorithm and its implementation, which efficiently detects bubble structures in contig graphs using graph decomposition. These bubbles represent variable genomic regions in closely related strains in metagenomic samples. The variation found is presented in a condensed Circos-based visualization, which allows for easy exploration and interpretation of the found variation.

We validated the algorithm on two simulated datasets containing three respectively seven Escherichia coli genomes and showed that finding allelic variation in these genomes improves assemblies. Additionally, we applied MaryGold to publicly available real metagenomic datasets, enabling us to find within-sample genomic variation in the metagenomes of a kimchi fermentation process, the microbiome of a premature infant and in microbial communities living on acid mine drainage. Moreover, we used MaryGold for between-sample variation detection and exploration by comparing sequencing data sampled at different time points for both of these datasets.

Availability: MaryGold has been written in C++ and Python and can be downloaded from http://bioinformatics.tudelft.nl/software

Contact: d.deridder@tudelft.nl

1 INTRODUCTION

Recently, large-scale microbiome analyses, such as metaHIT (Qin et al., 2010) and the National Institutes of Health Human Microbiome Project (Human Microbiome Project Consortium, 2012), have demonstrated the importance and the richness of our second genome: the microbes inhabiting many different sites of our bodies. To get the complete picture of all DNA present, its biological functions and the genetic variation, increasingly whole-metagenome sequencing is performed (Hess et al., 2011; Qin et al., 2010). Large-scale analysis of variation within and between the resulting metagenomes—single nucleotide variants, short insertions and deletions (indels) and structural variaton—is essential to fully understand their genetic makeup. However, relatively few studies have thus far ventured into such analyses. Schloissnig et al. (2013) combined data obtained from stool samples in the metaHIT and HMP projects and a study comparing leanness and obesity (Turnbaugh et al., 2009), taking a read mapping approach to detect millions of single nucleotide polymorphisms and other genetic variation in bacterial metagenomes. Morowitz et al. (2011) studied the metagenome of stool samples of a premature infant using an assembly approach. Manual analysis of the assembly output resulted in a genetic variation found in Citrobacter strains.

A major reason for this lack of metagenomic variation analysis is a shortage of available tools. Variation detectors have mainly been developed for the isolated genomes of single individuals and can be roughly divided in two categories: reference-based and reference-free. Several reference-based methods that map reads to a preconstructed reference genome are available to detect single nucleotide variants and structural variants, as reviewed in Nielsen et al. (2011) and Medvedev et al. (2009), respectively. However, in metagenomics, reference genomes are usually not available for all species. Moreover, many bacterial species are not cultivable in the laboratory, complicating construction of reference genomes.

Reference-free methods, in contrast, detect variation between sequencing samples directly, without resorting to reference genomes. Fasulo et al. (2002) showed that genomic regions with polymorphisms give rise to bubbles in the fragment assembly graph and presented an algorithm to find and smooth the bubbles, which was implemented in the Celera assembler. The Cortex assembler (Iqbal et al., 2012) was designed to coassemble multiple genomes and search for such bubbles in the de Bruijn graph that represent variation between the assembled genomes. Decomposition of a de Bruijn graph into biconnected components followed by bubble detection has been shown to be useful in detecting splicing variants in RNA sequencing data (Sacomoto et al., 2012).

Similar to co-assembly of individual genomes, metagenome assembly involves simultaneous assembly of multiple genomes. The presence of two closely related genomes in a sample leads to similar bubbles. The metagenome scaffolder Bambus 2 was designed to detect these bubbles and collapse them, thereby elongating scaffolds while preserving divergence in the data (Koren et al., 2011). Bambus 2 finds bubbles by looking for subgraphs where multiple paths begin at a source node and collapse to one sink node. To keep computation tractable, the number of hops considered is limited to two. Meta-IDBA similarly searches bubbles in a de Bruijn graph, but the search is limited to a maximum of 300 bp (Peng et al., 2011).

Here we set out to detect complex bubbles such as presented in Figure 2a, i.e. longer than can currently be detected by Bambus 2 and Cortex, typically found when >2 homologous sequences (closely related genomes) are present in a sample. We overcome the computational limitations in the aforementioned methods by developing an efficient way to find genome variation in assembly graphs, by introducing a graph decomposition into bi- and triconnected components that allows us to select a subset of the nodes as source nodes for bubble finding. Identifying bubbles representing multi-alleles has three applications. First, it can be used to detect sequence variation, i.e. multiple alleles, between strains within a single-sample metagenome. Second, co-assembling multiple metagenomes allows the detection of variation between samples. This latter application is particularly novel and is set to become more prominent as more metagenomics datasets will become available over the coming years. Third, although not the main focus in this article, it allows to simplify assemblies, generating longer scaffolds and contigs by collapsing bubbles into a single linear sequence instead of breaking into multiple contigs. Co-assembly has previously been used by Dutilh et al. (2012) to calculate global distances between metagenomes, but here we aim to find sequence-level differences.

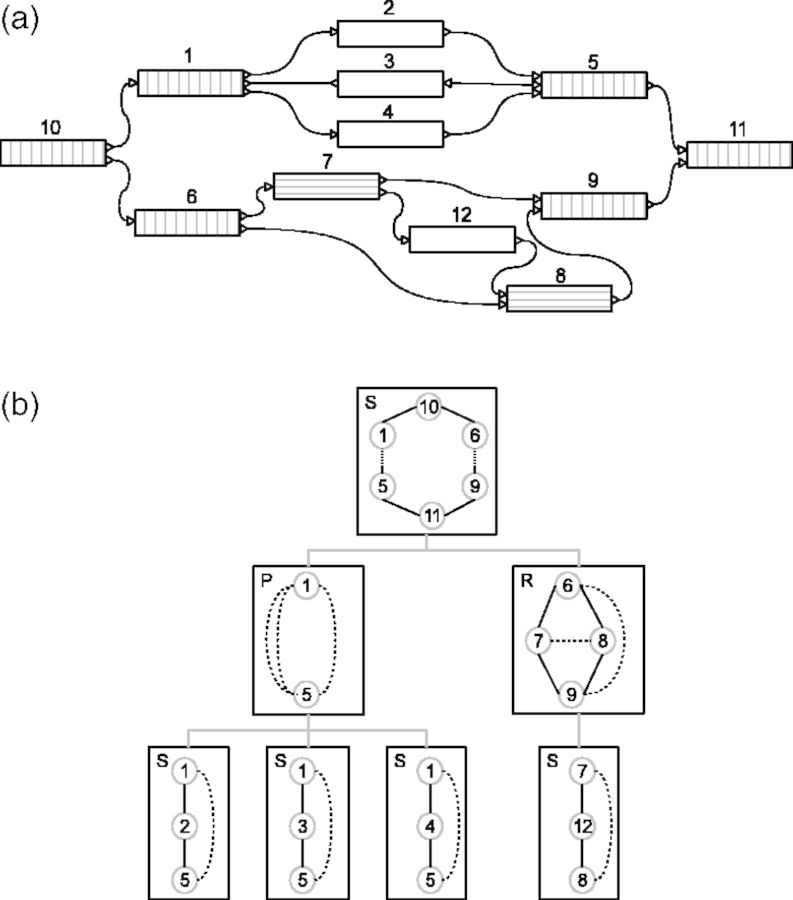
Fig. 2.

(a) Toy example of a biconnected contig graph. Separation pairs are hatched, but only valid source–sink pairs are hatched vertically, otherwise horizontally. (b) The corresponding SPQR tree describing the triconnected components. Virtual edges are indicated by dashed lines; branches in the SPQR tree link shared virtual edges. By merging these edges, the original graph can be reconstructed. A detailed description on how to construct an SPQR tree can be found in Weiskircher (2002)

We demonstrate MaryGold, our algorithm to find bubbles and compare them across samples using co-assembly, by comparing metagenome samples obtained using 454 technology of different time points obtained from the stool sample of a premature infant (Morowitz et al., 2011) and a fermentation process of the traditional Korean food kimchi (Jung et al., 2011). We also apply the algorithm on sequencing data of microbial populations found on acid mine drainage (Denef and Banfield, 2012), obtained using both 454 and Illumina technologies, and compare MaryGold with Bambus 2. MaryGold exports the variation detected in a format that can be visualized by Circos, allowing for a rich visual exploration and interpretation of the genomic variation in metagenomes.

2 ALGORITHM

2.1 Generating a contig graph

De novo assembly of metagenomes relies on the same principles as that of single genomes. It can be done either by assemblers based on de Bruijn graphs or overlap-layout-consensus assemblers as reviewed by Li et al. (2012). Both of these types of assembler use graphs to merge the millions of short reads into longer contiguous sequences, with the ultimate goal of reconstructing full genomes. Although de Bruijn graph and overlap-layout-consensus assemblers have different ways of building their graphs, i.e. by means of kmer hashing and pairwise read alignment, respectively, both paradigms produce graphs that contain similar information and have similar limitations. In both, repeats longer than the read length (or kmer length) will cause branching in the graph, and unique regions correspond to unambiguously reconstructable sequences.

The algorithm we propose uses the graphical output of assemblers to reconstruct metagenomes. The assembly graphs are assumed to have nodes representing contigs and edges representing reads spanning the connected contigs. The graph is bidirected because it has both contigs coming from the forward strand and from the reverse strand of the DNA molecule (Kundeti et al., 2010). From this point onward, we refer to this graph as the contig graph 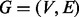that has a set of nodes 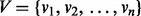and a set of edges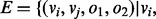 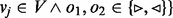. The set of nodes is created by assigning each contig 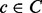to a unique node. A path from v_i to v_j through the bidirected-contig graph is a sequence of nodes and edges , such that each intermediate node 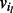in subsequence 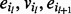has matching orientations of its incoming edge (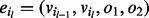) and outgoing edge (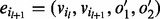), i.e. 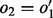(Kundeti et al., 2010). The DNA sequence corresponding to a node in a path depends on its traversal. The reverse complement DNA sequence of a node 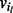is used when eithe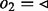r or 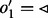(Fig. 1: node GGTG).

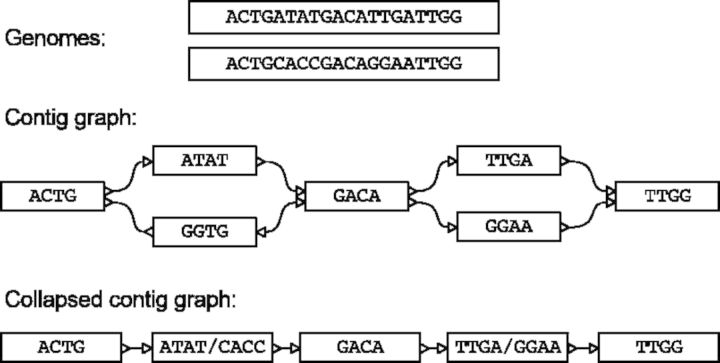
Fig. 1.

Two genomes, their contig graph and collapsed contig graph, where the two simple bubbles have been compressed into multi-allelic contigs. After compression the original seven contigs are connected by a simple path without branching, and can be merged into a single contig

2.2 Metagenome graph compression

In the contig graph, two contigs can be reliably concatenated, with or without a gap, if they are connected by a single edge and no other edge contradicts their concatenation. Ambiguity arises when multiple edges of a contig link to other contigs. In metagenome assemblies where we are dealing with closely related strains, such branches in the graph can be caused by sequence divergence between two strains of the same (or closely related) species in the sample, forming bubbles (Fig. 1). In this work we try to elongate scaffolds and contigs by identifying these regions and collapsing them to multi-allelic contigs.

The main challenge tackled here is the detection of complex bubble structures. We define a bubble as a subgraph where all maximally extended paths within the bubble start in a single source node and end in a single sink node or vice versa (the source and sink nodes are interchangeable because of the two-stranded nature of DNA, i.e. they can be swapped by taking the reverse complement of all nodes in the subgraph).

2.2.1 Finding separation pairs using graph decomposition

In Bambus 2, source–sink pairs are iteratively found by traversing all paths leaving a node and checking if these paths all collapse to a sink node within a certain number of hops. The number of hops is limited to two to keep this search tractable. Here we set out to find source–sink pairs efficiently, so that we can detect source and sink nodes that are >2 hops apart from each other in ≥1 of the connecting paths. This allows us to detect more complex multi-allelic sites. We achieve this by finding separation pairs, i.e. pairs of nodes that increase the number of connected components in a graph when they are removed. All source and sink pairs are a separation pair (Theorem 1), though the converse does not hold. We can, therefore, first find all separation pairs, and then select the subset of separation pairs that are also source–sink pairs.

Theorem 1 —

A separation pair is a source–sink pair of nodes forming a bubble if and only if all paths in the corresponding subgraph starting in the source node end in the sink node when extended, and all paths starting in the sink node end in the source node when extended.

Separation pairs are detected in an undirected version of the contig graph using graph decomposition methods. An initial set of separation pairs is found by decomposing each connected component into its biconnected components, which can be done in 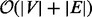. A biconnected component is a maximal biconnected subgraph. The cut vertices of a graph are the nodes, whose removal increases the number of connected components. If a biconnected component has exactly two such cut vertices, then these two are stored as a separation pair. The set of separation pairs is extended by decomposing each biconnected component into its triconnected components. The triconnected components of a biconnected component describe the 2-vertex cuts in a graph. A 2-vertex cut is a pair if nodes that, if removed, increase the number of connected components, i.e. a separation pair.

Battista and Tamassia (1989) developed an algorithm to decompose a biconnected undirected graph into its triconnected components by building an SPQR tree, which was later improved and implemented in time 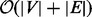by Gutwenger and Mutzel (2001). The SPQR tree represents all triconnected components of a biconnected graph from which all 2-vertex cuts can be extracted. Figure 2 shows such an SPQR tree for a toy graph example; an elaborate description of how to construct the SPQR tree can be found in Weiskircher (2002). The pairs of 1-vertex cuts obtained from the decomposition in biconnected components and the 2-vertex cuts obtained from the triconnected components form the set of separation pairs. These separation pairs are next validated to be source–sink pairs using the bubble search algorithm.

2.2.2 Validating separation pairs as source–sink pairs

The separation pairs are only source and sink pairs when all maximally extended paths inside the bubble originate from the source node and end in the sink node or vice versa. For example, the pair {1,6} in the biconnected component in Figure 2a is a separation pair because when it is removed, it increases the number of connected components, but it does not form a valid source–sink pair of a bubble. The only valid source–sink pairs in Figure 2a are {1,5}, {6,9} and {10,11}.

Theorem 2 —

Node v is part of a bubble if and only if all paths starting at v with a certain orientation o end in the source node when extended and all paths starting with the opposite orientation end in the sink node when extended.

Valid bubbles are found with a search based on breadth-first search in the bidirected-contig graph, starting from a random node in the list of nodes that form separation pairs. As a bubble can be present both upstream and downstream of the contig, the search is performed in two directions independently. In a normal breadth-first search, all outgoing edges of a node v that has been visited are queued for visiting. In our bubble search, edges of a node 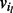with orientation 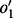are only queued when all its edges for which 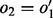have been visited, as Theorem 2 states that if there is no path from the source leading to one of these not-visited edges of 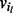, a valid bubble will never be present and there is no need for further exploration (Fig. 3).

Theorem 3 —

A contig can be the source of at most one bubble and the sink of at most one other bubble.

Fig. 3.

The bubble search algorithm. Solid edges indicate visited edges. (a) The search starts at node 1, and the queue Q holding the edges to be visited is initialized with all edges with a given orientation; 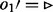in this case. (b) Edge 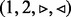is visited. As all edges incident to node 2 with 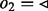have been visited, all edges of node 2 with 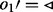are queued. (c) Edge 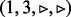is visited, but in this case, not all edges incident to node 3 with 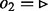have been visited yet, so the edges of node 3 are not queued. (d) The next edge 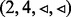in Q is traversed to target node 4. Again, not all edges incident to node 4 with have been visited, so no edges are added to Q. The Q is now empty and the algorithm terminates: node 1 in forward orientation is not a valid source node

To limit computation time, we try to minimize the number of bubble searches that we have to do by reducing the set of separation pairs. When a bubble is successfully found, all separation pairs that have at least one node in this bubble are removed from the set. Only the sink node can still be used to start the bubble search algorithm, if it forms a separation pair with another node outside the established bubble (Theorem 3). If we failed to find a bubble from a source node, then all separation pairs that contain the source node are removed from the set.

2.3 Assembly simplification by collapsing multi-allele bubbles

Scaffold and assembly graphs can be simplified by collapsing the bubbles into supercontigs. The inner contigs of the bubble are replaced in the contig graph by a single supernode (Fig. 1). All edges to and from the inner nodes are removed and replaced by two new edges: from source to supernode and from supernode to sink. Subsequently, a so-called unitigging step is performed, which is a search for simple paths without branches. The contigs in the simple paths are then combined into a single supercontig.

These supercontigs represent different alleles between the source and sink node present in the genomes in the sample. Any path from source to sink through this supercontig spells a valid assembly (Myers, 2005) and is a potential allele in one of the genomes. The native output of MaryGold is a graph describing the multi-allele. Nonetheless, downstream processing is facilitated by sequence-based tools, as there is also a sequence output, which is the highest depth path in the multi-allele (with ties broken arbitrarily).

2.4 Comparative metagenomics: genomic variation detection between metagenomes by co-assembly

The MaryGold algorithm enables variation detection between metagenome sequencing samples through co-assembly. By keeping track of the sample origin of the reads during assembly, a read depth per contig per sample can be calculated. Bubbles are then detected and the potential alleles are enumerated by finding all maximal paths from source to sink. The number of alleles corresponds to the number of paths from source to sink, although in reality there may be more possible paths than actual alleles present in genomes.

The alleles (and their carrying organisms) are present in unknown relative abundance. The sequencing depth for a single allele in a complex bubble, reflecting its relative abundance, is not trivial to find, as some nodes will be shared by two or more paths, e.g. node 5 in Figure 2a is shared by three paths between nodes 10 and 11. We infer the allele depth from the read depth of the contigs in its path, by minimizing the difference between the sum of the depths of the paths j that cross a node i and its read depth d_i for all node 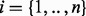using a non-negative linear least squares approach. The residual of node i for paths 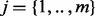in a multi-allele a then is

(1)

where X is the design matrix with binary regressors

(2)

and 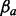is an m times 1 vector with the unknown path weights. The least squares method then finds path weights 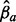that minimize the sum of the squared residuals

(3)

under the constraint that the allele read depths in 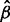are positive.

2.4.1 Measure of variation between alleles

To quantify the extent of the genomic difference in a bubble, we use a normalized version of the Levenshtein distance (or edit distance), summarizing the sequence distances of the alleles in a bubble. The average distance D_M is obtained by calculating the Levenshtein distance 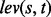for each pair of alleles s and t in a multi-allele M with N alleles and normalizing for the maximum length of the two alleles

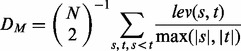(4)

3 METHODS

Most of the MaryGold algorithm is implemented in C++, with some additional Python scripts. The algorithm interfaces with the AMOS bank, where Bambus 2 and metAMOS store their assembly and scaffold information, using the AMOS library (Treangen et al., 2011). The graph decomposition in bi- and triconnected components uses the Open Graph Drawing Framework (Chimani et al., 2007). The multi-allele search algorithm is parallelized using OpenMP (Dagum and Menon, 1998). The non-negative least squares solver from the SciPy optimization package is used to obtain sequencing depths for the individual alleles, which is a wrapper around Fortran code (Lawson and Hanson, 1974).

Two shotgun datasets were simulated with the 454sim v1.04 package (Lysholm et al., 2011) using default settings from the genomes of three respectively seven Escherichia coli strains, to illustrate the effect on metagenome assembly of multiple closely related genomes. Four real sequencing datasets from the public domain were used to demonstrate the comparative metagenomics functionality of MaryGold. The first was obtained from the microbiome of a premature infant. Morowitz et al. (2011) sequenced the genomic DNA of the fecal microbiome, sampled on days 10, 16, 18 and 21 of the infant’s life. The second dataset was obtained at 10 different time points during the 29-day fermentation process of kimchi, the traditional Korean food (Jung et al., 2011). Both datasets are well suited for comparative metagenomics, as we can compare the metagenomes of the different time points. Finally, two sequencing datasets generated from samples obtained from the Richmond mine location C75 (Denef and Banfield, 2012) were downloaded from the Sequence Read Archive to compare performance on low coverage, but long 454 reads (SRA:SRR358990, 454 Titanium FLX, 133M bases) versus high coverage, but shorter Illumina reads (SRR359000, Illumina HiSeq2000 3.6G bases, 100 bp/read).

Assemblies were performed within the metAMOS v1.1 package (Treangen et al., 2013) using the Newbler v2.6 assembler (Roche, Branford, CT). Newbler was run with parameters ‘-a 0 -m -ace'. Additionally, the ‘-large' parameter was added for the assembly of the Illumina datasets to speed up the processing of the fragment assembly graph. Assigning taxonomic attributions was performed using the Fragment Classification Package v1.0 (Parks et al., 2011). Circular plots were generated with Circos v0.63 (Krzywinski et al., 2009), and graph layouts were performed with Cytoscape v2.8.3 (Shannon et al., 2003). The DAVID functional annotation tool (Huang et al., 2009) was applied on the genes in the kimchi sample that overlapped with the multi-alleles to find enrichment of functions and sequence features. DAVID was run with default settings, except that all predicted genes in the metagenome were used as background.

Performance was analyzed and compared with that of Bambus 2 based on the contig graphs of the simulated E.coli metagenomes. Ground-truth variation calls were obtained by aligning the K12 strain to each of the other strains individually, using nucmer [Mummer (Delcher et al., 2002)]. Subsequently, nucleotide variations were obtained using show-diff. Gapped alignments (labeled ‘GAP’) represent variation that could potentially lead to bubbles in the contig graph. Results from individual comparisons between K12 and all other strains were merged into a single list. Overlapping variation calls were merged. Next, MaryGold variation calls were related to a position on the K12 genome by aligning the source and sink node to its genome sequence. Bambus 2 variation calls were generated in FASTA format by the OutputMotifs program. Regions with the header ‘REPLACE_RANGE’ were extracted and aligned to the K12 genome to assign a genomic position to the variation call. Sensitivities were calculated as ( number of Mummer calls that overlap with a MaryGold bubble/number of Mummer calls). Precision was calculated as ( number of MaryGold bubbles that overlap with a Mummer call/number of MaryGold bubbles that mapped to the K12 genome). These calculations were made likewise for the Bambus variation calls.

Performance of MaryGold and Bambus 2 was also compared on the biofilm data. For Bambus 2, the OrientContigs program was run followed by OutputMotifs to output all multi-allelic regions. We then counted the number of bubbles and the number of contigs they contain. Bubbles were considered to overlap between the two methods if they shared at least three contigs.

4 RESULTS

4.1 MaryGold finds multi-allelic regions by detecting bubbles in the contig graph

The bubbles MaryGold detects are multi-allelic sites in the metagenome, meaning that for the genomic regions represented in the bubble, multiple alleles are present in the sample. Morowitz et al. (2011) resolved the bubbles in the assembly graph by manual curation. This was possible because only two Citrobacter strains were present, and therefore only bi-allelic bubbles had to be resolved. Our simulation experiments confirm that for a low number of strains, the contig graph is rather simple and bubbles can be resolved manually (Fig. 4a). If more strains are present, such as shown in our simulation experiment with seven E.coli genomes, the graph becomes too complex for manual curation (Fig. 4b).

Fig. 4.

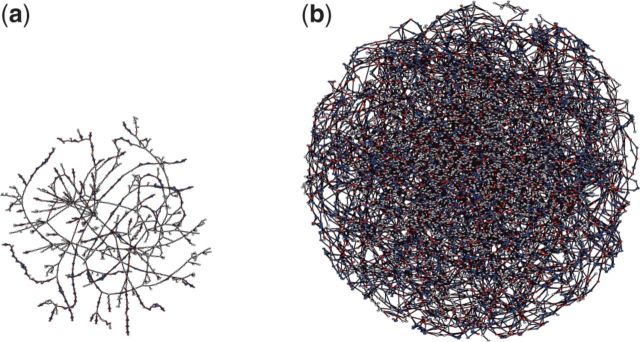
Largest connected components of the contig graphs for two simulated sequencing datasets for (a) three and (b) seven E.coli genomes

MaryGold detected 387 and 1582 bubbles in the simulated sequencing samples with three respectively seven strains (Table 1).The number of bubbles does not increase linearly with the number of strains, which is expected. If two genomes A and B differ at a locus, creating a bubble, then a third genome C that is again different at that locus will not result in an additional bubble, but just an additional path from source to sink within the bubble. Only at already present loci where A and B are identical, but C is different, the addition of genome C will result in an additional bubble.

Table 1.

Assembly statistics for two simulated E.coli and two real metagenomics datasets

Sample	Number of contigs	Number of multi-alleles	Number of contigs after simplification
Three E.coli strains	3445	387	2185
Seven E.coli strains	12 378	1582	6156
Kimchi fermentation	11 466	133	11 325
Infant microbiome	5686	154	5251

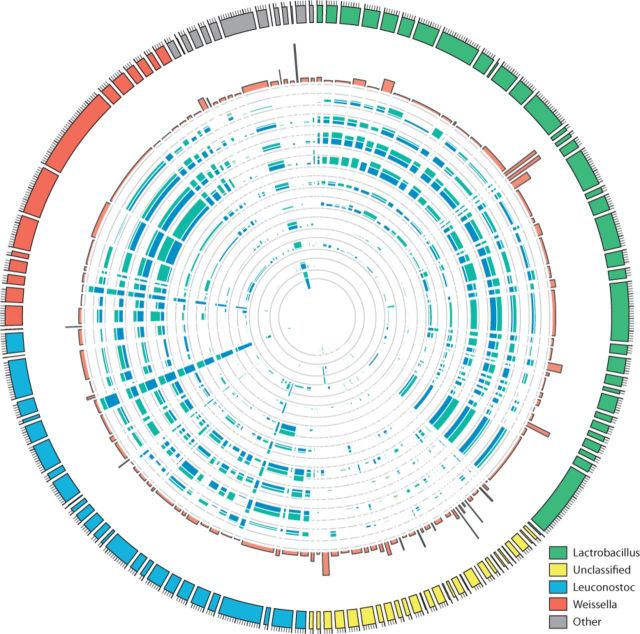
In the premature infant datasets, 154 bubbles were found (Table 1), predominantly in Citrobacter spp. (Fig. 5), as also described in the original article (Morowitz et al., 2011). In the original study of the kimchi fermentation, no allele variation study was performed. Here we show that allele variation is present by detecting 133 bubbles in Lactobacillus spp., Leuconostoc spp. and Weisella spp. (Fig. 6), which are thought to be the key players in this vegetable fermentation process (Jung et al., 2011).

Fig. 5.

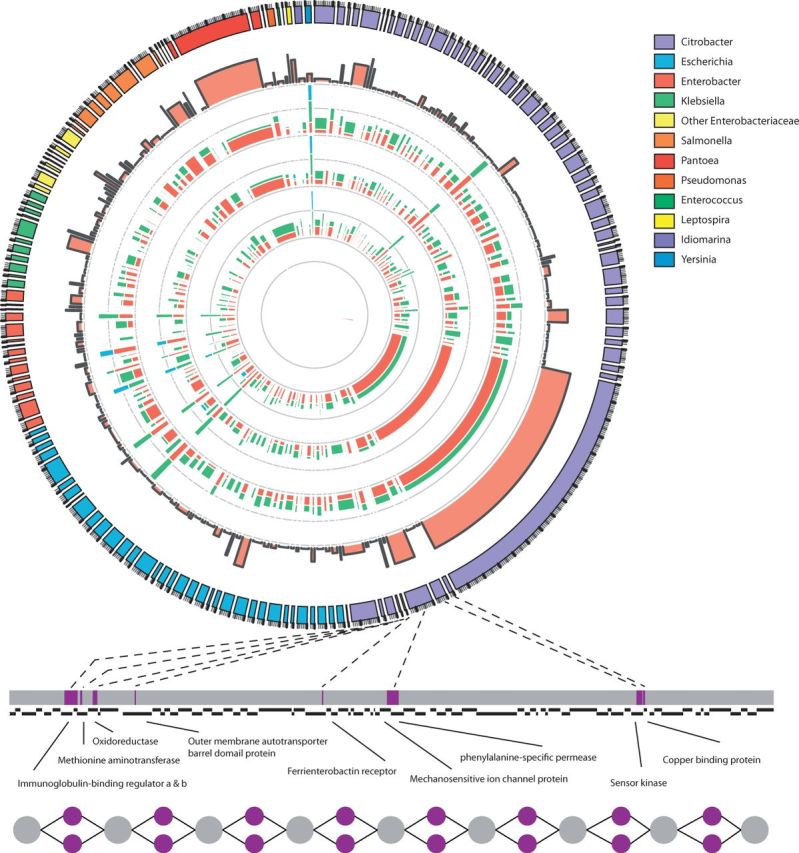
Overview of the multi-allele bubbles of the premature infant’s microbiome. Tracks in the circular plot from outside to inside are as follows: the multi-allele bubbles colored by species; their average length-weighted edit-distance D_M indicating variation; and the inferred sequencing depths 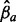for days 21, 18, 16 and 10 with each allele a indicated by a different color. Sequencing depths were scaled by 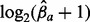to allow variable sequencing depths between genomes, and their gray axis is at 0.5. Below the circle is a zoomed version of one of the supercontigs, containing eight bubbles. Top: supercontig with the variable locations marked in purple. Middle: a gene track in which genes overlapping with a multi-allele site are functionally annotated. Bottom: the contig graph

Fig. 6.

Overview of the multi-allele bubbles of the kimchi fermentation. Tracks in the circular plot from outside to inside are as follows: the multi-allele bubbles colored by species; their average length-weighted edit-distance D_M indicating variation; and the inferred sequencing depths 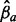for the time points chronologically sorted from inside to outside, with each allele a indicated by a different color. Sequencing depths were scaled by 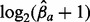to allow variable sequencing depths between genomes

4.2 Bubble collapsing allows studying genetic variation in genomic context

In the contig graph, contigs can be reliably concatenated into longer contiguous sequences, if they are connected by a simple path without branching. The contig graph branches at multi-allelic loci in the metagenome, leading to highly fragmented assemblies. By collapsing the bubbles that were detected by MaryGold (Fig. 1), the number of contigs in the assembly with three E.coli strains could be reduced by 28% and in the assembly of seven E.coli strains even by >50% (Table 1). The reduction in number of contigs in the real sequencing datasets was less apparent. In true metagenomic samples, genomes that have no close homologues are present. For such genomes, bubble compression does not reduce the number of contigs, as it only improves of the assembly of multiple closely related strains. Also, low sequencing depth causes low abundant strains to stay under the detection limit.

Bubbles are collapsed by choosing a single path from source to sink in the contig graph, with the highest average sequencing depth, to represent the multiple alleles, which allows the output of linear instead of fragmented sequences as generated by the assembler. The linear sequences aid further analysis, such as gene prediction and taxonomic assignments. Figure 5 shows a zoomed-in version of one such linear contig in the premature infant sample with gene annotations for each gene that overlaps with a multi-allelic locus. The genes that differed in the Citrobacter strains were found to be involved in iron and copper uptake as well as immunoglobulin (Ig) binding regulators, which bind to human Ig in a non-immune manner (Sandt and Hill, 2001).

Bubble collapsing enabled gene prediction across multi-allelic loci. The features ‘retrotransposable element Tf2’ and ‘E.coli ABC transporter YbhF’ were found to be significantly overrepresented (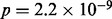 respectively 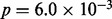, Bonferroni corrected) in genes in the kimchi sample that overlapped with the multi-alleles. Retrotransposons are expected to be found in multi-alleles, as they amplify themselves in a genome and create an additional allele after each insertion. The ABC transporter protein superfamily is involved in many cellular processes, including transport of a wide range of substrates and has been linked to development of resistance to multiple drugs, including antibiotics (Davidson et al., 2008).

4.3 Co-assembly finds variation between metagenomes

Co-assembly of multiple metagenomics samples followed by bubble detection using MaryGold allows for reference-free sequence variation detection. Subsequent visualization of the bubbles enables visual analysis and interpretation, such as in Figure 5, that shows the sequencing depths at the 4 days for which the microbiome of the infant was sampled. The alleles, and hence their carrying strains, vary in abundance over time. The bubble of the Pantoea spp. with the longest sequence (red in Fig. 5) also has a high average distance between the alleles. The sequencing depths show that the ‘green’ allele is the most abundant at the second time point (day 16), whereas for the two subsequent time points, this allele diminishes, and the red allele becomes the most abundant one.

4.4 Performance analysis of MaryGold and Bambus 2

We assessed performance of MaryGold and compared it with that of Bambus 2. Although Bambus 2 is optimized for contig graphs generated with paired-end data, i.e. scaffold graphs rather than assembly graphs, the methods could be compared, as they both output their bubbles. Other assemblers also contain bubble detection algorithms, such as Velvet (Zerbino and Birney, 2008), the Celera assembler (Fasulo et al., 2002) and meta-IDBA (Peng et al., 2011), but the bubble-finding algorithms are embedded in the assembler, and it is unclear how to access these methods. Moreover, the goal of these assemblers is to smooth the assemblies by collapsing bubbles, rather than using them for variation detection.

First, we tested the algorithms on simulated metagenome data. Mummer was applied on finished high-quality genomes instead of on sequencing reads, to find a list of ground-truth variation calls. Table 2 shows that MaryGold and Bambus found 16.8% respectively 2.0% of the nucleotide variation calls in the contig graph of the metagenome sample with three E.coli strains and 28.7% respectively 6.7% in the sample with seven strains. Bambus showed a higher precision, but the F1 score (the harmonic mean of the sensitivity and precision) was higher for MaryGold. The reference-free methods could not recover all ground-truth genomic differences, as de novo assemblies are hampered by the short read lengths, which cause fragmented assemblies in the presence of repeats. Additionally, the individual strains had ∼2× depth of coverage. If an allele appeared in only one strain, the bubble might have been removed by the assembler because it considered it to be a sequencing error.

Table 2.

Variation detected by Bambus 2 and MaryGold in simulated metagenomes compared with variation found by alignments of individual finished genomes to the E.coli K12 reference genome

Measure	Mummer	Bambus 2	MaryGold
Three E.coli
Number of calls	250	32	312
Sensitivity		2.0%	16.8%
Precision		15.6%	13.1%
F1-score		3.5%	14.7%
Seven E.coli
Number of calls	1177	114	1130
Sensitivity		6.7%	28.7%
Precision		30.7%	12.6%
F1-score		11.0%	17.5%

Note: The number of Bambus 2 and MaryGold calls is the number of bubbles that mapped to the K12 genome.

The difference in the number of bubbles found by MaryGold and Bambus 2 can be explained by looking at the algorithmic differences. Bambus 2 finds only bubbles detectable within two hops of the source node, which are then iteratively composed into larger bubbles. Additionally, the definition of a bubble slightly differs: unlike MaryGold, Bambus 2 allows for missing edges within the bubble due to lack of coverage and requires paths through a bubble to be roughly the same length.

Next, we applied both MaryGold and Bambus 2 on DNA sequences using both Illumina and 454 technology, which originated from biofilms at the same location within the Richmond Mine, but sampled on different dates (Denef and Banfield, 2012). This also allowed us to study the influence of the sequencing technology used and the accompanying difference in sequencing depth. More sequence could be assembled using the Illumina data because the higher number of sequenced bases allowed lower abundance bacterial strains to rise above the detection limit. In total, 16.8 Mb (N50 = 5850) were assembled with the Illumina data, whereas only 6.1 Mb (N50 = 1669) were assembled with the 454 data.

Both methods found more bubbles using the Illumina data than using the 454 data (Fig. 7). Although the samples were taken at different time points, we assume that they have similar microbial complexity because the sample location in the Richmond mine was identical. Therefore, we attribute the increased amount of variation found to the higher sequencing depth of the Illumina dataset. Figure 7 indicates the number of bubbles found by both methods and the extent to which they overlap (see Section 3). MaryGold found more bubbles than Bambus 2 in both datasets. On Illumina data, most of these bubbles overlapped (69, i.e. 73%); on 454 data, far less so (3, i.e. 27%). This corroborates the findings on the simulated data and shows that variation detection depends on assembly quality.

Fig. 7.

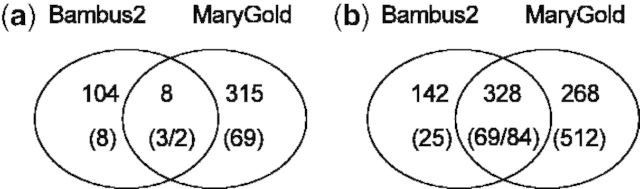
Comparison of the number of bubbles found by MaryGold and Bambus 2 for two acid mine drainage datasets: (a) the 454 dataset (SRR358990) and (b) the Illumina dataset (SRR359000). Indicated is the total number of contigs within the bubbles, with the number of bubbles between brackets

Finally, to give an idea of the computational complexity of MaryGold, we recorded its runtime on the contig graph with 31 191 nodes and 9586 edges of the Illumina acid mine drainage dataset, using an Intel Xeon CPU with four cores and four threads per core. Finding the set of separation pairs using graph decomposition took 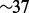s (CPU time). The subsequent bubble search algorithm took 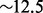min on a single core. Using two threads, the wall clock time spent by the bubble search algorithm dropped by 42%. The full analysis, from raw reads to MaryGold output, is mostly limited by the assembly step.

5 CONCLUSION

We presented MaryGold, a tool to detect and explore genomic variation within and between metagenomic sequencing samples, not reliant on reference genomes. MaryGold finds multi-allelic regions that reflect sequence variation and improves the contiguity of assemblies by collapsing these. As input, it expects a contig graph, which makes it generic and applicable to any type of sequencing data; we demonstrated the algorithm both on 454 and Illumina data. Here we generated contig graphs using links from fragment assembly string graphs, but the graphs can be extended using edges derived from other sources such as paired-end sequencing data, de Bruijn graphs or even reference genomes. Multi-allelic regions are efficiently detected by searching for bubble structures in the contig graph, enabled by its decomposition into bi- and triconnected components. Although MaryGold can detect local sequence variation, i.e. multiple alleles of a genomic locus, it ignores variation that not does not result in a detectable bubble, such as duplications and translocations, i.e. due to horizontal gene transfer.

Sequence variation in metagenomes and in particular between metagenomes, i.e. comparative metagenomics, is still a largely unexplored field. Our algorithm not only finds sequence variation within a single metagenomic sample but also between samples, and it allows for convenient visualization and interpretation of variation of even multiple metagenomic sequencing samples. The importance of sequence variation detection in metagenomes was demonstrated by finding variability in ABC transporters that are involved in resistance to multiple drugs in the kimchi sample and variability in bacterial cell surface proteins that bind to human Ig in the infant’s microbiome. Comparing data sampled at different time points in the infant’s microbiome showed varying relative abundance during the early colonization of its gut, suggesting competition between closely related strains until a stable composition is reached.

As sequencing gets cheaper, more assembly-grade metagenomics sequencing datasets become available. It will soon be possible to compare cohorts of samples and detect sequence-level difference in microbiomes or other environmental samples explaining specific phenotypes, and link the meta-genotypes to disease. The development of tools, such as MaryGold, that find this sequence variation and allow further analysis and interpretation is essential for effectively mining the metagenomics sequencing data.

Funding: This work was funded by Kluyver Centre for Genomics of Industrial Fermentation, a subsidiary of the Netherlands Genomics Initiative. The project was initiated during a visit of J.F.N. to the laboratory of M.P., supported by an EMBO short-term fellowship.

Conflicts of Interest: none declared.