Dependence of cancer cell adhesion kinetics on integrin ligand surface density measured by a high-throughput label-free resonant waveguide grating biosensor

Abstract

A novel high-throughput label-free resonant waveguide grating (RWG) imager biosensor, the Epic® BenchTop (BT), was utilized to determine the dependence of cell spreading kinetics on the average surface density (v_RGD) of integrin ligand RGD-motifs. v_RGD was tuned over four orders of magnitude by co-adsorbing the biologically inactive PLL-g-PEG and the RGD-functionalized PLL-g-PEG-RGD synthetic copolymers from their mixed solutions onto the sensor surface. Using highly adherent human cervical tumor (HeLa) cells as a model system, cell adhesion kinetic data of unprecedented quality were obtained. Spreading kinetics were fitted with the logistic equation to obtain the spreading rate constant (r) and the maximum biosensor response (Δλ_max), which is assumed to be directly proportional to the maximum spread contact area (A_max). r was found to be independent of the surface density of integrin ligands. In contrast, Δλ_max increased with increasing RGD surface density until saturation at high densities. Interpreting the latter behavior with a simple kinetic mass action model, a 2D dissociation constant of 1753 ± 243 μm⁻² (corresponding to a 3D dissociation constant of ~30 μM) was obtained for the binding between RGD-specific integrins embedded in the cell membrane and PLL-g-PEG-RGD. All of these results were obtained completely noninvasively without using any labels.

Integrins are heterodimer transmembrane receptors establishing a connection (anchorage) between the extracellular matrix (ECM, a molecularly diverse multi-functional biological scaffold for adherent cells¹,²) and the cytoskeleton of an ECM-supported cell (or between two adjacent cells). The connection is realized through non-covalent chemical bond formation with amino acid sequences in the ECM (or on the surface of the adjacent cell) complementary to the ligand recognition sites of integrins³,⁴,⁵. The particular α and β subunits constituting its heterodimers determine the specificity of an integrin as a receptor; the 24 known members of the superfamily are ordered into 4 subgroups on this basis⁶. The role of integrins is not, however, constrained to the mere establishment of anchorage; they also function as bidirectional signaling machines integrating several environmental clues, hence enabling the cell to dynamically respond to changes in its surroundings⁴,⁷.

It seems clear that the interaction between integrins and the complementary chemical entities in the substratum (e.g. certain amino acid sequences in the ECM, especially their dimensionality, availability, variability and spacing) provide the most important clues for spreading. It has, however, become increasingly evident that the physicochemical properties of the substratum – its topography, porosity, elasticity, and wettability – also play a role in determining whether a cell will spread, albeit less directly (e.g., the hydrophobicity of a carrier substratum can determine the orientation of proteins adsorbed to it⁸). If a metallic or ceramic material (e.g. an implant) acts as the underlying (carrier) substratum for cells, it must be coated with protein for specific cell adhesion and spreading to take place⁹,¹⁰; this protein coating, constituting the biological substratum, may be pre-applied or may be synthesized and secreted by the cells⁹,¹¹.

Today, research of unprecedented intensity is dedicated in biomaterials science to determine how the distinct biological, chemical and physical properties of candidate implant materials affect cell adhesion, spreading and, thus, fate¹². The hope of progress now lies in the possibility of individually tailoring those properties of a substratum which have the potential to modulate cell spreading¹³,¹⁴,¹⁵,¹⁶,¹⁷. Much work strives to tailor the topography, elasticity, or hydrophobicity of the carrier substratum, and the elasticity, topography, or the spatial organization of the biological substratum (see references18,19,20,21 for excellent reviews). Given the relative ease with which it can be accomplished, a distinctively great interest has been devoted to tailor the surface density of integrin ligands (especially that of the RGD tripeptide), and study its effects on cell spreading. Various approaches enable the average surface density of the RGD-motif (arginine-glycine-asparagine) – a minimal integrin recognition sequence present in several key proteins of the ECM (e.g. fibronectin, vitronectin, fibrinogen, van Willebrand factor)⁶,¹⁸ – to be tuned at will²²,²³,²⁴,²⁵,²⁶. In contrast, a more advanced technique, called block copolymer micelle nanolithography, is necessary to position the RGD motifs in a strict nanoscale order, yielding well defined interligand distances²⁷,²⁸,²⁹. The degree of nanoscale order of RGD motifs on a surface has been shown to have a serious impact on cell spreading²⁷. Cell attachment and spreading on an ordered nanopattern of ligands were highly restricted when the ligand spacing was increased beyond ~70 nm, while an average interligand distance larger than 92 nm was still sufficient to promote marked cell spreading on a disordered nanopattern²⁷. It has been claimed that the failure of cell spreading in the former case was due to the overly large interligand distances restricting effective integrin clustering, and the spreading observed in the latter case could be attributed to locally higher ligand densities that are sufficient to promote clustering²⁷.

Notwithstanding the impressive work done in the field, most investigations seem to get stuck at the level of quantifying cell adhesion and spreading at a single time point and, therefore, can only imperfectly describe the effect of substratum modifications (e.g., adhesion-enhancing or -inhibitory). The dynamic aspects of adhesion and spreading have hitherto very rarely been considered²²,²³,³⁰,³¹, mainly because few techniques enable these processes to be specifically monitored with adequate data quality, especially without the incorporation of labels, which may potentially perturb cellular behavior.

Nevertheless, surface-sensitive label-free biosensors suitable for cell-based assays are inherently capable of generating good quality kinetic data. Evanescent field-based label-free optical biosensors including optical waveguide lightmode spectroscopy (OWLS)¹⁰,¹¹,³²,³³,³⁴,³⁵, photonic crystal biosensors³⁶, grating coupling interferometry (GCI)³⁷,³⁸, and resonant waveguide grating (Epic®) biosensors³⁹ are considered to be especially straightforward means to monitor surface adhesion, since they detect refractive index changes only in the relevant 100–200 nm layer above the substratum⁴⁰. The biosensor response – integrating changes in both the size of the contact area, and the optical density therein (dependent on the extents of actin polymerization, integrin clustering, adhesion complex formation and maturation, etc.) – is a more accurate measure of cell adhesion and spreading than the ones predominantly used in microscope image analysis (number of attached cells and average contact area). However, in-depth comparative analysis of the kinetics requires a vast amount of high quality data recorded under various experimental conditions. First generation biosensing technologies were unable to satisfy these criteria due to their limited throughput – single measurements conducted hours or days apart could be hardly compared with each other since inter-experimental dynamic variability seems to be inherent in the nature of living cells. Quantitatively monitoring cellular responses to fine-tuning a known environmental regulator of cell adhesion and spreading was not, therefore, feasible until the appearance of a new generation of biosensors offering high throughput.

Here we exploit a novel high-throughput optical biosensor (Fig. 1) to quantitatively elucidate the relationship between the two-dimensional surface density of the integrin ligand RGD-motif and the kinetics of cell adhesion. Surface coatings for spreading studies were obtained using the mixtures of two synthetic copolymers, the biologically inactive PLL-g-PEG and its RGD-functionalized counterpart, simply referred to here as PLL-g-PEG-RGD. These molecules simultaneously attach to the mostly electron-donating substrata with their PLL moieties, leaving the PEG moieties free to prevent cell attachment and nonspecific protein adsorption²⁵. By mixing the two copolymers in appropriate proportions, we could generate well-defined average RGD surface densities at will, which were then used as substrata for cell spreading assays. Superior quality kinetic data were obtained with the novel resonant waveguide grating (RWG) system, which were then further analyzed by fitting the logistic equation to the spreading curves. The fitting parameters were connected to possible molecular biological processes and interpreted in terms of a simple kinetic mass action model. Unlike previous efforts, which have mostly been wedded to homogeneous reaction kinetics, with the surface-sensitive biosensor we can directly extract the biophysically, chemically, and physically relevant heterogeneous dissociation constant of the binding between integrins embedded in their native (cell) membrane and the RGD moieties.

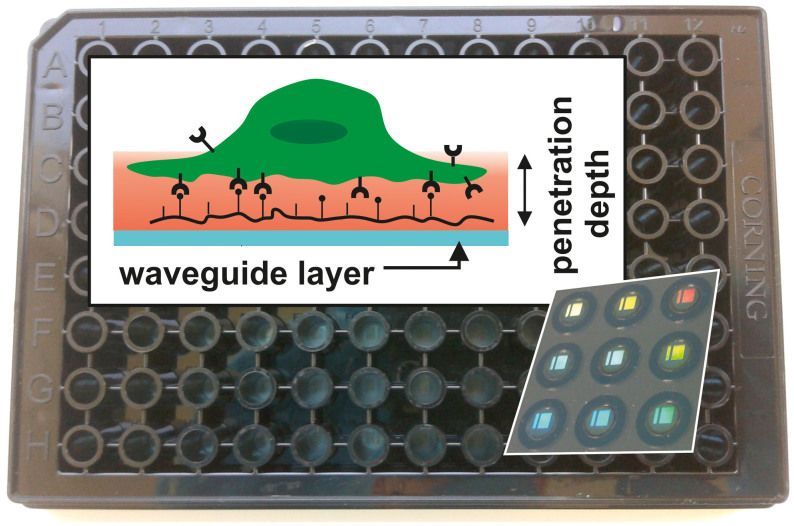
Figure 1. Detection scheme of the RWG imager with the microplate in background.

In the background, a photograph of an SBS-standard 96-well Epic® sensor microplate is shown. Each well contains a biosensor (a 2 × 2 mm nano-grating embedded in a high-refractive index waveguiding film) at its bottom, which is visible due to diffraction (shown for nine wells imaged from the back of the plate in the inset lower right). The upper left inset depicts the principle of detection (not to scale). The wavelength of the light source illuminating the sensors is swept in a 15000 pm range with a 0.25 pm resolution. At the resonant wavelength λ the light is incoupled to the waveguide and its evanescent field penetrates into a ~150 nm thick layer above the sensor (containing the PLL-g-PEG-(RGD) layer, the liquid medium, and the very bottom of the cell with its integrin receptors; shown in red), probing the local refractive index. The resonant wavelength λ is detected with a CMOS camera after it has been outcoupled. Refractive index changes in the sensing zone shift λ; thus the raw response of the wavelength-swept RWG-sensor is the wavelength change Δλ.

The present paper is the first to demonstrate the outstanding potential of a high-throughput label-free biosensor in studying the impact of an environmental regulator of cell adhesion on the kinetics of the process. As such, a high-throughput RWG biosensor can be readily applied in any study aiming at quantitatively elucidating the relative importance of environmental clues for cell adhesion and spreading. Furthermore, we emphasis that kinetic monitoring, especially in combination with appropriate kinetic analysis, provides a better insight into these processes than a static analysis, and sheds light on details that are otherwise unseen.

Results and discussions

Estimation of the molar surface density of ligand, ligand-ligand distances, and numbers of ligands per unit area

The molar surface density of the peptide (ρ_RGD) is approximated according to²⁶:

where Γ is the mass adsorbed to the smooth surface, M_Pol is the molecular weight of the RGD-functionalized copolymer, Q is the volume percent of the PLL-g-PEG-RGD solution (1 mg/ml) in the mixed solution of copolymers (1 mg/ml), N_Lys = 96 is the average number of lysine monomers in a PLL backbone, g = 3.7 is the grafting ratio (giving the number of Lys units per PEG side chain), and P = 12% is the fraction of functionalized PEG chains²⁶. M_Pol is estimated from the approximate molecular weights of the components of PLL-g-PEG-RGD, i.e. that of the PLL backbone (M_PLL = 14 kDa), the unfunctionalized PEG side chains (M_PEG = 2.3 kDa), the slighly longer PEG side chains for functionalization (M_PEG* = 3.4 kDa), and the peptide containing the RGD sequence (M_PGD = 1035 Da):

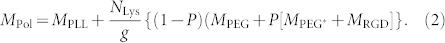This yields M_Pol = 80.3 kDa. The mass surface density of the copolymers adsorbed to a Nb₂O₅ substratum has been reported to be 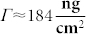(independently of g or P)²⁵. Assuming a hexagonal surface distribution of RGD-containing peptides, the average ligand-to-ligand distance (d_RGD-RGD) is formulated as²⁶:

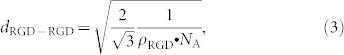where N_A is Avogadro's number (N_A = 6.022 · 10²³ mol⁻¹). We estimate the average number of ligands per unit area as:

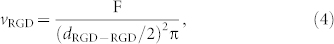where F ≈ 0.9069 is the proportion of the surface covered by non-overlapping circles of equal sizes packed in a hexagonal arrangement. Values of ρ_RGD, d_RGD-RGD and v_RGD calculated from Eqs. 1–4 are given in Table 1.

Table 1. Volume percent Q of 1 mg/ml PLL-g-PEG-RGD in the mixed solutions of copolymers used for coating the sensor surfaces; the calculated molar surface density of RGD-motifs (ρ_RGD); the estimated values of average ligand-to-ligand distance (d_RGD-RGD), and the average number of ligands per µm² (v_RGD).

Q (%)	ρRGD (pmol · cm−2)	dRGD-RGD (nm)	vRGD (μm−2)
0.0	0.0	∞	0
0.125	0.0089	147	54
0.25	0.0178	104	107
0.5	0.0356	73	214
1.0	0.0712	52	429
2.0	0.1423	37	858
4.0	0.2847	26	1715
10.0	0.7117	16	4288
25.0	1.7792	10	10720
50.0	3.5585	7	21440
100.0	7.1169	5	42880

PLL-g-PEG does not completely inhibit the adhesion of HEK293 cells

HEK293 cells seeded onto sensor surfaces coated with either 1 mg/ml PLL-g-PEG or 1 mg/ml PLL-g-PEG-RGD spread to a similar extent (data not shown). Schuler et al. hypothesized that porcine epithelial cells and Balb/c 3T3 fibroblasts could spread on a pure PLL-g-PEG coating due to the nonspecific adsorption of cell-adhesive proteins at locations of small defects in the PEG-brushes²⁶. Since we did not add FBS to our assay medium (in contrast to the work cited above), we must conclude that cell-adhesive proteins were produced and secreted by the cells themselves. In addition, the RGD-functionalized copolymer was unable to strongly enhance the spreading of the cells compared to that observed on a pure PLL-g-PEG coating, perhaps because of low expression levels of RGD-specific integrins in the HEK293 cell line. Although the first issue – the adsorption of spreading-promoting secretion to the PLL backbone – could perhaps be dealt with by creating ultradense PEG-surfaces⁴⁶, we could not overcome the second problem without genetic engineering. Therefore, we simply excluded the HEK293 cell line from further investigations in which the surface density of the RGD-motif was fine-tuned.

Spreading of HeLa cells on surfaces with fine-tuned RGD-densities

In contrast to the moderately adherent HEK293 cells, initial experiments indicated that the spreading of highly adherent HeLa cells⁴⁷ is totally inhibited by a pure PLL-g-PEG coating, and that they respond very sensitively to changes in the surface density of RGD-motifs. This made the latter cell line ideal for detailed spreading studies investigating the effect of fine-tuning the surface density of integrin ligands.

So far, 7–8 integrin heterodimers have been shown to be specific for the RGD-motif⁵,⁶, and many other promiscuous ones have been also shown to recognize and weakly bind it⁶. It is known that HeLa cells have at least 2-3 RGD-specific integrins, α5β1⁴⁸, αvβ5⁴⁸,⁴⁹ and αvβ3⁴⁹,⁵⁰. αvβ3 is overexpressed in HeLa cells and, being a critical factor for angiogenesis, its expression level is a general measure of the malignancy of tumorous cells⁵¹. The approximate number of these heterodimers per HeLa cell has not been determined, therefore we have to content ourselves with a rough estimate and assume that the number of RGD-specific integrins on an individual HeLa cell is around n_HeLa = 6 · 10⁵ (which is the same as the summed number of α5β1, αvβ5 and αvβ3 integrins on the surface of a single HUVEC endothelial cell⁵²).

Dependence of spreading kinetics of HeLa cells on ligand surface density measured with the RWG imager

Biosensor data obtained by monitoring cell spreading on surfaces coated with mixed solutions of PLL-g-PEG and PLL-g-PEG-RGD (Table 1) are presented as means ± standard deviations in Fig. 2a. We assume that the observed differences can fully be attributed to varying the average surface density of the RGD-motifs (v_RGD). We cannot exclude the possibility that cells modulate their spreading or that of others; secreted biomolecules such as ECM proteins or matrix metalloproteinases⁵³ all have the potential to regulate cell spreading. Nevertheless, secretions cannot contribute directly to the biosensor signal, since their amount is far too small to detectably increase the bulk refractive index, and the PLL-g-PEG coating reduce molecular adsorption to an insignificant level²⁵,⁵⁴. Therefore, the biosensor signal exclusively reflects the spreading and adhesion of a cell population on a given surface, whether it is promoted by direct interaction with the adhesion receptors or by (an altered) cellular secretion of molecules which further modulate cell spreading. This exclusivity might be violated if the number of spread cells is too high or too low. In the former case the lack of space may restrain spreading or provoke cellular responses that cannot be attributed to the differences in v_RGD (or, equivalently, to differences in d_RGD-RGD). We therefore seeded cells at a number low enough to avoid this issue. Thanks to the excellent sensitivity of the biosensor, the latter case was never a real problem: all spreading curves were reproducible and followed a sigmoidal evolution.

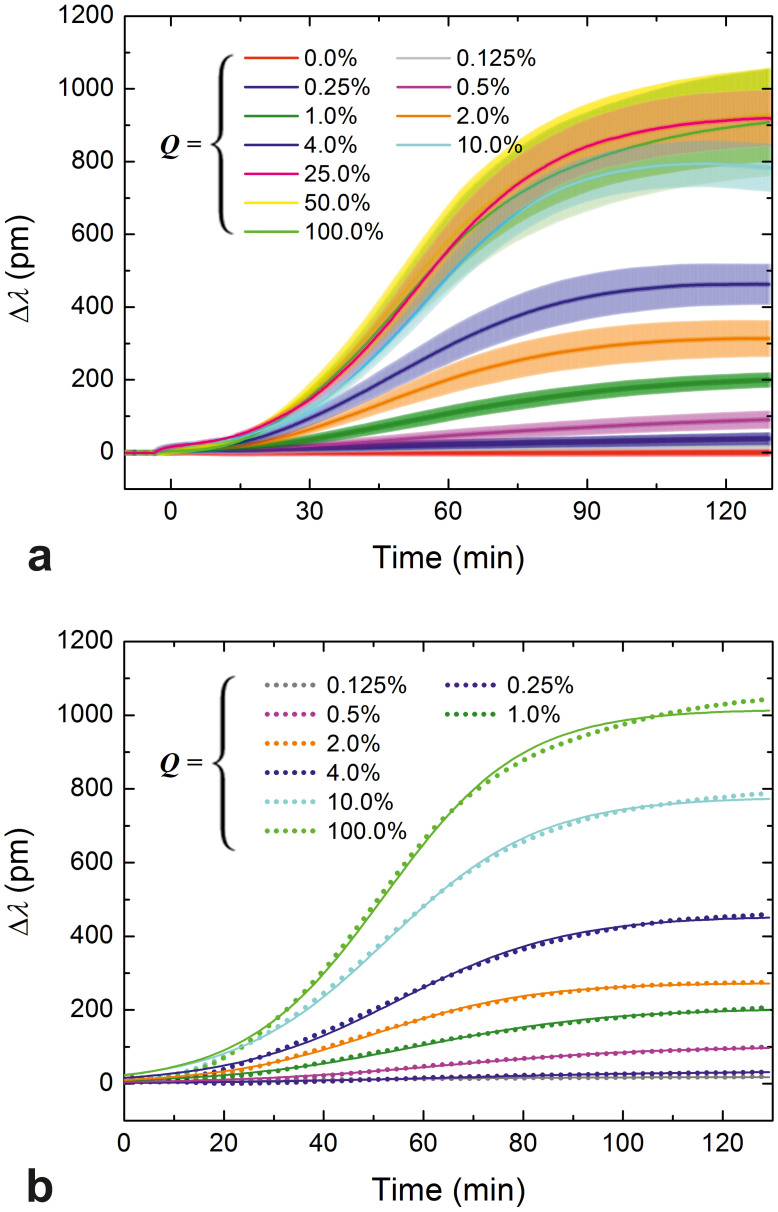
Figure 2. Spreading curves obtained at different RGD densities and their fits.

(a) Spreading curves of HeLa cells measured using the RWG imager. The surface density of integrin ligand RGD-motifs was fine-tuned by co-adsorbing the generally cell repellent and protein-resistant PLL-g-PEG copolymer and its cell adhesive, functionalized counterpart, PLL-g-PEG-RGD, from their mixed solutions. Data are presented as a function of the volume percent of a 1 mg/ml PLL-g-PEG-RGD solution in the mixed solution of copolymers (Q, bottom axes in the graphs), and the average interligand distances (d_RGD-RGD, top axes in the graphs). HeLa cells in serum-free buffer were seeded on the coated sensor surfaces (at epoch t = 0 min) and their spreading was monitored for approximately 2 h. Measurements were done in triplicate, data are presented as mean ± standard deviation. (b) Individual spreading curves registered by the RWG sensor and their fits (Eq. 5) can be hardly distinguished, which demonstrates the superior quality of the data (only one series of curves is shown, and some data and the corresponding fits have been omitted from this figure to avoid crowding and overlaps). Dots represent data, solid curves are the fits.

Given the excellent resolution and quality of the data, cellular responses to increasing Q from zero to as little as 0.125% could be easily detected; the corresponding biosensor signals can be perfectly distinguished (Fig. 2a). Maximum biosensor responses (Δλ_max) increased as a response to increasing Q until saturation was reached at around Q = 25.0% (d_RGD-RGD ≈ 10 nm). The saturation is not surprising considering that: i) the diameter of an integrin in the cell membrane is 8–12 nm²⁷, thus ligands closer to each other than this cannot be simultaneously bound; and ii) all integrins of a cell are expected to be bound at that level (~5 · 10⁶ ligands should lie under a cell having a moderately spread contact area of 500 µm², which is much more than the estimated value of n_HeLa).

Image analysis: end-point photomicrographs show the same trend as the biosensor data

Microscope image analysis is a traditional, widely used method to quantitatively characterize the extent of cell attachment and spreading on different substrata. Although much information can potentially be gained from image analysis, the ratio of the attached cells and the cell-substrate contact area are, by far, the two predominantly used measures for the extent of cellular adhesion and spreading.

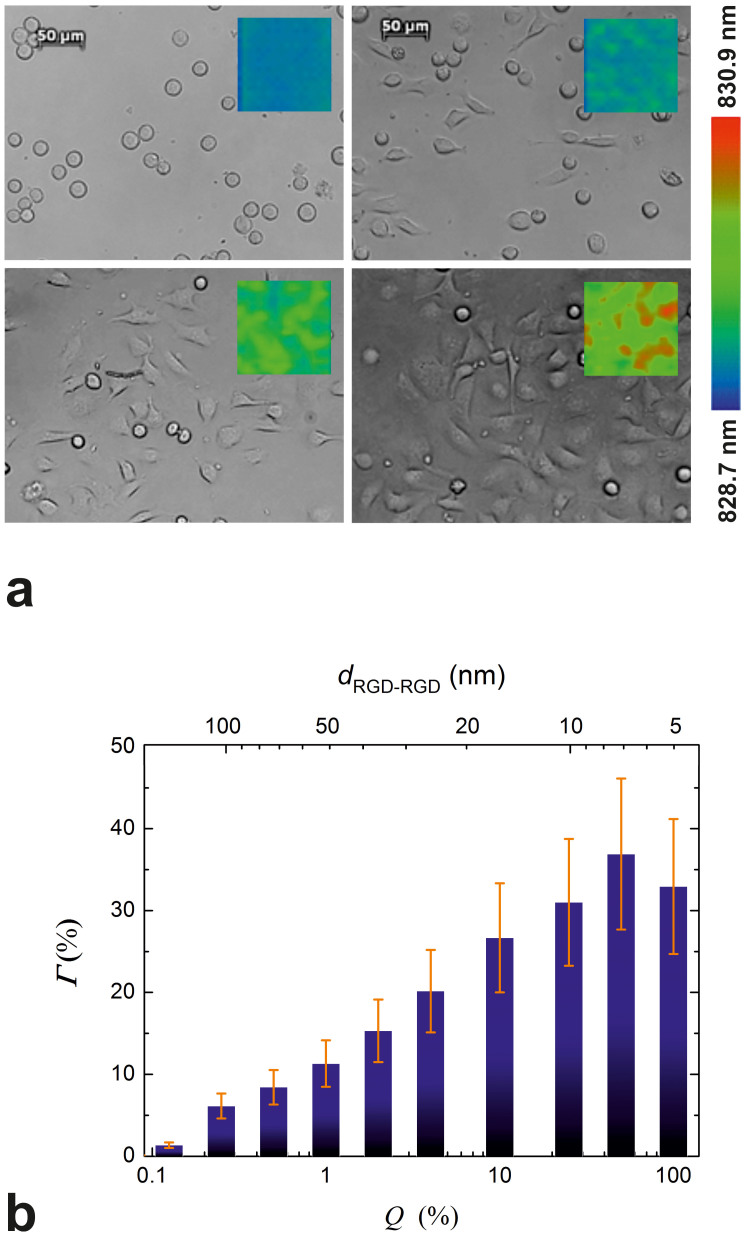
To allow for a rough comparison between biosensor data and the information that can be extracted using basic image analysis, cells were imaged with a microscope immediately after the biosensor experiment. Representative photomicrographs for Q = 0.0, 1.0, 4.0 and 50.0% (d_RGD-RGD = ∞, 52, 26 and 7 nm) are shown in Fig. 3a (the resonant wavelength distribution in the corresponding wells at the very end of the experiment is also shown as an inset in the photomicrographs). Image analysis revealed that both the number of spread cells and their average contact area were dependent on the integrin ligand surface density (data not shown individually). Thus, if normed with the number of seeded cells, these curves would reflect the spreading of an average cell in the whole cell population on a given surface. Using these quantities determined for each value of Q, we calculated the proportion of the surface that was occupied by spread cells (Γ, Fig. 3b). To a first approximation, spread cell coverage of the surface (Fig. 3b) is expected to be directly proportional to the biosensor response³². Indeed, comparing Γ shown in Fig. 3b with Δλ_max in Fig. 2b (end-point values of individual curves, or see Fig. 4a for average of triplicates), a general agreement in the tendencies is seen. A pure PLL-g-PEG coating completely blocked HeLa cell spreading: all cells remained small and round (Fig 3a, top left image). In contrast, a rather low RGD-surface density (e.g. at Q = 0.125% or Q = 0.25%) was already sufficient to promote spreading of a number of cells (not shown in microscope images, but see Fig. 3b). Increasing Q up to 25.0% engendered increases in both the extent of spreading and the number of spread cells (in Fig. 3a, compare the images corresponding to Q = 0.0, 1.0, 4.0 and 50.0%). However, further increasing the ligand density did not further increase cell spreading.

Figure 3. Microscope images taken at the end of the biosensor experiment and data obtained from image analysis.

(a) Photomicrographs of cells taken with an inverted microscope at the end of the biosensor experiments. Cells were allowed to spread on surfaces pre-coated with the mixed solutions of copolymers. Q was either 0.0, 1.0, 4.0 or 50.0% (from left to right, top to bottom). The scale bars on the top images represent 50 µm. Inset images in the photomicrographs (c.f. the color bar on the right) show the resonant wavelength distribution in the corresponding wells at the very end of the experiment. (b) The surface percent occupied by spread cells (Γ, bars) on each coating was obtained by performing image analysis on the photomicrographs taken at the end of the biosensor experiment. Data are presented as a function of the volume percent of a 1 mg/ml PLL-g-PEG-RGD solution in the mixed solution of copolymers (Q, bottom axes in the graphs), and the average interligand distances (d_RGD-RGD, top axes in the graphs). Error bars represent estimated errors, see text for details.

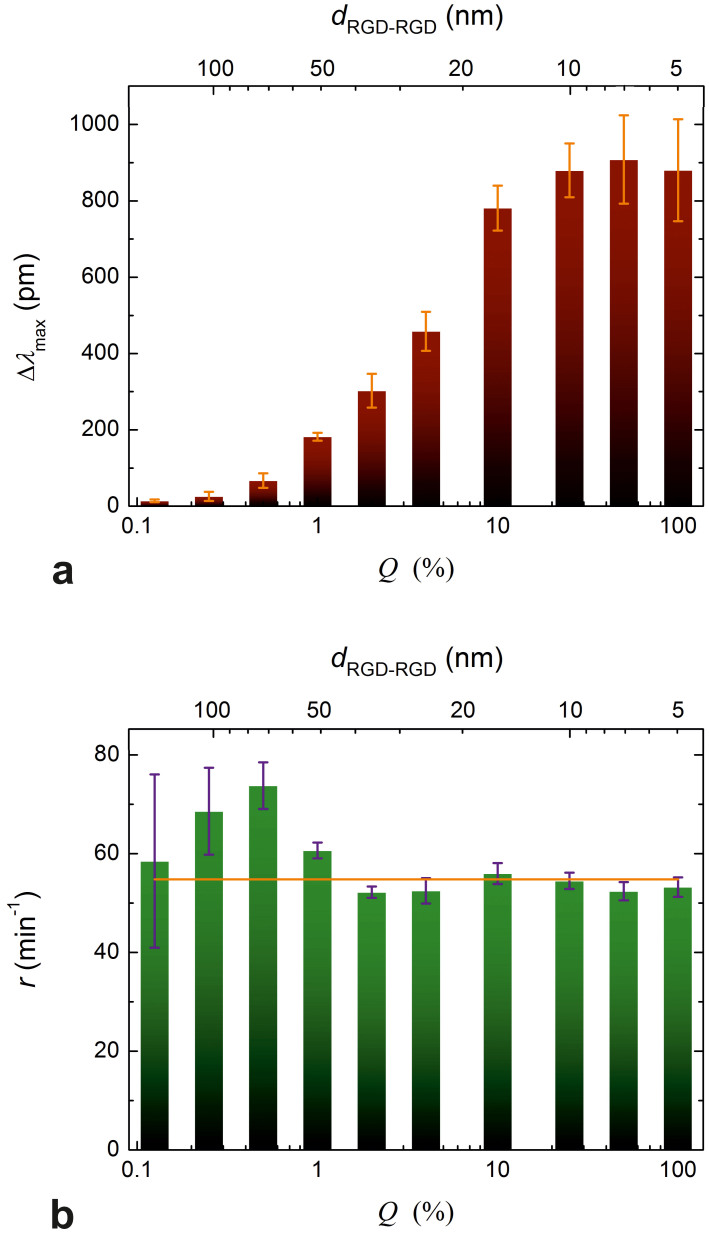
Figure 4. Maximum biosensor responses and the rate constants of spreading.

(a) Maximum biosensor response (Δλ_max) as a function of Q (bottom axis) and the d_RGD-RGD average interligand distance (top axis). The values were obtained by fitting Eq. 5 to the individual spreading curves and averaging the parameters obtained from triplicate fits. Error bars represent the standard deviation from the mean Δλ_max values (practically the same as the half-widths of the ‘clouds' drawn around the end-points of the curves in Fig. 2a). (b) The rate constant (r) as a function of Q (bottom axis) and the d_RGD-RGD average interligand distance (bars). Values and error bars were obtained the same way as for Δλ_max. The solid horizontal line represents the average value of all rate constants.

Importantly, the error of the data obtained from image analysis (error bars in Fig. 3b) should not be compared to the errors presented in Fig. 4a (as the latter represent the standard deviations from the mean values of triplicates), but to the negligible noise of the curves near the end-point values in Fig 2b. The quality of the data obtained from image analysis is, therefore, rather poor compared to that registered by the biosensor; further emphasizing the capabilities of the RWG sensor to generate superior quality cell spreading data.

Maximal spread contact areas and the rate constants of spreading obtained by fitting the data

Previously we have proposed to quantitatively characterize the spreading curves by fitting the logistic equation to them¹¹:

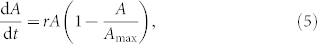where A_max is the maximum possible contact area, termed spreading constraint, and r is the rate constant of spreading. In the present work the logistic equation (Eq. 5) was individually fitted to each curve (and not to the averaged curves of triplicates), and Δλ and Δλ_max were used instead of the less accurately measured variable A and parameter A_max. (Note that Δλ is expected to be directly proportional to A¹⁰.) Adjusted R-square values characterizing the goodness of the fits were >0.969 in all thirty cases. Goodness of the fits is further demonstrated in Fig. 2b; it is seen there that the individual spreading curves and the corresponding fits are practically indistinguishable from each other (only a single set of curves is shown, and two curves have been omitted to avoid crowding and overlaps).

The fitting parameters (Δλ_max and r) of triplicates were averaged and their mean values plotted against Q and d_RGD-RGD as shown in Fig. 4. It is clearly seen on the graphs that the maximum biosensor response (Δλ_max) increase with decreasing d_RGD-RGD (Fig. 4a) until d_RGD-RGD ≈ 10 nm (Q ≈ 25.0% is reached, while r remains essentially constant. It is interesting to compare the dependence of Δλ_max on the average interligand distances with the findings of the Spatz group²⁷,²⁹, while noting that the nanoscale distribution of RGD-motifs on our surfaces is disordered, but not completely random (adsorption of PLL-g-PEG-RGD molecules corresponds to a random deposition of islands each with an average of 3 RGD motifs). In our case, no critical interligand distance was found above which spreading diminishes abruptly; this is characteristic of spreading promoted by ligands dispersed in a highly disordered manner²⁷. In accordance with expectations²⁷, we obtained the maximum biosensor response at around an average interligand distance of 10 nm – indeed, separation distances smaller than the diameter of an integrin in the cell membrane (corresponding to Q = 50.0, 100%) cannot possibly increase the biosensor response further.

Interpretation of the dependence of maximum biosensor response on ligand surface density

Let us suppose that the receptor-ligand interaction can be described as first order monovalent binding. Denoting the surface concentrations of the unbound ligand (RGD), unbound receptor (integrin), and their bound form as L, I and B, respectively, the receptor-ligand reaction is:

According to the kinetic mass action law (KMAL), at steady state (equilibrium) the attachment and detachment reactions (characterized by two-dimensional rate coefficients k_a and k_d, respectively) have equal rates and

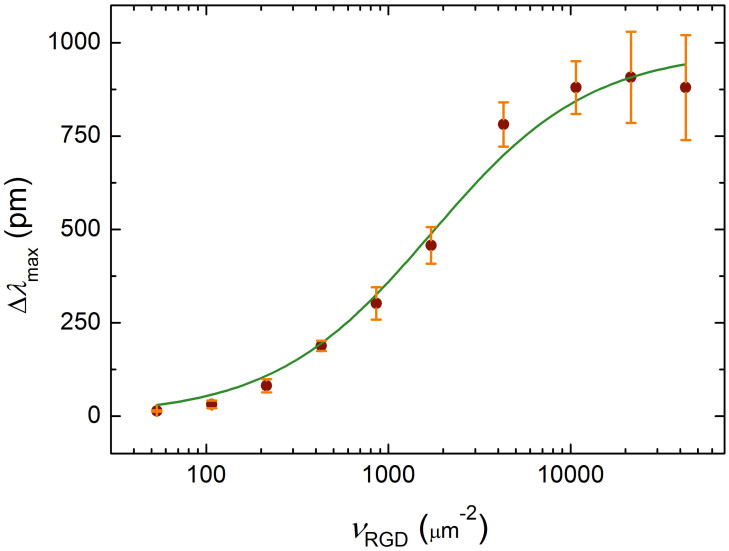
where L₀ = L + B and I₀ = I + B (i.e. L₀ = v_RGD), and ^2DK_d = k_d/k_a is the two-dimensional dissociation constant. We assume that B_eqm is directly proportional to the optical response measured at saturation (Δλ_max). By fitting Eq. 7 to the data replotted as Δλ_max vs. v_RGD (Fig. 5), we found that ^2DK_d = 1753 ± 243 μm⁻² (adjusted R-square value of the fit is 0.987).

Figure 5. Fit performed to derive the two dimensional dissociation constant.

Δλ_max as a function of the average number of ligands per unit contact area v_RGD (dots) was fitted with Eq. 7 (solid line) describing the steady-state of single-step monovalent binding. This yielded a 2D dissociation constant of ^2DK_d = 1753 ± 243 μm⁻² for the binding between integrins embedded in their native (cell) membrane and the RGD moieties. Error bars on the dots represent the standard deviation from the mean Δλ_max values (practically the same as the half-widths of the ‘clouds' around the end-points of the curves in Fig. 2a).

In order to compare these results with experimental data published elsewhere, the relation between the two and three-dimensional dissociation constants (^2DK_d and ^3DK_d, respectively) has to be established. Clearly, ^3DK_d equals ^2DK_d divided by some characteristic length of the interacting system:

l_c has been referred to as the confinement length⁵⁵,⁵⁶. We propose l_c to be the average cell-substrate separation distance: the extent of separation is the result of the combined effect of nonspecific repulsion and specific bonding forces between the cell and the underlying substrate⁵⁵. Various techniques including internal reflection microscopy⁵⁷, surface plasmon resonance microscopy⁵⁸, and impedance-based biosensing⁵⁹, have been utilized to determine the separation distance, and the obtained average values are typically in the range of 40–160 nm. Lacking more precise information, we assume an average separation distance and an equivalent confinement length of l_c = 100 nm, while keeping in mind that the repulsion exerted by the unfunctionalized PEG side chains on the cells may cause this value to be exceeded.

Using Eq. 7, the estimated value of the three dimensional dissociation constant is ^3DK_d ≈ 30 μM. In comparison, a dissociation constant of 0.03 μM was determined by total internal reflection fluorescence microscopy (TIRFM) for the binding of natural ligand fibrinogen to the RGD-specific αIIbβ3 integrin (platelet integrin) incorporated into a lipid bilayer⁶⁰. This discrepancy of three orders of magnitude can be partially explained by the different conformation of the RGD-site in the two molecules⁶¹. αIIbβ3 integrins incorporated into a lipid planar bilayer have indeed been found to show less affinity for an RGD-containing linear peptide (having a very similar amino acid sequence to that used to functionalize the PEG-chains) than for fibrinogen; the dissociation constant of the former was determined as 1.7 μM⁶⁰. Hence conformation differences between the native and the artificial linear RGD-ligands account for a roughly sixtyfold factor in ^3DK_d. The remaining (roughly twentyfold) discrepancy can be attributed to further differences between the investigated systems. First, the RGD-specific integrins of HeLa are unlikely to have exactly the same affinity for the same linear sequence as the platelet integrin αIIbβ3. Second, platelet integrins isolated with a detergent and grafted uniformly into planar lipid bilayers have been claimed to be all activated, thus showing maximum affinity for their ligands⁶⁰. In contrast, affinity regulation is an intrinsic property of αIIbβ3 integrins in platelets (they are able to switch from a low affinity ‘inactive' to a high affinity ‘activated' state upon induction)⁷; thus, they are expected to show a larger dissociation constant (smaller affinity) for a certain ligand when they are in their native environment compared to when embedded into a model cell membrane system. In addition, the incorporated labels used in most of the earlier studies may well have interfered with ligand binding. In summary, the simplest model described by Eq. 7 seems to be sufficient to characterize integrin–ligand interaction; it fitted our data remarkably well and yielded a dissociation constant with a reasonable value.

Interpretation of the independence of the rate constant of spreading on surface ligand density

In contrast to Δλ_max, the rate constant of spreading (r) was found to be practically independent of the RGD-surface density (Fig. 4b). This is in accordance with a previous report²³, where substrata were coated with varying amounts of fibronectin and the rate of increase in contact area of isotropically spreading fibroblasts was directly measured by TIRFM. Averaging our data resulted in r = 54.8 ± 1.3 min⁻¹ (Fig. 4b). We propose that r most probably depends on the growth of the filopodia governed by actin polymerization and is therefore naturally independent from ν_RGD: we appropriately called it “exploratory eagerness”¹¹. It would be interesting to test this hypothesis by treating cells with inhibitors of actin polymerization, but this is beyond the scope of the present study.

Conclusions

Optical biosensing has long been considered to be an especially valuable method in the label-free “zero-perturbation” monitoring of living cell behavior, but until recently could not cope with the demands for high-throughput indispensable for wide-scope studies. The Epic® technology has overcome the disadvantage of the limited throughput of first-generation biosensing technologies, and Epic® biosensors have indeed already become extremely powerful tools in the hands of large pharmaceutical companies, but were not hitherto available to financially more restricted academic research labs.

We report here for the first time the application of a novel high-throughput RWG-biosensor, and demonstrate its outstanding capabilities in a cell adhesion assay where the bulk RGD surface density was varied over four orders of magnitude while not affecting any other surface properties. Cell adhesion kinetic data of unprecedented quality were obtained, which is essential for critically testing kinetic models for the process. Our data were practically perfectly fitted with a logistic equation. The dependence of the resulting fitting parameters on RGD surface density was connected to possible molecular mechanisms. The maximum biosensor response Δλ_max, which was assumed to be linearly proportional to the number of bound integrins, obeyed a sigmoidal dependence on the surface density of RGD motifs. Importantly, the investigated cells (HeLa) responded to varying the average interligand distance only in a narrow window; RGD ligands separated by an average distance of ~10 nm promoted maximum spreading, while no adhesion and spreading were detected on surfaces where the separation distance exceeded ~150 nm. The observed behavior was interpreted in terms of a simple kinetic mass action model: fitting Eq. 7 to the data yielded a two-dimensional (heterogeneous) dissociation constant of ^2DK_d = 1753 ± 243 μm⁻² for the binding between integrins embedded in their native (cell) membrane and the RGD moieties. This was related to the three-dimensional (homogeneous) dissociation constant using Eq. 8 and assuming an average cell-substrate separation distance of 100 nm. The resulting ^3DK_d ≈ 30 μM was compared to previous experimental data recorded by others, and taking into account the multiple differences in both the investigated systems and the utilized techniques, it is considered to be a realistic value. In contrast to Δλ_max, the second parameter found by fitting Eq. 5 on the spreading curves, the r rate constant of spreading was found to be independent of the surface density of integrin ligands. Averaging our data resulted in r = 54.8 ± 1.3 min⁻¹. We propose that r most probably depends on the growth of the filopodia governed by actin polymerization and is therefore naturally independent from ν_RGD.

All of these results were obtained completely noninvasively without using any labels.

The presented methodology could be applied for other live cell assays to more deeply investigate the adhesion and spreading, especially when obtaining reliable and high quality kinetic data is critical.

We consider that the appearance of the small footprint Epic® BT will cause biosensors to become more widely spread and applied in many new fields, yielding an explosion in our knowledge and to further improvements in label-free detection. For example, further improvements would allow label-free biosensing to focus on the single cell level rather than studying a large population; a general trend in cell research nowadays.

Methods

The Epic® BenchTop (BT) resonant waveguide grating (RWG) imager biosensor

The Epic® BenchTop system (Corning Incorporated, Corning, NY, USA) employed in the present study is a next-generation resonant waveguide grating imager biosensor⁴¹ allowing high-throughput label-free detection at a solid–liquid interface³⁹,⁴²,⁴³. The RWG imager accepts 96- or 384-well Society for Biomolecular Screening (SBS) standard format biosensor microplates. In this work, a 96-well uncoated Epic® microplate (Corning) was used (Fig. 1). The bottom of an Epic® microplate serves as a planar optical waveguide – i.e. a thin, high refractive-index, transparent dielectric layer (waveguide layer, made of the biocompatible material niobium pentoxide³⁴) on a thicker substratum. At the position of each well, an optical grating is embedded into the waveguide layer to enable the incoupling of the illuminating light; thus separate biosensors are created (Fig. 1). Incoupled light beams undergo total internal reflections at the inner surfaces of the waveguide layer, and gain a phase shift upon each reflection. The extent of the acquired phase shift is dependent on the refractive index (RI) of the medium being closest to the reflecting surface (because an exponentially decaying electromagnetic field, called an evanescent field, penetrates into a ~150 nm thick layer of the neighboring medium and probes the local RI³²,⁴⁰). Light beams incoupled by the same grating interfere with each other, but only positive interference results in waveguiding (i.e. the phase shift between the interfering beams has to be 2πm, m = 0,1,2…). This criterion is met only at a certain illuminating wavelength, called the resonant wavelength (λ). Any process accompanied by RI-variations in the ~150 nm thick layer over the biosensor surface (bulk RI change, molecular adsorption, cell spreading, or dynamic mass redistribution in the cells) alters the acquired phase shift when the beams undergo reflections at the waveguide layer–sample interface. This untunes the resonance but waveguiding can resume at an illuminating wavelength λ′ ≠ λ. The primary signal output by the Epic® BT system is the shift of the resonant wavelength (Δλ = λ′ − λ) in each well. Δλ is proportional to the alteration in the effective refractive index N of the substrate-cell-medium system. At constant cell number and cell volume, N is related in a simple way to the degree of spreading¹⁰,³²,⁴⁴.

In practice, all wells of an Epic® microplate are simultaneously interrogated every 3 seconds by sweeping the illuminating wavelength through a range of 15000 pm with 0.25 pm precision⁴¹. The guided wavelength is outcoupled by the same grating as that used for incoupling, and the resonant wavelength distribution within each well is imaged with a spatial resolution of ~90 µm using a complementary metal-oxide semiconductor (CMOS) camera. The two-dimensional resonant wavelength map allows patterns in single wells (corresponding to areas of e.g. aggregated spread cells, or a group of dead ones in a cellular monolayer) to be identified and permits data filtration to improve assay quality⁴⁵. The small footprint and tolerance to high temperatures of the Epic® BT allows one to place it into a non-humidified cell incubator and, therefore, provide a better approximation to the environmental conditions cells experience in vivo.

Coating procedure for a fine-tuned surface density of RGD-motifs

The synthetic copolymers, poly(L-lysine)-graft-poly(ethylene glycol) (PLL-g-PEG) and its RGD-functionalized counterpart, PLL-g-PEG/PEG-GGGGYGRGDSP, (simply referred to as PLL-g-PEG-RGD throughout this work) were obtained as powders from SuSoS AG, Dübendorf, Switzerland. The materials were stored at −20°C until use. Each powder was then dissolved in 10 mM 4-(2-hydroxyethyl)-1-piperazine ethanesulfonic acid (HEPES, from Sigma-Aldrich Chemie GmbH, Munich, Germany) at pH 7.4 to make stock solutions with a concentration of 1.0 mg/ml. These were then sterile-filtered and stored at 4°C for a maximum of two weeks. Coating solutions with different concentrations of RGD-motifs were created by mixing the two stock solutions in eleven different ratios ranging from 0.0 to 1.0 (Table 1).

Assay buffer was prepared by adding 20 mM HEPES to Hank's balanced salt solution (HBSS, from Sigma-Aldrich) and adjusted to pH 7.0 with 1 mM NaOH.

Wells were given 50 µl assay buffer to pre-wet the sensors and establish a baseline with the RWG imager. Following the stabilization of the biosensor signal (typically 30 min), the measurement was stopped and the buffer was replaced with 50 µl of the desired coating solution and incubated for 0.5 h while gently shaking at room temperature. The biosensor plate was then replaced into the RWG imager and the signal was recorded. The coating solutions were then removed and the wells were rinsed three times with 50 µl of assay buffer; this did not provoke any decrease in the biosensor signal, indicating that the polymers had adsorbed to the surface irreversibly. Wells were then dosed with 50 µl assay buffer for the fourth time to establish a new baseline for the subsequent room temperature cell spreading assay.

Cell culture

HeLa and HEK293 cells were routinely cultured in tissue culture polystyrene Petri dishes (Greiner) placed in a humidified incubator (37°C, 5% CO₂). Culture medium was prepared by supplementing Dulbecco's modified Eagle's medium (DMEM) with 10% fetal bovine serum (FBS), 4 mM L-glutamine, 40 µg/ml gentamycin, and 0.25 µg/ml amphotericin B (all these substances were purchased from Sigma-Aldrich).

Adhesion and spreading assays

HEK293 cells were brought into suspension by gently pipetting the culture medium over them, while HeLa cells were trypsinized with 1.0% pre-warmed trypsin-EDTA. Trypsin was removed before complete detachment of HeLa cells and its activity arrested by adding culture medium containing 10% FBS. Harvested cells were centrifuged at 380 g for 7 min and the cell pellet was resuspended in assay buffer with intensive pipetting. Cells were then counted in a hematocymeter, and ~8000 cells in a volume of 100 µl were added to the sensor wells already containing 50 µl assay buffer. Wells for buffer control were also coated with the appropriate copolymers and treated the same way as the sample wells throughout the experiment, except that they received assay buffer instead of cell suspension. All experiments were done in triplicate in three different wells at room temperature. Spreading was monitored until saturation of the biosensor signals. Averaging every 5 subsequent data points, the effective sampling rate was 1/15 s⁻¹. The averaged response of the wells that had contained only unspread cells on a pure PLL-g-PEG coating was subtracted from the raw biosensor data (background correction).

Visualization of spread cells and image analysis

At the end of the biosensor measurement the microplate was placed under a Zeiss Observer microscope to visually observe and image the cells with a 20× objective (all wells were completely filled up with assay buffer and covered with a microscope slide to improve imaging quality by eliminating the disturbing meniscus). One representative photomicrograph per Q was taken to document the visual effects of integrin ligand surface density on cell adhesion and spreading. The obtained 11 images were one by one subjected to image analysis. First, the number of spread cells was determined, then the mean cell-substrate contact area was accessed by manually tracking the contour of 50 spread cells in each phase contrast image and averaging the enclosed contact areas (measured using ImageJ). When less than 50 spread cells could be observed in an image, the statistics consisted of the maximum possible number of cell area measurements. The relative errors of cell counts and that of the average contact areas were estimated to be 10% and 15%, respectively (the latter was estimated by measuring the contact area of an individual cell 10 times and comparing the results). The proportion of the different surfaces occupied by spread cells was determined from the number of spread cells, their average contact area and the total size of a field-of-view image.

Author Contributions

R.H. established the research line and supervised the current work. N.O. conducted all the experiments, Sz.B., B.Sz. and B.P. helped in experimental design. N.O. and R.H. analyzed the data. N.O. prepared the manuscript figures. Manuscript text was written by N.O., J.J.R. and R.H. The model introduced to determine the dissociation constant in live cells was developed by R.H. All authors reviewed and commented the manuscript.