Basic Concepts in Population Modeling, Simulation, and Model-Based Drug Development: Part 3—Introduction to Pharmacodynamic Modeling Methods

Abstract

Population pharmacodynamic (PD) models describe the time course of drug effects, relating exposure to response, and providing a more robust understanding of drug action than single assessments. PD models can test alternative dose regimens through simulation, allowing for informed assessment of potential dose regimens and study designs. This is the third paper in a three-part series, providing an introduction into methods for developing and evaluating population PD models. Example files are available in the Supplementary Data.

Background

Pharmacodynamics (PD) is defined as “what the drug does to the body”¹ and is a way of describing the mechanisms of drug action and defining the relationship between drug concentration and effect. Much of the science of PD began in the early 1960s with work by Levy² and others describing the correlation between reversible drug effects and drug concentrations. Population PD evaluates physiological and biochemical effects of drugs on the body or disease-causing agents at the population level. As described in the second paper in this series,³ these evaluations are conducted using nonlinear mixed-effects modeling approaches. Thus, during the development of population PD models, the same major aspects of data, structural, statistical, and covariate models must be addressed.

PD data can be continuous (e.g., can take any value in a range), such as weight, blood glucose, enzyme levels, or categorical (e.g., can take only discrete values in a range), such as grade of an adverse event, or physician's global assessment scales. Categorical data require special consideration and are usually handled with probability or count models. However, if the number of categories is sufficiently high (usually 6–10), ordered categorical data may be treated as continuous. Here, we focus on models for continuous PD data.

Continuous PD responses can be broadly classed as reversible or irreversible. An example of the former would be antihypertensive agents, which reduce blood pressure with drug effect reversing after the drug has cleared from the body. The latter might be a cytotoxic chemotherapeutic agent, which acts to destroy tumor cells. Within each of these classes, the behavior is commonly categorized depending on the duration of time between administering drug and achieving a measurable response. Thus, drugs can have an immediate effect (e.g., QT prolongation), or there can be a lag between measured concentration and response. The delay to effect can arise because the site of action is not readily accessible to a drug, which may result in maximum effects occurring later than maximum drug concentrations. The delay may also be because the drug affects something other than the measured response, such as inhibiting an enzyme, which increases substrate over time. In both types of systems, pharmacological effects may persist even when drug concentrations are no longer measurable.⁴

Before the inception of population-based approaches, data from multiple subjects or animals were evaluated using either a naive pooled approach, where data from all individuals are pooled and fit simultaneously ignoring individual differences in exposure and response, or the “two-step” method, where each individual's data are fit, and summary statistics were determined from the individual values. These approaches have been shown to produce biased parameter estimates⁵ and are consequently rarely used today. The naive pooled approach produces imprecise estimates of mean responses and cannot provide estimates of between-subject variability (BSV), whereas the two-step approach produces good estimates of mean response but biased and imprecise estimates of BSV.⁶

Population PD evaluations are useful both to identify appropriate dose regimens and to identify sources of variability that might contribute to lack of efficacy or predispose patients to adverse events. Other uses include extrapolation into different patient populations (e.g., pediatrics) or different therapeutic areas. PD modeling has been shown to be important during regulatory review of new therapeutics.⁷ The US Food and Drug Administration⁸ states that PD modeling can represent a well-controlled clinical study, contributing to substantial evidence of effectiveness where clinical end points or accepted surrogates are studied or can add to the weight of evidence supporting efficacy where the drug's mechanism of action is well understood. PD models can contribute to optimal study designs. For example, PD modeling of viral growth during therapy has been successful in explaining the dynamics of chronic infection.⁹ Models describing hepatitis C viral RNA decline over time suggested that the primary mode of action of interferon involved blocking viral production from infected cells rather than preventing infection.¹⁰ PD modeling has been used to stop further drug development¹¹ or can be used to develop clinical studies and facilitate identification of meaningful drug activity (e.g., boceprevir and telaprevir).^12,13

In this article, we examine fundamentals of population PD modeling of continuous data together with methods for comparing and evaluating population PD models.

Graphical Evaluations of Data

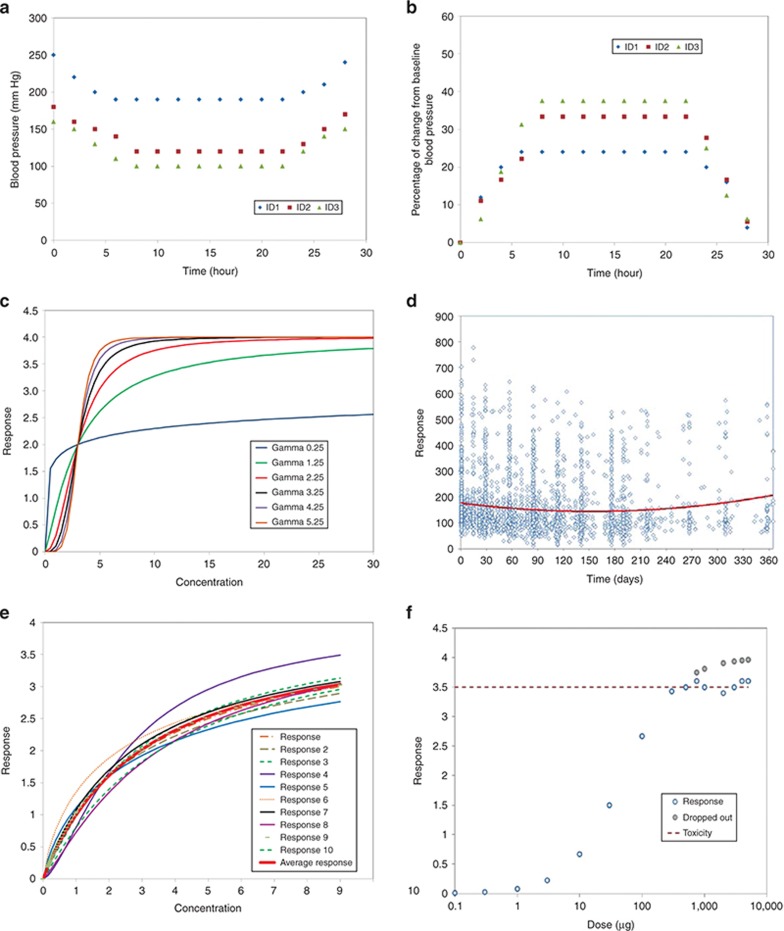
As mentioned in our previous paper,³ data preparation is a major component of modeling. Graphical evaluation of PD data is important not only to develop an understanding of the potential relationships between exposure and response, but to evaluate the data for missing or erroneous observations and to give insight into appropriate models to evaluate. Multiple plots are often generated, including plots of concentration and response vs. time and concentration vs. response. Generally, it is best to work with raw (untransformed) data, although transformations such as percent of baseline are commonly needed in reports. Figure 1 that plots systolic blood pressure over time in three subjects with severe (ID: 1), moderate (ID: 2), and mild (ID: 3) hypertension shows that such plots (and ensuing models) can result in biased assessments of the actual effect of drug. Panel a is the raw data, and the numerical drop in systolic blood pressure is the same regardless of the starting systolic blood pressure; panel b that shows the percentage of baseline SBP suggests that drug does not work well in severe hypertension.

Figure 1.

Basic plots of raw vs. transformed data and potential issues with mean and pooled data. In general, it is best to work with the raw (untransformed) data. (a) A plot of systolic blood pressure in three individuals with severe (ID 1), moderate (ID 2), and mild (ID 3) hypertension. (b) A plot of transformed data as percent of baseline for these same subjects. While the data in panel b appear to show a greater response in ID 1, the decrease in blood pressure for all three was 60 mm Hg. This visual bias is owing to the lower baseline blood pressure and not the effect of drug. (c) The effect of varying Hill coefficients¹⁴ (which define the steepness of the concentration–response relationship) on concentration–response curves. (d) Naive pooled plot of response vs. time—with different numbers of observations at varying times, trends in the data may become difficult to visualize. (e) The effect of drop out (here at high response) can lead to a truncated concentration–response curve. (f) Taking a mean of individual concentration response profiles can result in a shallower relationship than is evident in any individual subject.

Graphical evaluations are generally most useful when plotted on an individual basis; however, in many studies, there may be insufficient individual data to generate meaningful plots. In such cases, there are several options: (i) pool data from each dose group for plots or (ii) plot mean data from each dose group. However, plots of naive pooled or mean data can result in misleading representations of the data. Some potential issues are highlighted in Figure 1. Panel c shows individual data with varying sensitivity to drug as reflected in the Hill coefficient,¹⁴ which describes the steepness of the concentration–response curve. Panel d demonstrates the potential impact of high variability together with different values of observations at given times on finding trends in the data, making the mean response (shown as a solid smoothed line) appear blunted. Panel e shows that the mean of several individual PD time curves can misrepresent individual tendencies. Thus, while there may no choice but to evaluate pooled or mean data, care should be taken in the interpretation of such graphical explorations. Care should always be taken with graphical evaluations as the true concentration–response relationship can be obscured by hysteresis or with highly variable data.

Graphical evaluations of data with dropout

Subject withdrawal from a study (e.g., dropout, right censoring) is common in clinical trials. Rubin¹⁵ suggested that the only time it was feasible to ignore the process that caused the missing data was if the missing data are “missing completely at random” and are independent of observable variables and unobservable parameters of interest. Conversely, data that are “not missing at random” are missing for a specific reason (e.g., nonignorable) because the value of the variable that is missing is related to the reason it is missing, as is shown in Figure 1. Panel f shows the potential impact of dropout on the perceived concentration–response relationship. Here, high PD response results in patients' dropping out which would bias graphical (and model based) evaluations. A number of methods dealing with dropout have been used in practice, the most common being “last observation carried forward”, which implies that PD measurement stays fixed at the last observed value after drop out. Many methods, including last observation carried forward, yield biased estimates of the efficacy or potency,¹⁶ especially with modeling. If the likelihood of dropout is correlated to underlying, unobserved data, dropout is informative and cannot be ignored in the modeling process.¹⁷ Hu and Sale¹⁸ provided a good summary of the concept of accounting for dropout. Thus, it is important to inspect the potential impact of dropout during the preliminary evaluations of data prior to modeling.

Graphical evaluations of data with lag

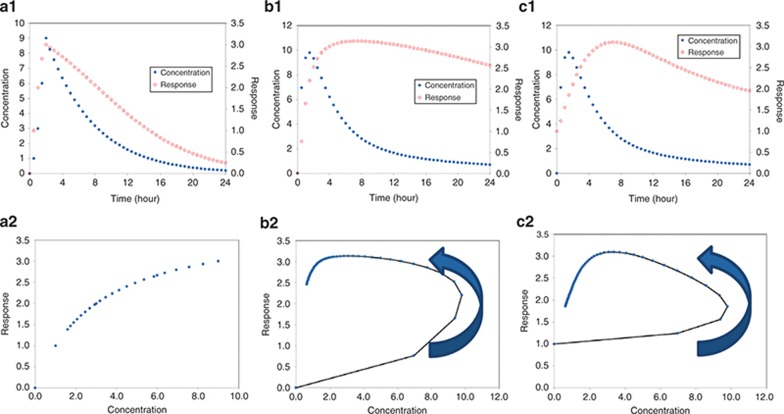
PD can correlate directly with concentration, or there may be a delay between measured concentrations and response. Figure 2 shows example plots of concentration with progressively delayed response. Note that when there is a delay between concentration and response, the plot of response vs. concentration will exhibit a counterclockwise loop referred to as “hysteresis.” Hysteresis is the dependence of a system on both its current and past environments. The term was coined around 1890 by Sir James Ewing to describe magnetic material behavior but is also used to describe situations where PD response lags behind concentrations such as is seen with neuromuscular blocking agents¹⁹ or with anxiolytics, sedatives, and anesthetic agents.²⁰ Hysteresis can also result from active metabolite formation. Clockwise hysteresis is possible with PD tolerance. If a drug depletes a reservoir such as an enzyme pool, when drug exposure is protracted, PD response may decline while drug levels are still high. The resultant clockwise hysteresis curve in a plot of response vs. concentration (see Supplementary Data) can be useful to support testing models of tolerance. The area enclosed by a hysteresis plot is indicative of the magnitude of the delay between concentration and response—a larger loop implies a longer delay, although the magnitude of the delay is not readily quantitated from such plots.²¹

Figure 2.

Interpreting pharmacodynamic plots. (a1) Plot of concentration and response vs. time for a direct effect drug. Note that the peak response and peak concentration are correlated. (a2) Shows the concentration vs. response, which shows the expected sigmoidal curve. (b1) Shows concentration and response vs. time for a drug with a delayed onset of effect. Note that the peak concentration and peak response are shifted, reflecting a delay. (b2) Shows the plot of concentration vs. time that results in hysteresis. (c1,c2) Represent a longer delay between concentration and response—as the delay increases, the plot of concentration vs. response will become less and less useful.

Concentration–Effect Relationships

Concentration–effect relationships are central to PD models. The origins of the four fundamental relationships in common use can be traced to receptor theory.²² A drug (D) binds with a specific three-dimensional receptor (R) in the body forming a drug–receptor complex (DR). The altered drug–receptor complex initiates an immediate (e.g., ion channel) or delayed (e.g., change in protein expression) sequence of events leading to an observable drug effect (E):

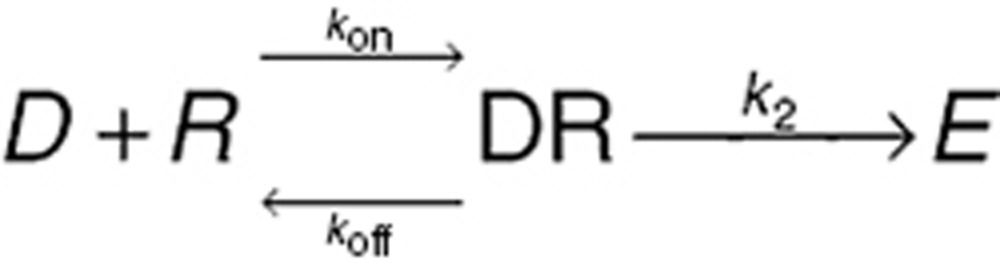While irreversible binding is possible (e.g., phenoxybenzamine and the α adrenergic receptor), typically binding is a dynamic process with the net concentration of the drug–receptor complex being a balance between the rate of drug and receptor association (k_on) and the rate the complex dissociates (k_off). The classical chemical equilibrium equation shows the ratio of free receptor concentration [R] to bound receptor concentration [DR] is a function of the drug concentration [D] and the ratio of k_off/k_on (the receptor dissociation rate constant, K_d):

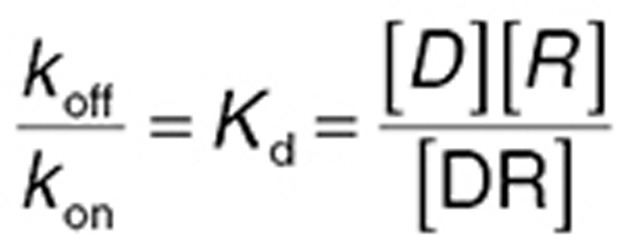Pharmacologists have devised many ingenious methods of estimating K_d. While more complex classes of receptor binding kinetics are possible, Eq. 2 illustrates a fundamental principle of PD: as K_d is a constant, it can be seen that increasing drug concentration reduces [R] and increases [DR], hence increasing drug effect. If [D] is very high, receptors are saturated; further increasing the drug concentration produces no additional increase in drug effect—there is therefore a maximal effect (E_max) for all drugs.

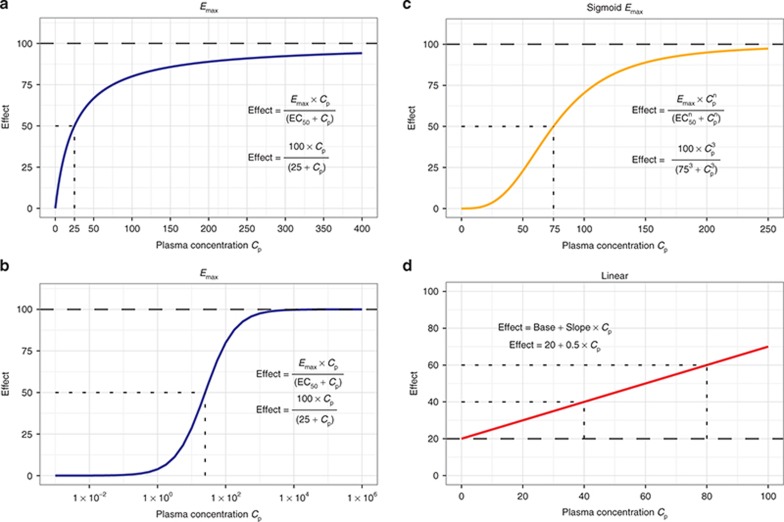
Sigmoid E_max concentration effect

Eq. 2 can be used to derive (see Supplementary Data online) a general equation for the relationship between drug concentration (using C now used instead of [D]) and effect (E)—the sigmoid E_max relationship:

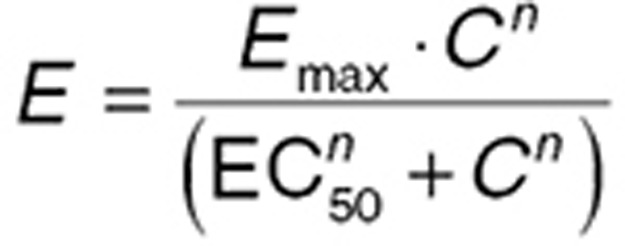In this general case, “n” drug molecules bind with each receptor, and K_d is expressed as the EC₅₀, the concentration at which E is 50% of E_max. The shape of the concentration–effect relationship implied by Eq. 3 is summarized in Figure 3. When the drug acts to inhibit a response, E_max and EC₅₀ may be referred to as I_max and IC₅₀, where I indicates inhibition, but this is a nomenclature of convenience, and the fundamental equations are unchanged. The parameter n (the “Hill” coefficient) affects the “steepness” of the concentration–effect relationship. When n is high (>5), the concentration–effect relationship may become steep enough for the effect to be functionally present or absent (i.e., the EC₅₀ is a threshold concentration for drug effect).

Figure 3.

Fundamental concentration–effect relationships. (a) The E_max concentration–effect relationship that arises from receptor theory for the binding of a single drug to a single receptor. Fifty percent of the maximum effect is achieved at the EC₅₀ concentration. (b) The same relationship over a much wider log-concentration scale. (c) The sigmoid E_max concentration–effect relationship that arises from receptor theory when there is allosteric inhibition or simulation of binding. The “Hill factor” n controls the steepness of the middle part of the curve. (d) A linear concentration–effect relationship that is a semiempirical but sometimes useful substitute for an E_max relationship when the range of concentration is relatively small and the drug effect is well below E_max.

E_max concentration effect

When only one drug molecule binds with one receptor, n = 1, and Eq. 3 can be simplified (Eq. 4). While the origin of the parameter n is based on receptor theory, in practice, it is often an empirical device that can improve the fit of PD data. Hence, if Eq. 4 is found to fit a data set, it may be worthwhile also to try Eq. 3, with the initial parameter value set at 1, and the parameter range bounded to plausible values (e.g., 0.1–10). There are few data sets where the BSV of n can be estimated with precision.

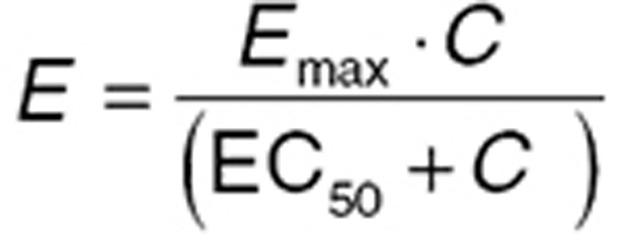Linear concentration effect

Eq. 4 can be simplified further when C is much less than EC₅₀. This represents the apparent linear segment of the concentration relationship, which has an approximate slope of E_max/EC₅₀ that can be represented by a single “slope” parameter. An apparent linear relationship may describe studies where the range of doses used is relatively narrow (e.g., clinically used doses) but should only be used for interpolation rather than extrapolation of drug effects beyond the dose studied.

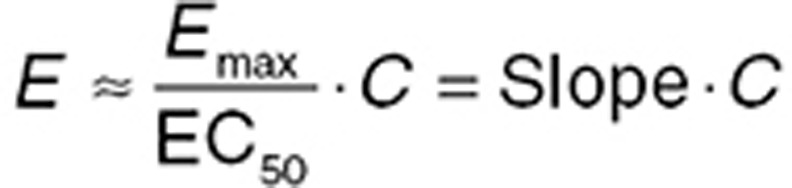Log-linear concentration effect

The apparent linear segment of the concentration–effect relationship can be extended by plotting effect against log concentration (Eq. 6). However, this equation cannot represent the case where C is zero and is problematical for this reason when baseline or placebo data are modeled. While not ideal, a log-linear relationship may be the only option for data with very high intrinsic variability (e.g., cytokines), when more physiologic models fail.

Note that all of the concentration–effect relationships described here should be used with caution when extrapolating outside the range of data use to develop the model.

Concepts of additive and proportional drug effect

The fundamental concentration–effect relationships outlined above assume that the drug effect is zero when the drug concentration is zero. However, a more common scenario is that the drug effect has a baseline (predrug) value, and the relationship between the drug effect and the baseline effect value (E_base) needs to be considered. Using a linear concentration–effect relationship as an example, two common relationships are additive (Eq. 7) and proportional (Eq. 8).

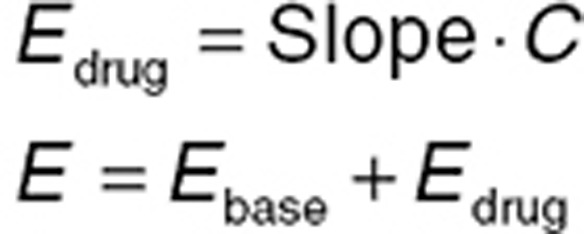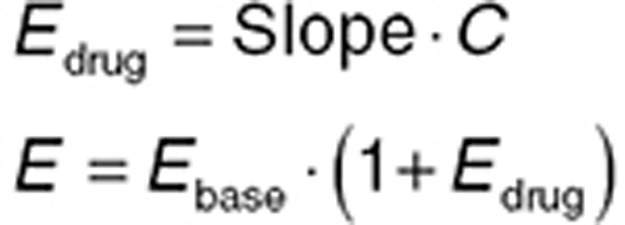The difference between the two is summarized graphically in the Supplementary Data. Notably, for a proportional relationship, a higher baseline is associated with a greater drug effect. In practice, both relationships should be considered during model building (ideally in consultation with clinical experts), unless there is an established mechanistic understanding allowing informed selection. The Supplementary Data provide examples of visualizing concentration–effect relationships using the R language.

Drug combinations

While a full understanding of pharmacokinetic (PK) –PD relationships requires data on the drug given alone, clinically, most drugs are given in combination (whether by design or as a consequence of polypharmacy). The potential for PK drug–drug interactions through metabolic enzymes²³ or transporters are well recognized.²⁴ PD drug–drug interactions become important when drugs act on the same receptor or share components of a PD pathway. When two drugs act on the same PD effect, the concentration–effect relationship is a three-dimensional surface (a “response surface”), and defining the shape of this surface can be a complex task. Modeling response surfaces can quantify additive or synergistic PD effects.^25,26 Furthermore, the E_max receptor model can be modified to account for competitive and noncompetitive antagonism,^27,38 and these relationships have been implemented in population models.^29,30 Eq. 9 summarizes how Eq. 4 can be modified to account for the interaction with an inhibitory drug (concentration C_i).

An important class of PD drug–drug interactions occurs when a drug has active metabolites. The proportion of dose converted to metabolite can differ between oral and parenteral doses with hepatic first-pass metabolism, and the metabolite can act as a second drug with either agonist (e.g., morphine-6-glucuronide) or antagonist (morphine-3-glucuronide) properties. A PK–PD model that ignores known active metabolites requires careful justification.

Continuous PD Models

While concentration–effect relationships are the building block of continuous PD models, there is a variety of continuous PD models which differ in terms of the site at which the concentration–effect relationship “drives” the PD process or the representation of the PD process itself. The ideal PD model is not always possible, but it is best to describe the data using the most physiologically relevant model possible. The model chosen will be dependent on the type of data and how frequently it is measured. Well-constructed continuous PD models allow simulation of the whole time course of drug effect. This allows improved understanding of drug onset, when to expect maximal effects, when to expect steady state for efficacy, and the best times for evaluating efficacy.

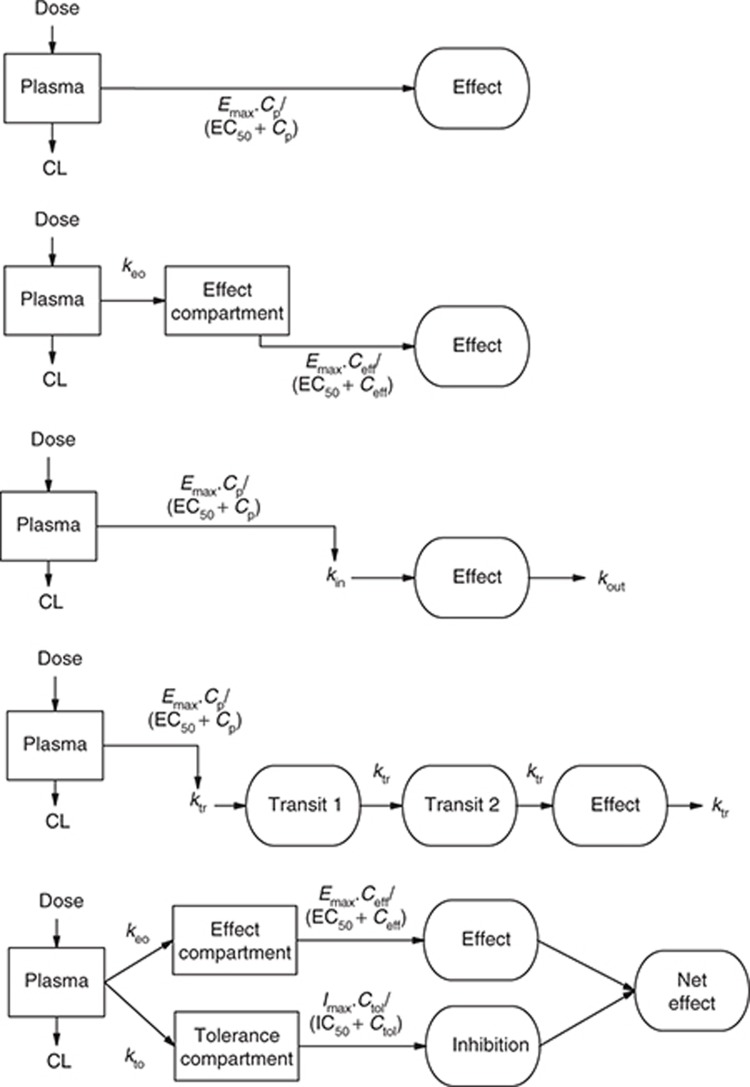
There are at least five categories of continuous PK/PD models, and the relationship between them is summarized in Figure 4. These models are broadly differentiated by the duration of time between measurable concentration and observed effect.

Figure 4.

Representative continuous pharmacodynamic models. (a) A direct response model where effect is driven by the plasma drug concentration. (b) An effect compartment model where effect is driven by the effect compartment drug concentration, which is delayed relative to the plasma concentration by a first-order rate constant k_e0. (c) A turnover model where drug effect is a balance between an apparent production rate (k_in) and an apparent removal rate (k_out). Drug affects the net effect by altering k_in or (k_out). (d) A transit compartment model, where the drug effect is at the end of chain of processes and drug action is on the first process. (e) A tolerance compartment model, where the drug effect is described by an effect compartment and the development of tolerance is described by a slower inhibitory compartment that reduces the net drug effect with time.

Direct effect

When the apparent biophase equilibration is sufficiently rapid relative to the time scale of drug administration (e.g., chronic oral dosing), biophase equilibrium is less important. Plots of concentration vs. effect show minimal hysteresis, and a model directly linking plasma concentrations and effect can be used (Figure 4a)

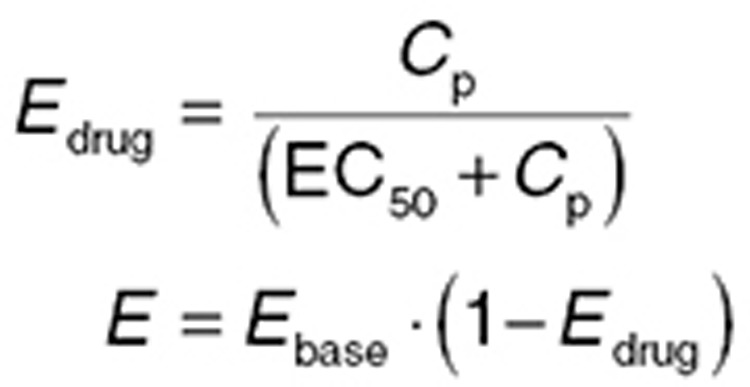Link effect/effect compartment

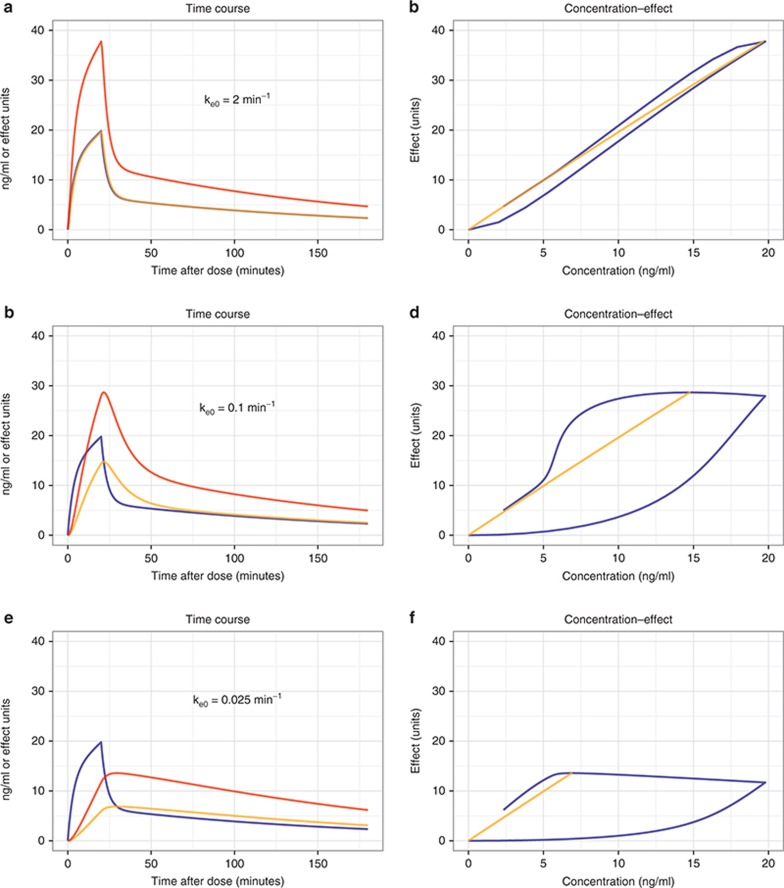
Commonly, drug concentrations are measured in venous plasma, but this site in the body is largely a matter of convenience. Theoretically, it is more advantageous to measure drug concentration at the site responsible for “driving” the PD effect—that is the concentration at the receptor site linked to drug action. There are few drugs that act in venous plasma, and hence, there are convection transport (blood flow) and diffusion processes that “deliver” the drug to its site of action. These factors may contribute to the temporal difference (hysteresis) between the drug concentration in venous blood and the drug effect discussed previously. Effect compartment models^19,31 account for this delay by representing it as an additional compartment between the blood concentration and effect defined by a first-order effect compartment rate constant k_e0. It is the apparent (unmeasured) drug concentration in this effect (or link) compartment that drives drug effect (Eq. 11). A large k_e0 value means that the effect compartment is rapidly equilibrating and effect compartment concentrations closely follow the plasma concentration; a small k_e0 value means the effect compartment equilibrates slowly and effect compartment concentrations (and hence effect) are delayed relative to plasma concentrations (Figure 5).

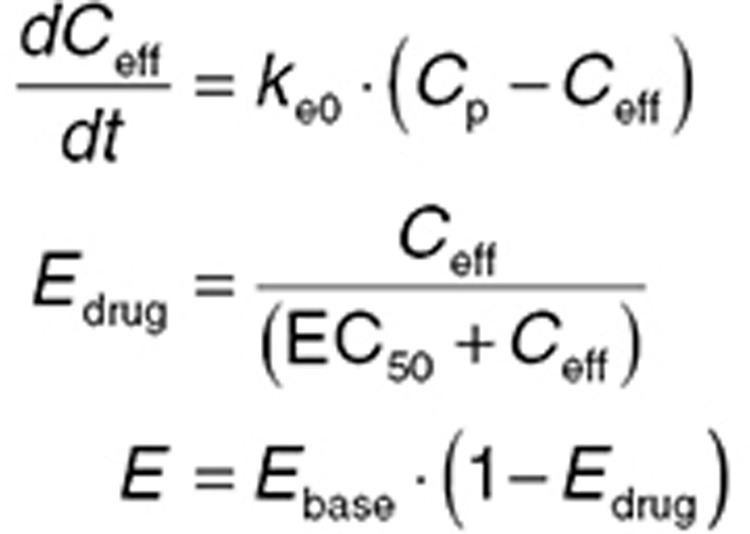Figure 5.

Effect compartment models—influence of k_e0. A simulation where a hypothetical drug is infused for 20 min, with resultant plasma concentrations (C_p) shown by blue. Each row shows the effect compartment concentrations (C_eff, orange) for a different effect compartment rate constant. Drug effect in arbitrary units (E, red) is related to the effect compartment concentrations by an E_max model with E_max = 1,000 and EC₅₀ = 500. The left column shows the time course of C_p, C_eff, and E. The right column shows a hysteresis plot of E vs. C_p (blue) and E vs. C_eff (orange). (a) The time course of C_eff is similar to C_p for this value of k_e0 and this study time scale. (b) As the maximum C_p is ~20 ng/ml, the E–C_eff relationship is essentially linear with a slope of 2 (1,000/500). The E–C_p relationship shows minimal hysteresis. (c) The time course of C_eff now lags behind C_p, and the peak C_eff occurs later than the peak C_p (although at equilibrium, C_eff = C_p by definition). (d) The E–C_eff relationship is unchanged, but the E–C_p relationship now shows hysteresis. The hysteresis is anticlockwise—the rise in concentration precedes the rise in effect. (e) The time course of C_eff is now substantially different to C_p. The transient peak in effect associated with the high C_p during the infusion is now absent. (f) The E–C_p relationship now shows hysteresis, with a complex shape dictated in part by the shape of the C_p time course.

While it is tempting to interpret the effect compartment rate constant as a physiologically based description of biophase equilibration, this is only the case in specific limited cases such as when the drug concentration is measured in arterial blood and the drug acts in an identifiable target organ or tissue (e.g., central nervous system or myocardium).³³ The effect compartment can then be substituted with a physiological representation of the target organ.³³ Commonly, when venous blood concentration is measured, the effect compartment rate constant represents the net difference between the equilibration rate of the arm (if venous blood is drawn from an arm vein) and the target organ. Indeed, with rapid target organ equilibration and slow arm equilibration, drug effect can precede the measured concentration resulting in clockwise rather than anticlockwise hysteresis plots. When the rate of target organ equilibration and arm equilibration are the same, no hysteresis will be observed, but this is an artifact—not an indication—that biophase equilibration does not occur.

Algebraic solutions for common PK models including an effect compartment are implemented by some software (e.g., Monolix, Lixoft, France), but more generally, effect compartment models can be implemented as differential equations.¹ The effect compartment rate constant is sometimes more usefully parameterized as an equilibration half-life (Ln(2)/k_e0).

Indirect effect/turnover

When the apparent delay between drug concentration and effect is due more to lag in PD processes than biophase equilibration, indirect or turnover PD models^34,35 may be appropriate. The observed effect is considered a dynamic process. The net baseline effect is a balance between the apparent rate of “production” of the effect and rate of “removal” of the effect. While production and removal of the effect can be complex, multistep processes in vivo, generally one step is rate limiting, and these are represented by first-order rate constants k_in and k_out, respectively. Turnover models are best conceptualized when the effect is an endogenous biomarker. For example, serum creatinine level at any given time is the net balance of production via breakdown of creatine phosphate in muscle and removal via glomerular filtration. If production rate increases, or removal rate is reduced, serum creatinine will rise and vice versa. Turnover systems are defined by two important relationships. First, baseline steady-state level of the effect (E_base) is given by the ratio of the rate constants (Eq. 12). Second, turnover time of the system is given by the inverse of k_out (Eq. 13). Longer turnover times are associated with longer times for a new steady state to be established following a step change in one of the rate constants.

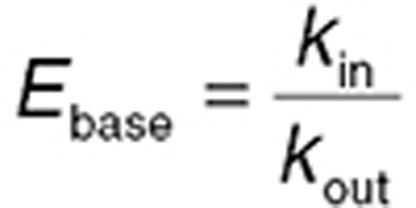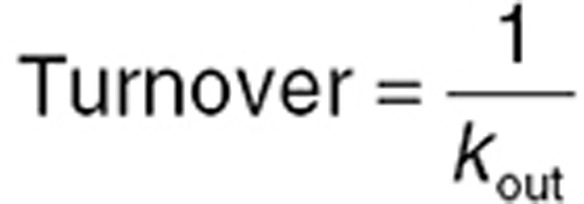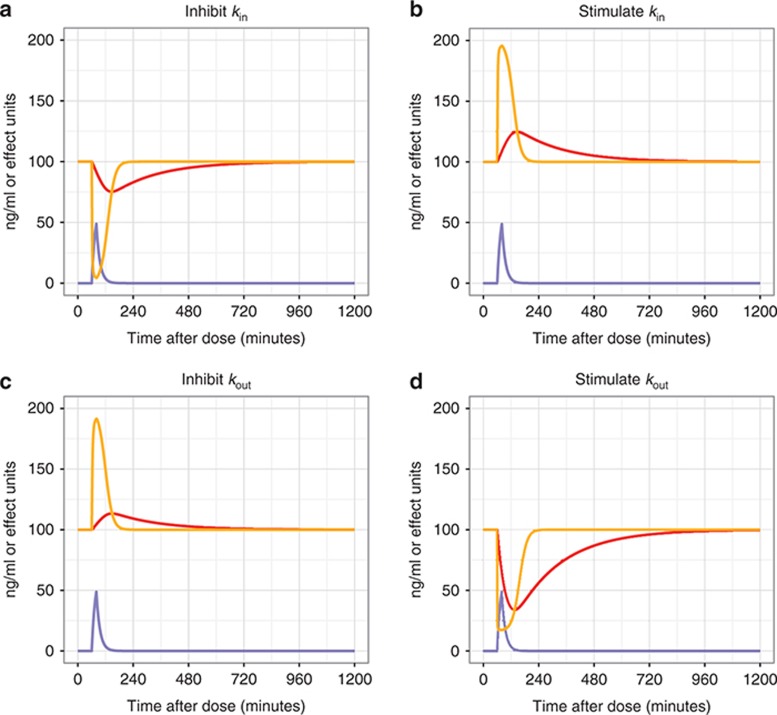
Drugs can affect turnover systems by four main mechanisms—inhibiting production, stimulating production, inhibiting removal, or stimulating removal (Figure 6). Eq. 14 shows an example system of equations for a turnover model where a drug has an inhibitory effect on k_in (k_in0 is the baseline value of k_in). Other examples are given in the Supplementary Data.

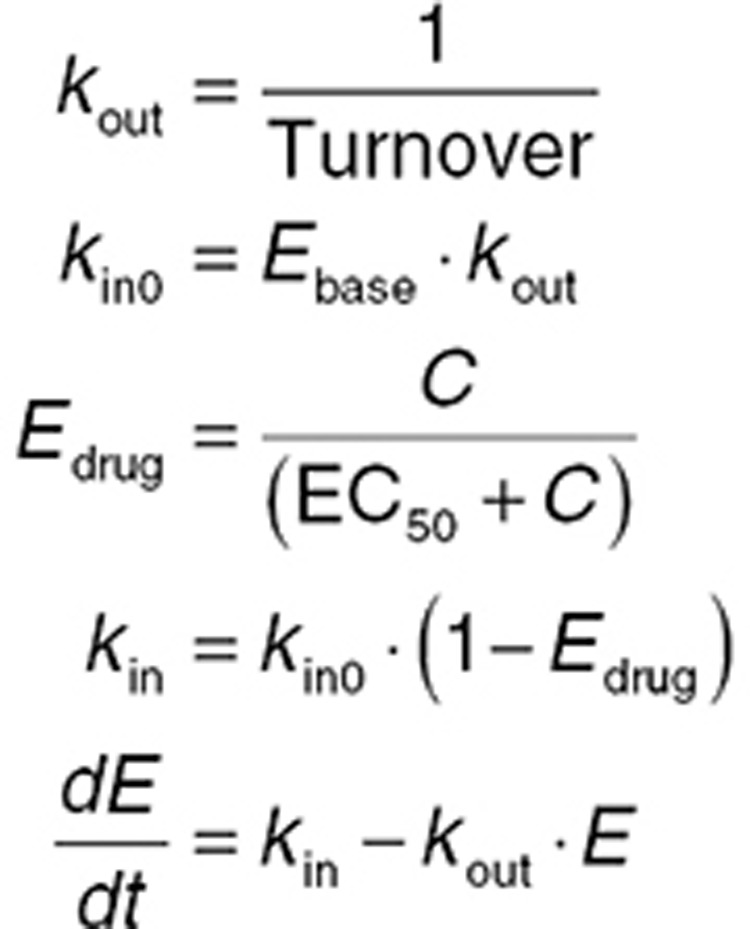Figure 6.

Drug effects on turnover models. A simulation where a hypothetical drug is infused for 20 min after 60 min of baseline observations of drug effect that is described by a turnover compartment. The resultant plasma concentrations (C_p) are shown in blue. The drug effect has a baseline of 100 units, and the time course of effect is shown for system that turns over rapidly (turnover = 1 min, orange) or slowly (turnover = 200 min, red). The four scenarios show drug affecting turnover by: (a) inhibiting production (k_in), (b) stimulating production (k_in), (c) inhibiting removal (k_out), and (d) stimulating removal (k_out). Drug effect on turnover compartment rate constants (k_in or k_out) was via an E_max relationship. The EC₅₀ was 50 ng/ml, and E_max was 1, 1, 0.5, and 5 for a–d, respectively.

Both an effect compartment model and turnover model may fit a given data set equally well, and the choice between the two may need to be made on mechanistic grounds. Effect compartment models are perhaps better suited to relatively short delays; turnover models may favor longer delays. Indeed, both an effect compartment process (biophase equilibration) and turnover process can be concurrent in vivo, but few data sets have enough information to support such combined models.

Transit models

The turnover model can be extended by adding more turnover (transit) compartments,^36,37 each representing a step in the progression of observed drug effect (Figure 4). This strategy is useful with long delays between drug administration and observable effect. An example is the effect of antineoplastics on neutrophils.³⁶ Neutrophils are formed from progenitor myeloblasts in the bone marrow which undergo maturation through at least five distinct cell populations before becoming neutrophils. Antineoplastics affect myeloblast formation, lowering neutrophil counts only when the decreased production rate has propagated down the maturation pathway—often 5–7 days after antineoplastic administration. Each distinct cell population can be represented as transit compartment linked in series. While it may be feasible to define the k_in and k_out rate constants for each transit compartment, in practice, only one step is rate limiting, which is represented as a transit compartment rate constant (k_tr), which is the same for each compartment (Figure 4). The greater the number of transit compartments and the slower k_tr, the greater the delay between drug administration and first observable effect and the time of the peak drug effect. Transit compartment models are most easily represented as differential equations.

Tolerance models

Many biological systems are under homeostatic control, and when perturbed by drug, they tend to return to baseline state (set point), which can produce characteristic differences in the concentration–effect time course with clockwise hysteresis. An example is the development of tolerance to opioids.³⁸ While the physiological mechanism of opioid tolerance is complex and multifactorial,³⁸ relatively simple models can account for both the dose- and time-dependent nature of the development of tolerance. One approach is the use of a parallel, slower equilibrating hypothetical tolerance compartment (Figure 4, Supplementary Data) which represents the time course of hypothetical inhibitory drug. The inhibitory drug modifies the effect produced by the “real” drug via reverse agonist, competitive antagonist, noncompetitive antagonist, or partial agonist mechanisms.³⁸ Tolerance models can also be derived from turnover models, where tolerance acts by altering k_in or k_out²⁷ or via depletion of a precursor pool when additional compartments are added to turnover models.²⁸

Placebo Models/Disease Progress

Baseline (predrug) and placebo (vehicle dose) data are as important for PD modeling as the drug treated data and should be given equal attention. It is only with a faithful model of baseline and placebo data that it is possible to distinguish drug effect from placebo effect and from noise in the data.

Placebo models

Placebo models account for the time course of PD effects in the absence of drug. Time-dependent changes in effect in placebo cohorts can occur for a variety of reasons. Models can be either empirical (e.g., linear or curvilinear compensation for a drift in a PD measurement)³⁹ or mechanistically based (e.g., a circadian rhythm). In both cases, the relationship between baseline values, placebo effect, and drug effect must be carefully considered. A common assumption is that changes that occurred with placebo also happened with drug treatment, and the effect of the drug is referenced to these changes. Eq. 15 shows a system where placebo effect changes linearly over time, while the drug reduces the effect via an E_max relationship. Both act proportionally relative to the baseline effect. An empirical curvilinear relationship can be achieved using a quadratic equation (Eq. 16), but, like all polynomial functions, should not be used for extrapolation.

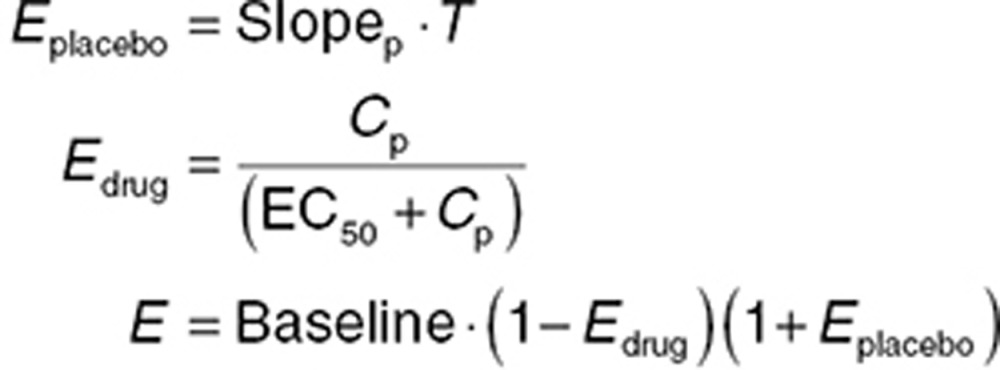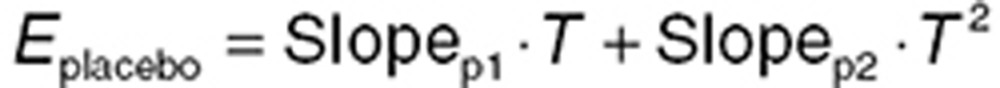Circadian rhythms are evident in many behavioral, physiological, and endocrine systems.^40,41 If placebo data are collected over more than 24 hours, circadian patterns may be evident. Caution is needed when placebo data are collected at times that are only multiples of 24 hours (e.g., daily), as a potential circadian rhythm may be hidden by “temporal aliasing” (where an oscillating signal is masked because it is sampled at times that only reflect the same part of the curve). Circadian rhythms can be represented using trigonometric functions that oscillate over 24 h (Eq. 17).

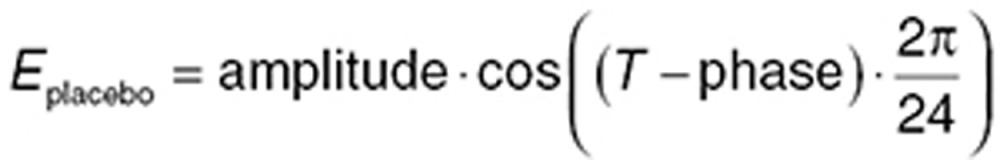Unrecognized circadian rhythms can obscure significant concentration–effect relationships. Seasonal variation, which affects temporal response, can also mask drug effect and is handled the same way.

Insult/disease models

Placebo data may reflect an active experimental insult or disease progression. The latter is a complex area and has been covered in detail elsewhere.⁴² An example of the former is the induction of adjuvant-induced arthritis in rats,⁴³ where adjuvant injection causes paw swelling, which evolves until it reaches a maximum value and subsequently resolves with time. Efficacy is measured as the ability to prevent or treat swelling. A modeling approach is very useful for resolving the competing time-dependent process of experimental injury and drug effect. Turnover models can be adapted using time-dependent rate constants representing the increase from and return to baseline in the placebo group (see Supplementary Data).

Population PD Model Development

Generally, methods used to develop and evaluate PD models are similar to methods used for PK evaluations. However, there are a few exceptions that can require specialized techniques. One issue arises from the increased complexity of PK/PD modeling, which requires robust estimation methods, although the ensuing run times must also be considered. Plan et al.⁴⁴ investigated parametric approaches for maximum likelihood estimation: first-order conditional estimation in NONMEM and R, LAPLACE in NONMEM and SAS, adaptive Gaussian quadrature in SAS, and stochastic approximation expectation maximization in NONMEM and MONOLIX (both stochastic approximation expectation maximization approaches with default and modified settings). They noted that run times were shortest with first-order conditional estimation and LAPLACE and longest with adaptive Gaussian quadrature; when the initial estimates were incorrect, adaptive Gaussian quadrature, and first-order conditional estimation in NONMEM, LAPLACE in SAS, and stochastic approximation expectation maximization in NONMEM and MONOLIX had lower relative root mean squared error than the other methods. Thus, it may be necessary to explore different estimation approaches depending on the needs of the individual projects.

Model building methods

When developing population PD models, several approaches can be taken: both the PK and dynamic models can be fit simultaneously to both data types (“simultaneous” method), or first a PK model can be developed and then the PD model can be developed. This second approach can either condition on the PK information using fixed parameter estimates with or without the PK data, or individual estimates of the PK parameters can be added to the database in lieu of the PK data (“sequential” methods). Zhang et al.⁴⁵ investigated these approaches and found that the best approach in terms of computational time, convergence, and estimated parameter precision was to fix the PK parameters and retain the PK data in the database. It should be noted, however, that these results apply to models where the PKs are independent of the PD. For example, the PKs of many biological agents are highly dependent on the PD response,^46,47 which often necessitates simultaneous fitting of the data. In such situations, it may be reasonable to first include the PD assessment as a covariate to allow preliminary evaluations of the PK data, followed by simultaneous model development.

In some situations, PK data may not be available or may be unreliable (e.g., the presence of interfering substrate may result in concentration data that are questionable). In this situation, the use of “kinetic-pharmacodynamic (K-PD) K-PD” models,⁴⁸ which implements a forcing function to replicate drug exposure, becomes necessary. This approach involves setting up a one compartment intravenous bolus model with first-order clearance as a forcing function that represents dose regimens. This forcing function can then be used to drive the PD model and is commonly used in meta-analyses,⁴⁹ which is a means of modeling aggregate (e.g., mean) data from multiple studies. In the setting of meta-analysis, where only the PD data are available, a K-PD model is useful to reflect different dose regimens tested in different studies.⁵⁰ A K-PD model was also used for characterizing the PD of ibandronate⁵¹ owing to its PK complexity and substantial time dissociation between measured concentrations and changes in urinary excretion of the C-telopeptide of the α chain of type I collagen (uCTX, a marker of ibandronate activity). Zhang et al.⁵² tested using forcing functions when modeling complex, multiresponse PD systems. They found that final parameter estimates cannot be trusted when the multiresponse system being modeled involves feedback. They also noted that with forcing functions, it is difficult to impose “realistic” global constraints on the “piecewise” solutions described with a forcing function, and these models will have problems estimating standard errors. Thus, using forcing functions (“K-PD” Kinetic - Pharmacodynamic) models should not be the first choice. This would be particularly true with many biological agents since the PKs often depends on the PD response.

Identification of appropriate structural models

Model selection is usually initially guided by the drug's pharmacology. Most PD models are semi-physiologic and are parameterized to reflect what is known about the drug's mechanism of action. Despite this, identification of appropriate structural models for PD evaluations is not straightforward. Comparing models with a linear drug effect vs. a nonlinear drug effect are not nested (such that fixing one new parameter to 0 simplifies the test model to the reference linear model), thus the likelihood ratio test is generally not an appropriate metric to compare different models. Instead, the use of the Akaike Information Criteria or similar comparisons should be used.³ Preference is generally given to models that converge and provide robust parameter estimates. Other diagnostics such as goodness-of-fit plots, as were used for PK evaluations, are also used to help select appropriate models.

Parameterization can be important with PD models. PD data are often more variable than PK data; appropriate parameterization can improve stability and ensure convergence. For example, EC₅₀ was parameterized as shown below to improve stability and ensure that EC₅₀ remains positive. Providing a parameterization that does not require fixing boundaries is beneficial because it does not constrain minimization.

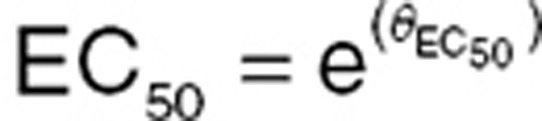Other functions are often used to ensure values fall within specific intervals. Logit transforms, for example, are often used to constrain models to measurement scales. Below, E_max was parameterized using a logit function to ensure that the parameter remains positive in the open interval (0,1).

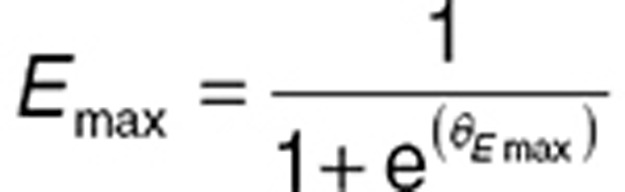Therapeutic monoclonal antibodies bind to a target antigen with high affinity, lowering the reservoir of free antigen and occasionally depleting it. If antigen turnover is slow, concentrations of free antigen may be zero for a long period of time, resulting in a large number of “zero” observations. Such data are referred to as being heavy at the boundary (e.g., the limit of the measurement scale or assay). Models generally do not predict boundary values well and removing all zero values is not appropriate because the zero in this example is an important response. Consequently, “standard modeling approaches” often result in models with upwardly biased predictions, and the estimated random-effects distributions may exhibit severe departures from normality.⁵³ This situation occurs when response to drug results in a maximum response for protracted periods.

A “two-part model” should be used for dealing with data that are heavy at the boundary.^53,54 Two-part models describe zeros (or boundary values) as discreet values such that the probability of a zero response given a drug concentration is modeled. Responses with values that are outside the boundary are modeled as a continuous function. Such models can reproduce zero (boundary) observations. In some extreme cases, where data are heavy at two boundaries (e.g., 0 and 100%), a three-part model can also be developed.

The two-part model first describes the probability of a zero or boundary value (π_Aij,) for the ith subject at the jth time point using a binomial logistic function:

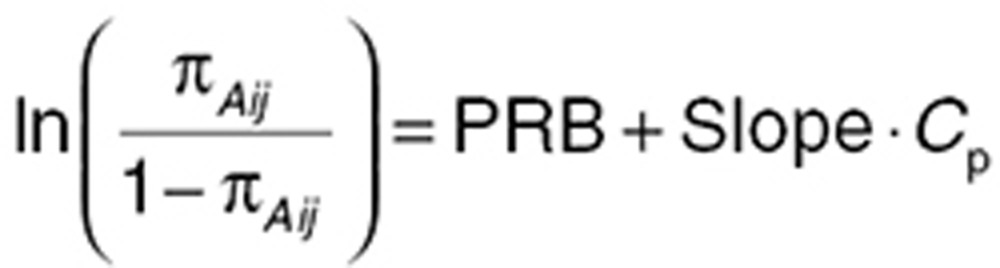where PRB describes the probability that the PD observation is zero in the absence of measurable drug levels, and Slope is the estimated effect of active drug concentration (C_p). The second component of the model describes the continuous portion of the data with probability 1−π_A as truncated log-normal distribution using a sigmoidal E_max function:

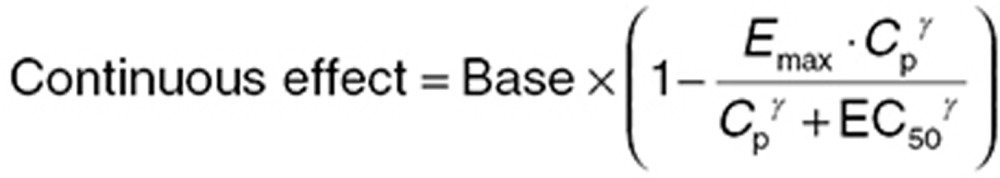where Base is the baseline value for free receptor, E_max is maximal drug effect, C_p is drug concentration, EC₅₀ is the concentration of drug at half-maximal response, and γ is the Hill coefficient. The likelihood of the data (L(A_ij)) is as described below:

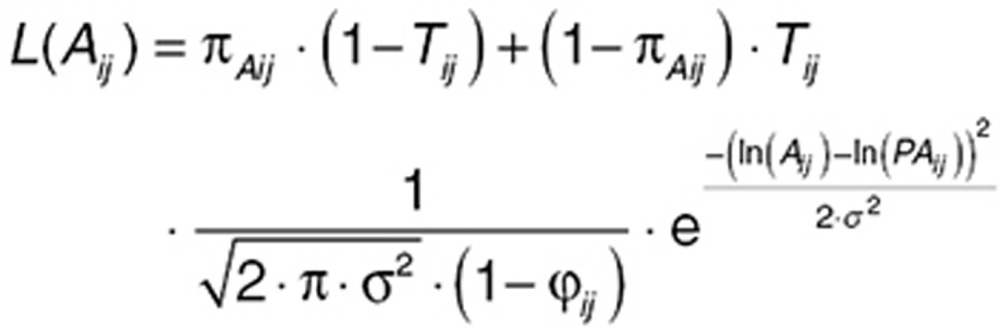where A_ij and PA_ij are observed and predicted PD values, respectively. In this equation, T_ij = 1 if A_ij > 0, else T_ij = 0; σ is the estimated within-subject variability as a SD (in the log space) for continuous data above the cutoff. The factor (1−ϕ_ij) in the denominator of the normal density portion of the likelihood is a normalizing factor representing the probability that PA_ij is greater than half the cutoff. This correction allows the function to integrate to unity, necessary for a probability model; ϕ_ij is computed using Chebychef polynomials.

Development of statistical models

As with PK models, the statistical model describes variability around the structural model, including BSV (variance of a parameter across individuals), between-occasion variability (BOV) (variance within individuals), and residual variability (unexplained variability after controlling for other sources of variability).³ Between-subject differences in response to drug may have a PK basis, a PD basis, or both. When assessing pharmacologic response, it is important to determine BSV and BOV for both the PKs and the dynamics and to explore the possible influence of underlying diseases and other physiologic variables on concentration–effect relationships.

Between-subject variability. Developing models for PD BSV is similar to the approach used for PKs. However, while PK BSV is frequently described using a log-normal distribution because parameters such as clearance must be constrained to be positive and are often right skewed, for some PD parameters such as baseline, BSV can be described using an additive (normal) distribution:

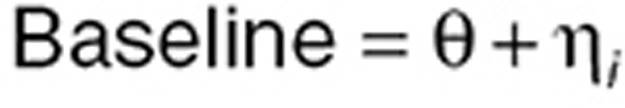where Θ is the population mean and η_i is the deviation from the mean for the ith subject such that η~N(0, ω²). The SD in the population is the square root of ω², and the coefficient of variation (CV) in the population is

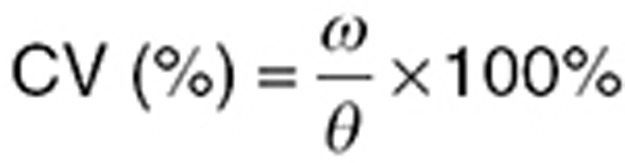An additive BSV is also necessary when a parameter can take positive and negative values (e.g., slope in a linear concentration–effect relationship if negative slope is physiologically plausible). The distributions of individual η values must be checked to ensure the appropriate function is being used to describe the distribution. When modeling dense data, it is possible to examine the distribution of the η estimates and graphically determine (via histograms or quantile–quantile plots) if parameters are normally or log-normally distributed. With sparse data, one might test both normal and log-normal distributions and examine the objective function value or simulate using both distributions to determine which assumption appears to best reproduce the data, although the use of the likelihood ratio test as a criterion for including BSV terms is inappropriate. However, because the objective function is a measure of how well a model describes the data, it can be used to make some distinctions between distributional assumptions.

Note that BSV can be different in different patient types due to varying sensitivity to the drug, or disease severity for instance. Thus, combining data from patients with data from healthy volunteers may require separate variance components for each subject type.

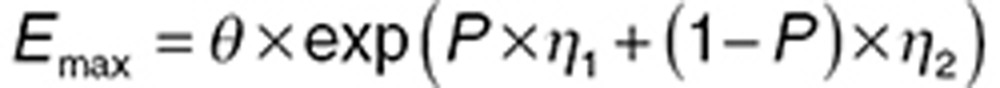where P is an indicator variable that takes values of either 0 (if the subject is healthy) or 1 (if the subject has disease), ω₁² is the variance of subjects with disease, and ω₂² is the variance of healthy volunteers.

BSV on parameters can often be correlated. This is particularly true for PD models and using ω block structures for PD random effects describing this correlation is encouraged. For example considering a simple E_max model:

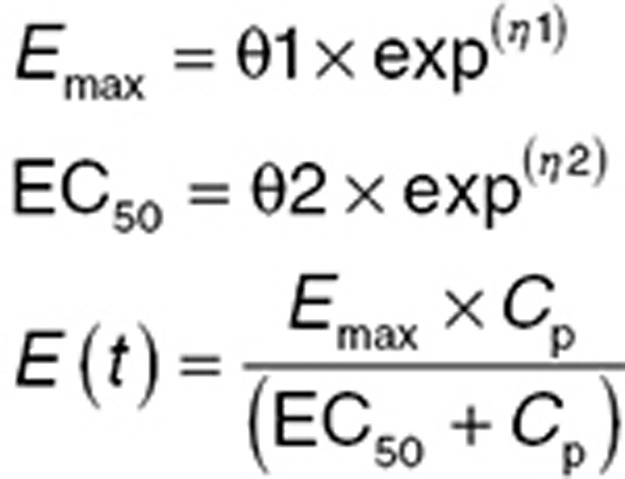where E_max is the maximum effect a drug can elicit, EC₅₀ is the concentration at half-maximal response, C_p is the concentration of drug, and E(t) is the measured PD effect at time t. In this function, the parameters E_max and EC₅₀ are often correlated, and BSV can often be estimated more reliably for both parameters when correlation is described. For some biologic agents, the PKs are dependent on the PD. For example, Campath (Sanofi, Paris, France), a monoclonal antibody directed against CD52, a protein present on the surface of mature lymphocytes, acts to reduce the lymphocyte counts but is also cleared by these cells. Response to Campath results in substantially decreased clearance.⁵⁵ When fitting such models, describing the correlation between PKs and PD via off-diagonal elements of the omega matrix is recommended.

Owing to varying response to drugs, η distributions for PD parameters may be skewed or multimodal (Figure 7). In our previous paper,³ we investigated methods for dealing with skewed distributions. There may be situations where transforming the η distribution does not resolve the skewness. Using a mixture model to account for a heavy-tails in the distribution does not necessarily imply the existence of subpopulations unless the tail of the distribution arises from patients who are inherently (usually) less sensitive to drug effects. When parameter distributions are clearly multimodal, mixture models may be used to identify subpopulations contained within the distribution of a random effect when there are no covariates that are predictive of a patient belonging to one subpopulation or other.

Figure 7.

Multimodal and skewed distributions, responders, and nonresponders. This figure shows two common, non-normal distributions. (a) A bimodal distribution suggesting two subpopulations. (b) A highly skewed distribution. In both cases, a mixture model may be used. For the bimodal distribution, the identification of two populations may reflect patients who are more or less sensitive to a drug effect. For the skewed distribution, a mixture model does not necessarily imply a subpopulation but can be a useful tool for resolving highly skewed distributions. (c) Shows two populations, responders, and nonresponders. These two populations may not arise from bimodal distribution of pharmacodynamic parameters, but may instead be described using a mixture of models, allowing the non-responders to follow one trajectory while responders follow a different one.

Traditionally, mixture models represent a situation where we have unobserved (latent) variables (e.g., missing genotypes) in our data. Latent variables may be continuous, discrete, or a combination. Mixture modeling refers to modeling with categorical (discrete) latent variables that represent subpopulations where population membership is not known but is inferred from the data. This is referred to as finite mixture modeling in statistics.⁵⁶ The likelihood ratio test is not a good test of the appropriateness of using a mixture model because mixture models are not nested. Implementation of a mixture model always decreases the objective function because effectively, the data are split into subsets and fit using different functions. Mixture models are used when multimodal behavior cannot be removed or made symmetric by inclusion of a covariate, transformation of η values or other “tweaking,” and there is a good physiological reason to suspect the existence of subpopulations. Frame provides an excellent reference for the use of mixture models.⁵⁷

Coding for mixture models depends on the modeling software. The code below is used with NONMEM to describe two populations, one with a high response and one with a low response. The parameterization for each population prevents aliasing, which is that the subpopulation associations may switch during estimation and simulation. The parameterization used for the probability of a subject being in one population is coded to avoid placing constraints on the parameters. The probability must range between 0 and 1, but using this parameterization, the value of Θ can range from −∞ to +∞. When the probability is coded as P1 = Θ and P2 = (1−Θ), the confidence intervals of the mixing probabilities can include boundary points, resulting in model instability.

These mixture models describe subpopulations on an individual level, whereby an individual is assigned to a subpopulation and cannot change populations. The two-part models described previously are mixture models at the observation level.

Between-occasion variability. The concept of BOV,³ where response to drug varies between occasions, is also important with PD evaluations, particularly in crossover study designs where the baseline drug effect can differ between treatment arms within a subject. In some settings owing to tolerance to drug or to progressing disease, a patient's response to treatment can change over time. Describing BOV can be an important tool for identifying underlying reasons for altered response over time.

Residual variability. As mentioned previously, PD data are generally more variable than PK data. This is often a result of the assays used to measure response, which are less precise than the methods used to measure drug concentration. Coding for residual variability with PD data therefore follows the same process used for PK data. The modeler should determine if the PD marker can take negative values. Some markers, such as cell and receptor counts can never be negative. With such data, the log transform both sides approach is useful to ensure that negative values cannot be simulated.

With some therapeutic agents, PD may be impacted due to low receptor expression, the disease being dependent on other pathways, or may be affected due to other events resulting in erratic response, leading to subpopulations of responders and nonresponders (Figure 7c). In some situations, nonresponders exhibit a random walk around the placebo trajectory, resulting in high residual variability. Attempting to use a traditional mixture model as described previously results in both high residual variability and biased or highly skewed distributions of PD parameters. Note that with a nonresponder population, the distribution of individual η values is generally not bimodal. In this situation, describing the PD of the entire population using a single function is inappropriate as response trajectories are different. In this setting, a “mixture of models”⁵⁸ or an “indescribable” mixture model,⁵⁹ which applies separate submodels to each subpopulation can be used to separate nonresponders from responders. This approach provides unbiased estimates of BSV and residual variability and allows estimation of the percentage of patients likely to be unresponsive to treatment, which is important in clinical trial simulation and study design.

The implementation of this sort of mixture model requires that the data be flagged depending on type (PK (DVID = 1 where DVID is a flag defining the type of observation) or dynamic (DVID = 2)). In the example equations below, the responders were described using one function, the nonresponders were assumed to stay at baseline. Other functions for nonresponders can be implemented. This approach was used to describe responder/nonresponder PD for HIV agents.⁶⁰

where WPD is the residual error of the PD observations in the log domain, IPRED is the individual predicted response, and the PD function can be any of the models described in previous sections.

Evaluation of model performance and when to evaluate

Population PD models should be evaluated to ensure that they are fit for purpose. The same evaluations described previously³ are applicable for PD models. However, model evaluation should be tailored to the pharmacology of the drug which requires understanding the pharmacology. For example, with models describing the time course of neutrophils following chemotherapy, the nadir is an important component of the model, and the ability of the model to reproduce nadir cell counts would be an important additional evaluation. Similarly, for safety and efficacy, models of international normalized ratio used to evaluate anticoagulants need to accurately describe both the lowest and highest expected international normalized ratio values.

The visual predictive check may also need special consideration because drugs are often adaptively dosed to ensure patient safety and allow adjustment of individual patient doses based on measured responses to achieve a response within a target range. During the conduct of the study, individual patient doses may stay the same, increase, or decrease over time; or a patient may be put on hold until the response of interest returns to some satisfactory range. Dose adjustments may be based on recent measurements, time averaged measurements, or may take into account multiple types of responses.

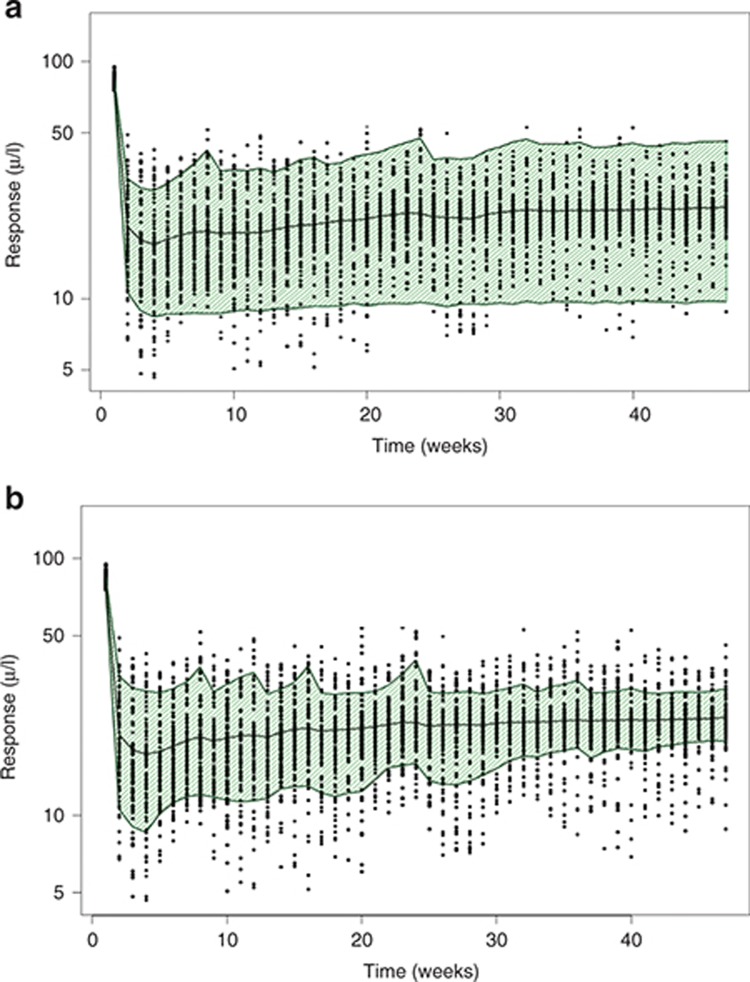
In such cases, the dose adjustment strategy used in the trial must be implemented for model evaluation and simulation⁵⁹ as other strategies (e.g., validation databases or other visual predictive check options such as prediction-corrected visual predictive checks)⁶¹ will not address this issue. Simulations using the original dosing records are usually inappropriate in this setting because the simulation scenarios often contain much higher and lower responses than those observed with the index data, producing prediction intervals that are inflated and potentially biased. The potential impact of ignoring dose adjustments is shown in Figure 8. Typically, PK models are not affected, although in some cases, PD response alters PK behavior.

Figure 8.

Visual predictive check (VPC) with and without adaptive dosing simulations. This figure shows the impact of failing to account for adaptive dosing in a clinical trial on the simulated responses. (a) Shows a VPC without accounting for adaptive dosing. The open symbols are observed data and the shaded area is the 80% prediction interval, which covers most of the data due the fact that dose adaptations used in the study are not implemented here. (b) Shows the VPC after accounting for adaptive dosing. Note the 80% prediction intervals now cover only the expected 80% of the observed data with approximately equal distributions of data above and below the prediction intervals .

The simulated subject's response to the drug rarely reflects the original patient's sensitivity, so dose adjustments in the original dose records are not appropriate for the simulated subject. The discrepancy arises when the BSV drawn during simulation results in simulated subjects who's responsiveness to drug effect differs from the original patient's sensitivity. Using the original dose records is not realistic because in a clinical setting, the clinician would not have dosed the simulated subject without regard for response. There are four check statistics that should be considered when simulating data arising from a study implementing adaptive dosing:

1. Number of subjects never in therapeutic range

2. Number of subjects put on hold for no reason

3. Number of subjects that received inappropriate dose increases

4. Number of subjects that received inappropriate dose decreases

Owing to BSV, some subjects may be simulated that are never in the therapeutic range even with adaptive dosing. However, simulations using the adaptive dosing paradigm used in the clinical trial will not generate subjects that fit the last three check statistics.

Conclusions

There is no “correct” method for developing and evaluating population PD models of continuous PD data. The nature of the model is very dependent on the data and the intended purpose of the model. However, more than population PK modeling, there is the potential for constructing models that perform poorly due to parameters or variables taking values in some circumstances that are mechanistically impossible or biologically implausible. Using a systematic piece-wise model building process where the behavior of each subcomponent of the model is well understood by test simulations and plots help guard against this (see Supplementary Data). Errors can be further minimized by testing that the steady-state solution of the coded model (either by algebra or simulation; see Supplementary Data) meets expectations and by checking that the units of all parameters and variables are consistent with expectations.

Like all population modeling, population PD requires a clear understanding of the assumptions made and a rigorous examination of model performance in describing the index data. As always, the model should be challenged and modified by comparison of its predictions with new data as part of the “learn and confirm” cycle of model development.^61,62 PD modeling, although more challenging than PK modeling, can provide substantial benefits including providing a basis for evaluating alternative dosing strategies and study design. A well-conducted evaluation can add to the weight of evidence supporting efficacy where mechanism of action is well understood. Even if concentration data are not available, evaluating the PD time course leads to substantial benefits.

Author contributions

Both authors contributed equally to the manuscript.

Conflict of Interest

The authors declared no conflict of interest.