Rewards and the evolution of cooperation in public good games

Abstract

Properly coordinating cooperation is relevant for resolving public good problems, such as clean energy and environmental protection. However, little is known about how individuals can coordinate themselves for a certain level of cooperation in large populations of strangers. In a typical situation, a consensus-building process rarely succeeds, owing to a lack of face and standing. The evolution of cooperation in this type of situation is studied here using threshold public good games, in which cooperation prevails when it is initially sufficient, or otherwise it perishes. While punishment is a powerful tool for shaping human behaviours, institutional punishment is often too costly to start with only a few contributors, which is another coordination problem. Here, we show that whatever the initial conditions, reward funds based on voluntary contribution can evolve. The voluntary reward paves the way for effectively overcoming the coordination problem and efficiently transforms freeloaders into cooperators with a perceived small risk of collective failure.

1. Introduction

Public goods, such as clean energy and environmental protection, are the building blocks of sustainable human societies and failures in these areas can have far-reaching effects. However, the private provision of public goods can pose a challenge, as often cooperation and coordination do not succeed (e.g. [1]). First, voluntary cooperation to provide public goods suffers from self-interest behaviours. Exploiters can freeload on the efforts of others. In collective actions, proper coordination among individuals is usually required to attain a cooperation equilibrium. Otherwise, freeloading leads individuals to the non-cooperation equilibrium, which is a social trap.

The coordination problem has been broadly studied by game theory and its ubiquity is indicated by a variety of names: coordination game, assurance game, stag-hunt game, volunteer's dilemma or start-up problem [2–4]. Evolutionary game models tackling sizeable groups are often built on public good games of cooperation and defection but have generally resulted in a system that has two equilibria (ones with no cooperation and certain-level cooperation) [5,6]. Thus, it is a challenge to develop a mechanism that allows populations to evolve towards the cooperation equilibrium, independent of the initial conditions. The situation is most stringent in cases where unanimous agreement is required for the public good, as the only desirable initial condition is a state in which almost all cooperate. Theoretical and empirical analyses have clarified that prior communication [7] or social exchange situations [8] can facilitate the selection of the cooperation equilibrium. Little is known, however, about how equilibrium selection can materialize from one-shot anonymous interactions in large populations, where such a consensus-building process is less likely to succeed. Previous studies showed that the higher the risk perception of collective failure, the higher the chance of coordinating cooperative actions [9–11]. Recent research has shown that considering institutional punishment can further relax the initial conditions for establishing cooperation [12].

What happens if reward is considered instead of punishment? Reward is one of the most studied structural solutions for cooperation in sizeable groups and inspires cooperation [13,14]. While in real life there exists an array of subsidy systems for encouraging cooperative actions, here we turn to endogenous fundraising (see [15] for formal rewards). Early work revealed that replicator dynamics [16], whereby the more successful strategy spreads further, can lead to the dynamic maintenance of cooperation in public good games with reward funds [17]. This model considered three strategies: (i) a cooperator or (ii) defector in the standard public goods game, or (iii) a rewarder that contributes to both the public good and reward fund. Only those who contribute to the public good are invited to share the returns from the reward fund. Rewarders can spread even in a population of defectors, because defectors are excluded from the rewards. The fundraising itself, however, is voluntary and costly. Thus, this incentive scheme can easily be subverted by ‘second-order freeloading’ cooperators who contribute to the public good but not the rewards. In the next step, as contribution to the public good is also costly, cooperators will be displaced by ‘first-order freeloading’ defectors. This leads to a rock–scissors–paper type of cyclical replacement among the three strategies.

2. Model

We extend public good games with reward funds [17] with a provision threshold [12], which can easily generate a coordination situation. We consider infinitely large, well-mixed populations from which n individuals with n > 2 are randomly sampled and form a gaming group. After one interaction, the group is dissolved. We assume the three strategies as before: both the rewarder and cooperator are willing to contribute with a personal cost c > 0; the defector contributes nothing and incurs no cost. All of the public benefit is provided only if the number of contributors m (0 ≤ m ≤ n) exceeds or equals a threshold value k (1 ≤ k ≤ n); otherwise, just part of the public benefit, discounted by a risk factor p (0 ≤ p ≤ 1), is provided. However, the resulting benefit goes to every player equally, whatever she/he contributes. The individual benefit is given by B(m) = 1, if m ≥ k; otherwise, B(m) = 1 − p (figure 1).

Figure 1.

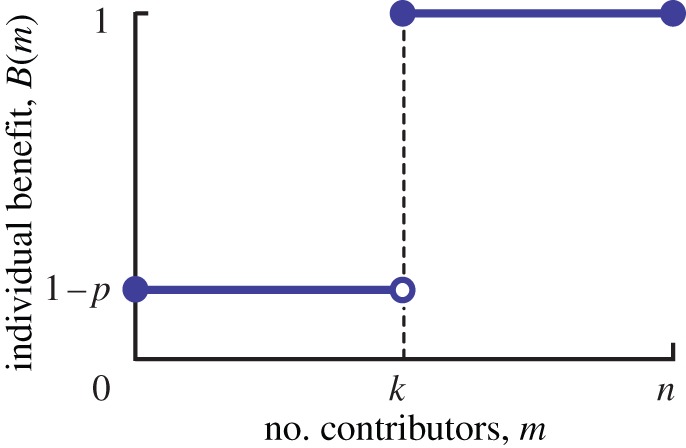
Step returns in the public good. Each member receives benefits given by 1 if the number of contributors in the group m exceeds or equals threshold k (1 ≤ k ≤ n); otherwise, 1 − p. (Online version in colour.)

Next, we consider a voluntary reward fund for the threshold public good game. Beforehand, only the rewarders are willing to contribute c′ > 0 to the fund; after the game, the integrated fund multiplied by interest rate r′ > 1 will be shared equally among m contributors (i rewarders and m − i cooperators) to the public good. The reward fund is thus a ‘club’ good, excluding the defectors. In summary, a rewarder earns B(m) − c + c′r′i/m − c′, a cooperator B(m) − c + c′r′i/m and a defector B(m). (The corresponding replicator equations are available in the electronic supplementary material.) Furthermore, if the reward fund is very beneficial with r′ ≥ n (i.e. its marginal return is non-negative, c′r′/n − c′ ≥ 0) the reward fund is sustainable against the second-order freeloaders. Thus, we assume r′ < n.

3. Results

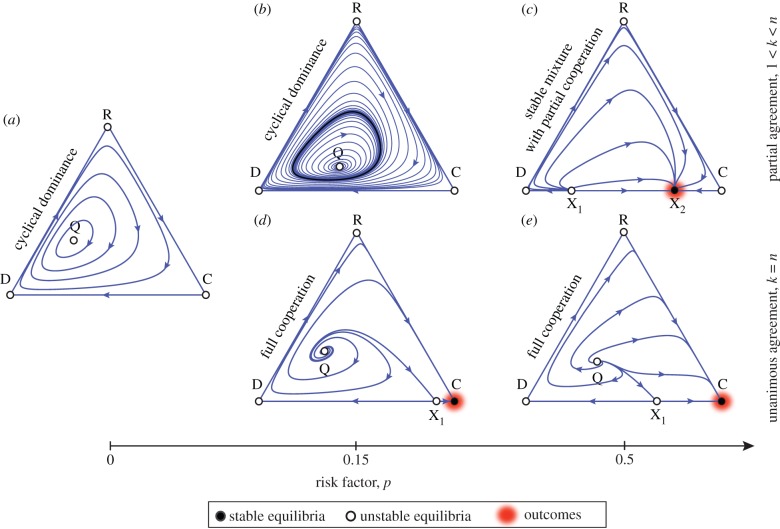
First, we look at the evolutionary outcomes without rewarders. The step function B(m) with the intermediate threshold value k (figure 1) can lead to the bistability of both no cooperation and a mixture of cooperation and defection for a sufficiently large risk factor p for 1 < k < n, and for k = 1, with just mixed cooperation [10,18]. Pure coordination between no and 100% cooperation only occurs if k = n, a case where avoiding a collective failure requires homogeneous cooperation among all participants. It holds for 1 < k ≤ n that the larger the risk p, the smaller (larger) the attraction for a no (certain) cooperation equilibrium [10]. To bring about bistability, the critical risk factor p* takes its smallest value in the case of unanimous agreement.

Evolutionary outcomes change dramatically with rewarders (figure 2; the electronic supplementary materials for details). The analytical investigation shows that if a certain level of rewards is considered, the replicator dynamics first lead the rewarders to invade a state where all individuals defect. Individuals are better off rewarding in mixed groups (defectors and rewarders) as long as the most promising return of the fund c′r′ is greater than the total cost c + c′. The non-rewarding cooperators then invade the population of the rewarders and propagate. This is common for whatever the risk factor p and provision threshold k and leads to a state where all individuals cooperate.

Figure 2.

Threshold public good games with reward funds. The simplex represents the state space. The three nodes, D: 100% defectors, C: 100% cooperators and R: 100% rewarders, are trivial equilibria. (a) Risk zero (p = 0). The unique interior equilibrium Q is surrounded by closed orbits, along which the three strategies dynamically coexist. Boundary orbits form a cycle connecting the three nodes. (b,c) Partial agreement (1 < k < n). For a small risk p, there can exist a stable closed orbit (bold, black line) (b). When p goes beyond a critical value p*, a mix among the three strategies is no longer sustainable, and only cooperators can stably coexist with defectors at point X₂. All interior population states evolve to this state (c). (d,e) Unanimous agreement (k = n). When p increases beyond p*, all individuals end up with the all-cooperation equilibrium C. Parameters: n = 5, c = c′ = 0.1, r′ = 2.5, and for (b,c), k = 3. (Online version in colour.)

In the absence of bistability for the threshold public good game, the population state pulls back to states in which defectors are the majority. Thus, the population ends up with a rock–scissors–paper cycle, and the dominant strategy is replaced by a rotation from defector to rewarder to cooperator to defector (figure 2a,b). Similar oscillatory dynamics for cooperation and rewards have been obtained in complicated models with reputation systems [14]. In the presence of the bistability, the resulting mixed state of defectors and cooperators is sustainable, even after the reward fund falls. Once escaping the state of 100% defectors, the population evolves to the mixed state for 1 < k < n (figure 2c), with k = n being the state of 100% cooperators (figure 2d,e). Therefore, it is through the rise and fall of the reward that the coordination problem is resolved.

4. Discussion

Voluntary rewards can provide a powerful mechanism for overcoming coordination problems, without considering second-order punishment. This is an intriguing scenario that is not easily predicted using traditional models with voluntary punishment [16]. Furthermore, second-order freeloading has been an issue that needs to be defeated or suppressed [13,19,20]. The present model is in striking contrast to previous models and can generate 100% cooperation when second-order freeloading terminates the voluntary rewarders.

There are three key steps for evolving to the cooperation equilibrium. First, the rewarders need to evolve among the defectors. This requires that the average fitness of the rewarders is higher than that of the defectors. This is the case when the returning reward offsets the costs to the public good and reward fund (c′r′ > c + c′). We note that the degree of risk factor p does not affect this result, because there is positive feedback between the increase in the number of rewarders and the jump in the return. Second, the rewarders are replaced with cooperators because, assuming mild rewards (r′ < n), switching to cooperators causes an increase in fitness (c′ − c′r′/n > 0). Finally, the resulting state needs to be stable, despite the fact that a single mutant defector has a higher net benefit in a group of cooperators. For a sufficiently large p, however, switching to defection leads to a loss where the average fitness of the defectors falls below that of cooperators, and thus the cooperation equilibrium is stabilized.

Collaboration results for transforming defectors into cooperators in coordination games have been obtained by considering optional participation [21,22] or institutional punishment [12]. Optional participation can provide a simple but effective resolution for escaping the social trap [13,16]. In human societies, however, there are many issues at play, such as nationality, religion, energy and environment. The present model focuses on such an unavoidable situation, and thus players are forcibly admitted to games.

Although institutional punishment influences the establishment of a stable level of cooperation, in large groups it may face a coordination problem in itself [7,23]. Thus, it would be difficult for a single punisher to make an impact that activates a sanctioning system that covers the whole group. What about punishing those who do not make any contribution to institutional punishment? This triggers an infinite regression to the question: who pays for (higher order) punishment? By contrast, a reward fund can rise in response to a single volunteer and then spread in a population of defectors.

We revealed that cooperation with a reward fund is a more powerful tool than institutional punishment. Voluntary rewarding is an efficient mechanism that enables the resolution of coordination problems with minimal risk.

Funding statement

T.S. was supported by the Foundational Questions in Evolutionary Biology Fund (grant no. RFP-12-21).