Abstract
Understanding decisions is the fundamental aim of the behavioural sciences. The theory of rational choice is based on axiomatic principles such as transitivity and independence of irrelevant alternatives (IIA). Empirical studies have demonstrated that the behaviour of humans and other animals often seems irrational; there can be a lack of transitivity in choice and seemingly irrelevant alternatives can alter decisions. These violations of transitivity and IIA undermine rational choice theory. However, we show that an individual that is maximizing its rate of food gain can exhibit failure of transitivity and IIA. We show that such violations can be caused because a current option may disappear in the near future or a better option may reappear soon. Current food options can be indicative of food availability in the near future, and this key feature can result in apparently irrational behaviour.
Keywords: rate maximization, transitivity, independence of irrelevant alternatives, rationality, decision-making
1. Introduction
Rational choice is typically assumed to conform to axiomatic principles such as transitivity (if A is preferred to B and B preferred to C, then A is preferred to C) and independence of irrelevant alternatives (IIA; if A is the preferred option when A, B and C are all available, then A will be preferred to B when C is not available; see IIA(R-M) in [1]. Empirical studies have demonstrated that the behaviour of humans and other animals can violate transitivity [2,3] and IIA [4,5], leading to the claim that such behaviour is irrational.
We use simple models to show that such behaviour can be optimal; i.e. can be favoured by natural selection. The models are based on the standard prey-choice paradigm in which a forager chooses items in such a way that its long-term rate of energy gain is maximized [6]. Our aim is not to claim that real animals always behave so as to maximize their long-term rate of energy gain; this is simply a plausible and straightforward currency that enables us to expose the logic of behaviour which might appear to be irrational.
2. Modelling approach
We consider a foraging individual that is attempting to maximize its average rate of energy gain over an extended foraging period. Three sources of food are labelled options A, B and C. In contrast to standard models of prey choice (e.g. [6]) options are not always available. Sometimes there may be no options available to the individual, sometimes one option, sometimes two to choose between and sometimes all three options are available. If option X is chosen at a given time, the individual obtains a food item of energy content eX that takes time hX to handle. While it is handling a food item the individual is not able to forage; it is only when it has finished handling that it again chooses from the available options. This means that there is an opportunity cost associated with choosing an item, since a better option may appear while it is handling the current item. Consequently, the decision about whether to accept an option needs to take into account the alternative options currently available, the alternatives that may be missed as a result of handling, and what is likely to be available after handling the current option that is chosen.
Without loss of generality, we rank the items according to their profitability, e/h: eA/hA < eB/hB < eC/hC.
When the individual is not handling it can choose an available item (if there are any) or choose to do nothing for a unit of time.
Suppose all options are always present. When a choice is made between simultaneously available items, the behaviour that maximizes the rate of energetic gain depends on the time between decisions [7]. In our model, the next choice is made at the end of the current handling time. Under such conditions (i.e. with no delay between handling one item and starting the next), rate of gain is maximized by repeatedly choosing the option with the highest profitability; i.e. C is chosen, the individual handles the resultant item for time hC, chooses C again, and so on. Similarly, if the set of available options is the same fixed subset of those that are possible, it is always optimal to take the option with the greatest profitability. Thus there is a strict preference order A < B < C. Consequently, there are no IIA or transitivity violations.
However, in the real world possibilities change over time. It may be worth taking an option before it becomes unavailable or ignoring a profitable option in the expectation that a better one will soon appear. To allow for such possibilities we suppose that an option that is present at a given time has a probability of disappearing in each unit of time. Similarly, if an option is not present it may reappear and become available in the next unit of time. We assume that when the individual has chosen not to take an item (or been forced by lack of availability), a unit of time elapses before options are assessed again. Each of the three options A, B, C is assumed to appear and disappear independently the others, and independently of choices made (i.e. there is no depletion effect from taking an option).
When the options that are available can change, both the profitability of an item and the absolute amount of energy that the item yields are relevant to choice, as the two following examples illustrate.
3. Disappearance of options
Consider the options as shown in table 1.
Table 1.
Baseline parameters (disappearance case).
| option | energy content, e | handling time, h | P (disappear), μ | P (reappear), λ |
|---|---|---|---|---|
| A | 20 | 20 | 0.5 | 0.001 |
| B | 8 | 5 | 0.001 | 0.001 |
| C | 18 | 10 | 0.5 | 0.001 |
A strategy specifies which option to choose for each possible combination of available options; i.e. it is a contingent rule for choice. The long term mean rate of energy gain to an individual depends on the strategy that the individual follows. For the options shown in table 1, computations of the optimal strategy (see the electronic supplementary material) reveal the preferences given in table 2. The table also gives the intuitive reasons why these preferences occur.
Table 2.
Preferences between options from table 1.
| combination of options | preferred option | reason |
|---|---|---|
| A and B | B | B is more profitable (yields greater energy per unit time) than A |
| B and C | C | C is more profitable (yields greater energy per unit time) than B |
| C and A | A | whichever option is chosen, after handling of the prey item none of the three options is likely to be available. Thus, it is best to choose the option which yields the greatest energy gain |
| A, B and C | C | option A yields 20 units of energy in 20 time units. In this time it is possible to choose option C and then (since C will no longer be available) option B twice, so gaining 34 units of energy |
When only two options are available at a time, it can be seen that B is preferred to A, C is preferred to B and A is preferred to C. Thus transitivity is violated.
It can be seen that A is preferred to C when B is not available but C is preferred when B is also available. Thus, the introduction of a non-preferred option (B) changes the preference between A and C; i.e. the principle of IIA is violated.
By varying the energy content and handling time of option B, we obtain figure 1.
Figure 1.
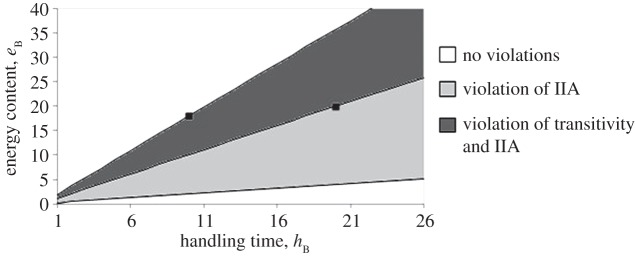
Energy and handling time parameters associated with option B that produce violations of transitivity and IIA. Above the region of transitivity violation, option B is always preferred. Below the region of IIA violation, B is never preferred. Options A and C are shown as black squares on the graph.
The violations in figure 1 are driven by the different probabilities of options disappearing.
4. Reappearance of options
Table 3 shows parameter values for the options which result in the optimal preferences that are shown in table 4. Again, this shows violations of transitivity and IIA, but rather than being driven by the probable disappearance of currently available options (as above), the effect is largely driven by the probable reappearance of option B (when it is not currently available).
Table 3.
Baseline parameters (reappearance case).
| option | energy content, e | handling time, h | P (disappear), μ | P (re-appear), λ |
|---|---|---|---|---|
| A | 5 | 6 | 0.5 | 0.01 |
| B | 2 | 2 | 0.5 | 0.5 |
| C | 1 | 1 | 0.5 | 0.01 |
Table 4.
Preferences between options from table 3.
| combination of options | preferred option | reason |
|---|---|---|
| A and B | A | whichever option is chosen there may be no option available once handling is completed. Thus, it is best to go for the option that gives the greatest energy gain, i.e. A |
| B and C | B | B guarantees 2 units of energy in 2 time steps, whereas if C is chosen, there may not be an option to take after 1 time step |
| C and A | C | C has the higher profitability and, even if it is not still available after handling, B (which also has a higher profitability than A) is likely to reappear soon |
| A, B and C | B | B and C have the same profitability and B gives a greater energy than C. Both A and C act as backup options for subsequent choices |
Figure 2 shows that violations of IIA and transitivity occur over a range of parameter values. If the probability of option B reappearing is low, option A is preferred to option C since it gives the greater amount of energy and the system is transitive. If option B is almost certain to reappear, it is preferred to option A since it has a greater rate of gain, again resulting in a transitive system.
Figure 2.
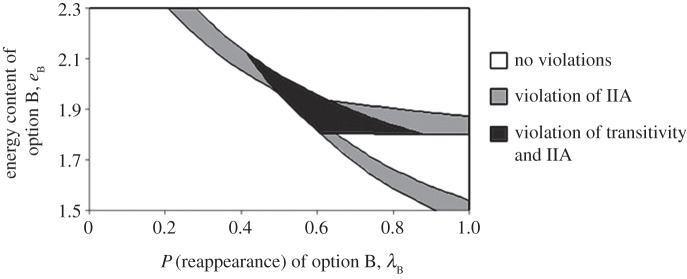
Regions of violation with respect to probability of reappearance and energy content of option B, holding all other values at those of table 3.
5. Discussion
Individuals sometimes make decisions which conform with transitivity and IIA [8] but violations of these principles are reported in many situations [4,9–12]. We have shown that it can be adaptive for these principles to be broken.
The long-term mean rate of energy gain to an individual depends on the strategy that the individual follows. Different strategies can be ranked in order of their mean rate of energy gain. Thus, in comparing different strategies, there cannot be any violations of transitivity or IIA. We have based our analysis on the choices made under the optimal strategy, i.e. the strategy maximizing mean gain rate. Although there is a strict ordering of strategies, it does not mean that there is a strict ordering of preference for food options under the optimal strategy; transitivity and IIA can fail to hold when an individual follows this strategy.
Our results are stronger than any previously obtained in this area. Houston [13] shows that stochastic transitivity can be violated when an individual maximizes the rate subject to errors and costly errors are rare. We obtain violations when choice is deterministic and not subject to errors. Houston et al. [14] assume that an individual makes optimal choices between options on the basis of its level of energy reserves. They show that transitivity can be violated at particular (intermediate) levels of reserves. Trimmer [15] uses the same approach to show that IIA can be violated. In both cases decisions are context-dependent because the available options influence the individual's future expectations. The effect of the future arises because future levels of energy reserves might require the non-selected option to be chosen. We have shown in the simple context of rate maximization that violations of transitivity and IIA do not require errors or decisions that depend on energy reserves.
IIA is very similar (or equivalent) to principles which go by other names: the principle of regularity, Sen's property, α, the constant-ratio-rule and Luce's choice axiom. For a summary of various definitions and their logical differences, see Ray [1]. Behaviour which does not conform to IIA also goes by more than one name, such as the violation of regularity, and the asymmetrically dominated decoy effect. Others (e.g. Tsetsos et al. [16]) have attempted to explain such violations by referring to mechanistic models of computational processes—i.e. they assume that such behaviour comes about through constraints. By dealing with cases where individuals always make the same choice given the same range of options, we have demonstrated that all forms of IIA can be violated by an optimal decision-maker.
A formal logician might argue that neither transitivity nor IIA has necessarily been violated, because the choice sets can alter over time. However, it would not be possible to test for transitivity or IIA if the choice set could not alter, so from an operational perspective (i.e. measuring the preferences of animals by giving them options), it is clear that the principles of transitivity and IIA should sometimes be violated if fitness is to be maximized.
Rationality is a fundamental principle of decision-making in economics, psychology and philosophy. Economic rationality is based on the maximization of utility [17]. The existence of a utility function is guaranteed given certain consistency conditions on decisions. The consequence is that utility is inferred from the data. In evolutionary biology, there is always a utility measure known as reproductive value. The reproductive value of an individual is defined as its expected future lifetime reproductive success; this typically depends on the state of the individual [18]. In our model, the state of the animal is the set of options which are currently available. Each possible action has an associated reproductive value. Natural selection favours individuals that behave as if they are maximizing reproductive value [18]. This means that in contrast to the descriptive utility function in economics, reproductive value is a normative measure of utility, i.e. it specifies the decision that should be made [17,19]. As we show, even individuals that behave optimally can violate IIA and transitivity. This can occur because options do not have absolute reproductive values; the value of an option depends on the future [13]. The key point is that reproductive value is a future expectation and currently available options provide information about the future and hence affect reproductive value. In other words reproductive value cannot be assigned to options individually; the value of choosing an option depends on the other options that are present. The options presented to humans and other animals often give information about an individual's future prospects. Thus, the insight gained from our particular model applies to a whole range of choice phenomena, with widespread implications for how human choices—and the behaviour of other animals—should be analysed.
Acknowledgements
Thanks to Sean Collins for mathematical help with the appendix (available as the supplementary material).
Funding statement
This work was supported by the European Research Council (Evomech Advanced grant no. 250209 to A.I.H.).
References
- 1.Ray P. 1973. Independence of irrelevant alternatives. Econometrica 41, 987–991 (doi:10.2307/1913820) [Google Scholar]
- 2.Tversky A. 1969. Intransitivity of preferences. Psychol. Rev. 76, 31–48 (doi:10.1037/h0026750) [Google Scholar]
- 3.Waite TA. 2001. Intransitive preferences in hoarding gray jays (Perisoreus canadensis). Behav. Ecol. Sociobiol. 50, 116–121 (doi:10.1007/s002650100346) [Google Scholar]
- 4.Shafir S, Waite TA, Smith BH. 2002. Context-dependent violations of rational choice in honeybees (Apis mellifera) and gray jays (Perisoreus canadensis). Behav. Ecol. Sociobiol. 51, 180–187 (doi:10.1007/s00265-001-0420-8) [Google Scholar]
- 5.Doyle JR, O'Connor DJ, Reynolds GM, Bottomley PA. 1999. The robustness of the asymmetrically dominated effect: buying frames, phantom alternatives, and in-store purchases. Psychol. Market. 16, 225–243 (doi:10.1002/(Sici)1520-6793(199905)16:3<225::Aid-Mar3>3.0.Co;2-X) [Google Scholar]
- 6.Stephens DW, Krebs JR. 1986. Foraging theory. Princeton, NJ: Princeton University Press [Google Scholar]
- 7.Stephens DW, Lynch JF, Sorensen AE, Gordon C. 1986. Preference and profitability—theory and experiment. Am. Nat. 127, 533–553 (doi:10.1086/284501) [Google Scholar]
- 8.Monteiro T, Vasconcelos M, Kacelnik A. 2013. Starlings uphold principles of economic rationality for delay and probability of reward. Proc. R. Soc. B 280, 20122386 (doi:10.1098/rspb.2012.2386) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Navarick DJ, Fantino E. 1974. Stochastic transitivity and unidimensional behavior theories. Psychol. Rev. 81, 426–441 (doi:10.1037/H0036953) [Google Scholar]
- 10.Latty T, Beekman M. 2011. Irrational decision-making in an amoeboid organism: transitivity and context-dependent preferences. Proc. R. Soc. B 278, 307–312 (doi:10.1098/rspb.2010.1045) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hurly TA, Oseen MD. 1999. Context-dependent, risk-sensitive foraging preferences in wild rufous hummingbirds. Anim. Behav. 58, 59–66 (doi:10.1006/anbe.1999.1130) [DOI] [PubMed] [Google Scholar]
- 12.Bateson M, Healy SD, Hurly TA. 2002. Irrational choices in hummingbird foraging behaviour. Anim. Behav. 63, 587–596 (doi:10.1006/anbe.2001.1925) [Google Scholar]
- 13.Houston AI. 1997. Natural selection and context-dependent values. Proc. R. Soc. Lond. B 264, 1539–1541 (doi:10.1098/rspb.1997.0213) [Google Scholar]
- 14.Houston AI, McNamara JM, Steer MD. 2007. Violations of transitivity under fitness maximization. Biol. Lett. 3, 365–367 (doi:10.1098/rsbl.2007.0111) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Trimmer PC. 2013. Optimal behaviour can violate the principle of regularity. Proc. R. Soc. B 280, 20130858 (doi:10.1098/rspb.2013.0858) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Tsetsos K, Usher M, Chater N. 2010. Preference reversal in multiattribute choice. Psychol. Rev. 117, 1275–1293 (doi:10.1037/a0020580) [DOI] [PubMed] [Google Scholar]
- 17.Kacelnik A. 2006. Meanings of rationality. In Rational animals? (ed. Hurley S, Nudds M.), pp. 87–106 Oxford, UK: Oxford University Press [Google Scholar]
- 18.Houston AI, McNamara JM. 1999. Models of adaptive behaviour. Cambridge, UK: Cambridge University Press [Google Scholar]
- 19.Houston AI, McNamara JM, Steer MD. 2007. Do we expect natural selection to produce rational behaviour? Phil. Trans. R. Soc. B 362, 1531–1543 (doi:10.1098/rstb.2007.2051) [DOI] [PMC free article] [PubMed] [Google Scholar]


