Biomechanical Measurement of Kinocilium

Abstract

Vestibular hair cell bundles in the inner ear each contain a single kinocilium that has the classic 9+2 axoneme microtubule structure. Kinocilia transmit movement of the overlying otoconial membrane mass and cupula to the mechanotransducing portion of the hair cell bundle. Force deflection techniques were used to measure turtle utricle kinocilium shaft and base rotational stiffness. Kinocilia were modeled as homogenous cylindrical rods and their deformation examined as both isotropic Euler–Bernoulli beams (bending only) and as transversely isotropic Timoshenko beams (combined shear and bending). The measurements fit the transversely isotropic model much better with flexural rigidity EI = 10,400 pN·μm² (95% confidence interval: 7182 to 13,630) and shear rigidity kGA = 247 pN (180 to 314). Resulting in a shear modulus (G=1.9 kPa) that was four orders of magnitude less than Young’s modulus (E=14.1 MPa), indicating that significant shear deformation occurs within deflected kinocilia. The base rotational stiffness (κ) was measured following BAPTA treatment to break the kinocilial links that bind the kinocilium to the bundle along its shaft, and κ was measured as 177±47 pN·μm/rad. These parameters are important for understanding how forces arising from head movement are transduced and encoded.

1. INTRODUCTION

1.1 Vestibular hair cells

Vestibular hair cells are mechanoreceptors in vestibular organs of the inner ear that detect movement and accelerations of the head. Their mechanosensitive organelle is the hair bundle, which is composed of multiple stereocilia and a single kinocilium. The stereocilia are arranged in rows of increasing height with the kinocilium eccentrically positioned at the tall edge of the bundle. While considerable attention has been focused on the behavior of stereocilia during mechanotransduction, much less is known about kinocilia.

The kinocilia play an important role in the development of inner ear hair cell polarization (Denman-Johnson and Forge, 1999; Jones et al., 2008), but they are lost during the maturation of hair cells in the mammalian and avian cochlea. Their persistence in mature vestibular bundles of all species suggests kinocilia have lifelong functional significance in these endorgans. Like other true cilia, including motile cilia, kinocilia posses a microtubule core of 9 peripheral doublets circumferencing up to 2 single tubules and are rooted in a basal body (Fig. 1A). There is conflicting evidence regarding the motility of vestibular kinocilia. A limited number of spontaneous flagella like oscillations were observed in ampullary kinocilia, but a correlation between frequency and length of the experiment suggested they were the result of tissue degradation (Flock et al., 1977; Rüsch and Thrum, 1986; Rüsch and Thurm, 1990). Other work shows that the inner arms of the motor protein dynein that is essential for motility are absent in kinocilia (Kikuchi et al., 1989).

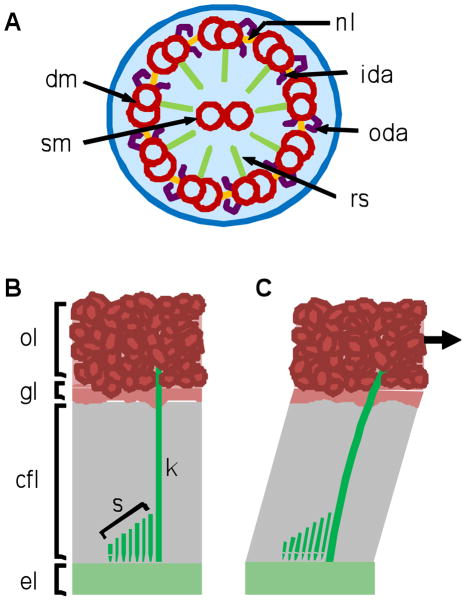
FIGURE 1.

(A) A cross section of the classic 9+2 axoneme of cilia shows nine peripheral doublet microtubules (dm) surrounding two single microtubules (sm). The peripheral doublets connect to each other through nexin links (nl) and to the central tubules through radial spokes (rs). Inner (ida) and outer dynein arms (oda) interact with neighboring peripheral tubules. Kinocilia posses this 9+2 microtubule structure, but have been shown to lack ida (Kikuchi et al., 1989). (B–C) In medial extrastriola hair bundles from the turtle utricle, the kinocilia (k) are much taller than the stereocilia (s). The kinocilia project from basal bodies in the epithelial layer (el) through the gelatinous column filament (cfl) and gel (gl) layers, and embed in the otoconial layer (ol). Movement of the ol produces shearing of the cfl and gl. The kinocilium deflects in response to movement of the ol which in turn deflects the stereocilia resulting in signal transduction.

Each stereocilium in a vestibular hair cell bundle contains a tip link that runs diagonally up to the next taller stereocilium. These tip links have a mechanotransduction ion channel, attached the top of the stereocilium, that is opened by mechanical tension in this link (Beurg et al., 2009). When the bundle is deflected in an excitatory direction these tip links are tensioned and the ion channel opened. The kinocilia do not directly contribute to mechanotransduction, as there are no tip links connecting kinocilia to their adjacent stereocilia (Hackney et al., 1993). Additionally, deflection of kinocilia intact but separated from the stereocilia of transducing bundles produced no intracellular receptor potential (Hudspeth and Jacobs, 1979).

Evidence shows that the kinocilia of vestibular bundles play a strictly mechanical role. The kinocilia are thought to passively transmit force to the mechanotransducing portion of the bundle including the stereocilia, tip links and transduction channels. This mechanical role is clearest in otoconial organs, the utricle and saccule. In these vestibular organs, head movements result in displacement of the otoconial layer (OL) in which kinocilia tips are embedded (Fig. 1B,C). Movement of the OL causes deflection of the kinocilium and of the stereocilia to which the kinocilium is attached. The resulting bundle deflection modulates the output of the hair cell and thus the signal that the inner ear sends to the central nervous system.

Given the importance of kinocilia in transmitting forces generated by head movements, it is important to know their mechanical properties. This study measures the important mechanical deformation properties of kinocilia in vestibular hair bundles. The kinocilia can be thought of as flexible beams tethered to the OL which are able to bend along their shaft and rotate about their insertion in response to shearing of the column filament and gel layers.

The kinocilium remains upright when the links between it and neighboring stereocilia are broken, and a kinocilium separated from the stereocilia and pinned to the epithelial surface returns to an upright position within seconds of release (Hudspeth and Jacobs, 1979). Both behaviors indicate that the insertion of the kinocilium possesses an inherent rotational stiffness.

There are two morphologically distinct bundle populations in the utricle differ in regional location. The ratio of kinocilium height to tallest stereocilia height is termed the KS ratio. Bundles in a crescent shaped band known as the striola have KS ratios of one or near one, while extrastriola (ES) bundles have values of 3 to 4 on average (Fig. 1B, C; Xue and Peterson, 2006). Previous computational studies have shown that the tall kinocilia of ES bundles dominate their mechanics and increases their operating range, the range of displacements the vestibular sensory cell can encode, to several microns compared to that of striolar bundles which is less than 1 micron (Nam et al., 2005; Grant et al., 2007). Knowing the correct mechanical properties of the kinocilium is crucial to further understanding the function of ES hair bundles.

In this study, we have taken advantage of the ES population of vestibular hair bundles from turtle utricle. Their structure makes it easy to identify and isolate the kinocilia for experimental manipulation. A force-deflection technique was used to measure kinocilium stiffness. These stiffness values were fit to two beam deformation models that showed kinocilia have significant bending and shear deformation.

1.2 Beam Models for Kinocilia

The kinocilium was modeled as a vertically oriented cantilever beam with elastic properties using the Euler–Bernoulli and Timoshenko beam theories (Fig. 2A). The Euler–Bernoulli theory omits the effect of transverse shear deformation. It assumes that, during bending, the transverse cross-sections of the beam remain planar and perpendicular to the bending axis. The kinocilium was assumed to be homogenous and isotropic, meaning the mechanical properties are the same in all directions. For a Euler cantilever beam with a point load at the tip, the transverse deflection (δ_E) at the tip or free end that is available for deflection, is given by

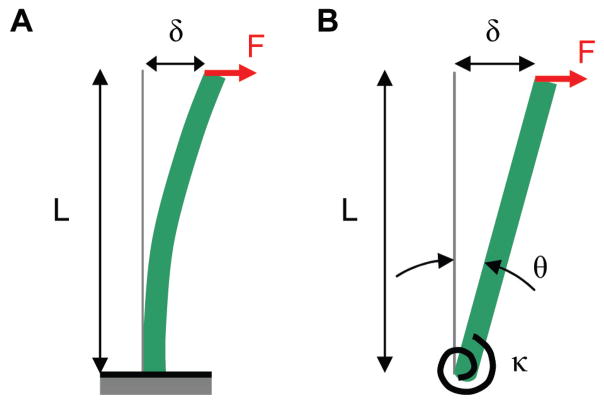
FIGURE 2.

(A) Kinocilium modeled as a vertically oriented cantilevered beam. Force F, applied at length L, at the tip of the kinocilium induces a deflection δ. (B) Kinocilium insertion into its neuro-epithelial base, modeled as a rotational spring. Shown as a rigid bar that pivots about its base, resisted by a rotational spring of stiffness κ. For small angles of deflection θ, κ can be determined from the length L, applied force F, and deflection δ. Bending of the kinocilium was also included in the analysis.

$${\delta }_E=\frac{{FL}^3}{3EI}$$ (1)

where: F is the force applied at the free end, L is the length of the beam, E = Young’s modulus, I is the second moment of inertia, and EI is the flexural rigidity.

The Timoshenko beam theory includes transverse shear as well as bending. The assumption here are that the cross-sections remain planar but are not restrained to be perpendicular to the bending axis. The structure of the kinocilium, with its longitudinally aligned microtubules, is loosely analogous to a composite beam reinforced by unidirectional longitudinally oriented fibers. For this reason, the kinocilium was modeled as a transversely isotropic material, meaning the transverse cross-sections are considered isotropic and the material properties in the transverse direction differ from those in the longitudinal direction. The deflection at the free end of a Timoshenko cantilever beam (δ_T) with a point load at the tip is the sum of the deflection due to bending (Eqn. 1) and the deflection due to shear, and is given by (Wang et al., 2000; Kollar and Springer, 2003)

$${\delta }_T=\frac{{FL}^3}{3EI}+\frac{FL}{\mathit{kGA}}$$ (2)

where: E is now specific to the longitudinal Young’s modulus, k is a shear correction factor equal to 3/4 for a cylindrical beam (Boresi and Schmidt, 2003), G is the transverse shear modulus, and A is the cross-sectional area.

The beam analysis employed here for each model, assumes that kinocilia are homogenous beams, meaning their composition and elastic properties are the same at every point. Even though kinocilia are not homogenous because of their microtubular structure, this assumption is necessary for the type of simplified beam analysis presented here and the same as made in previous studies of kinocilia and flagella mechanics (McHenry and van Netten, 2007; Okuno and Hiramoto, 1979; Okuno, 1980; Ishijima and Hiramoto, 1994). In consequence, the determined values of EI and kGA serve as effective values, meaning that the kinocilia effectively function, or can be effectively modeled, as homogenous beams with these properties.

1.3 Accuracy of small-deflection beam theory

Both the Euler–Bernoulli and Timoshenko beam analyses used here is based on small-deflection beam theory. The accuracy of this small-deflection formulation is dependent on the force loading condition. To determine accuracy, we compared results from small-deflection theory with those from large- or finite deflection theory in which nonlinearities in the deflection gradient are taken into account (Timoshenko and Gere, 1972). This was done by numerical solution of the governing equations for large deflection, compared to small deflection of equal displacement. Comparison showed that for the small-deflection theory using a point load at the top of the kinocilium, has an accuracy that is better than 1.3% for δ/L = 0.1, and the error increases to 10% with δ/L = 0.3. All our δ/L values are well below 0.1, with a maximum of 0.07 and error less then 1%. Thus, the application of the small-deflection beam theory to our kinocilia measurements has better than 1% accuracy.

1.4 Rotational stiffness

The rotation stiffness κ of a torsional spring is related to its angular rotation θ due to an applied moment M = κθ. Fig. 2B illustrates a rigid bar pivoting about a rotational spring at its base. For small angular deflections, the angle of rotation can be approximated as $\theta \simeq sin\theta =\frac{{\delta }_R}{L}$, where δ_R is the tip deflection and L = length of the rigid bar. The applied moment as M = FL, where F = force applied at distance L from the spring pivot, the rotational stiffness relationship becomes

$${\delta }_R=\frac{1}{\kappa }{FL}^3$$ (3)

This approach has previously been used to determine the κ of intact hair bundles where the kinocilium was approximately the same height as the tallest stereocilia (Crawford and Fettiplace, 1985; Howard and Ashmore, 1986). Here, the insertion of the kinocilium is modeled as a rotational spring and the tall kinocilium shaft as a flexible beam. To measure the κ of kinocilia, the filamentous links connecting the kinocilia to their adjacent stereocilia were broken (see Materials and Methods). A force applied to the tip of a kinocilium that is disconnected from the adjacent stereocilia induces both rotation about its insertion in the epithelial base and bending of the shaft. In the experiment, the total deflection at the tip of the kinocilium δ includes the sum of the rotational deflection δ_R and the bending deflection δ_T from the Timoshenko beam

$$\delta ={\delta }_R+{\delta }_T=\frac{1}{\kappa }{FL}^2+\frac{{FL}^3}{3EI}+\frac{FL}{\mathit{kGA}}$$ (4)

This expression will be used to evaluate rotational stiffness.

1.5 Previous measurements of tubule and kinocilium mechanical properties

Flexural rigidity (EI) is a measure of a beam’s ability to resist bending based on material deformation properties and geometry. It has been measured for non-kinocilial structures with a 9+2 axoneme, including compound cilia (Baba, 1972) and echinoderm sperm flagella (Okuno and Hiramoto, 1979; Okuno, 1980; Ishijima and Hiramoto, 1994; Pelle et al., 2009). In these studies, the EI measured was based on the Euler–Bernoulli beam theory and assumptions that these 9+2 microtubular structures behave as homogenous, linearly elastic, and isotropic beams (Okuno and Hiramoto, 1979; Okuno, 1980; Ishijima and Hiramoto, 1994). Shear deformation due to the sliding of adjacent doublets was only considered in one study of passive sea sperm flagella (Pelle et al., 2009). The reported values for echinoderm sperm flagella EI ranged from 300 to 15,000 pN·μm² and varied with a number of factors, including immobilization with CO² (Okuno and Hiramoto, 1979; Ishijima and Hiramoto, 1994), exposure to ATP and vanadate (Okuno and Hiramoto, 1979; Okuno, 1980; Ishijima and Hiramoto, 1994; Pelle et al., 2009). A 12- to 14-fold difference in EI was found when it was measured within and perpendicular to the beating plane (Ishijima and Hiramoto, 1994). The only reported value of kinocilium EI (2400 pN·μm²) was measured from the superficial neuromasts of the zebrafish lateral line (McHenry and van Netten, 2007). This value was cleverly inferred from the number of kinocilia and the overall EI of the neuromast cupula.

Single microtubules (MTs) have also been analyzed using elastic beam theories to quantify their mechanical properties. Experimental measurements suggest that the EI of microtubules is height dependent, such that shorter microtubules have lower values of EI (Kurachi et al., 1995; Takasone et al., 2002; Pampaloni et al., 2006), but this height dependence is not expected for an isotropic Euler–Bernoulli beam, demonstrating that the MT is not accurately modeled as such. Indeed, atomic force microscopy shows that MTs are highly anisotropic because the longitudinal bond strength between tubulin dimmers along the protofilaments is greater than the lateral bond strength between protofilaments (Kis et al., 2002). Computational studies in which the MT was modeled as a two-dimensional orthotropic shell or a one-dimensional Timoshenko beam predict a length dependence of EI that results from an extremely low shear modulus relative to the longitudinal Young’s modulus (E) (Li et al., 2006; Pampaloni et al., 2006; Shi et al., 2008). Use of the Euler–Bernoulli model, which does not account for shear deformation, leads to an underestimate of EI for shorter MTs (Li et al., 2006). The Timoshenko beam theory, which can account for shear deformation, was applied to MTs, yielding results comparable to that of the more complicated orthotropic shell model, which includes transverse shearing (Gu et al., 2009). These findings regarding MTs are relevant to the study of kinocilium mechanical properties in two ways. First, microtubules are the building blocks and main structural elements of the kinocilium’s 9+2 axoneme, contributing an inherent anisotropy to the microtubular structure. Second, there is potential for sliding between doublet microtubules during bending, further disposing them to translational shearing. Both reasons suggest that a shear-deformable Timoshenko beam would be a more accurate model for a kinocilium than an Euler Bernoulli beam.

1.6 The study reported on here

Stiffness of the kinocilium (s_k) was measure in this study by applying a force F at the top of individual kinocilia and measuring the resulting deflection (δ) where

$$s_k=\frac{F}{\delta }$$ (5)

The kinocilia used were also of various heights. The base was supported to simulate a fixed base kinocilium. The measurements of kinocilia stiffness are analyzed using two mechanical beam theories, the Euler–Bernoulli and the Timoshenko beam theories, to determine EI and kGA. We then asked which model produces results that most accurately reflect our experimental data.

The rotational stiffness (κ) of the kinocilium’s insertion into the apical surface of the hair cell was also measured. The kinocilium remains upright when the links between it and neighboring stereocilia are broken, and a kinocilium separated from the stereocilia and pinned to the epithelial surface returns to an upright position within seconds of release (Hudspeth and Jacobs, 1979). Both behaviors indicate that the insertion of the kinocilium possesses an inherent rotational stiffness, which is quantified here.

1.7 Kinocilium motion in fluid as a measure of its mechanical properties

The technique described in this section was implemented, however, it did not fit well with the direct force-deflection measurement described in the previous section. This technique is described briefly here along its inherent errors. It is included to highlight the potential problems and difficulty with this approach.

When a kinocilium is submerged in fluid, deflected and released, fluid drag force impedes its return to its equilibrium position. These fluid drag forces are distributed along its height and are directly proportional to the velocity of the kinocilium as it moves through the suspending fluid. The velocity increases linearly from zero at the base of the kinocilium to a maximum at its tip. These velocity magnitudes also decreasing as the kinocilium approaches its equilibrium position.

The problems begin with the large deflections that are required for implementation. The error is approximately 10% for δ/L = 0.3, and this technique required deflections up to this magnitude. Defining the drag force in this low Reynolds experiment (10⁻³ to 10⁻²) is in a range below where drag data have been measured, requiring extrapolation of experimental data for a cylinder, and the slope of this extrapolation is not clear. With the large deflections the relative velocity between the kinocilium and fluid was not always perpendicular to the kinocilium shaft, a basic assumption in the drag data. All this information was incorporated into a first order differential equations that describes the tip motion return to its equilibrium position. A time constant containing the parameters of interest was determined from this differential equation. During an experiment, the kinocilium was released from a deflected position and the displacement at the tip of the kinocilium was tracked using high-speed video and a time constant for this motion determined. The compounding of errors proved to produce data that was not consistent with that of the force-deflection method. So this technique was abandoned. For details of this technique see Spoon, 2007b.

2. MATERIALS and METHODS

2.1 Experimental Preparation

Experiments were performed on hair cell bundles in isolated turtle utricles, Trachemys (Pseudemys) scripta elegans. Animals were euthanized following guidelines of the Virginia Tech Institutional Animal Care and Use Committee. Utricles were removed and maintained at room temperature in Hanks’ balanced salt solution (HBSS), with 10 mM HEPES added as a buffering agent, resulting in 7.2 pH; 300 mOsm osmotic concentration. The utricles were folded along a medial to lateral transect and securely pinned in an experimental chamber. The otoconial membrane was peeled away using an eyelash. The folded bundle edge were viewed from the side using a Zeiss Axioskop with DIC 100X water immersion objective, 10X oculars, and an oil immersion substage condenser. Experiments were performed on a vibration isolation table. Measurements of the kinocilia’s properties were made from hair bundles located in the medial extrastriola of the turtle utricle. The kinocilia in this region are very tall (10–40+ μm) and the stereocilia are short (2–5 μm).

To measure the stiffness of the kinocilium shaft, the portion of the kinocilium projecting above the tallest stereocilia was backed up with a rigid glass probe, mechanically fixing it between the stereocilia and the probe (Fig. 3A, B). The supporting probe was fabricated from a solid pipette pulled and trimmed to have a flat end 5 μm in diameter. The supporting probe was trimmed while under tension to produce a smooth flat surface. The glass probe was positioned with its top edge at the height of the tallest stereocilia so that when the kinocilium was deflected in the excitatory direction, the exposed portion bent in flexure (Fig. 3B). This produced a stiffness measurement for each kinocilia did not include the stereocilia bundle effects.

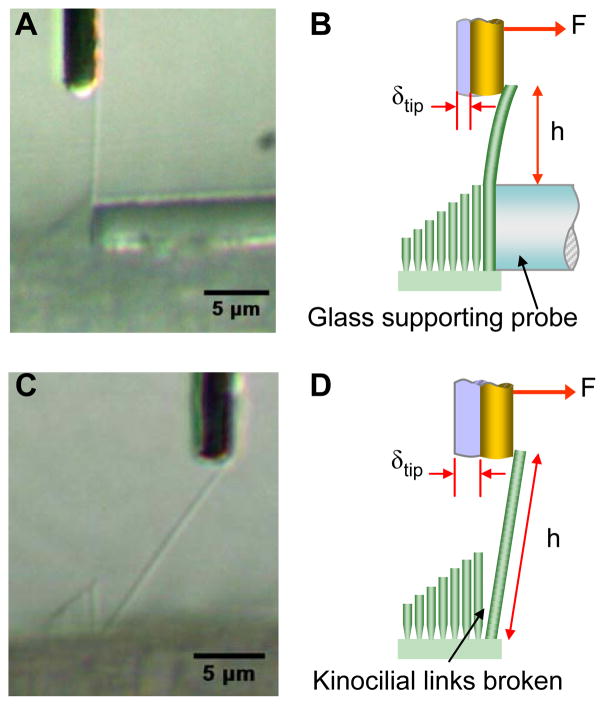
FIGURE 3.

(A) For EI measurements, bundles were backed up with a supporting probe to fix the kinocilium at the height of the tallest stereocilia. When pushed in the excitatory direction with a flexible glass fiber, the kinocilium bent in flexure. (B) Measurements of applied force F, tip deflection δ_tip, and height projecting above the supporting probe h, were used to calculate EI and kGA. (C) Exposure to BAPTA broke the kinocilial links connecting the kinocilia with their neighboring stereocilia. This photograph of a large deflection shows there was complete separation. (D) Following BAPTA treatment, κ was determined from the force F applied through a flexible glass fiber and measurements of the kinocilium’s tip deflection δ_tip, length L, and measured values of EI and kGA.

For measurements of the insertion rotational stiffnes κ, the kinocilium was detached from the adjacent stereocilia by using the calcium chelator BAPTA (Sigma-Aldrich). BAPTA has been shown to sever kinocilial links in chick utricular bundles (Goodyear and Richardson, 2003). A 5 mM solution of BAPTA was prepared in Ca²⁺ and Mg²⁺ free HBSS, with 0.9 mM MgCl₂ and 10mM HEPES added, pH 7.2; 300 mOsm. The BAPTA solution was prepared in plastic containers. A peristaltic pump was used to exchange the fluid in the experimental chamber with the BAPTA solution. Measurements of κ were begun after at least 10 minutes of BAPTA solution exposure. It is assumed that the BAPTA treatment did not otherwise damage the kinocilia or the epithelium at the apical insertions. Fig. 4C demonstrates a kinocilium fully detached and rotated about its insertion for a large displacement. Note that the displacements of the kinocilia during actual measurements were much smaller (< 1 μm) than shown in the photograph. The angular displacements (≤ 0.09 rad) during experiments complied with the small angle approximation applied to obtain Eqn. 4.

FIGURE 4.

(A) A flexible glass fiber, sputter coated with gold to enhance its contrast, deflects the tip of a kinocilium. The magnified image of the tip of the fiber is projected onto a dual array of photodiodes, positioned at the camera port of the microscope. Movement of the glass fiber changes the distribution of light on the photodiodes. (B) As the fiber passes between the two diodes, the diode output voltage is linearly related to fiber position, the plot is an illustration.

2.2 Force-Displacement Technique

For measurements, kinocilia were deflected in their excitatory directions with flexible glass fibers (Fig. 3A, B). The glass fibers were made from solid borosilicate glass pipettes using a microforge. The fibers were drawn perpendicular to the shank of the rod by quickly retracting a platinum-heating element. The fibers had tip diameters of 2.9–4.2 μm, were trimmed to lengths of 2.8 – 3.5 mm, and were sputter coated with 200 Å of gold to improve their optical contrast. The stiffness of the fibers was determined by measuring the deflection of a horizontally positioned fiber from the weight of micro beads of 30–100 μm in diameter that were electro-statically attached. From the bead weight, fiber length, and vertical deflection, the stiffness was determined using a cantilever beam equation. The fibers used had stiffness values of 6–47 pN/m.

The free end of a flexible glass fiber was brought into contact with the tip of the kinocilium such that their shafts were parallel. The base of the fiber was displaced using a piezoelectric linear actuator, and measured using a fiber optic displacement sensor, an extrinsic Fabry-Perot interferometer (Luna Innovations, Blacksburg, VA). Deflections at the tip of the glass fiber, in contact with the kinocilium, were measured using a dual array of photodiodes housed at the camera port of the microscope (Fig. 4A). The rectangular photodiodes were located side by side and the gap separating them was aligned with the projected image of the fiber. As the magnified image of the fiber passed between the two diodes their differential output voltage was proportional to fiber position (Fig. 4B). The force applied to the kinocilium by the glass fiber was quantified by multiplying the fiber stiffness by the deflection of the glass fiber (ie., the difference between the fiber’s base and tip deflections).

With the fiber contacting the kinocilium’s tip, the base of the glass fiber was sinusoidally oscillated a peak-to-peak distance of 1 μm at 0.5 Hz. Signals from the displacement sensor and photodiodes were recorded for 30 sec. trials with a sampling frequency of 1 kHz using LabVIEW 7.0 (National Instruments, Austin, Texas). The photodiodes were calibrated at the end of each trial by positioning the oscillating fiber just above the kinocilium in the same horizontal plane. Again, the displacement sensor and photodiode outputs were recorded in 30 sec. trials. This was used to determine a calibration factor relating photodiode output voltage to displacements of the fiber tip. Testing showed that drag on the fiber was negligible at 0.5 Hz.

The force applied to the kinocilium was determined from the peak-to-peak base and tip deflections of each oscillation and averaged per trial. The reported EI, kGA, and κ measurements are the averages of multiple trials. Kinocilium heights for these calculations were measured from high-resolution digital photographs using Image J software (NIH, public domain).

2.3 Error analysis of force-deflection technique

To assess the error in the force-deflection measurements, seven borosilicate glass fibers were made. Stiffness of these fibers was measured using: (1) microbeads (as previously described) and (2) the force-deflection technique, where a stationary glass fiber was positioned opposite the forcing fiber. The seven fibers (with a stiffness range of 7.6–1107 μN/m) were paired 17 ways with ratios of forcing fiber to stationary fiber stiffness (k_f/k_s) ranging from 0.01 to 22.11. The percent difference between the photodiode system and bead-calibrated stiffness measurements depended on the k_f/k_s ratio. For k_f/k_s>0.17, the percent difference was 10% or less. For k_f/k_s<0.17, the percent difference steadily increased from 30 to 90% as the k_f/k_s decreased. In the present study, the ratio of fiber stiffness to kinocilium stiffness for all measurements ranged from 0.4 to 14, indicating that the error, measured as the percent difference between the force-deflection and bead-calibrated results, ranged between 0 and 10%.

Additionally, we determined the uncertainty in EI and kGA calculations due to propagation of the uncertainty of each individually measured value: kinocilium height, fiber base deflection, fiber tip deflection and fiber stiffness (Taylor, 1982). The error in the force-deflection measurements was determined to have a maximum value of 9%. The measurements of fiber stiffness using the bead-calibration method yielded the largest fractional uncertainties of all measured values.

3. RESULTS

3.1 Properties of the kinocilium shaft

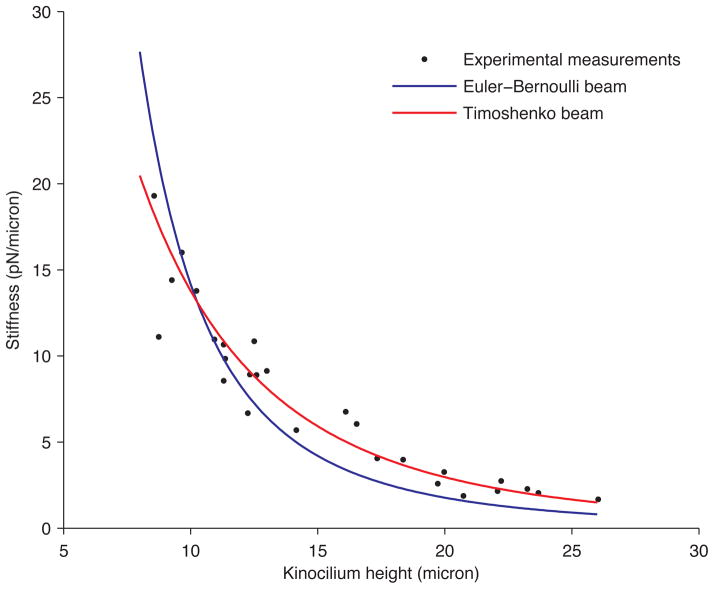
Using the force-deflection technique, we took a stiffness measurement from 27 kinocilia of differing heights located in the medial extrastriolar region of the turtle utricle. These results are plotted in Fig. 5. The stiffness values ranged from 2 to 19 pN/μm for kinocilia with heights projecting above the tallest stereocilia of 8.5–26.0 μm. Kinocilium stiffness decreased with height, as expected from both the Euler–Bernoulli and Timoshenko beam theories: Eqns. 1 and 2 for both beam theories show that stiffness (F/δ) is inversely proportional to the height cubed. Values of EI and kGA were determined in two ways. In one technique, the stiffness measurements from all 27 kinocilia were curve-fit using the Timoshenko and Euler–Bernoulli beam equations (Eqns 1 and 2) to predict single values of EI (for both) and kGA (for the Timoshenko equation only) for the whole data set. The Timoshenko beam model produced a better fit to the experimental data than the Euler–Bernoulli model with R² values of 0.94 and 0.83 respectively. The predicted curve-fit values and their 95% confidence intervals are given in Table 1.

FIGURE 5.

Each data point represents the experimentally measured stiffness of a single kinocilium versus its height above the tallest stereocilia. These stiffness measurements are curve-fit with the Euler–Bernoulli (blue) and Timoshenko beam (red) theories.

Table 1.

Mechanical deformation values of turtle kinocilia.

Deformation Parameter	Euler-Bernoulli	Timoshenko
EI ~ pN·mm2	4721 (4327, 5115)	10,400 (7182, 13,630)
kGA ~ pN	--	247 (180, 314)
E ~ MPa	6.4	14.1
G ~ kPa	--	1.9

Values of EI and kGA were predicted from the curve-fits shown in Fig. 5. Numbers in parentheses give the 95% confidence intervals. Effective values of E and G were calculated from the curve-fit predictions of EI and kGA by assuming the kinocilium is a homogenous rod with a constant diameter of 0.35 μm.

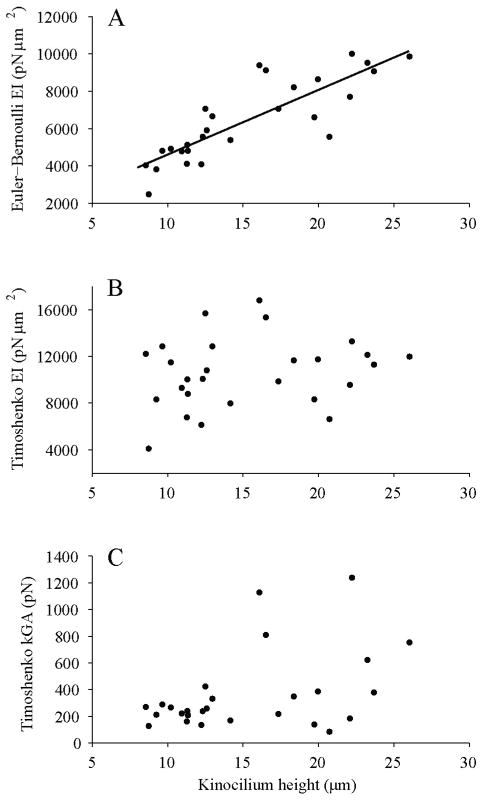
Using a second technique, values of EI and kGA were determined for each of the 27 kinocilia measured. From the Euler–Bernoulli beam equation, the EI of an individual kinocilium can be calculated based on measured values of its stiffness and kinocilium height. EI calculated in this way demonstrates a dependence on kinocilium height, increasing by ~6000 pN μm² as the height increases by ~17 μm (Fig. 6A). Regression analysis demonstrates a significant (P<0.0001) linear dependence of Euler EI on height.

FIGURE 6.

(A) Values of EI calculated using Euler–Bernoulli beam equation (Eqn. 1) from measured values of stiffness as a function of kinocilium height above the tallest stereocilium. Linear regression demonstrates Euler–Bernoulli EI is significantly dependent on kinocilium height. (B) Individual kinocilia EI calculated using, the Timoshenko beam equation (Eqn 2), measured values of stiffness, kinocilium height, and the curve-fit prediction of kGA=247 pN. A linear regression showed no significant relationship between the Timoshenko EI and kinocilium height. (C) The kGA of individual kinocilia calculated from, the Timoshenko beam equation (Eqn 2), measured values of stiffness, kinocilium height, and the Timoshenko EI curve-fit prediction of 10,400 pN·μm². A linear regression using bisquare weights was performed to reduce the impact of outliers. The regression showed that there is not a significant dependence of kGA on kinocilium height.

Using the Timoshenko beam theory, EI cannot be directly calculated from our measured values of stiffness and kinocilium length because of the additionally unknown kGA term. For this reason, the curve-fit predicted value of kGA was used in combination with the measured values to calculate the EI of individual kinocilia; conversely, the predicted EI was used to calculate the kGA of individual kinocilia (Fig. 6B, C). Using the curve-fit values introduces any error associated with the curve-fit parameters. This is probably the reason the Timoshenko EI values determined in this way demonstrate more scatter than the Euler EI calculations (cf. Fig. 6A and B). Linear regression analysis of these data shows no significant EI dependence on kinocilium height (P=0.29).

Determining kGA in this way resulted in several extreme outliers (Fig. 6C). We found that calculated values of kGA are extremely sensitive to variation in kinocilium height. In one case, a change in kinocilium height of only 0.2 mm produced a 700 pN change in the kGA calculation. The resolution of the digital images from which kinocilium height was measured is ~0.1 mm/pixel, so it is very likely that small errors in the measurements of kinocilia height are responsible for the extreme outliers and the increased variation in kGA observed for taller kinocilia. In addition, it is difficult to find tall kinocilia that lie perfectly in the focal plane, which may also decrease the accuracy of their height measurements. A linear regression was performed using the Bisquare weights robust method, which lessens the impact of outliers (MATLAB Curve Fitting Toolbox, MathWorks, Natick, MA, USA). The regression produces the line kGA=8.7L+132 (R²=0.72). The 95% confidence intervals for both the slope and intercept include zero, showing that they are not significantly different from zero and thus that kGA is not significantly dependent on height.

Effective values of Young’s modulus (E) and the shear modulus (G) in Table 1 were determined from the curve-fit values of EI and kGA, assuming a constant kinocilium diameter of 0.35 μm (Silber et al., 2004) and a shear correction factor for a circular cross-section (k) of 3/4 (Boresi and Schmidt, 2003). Based on the Timoshenko fit, the shear modulus is four orders of magnitude less than the Young’s modulus, indicating that kinocilia will experience shear deformation during bending.

3.2 Rotational stiffness of the insertion

The rotational stiffness was measured for a total of five kinocilia. Multiple trials were performed for each kinocilium. Except for three outliers from the second kinocilium, the measured rotational stiffness ranged from 86 to 240 pN·μm/rad. The mean rotational stiffness and standard deviation for all measurements is 177±47 pN μm/rad. A Kruskal–Wallis ranked sum test demonstrates that there is not a significant difference between the rotational stiffness of the five kinocilia measured (P>0.18). The three outlying measurements occurred for the same kinocilium, suggesting that there was something unusual about the arrangement of that particular bundle. For example, it is possible that the deflecting fiber was contacting a neighboring kinocilium during the three outlying trials, giving a rotational stiffness approximately two to three times greater than normal. The amount of kinocilium tip deflection due to rotation was 12% as determined using Eqn. 4.

4. DISCUSSION

4.1 Euler–Bernoulli vs. Timoshenko beam analysis

Curve-fitting experimental measurements of kinocilia shaft stiffness demonstrated that the Timoshenko beam is a more accurate model of the kinocilium than the Euler– Bernoulli model; R²-value is higher for the Timoshenko model (0.94 compared with 0.83). When EI is calculated for individual kinocilia directly from measured stiffness using the Euler–Bernoulli theory, the EI shows a linear dependence on height. This observed height dependence is not consistent with the Euler–Bernoulli theory. For a homogenous isotropic beam with a constant cross section, the EI is expected to be constant regardless of length. The observed EI length dependence indicates that the isotropic Euler beam is not an appropriate model for the kinocilium.

Similar results have been observed for MTs. Measurements of MTs have shown that EI is length dependent when modeled as a Euler-Bernoulli beam (Kurachi et al., 1995; Takasone et al., 2002; Pampaloni et al., 2006), and leads to underestimates of EI for shorter MTs (Li et al., 2006). A Timoshenko beam model of an MT predicts an EI length dependence that matches experimental results, provided the shear modulus is five to six orders of magnitude lower than the longitudinal Young’s modulus (Shi et al., 2008). Our results for the kinocilia differ from those of MTs in that a significant EI length dependence was not observed using the Timoshenko analysis. However, our results show that the effective shear modulus for kinocilia is only four orders of magnitude less than the effective Young’s modulus. Also, the MT analysis examined a much wider range of heights (100 μm) compared with the range of kinocilia heights examined (17.5 μm).

The curve-fit predicted value of EI is more than two times greater for the Timoshenko compared with the Euler–Bernoulli analysis (10,400 compared with 4700 pN·μm²). We conclude that the Euler–Bernoulli theory underestimates the EI of kinocilia because it does not account for shear deformation. For any shear-deformable beam, the impact of shear deformation during bending will be more evident in beams with shorter lengths. Because the Euler–Bernoulli theory does not account for shear, all the deflection at the tip of the kinocilium is attributed to bending, which results in an underestimate of EI for shorter kinocilia.

The deflection of the OL in the utricle is proportional to head acceleration. The kinocilia are the links that transfer OL deflection to the mechanotransducing portion of the hair cell bundle. Hair cell bundles in the turtle have a spectrum of bundle morphologies that systematically vary with epithelium location (Xue and Peterson, 2006). In the striolar region, the heights of tallest stereocilia are approximately the same as those of the kinocilia (10 μm). In addition, the height at which the kinocilia insert into the otoconial layer is also ~10 μm (Xue and Peterson, 2002). At the other end of the spectrum, the heights of the tallest stereocilia in the medial extrastriolar region are much less (3–4 μm), and the kinocilia insert into the otoconial layer at heights of 13–14 μm (Xue and Peterson, 2002). Thus, in the medial extrastriolar region, there is a ~10 μm portion of the kinocilium that can bend in response to otoconial layer deflections. Bending of the kinocilium in the extrastriola hair cells enable the hair cell bundles to respond to larger deflections of the OL.

We examined the bending deformation profile of the kinocilium in a medial extrastriolar bundle using a computational model in which the kinocilium was modeled as a cantilever beam (14 mm tall) and the stereocilia portion (4 mm tall) was represented by its deflection stiffness. The kinocilium was modeled as both Euler–Bernoulli and Timoshenko beams with an EI of 10,400 pN μm² (for both cases) and a kGA of 247 pN (for the Timoshenko case). A stiffness of the stereociliary bundle of 400 pN/μm was utilized for the bundle model. This computational model showed that a smaller percentage of the tip deflection was transferred to the stereocilia bundle when the kinocilium was modeled as a Timoshenko (2.8%) versus an Euler–Bernoulli (8.0%) beam. For example, a 3 μm deflection at the tip of the kinocilium produces a deflection at the height of the tallest stereocilia of 84 and 240 nm for the Timoshenko and Euler– Bernoulli models, respectively. The shear deformation present in the kinocilium reduces the deflection of the stereocilia bundle in this medial extrastriolar region. This reduced deflection of the stereocilia extends the operating rage of these bundles so they can transduce accelerations of a much broader range. These results suggest that the physiological importance of shear deformation in the kinocilium is to extend the range of OL deflections that the bundle can detect before saturating the hair cell transduction.

4.2 Comparison with literature

Although there are no direct kinocilium stiffness measurements in the literature, there are studies that quantify the EI of kinocilia and flagella with which our data can be compared. The only reported value of kinocilium EI was derived from the superficial neuromast in the lateral line of zebrafish (McHenry and vanNetten, 2007). The superficial neuromast is a structure that contains hair cells with tall kinocilia embedded in an elongated cupula. Its function is to detect water flow across the surface of the lateral line of fish. In this study, the neuromast’s entire cupular structure was modeled as a Euler–Bernoulli beam, and its EI was measured using a force-deflection technique. A linear relationship was observed between the cupula EI and the number of kinocilia per cupula. The slope of this linear relationship gave the EI of a single kinocilium as 2400 pN·μm². This value is less than the EI we measured for vestibular kinocilia of the same height. The majority of kinocilia heights in the neuromasts cupula were reported to range between 16 and 24 μm. Using the Euler–Bernoulli theory to directly calculate EI from stiffness measurements (Fig. 6A) yields EI values of 5500–10,000 pN·μm² for kinocilia within this same height range, which is approximately two to four times greater than calculated values for neuromast kinocilia. The difference from Timoshenko curve-fit prediction was approximately four times greater than the EI measured for the neuromast’s kinocilia. The discrepancy between EI measurements of vestibular and neuromast kinocilia may result from differences between the kinocilia of different neurosensory systems, differences between species, deformation of the cupula matrix, and/or differences between measurement techniques.

The literature also contains information regarding the EI of flagella, which can be compared with the kinocilia. Though kinocilia and flagella are not identical in composition (kinocilia lack inner dynein arms), both derive structural integrity from a 9+2 microtubular core. The echinoderm sperm flagellum provides a good comparison for kinocilia because they lack coarse fibers that are observed in other flagella (e.g. bull sperm flagellum), which likely influence the stiffness (Okuno and Hiramoto, 1979). Experimental measurements from echinoderm sperm flagella suggest that dynein cross-bridging greatly influences EI, presumably by preventing sliding between microtubule doublets. In the absence of ATP, demembranated flagella acquire a state of rigor attributed to stable dynein cross-bridges (Okuno, 1980). In this rigor state, the EI ranges from 11,000 to 15,000 pN·μm² (Okuno and Hiramoto, 1979; Okuno, 1980; Ishijima and Hiramoto, 1994), which overlaps the 95% confidence interval of kinocilia EI determined through the Timoshenko analysis (7200–13,600 pN·μm²). When exposed to Mg-ATP in addition to vanadate (NaVO³), a compound that disables the dynein motors, demembranated flagella assume a relaxed state and EI is greatly reduced to 600–900 pN·μm² (Okuno, 1980; Pelle et al., 2009). Comparing the EI of kinocilia with that of demembranated flagella in states of rigor and relaxation suggests that cross-bridging contributes greatly to the stiffness of the kinocilium. Because the inner dynein arms are absent in the kinocilium, results suggest that cross-bridging of the outer arms contributes to kinocilia stiffness.

A theoretical study determined the EI of a 9+2 axoneme based on detailed calculation of its moment of inertia (Schoutens, 1994). Assuming no connections between the microtubules, a lower EI value of 680 pN·μm² was determined, which is in remarkable agreement with measured values of the relaxed flagellum. For the case where the doublet and central microtubules are rigidly bound and therefore not permitted to slide, an EI of 74,000 pN·μm² was calculated. This upper value is greater than five times the EI of the kinocilium and the flagellum in a state of rigor, suggesting that even with cross-bridging the microtubules are not rigidly bound. These findings are additional evidence that microtubule sliding occurs during kinocilium bending and supports our conclusion that a beam theory, such as the Timoshenko theory, that incorporates shear deformation should be used to model the kinocilium.

List of Variables

A

Cross-sectional area

E

Young’s modulus

EI

Flexural rigidity

F

Applied force

G

Shear modulus

I

Second moment of inertia

k

shear correction factor

kGA

shear rigidity

L

effective kinocilium height or beam length/height

M

moment

Re

Reynolds number

s_k

stiffness of kinocilium

δ

Displacement

δ_E

deflection due to bending for an Euler–Bernoulli beam

δ_R

deflection due to rotation

δ_T

deflection due to bending and shear for a Timoshenko beam

θ

Angle of rotation

κ

Rotational stiffness

List of Abbreviations

DIC

Differential interference contrast

ES

Extrastriola

HBSS

Hanks’ balanced salt solution

MT

Microtubule

KS

Height of kinocilium divided by height of stereocilia

OL

Otoconial layer