Abstract
BACKGROUND AND PURPOSE:
Hemodynamics play an important role in the mechanisms that govern the initiation, growth, and possible rupture of intracranial aneurysms. The purpose of this study was to objectively characterize these dynamics, classify them, and connect them to aneurysm rupture.
MATERIALS AND METHODS:
Image-based computational fluid dynamic simulations were used to re-create the hemodynamics of 210 patient-specific intracranial aneurysm geometries. The hemodynamics were then classified according to their spatial complexity and temporal stability by using quantities derived from vortex core lines and proper orthogonal decomposition.
RESULTS:
The quantitative classification was compared with a previous qualitative classification performed by visual inspection. Receiver operating characteristic curves provided area-under-the-curve estimates for spatial complexity (0.905) and temporal stability (0.85) to show that the 2 classifications were in agreement. Statistically significant differences were observed in the quantities describing the hemodynamics of ruptured and unruptured intracranial aneurysms. Specifically, ruptured aneurysms had more complex and more unstable flow patterns than unruptured aneurysms. Spatial complexity was more strongly associated with rupture than temporal stability.
CONCLUSIONS:
Complex-unstable blood flow dynamics characterized by longer core line length and higher entropy could induce biologic processes that predispose an aneurysm for rupture.
Endothelial cells in blood vessel walls continuously sense and respond to hemodynamic wall shear stresses. Responses to normal wall shear stresses typically involve short-term vessel adaptation through vasodilation, or long-term, nonpathologic tissue remodeling. Under abnormal wall shear stresses, degenerative processes can take place in the vessel wall and lead to the pathologic formation, growth, and rupture of an intracranial aneurysm (IA).1–6 The coupling between the local (near wall) and global (far from wall) hemodynamics makes it possible to identify large-scale spatiotemporal blood flow patterns that result in dangerous wall shear stress conditions.
The connection between large-scale hemodynamics and aneurysm rupture was previously studied.7,8 Qualitative descriptions of spatial flow complexity and temporal flow stability were outlined and used to visually assess the hemodynamics of patient-specific IA geometries. The clinical history of each patient was used to correlate rupture events with spatially complex and temporally unstable flow patterns.
In this study, we use vortex core lines and proper orthogonal decomposition (POD) to quantify the large-scale hemodynamics of IAs. These methods are commonly used to visualize spatially complex fluid flows9,10 and create low-dimensional models of turbulence.11,12 However, their use in analyzing biofluids is novel. Quantitative representations of spatial flow complexity and temporal flow stability are outlined and used to provide a more objective hemodynamic classification. This quantitative approach also allows us to connect specific large-scale dynamical quantities to rupture.
Materials and Methods
Hemodynamic Modeling
Patient-specific geometries of cerebral aneurysms were reconstructed from 3D rotational angiography images.13 Digital subtraction imaging was performed by use of a constant injection of contrast agent at 24 mL/s for a 180° rotation in 8 seconds. Imaging was performed at 15 frames per second. Data from these images was transferred to a workstation (Phillips Healthcare, Best, The Netherlands) and reconstructed into 3D voxel data with the use of the standard proprietary software. 3D reconstructions were compared with views from the conventional angiogram to assess the completeness of the rendering. Cases with incomplete rendering or inadequate filling of the parent artery or the aneurysm were discarded.
Unstructured grids composed of tetrahedral elements were generated with a resolution of approximately 0.1 mm, resulting in grids of roughly 2–5 million elements. Vessel walls were assumed rigid, and blood flow was considered incompressible and Newtonian. Numeric solutions of the unsteady 3D Navier-Stokes equations were obtained under “typical” pulsatile flow conditions.14 The inlet boundaries of all models were located in the internal carotid artery, the vertebral artery, or the basilar artery.
Two cardiac cycles were simulated with a time-step size of 0.01 second for a heart rate of 60 bpm. The analysis in this work was based on 100 snapshots of the velocity vector field generated during the second cycle. IA necks were identified on the reconstructed vascular models and used to label the aneurysm and the parent artery.15 Subsequent flow characterizations were restricted to the aneurysm.
Qualitative Assessments of Spatial Complexity and Temporal Stability
The hemodynamics of 210 IA geometries (83 ruptured) were classified according to Cebral et al.7,16 Flows were classified according to visual assessments of spatial complexity and temporal stability, on the basis of the following qualitative criteria.
Flow Complexity.
“Simple” refers to flow patterns that consist of a single recirculation zone or vortex structure within the IA. “Complex” refers to flow patterns that exhibit flow divisions or separations within the aneurysm sac and contain more than one recirculation zone or vortex structure.
Flow Stability.
“Stable” refers to flow patterns that persist (do not move or change) during the cardiac cycle. “Unstable” refers to flow patterns in which the flow divisions and/or vortex structures move or are created or destroyed during the cardiac cycle.
Streamline plots were used to assess spatial flow complexity. Two examples are shown in Fig 1. Temporal flow stability was assessed by animating the streamline plots over the cardiac cycle.
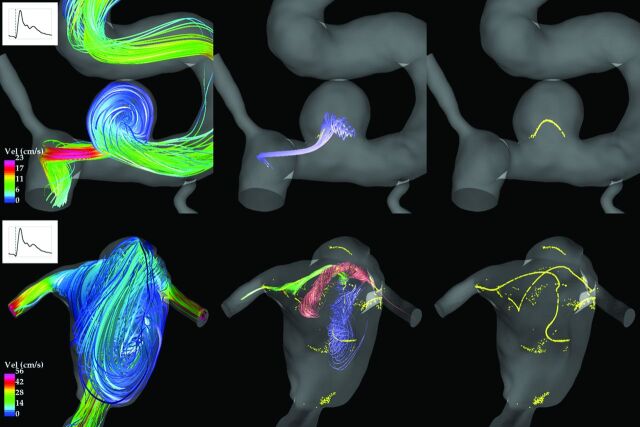
Fig 1.
Qualitative assessments of spatial flow complexity were made by visually inspecting streamline plots. Top left: This flow formed a single vortex and was classified as simple. Bottom left: This flow formed multiple vortices and was classified as complex. Center column: Streamline trajectories around the vortex core lines help to distinguish the individual vortices. Right column: Core lines are also known as vortex skeletons because they provide simplified representations of the large-scale flow structure.
Quantifying Spatial Flow Complexity
Many algorithms have been proposed to visualize vortices in datasets generated by computational fluid dynamic (CFD) simulations.10 Vortices were identified in this study by constructing vortex core lines: 1D sets that pass through centers of swirling flow. Vortex core lines provide a simple but accurate way of representing the spatial structures that underpin blood flow patterns in an aneurysm.
Vortex core lines were identified by use of a co-linearity condition between the instantaneous vorticity ω⃗ and velocity ν⃗ vectors. Mathematically, this condition can be expressed as
where ω⃗ = ∇ × ν⃗.
Our numeric algorithm consisted of a parallel search across multiple processors for tetrahedral mesh elements that satisfied Equation 1. Each processor formed and diagonalized the velocity gradient tensor in an element. If a pair of complex conjugate eigenvalues was found, the vorticity vector ω⃗ was formed to test whether Equation 1 was satisfied in the element. Reduced velocities17 were formed at the element nodes by subtracting the velocity component in the direction of the vorticity vector. Element faces that contained a point where the reduced velocity was zero were marked. If 2 or more faces of an element were found to contain a zero, a vortex core line passes through the element. A segment approximating this core line was constructed by connecting the points along the faces containing the zeros of the reduced velocity.
The vortex core line segments in each mesh element at the ith snapshot were summed up to produce a total length Li. Spatial complexity was quantified taking the average vortex core line length over the N snapshots
Complex flows (with multiple vortices) are expected to have longer average vortex core lines than simple flows (with a single vortex). Fig 1 shows the vortex core lines for a simple and a complex flow. The simple flow (top) contains a single core line with an average length 〈L〉 = 0.93, whereas the complex flow (bottom) contains multiple core lines with an average length 〈L〉 = 17.5.
Quantifying Temporal Flow Stability
Temporal flow stability is characterized by the creation, destruction, or motion of spatial flow patterns during the cardiac cycle. These patterns are defined by both vortex structures and flow divisions created by inflow jets. Temporal tracking of the vortex core lines was not used to quantify flow stability because of an alternate method that captures both flow divisions and recirculation zones.
The first step in quantifying the temporal flow stability was to separate the temporal dynamics from the spatial dynamics. This was achieved by expressing the velocity vector field ensemble as a linear combination of orthogonal, vector-based modes ϕ(x) and scalar coefficients α(tj) that govern their temporal evolution
where N is the number of snapshots in the ensemble. POD was used to generate the orthogonal set of basis modes ϕo(x).11 Although this decomposition may not be unique, we chose the POD procedure to form the basis set because it identifies fundamental spatial flow patterns that, on average, capture more of the fluid kinetic energy per mode than any other basis set.
The POD basis was computed by use of a snapshot method that builds an N×N 2-point velocity correlation tensor.18 When diagonalized, the correlation tensor forms an energy matrix η with energy eigenvalues λi running along the diagonal in decreasing order. Each mode ϕ(x) is associated with energy eigenvalue λi that can be recovered from the mean squared value of the corresponding temporal coefficients λi = (αi(tj),αi(tj))/N, where (.,.) is the Euclidean inner product. The trace of the energy matrix Tr(η) = is a measure of the total fluid kinetic energy in the aneurysm. The relative energy Pi = quantifies the energy content of the ith mode, whereas the entropy
quantifies the average energy distributed across the N modes. It is used here to measure the temporal stability of hemodynamic flows. Entropy is maximized when the energy is evenly spread over the modes and minimized when it is concentrated in a single mode.
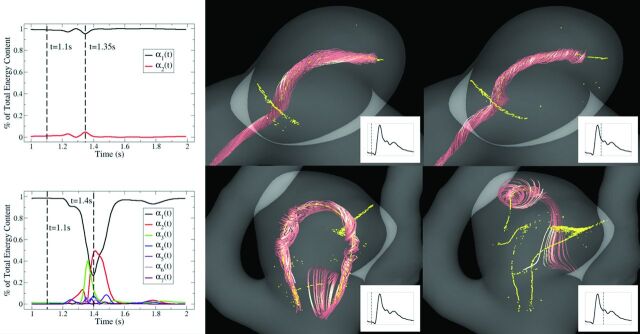
An example is provided in Fig 2. The first column contains plots of the temporal coefficients αi(tj) for a stable (top) and unstable (bottom) flow. The temporal coefficients were scaled to plot the fractional energy content contained in each corresponding basis mode. For visualization purposes, only the temporal coefficients accounting for 99% of the total energy are plotted. The vortex core lines and a few neighboring streamlines are shown in the center and right hand columns at 2 different points in the cardiac cycle. Two coefficients are required to meet the 99% energy threshold for the stable flow while 7 coefficients are required for the unstable flow.
Fig 2.
The temporal coefficients accounting for 99% of the total energy are plotted for stable (top) and unstable (bottom) flows. Vortex core lines (yellow) and neighboring streamline trajectories (red) are used to visualize the spatial structure of the flow at 2 instants during the cardiac cycle. The stable flow retains its spatial structure during the cardiac cycle. Very little energy is transferred between the temporal coefficients resulting in an entropy of S = 0.0713. The unstable flow undergoes large fluctuations and changes its spatial structure. Large amounts of energy are transferred between the temporal coefficients resulting in an entropy of S = 0.674.
The value of the entropy for the stable flow is S = 0.0713. Most of the energy during the cardiac cycle is concentrated in the first spatial mode ϕ1(x). No flow structures are created, destroyed, or undergo significant motion. The value of the entropy for the unstable flow is S = 0.674, approximately 9.5 times greater than the stable flow. Large amounts of energy are transferred from α1(t) to the remaining 6 coefficients. Significant changes are also observed to occur in the spatial organization of the flow during the cardiac cycle.
Results
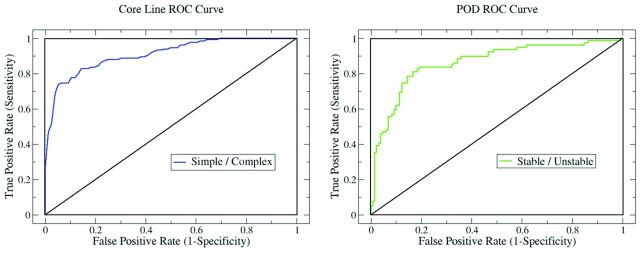
The spatial flow complexity and temporal flow stability in all 210 IA geometries were quantified by use of the average core line length 〈L〉 and entropy S. Flow classification was based on discrimination thresholds for each of the 2 variables. True- and false-positive rates were computed by sweeping over the discrimination thresholds and comparing the quantitative classifications to the qualitative classifications. The results are summarized by the 2 receiver operating characteristic (ROC) curves in Fig 3. The accuracy of the qualitative classification was measured by integrating the ROC curves. The resulting areas under the curve (AUCs) are presented in Table 1. An AUC of 1 indicates exact agreement for all cases. The AUC is 0.905 for spatial complexity and 0.86 for temporal stability. These results are considered “excellent” and “very good.”19
Fig 3.
ROC curves summarizing the ability of our flow variables to correctly identify spatially simple (left) and temporally stable (right) hemodynamic flows in our aneurysm data base. The ROC curves were generated by comparing the quantitative classification against qualitative classification.
Table 1:
Summary and performance statistics of the variables used to quantify spatial flow complexity and temporal flow stability
| Category | Mean Core Line Length | Category | Mean Entropy |
|---|---|---|---|
| Simple | 0.4564 | Stable | 0.1224 |
| Complex | 3.2094 | Unstable | 0.2458 |
| P value | <2.12 × 10−22 | P value | <8.4 × 10−19 |
| AUC | 0.905 | AUC | 0.86 |
Table 1 also compares the variable means for each flow group as established by the qualitative classification. The P values were generated by use of the Wilcoxon rank sum test. The mean core line length is higher in the complex flow group than in the simple flow group. Likewise, the mean entropy is higher in the unstable flow group than in the stable flow group. The differences between the means are statistically significant (P < .05).
The same statistical comparison was applied to the group means of the ruptured and unruptured IAs. These results, presented in Table 2, indicate that ruptured IAs tend to have larger core line lengths (ie, more complex spatial flow patterns) and larger entropies (ie, more temporally unstable flow patterns) than unruptured IAs. Again, the differences between the means are statistically significant.
Table 2:
Summary and performance statistics of the variables used to quantify spatial flow complexity and temporal flow stability in ruptured and unruptured aneurysms
| Category | Mean Core Line Length | Mean Entropy | Combined |
|---|---|---|---|
| Unruptured | 1.4551 | 0.181 | – |
| Ruptured | 3.407 | 0.2275 | – |
| P value | <7.6 × 10−8 | <0.0002 | – |
| AUC | 0.72 | 0.648 | 0.716 |
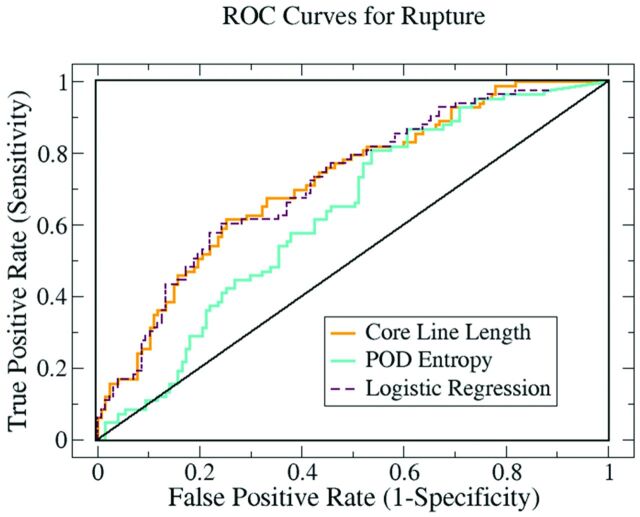
Rupture prediction was based on the ability to quantitatively discriminate between ruptured and unruptured aneurysms. The true- and false-positive rates were established by comparing the predicted state of rupture to the clinical records. A third variable, based on a logistic regression of spatial complexity and temporal stability, was also developed and tested for enhanced predictive power. The 3 ROC curves for rupture are shown in Fig 4. The corresponding AUCs are reported in Table 2. The average vortex core line length had the highest AUC, suggesting that spatial complexity may play a more important role than temporal stability in the rupture of IAs.
Fig 4.
ROC curves summarizing the ability of our flow variables to discriminate between ruptured and unruptured aneurysms. The average core line length 〈L〉 measured the flow complexity and the entropy S measured flow stability. A logistic regression was used to combine these 2 variables into a third variable that was tested for enhanced predictive power.
Discussion
The results presented in this report confirm and extend previous results that compared qualitative flow characteristics in ruptured and unruptured IAs. Important spatiotemporal flow features (ie, flow complexity and flow stability) previously identified by visual inspection were successfully extracted from the velocity vector fields by using objective quantitative methods based on vortex core lines and POD. Quantitative results confirmed previous observations that ruptured aneurysms tend to have complex-unstable flows and that unruptured aneurysms tend to have simple-stable flows. The results also indicated that flow complexity is a better discriminant of rupture state than flow stability.
The effect of rupture on IA geometries was previously studied.20 The results indicated small changes in 20% of the IAs and no changes in 80% of the IAs between the pre-ruptured and post-ruptured state. The small changes found in 20% of the ruptured IAs' geometry were assumed to have a negligible impact on the large-scale hemodynamic properties.
Isosurface methods have been used to visualize vortices in aortic aneurysms.21,22 However, the frequent need for a user supplied threshold to construct these surfaces led us to use line-type methods for visualizing and analyzing the spatial structure of hemodynamic flows.23–26 Irregular aneurysm geometries make the task of identifying a “characteristic length” difficult and subjective. As a result, we used the unnormalized length.
Our metric for spatial complexity is limited in the sense that it does not measure the number of discrete vortices formed within the aneurysm or account for their topologic structure. Other measures of spatial complexity on the basis of a more detailed analysis of the core line structure (geometry, connectivity, or topology) are also possible and may provide a more accurate representation of the original qualitative criteria.
Discontinuities between neighboring core line segments were observed because the velocity gradient is piecewise linear over the computational domain. Segments oriented end-to-end created well-defined vortex core lines. Segments that were not oriented end-to-end often formed 2D structures that resembled vortex sheets. Vortices smaller than the mesh elements are unable to be resolved and were ignored in our study. Isolated segments in the domain that were not part of any visible fluid structure could be the result of noise produced by the computation of numeric derivatives.
Mesh sensitivity studies were not performed. The core lines extracted and analyzed in this work were consistent with the degree of approximation of the CFD simulations. Mesh refinement should capture smaller vortices and improve the linear approximation used for the vortex core segments. It should also reduce the gaps in vortex segments between neighboring elements.
The AUC values in Table 2 represent the probability that a ruptured aneurysm randomly selected from the data base will be ranked as “higher risk” than a randomly selected unruptured aneurysm. They indicate that the logistic regression variable performed about the same as the spatial complexity variable. This is an interesting result that further highlights the fact that most spatially complex flows are unstable and that most simple flows are stable. We attribute the lack of improvement in the AUC of the logistic variable to this correlation. One of the limitations of the rupture prediction study was the lack of long-term clinical data. As a result, we would like to point out that caution must be used when interpreting the low values of the AUCs found in Table 2. Artificially high false-positive rates can be generated by IAs that were quantitatively classified as “high risk,” but that have not yet undergone a rupture. A study with an extended clinical history would be required to make a more accurate assessment of rupture prediction on the basis of these variables.
CFD calculations were carried out under pulsatile flow condition at 2 heart rates (60 bpm and 100 bpm). For each heart rate, the corresponding flow waveforms were prescribed from measurements in the cerebral arteries reported in the literature.27 Under these different flow conditions, the vortex core line lengths were not significantly different, and the statistical results were largely unaffected (within a 1% difference). This suggests that the large-scale hemodynamics are independent of relatively small variations in the physiologic conditions.
Conclusions
The observations and methods described in this study can better help us to understand the underlying mechanisms that govern IA initiation, evolution, and rupture. Our quantitative approach for assessing spatial flow complexity and temporal flow stability was consistent with the assessments made using well-defined qualitative approach. Statistically significant differences were found in the variables quantifying the hemodynamics of ruptured and unruptured aneurysms. Complex-unstable flow dynamics were more commonly observed in ruptured aneurysms, whereas simple-stable flow dynamics were more commonly observed in unruptured aneurysms. Spatial complexity was found to be more strongly associated with rupture than temporal stability. This result indicates that complex flows producing high spatial gradients of the wall shear stress vector may play a more fundamental role in predisposing the aneurysm wall for rupture than unstable flows producing temporal oscillations of the wall shear stress vector.
ABBREVIATIONS:
- IA
intracranial aneurysm
- POD
proper orthogonal decomposition
- CFD
computational fluid dynamic
- ROC
receiver operating characteristic
- AUC
area under the curve
Footnotes
Disclosures: Greg Byrne—RELATED: Grant: NIH,* Comments: Research grant; Support for Travel to Meetings for the Study or Other Purposes: George Mason University, Comments: GMU student travel fund for the March APS conference 2012. Fernando Mut—RELATED: Grant: NIH.* Juan Cebral—RELATED: Grant: NIH,* Comments: Research grant; UNRELATED: Consultancy: Cardiatis; Grants/Grants Pending: NIH,* Philips* (*money paid to institution).
This work was supported by the National Institutes of Health, grant No. R01NS059063.
References
- 1. Sforza D, Putman CM, Cebral JR. Hemodynamics of cerebral aneurysms. Annu Rev Fluid Mech 2009;41:91–107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Chalouhi N, Ali MS, Jabbour PM, et al. Biology of intracranial aneurysms: role of inflammation. J Cereb Blood Flow Metab 2012;32:1659–76 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Penn DL, Komotar RJ, Connolly ES. Hemodynamic mechanisms underlying cerebral aneurysm pathogenesis. J Clin Neurosci 2011;18:1435–38 [DOI] [PubMed] [Google Scholar]
- 4. Kadirvel R, Ding YH, Dai D, et al. The influence of hemodynamic forces on biomarkers in the walls of elastase-induced aneurysms in rabbits. Neuroradiology 2007;49:1041–53 [DOI] [PubMed] [Google Scholar]
- 5. Hashimoto T, Meng H, Young WL. Intracranial aneurysms: links among inflammation, hemodynamics and vascular remodeling. Neurol Res 2006;28:372–80 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Frosen J, Tulamo R, Paetau A, et al. Saccular intracranial aneurysm: pathology and mechanisms. Acta Neuropathol 2012;123:773–86 [DOI] [PubMed] [Google Scholar]
- 7. Cebral JR, Mut F, Weir J, et al. Association of hemodynamic characteristics and cerebral aneurysm rupture. AJNR Am J Neuroradiol 2011;32:264–70 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Cebral JR, Castro MA, Burgess JE, et al. Characterization of cerebral aneurysm for assessing risk of rupture using patient-specific computational hemodynamics models. AJNR Am J Neuroradiol 2005;26:2550–59 [PMC free article] [PubMed] [Google Scholar]
- 9. Roth M, Peikert R. Flow visualization for turbomachinery design. In: 7th IEEE Visualization Conference (VIS'96). San Francisco: IEEE Computer Society Press; 1996:381–84 [Google Scholar]
- 10. Jiang M, Machiraju R, Thompson DS. Detection and visualization of vortices. In, Hansen CD, Johnson CR, ed: Visualization Handbook. Burlington, Massachusetts: Elsevier Butterworth-Heinemann; 2005:287–301 [Google Scholar]
- 11. Holmes P, Lumley J, Berkooz G. Turbulence, Coherent Structures, Dynamical Systems and Symmetry. Cambridge, UK: Cambridge University Press; 1996 [Google Scholar]
- 12. Aubry N, Guyonnet R, Lima R. Spatiotemporal analysis of complex signals: theory and applications. J Stat Phys 1991;64:683–739 [Google Scholar]
- 13. Cebral JR, Castro MA, Appanaboyina S, et al. Efficient pipeline for image-based patient-specific analysis of cerebral aneurysm hemodynamics: technique and sensitivity. IEEE Trans Med Imaging 2005;24:457–67 [DOI] [PubMed] [Google Scholar]
- 14. Ford MD, Alperin N, Lee SH, et al. Characterization of volumetric flow rate waveforms in the normal internal carotid and vertebral arteries. Physiol Meas 2005;26:477–88 [DOI] [PubMed] [Google Scholar]
- 15. Mut F, Löhner R, Chien A, et al. Computational hemodynamics framework for the analysis of cerebral aneurysms. Int J Numer Method Biomed Eng 2011;27:822–39 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Cebral JR, Mut F, Weir J, et al. Quantitative characterization of the hemodynamic environment in ruptured and unruptured brain aneurysms. AJNR Am J Neuroradiol 2011;32:145–51 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Sujudi D, Haimes R. Identification of Swirling Flow in 3D Vector Fields. Technical Report, Department of Aeronautics and Astronautics, MIT, Cambridge, Massachusetts: 1995 [Google Scholar]
- 18. Sirovich L. Turbulence and the dynamics of coherent structures: I, coherent structures; II, symmetry and transformations; III, dynamics and scaling. Quart Appl Mathematics 1987;45:561–90 [Google Scholar]
- 19. Zweig MH, Campbell G. Receiver-operating characteristic (ROC) plots: a fundamental evaluation tool in clinical medicine. Clin Chem 1993;39:561–77 [PubMed] [Google Scholar]
- 20. Ishikawa T, Nakayama N, Yoshimoto T, et al. How does spontaneous hemostasis occur in ruptured cerebral aneurysms? Preliminary investigation on 247 clipping surgeries. Surg Neurol 2006;66:269–75 [DOI] [PubMed] [Google Scholar]
- 21. Biasetti J, Hussain F, Gasser TC. Blood flow and coherent vortices in the normal and aneurysmatic aortas: a fluid dynamical approach to intra-luminal thrombus formation. J R Soc Interface 2011;8:1449–61 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Arzani A, Shadden SC. Characterization of the transport topology in patient-specific abdominal aortic aneurysm models. Phys Fluids 2012;24:81901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Byrne G, Mut F, Cebral JR. Vortex Coreline Detetction for the Analysis of Blood Flow Patterns in Cerebral Aneurysms. In: 2nd International Conference on Mathematical and Computational Biomedical Engineering, CMBE. 2011, Washington, DC. 2011 [Google Scholar]
- 24. Byrne G, Mut F, Cebral JR. Using Vortex Detection to Characterize Aneurismal Flow Activity. In: Proceedings of the ASME 2012 Summer Bioengineering Conference, Fajardo, Puerto Rico. 2012 [Google Scholar]
- 25. Raschi M, Mut F, Byrne G, et al. CFD and PIV analysis of hemodynamics in a growing intracranial aneurysm. Int J Numer Method Biomed Eng 2012;28:214–28 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Gambaruto AM, Joao AJ. Flow structures in cerebral aneurysms. Comp Fluids 2012;65:56–65 [Google Scholar]
- 27. Jiang J, Strother CM. Computational fluid dynamics simulations of intracranial aneurysms at varying heart rates: a “patient-specific” study. J Biomech Eng 2009;131:91–101 [DOI] [PubMed] [Google Scholar]