PROBABILISTIC PREDICTION OF NEUROLOGICAL DISORDERS WITH A STATISTICAL ASSESSMENT OF NEUROIMAGING DATA MODALITIES

Abstract

For many neurological disorders, prediction of disease state is an important clinical aim. Neuroimaging provides detailed information about brain structure and function from which such predictions may be statistically derived. A multinomial logit model with Gaussian process priors is proposed to: (i) predict disease state based on whole-brain neuroimaging data and (ii) analyze the relative informativeness of different image modalities and brain regions. Advanced Markov chain Monte Carlo methods are employed to perform posterior inference over the model. This paper reports a statistical assessment of multiple neuroimaging modalities applied to the discrimination of three Parkinsonian neurological disorders from one another and healthy controls, showing promising predictive performance of disease states when compared to nonprobabilistic classifiers based on multiple modalities. The statistical analysis also quantifies the relative importance of different neuroimaging measures and brain regions in discriminating between these diseases and suggests that for prediction there is little benefit in acquiring multiple neuroimaging sequences. Finally, the predictive capability of different brain regions is found to be in accordance with the regional pathology of the diseases as reported in the clinical literature.

1. Introduction

For many neurological and psychiatric disorders, making a definitive diagnosis and predicting clinical outcome are complex and difficult problems. Difficulties arise due to many factors, including overlapping symptom profiles, comorbidities in clinical populations and individual variation in disease phenotype or disease course. In addition, for many neurological disorders the diagnosis can only be confirmed via analysis of brain tissue post-mortem. Thus, technological advances that improve the efficiency or accuracy of clinical assessments hold the potential to improve mainstream clinical practice and to provide more cost-effective and personalized approaches to treatment.

In this regard, combining data obtained from neuroimaging measures with statistical discriminant analysis has recently attracted substantial interest among the neuroimaging community [e.g., Klöppel et al. (2008), Marquand et al. (2008)]. Neuroimaging data present particular statistical challenges in that they are often extremely high dimensional (in the order of hundreds of thousands to millions of variates) with very few samples (tens to hundreds). Further, multiple imaging sequences may be acquired for each participant, each aiming to measure different properties of brain tissue. Each sequence may in turn give rise to several different measurements. In the present work, we will use the term “modality” to describe such a set of measurements. In response to those challenges, most attempts to predict disease state from neuroimaging data employ the Support Vector Machine [SVM; see, e.g., Schölkopf and Smola (2001)] based on information obtained from a single modality. Such an approach, however, is not able, in any statistical manner, to fully address questions related to the importance of different modalities. As we will show in the experimental section of this paper, even the multi-modality SVM-based classifier proposed in Rakotomamonjy et al. (2008) lacks a systematic way of characterizing the uncertainty in the predictions and in the assessment of the relative importance of different modalities.

In this work, we adopt a multinomial logit model based on Gaussian process (GP) priors [Williams and Barber (1998)] as a probabilistic prediction method that provides the means to incorporate measures from different imaging modalities. We apply this approach to discriminate between three relatively common neurological disorders of the motor system based on data modalities derived from three distinct neuroimaging sequences. In this application we aim to characterize uncertainty without resorting to potentially inaccurate deterministic approximations to the integrals involved in the inference process. Therefore, we propose to employ Markov chain Monte Carlo (MCMC) methods to estimate the analytically intractable integrals, as they provide guarantees of asymptotic convergence to the correct results. The particular structure of the model and the large number of variables involved, however, make the use of MCMC techniques seriously challenging [Filippone, Zhong and Girolami (2012), Murray and Adams (2010)]. In this work, we make use of reparametrization techniques [Yu and Meng (2011)] and state-of-the-art sampling methods based on the geometry of the underlying statistical model [Girolami and Calderhead (2011)] to achieve efficient sampling.

The remainder of the paper is structured as follows: In Section 2 we describe the motivating application of statistical discrimination of movement disorders from brain images. In Section 3 we introduce the multinomial logit model with GP priors and in Section 4 we present the associated MCMC methodology. In Section 5 we report a comparison of MCMC strategies applied to our brain imaging data and in Section 6 we investigate the predictive ability of different data sources and brain regions, comparing the results with a nonprobabilistic multi-modality classifier based on SVMs. Section 7 shows how predictive probabilities can be used to refine predictions, and Section 8 draws conclusions commenting on the questions that this methodology addresses in this particular application.

2. Discriminating among Parkinsonian disorders

2.1. Introduction to the disorders

For this application, we aim to discriminate between healthy control subjects (HCs) and subjects with either multiple system atrophy (MSA), progressive supranuclear palsy (PSP) or idiopathic Parkinson’s disease (IPD), which are behaviorally diagnosed motor conditions collectively referred to as “Parkinsonian disorders.” MSA, PSP and IPD can be difficult to distinguish clinically in the early stages [Litvan et al. (2003)] and carry a high rate of misdiagnosis, even though early diagnosis is important in predicting clinical outcome and formulating a treatment strategy [Seppi (2007)]. For example, MSA and PSP have a much more rapid disease progression relative to IPD and carry a shorter life expectancy after diagnosis. Further, IPD responds relatively well to pharmacotherapy, while MSA and PSP are both associated with a modest to poor response. Thus, automated diagnostic tools to discriminate between the disorders is of clinical relevance where they may help to reduce the rate of misdiagnosis and ultimately lead to more favorable outcomes for patients.

2.2. The clinical problem of discriminating among Parkinsonian disorders

In this study we employed magnetic resonance imaging (MRI), as it is noninvasive, widely available and, unlike alternative measures such as positron emission tomography, does not involve exposing subjects to ionizing radiation. A detailed discussion of the imaging modalities employed in this study is beyond the scope of the present work, but see Farrall (2006) for an overview. Briefly, the different imaging modalities employed here measure different properties of brain tissue: T1-weighted imaging is well-suited to visualizing anatomical structure, while T2-weighted structural imaging often shows focal tissue abnormalities more clearly. Diffusion tensor imaging (DTI) does not measure brain structure directly, but instead measures the diffusion of water molecules along fibre tracts in the brain, thus quantifying the integrity of the fibre bundles that connect different brain regions [see Basser and Jones (2002) for an introduction to DTI].

A review of the neuropathology of the Parkinsonian disorders is also beyond the scope of this work, but briefly we note that MSA and PSP are characterized by distinct cellular pathologies and subsequent degeneration of widespread and partially overlapping brain regions. For MSA, affected regions include the brainstem, basal ganglia (e.g., caudate and putamen), cerebellum and cerebral cortex [Wenning et al. (1997)]. Note that MSA is sometimes subdivided into Parkinsonian and cerebellar subtypes (MSA-P and MSA-C, resp.), but for the present work we included both variants in the same class. For PSP the brainstem and basal ganglia both undergo severe degeneration [Hauw et al. (1994)], although cortical areas are also affected. In contrast, IPD is characterized in the early stages by relatively focal pathology in the substantia nigra (a pair of small nuclei in the brainstem), which is difficult to detect using conventional structural MRI where the scans of IPD patients can appear effectively normal [Seppi (2007)].

There is, however, some evidence that changes in IPD can be detected using DTI [see, e.g., Yoshikawa et al. (2004)]. Thus, it is of interest to investigate which data modalities are best suited to discriminating between MSA, PSP, IPD and HCs, which has practical implications in planning future diagnostic studies: MRI scans are costly, so it is desirable to know which data modalities provide the best discrimination of the diagnostic groups and which scans can be omitted from a scanning protocol to avoid wasting money acquiring scans that do not provide additional predictive value.

2.3. State of the art in diagnosis and prediction

We are aware of only one existing study that employed a discriminant approach to diagnose these diseases based on whole-brain neuroimaging measures [Focke et al. (2011)]. This study employed binary SVM classifiers to discriminate MSA-P from IPD, PSP and HCs based on a similar sample to the present study. The authors reported that (i) PSP could be accurately discriminated from IPD, (ii) that separation of the MSA-P group from IPS and from controls was only marginally better than chance and (iii) that no separation of the IPD group from HCs was possible. The authors did not attempt to combine the distinct binary classifiers to provide multi-class predictions.

The problem of combining different modalities in classification models can be seen as a Multiple Kernel Learning (MKL) problem [Lanckriet et al. (2004), Sonnenburg et al. (2006)]. A recent MKL approach to classification referred to as “simpleMKL” has been proposed by Rakotomamonjy et al. (2008). SimpleMKL is based on a SVM learning algorithm and shows good performance relative to other MKL approaches; for this reason we will consider it as a baseline against which we aim to compare the performance of the proposed approach.

2.4. Data acquisition and preprocessing

Eighteen subjects with MSA, 16 subjects with PSP, 14 subjects with IPD (all in mid-disease stage) and 14 HCs were recruited according to clinical and experimental criteria described in Blain et al. (2006). For each subject, a T2-weighted structural image, a T1-weighted spoiled gradient recalled (SPGR) structural image and a DTI sequence were acquired and preprocessed (see the Appendix for the details on acquisition).

All images were screened by a trained radiologist and were examined for gross structural abnormalities, including white matter abnormalities. Diffusion tensor images were then preprocessed according to an in-house protocol and were summarized by measures of fractional anisotropy (FA) and mean diffusivity (MD) at every brain location [see Basser and Jones (2002)]. SPGR images were preprocessed using the DARTEL toolbox included in the SPM software package (www.fil.ion.ucl.ac.uk/spm), which involved nonlinear registration to a common reference space, segmentation into grey matter (GM), white matter (WM) and cerebrospinal fluid (CSF) in addition to smoothing with a 6mm isotropic Gaussian kernel.

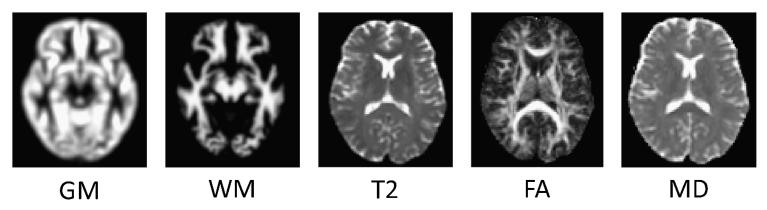
For this analysis, whole-brain (unmodulated) GM and WM images derived from the SPGR scans, the T2 structural images plus the FA and MD images derived from the DTI sequence were used for classification, yielding a total of five distinct modalities for each subject. For illustrative purposes, an example of each type of image after preprocessing is provided in Figure 1.

Fig. 1.

Examples of each data source (after preprocessing), taken from the same slice and subject.

3. Multinomial logit model with GP priors

The aim of this study is twofold: the first is to reliably estimate the probability that new subjects have MSA, PSP, IPD or none of them, and the second is to assess the importance of different sources of information in the discrimination among these diseases. We cast this problem as a multi-modality classification problem, whereby we associate class labels corresponding to MSA, PSP, IPD and HCs to n subjects described by s = 1, … , q distinct representations (i.e., modalities), each defined by d_s covariates.

Denote each modality by an n × d_s matrix X_s. Let {y₁, … , y_n} be the set of observed labels for the n subjects. Assume a 1-of-m coding scheme (m = 4 in our application), whereby the membership of subject i to class c is represented by a vector y_i of length m where (y_i)_r = 1 if r = c and zero otherwise.

In this work we propose a probabilistic multinomial logit classification model based on Gaussian process (GP) priors to model the probability π_ic := p(y_ic = 1∣X₁, … , X_q) that subject i belongs to class c. The multinomial logit model assumes that the class labels y_i are conditionally independent given a set of m latent functions f_c that model the π_ic using the following transformation:

$${\pi }_{\mathit{ic}}=\frac{{\left[\exp \right({\mathbf{f}}_c\left)\right]}_i}{{\left[{\Sigma }_{r=1}^m\exp \right({\mathbf{f}}_r\left)\right]}_i}.$$ (1)

We assume that the latent variables f_c are independent across classes and drawn from GPs, so that ${\mathbf{f}}_c~\mathcal{N}(0,K_c)$. The assumption of independence between variables belonging to different classes can be relaxed in cases where there is prior knowledge about that. Note that the assumption of conditional independence of the class labels given the latent variables is not restrictive, as the prior over the latent variables imposes a covariance structure that is reflected on the class labels.

In order to assess the importance of each modality in the classification task, we propose to model each covariance K_c as a linear combination of covariances obtained from the q modalities, say, C_s with s = 1, … , q. We constrain the linear combination of covariance functions to be positive definite by modeling $K_c={\Sigma }_{s=1}^q\exp \left[{\theta }_{\mathit{cs}}\right]C_s$. Note that given the additivity of the linear model under the GP, it is possible to interpret this model as one where each latent function is a linear combination of basis functions with covariances C_s. Since the data modalities employed in this study potentially have different numbers of features which are are also scaled differently, we employed two simple operations to normalize the images prior to classification. First we divided each feature vector by its Euclidean norm, then standardized each feature to have zero mean and unit variance across all scans. We then chose a covariance for each modality to be $C_s=X_s{X}_s^T$ . Given that the modalities are normalized and that the covariances are linear in the data sources X_s, the inference of the corresponding weights allows to draw conclusions on their relative importance in the classification task. In this work we imposed Gamma priors on the weights exp[θ_cs], but for the sake of completeness and to rule out any dependencies of the results from the parametrization of the weights and the specification of the prior, we have also explored the possibility to use a Dirichlet prior inferring the concentration parameter; we will discuss this in more detail in the sections reporting the results.

We note here that the representation in equation (1) is redundant, as class probabilities are defined up to a scaling factor of the exponential of the latent variables. Choosing a model in which m – 1 latent functions are modeled and one is fixed would remove any redundancy, but, as described in Neal (1999), “forcing the latent values for one of the classes to be zero would introduce an arbitrary asymmetry into the prior.” Also, modeling m–1 latent functions would not allow a direct interpretation of the importance of different modalities given by the hyper-parameters.

We used all features to perform the classification, because in our experience feature selection does not provide a benefit in terms of increasing the accuracy of classification models for neuroimaging data but does increase their complexity. In line with this, a recent comparative analysis of alternative data preprocessing methods on a publicly available neuroimaging data set indicated that feature selection did not improve classification performance but did substantially increase the computation time [Cuingnet et al. (2011)].

We now discuss how to make inference for the proposed model. In order to keep the notation uncluttered, we will drop the explicit conditioning on X_s. We will denote by f the (nc) × 1 vector obtained by concatenating the class specific latent functions f_c, and similarly by y and π the vectors obtained by concatenating the vectors y_·c and π_·c. Finally, let the m × q matrix θ denote the set of hyper-parameters, and K be the matrix obtained by block-concatenating the covariance matrices K_c.

Given the likelihood for the observed labels, the prior over the latent functions and the prior over the hyper-parameters, we can write the log-joint density as

$$\mathcal{L}=\log \left[p\right(\mathbf{y},\mathbf{f},\theta \left)\right]=\log \left[p\right(\mathbf{y}\mid \mathbf{f}\left)\right]+\log \left[p\right(\mathbf{f}\mid \theta \left)\right]+\log \left[p\right(\theta \left)\right].$$

One of the goals of our analysis is to obtain predictive distributions for new subjects. Let y_* denote the corresponding label; the predictive density is obtained by marginalizing out parameters and latent functions via

$$p({\mathbf{y}}_{\ast }\mid \mathbf{y})=\int p({\mathbf{y}}_{\ast }\mid {\mathbf{f}}_{\ast })p({\mathbf{f}}_{\ast }\mid \mathbf{f},\theta )p(\mathbf{f},\theta \mid \mathbf{y})d{\mathbf{f}}_{\ast }d\mathbf{f}d\theta .$$

In this work, we propose to estimate this integral by obtaining posterior samples from p(f, θ∣y) using MCMC methods. The Appendix gives details of how Monte-Carlo estimates of this predictive distribution may be obtained. Obtaining samples from p(f, θ∣y) is complex because of the structure of the model that makes f and θ strongly coupled a posteriori. Also, there is no closed form for updating f and θ using a standard Gibbs sampler, so samplers based on an accept/reject mechanism need to be employed (Metropolis-within-Gibbs samplers) with the effect of reducing efficiency. This motivates the use of efficient samplers to alleviate this problem as discussed next.

4. MCMC sampling strategies

4.1. Riemann manifold MCMC methods

The proposed model comprises a set of m latent functions, each of which has dimension n, and a set of q × m weights. Given the large number of strongly correlated variables involved in the model, we need to employ statistically efficient sampling methods to characterize the posterior distribution p(f, θ∣y).

Recently, a set of novel Monte Carlo methods for efficient posterior sampling has been proposed in Girolami and Calderhead (2011) which provides promising capability for challenging and high-dimensional problems such as the one considered in this paper. In most sampling methods (with the exception of Gibbs sampling) it is crucial to tune any parameters of the proposal distributions in order to avoid strong dependency within the chain or the possibility that the chain does not move at all. As the dimensionality increases, this becomes a hugely challenging issue, given that several parameters need to be tuned and are crucial to the effectiveness of the sampler.

The sampling methods developed in Girolami and Calderhead (2011) aim at providing a systematic way of designing such proposals by exploiting the differential geometry of the underlying statistical model. The main quantity in this differential geometric approach to MCMC is the local Riemannian metric tensor which is the expected Fisher Information (FI) that defines the statistical manifold; see Girolami and Calderhead (2011) for full details. The intuition behind manifold MCMC methods is that the statistical manifold provides a structure that is suitable for making efficient proposals based on Langevin diffusion or Hamiltonian dynamics. In the case of the sampling of f using RM–HMC, let G_f be the metric tensor computed as the FI for the statistical manifold of p(y∣f) plus the negative Hessian of p(f∣θ) (see the Appendix for further details). Introducing an auxiliary momentum variable $\mathbf{p}~\mathcal{N}(\mathbf{p}\mid 0,G_{\mathbf{f}})$ as in HMC, RM–HMC can be derived by solving the dynamics associated with the Hamiltonian:

$$H(\mathbf{f},\mathbf{p})=-\log \left[p\right(\mathbf{y},\mathbf{f}\mid \theta \left)\right]+\frac{1}{2}\log \mid G_{\mathbf{f}}\mid +\frac{1}{2}{\mathbf{p}}^{\mathrm{T}}{G}_{\mathbf{f}}^{-1}\mathbf{p}+\text{const}.$$

Given that the metric tensor is dependent on the value of f, the Hamiltonian is therefore nonseparable between p and f, and a generalized leapfrog integrator must be employed [Girolami and Calderhead (2011)]. RM–HMC can be seen as a generalization of Hybrid Monte Carlo (HMC) [Neal (1993)], where the mass matrix is now substituted by the metric tensor.

4.2. Ancillary and sufficient augmentation

The proposed classification model is hierarchical, and the application of a Metropolis-within-Gibbs style scheme, sampling f∣θ, y then θ∣f, y, leads to poor efficiency and slow convergence. This effect has drawn a lot of attention in the case of hierarchical models in general [Papaspiliopoulos, Roberts and Sköld (2007), Yu and Meng (2011)] and recently in latent Gaussian models [Murray and Adams (2010), Filippone, Zhong and Girolami (2012)]. In order to decouple the strong posterior dependency between θ and f, we can apply reparametrization techniques, whereby we introduce a new set of variables ν_c related to the old set of latent variables by a transformation f_c = g(ν_c, θ_c). This transformation can be chosen to achieve faster convergence as studied, for example, in Papaspiliopoulos, Roberts and Sköld (2007), and should be designed to handle both strong and weak data limits, namely, situations where data overwhelm the prior or not. In the terminology of Yu and Meng (2011), we identify two particular cases, namely, Sufficient augmentation (SA) and Ancillary augmentation (AA). In the SA scheme the sampling of θ is done by proposing θ′∣θ, f, y. In the case of weak data, as it is the case in this application, the SA parametrization is inefficient, given the strong coupling between f and θ. In contrast, in the AA scheme, the new set of latent variables ν_c is constructed to be a priori independent from θ; this is a good candidate to provide an efficient parametrization in cases of weak data. To see this, in the case of no data, the posterior over hyper-parameters and the newly defined latent variables ν_c corresponds to the prior which is factorized and easy to explore.

This parametrization makes the ν_c ancillary for y. We propose to realize this by defining f_c = L_cν_c, where L_c is any square root of K_c (in the remainder of this paper we will consider L_c as the Cholesky factor of K_c). This sampling scheme amounts to sampling θ′∣θ, ν₁, … , ν_m, y. In the next section we will report experiments showing the relative merits of SA and AA combined with manifold methods, with the ultimate goal of achieving efficiency in inferring latent functions and hyper-parameters in our application. All implemented methods were tested for correctness as proposed by Geweke (2004), and convergence analysis was performed using the $\widehat{R}$ potential scale reduction factor [Gelman and Rubin (1992)].

5. Comparison of MCMC sampling strategies

In this section we investigate the efficiency of various MCMC sampling strategies in our application. Table 1 lists the sampling approaches that we considered for this study. All approaches make use of RM–HMC for sampling the latent variables with different metrics. Approach (a) uses a simple isotropic metric so that RM–HMC is effectively HMC with an identity mass matrix. Approaches (c), (d) and (f) use the metric derived from the FI (see the Appendix), while approaches (b) and (e) use an alternative homogeneous metric, defined as $\widehat{F}=K^{-1}+\text{diag}\left({\pi }_p\right)-{\Phi }_p{\Phi }_p^T$. Note that this is similar to the definition of the metric tensor outlined in the Appendix, except πp and Φ_p are defined by the prior frequency of the classes in the training set instead of by the likelihood. Employing this homogeneous metric is less efficient than employing a position specific metric, but it holds two practical advantages: (i) it has a substantially lower computational cost since it does not recompute and invert the metric tensor at every step and (ii) the explicit leapfrog integrator may be used in place of the generalized (implicit) leapfrog integrator used in Girolami and Calderhead (2011).

Table 1.

Sampling schemes evaluated

	p(f′|f,θ)		p(θ′|f,θ)
Approach	Sampler	Metric	Sampler	Metric	Scheme
(a)	RM–HMC	I	RM–HMC	I	SA
(b)	RM–HMC	$\widehat{F}$	RM–HMC	I	SA
(c)	RM–HMC	G f	RM–HMC	I	SA
(d)	RM–HMC	G f	RM–HMC	Gθ	SA
(e)	RM–HMC	$\widehat{F}$	MH	–	AA
(f)	RM–HMC	G f	MH	–	AA

In sampling the hyper-parameters, approaches (a)–(c) effectively employ an HMC proposal with identity mass matrix with SA parametrization. Approach (d) uses RM–HMC with metric derived from the FI as shown in the Appendix, whereas approaches (e) and (f) make use of Metropolis–Hastings (MH) with an identity covariance with AA parametrization.

Approach (a) can be viewed as a simple baseline approach since it does not incorporate any knowledge on the curvature of the target distribution and attempts to explore the parameter space by isotropic proposals. It is presented primarily as a reference for the other approaches. Approaches (b) and (c) employ manifold methods to efficiently sample the latent variables only while approach (d) also applies them to sample the hyper-parameters. Approaches (e) and (f) employ manifold methods for the latent variables and an MH sampler with AA for the hyper-parameters.

For all the experiments that follow, we applied an independent Gamma prior to each weight exp(θ_cs), with a = b = 2, where a and b refer, respectively, to shape and rate parameters. This prior is relatively vague but nevertheless constrained the sampler to a plausible parameter range.

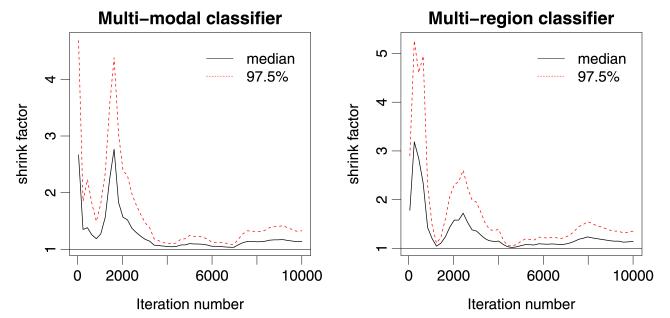
We tuned each of the sampling approaches described above using pilot runs and assessed convergence by recording when all sampled variables had $\widehat{R}<1.1$. According to this criterion, sampling approaches (e) and (f) converged after 1000 iterations for the latent function variables and after a few thousands of iterations for the hyper-parameters. Sampling approaches (a)–(d) did not converge even after 100,000 iterations, so will not be considered further. This demonstrates that the structure of the model poses a serious challenge in efficiently sampling f and θ, no matter how efficient are the individual samplers employed in the Metropolis-within-Gibbs sampler. For all subsequent analysis, we discarded all samples acquired prior to convergence (burn-in). A plot reporting the evolution of Gelman and Rubin’s shrink factor vs the number of iterations (for the first 10,000 iterations) for the slowest variable to converge is reported in Figure 2. The left and right panel of Figure 2 correspond to the slowest variable in the approach (e) for the multi-modality and multi-region classifiers (see next section), respectively; in both cases the slowest variable was one of the hyper-parameters.

Fig. 2.

Convergence analysis: plot reporting the evolution of Gelman and Rubin’s shrink factor vs the number of iterations for the slowest variable to converge in approach (e) for the multi-modality classifier (left panel) and the multi-region classifier (right panel).

For the latent function variables, we used an RM–HMC trajectory length of 10 leapfrog steps and a step size of 0.5 for sampling approaches (e) and (f). This appeared to be near optimal and yielded an acceptance rate in the range of 60–70%, while keeping correlation between successive samples relatively low. For the hyperparameters, a step size of 0.2 yielded an acceptance rate in the range of 60–70%, although correlation between successive samples remained high (see below).

We report the Effective Sample Size (ESS) [Geyer (1992)] for each method in Table 2, expressed as a percentage of the total number of samples. The ESS is an autocorrelation based method that is used to estimate the number of independent samples within a set of samples obtained from an MCMC method. Both approaches (e) and (f) sampled the latent function variables relatively efficiently, although there was some variability between different variables. Sampling of the hyper-parameters was much more challenging than the sampling of the latent function variables, and the MH samplers achieved an ESS less than 0.5% for all variables. Thus, for subsequent analysis we ran a relatively long Markov chain (5 million iterations) which we thinned by a factor of 500, ensuring independent sampling for all variables. Note that RM–HMC with metric $\widehat{F}$ and RM–HMC with matrix G_f [approaches (e) and (f)] performed approximately equivalently for sampling the latent function variables. Thus, for the remainder of this paper we focus on the results obtained from the sampler that employed the homogeneous metric $\widehat{F}$ for the latent functions and MH for the hyper-parameters [i.e., approach (e)], owing to its lower computational cost. The results reported in this section are in line with what is observed in a recent extensive study on the fully Bayesian treatment of models involving GP priors [Filippone, Zhong and Girolami (2012)]. In particular, it has been reported that the sampling of the latent variables can be done efficiently using RM–HMC and a variant with the homogeneous metric $\widehat{F}$, and that for the hyper-parameters the MH proposal with the AA parametrization is a good compromise between efficiency and computational cost.

Table 2.

Efficiency of converged sampling schemes (multi-source classifier). Min and max refer to the minimum and maximum ESS across all sampled variables

Approach	Mean % ESSf (min, max)	Mean % ESSθ (min, max)
(e)	27.04 (5.31, 48.06)	0.34 (0.21, 0.48)
(f)	24.11 (5.71, 42.86)	0.31 (0.19, 0.42)

6. Predictive accuracy and assessment of neuroimaging data modalities

In this section we have three main objectives: first, we aim to demonstrate that the predictive approach we propose can accurately discriminate between multiple neurological conditions. Second, we investigate which neuroimaging data modalities carry discriminating information for these disorders and whether greater predictive performance can be achieved by combining multiple modalities. Finally, we investigate the predictive ability of different brain regions for discriminating between each of the disorders.

For estimating the predictive ability of the classifiers we performed four-fold cross-validation (CV). In the CV procedure, we randomly partitioned the data into four folds so that each CV fold contained approximately the same frequency of classes as in the entire data set. We then carried out the inference leaving out one fold that we used to assess the accuracy of the proposed method; leaving out one fold at a time, it is possible to obtain an estimate of performance on unseen data.

We compared the performance of the proposed multinomial logit model with simpleMKL. Similar to the proposed method, simpleMKL allows an optimal linear combination of data sources or brain regions to be inferred from the data, but, unlike the proposed approach, simpleMKL is not a probabilistic model. In the MKL literature, each data source is referred to as a “kernel” which corresponds to a covariance function for the proposed multinomial logit model. Since SVMs do not support true multi-class classification, we employed a “one-vs-all” approach to combine multiple binary classifiers to provide a multi-class decision function. This has the consequence that simpleMKL estimates a linear combination of kernels that provides optimal accuracy across all binary classification decisions, and is therefore not able to estimate an independent set of kernel weighting factors for each class. To ensure the comparison with the multinomial logit model was as fair as possible, we used nested cross-validation to find an optimal value for the SVM regularization parameter C. We achieved this by performing an inner “leave-one-out” cross validation cycle (“validation”) within each outer four-fold cycle (“test”) while we varied C logarithmically across a wide range of values (10⁻⁵ to 10⁵ in steps of 10). We selected the value of C that provided the optimal accuracy on the validation set, before applying it to the test set. To further examine whether any performance difference could be attributed to the extension of simpleMKL to multiclass classification, we also compared the accuracy of simpleMKL and the proposed model on all possible binary classification decisions. For simpleMKL, we used the implementation provided by Rakotomamonjy et al. (2008) where we used the “weight variation” stopping criterion and the default options.

We employed two measures of predictive performance: (i) balanced classification accuracy, which measures the mean number of correct predictions across all classes assuming a zero–one loss and (ii) a multi-class Brier score, which also quantifies the confidence of classifier predictions on w unseen samples and can be computed as the following error measure: $B=\frac{1}{w}{\Sigma }_{i=1}^w{\Sigma }_{c=1}^m{({\pi }_{\mathit{ic}}^{\ast }-y_{\mathit{ic}}^{\ast })}^2$. Note that simpleMKL does not provide probabilistic predictions, so the Brier score is not appropriate to evaluate the performance of this algorithm. Gneiting and Raftery (2007) reported studies on the connections between the Brier score and predictive accuracy in the case of two-class classification, reporting that simple accuracy is a proper score unlike the Brier score which is strictly proper. We are unaware of any results on the connections between the two scores in the case of multi-class classification.

For comparison we also present predictive accuracy measures derived from classifiers using each data source independently, and a classifier using an unweighted linear sum of data sources (i.e., $K_c={\Sigma }_{s=1}^q{C}_s$ for all c).

6.1. Multi-modal classifier

We first studied the classification problem based on the five data sources obtained from the three modalities, namely, GM, WM, T2, FA and MD, as explained in Section 2, so that q = 5. The overall performance of each model is summarized in Table 3. Note that all classifiers exceeded the predictive accuracy that would be expected by chance (i.e., p < 0.05, χ² test).

Table 3.

Predictive accuracy (multi-source classifier). Min and max values refer to minimum and maximum values across CV folds

	Input data	Accuracy (min, max)	Brier score (min, max)
1	GM only	0.627 (0.321, 0.854)	0.667 (0.636, 0.712)
2	WM only	0.603 (0.350, 0.771)	0.653 (0.609, 0.710)
3	T2 only	0.545 (0.500, 0.604)	0.663 (0.619, 0.695)
4	FA only	0.569 (0.442, 0.688)	0.675 (0.645, 0.703)
5	MD only	0.623 (0.533, 0.750)	0.631 (0.588, 0.680)
6	Weighted sum	0.598 (0.350, 0.708)	0.588 (0.517, 0.662)
7	Unweighted sum	0.610 (0.400, 0.708)	0.553 (0.469, 0.646)
8	SimpleMKL	0.418 (0.143, 0.625)	–

From Table 3, it is apparent that classifiers based on the T2 and FA data sources achieved lower classification accuracy than all the other data sources, suggesting they are not ideally suited to discriminating between these disorders. Further, the linear combinations of sources did not achieve higher accuracy than the best individual data source and the highest accuracy was obtained using the GM images only, although the difference is relatively small. The simpleMKL classifier produced lower accuracy than either linear combination derived from the multinomial logit model. The mean accuracy for the binary classifiers over all pairs of classes was slightly higher for the GP classifiers (0.807) relative to simpleMKL (0.741), suggesting that most of the performance difference between simpleMKL and the proposed multinomial logit approach can be attributed to the extension of simpleMKL to the multi-class case.

In contrast to the outcomes for classification accuracy, the linear combinations of data sources produced more accurate probabilistic predictions than any of the individual modalities, indicative of a disjunction between categorical classification accuracy and accurate quantification of predictive uncertainty (Table 3). This is probably a result of this model having greater flexibility to scale the magnitude of the latent function variables.

6.1.1. Covariance parameters for the latent functions

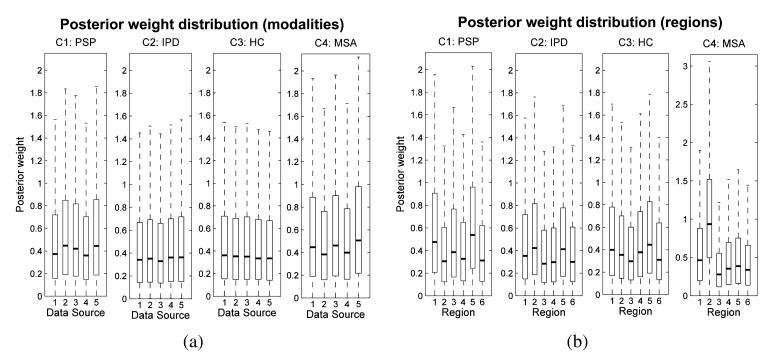
The posterior distribution of the weights is an important secondary outcome from this model and is summarized in Figure 3(a). These hyper-parameters collectively describe the relative contribution (or weighting factors) for each modality in deriving the prediction for each class.

Fig. 3.

Posterior distributions for the predictive weights for the multi-modality classifier (a) and the multi-region classifier (b). Panel (a): Data sources: (1) GM, (2) WM, (3) T2, (4) FA, (5) MD. Panel (b): Regions: (1) brainstem, (2) cerebellum, (3) caudate, (4) middle occipital gyrus, (5) putamen, (6) all other regions.

The posterior class distribution for covariance weights in this model is relatively flat across all modalities for each class although each weight has slightly greater magnitude for the PSP and MSA classes relative to the other classes. Overall, the results from this section provide evidence that all imaging modalities contain similar information for discriminating disease groups. In other words, we found little benefit from combining multiple neuroimaging sequences. This has the important implication that for the purposes of discrimination it appears sufficient to acquire a single structural MRI scan (i.e., SPGR image), which is comparatively rapid and inexpensive to acquire. Although the T2 images are also relatively inexpensive, they do not offer the same discriminative value and the DTI images, which are time-consuming and expensive to acquire, and appear to offer little additional benefit.

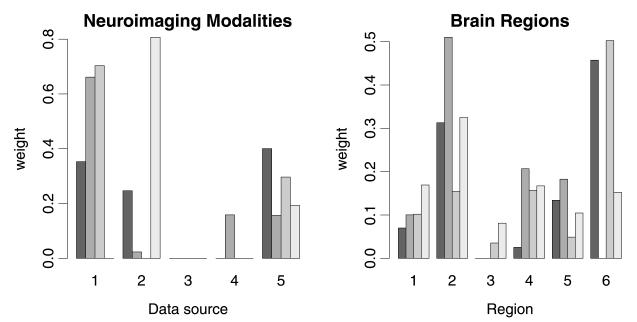
In the left panel of Figure 4 we report the kernel weights obtained by simpleMKL across the four folds. We can see how the values of the weights are not consistent across the folds; for example, GM is given zero weight in the fourth fold, whereas it seems to be important for the other three cases. Modality T2, instead, is consistently given zero weight across the four folds, suggesting that this might not add any information to the other modalities. This is in contrast with the results of the probabilistic classifier that suggests that there is not much evidence in the data to completely ignore the information from one of the modalities.

Fig. 4.

Weights of the neuroimaging modalities (left panel) and brain regions (right panel) obtained by simpleMKL across the four folds. Left panel: Data sources: (1) GM, (2) WM, (3) T2, (4) FA, (5) MD. Right panel: Regions: (1) brainstem, (2) cerebellum, (3) caudate, (4) middle occipital gyrus, (5) putamen, (6) all other regions.

6.2. Multi-region classifier

In this section we illustrate how the proposed methodology may be used to estimate the predictive value of different brain regions for classification, although we will investigate the relative contribution of different brain regions in greater detail and comment on the clinical significance of these findings in a separate report. For neurological applications, it is primarily important to assist interpretation, since it is desirable to identify differential patterns of regional pathology for each disease. While there are other methods to achieve this goal, an advantage of the proposed approach is that it provides a full posterior distribution over regional weighting parameters. For this analysis we used only the GM data modality, since it showed the highest discrimination accuracy, and used an anatomical template [Shattuck et al. (2008)] to parcellate the GM images into six regions: (i) brainstem, (ii) bilateral cerebellum, (iii) bilateral caudate, (iv) bilateral middle occipital gyrus, (v) bilateral putamen and (vi) all other regions, so that now q = 6. As described above, the cerebellum, brainstem, caudate and putamen are affected to varying degrees in MSA, PSP or IPD. The middle occipital gyrus region was selected as a control region, as this is hypothesized to contain minimal discriminatory information.

All sampling approaches performed similarly for this problem in that none of the sampling approaches (a–d) converged after 100,000 iterations and sampling approaches (e) and (f) converged after 1000 iterations for the latent function variables and after a few thousands of iterations for the hyper-parameters (see the right panel of Figure 2). Table 4 reports the efficiency of the sampling approaches (e) and (f), as they were the only ones that converged in a reasonable number of iterations.

Table 4.

Efficiency of converged sampling schemes (multi-region classifier). Min and max refer to the minimum and maximum ESS across all sampled variables

Approach	Mean % ESSf (min, max)	Mean %ESSθ (min, max)
(e)	8.52 (2.37, 34.85)	0.28 (0.11, 0.64)
(f)	9.42 (2.32, 35.44)	0.31 (0.11, 0.50)

The sampling efficiency for the latent function values was somewhat lower for this problem than for the multi-modal prediction problem described in the previous section. On average, the sampling efficiency for the hyper-parameters was approximately equivalent to the values reported above, but the minimum ESS was slightly lower. To accommodate this, we thinned all Markov chains by a factor of 1000, ensuring approximately independent sampling for all variables.

Predictive accuracy measures for the multi-region classifier are presented in Table 5. All classifiers exceeded the predictive accuracy that would be expected by chance (p < 0.05, χ² test) except the simpleMKL classifier which performed very poorly for this data set. As for the multi-modal classifier, we compared the predictive accuracy of simpleMKL to the logit model across all binary classification decisions. In this case, the models produced similar accuracy (0.765 for the GP classifiers, 0.780 for simpleMKL). This provides further evidence that the suboptimal performances of simpleMKL can be traced to the extension of the binary SVM to the multi-class setting. In particular, it is likely that the suboptimal performance of simpleMKL in the multi-class context is due to the fact that it does not support different weighting factors for each class. In this case, the classifiers using weighted and unweighted covariance sums of brain regions produced the most accurate predictions and quantified predictive confidence most accurately. Again, there was negligible difference between the classifiers using the weighted and unweighted sums.

Table 5.

Predictive accuracy (multi-region classifier). Min and max values refer to minimum and maximum values across CV folds

	Input data	Accuracy (min, max)	Brier score (min, max)
1	Brainstem only	0.578 (0.500, 0.688)	0.595 (0.555, 0.643)
2	Cerebellum only	0.478 (0.333, 0.562)	0.634 (0.593, 0.643)
3	Caudate only	0.349 (0.221, 0.520)	0.737 (0.693, 0.764)
4	Mid. occipital gyrus only	0.419 (0.333, 0.479)	0.741 (0.677, 0.773)
5	Putamen only	0.438 (0.354, 0.521)	0.668 (0.604, 0.718)
6	All other regions	0.424 (0.321, 0.563)	0.753 (0.724, 0.779)
7	Weighted sum	0.614 (0.500, 0.708)	0.547 (0.499, 0.593)
8	Unweighted sum	0.624 (0.500, 0.708)	0.546 (0.501, 0.592)
9	simpleMKL	0.229 (0.111, 0.375)	–

6.2.1. Covariance parameters for the latent functions

The posterior distribution of the weights for the multi-region classifiers is summarized in Figure 3(b). The posterior means of the weighting factors were again relatively constant between brain regions and also showed a high variance. This indicates that the relative contribution of different brain regions was not strongly determined by the data and that we should be cautious about interpreting the relative contributions of the different brain regions using this approach. Nevertheless, the clearest differential effect among regions was for the cerebellum, where the lower quartile of the posterior distribution for the MSA class was greater than the mean of all other regions. In addition, the brainstem also made a small positive contribution toward predicting the MSA class. As described above, both the cerebellum and brainstem are known to undergo severe degeneration in MSA. The strongest positive contributions to predicting the PSP class were obtained from the brainstem, caudate and putamen, which once again are regions known to show the extensive degeneration in PSP. The regional weighting factors for the IPD and control groups were somewhat flatter, which is consistent with the focal nature of the degeneration in early-mid IPD and with the observation that the brain scans of these groups are difficult to discriminate from one another. However, the posterior suggests that the cerebellum showed a relatively increased weighting relative to other regions for the IPD class, and that the putamen was assigned a relatively increased weighting for the IPD and HC classes, which is congruent with the expectation that these classes are characterized by greater GM concentration in those regions relative to the PSP and MSA classes respectively. From the current analysis, it is difficult to determine the regions having the greatest predictive value for discriminating the PD from the HC group. As future work, separate binary classifiers trained to discriminate these classes directly may be beneficial in this respect. We notice also that the control region (i.e., the middle occipital gyrus) was assigned comparatively low weighting for every class.

Overall, the results from this section suggest that distributed patterns of abnormality across multiple brain regions are necessary to accurately discriminate between classes. The neurodegenerative disorders studied in the present work have relatively well-defined regional pathology, but even in this case the most accurate predictions were obtained from the classifiers using all brain regions.

Again, the analysis of the weights obtained by simpleMKL (right panel of Figure 4) shows that the nonprobabilistic classifier obtains sparse solutions for the weights that are not consistent across the folds, thus preventing one from being able to properly assess the role played by each region in the classification task.

6.3. Results with the Dirichlet prior

Here we briefly discuss the results obtained when imposing a Dirichlet prior on the weights exp(θ_cs), focusing only on the multi-region classifier for the sake of brevity. The sampling strategy was as in approach (e), with the difference that the update of the hyper-parameters followed a MH sampling with proposal based on Dirichlet distributions. In order to test the robustness to prior specification, we added a further level in the hierarchy of the model by imposing a prior over the concentration parameter of the Dirichlet distribution, so that the model had a joint density p(y, f, θ, α) = p(y∣f)p(f∣θ)p(θ∣α)p(α). Including a hyper-prior over the concentration parameter has the effect of averaging out the choice of the prior and inferring the concentration parameter allows inference of levels of sparsity from the data.

From the computational perspective, the sampling of α induces a further level of correlation in the chains. We ran thorough convergence tests, and we obtained similar convergence and efficiency results as in the previous analysis. We chose a fairly diffuse hyper-prior p(α) as exponential with unit rate, so that E[α] = 1, which corresponds to a uniform prior over the simplex for the weights.

Note that data has quite a weak effect in informing the posterior over the concentration parameter, as they are three levels apart in the hierarchy [Goel and DeGroot (1981)]. Nevertheless, comparing prior and posterior over α, we notice a slight reduction in the interquartile range from [0.29, 1.39] to [0.51, 1.49] and a shift of the mean from 1 to 1.16, thus supporting a diffuse (nonsparse) prior over the weights. In terms of questions addressed in this particular application, the results obtained by adding a hyper-prior lead to the same conclusions.

7. Refining predictions using predictive probabilities

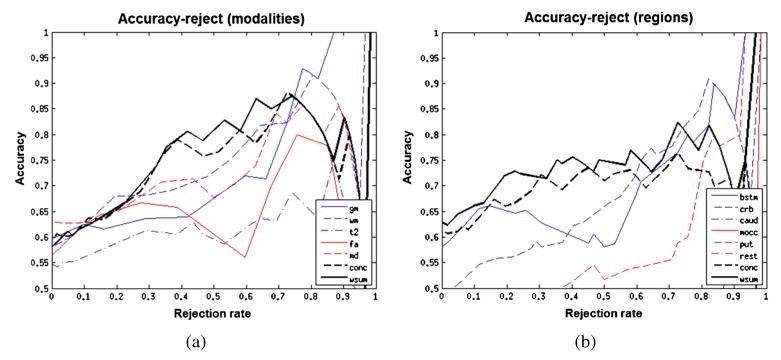
We have discussed how a probabilistic approach allows us to assess the importance of different neuroimaging modalities in disease classification. Another advantage of employing a probabilistic classification model is that predictive probabilities quantify the uncertainty in the outcome, which allow a “reject option” to be specified. Under this framework, the researcher specifies in advance a confidence threshold below which a prediction is considered to be inconclusive. In cases where the maximum class probability does not exceed this threshold, the final decision may be deferred to another classification model or a human expert. To investigate the suitability of the proposed classifier for this approach and to assess the accuracy of the classifier across varying rejection thresholds, we plotted accuracy–reject curves for each of the classifiers investigated in this work (Figure 5). These were constructed by varying the rejection threshold monotonically from 0 to 1 in steps of 0.01. At each threshold, we computed the rejection rate as the proportion of samples for which the most confident class prediction did not exceed the rejection threshold and measured the accuracy of the remaining samples. The accuracy–reject curves were then generated by plotting accuracy as a function of rejection rate.

Fig. 5.

(a) Accuracy–reject curve for multi-modality classifiers. (b) Accuracy–reject curve for multi-region classifiers.

The accuracy–reject curves show that: (i) predictive performance increases monotonically across most rejection rates and (ii) the multi-source classifiers perform better than any of the individual modalities or brain regions across most rejection rates. This implies that the multi-source classifiers not only make fewer errors, but also quantify predictive uncertainty more accurately than any of the individual regions. At high rejection thresholds, the multi-modality classifier is outperformed by the GM modality, owing to two confident misclassifications deriving from the FA and MD modalities, suggesting the possibility of atypical white matter pathology in these subjects.

8. Conclusions

In this paper we presented the application of a multinomial logit model based on GP priors to the problem of classification of neurological disorders based on neuroimaging measures. The proposed model is flexible and highly descriptive, and it can be employed in scenarios where the focus is on gaining insights into the relative importance of different data modalities or brain regions in the application under study. Also, it allows accurate quantification of the uncertainty in the predictions, which is crucial in several applications and especially for predicting disease state in clinical applications.

From a statistical perspective, carrying out the inference task in the model presented in this paper and in latent Gaussian models in general represents a serious challenge. This paper presented a combination of advanced inference techniques based on MCMC methods that allowed us to tackle this problem in an efficient way. Predictions for unseen data were obtained by integrating out all the parameters in the model, thus capturing the uncertainty in the inferred parameters. We also investigated the use of a hyper-prior to integrate out the choice of the prior.

The motivating application for this study aimed to use neuroimaging measures to classify a cohort of 62 participants, consisting of both healthy controls and patients affected by one of three variants of Parkinsonian disorder. We demonstrated accurate classification of disease state that compares favorably with the only existing study of which we are aware of employing whole-brain neuroimaging measures to discriminate between these disorders [Focke et al. (2011)]. For future work it will be important to: (i) validate how well the predictive accuracy obtained here generalizes to earlier disease stages and (ii) investigate methods to improve the predictive accuracy beyond what was reached here, which will become increasingly important when the proposed method is evaluated in early stage disease. Construction of classification features from brain images that better reflect the underlying pathology may be particularly beneficial in this regard. We showed how the results of the inference allowed us to draw conclusions regarding the relative importance of neuroimaging measures and brain regions in discriminating between classes. We also compared the results with simpleMKL, a nonprobabilistic multi-modality classifier based on SVMs, which shows lower accuracy and, most importantly, is not able to address questions regarding the relative importance of neuroimaging measures and brain regions in a statistically consistent way. In contrast, the proposed method was able to give insights into the predictive ability of the different neuroimaging sequences, and suggested that all the modalities investigated in this study carry similar discriminative information. This has important implications for planning future studies, and suggests that there is little benefit in acquiring multiple neuroimaging sequences. Instead, for the purposes of prediction, acquiring a single structural brain image is probably the most cost-effective approach. Another level of the analysis showed that the proposed method was able to quantify the predictive ability of different brain regions for discriminating between classes. Similar to the previous analysis, this analysis showed that all regions carry some discriminative information, but at the same time seems to indicate that some of them have greater predictive ability than others for different classes. Further, the regional distribution of these regions is in accordance with the known pathology of the disorders based on the clinical literature.

APPENDIX A. DATA ACQUISITION DETAILS

For each subject, a T2-weighted structural image, a T1-weighted spoiled gradient recalled (SPGR) structural image and a DTI sequence were acquired using a 1.5T GE Signa LX NVi scanner (General Electric, WI, USA). All images had whole brain coverage and imaging parameters for the T2 weighted images and DTI sequences have been described previously [Blain et al. (2006)]. Imaging parameters for the SPGR imaging sequence were as follows: repetition time = 18 ms, echo time = 5.1 ms, inversion time = 450 ms, matrix size = 256 × 152, field of view (FOV) = 240 × 240. SPGR Images were reconstructed over a 240 × 240 FOV, yielding an in-plane resolution of 0.94 × 0.94 mm and 124 1.5 mm thick slices. Subjects provided informed written consent, and the study was approved by the local Research Ethics Committee.

APPENDIX B. MCMC ADDITIONAL DETAILS

Let K_*. be an m × (mn) block diagonal rectangular matrix where entries in the rth diagonal block contain the covariance of the test sample with the training samples corresponding to the rth covariance K_r. Also, let K_** be an m × m matrix where the i, j entry is the covariance of the test sample corresponding to the covariances K_i and K_j . A priori we assumed zero covariance across latent functions, so K_** will be diagonal. Using the properties of GPs, given f and θ, then $p({\mathbf{f}}_{\ast }\mid \mathbf{f},\theta )=\mathcal{N}({\mathbf{f}}_{\ast }\mid {\mu }_{\ast },{\Sigma }_{\ast })$ with μ_* = K_*·K⁻¹f and Σ_* = K_** – K_*·K⁻¹K_·*. Given N₁ independent posterior samples for f and θ, we can estimate the integral by

$$p({\mathbf{y}}_{\ast }\mid \mathbf{y})\approx \frac{1}{N_1}\sum _{i=1}^{N_1}\int p({\mathbf{y}}_{\ast }\mid {\mathbf{f}}_{\ast })p({\mathbf{f}}_{\ast }\mid {\mathbf{f}}_{\left(i\right)},{\theta }_{\left(i\right)})d{\mathbf{f}}_{\ast }.$$

Each of the former integrals can be estimated again by a Monte Carlo sum, by drawing N₂ independent samples from p(f_*∣f_(i), θ(i)) which is Gaussian:

$$\int p({\mathbf{y}}_{\ast }\mid {\mathbf{f}}_{\ast })p({\mathbf{f}}_{\ast }\mid {\mathbf{f}}_{\left(i\right)},{\theta }_{\left(i\right)})d{\mathbf{f}}_{\ast }\approx \frac{1}{N_2}\sum _{j=1}^{N_2}p({\mathbf{y}}_{\ast }\mid {\left({\mathbf{f}}_{\ast }\right)}_{\left(j\right)}).$$

The required gradients of the joint log-density follow as ${\nabla }_{\mathbf{f}}\mathcal{L}=-K^{-1}\mathbf{f}+\mathbf{y}-\pi$ and

$$\frac{\partial \mathcal{L}}{\partial {\theta }_{\mathit{cj}}}=-\frac{1}{2}\exp \left[{\theta }_{\mathit{cj}}\right]\mathrm{Tr}\left(K_c^{-1}{C}_j\right)+\frac{1}{2}\exp \left[{\theta }_{\mathit{cj}}\right]{\mathbf{f}}_c^T{K}_c^{-1}{C}_j{K}_c^{-1}{\mathbf{f}}_c+\frac{\partial p\left({\theta }_c\right)}{\partial {\theta }_{\mathit{cj}}},$$

and the FI for the two groups of variables, along with the negative Hessian of the priors are G_f = K⁻¹ + diag(π) – ΦΦ^T and ${\left(G_{\theta }\right)}_{\mathit{cjr}}=\frac{1}{2}\exp [{\theta }_{\mathit{cr}}+{\theta }_{\mathit{cj}}]\mathrm{Tr}\left(K_c^{-1}{C}_r{K}_c^{-1}{C}_j\right)$, where Φ is a (mn) × n matrix obtained by stacking by row the matrices diag(π_c). The derivatives of the two metric tensors needed to apply RM–HMC can be computed by using standard properties of derivatives of expressions involving matrices.