Multi-resolutional Brain Network Filtering and Analysis via Wavelets on Non-Euclidean Space

Abstract

Advances in resting state fMRI and diffusion weighted imaging (DWI) have led to much interest in studies that evaluate hypotheses focused on how brain connectivity networks show variations across clinically disparate groups. However, various sources of error (e.g., tractography errors, magnetic field distortion, and motion artifacts) leak into the data, and make downstream statistical analysis problematic. In small sample size studies, such noise have an unfortunate effect that the differential signal may not be identifiable and so the null hypothesis cannot be rejected. Traditionally, smoothing is often used to filter out noise. But the construction of convolving with a Gaussian kernel is not well understood on arbitrarily connected graphs. Furthermore, there are no direct analogues of scale-space theory for graphs — ones which allow to view the signal at multiple resolutions. We provide rigorous frameworks for performing ‘multi-resolutional’ analysis on brain connectivity graphs. These are based on the recent theory of non-Euclidean wavelets. We provide strong evidence, on brain connectivity data from a network analysis study (structural connectivity differences in adult euthymic bipolar subjects), that the proposed algorithm allows identifying statistically significant network variations, which are clinically meaningful, where classical statistical tests, if applied directly, fail.

1 Introduction

The development of diffusion weighted imaging (DWI) and functional magnetic resonance imaging (fMRI) have laid the groundwork for ambitious initiatives towards a full characterization of the human connectome (the brain’s wiring diagram) to better understand the structural and functional aspects of brain connectivity. While such large scale projects will clearly push the frontiers of neuroscience forward, these efforts must necessarily go hand in hand with studies seeking to answer more focused questions pertaining to the variations in the connectivity structure in the context of specific neurodegenerative diseases, and how its manifestation is modulated by genetic and demographic factors. As such these studies operate in the small sample size regime, and the first order requirement on analysis methods appropriate for such applications is to maximize statistical power — in other words, the likelihood of observing a differential signal in the connectivity data given the limited size of the cohort.

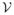Consider a brain connectivity network modeled as an undirected weighted graph denoted as = ( , , ω). The vertices, may denote anatomically meaningful parcellations [5] or regions exhibiting spatially contiguous BOLD activations where as the weighted edges may correspond to temporal correlations or strength of tract connectivity. Now, our interest is to perform statistical analysis on a population of such brain connectivity networks in clinically disparate groups, to understand which connections are severely affected by the disease. The overwhelming majority of current literature suggests applying standard hypothesis testing at the level of individual network edges. This approach generally works well, but when the group-wise differences are weak to begin with, one finds that after correcting for multiple comparisons, a statistically significant signal may be unidentifiable. One may smooth out the noise variance in 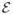and 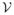, but it is still an issue in brain connectivity analysis. For example, even a small head motion in the scanner can influence the DTI connectivity information. [15] The standard procedure to improve the signal to noise ratio is to smooth the input signal. In image processing, the measurements are defined on a uniformly sampled lattice (Euclidean space) where the standard notions of a convolution filter apply directly. The few instances in the literature which implement a smoothing process on brain network data essentially average the measurements within a the node or edge ROIs with isotropic Gaussian kernels [17,13], discarding the network structure. In computer vision, anisotropic diffusion kernels [14], heat kernels [19] and pyramids [10] have been used extensively, but mostly in the context of a regular lattice over pixels. Developments of these ideas have led to much work in scale space theory, towards deriving multi-resolution representations of the image by incremental smoothing. The question we investigate is whether such connections can be exploited to analyze brain connectivity network data with enhanced statistical sensitivity. The literature offers few strategies for filtering of signals on the edges of a brain connectivity network.

Key contributions

The most natural mathematical tool which offers multi-resolution behavior, i.e., wavelets, was until recently, restricted to the Euclidean space. But the objects of interest here are networks with arbitrary topology (non-Euclidean). a) We make use of a recent harmonic analysis results to show how non-Euclidean wavelets provide tools for defining multi-scale representations of brain networks. b) We demonstrate an application to analyzing structural connectivity differences between euthymic bipolar disorder and healthy subjects. Our framework applies multi-resolutional analysis on the information defined on the edges, not on the vertices. The noise in raw connectivity data has the effect that few edges show up as statistically significant after accounting for multiple comparisons correction. But applying the proposed method, clinically meaningful group differences can be detected at the Bonferroni threshold of α < 0.01.

2 Non-Euclidean Wavelets

Wavelet transform is conceptually similar to the well-known Fourier transform, however, it uses a certain shape of oscillating function as a basis with finite duration instead of the sine and cosine basis with infinite duration. The traditional construction of wavelets is defined by a mother wavelet function ψ and a scaling function φ, which are band and low-pass filters in the frequency domain.

The wavelet function ψ on x is a function defined by two parameters, the scale parameter s and translation parameters a

$${\psi }_{s,a}(x)=\frac{1}{a}\psi (\frac{x-a}{s}).$$ (1)

Change in s varies the dilation of the wavelet, and together with a translation parameter a, approximates a signal in harmonics using wavelet expansion. The function ψ_s;a(x) forms bases for the signal and can be used with other basis at different scales to decompose a signal. The wavelet transform of a signal f(x) is defined as the inner product of the wavelet basis ψ_s;a and f(x),

$$W_f(s,a)=\langle f,\psi \rangle =\frac{1}{a}\int f(x){\psi }^{\ast }(\frac{x-a}{s})\mathrm{d}x,$$ (2)

where W_f (s, a) is the wavelet coeficient at scale s and at location a. The original signal f(x) can be reconstructed from W_f (s, a) and basis function without loss of information; the inverse transformation is

$$f(x)=\frac{1}{C_{\psi }}\int \int W_f(s,a){\psi }_{s,a}(x)\mathrm{d}a\mathrm{d}s$$ (3)

where $C_{\psi }=\int \frac{{\mid \mathit{\Psi }(j\omega )\mid }^2}{\mid \omega \mid }\mathrm{d}\omega$ is known as the admissibility condition constant, Ψ is the Fourier transform of the wavelet [8], and ω denotes the frequency domain.

Recent work in harmonic analysis [6] provides wavelet basis on structured data which expresses in a wide spectrum of frequencies. The solution in [6] relies on a graph Fourier transform to derive a spectral graph wavelet transform (SGWT). It is shown that SGWT formalization preserves the localization properties at fine scales as well as other wavelet specific properties, while addressing the bottleneck of defining scales on a domain where the space is non-Euclidean.

Let a graph = { 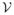, , 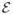ω} be a undirected graph with a vertex set 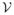with N vertices, an edge set 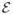and corresponding edge weight ω ≥ 0. The adjacency matrix A of is given as a N × N matrix whose elements a_ij are the edge weight ω_ij if i^th and j^th nodes are connected. The degree matrix D is computed as a N × N diagonal matrix whose i^th diagonal is Σ_j ω_ij. The graph Laplacian from these graph matrices is defined in the usual way as L = D − A. Then, the complete orthonormal basis χ_l and eigenvalues λ_l, l ∈ {0, 1, ···, N − 1} obtained from the graph Laplacian, a self-adjoint operator, forms the basis for the graph Fourier transformation. Note that the λ_l are increasingly ordered, and are irrelevant to the order of vertex index in the graph domain. Using these basis, the forward and inverse graph Fourier transformation are defined using the eigenvalues and eigenvectors of L as,

$$\widehat{f}(l)=\langle {\chi }_l,f\rangle =\sum _{n=1}^N{\chi }_l^{\ast }(n)f(n)\text{and}f(n)=\sum _{l=0}^{N-1}\widehat{f}(l){\chi }_l(n)$$ (4)

Using these transforms, we construct spectral graph wavelets by applying bandpass filters at multiple scales and localizing it with an impulse function and low-pass filter for the scaling function.

Here, λ_l, the spectrum of the Laplacian, serves as an analog of the 1-D frequency domain, where scales can be easily defined. This directly provides the key component in obtaining a multi-resolutional view of the signal localized at n. Constructing a kernel function g which acts as band-pass filter in the frequency domain, when g is transformed back to the original graph domain, we directly obtain a representation of the signal for that scale. Repeating this procedure for multiple scales, the set of coefficients obtained for each s ∈ S gives a multi-resolution representation for that particular vertex.

Since the transformed impulse function in the frequency domain is equivalent to a unit function, the wavelet localized at vertex n can now be defined as,

$${\psi }_{s,n}(m)=\sum _{l=0}^{N-1}g(s{\lambda }_l){\chi }_l^{\ast }(n){\chi }_l(m)$$ (5)

where m is a graph vertex. With this in hand, the wavelet coefficients of a given function f(n) is given by the inner product of wavelets and the function,

$$W_f(s,n)=\langle {\psi }_{s,n}f\rangle =\sum _{l=0}^{N-1}g(s{\lambda }_l)\widehat{f}(l){\chi }_l(n)$$ (6)

SGWT follows the same procedure of constructing wavelets as in the continuous wavelet transform. In the fine scale limit, SGWT maintains many of the properties of the traditional wavelet transform, including localization.

Remark

Wavelets in Euclidean space have a rich history in Signal processing. However, defining wavelets in non-Euclidean space is a recent development [6,4], and is especially interesting for network analysis in Neuroimaging.

3 Deriving a Multi-Resolution Perspective of a Network

Line Graphs

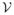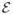In graph theory, one defines the line graph L( ) as a dual form of graph . The L( ) is formed by interchanging the roles of and in . Two vertices in L( ) are connected when the corresponding edges in share a common vertex. The line graph L( ) = { 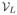, , 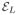ω_L} has a vertex set for the edges { 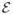, ω} and a edge set that corresponds to the vertices 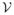in [7].

The transformation of L( ) from a graph is defined as follows. Let g_ij be the elements in the adjacency matrix A_L of L( ), then

$$g_{ij}=\{\begin{array}{ll}1\hfill & \text{if}v\in \mathcal{V},v\backsim e_i,e_j\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (7)

where v is a vertex in 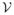and e is an edge in 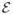. This means that when two edges share a common vertex in , these edges are connected to each other by the common vertex. After this transformation, the isolated vertices in are completely neglected in L( ). If there are no isolated vertices in , then and L( ) have equal number of components. After constructing a line graph L( ) of a graph , the edges in form a completely new domain of analysis and the edge weight ω can be defined as a function defined on each vertex in 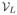, where the connection between each vertex in 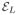is given from 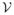. Toy examples of this transformation are shown in Fig. 1.

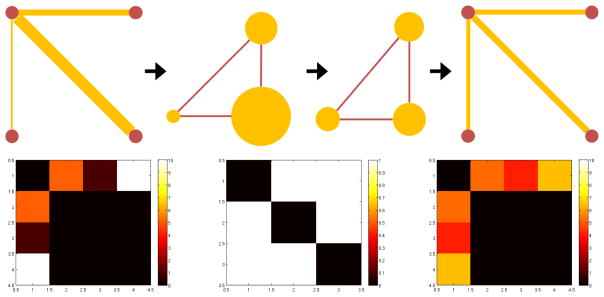
Fig. 1.

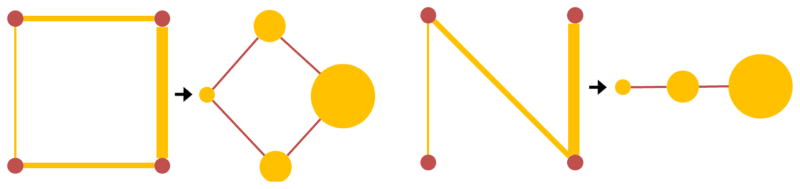
Examples of graphs and the corresponding line graphs. Original graphs with vertices (red) and edges (yellow) with edge weights (thickness), and corresponding line graphs with vertices (yellow) with function (vertex size) and edges (red).

In a measured signal, the true signal tends to change smoothly while noise varies very rapidly in high frequencies. Using wavelets, smoothing can be efficiently performed by removing high frequency components tied to the finer scales, moreover, due to the bandpass property of wavelet, we can get a multi-resolutional view of the given signal. The multi-scale view comes from the inverse wavelet transformation of the resultant function that provides the estimate of the signal at various scales. Rewriting (3) in terms of the graph Fourier basis,

$$f(m)=\frac{1}{C_g}\sum _l\left({\int }_0^{\infty }\frac{g^2(s{\lambda }_l)}{s}\mathrm{d}s\right)\widehat{f}(l){\chi }_l(m)$$ (8)

which sums over the entire scale s. Limiting the scales to the coarse scales will reconstruct the smoothed approximation of the original signal, and the original signal can be reconstructed by adding finer scales.

In order to filter the network structure, it is necessary to bring the network connectivity information as a signal into another domain. As described above, the transformation of a graph domain to a line graph L( ) enables us to view the edge weights as a signal defined in the domain of L( ). We can therefore define the connectivity as a signal on each vertex of L( ), and continue with the smoothing technique using wavelet. An illustrative example of the framework for the network smoothing is given in Fig. 2, where the edge weights are filtered along their connection and not losing the original topology of . The corresponding adjacency matrices are displayed at the bottom.

Fig. 2.

A toy example of graph structure filtering. The top panel shows the graph filtering steps: (1) Construction of the line graph, (2) filtering the signal on the line graph vertices, (3) reconstructing the filtered graph. The bottom panel shows the corresponding adjacency matrices.

In addition to the filtering, we define Wavelet Multi-scale Descriptor (WMD) using the wavelet wavelet coefficients over the signal defined on each vertex as

$${\text{WMD}}_f(n)=\{W_f(s,n)\mid s\in S\}$$ (9)

which characterizes the signal at multi-resolutions on the vertex according to the geometry of the graph. While [18] uses a sphere to obtain the descriptor, which causes data distortion by mapping process, WMD is derived based on the eigenfunction of the original graph itself, and thus avoids ‘ballooning’ [9].

4 Connectivity Differences in Bipolar Disorder

Dataset

We scanned 25 healthy subjects (13 male and 12 female; age: 42.2 ± 10.8) and 25 gender and age matched bipolar subjects (14 male, 11 female; age: 41.7 ± 12.6). All bipolar subjects received comprehensive psychiatric evaluations using the structured clinical interview for DSM disorders (SCID) and met the DSM IV criteria for bipolar I disorder (at the time of image acquisition all subjects have been in an euthymic state for at least 30 days). A Siemens 3T Trio scanner was used to acquire the brain MRI data. High resolution T1-weighted images were acquired with MPRAGE sequence (FOV = 250×250 mm²; TR/TE = 1900/2.26 ms; flip angle = 9°; voxel size = 1×1×1 mm³). Diffusion weighted (DW) images were acquired using SS-SE-EPI sequences (FOV = 190×190 mm²; resolution 2 × 2 × 2 mm³; TR/TE = 8400/93 ms; 64 gradient directions, b = 1000 s/mm² and one minimally DW scan: b=0 image).

Structural brain networks were generated using a pipeline which integrates multiple image processing steps. First, DW images were eddy current corrected using FSL by registering all DW images to their corresponding b=0 images with 12-parameter affine transformations. This was followed by the computation of diffusion tensors and then deterministic tractography using the FACT algorithm [12] built into the DTI Studio program (maximum bending angle 60 degrees; FA cut-off 0.25). T1-weighted images were used to generate label maps using Freesurfer. The number of tracts connecting 87 cortical/subcortical regions were used in constructing 87 × 87 connectivity matrix for each subject.

Group Analysis

There are total 3741 edges in the network. In order to detect connectivity differences between the two groups, we performed a Hotellings T²- test using WMD. WMD was realized by a Mexican-hat wavelet, which was defined at 5 scales over the spectrum of λ. Since typically noise lies in high frequency, we dropped 2 scales that correspond to larger λ, and used the rest for the statistical analysis. When using the raw edge weights, we could not detect any significant difference between the two groups after accounting for Bonferroni correction at α = 0.05 significance level. However, after applying WMD on smoothed edge weights with the proposed method, we identified 5 connections over 9 different brain regions as having significant connectivity differences at a very conservative Bonferroni correction level, 10⁻⁷.

Interpretation

Results showed that relative to control subjects, bipolar patients on average exhibited weaker strength for the connections within the frontal lobe (bilateral precentral to superior frontal) as well as in fiber tracts linking the bilateral hippocampus. These findings are consistent with past studies where abnormalities in the frontal, limbic, and callosal systems have been reported (for a review, see for example [11]). Additionally, previous fMRI studies of euthymic bipolar patients have also consistently revealed frontal hypoactivation [3,2,16]. In contrast, bipolar subjects exhibit a stronger connection, relative to controls, between the left amygdala and the left temporal pole and between the left superior frontal gyrus and the right caudal anterior cingulate. Although our subjects were in euthymia at the time of the scan, these stronger connections in bipolar may be related to amygdala activation during mania as reported in [1].

5 Conclusion

In this paper, we introduced a novel signal filtering approach for brain network data that takes into account the non-Euclidean nature of the structured data. Using a line graph construction from the original network, we perform band-pass filtering of signals defined on network edges to obtain a multi-resolutional view. The algorithm siginficantly improves the statistical sensitivity of connectivity differences using Hotelling’s T²-tests and Bonferroni correction. We believe that adapting non-Euclidean wavelets for improving the statistical properties of brain connectivity networks may improve analysis of a much wider variety of studies.

Fig. 3.

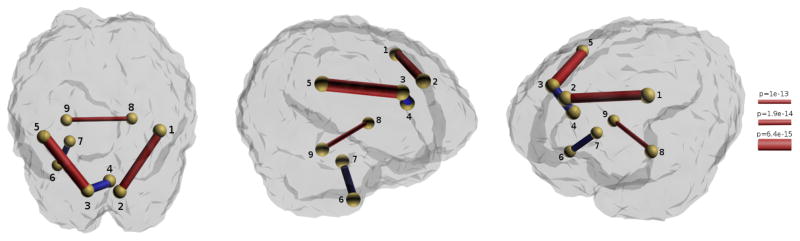
Anatomical connectivity showing group differences between bipolar and controls after Bonferroni threshold at α = 10⁻⁷. Connection thickness represents the p-value in negative log scale; color gives sign of strength: red (and blue) are stronger in controls (and bipolar group). Region labels are: 1. ctx-rh-precentral, 2. ctx-rh-superiorfrontal, 3. ctx-lh-superiorfrontal, 4. ctx-rh-caudal anterior cingulate, 5. ctx-lh-precentral, 6. ctx-lh-temporalpole, 7. left amygdala, 8. right hippocampus, 9. left hippocampus.