Multi-Atlas Segmentation without Registration: A Supervoxel-based Approach

Abstract

Multi-atlas segmentation is a powerful segmentation technique. It has two components: label transfer that transfers segmentation labels from prelabeled atlases to a novel image and label fusion that combines the label transfer results. For reliable label transfer, most methods assume that the structure of interest to be segmented have localized spatial support across different subjects. Although the technique has been successful for many applications, the strong assumption also limits its applicability. For example, multi-atlas segmentation has not been applied for tumor segmentation because it is difficult to derive reliable label transfer for such applications due to the substantial variation in tumor locations. To address this limitation, we propose a label transfer technique for multi-atlas segmentation. Inspired by the Superparsing work [13], we approach this problem in two steps. Our method first oversegments images into homogeneous regions, called supervoxels. For a voxel in a novel image, to find its correspondence in atlases for label transfer, we first locate supervoxels in atlases that are most similar to the supervoxel the target voxel belongs to. Then, voxel-wise correspondence is found through searching for voxels that have most similar patches to the target voxel within the selected atlas supervoxels. We apply this technique for brain tumor segmentation and show promising results.

1 Introduction

Multi-atlas segmentation has been widely applied in medical image analysis, e.g. [10, 8, 9, 4, 11, 15]. This technique has two main components: label transfer and label fusion. In the label transfer step, it computes voxel-wise correspondence between pre-labeled images, called atlases, and a novel target image, from which the atlas segmentation labels are transferred to the target image. Label fusion is then applied to derive a consensus segmentation to reduce segmentation errors produced by label transfer.

So far, multi-atlas segmentation has been mostly applied to problems, where deformable image registration can establish reliable voxel-wise correspondences for label transfer. The advantage of image registration is that it enforces spatial regularization, such as smoothness on the correspondence map, to improve the reliability of voxel-wise correspondences obtained from local appearance matching. For applications such as brain parcellation where the structures of interest have stable spatial structures, registration usually can provide high quality label transfer. However, for problems such as tumor and lesion segmentation where the assumption of localized spatial support does not hold, it is not straightforward to apply registration for label transfer across different subjects. Note that although non-local mean label fusion [4, 11] does not require non-rigid registration for label transfer, it still requires the structure of interest to have localized spatial support across subjects to make the technique practical due to its high computational cost for non-local averaging. In order to extend multi-atlas segmentation to problems where the structure of interest does not have localized spatial support, our contribution is to develop a supervoxel-based label transfer scheme for multi-atlas segmentation.

Our work is inspired by the Superparsing work [13], which was developed for semantic natural scene segmentation. Given pre-labeled training images and a novel target image, this technique first generates oversegmentation for all images using bottom-up segmentation techniques. Each segmented region is treated as a superpixel (or supervoxel in 3D). Typically, an image is represented by hundreds or thousands of superpixels. To segment a novel image, segmentation labels of superpixels in training images are transferred to superpixels in the novel image. For this task, each superpixel is described by a feature vector, which may include intensity, texture histograms and shape features extracted from all pixels within the superpixel. For each superpixel in the target image, the most similar superpixels in the training images are selected based on feature matching for label transfer. After label fusion, the consensus label produced for a superpixel in the target image is assigned to all pixels within the superpixel.

The advantages of employing superpixel for label transfer are three fold: 1) it can be applied to structures that do not have localized spatial support, 2) it significantly reduces the computational burden, making label transfer based multi-atlas segmentation practical for large datasets, and 3) feature matching between superpixels allows more reliable image statistics to be used, which gives more accurate matching than voxel-wise patch matching. The technique also has limitations. First, bottom up oversegmentation may contain errors, i.e. mixing pixels from different label classes into a single superpixel. Hence, its performance is limited by the performance of bottom-up oversegmentation. Second, as extensive studies in the multi-atlas segmentation literature have verified, label fusion should be performed in a way that spatially varies the relative contribution of atlases to accommodate spatially varying performance of label transfer [1, 12]. Performing label fusion at the superpixel level can be considered as a semi-local approach, which may not fully capture spatial variations for optimal label fusion.

To address these limitations, instead of label transfer and fusion at the superpixel level, we propose to use superpixel matching as an additional matching constraint for establishing voxel-wise label transfer and fusion. For each voxel in a novel target image, we first find supervoxels in the atlases that are most similar to the supervoxel it belongs to. Then voxel-wise correspondences of the target voxel are located by searching the most similar voxels within the selected atlas supervoxels by appearance patch matching. This technique maintains the computational efficiency achieved by employing supervoxels and also improves the accuracy of voxel-wise correspondences produced by local patch matching. For validation, we apply our multi-atlas segmentation technique to multimodal brain tumor segmentation and show promising results.

2 Method

2.1 Supervoxel generation and feature extraction

To generate supervoxel representations, we apply the efficient graph-based segmentation technique [6] to oversegment images into homogeneous regions. [6] groups neighboring voxels based on their intensity differences, such that similar voxels are more likely to be grouped together. Since for the tumor segmentation problem addressed in our experiments, multi-modality magnetic resonance (MR) images, including T1, contrast-enhanced T1, T2, and FLAIR, are available, we define intensity difference between two neighboring voxels as the maximal absolute intensity difference between them in all modality channels. In addition, we specify the minimal region size in the resulting oversegmentation to be 100 voxels. These parameters were chosen so that about 1000~2000 supervoxels are produced for each brain image (see Fig. 1 for examples of produced oversegemtnations). With such specifications, an image can be segmented within a few seconds on a single 2GHZ CPU.

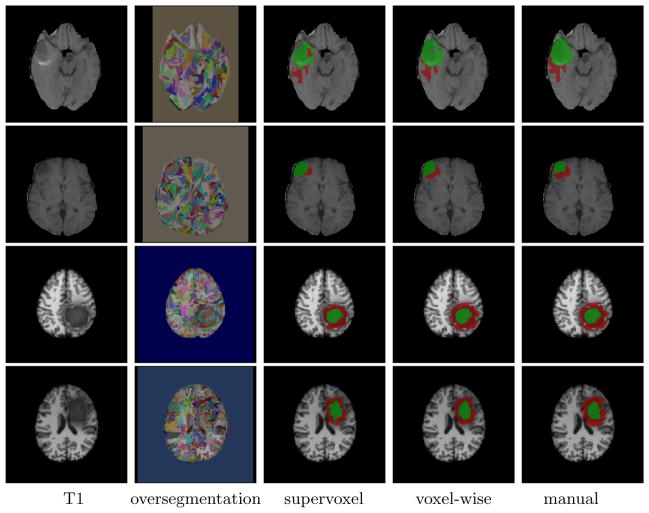
Fig. 1.

Edema (red) and tumor (green) segmentation produced by supervoxel label fusion and our voxel-wise label fusion. From first row to fourth row: high/low grade real data, high/low grade simulated data.

Before extracting features, we apply image histogram equalization implemented by the histeq function in Matlab with default parameters to reduce the intensity scale variations across different subjects. After histogram equalization, the image intensities are normalized into [0, 1] and all processed images have similar intensity histogram profiles. We include the following features to represent each supervoxel: the mean and standard deviation of voxel intensity and gradient within each supervoxel from each modality channel, the intensity and gradient histogram from each modality channel. The histograms are computed with 41 bins. Hence, each supervoxel is described by 344 features in total.

2.2 Supervoxel-based voxel-wise label transfer

Our goal is to find voxel-wise correspondence between a target image and all atlases for label fusion. For this task, we apply image patch based appearance matching. However, directly searching voxel-wise correspondences based on local appearance similarity has limitations. First, local image appearance similarity is not always a reliable indicator for correspondence. Additional regularization constraints, such as smoothness on the correspondence map used in image registration, are often required to make local appearance matching based correspondence searching more reliable. Second, the computation cost for global voxel-wise correspondence searching is too high. Hence, the assumption of localized spatial support for the structure of interest across subjects is necessary for limiting the searching area [4, 11].

One insight provided by the Superparsing work [13] is that regions obtained from bottom up segmentation provide meaningful information for correspondence matching. Hence, we propose to use supervoxel-based region matching as an additional constraint to guide voxel-wise correspondence searching. For each supervoxel in a novel target image, we find K most similar supervoxels in the atlases based on their feature vectors using L1 norm. Based on the selected corresponding supervoxels, we apply label fusion to derive the consensus label for the target supervoxel, as described below. If the target supervoxel is labeled as the structure of interest, then for each voxel within the target supervoxel, we search its corresponding voxels within the K selected atlas supervoxels. Again, L1 norm on appearance patches extracted for the voxels from all modality channels are used for voxel matching. N most similar voxels are selected as the correspondences of the target voxel. Their segmentation labels are transferred and fused into a consensus label for the target voxel.

Limiting the voxel-wise correspondence searching within selected corresponding atlas supervoxels significantly reduces potential matches into a small set of regions that are most likely to contain the correct correspondence and enforces weak spatial regularization on the voxel-wise correspondences. The above mentioned drawbacks in directly using local appearance matching for searching voxel-wise correspondence are properly addressed.

2.3 Label fusion

For label fusion, we apply local weighted voting. The fused consensus label probability for a novel target image T_F is obtained by:

$$p(l\mid x,T_F)=\sum _{j=1}^N{w}_{x(j)}p(l\mid x(j),A),$$ (1)

where x indexes through all voxels in the target image and l indexes through all possible labels. A is the set of all atlases. x(j) is the j_th selected corresponding voxel for x from A using the method described in section 2.2. p(l|x(j), A) is the probability that x(j) votes for label l, which is 1 if x(j) has label l and 0 otherwise. w_x(j) is the voting weights for x(j), with ${\sum }_{j=1}^N{w}_{x(j)}=1$. The consensus segmentation is obtained by selecting the label with the maximal probability for each voxel in the target image. To compute the voting weights, we apply the joint label fusion technique [15], and the solutions are given as:

$${\mathbf{w}}_x=\frac{M_x^{-1}{1}_N}{1_N^t{M}_x^{-1}{1}_N},$$ (2)

where 1_N = [1; 1; …; 1] is a vector of size N. M_x is a dependency matrix capturing the pairwise dependencies of the N selected corresponding atlas voxels voting for wrong labels for the target voxel x, which is computed as:

$$M_x(j,k)~\sum _{m=1}^{L_M}\langle \mid A_F^m(\mathcal{N}(x(j)))-T_F^m(\mathcal{N}(x))\mid ,\mid A_F^m(\mathcal{N}(x(k)))-T_F^m(\mathcal{N}(x))\mid \rangle ,$$ (3)

where m indexes through all modality channels and $\mid A_F^m(\mathcal{N}(x(j)))-T_F^m(\mathcal{N}(x))\mid$ is the vector of absolute intensity difference between a selected atlas image and the target image over local patches centered at voxel x(j) and voxel x, respectively. In our experiments, we applied a patch size 5 × 5 × 5. 〈·, ·〉 is the dot product. L_M is the total number of modality channels.

Label fusion at the supervoxel level

In our experiments, we compare our voxel-wise label transfer and fusion approach with the standard supervoxel-wise label transfer and fusion approach [13]. For supervoxel-wise label fusion, we compute the label distribution of all voxels within an atlas supervoxel to represent its label votes. As in [13], we apply majority voting to fuse the votes from the K selected corresponding supervoxels. The label that has the greatest consensus vote is assigned to all voxels within the target supervoxel.

Machine learning based error correction

Multi-atlas segmentation may produce systematic segmentation errors with respect to manual segmentation. We apply the technique described in [14] to train AdaBoost classifiers [7] to automatically correct systematic errors produced by our multi-atlas segmentation method on a voxel by voxel basis.

3 Experiments

We evaluate our method on brain tumor segmentation. Tumor segmentation is an ideal application for testing our method because the classical deformable registration based multi-atlas segmentation technique and non-local mean methods cannot be directly applied due to the substantial variation in tumor locations.

3.1 Data and experiment setup

To facilitate comparisons with state-of-the-art brain tumor segmentation techniques, we evaluate our method on the data from MICCAI 2012 Multimodal Brain Tumor Segmentation (BRATS) challenge. This dataset contains both real patient data and simulated data. The images are skull-stripped multimodal MR images, including T1, contrast enhanced T1, T2, and FLAIR. Both high grade and low grade tumor data are available for real patient data and simulated data. Overall, there are 20 real patient data with high grade tumors, 10 real patient data with low grade tumors. For simulated data, both high grade and low grade tumor data contain 25 image sets. For evaluation, we conduct leave-one-out cross-validation for each of the four datasets separately, i.e. each image is segmented by the remaining images of its kind.

Since empirical studies have shown that the performance of multi-atlas segmentation usually reaches saturated levels when 20 or more atlases are used, e.g. [2], we fixed the parameter K, the number of selected candidate corresponding atlas supervoxels, and N, the number of selected corresponding voxels for label transfer, to be 20 in our experiments.

3.2 Results

Table 1 summarizes the performance for edema and tumor segmentation in terms of Dice Similarity Coefficient (DSC) produced by each method for each of the four datasets. Overall, automatic segmentation algorithms all produced more accurate results for simulated data, possibly due to the fact that simulated data have better image quality. Our supervoxel matching based voxel-wise label fusion approach produced substantial improvements over the supervoxel-wise label fusion approach. Machine learning based error correction (EC) produced substantial improvement over our voxel-wise label fusion approach for real patient data, but did not produce much improvement for the simulated data, indicating that our method did not produce prominent systematic errors for simulated data. In terms of computational cost, supervoxel-wise label fusion segments an image within a few minutes using ten or twenty atlases. Supervoxel matching based voxel-wise label fusion usually takes about 30 minutes to segment one image, which is significantly faster than deformable registration-based label fusion.

Table 1.

The performance of edema and tumor segmentation in terms of Dice similarity coefficient (2|A ∩ B|/|A| + |B|) produced by each method.

Real patient	edema(High)	tumor (High)	edema(Low)	tumor (Low)
supervoxel	0.58±0.20	0.62±0.29	0.32±0.14	0.41±0.27
voxel-wise	0.64±0.17	0.63±0.28	0.37±0.16	0.54±0.22
voxel-wise + EC	0.66±0.15	0.67±0.28	0.41±0.15	0.60±0.25
[16]	0.70±0.09	0.71±0.24	0.44±0.18	0.62±0.27
[3]	0.61±0.15	0.62±0.27	0.35±0.18	0.49±0.26

Simulated	edema(High)	tumor (High)	edema(Low)	tumor (Low)
supervoxel	0.55±0.29	0.86±0.05	0.39±0.24	0.74±0.07
voxel-wise	0.65±0.29	0.92±0.04	0.61±0.25	0.82±0.06
voxel-wise + EC	0.67±0.28	0.92±0.04	0.59±0.26	0.83±0.06
[16]	0.65±0.27	0.90±0.05	0.55±0.23	0.71±0.20
[3]	0.68±0.26	0.90±0.06	0.57±0.24	0.74±0.10

Overall, our method compares well with the state-of-the-art algorithms [16] and [3], which finished in the top two places in the BRATS challenge.¹ Both methods apply decision forest based classification technique [5]. Our results are consistently better than those reported in [3], except for edema segmentation for high grade real patient data. In comparison with [16], our results on real patient data are worse but our results on simulated data are better. Note that classification-based approach implicitly chooses training samples for classifying new data. The key difference from our method is that no spatial regularization is used for locating training samples for classifying target voxels, which may compromise the reliability of the located training samples.

Fig. 1 shows a few segmentation results produced by supervoxel label fusion and our voxel-wise label fusion. Note that since the supervoxels produced by bottom up segmentation have irregular shapes, the results produced by super-voxel label fusion also have irregular shapes. This effect is greatly reduced when voxel-wise label fusion is applied.

4 Conclusions

We introduced a novel region matching based voxel-wise label transfer scheme for multi-atlas segmentation. This technique is much faster than registration-based label transfer and can be easily applied on large datasets. As a proof of concept, we showed promising performance on a brain tumor segmentation problem.

In our current experiments, a fairly crude set of criteria and simple features were used to create supervoxel representations. There is room left for improvement by specially tuning the supervoxel representation for multimodal MRI tumor segmentation. We will also explore the performance of the supervoxel-based label transfer scheme for segmenting structures with less distinctive appearance patterns than tumors.