Nonautonomous contact guidance signaling during collective cell migration

Significance

Group cell migration in response to guidance signals is a critical process in determining tissue organization. Here we explore the response of groups of cells to topographic guidance signals and reveal that guidance information can be transmitted between cells within the group. Significantly, we show that guidance information transmission is not dependent on cell–cell junctions or tensional forces within cells. Instead, we propose that signal transmission arises from a volume exclusion-type mechanism and is an emergent property that can arise in dense cell populations.

Abstract

Directed migration of groups of cells is a critical aspect of tissue morphogenesis that ensures proper tissue organization and, consequently, function. Cells moving in groups, unlike single cells, must coordinate their migratory behavior to maintain tissue integrity. During directed migration, cells are guided by a combination of mechanical and chemical cues presented by neighboring cells and the surrounding extracellular matrix. One important class of signals that guide cell migration includes topographic cues. Although the contact guidance response of individual cells to topographic cues has been extensively characterized, little is known about the response of groups of cells to topographic cues, the impact of such cues on cell–cell coordination within groups, and the transmission of nonautonomous contact guidance information between neighboring cells. Here, we explore these phenomena by quantifying the migratory response of confluent monolayers of epithelial and fibroblast cells to contact guidance cues provided by grooved topography. We show that, in both sparse clusters and confluent sheets, individual cells are contact-guided by grooves and show more coordinated behavior on grooved versus flat substrates. Furthermore, we demonstrate both in vitro and in silico that the guidance signal provided by a groove can propagate between neighboring cells in a confluent monolayer, and that the distance over which signal propagation occurs is not significantly influenced by the strength of cell–cell junctions but is an emergent property, similar to cellular streaming, triggered by mechanical exclusion interactions within the collective system.

Directed collective cell migration is a fundamental process during embryo development (1), adult organ regeneration (2, 3), wound healing (4), and the progression of metastatic cancer (4). During collective migration, individual cells must coordinate their motion both locally and globally and move as a cohesive group with intact, often cadherin-based, junctions and supracellular organization of the actin cytoskeletons of all cells within the group (4). Mechanical cooperation of intercellular tensional forces via cell–cell junctions is thought to underlie coordination between neighboring cells during collective movement (5–7). The local microenvironment of the cells provides the chemical and mechanical guidance signals that help direct collective migration. The rigidity and topographic texture of the local environment, as well as the tissue-level geometrical confinement of the cell population, can influence cell coordination and invasiveness (4, 8). Despite the fact that the topographic texture of the extracellular matrix is known to play a role in tumor cell dispersion into the surrounding tissue (9), little is known about the role of topographic cues on the collective guidance of cell populations in vivo and in vitro.

A number of cell types have shown contact-guided migration along grooved substrates (10–13) when cultured as single cells. The exact mechanism underlying contact guidance is not completely understood, but it is clear that, above a cell type-specific threshold groove depth, topographic features influence the organization of the actin cytoskeleton (11, 12, 14–17) and of focal adhesions (11, 12, 15–18) and that this altered organization is translated into directed migration (11, 13, 19–22). In contrast to single cells, the collective response of cohorts of cells to topographic signals is not well understood (12, 23), in particular in confined space (defined here as no free space available within or surrounding the sheet) where cells are not experiencing a polarization cue from the presence of open space. Contact guidance within a group of cells is a more complex process than in the single cell case; in groups, changes in cytoskeletal organization induced by the topographic feature must be compatible with the cytoskeletal coordination required between neighboring cells. Furthermore, it is not known whether each of the cells moving within a group responds autonomously to guidance cues or whether guidance signals can act nonautonomously (i.e., be transmitted between neighbors to act on cells with which they are not in direct contact) as a result of local steric interactions within the group and the need for local intercellular coordination.

Here, we set out to explore these fundamental questions by characterizing the guidance of individual cells and dense cell sheets in response to a topographic signal. We also presented confluent cell sheets with a hybrid surface containing a defined interface between a grooved and a flat region. This allowed us to determine whether the contact guidance signal from the grooved region of the substrate would act nonautonomously through a sheet of connected cells to guide cell migration in nongrooved regions. Our results demonstrate that, within both clusters and confluent cell sheets, cells move in streams oriented along the grooves and that guidance signals can propagate within continuous cell sheets to neighboring cells that are not exposed to the topographic cue. Surprisingly, we found both experimentally and using computational modeling that the distance over which the guidance signal propagates is independent of junction strength, suggesting a nontensional-based mechanism of cell–cell coordination underlies guidance signal propagation in confined monolayers. Furthermore, we show that signal propagation extends over a similar length scale as cooperative cell streams, and that both phenomena are dependent on similar physical parameters of the cells, consistent with a volume exclusion-type mechanism.

Results

Guidance of Cell Migration by Grooves.

We tracked the migration paths of individual human retinal pigment epithelial cells (ARPE-19) and human foreskin fibroblast (BJ) cells at both sparse and confluent densities on flat and grooved topography using a custom-built grooved 96-well plate (Fig. S1A). ARPE-19 cells were selected because they form confluent epithelial monolayer sheets, and BJ cells were selected to assess the behavior of a nonepithelial cell type in which continuous cell–cell junctions are not formed within the sheet (24). On grooves, both ARPE-19 and BJ cells migrated parallel to the direction of the grooves (Movie S1), as demonstrated by the large peaks between −25° and 25° in the distribution of cell migration angles shown in Fig. 1 A and B. As a measure of guidance effectiveness, we quantified the percent of cells within this peak (i.e., within the range −25° to 25°). At sparse densities, 52.1% of ARPE-19 and 70.7% of BJ cells migrated in a direction parallel to the grooves. This effect was more pronounced at confluent densities, with 59.1% of ARPE-19 and 80.6% of BJ cells lying within the peak. These data suggest that grooves are capable of producing robust guidance of cell migration at both sparse and confluent cell densities in the epithelial and fibroblast cell types tested.

Fig. 1.

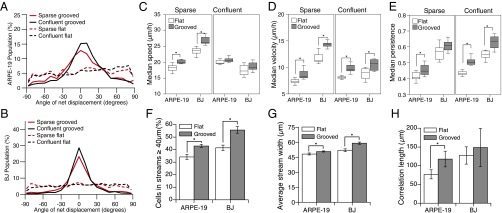
Quantification of cell migration and coordination behavior on flat and grooved substrates. Cell migration characteristics of ARPE-19 and BJ cells at sparse and confluent cell densities on flat versus grooved substrates. (A and B) Distribution of cell migration direction on flat versus grooved substrates for (A) ARPE-19 and (B) BJ cells. The peak created by the grooved substrates between −25° and 25° indicates cell migration guidance. (C) Cell speed was significantly increased by grooves in sparse ARPE-19 and BJ cells, but not in confluent cell sheets of ARPE-19 or BJ cells. (D) Cell velocity was significantly increased by grooves in sparse ARPE-19 and BJ cells and in confluent cell sheets of ARPE-19 and BJ. (E) Cell persistence was significantly increased by grooves in sparse ARPE-19 and in confluent cell sheets of ARPE-19 and BJ but not significantly different in sparse BJ cells. (F) Grooves significantly increased the percentage of cells participating in streams of width greater than 40 µm for both ARPE-19 and BJ cells. (G) Grooves significantly increased stream width in both ARPE-19 and BJ cells. (H) Grooves significantly increased correlation length in ARPE-19 but not BJ cells. Error bars represent 95% confidence intervals.

Grooved Topography Increases Confluent Cell Velocity and Persistence but Not Speed.

We next sought to quantify the impact of contact guidance on the migratory properties of cells. We quantified cellular speed (total distance traveled over time), velocity (net distance traveled over time), and persistence (velocity divided by speed) of cells on flat versus grooved substrates. As observed previously (22, 25) at sparse densities, cell migration speeds were moderately enhanced on grooves compared with flat substrates by 10.5% and 14.4% for ARPE-19 and BJ cells, respectively. No significant differences were observed, however, for confluent cells (Fig. 1C). This occurred despite the fact that, at both seeding densities, we observed alignment of the actin cytoskeleton with the grooves (Fig. S2), which has been hypothesized to account for more efficient migration, and hence increased speed, in sparse cells migrating on grooves (22). In contrast, cell velocity was significantly increased on grooves at both cell densities (Fig. 1D). Consistent with this increase in velocity, the grooved substrates increased persistence in confluent cells by 16.5% and 14.5% for ARPE-19 and BJ cells, respectively (Fig. 1E), indicating that within confluent sheets, grooves cause individual cells to move in a more directed fashion.

Grooved Topography Increases Intercellular Coordination.

We next wanted to determine whether contact guidance affected cell–cell cooperation between neighbors within confluent sheets. Groups of epithelial cells within confluent sheets have previously been described to form cooperative “streams” whose internal dynamics are reminiscent of glass-like behavior (26, 27). Narrow streams of coordinated groups of cells formed within confluent sheets of both ARPE-19 epithelial cells and BJ fibroblast cells on both flat and grooved substrates (Fig. S3). As a quantitative measure of cell–cell cooperation, we quantified both the percentage of cells migrating in streams (i.e., cells in streams ≥40 μm or more than two cells wide) and the width of the streams. We also calculated a correlation length, which assesses the distance over which cell behavior is coordinated (28). Grooves significantly increased the percentage of cells participating in streams (Fig. 1F), stream width (Fig. 1G), and the correlation length (in ARPE-19 cells only) (Fig. 1H). However, the increase in the number of cells that participate in streams and the distance over which streams extend could simply be attributed to the response of individual cells. By restricting the motion of the cells to directions parallel to the grooves, the number of cells moving in the same direction could increase independently of any increased coordination between neighboring cells. It is therefore unclear from this result whether the increased cooperation observed arises from autonomous but restricted directed motion of individual cells within the sheet or whether the guidance signal from the grooves acting on one cell propagates to nonautonomously guide neighboring cells and increase cell–cell coordination.

Propagation of Contact Guidance Signals from a Topographic Feature.

To better understand the impact of topographic cues on cell–cell coordination and distinguish between autonomous and nonautonomous guidance effects, we next set out to determine whether guidance signals can propagate from a groove feature through a sheet of cells to induce guided motion of cells some distance from the groove feature. To do this, we created hybrid substrates with a defined interface between flat and grooved regions (Fig. S1B). We cultured cells as a continuous confluent sheet over the whole substrate and quantified cell migration at the interface region between the grooved and nongrooved sections of the substrate. To investigate guidance propagation, we determined how far from this interface cells migrated in a guided manner.

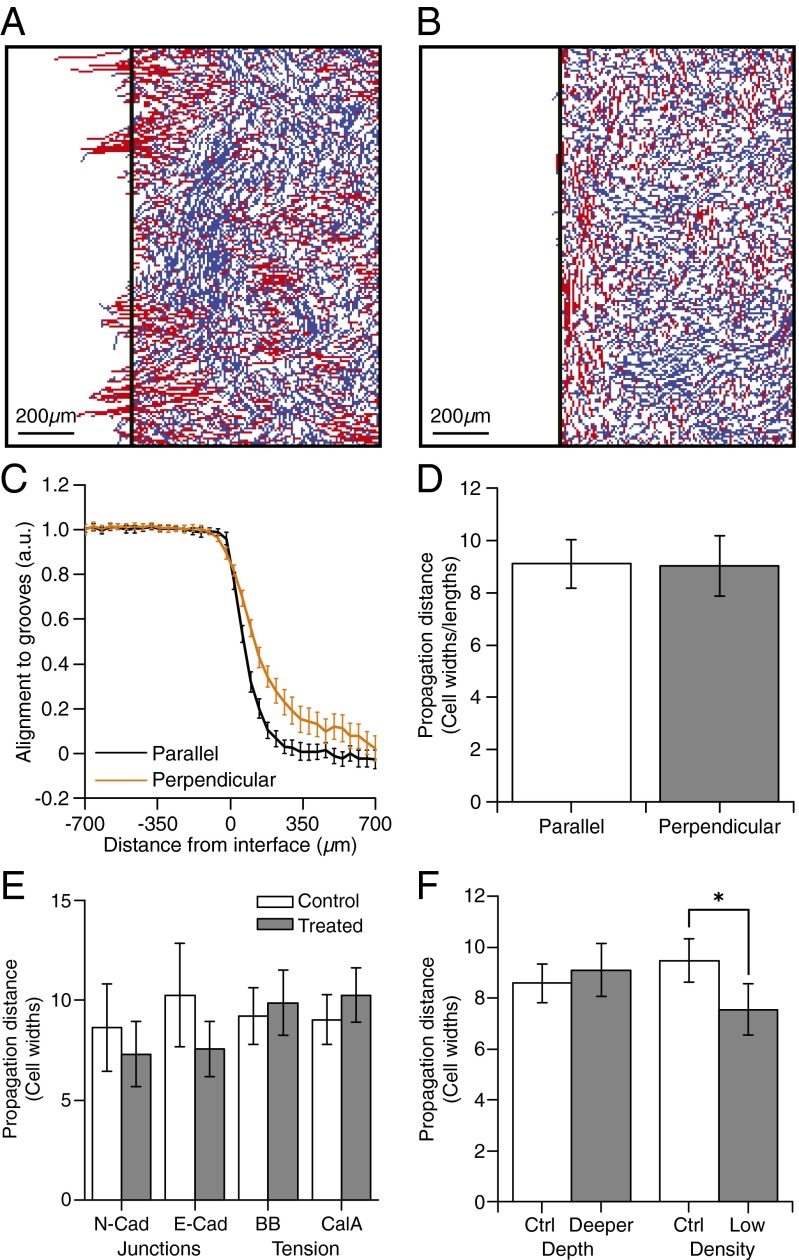
Continuous ARPE-19 cell sheets showed normal morphology (Fig. S4 A–C) within the cell sheet on the hybrid surfaces, and cell–cell junctions were not disrupted over the interface. Cells on the grooved side of the interface and on the interface itself showed aligned actin, whereas cells on the flat side, as little as three cells away from the interface, showed isotropically distributed actin (quantification is shown in Fig. S4D). We tracked cell migration at grooved–flat interfaces for substrates with grooves parallel or perpendicular to the interface and colored cell tracks red if migrating within ±25° of the groove direction, or blue otherwise (Fig. 2 A and B). In both cases, cells on grooves showed guided behavior, whereas cells on flat surfaces showed an isotropic distribution of movement direction. The transition from guided to random cell migration, however, was not exactly at the flat–grooved interface. To determine where the transition from guided to random cell migration occurred, we quantified the component of the velocity vector parallel to the groove direction as a function of the horizontal position within the sheet (Fig. 2C) and scaled values between 0 (fully random movement) and 1 (aligned migration). The distance at which this scaled value dropped to 0.321 (i.e., when the average cell velocity vector deviated more than 25° from the groove direction) was defined as the propagation distance (see SI Methods for calculation details).

Fig. 2.

Quantification of guidance propagation from a topographic feature. Guidance propagates about nine cells. Groove depth, adherens junctions, and myosin activity do not affect propagation distance. (A and B) Migration tracks of cells located on the flat region at start of the experiment on surfaces with (A) grooves perpendicular or (B) grooves parallel to the interface. Tracks are colored according to their angles [guided (red) versus nonguided (blue)]. (C) Quantification of alignment of cell migration direction with groove direction as a function of distance from the interface for grooves parallel or perpendicular to the interface. (D) Propagation distance from the interface, quantified as the distance at which the curves in C reach 0.321 (i.e., cells no longer move within 25° of the groove direction) for grooves parallel and perpendicular to the interface. (E) Propagation of guidance signals from the interface for parallel grooves in GFP-N-cadherin overexpressing ARPE-19 cells, anti–E-cadherin-treated ARPE-19 cells, blebbistain (BB)-treated cells, and calyculin A (CalA)-treated cells. No significant difference in signal propagation distance was observed between treated and control cells. Measurements were made on at least 19 wells from at least three independent experiments. (F) Propagation distance from the interface measured for parallel grooves of different depths and for cell sheets at different densities. No significant difference in signal propagation distance was observed between deep and shallow grooves. Sheets with a high cell density did, however, show a significantly higher propagation distance than cells in low-density sheets.

When grooves were oriented perpendicular to the interface, groups of cells from the flat region randomly migrated over the interface onto grooved regions and became guided by the grooves (Fig. 2A). This transition from random to guided migration as cells cross the interface led to increased migration of cells on flat substrate regions toward the interface extending several rows of cells (Fig. 2 C and D). The average distance from the interface at which cells continued to migrate in a directed fashion was 217 ± 29 μm (95% confidence intervals) or 9 ± 1 cell lengths (cells are elongated perpendicular to the interface) into the flat substrate. We speculate that as groups of cells randomly cross the interface they migrate along the grooves in a directed fashion, pushing or pulling cells located at the vicinity of the interface; this biases the migration of the cells proximal to the interface, leading to funneling of the cells across the flat–groove interface and disruption of random migration in a portion of the flat region. When grooves were oriented parallel to the interface, however, cells tended not to cross the interface between the grooved and flat region (Fig. 2B). Guided cell behavior was still observed to propagate a distance of 111 ± 12 µm (95% confidence interval) or 9 ± 1 cell widths (cells are elongated parallel to the interface) beyond the grooved–flat interface into the flat region of the substrate, suggesting that cells do not need to cross the interface and make contact with the groove for aligned cell migration to occur on the flat region proximal to the interface (Movie S2). In this case, guidance arose only from propagation of the guidance signal between cells in contact with the grooves and cells located on flat regions of the substrate (Fig. 2D), allowing us to better probe the mechanism of nonautonomous guidance.

Based on existing models that describe tension-based mechanisms of cell–cell coordination (5–7), we hypothesized that tensional forces transmitted between the cells via cell–cell junctions would underlie this guidance signal propagation and that the distance from the interface that the guidance signal propagates should depend on junction strength. To test this hypothesis, we characterized signal propagation in ARPE-19 cells with modified adhesion and contractility. Specifically, we overexpressed GFP-N-cadherin to increase cell–cell adhesion (overexpression of N-cadherin levels at membrane and impact on cell migration properties are quantified in Fig. S5) and disrupted junctions by incubation in medium with a calcium chelator followed by incubation with anti–E-cadherin antibodies to prevent reformation of the junctions (junction marker expression is characterized in Fig. S6). Surprisingly, we found that neither increasing nor decreasing cell–cell adhesion affected the signal propagation distance within the sheet (Fig. 2E). To further explore the influence of tension, we measured propagation distance in cells treated with calyculin A or blebbistatin to increase or decrease myosin activity (Fig. S7) and the ability of the cells to generate tension, respectively. Consistent with our observations of cells with modified junction strength, neither treatment significantly changed the distance over which the guidance signal propagated (Fig. 2E), providing evidence that a nontensional-based mechanism dominates signal propagation in this context.

We next asked whether geometric parameters in the system could influence signal propagation. Because groove depth has been shown to be the key geometric feature that influences contact guidance of migration in single cells (13), we first assessed whether groove depth affected propagation distance but found that propagation measurements made on deep versus shallow grooves showed no significant differences (Fig. 2F). We next hypothesized that signal propagation could result from tight packing of the cells in the sheet because space availability has previously been shown to affect cell migration and coordination behavior (8). We therefore conducted experiments at high and low cell densities to be able to vary cell size and change the sheet packing. We found that decreasing cell density (and therefore increasing cell area) significantly decreased the distance of signal propagation (Fig. 2F). This suggested that sheet architecture and limited free space available for cell reorganization could provide a nontensional-based mechanism for signal propagation.

Cellular Streaming Model of Signal Propagation.

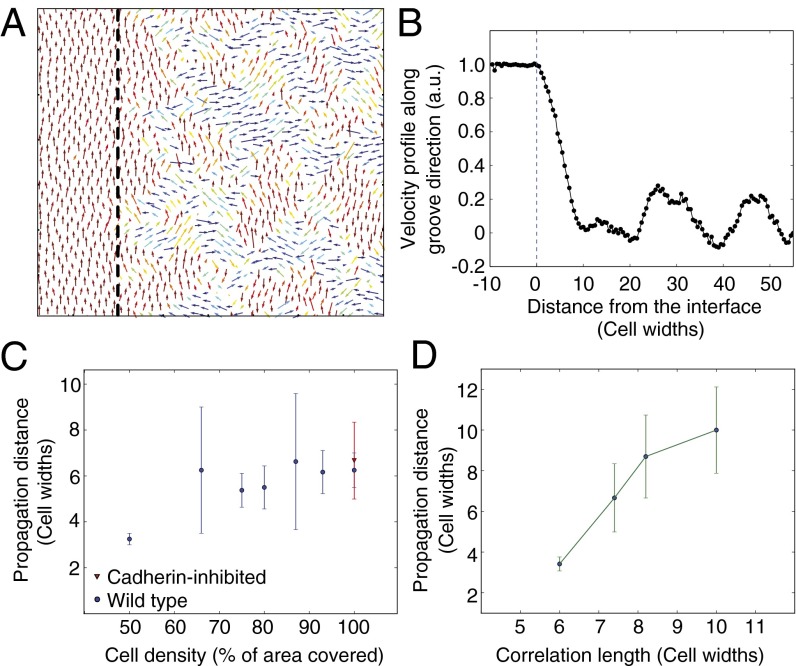
To further probe the possibility that the underlying mechanism of signal propagation originates from steric constraints owing to limited free space, we adapted an existing computational model of cell streaming in confluent sheets (8, 29, 30) to model cell behavior on our hybrid substrates in the parallel case configuration. The main biophysical parameters in the model are (i) membrane energy of cell–cell junctions and any unbound membrane (controlling the cohesion of the cell population) and (ii) the motile force that cells exert on the substrate and persistence of cell polarization. The volume of each cell is constrained by a high incompressibility, enabling steric mechanical interactions between neighboring cells owing to volume exclusion. Two different domains were introduced: Cells on the grooved region were modeled by biasing their migration direction to be parallel to the interface, whereas cells in the flat region had no preferred velocity direction. Model parameters for each cell type (wild-type cells and cells with modified junction strengths) were derived from our experimental measurements of bulk migration dynamics on flat substrates (29). We then analyzed how far guided migration propagated from the grooved domain into the flat domain. Consistent with experimental observations, our model predicted guided migration extending past the grooves, decaying to random behavior 10 cell diameters into the flat region (Fig. 3 A and B and Movie S3) in the parallel interface case. Furthermore, for cells with reduced junction strength (and hence cohesion), we found that as long as the cell density remained above 80% of confluence, there was no difference in guidance signal propagation distance compared with wild-type cells and that steric mechanical interactions alone, arising from the incompressibility of the cells, were sufficient to propagate the directional effect of the grooves (i.e., movement within ±25° of the grooves) up to six cells away from the boundary (Fig. 3C and Movie S4). Although the representation of cohesive forces is very simplistic in the model, this observation nevertheless shows that steric mechanical interactions owing to cell incompressibility are sufficient to trigger collective effects and propagate the guidance signal away from the interface and that, consistent with our experimental observations, this effect is independent of junction strength.

Fig. 3.

Propagation distance predictions from computational modeling. (A) Cell velocity field from computational model. Cells to the left of the interface (indicated by the dashed line) were biased to move vertically, mimicking cells on grooves. No bias was applied to cells to the right of the interface. Arrows are placed at the center of each cell within the sheet. Colors indicate the direction of migration. (B) Mean vertical velocity as a function of the distance from the interface for the parallel grooves case. The data are normalized so that the mean vertical velocity on the grooves is 1. The propagation distance is defined by the intersection between the curve and 0.321. (C) Propagation as a function of cell density for wild-type (blue) and cadherin-inhibited (red) cells. (D) Propagation distance as a function of the correlation of the cell population. According to the model, a correlation exists between propagation distance and correlation length. Error bars represent 95% confidence intervals.

Discussion

Previous work has extensively characterized contact guidance in single cells. Here, we describe the collective response of confined confluent cell sheets to grooved topographic guidance signals. We found that interactions between neighboring cells do not prevent guidance by the grooves and that individual cells within the confluent sheet migrate in narrow streams ∼50 μm wide (three or four cells), parallel to the direction of the grooves. As with single cells, the presence of the groove guidance signal increases velocity and persistence in confluent cell sheets. Unlike in sparse cell experiments, however, grooves do not increase migration speed in confluent cell sheets. Increases in sparse cell migration speed on grooves have previously been explained by the increased organization of the cytoskeleton leading to more efficient migration (22). However, on grooved substrates, not only sparse but also confluent cells exhibited actin alignment parallel to the grooves. This suggests that either changes in cytoskeletal organization induced by the grooves in confluent cell sheets are not sufficient to increase cell speed or that factors alternative to actin organization, such as cell junction properties or lack of free space, limit maximum cell speed in confluent sheets. Of these two possibilities, lack of free space seems most likely, given that that reducing cell junction strength has no effect on cell speed within confluent sheets (Fig. S6).

In addition to increases in cellular persistence and velocity, grooves increased the percentage of cells moving as streams, the average stream width, and the average correlation length (for ARPE-19 cells only), all measures of cell–cell coordination within confluent sheets. Furthermore, we found that topographic cues have the potential to afffect cell–cell coordination beyond just autonomously limiting the migration direction of individual cells and that the impact of this propagation depends on groove orientation. When monolayers were observed on hybrid surfaces containing a sharp interface between grooved and nongrooved regions in which the grooves were perpendicular to the interface, cells from flat regions that randomly crossed the interface induced the movement of neighboring cells to also cross the interface and become guided by the grooves. When the grooves were parallel to the interface, cells moved along the interface, rarely crossing it, and guidance information from grooved regions was transmitted between neighboring cells to affect cells on flat regions that never make contact with the groove. Interestingly, in this situation, guidance of cells in flat regions proximal to the grooved–flat interface seems to be an emergent property characteristic of groups of densely packed cells and is not due to alignment of the actin cytoskeleton, because cells more than three cells from the interface did not show aligned actin (as quantified in Fig. S4D). Furthermore, increasing groove depth, which is known to increase extent of cell alignment with the groove, and likely therefore actin alignment (31), had no impact on propagation distance. Surprisingly, the distance over which signal propagation occurred was also independent of cell junction properties or tension within the cell (Figs. 2F and 3C).

To probe alternative nontension-based mechanisms that may explain the observed guidance signal propagation behavior, we compared the properties of signal propagation to cellular streaming, a cooperative process observed in dense cell sheets. Cell streaming also requires cell–cell coordination and is observed above a threshold cell density (32) and has previously been compared with behavior in crowded particulate systems (26, 33). In such systems, cooperative movement arises owing to volume exclusion and forced reorganization of the particles within a confined space. Consistent with this nontension-based description of streaming, we found that modifications to junction strength and myosin activity (tension) have no significant effect on streaming correlation length (Fig. S8). By characterizing the behavior of noncohesive cell populations in silico, we also observed that simple steric interactions are sufficient to trigger collective effects, spatial correlations, and signal propagation (Fig. 3C). We therefore propose that guidance signal propagation in confined confluent cell sheets arises from the same volume exclusion phenomenon that produces cell streaming.

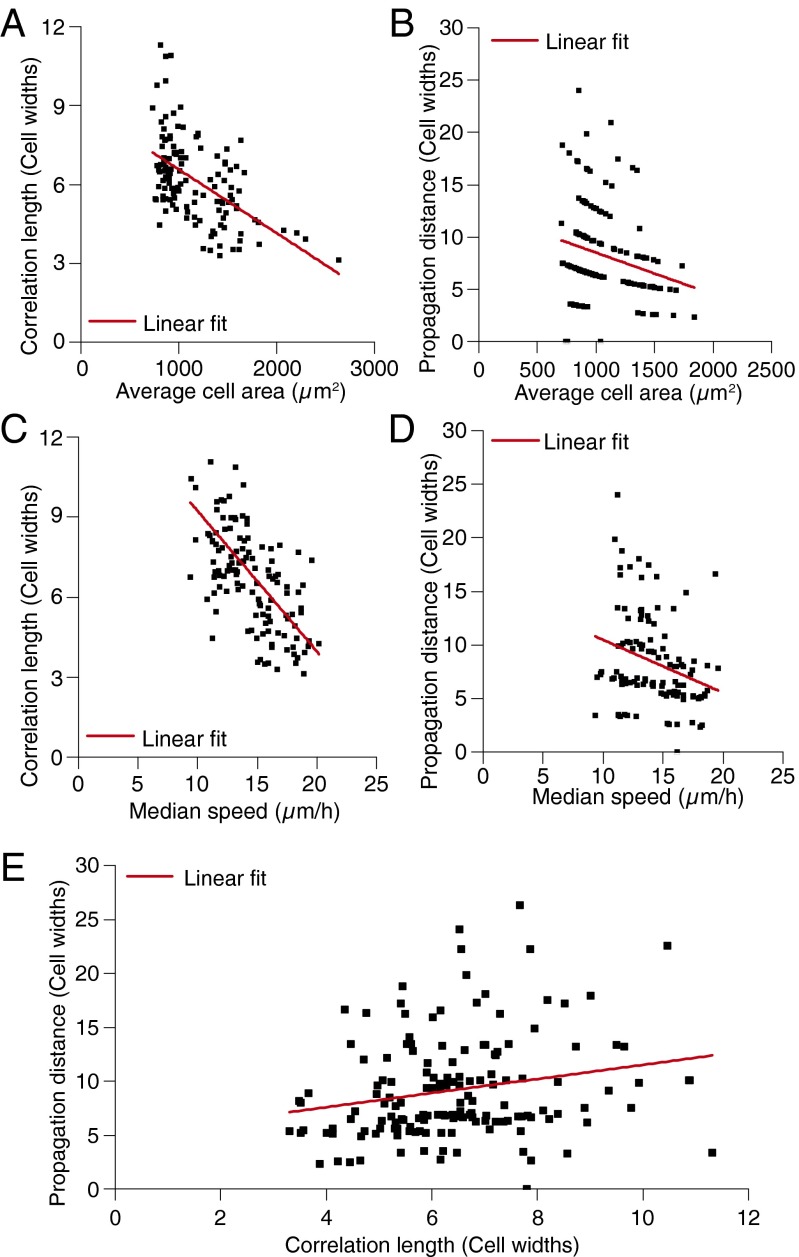
Consistent with a volume exclusion mechanism and our in silico results (Fig. 3C), our experimental data show that both correlation length (Fig. 4A) and signal propagation distance (Figs. 2F and 4B) correlate with cell density. Depending on the properties of the crowded particles, the length over which correlated behavior extends is also predicted to depend on particle speed (28). These trends are reproduced in the model, because larger cell velocities arise owing to larger motile forces, which are also responsible for a decrease in cell–cell coordination (29) (Fig. S9). Experimentally, we also observe this dependence: our data show a statistically significant inverse relationship between correlation length and cell speed (Fig. 4C), where faster objects show correlated behavior over a shorter range. Similarly, propagation distance is inversely proportional to cell speed (Fig. 4D). Because correlation length and propagation length both show similar dependencies on object size (cell area) and object speed, we assessed the correlation of these parameters in both our in silico and in vitro data. Both our model (Fig. 3D) and our experimental data (Fig. 4E) show a statistically significant correlation between correlation length and propagation distance, providing further evidence that the volume exclusion mechanism underlying cell streaming also determines signal propagation distance in this context.

Fig. 4.

Identifying relationships between propagation distance, correlation length, cell density, and cell speed from in vitro data. (A) Correlation length as a function of average cell area measured from cells on flat substrate regions showing a significant correlation (R = 0.538 versus R_significant = 0.195 for n = 127). (B) Signal propagation distance as a function of average cell area measured at the interface showing a significant correlation (R = 0.241 versus R_significant = 0.138 for n = 154). Propagation distance being measured in 40-µm bins results in the observed banding/segregation of the data. (C) Correlation length as a function of median cell speed measured from cells on flat substrate regions showing a significant correlation (R = 0.623 versus R_significant = 0.195 for n = 127). (D) Signal propagation distance as a function of median cell speed (speed measurements made on flat substrate regions) showing a significant correlation (R = 0.284 versus R_significant = 0.195 for n = 116). (E) Propagation distance as a function of correlation length (correlation length measured from cells on flat substrate regions) showing a significant correlation (R = 0.214 versus R_significant = 0.138 for n = 153).

Taken together, our data suggest that when cells are in constrained space tension-based forces at junctions, which are typically used to explain cell–cell cooperation during group migration, are not in fact a dominant factor in determining cooperative behaviors such as cell streaming and propagation of guidance signals. The spatial range over which cooperative behaviors such as streaming and signal propagation extend falls within a limited range (six to nine cells) over a wide range of experimental conditions. This is consistent with a model in which intrinsic physical properties of the cells are critical parameters that affect cell migration but are essentially unchangeable in typical culture conditions. For example, altering cell viscosity (which affects cell compressibility) could change collective migration but would also disrupt the viability and confluence of the cell sheet. Even cell area, which we found affects cooperation, can only vary within a limited range while maintaining confluence. A key challenge for the future will be to better understand the underlying mechanism driving stream formation in dense cell sheets and hence determine what cellular parameters, in addition to area, dictate the number of cells that participate in a particular stream. Although our work provides a better understanding of the factors that affect how cells cooperate during group migration in a constrained and textured space, a complete understanding of cell cooperation is still required to provide important tools for engineering tissue morphogenesis for regenerative medicine applications and to provide insight into tissue formation in the developing embryo.

Methods

Grooved Plate Formation and Characterization.

We assembled a 96-well plate with 48 flat-bottom and 48 grooved-bottom wells. The grooves were sinusoidal in shape, 1 μm in pitch, and 152.7 ± 1.5 nm (SEM) in depth (characterized by atomic force microscopy). Complete fabrication details are given in SI Methods.

Cell Culture and Live Cell Imaging.

We conducted experiments using human retinal epithelial ARPE-19 cells (ATTC) and human foreskin fibroblast BJ cells (ATTC). Before live cell imaging, cells were stained with 500 ng/mL Hoechst 33342 (Invitrogen) in cell culture medium for 30 min. An ImageXpress Micro high-content screening microscope with a live-cell imaging module (Molecular Devices) was used to image the cells every 20 min for 8 h.

Cell Migration and Signal Propagation Analysis.

Cell tracking was performed using the Multi-Dimensional Motion Analysis application module in the MetaXpress software package (Molecular Devices). Full details of the tracking parameters and method to quantify guidance signal propagation are given in SI Methods.

Junction and Tension Modifications.

Adherens junction strength was increased by overexpression of N-cadherin using lentivirus. Adherens junctions were disrupted by EGTA treatment and E-cadherin antibody inhibition by modifying a previously published protocol (34). Myosin II activity was modified using blebbistatin and calyculin A. SI Methods gives full details.

Modeling Cell Streaming and Signal Guidance Propagation.

A numerical model of self-propelled cells was used to study cell interactions across the boundary between grooved and flat domains. The algorithm used in this study is based on a cellular Potts model and has been characterized in detail in (29). Full information about the parameters for the model is provided in SI Methods.