Gene-centric approach to integrating environmental genomics and biogeochemical models

Significance

Modern molecular tools provide an invaluable window into the marine microbial world by identifying organisms and their metabolisms through the analysis of genetic material. Microbial communities are ubiquitous throughout the oceans and exert great influence over ocean chemistry, yet they are rarely included explicitly in models of marine biogeochemistry, such as those used to predict the response of the oceans to environmental problems (e.g., climate change). Here, we present a unique way of integrating genetic data from state-of-the-art molecular tools into biogeochemical models to improve their predictive power, better constrain geochemical processes—especially those that are not apparent from chemical measurements—and gain a deeper insight into ocean chemistry and microbiology.

Abstract

Rapid advances in molecular microbial ecology have yielded an unprecedented amount of data about the evolutionary relationships and functional traits of microbial communities that regulate global geochemical cycles. Biogeochemical models, however, are trailing in the wake of the environmental genomics revolution, and such models rarely incorporate explicit representations of bacteria and archaea, nor are they compatible with nucleic acid or protein sequence data. Here, we present a functional gene-based framework for describing microbial communities in biogeochemical models by incorporating genomics data to provide predictions that are readily testable. To demonstrate the approach in practice, nitrogen cycling in the Arabian Sea oxygen minimum zone (OMZ) was modeled to examine key questions about cryptic sulfur cycling and dinitrogen production pathways in OMZs. Simulations support previous assertions that denitrification dominates over anammox in the central Arabian Sea, which has important implications for the loss of fixed nitrogen from the oceans. Furthermore, cryptic sulfur cycling was shown to attenuate the secondary nitrite maximum often observed in OMZs owing to changes in the composition of the chemolithoautotrophic community and dominant metabolic pathways. Results underscore the need to explicitly integrate microbes into biogeochemical models rather than just the metabolisms they mediate. By directly linking geochemical dynamics to the genetic composition of microbial communities, the method provides a framework for achieving mechanistic insights into patterns and biogeochemical consequences of marine microbes. Such an approach is critical for informing our understanding of the key role microbes play in modulating Earth’s biogeochemistry.

Environmental policies are increasingly founded on the results of computer simulations. For example, large-scale biogeochemical models, like those used by the Intergovernmental Panel on Climate Change, are often used to examine the impacts of climate change and to make projections about the future of the Earth. These models rely on observations to constrain and parameterize processes, as well as to validate results, and thus benefit from drawing on all available datasets. An underexploited yet rapidly growing source of data is the field of environmental “-omics” (e.g., genomics, transcriptomics, proteomics, and their “meta-” counterparts), which employs molecular biological tools to determine the identity and activity of microbial communities. These approaches were key in establishing the existence of important but difficult-to-elucidate biogeochemical pathways that are mediated by microbes, such as anaerobic oxidation of ammonia (anammox; ref. 1), aerobic nitrification by archaea (2), and cryptic sulfur cycling (3, 4).

A major impediment to using these experimental techniques in concert with biogeochemical models is that they differ in terms of currency. Data refer to genomes, proteins, and metabolites, whereas biogeochemical models typically simulate chemical concentrations and biomass, grouping organisms according to their function as opposed to genetic identity. At present, a clear divide exists between modeling efforts and genomics studies, yet there is much to be gained by integrating these fields (e.g., mechanistic insight into biogeochemical processes, model-based hypothesis development for guiding meta’omic studies, and improved predictive power). With this in mind, a unique modeling approach was developed that adopts a gene-centric view, incorporates genomics data, provides output that can be compared directly to experimental observations, and can be combined with traditional biogeochemical modeling methods. The proposed approach was used to explore nitrogen dynamics and cryptic sulfur cycling in oxygen minimum zones (OMZs), regions that account for 30–50% of marine nitrogen loss and play an important role in the production of greenhouse gases (5–7). These simulations address the relative contributions of anammox and denitrification to N₂ production and examine how cryptic sulfur cycling alters biogeochemical dynamics.

Integrated Modeling Framework

To date, numerous strategies have been advanced for modeling individual microbes, microbial communities, and encompassing ecosystems (ref. 8 and references therein and refs. 9 and 10). Within a reactive-transport framework, microbial ecology and geochemistry are usually coupled either by modeling metabolic networks associated with specific organisms (e.g., Geobacter sulfurreducens 11, 12) or by modeling functional groups of organisms, whereby each group corresponds to a particular metabolism (e.g., refs. 13 and 14). The former approach, although insightful for laboratory studies, is infeasible for use in conjunction with environmental genomics data because the majority of microbes are uncultured and their metabolic networks are thus unknown. The latter approach is better suited for modeling these data, although biomass of functional groups is not a metric that is typically measured in environmental genomic studies. With this in mind, we propose a functional gene approach where microbes are grouped according to their functional genes and, therefore, their metabolisms. Functional gene abundance is an appropriate state variable when modeling microbial communities because it allows for the integration of environmental genomics data and biogeochemical models via a common currency. It also provides direct mechanistic links to biogeochemical function.

In the model, the dependence of microbial growth on substrate and nutrient availability is described using Michaelis–Menten kinetics with inhibition (e.g., ref. 14), whereas the thermodynamic potential factor (F_T; ref. 15) accounts for the chemical energy available to drive the metabolism. Accordingly, we define the rate of gene production as

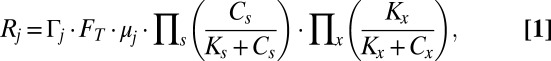where 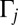is gene abundance (genes per liter), μ_j is the specific growth rate (seconds⁻¹), 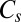is the concentration of reactant or nutrient s (molar), 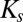is the half-saturation constant of reactant or nutrient s (molar), 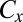is the concentration of inhibitor x (molar), and 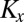is the half-saturation constant of inhibitor x (molar). (Here, s belongs to the set of all potentially limiting nutrients or substrates for the pathway associated with gene j, whereas x belongs to the set off all potential inhibitors.) This equation describes the rate at which j genes [e.g., nitrite reductase (nirK), nitrate reductase (narG), dissimilatory sulfite reductase (dsr)] are produced as a result of the metabolism associated with the gene. In addition, metabolic plasticity, whereby growth via one metabolism can lead to the propagation of functional genes associated with other metabolisms, is accounted for in the model. For example, the Gammaproteobacteria SUP05 possesses genes for both hydrogen and sulfur oxidation (16) and growth from hydrogen oxidation thus leads to an increase in sulfur oxidizing genes. Metabolic plasticity of this sort is incorporated into the model as shown below:

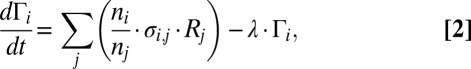where 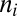is the number of i genes per g of cells that contains this gene (genes per gram), 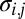is a probabilistic measure of co-occurrence of genes i and j within a genome (unitless), and λ is the “mortality rate” constant of a gene (seconds⁻¹). Nonzero values for 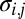account for metabolic versatility: Its magnitude—which can be estimated via complete genome sequence data—reflects the likelihood that a microbe is capable of the metabolisms associated with both genes i and j. Finally, the equations describing the microbial community are coupled to chemical dynamics:

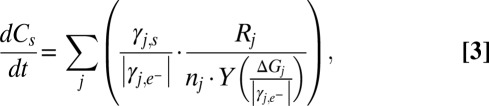where 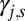is the stoichiometric coefficient for chemical species s in the reaction associated with gene j (negative for reactant and positive for product), 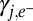is the stoichiometric coefficient of the electron donor in the metabolism, and Y is biomass production per mole of electron donor and is a function of free energy yield [grams of biomass (moles e⁻ donor)⁻¹; ref. 17]. The expressions above are given in a zero-dimensional context but are easily expanded into higher dimensions to include transport terms or for incorporation into existing biogeochemical models.

There are several noteworthy aspects of this model formulation. First, its parameters are experimentally tractable, drawing on both traditional microbiology and state-of-the-art molecular tools: μ and 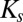are commonly measured parameters, 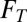and 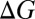are easily calculated from chemical concentrations, and mortality (i.e., λ) is a standard parameter in biogeochemical models. Metagenomic assembly or genomes from pure cultures or single-cell amplified genomes can be used to estimate the co-occurrence and number of genes per genome (i.e., 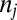and 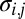). That is, the proportion of genomes that bear gene i that also contain gene j can be readily calculated. Second, measured gene abundances represent additional data with which to validate and constrain biogeochemical dynamics in a model. By reproducing observed spatial and temporal variation in functional genes, this approach also provides insight into the mechanisms that determine the distribution of organisms within the environment. Next, model solutions give gene abundances and chemical concentrations, thus allowing direct comparisons between model output and experimental data. Quantitative real-time PCR (qPCR) analysis, for example, can be used to estimate gene abundances. Finally, the model explicitly includes metabolic plasticity, which is a potentially important—albeit poorly understood—trait in the context of microbial community dynamics. By incorporating a quantitative measure of metabolic plasticity, the causes and impacts of functional versatility on microbial ecology and geochemical cycles can be readily explored.

Example Application: Nitrogen Cycling in the Arabian Sea

To demonstrate the proposed strategy in practice, a 1D steady-state model of nitrogen cycling across the Arabian Sea OMZ was developed. This OMZ is a well-studied marine region that is an important sink for fixed nitrogen and is characterized by sharp microbial and geochemical gradients (18). Key chemical species (i.e., O₂, , , and 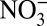) and known functional genes associated with nitrogen cycling (i.e., amoA and hzo) were the focus of the modeling effort, although the model includes the full nitrogen cycle (Supporting Information). Data from Pitcher et al. (18) are used for comparisons and to prescribe model parameters (e.g., temperature and density), whereas additional parameters for the model are determined from empirical relationships and other literature sources. Where possible, boundary conditions were derived from observations (18), specifically gene abundances and chemical concentrations. In the absence of data, we prescribe zero gradient boundary conditions with the exception of sulfate, which has a concentration of 28 mM throughout most of the ocean.

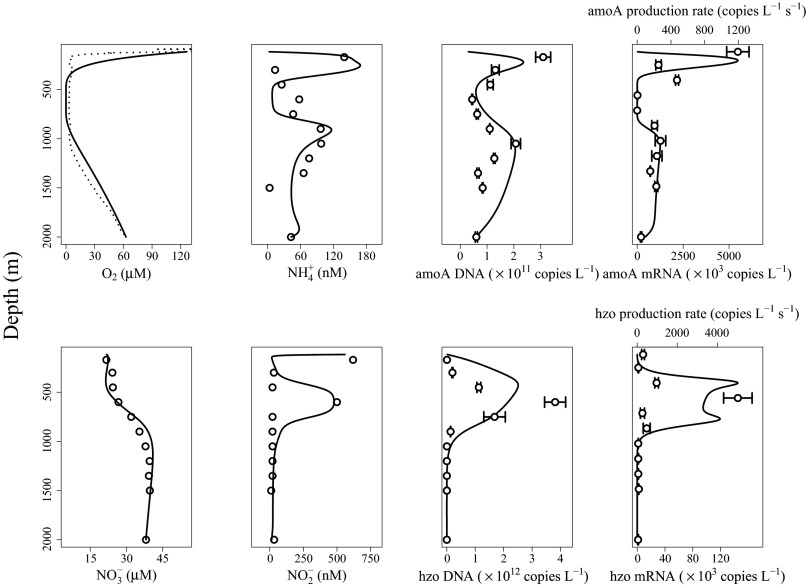
Fig. 1 compares model predictions with measured profiles of oxygen, nitrogen species, and gene abundances. Also plotted is measured gene expression (mRNA) and modeled gene production rate. Despite the complexities of nitrogen cycling across redox gradients and the dynamic nature of the Arabian Sea (e.g., monsoons), this relatively simple model is able to reproduce the general trends observed in chemistry, gene expression, and gene abundances.

Fig. 1.

A comparison of model results and data from Pitcher et al. (18). Solid lines represents model output, whereas individual points and dotted line are observations. Chemical profiles are as labeled, and hydrazine oxidoreductase (hzo) and ammonia monooxygenase (amoA) genes are associated with anammox and aerobic ammonia oxidation pathways, respectively. Error bars represent SDs.

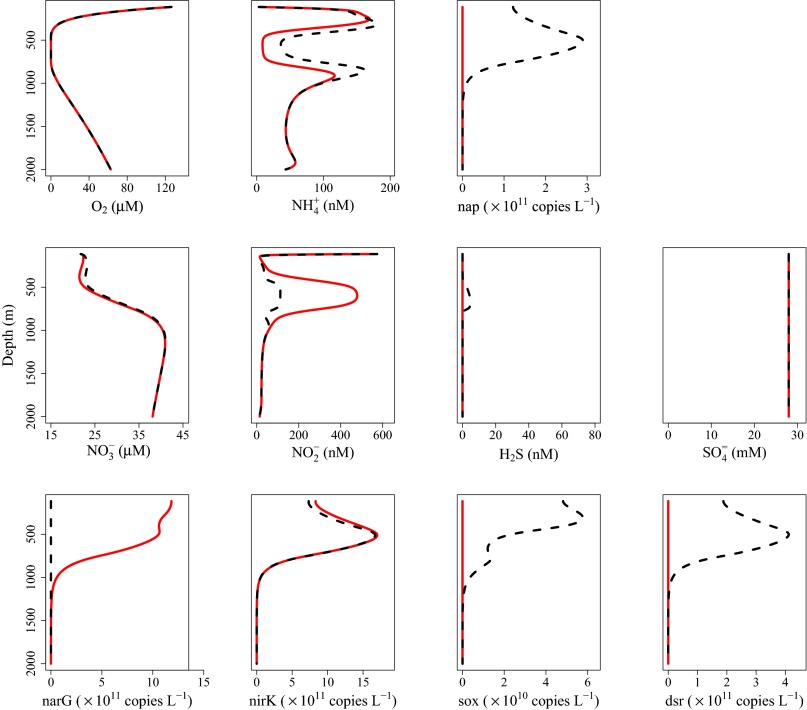
Sulfur cycling is coupled to nitrogen dynamics in the model, as observed recently in the OMZ off the Chilean coast (3), where hydrogen sulfide produced by heterotrophic sulfate reduction is rapidly oxidized to sulfate with nitrate. These processes are negligible in the simulation shown in Fig. 1, which is to be expected given that there have been no reports of cryptic sulfur cycling in the Arabian Sea. Nevertheless, cryptic sulfur cycling can be induced in the model by increasing the half-saturation constant for nitrate in dissimilatory nitrate reduction within a published range (19). This parameter defines the point at which dissimilatory nitrate reduction slows owing to nitrate limitation, thus attenuating the rate of organic matter degradation via this pathway. As a result, there is more organic matter available for less energetically favorable metabolisms (i.e., sulfate reduction) and crytpic sulfur cycling is initiated.

Comparing scenarios with and without prominent sulfur cycling reveals only subtle differences in most chemical profiles, with the exception of nitrite (Fig. 2, discussed below). These differences may be masked by spatial and temporal variability (e.g., stochastic mixing, seasonal export from surface waters) or attributed to other processes, and traditional models cannot distinguish between the two scenarios, because they do not consider biomarkers (e.g., genes) that are indicative of cryptic biogeochemical processes. Comparing the overall reaction for sulfate reduction coupled to nitrate reduction by hydrogen sulfide with organotrophic dissimilatory nitrate reduction reveals that these two competing pathways are effectively equivalent in terms of stoichiometry, explaining the absence of a clear chemical signal (Table 1). Nevertheless, these pathways differ in two important ways. First, the total energy yield of the metabolisms differs, resulting in different growth rates and nutrient demands. Specifically, cryptic sulfur cycling generates a lower microbial biomass and therefore requires less ammonia as a nutrient. Second, cryptic sulfur cycling is a two-step process: Hydrogen sulfide generated by sulfate reduction is then used to drive nitrate reduction (Table 1). Some of this hydrogen sulfide is lost to aerobic oxidation, however, meaning less is available for nitrate reduction. As a result, there is less nitrite produced per mole of organic matter during cryptic sulfur cycling and the second nitrite peak is lower (Fig. 2). When cryptic sulfur cycling is active there is no apparent accumulation of hydrogen sulfide (<5 nM), nor is there an evident decrease in sulfate concentration; there is, however, an abundance of associated genes (Fig. 2). Processes that lack obvious geochemical signatures yet are clearly active from genetic data, such as cryptic sulfur cycling, underscore the importance of integrating environmental genomics data into biogeochemical models if geochemical dynamics are to be characterized correctly.

Fig. 2.

Model output from simulations with (black dashed lines) and without (red solid lines) cryptic sulfur cycling active. The half-saturation constant for nitrate in the dissimilatory nitrate reduction to nitrite pathway is increased to 80 μM to induce sulfate reduction and, consequently, initiate cryptic sulfur cycling. Chemical profiles are as labeled, and sox, nap, narG, nirK, and dsr genes correspond to aerobic sulfide oxidation, sulfide oxidation by nitrate, organotrophic dissimilatory nitrate reduction, organotrophic dissimilatory nitrite reduction, and dissimilatory sulfate reduction, respectively.

Table 1.

A comparison of stoichiometry between dissimilatory nitrate reduction and dissimilatory sulfate reduction coupled to nitrate reduction by hydrogen sulfide

Pathway	Reaction
Cryptic sulfur cycling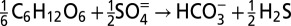
	- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
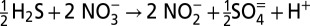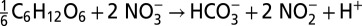Organotrophic dissimilatory nitrate reduction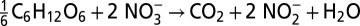

An additional key question regarding OMZ biogeochemistry is the relative contribution of denitrification and anammox to N₂ production, because OMZs account for 30–50% of marine nitrogen loss (5). Anammox dominates in many OMZs (e.g., refs. 20 and 21), but recent studies suggest that denitrification is the dominant nitrogen loss pathway in the central Arabian Sea OMZ (22, 23). To address this point, the rates of N₂ production within the model were calculated for both heterotrophic denitrification and anammox. These calculations support the latter argument, demonstrating that rates of N₂ production via heterotrophic denitrification in the central Arabian Sea may surpass 1 nM N₂⋅d⁻¹ in places, whereas the maximal anammox rate is an order of magnitude lower. Furthermore, depth-integrated heterotrophic denitrification is a factor of 3 greater than anammox.

Simulations not only shed light on which metabolisms are active, but also on the organisms that mediate these metabolisms. When adopting Michaelis–Menten kinetics, the half-saturation constant for ammonia during aerobic ammonia oxidation 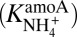must be on the order of 107 μM for the model to accurately reproduce observations. This value is consistent with ammonia-oxidizing bacteria (AOB) yet is several orders of magnitude higher than estimated values for ammonia-oxidizing archaea (AOA) (24). Although AOA are much more abundant than AOB in the region (25), mRNA analysis reveals that AOB are significantly more transcriptionally active, indicating an important role in ammonia oxidation (26). These observations support model results suggesting that coupled microbial–geochemical models can also furnish insight into the most active members of community.

Sensitivity Analysis

An extensive sensitivity analysis was undertaken (44 parameters and 17 state variables) to identify the most influential parameters in the model and to assess their impact. Results revealed 16 parameters that are important in modulating the biogeochemistry of the system and that there is a tight coupling between numerous state variables (Supporting Information). That is to say, perturbing a parameter does not simply affect a single state variable, but rather causes broad shifts in biogeochemical dynamics. These interdependencies greatly limit possible parameter space, as do published parameter values or ranges, imposing stringent constraints on parameter selection. Therefore, although state variables may exhibit marked sensitivity to some parameters, multiple constraints bolster confidence in parameter choices (19). These most influential parameters and their effects are discussed below.

Analysis results demonstrate that state variables are most sensitive to the mortality constant (λ), because this parameter directly affects all microbial communities, which in turn affect reaction rates and thus chemical distributions. Mortality is notoriously difficult to determine a priori and is therefore often estimated through model application. Providing mortality affects all subpopulations in the same way, the mortality constant can be tightly constrained in this manner.

As one would expect, parameters pertaining to organic matter dynamics play an important role in OMZ biogeochemistry. Half-saturation constants that define microbial affinity for dissolved organic matter 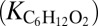and oxygen during aerobic respiration 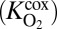show marked influence over the system, as does the export flux of organic matter from surface waters 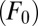and the rate constant for aerobic respiration 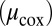. These parameters shift the location of the chemocline, altering where in the water column different processes dominate nitrogen cycling. Simulation results agree with experimental studies that N₂ production is a function of organic matter supply (27). Furthermore, rate constants and half-saturation constants for other catabolic pathways, specifically dissimilatory reduction of nitrate and nitrite, also affect microbial and chemical distributions.

More than half the parameters identified as important by the sensitivity analysis are half-saturation or inhibition constants. These results illustrate that half-saturation constants are key parameters because they define when pathways shutdown, effectively delineating chemical and biological boundaries. In environments characterized by chemical gradients, such as OMZs and coastal sediments, these parameters are understandably important.

Finally, physical transport parameters (K_z and ν) also influence model simulations because they prescribe exchange between regions with different chemical attributes and microbial communities. As a result, they introduce reactants to one another, export metabolites, and attenuate local populations by dispersing organisms throughout the environment, all of which affect biogeochemical dynamics.

In short, the sensitivity analysis demonstrates that although parameters pertaining to mortality, organic matter dynamics, transport, and geochemical boundaries (i.e., half-saturation constants) play an important role in defining the biogeochemistry of the system, multiple constraints on these parameters promote confidence in their values.

Limitations of the Functional Gene Approach

Like any modeling approach, the method proposed here has inherent assumptions, strengths, and limitations. The functional gene approach requires that the reactions mediated by modeled microbial communities and associated marker genes are defined a priori. This allows the model to track the reactants, products, and genes involved in the metabolism, in addition to calculating the energetics of the reaction. Therefore, the functional gene approach readily lends itself to modeling chemolithoautotrophs with well-defined metabolisms, such as ammonia oxidation, because there is a known marker gene (i.e., amoA) and the reaction can be stated with confidence (i.e., 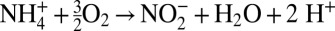). This is not necessarily the case, however. Even for cultured organisms that have been studied in the laboratory for decades, such as Escherichia coli, a large proportion of genes are of unknown function (28). The incidence of novel genes in uncultured microbial communities is even higher (29), and the continuing discovery of new metabolisms underscores the large gaps remaining in understanding the energy metabolism of uncultured organisms and its genetic basis. Hence, it may not currently be possible to identify an appropriate marker gene for a particular metabolic pathway. Furthermore, the reactants, products, and stoichiometry of metabolisms may be unclear, especially for novel pathways observed in situ beyond the rigorous controls of the laboratory. Nevertheless, applying the approach in the absence of these data may potentially highlight gaps in knowledge and offer insight into bridging these gaps.

Environmental genomics provides great insight into many aspects of uncultured microbes yet sheds little light on growth parameters. These parameters must then be estimated either through analogy with similar cultured organisms or by fitting model solutions to observations. In the latter case, parameters are tuned within reasonable ranges to reproduce measured gene abundances and chemical concentrations. This is a powerful method for quantitatively constraining the dynamics of poorly understood subpopulations that do not yield to traditional laboratory techniques, providing there are robust estimates for other model parameters. Confidence in such estimates diminishes, however, as the number of unconstrained parameters in the system increases. Ultimately, the power of our modeling approach is limited by biochemical and physiological data derived from laboratory experiments on cultured organisms and environmental data from observations.

Organotrophs are somewhat more challenging to model by means of the functional gene approach. Identifying the organic molecules used by different organotrophs in complex communities is not straightforward, creating difficulties with regards to thermodynamic calculations and chemical measurements. Moreover, characterizing dissolved organic matter that is relevant to microbial growth and determining in situ concentrations remains difficult (30). These issues likely preclude the use of functional genes for tracking microbial populations in the detailed fashion described above (i.e., for specific electron donors). Modeling generic organotrophic groups based on terminal electron acceptors (e.g., ref. 13) with average organic matter composition as a proxy for availability of specific organic molecules is perhaps more appropriate given the current available data. Thus, although the functional gene approach is well-suited to chemolithoautotrophs, which constitute a significant proportion of microbial biomass in the ocean, it does not represent a substantial improvement over the functional group approach when modeling organotrophs (13).

In contrast to chemoautotrophs, which rely on many diverse metabolisms to generate energy, photoautotrophs cannot be differentiated from one another based on their energy source. Instead, these organisms establish ecological niches through different functional traits, such as their source of inorganic nutrients (e.g., N₂ or ), physiological structures (e.g., calcareous exoskeletons or siliceous frustules), light-harvesting pigments, motility, and size (31). Thus, genetic markers for these traits are more suitable for tracking these communities as opposed to functional genes for photosynthesis. In addition to the presented model formulation, factors would also need to be added to Eq. 1 to account for light limitation and photoinhibition when modeling photoautotrophs. Although these factors complicate applying the technique to phytoplankton communities, the approach does offer one distinct advantage. Traditionally, phytoplankton taxonomy is determined by microscopy, although HPLC offers an alternative approach by characterizing phytoplankton according to pigment. The former technique is labor intensive and requires substantial expertise but provides good resolution, whereas the latter method is less time-consuming but offers a coarser view as some pigments are common to a number of organisms. Metagenomics offers an appealing alternative in that it affords a high-resolution perspective via high-throughput methods and produces data that may be readily incorporated into biogeochemical models as outlined above.

Finally, it should be noted that in adopting an ecosystem-level perspective the proposed approach relies on bulk concentrations, which may be radically different from those experienced by individual microbes (32). Nevertheless, there is presently no consistent overarching framework for casting cell-scale dynamics, which occur in heterogenous microenvironments, in an ecosystem context.

Model–Data Comparisons

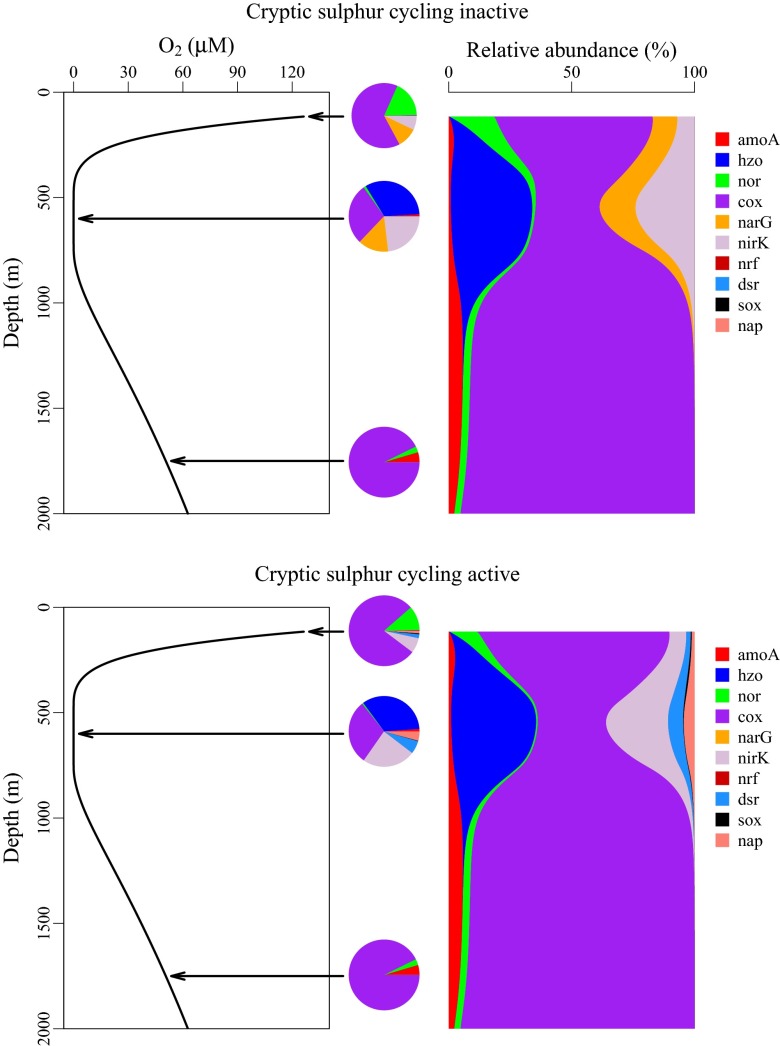
Whereas qPCR only provides data for a limited number of specific genes, metagenomic data provide a broad view of genes present in the environment and metagenomic assemblies (or single-cell genomics) can provide estimates of gene co-occurrences. Unlike qPCR, however, metagenomic data do not furnish absolute measures of gene abundances (e.g., number of genes per milliliter), but are typically expressed in a relative sense. Reconciling metagenomic data and model output therefore requires that modeled gene abundances are expressed in a relative form (i.e., as proportions of the total gene abundance) and that the dataset used for comparison should only consider the functional genes that are explicitly modeled. For example, Fig. 3 shows how modeled genes can be expressed as relative abundances at discrete locations, as is common in metagenomics. Adopting this approach allows metagenomic data to be easily incorporated into the modeling framework. Of particular importance is the ability to provide mechanistic explanations for observed relative gene abundances. As an example, Fig. 3 demonstrates the shift in the metagenome owing to the onset of cryptic sulfur cycling. These changes in the genetic composition of the microbial community can be directly linked to biogeochemical processes in the model.

Fig. 3.

Profiles of oxygen and relative gene abundances from model simulation without and with cryptic sulfur cycling active. At three depths, gene abundances are plotted in pie charts demonstrating how direct comparisons can be made between model output and metagenomic data, which are typically expressed in relative terms at discrete points in space. cox, cytochrome-c oxidase.

Proteomic and transcriptomic data are more challenging to integrate into biogeochemical models owing to complex, poorly characterized relationships between mRNA, proteins, and metabolic rates (33). Although this may preclude accurate predictions of transcript or protein abundances at present, coupled microbial–geochemical modeling may prove a useful tool for establishing and exploring these relationships. For instance, in the model application above, trends in mRNA abundances seem to be accurately approximated by metabolic (or gene production) rates within the model, suggesting a direct link in this scenario. Nevertheless, this is not always the case (33), and discrepancies between model output and observations may offer insight into the processes responsible for these disagreements.

Well-constrained model applications are dependent on suitable datasets. Ideally, datasets should have a high spatial resolution that covers environmental gradients to ensure that processes are accurately described for a broad range of conditions. These data should include abundances—either relative or absolute—of several functional genes that are coupled through interacting reactants and products, because interwoven metabolisms provide tighter constraints on system dynamics. These genetic data should be complemented by comprehensive chemical measurements of all species involved in the modeled metabolisms, because these data ensure that the microbial–geochemical interactions are accurately represented. Rate measurements (e.g., from isotopic labeling) are also incredibly useful in constraining models. Finally, environmental parameters, such as mixing rates, advective velocities, and fluxes of particulate matter are essential because they provide a physical context to the biogeochemical processes. Together, these data provide an integrated perspective of marine biogeochemistry when aggregated by means of the proposed modeling approach.

Conclusions

In summary, adopting an integrated modeling approach to biogeochemistry and environmental genomics data is a powerful means of exploring the nexus between microbial ecology and geochemistry. In particular, these tools serve to (i) extricate and quantify elusive chemical processes, where genetic data represents a pertinent and more sensitive tracer of biogeochemistry, and (ii) synthesize large, complex environmental genomic datasets in the context of biogeochemistry. Although in its infancy, results suggest that the functional gene approach holds great promise in describing the biogeochemical dynamics of complex ecosystems and their resident microbial communities with the potential to increase the predictive power of biogeochemical models on local to global scales. Simulations are consistent with experimental studies in the central Arabian Sea in showing that denitrification dominates over anammox and that cryptic sulfur cycling is absent. When cryptic sulfur cycling is induced by altering the concentration at which nitrate reducers become nitrate-limited, the secondary nitrite maximum often observed in OMZs is attenuated owing to a shift in the chemolithoautotrophic community and dominant metabolic pathways. Our results further emphasize the need to explicitly incorporate microbes into biogeochemical models.