Toward rationally redesigning bacterial two-component signaling systems using coevolutionary information

Significance

Our study uses amino acid coevolutionary information to better understand how bacterial two-component signaling (TCS) proteins preferentially interact with their correct partners while avoiding interactions with nonpartners. We extract coevolutionary couplings from sequences of TCS partners and study how coevolution is necessary to maintain their ability to transfer signals with high specificity. We use these coevolving couplings to devise a metric, which can predict the effects of mutations in the quality of signal transmission observed in vitro and provide support to the hypothesis that hybrid TCS proteins have reduced specificity. Our metric can potentially be used to redesign a TCS protein to preferentially interact with a nonpartner. Furthermore, our study can potentially be extended to networks of interacting proteins.

Abstract

A challenge in molecular biology is to distinguish the key subset of residues that allow two-component signaling (TCS) proteins to recognize their correct signaling partner such that they can transiently bind and transfer signal, i.e., phosphoryl group. Detailed knowledge of this information would allow one to search sequence space for mutations that can be used to systematically tune the signal transmission between TCS partners as well as potentially encode a TCS protein to preferentially transfer signals to a nonpartner. Motivated by the notion that this detailed information is found in sequence data, we explore the sequence coevolution between signaling partners to better understand how mutations can positively or negatively alter their ability to transfer signal. Using direct coupling analysis for determining evolutionarily conserved protein–protein interactions, we apply a metric called the direct information score to quantify mutational changes in the interaction between TCS proteins and demonstrate that it accurately correlates with experimental mutagenesis studies probing the mutational change in measured in vitro phosphotransfer. Furthermore, by subtracting from our metric an appropriate null model corresponding to generic, conserved features in TCS signaling pairs, we can isolate the determinants that give rise to interaction specificity and recognition, which are variable among different TCS partners. Our methodology forms a potential framework for the rational design of TCS systems by allowing one to quickly search sequence space for mutations or even entirely new sequences that can increase or decrease our metric, as a proxy for increasing or decreasing phosphotransfer ability between TCS proteins.

Cellular signal transduction in which an extracellular or intracellular stimulus elicits a physiological response is critical for cells to adapt and survive in a changing environment. To respond to a diverse range of stimuli, bacteria have adopted a robust two-component signaling (TCS) mechanism involving a histidine kinase (HK) protein and a response regulator (RR) protein (1–3). Conventional TCS begins with the detection of a stimulus resulting in the autophosphorylation of a conserved histidine residue on the HK protein. This phosphoryl group (i.e., signal) is then transferred from the HK to a conserved aspartic acid residue on its RR signaling partner following the formation of a transient HK/RR complex. In many cases, phosphorylation of the RR thereby activates its function as a transcription factor that generates a physiological response through the repression or activation of genes. A number of closely related evolutionary extensions to the TCS motif can also be found in bacteria such as the phosphorelay (3). Due to the robust and effective nature of TCS proteins in transducing signals, bacteria have evolved to use as many as tens to hundreds of TCS pairs that regulate a wide variety of biological processes ranging from environmental response to the regulation of the cell cycle.

Because both TCS and its related extensions require signaling proteins to faithfully bind and transfer a phosphoryl group to and from their signaling partner(s), an important question arises: How are the various signaling proteins able to interact with their signaling partners with high specificity while keeping interactions with signaling proteins from other signaling pathways (i.e., “cross-talk”) at a minimum? Decoding the determinants of specificity has been the subject of many studies (reviews in refs. 4 and 5). Although bacteria may use a number of mechanisms to maintain specificity such as spatial localization of the signaling proteins, it is clear that much of the code for maintaining specificity is contained in the specific interprotein residue–residue interactions that give rise to mutual recognition of the signaling partners as well as their unique binding interface. Extracting this molecular code is of great importance for understanding the network of signaling systems in bacteria as well as the rational redesign of TCS signaling systems.

In principle, the molecular determinants of recognition among the signaling proteins are contained within the structural data of the interacting proteins. Although significant amounts of structural data exist for individual signaling proteins, shedding light on their functional domains, limited structural data exist for the functional complexes (6–9) of the signaling proteins due to the transient nature of their interactions. Furthermore, structural data do not distinguish the subset of molecular interactions that are critical for ensuring specificity nor do they easily differentiate between residues that are critical for protein–protein recognition and residues directly involved in the catalytic activity. Complementing these structural studies, alanine-scanning mutagenesis (10, 11) and cysteine-scanning mutagenesis (12) have been performed on signaling proteins to help identify residues that are key to maintaining the interaction and phosphotransfer functionality between the signaling proteins. Although these studies are informative, a systematic exploration of the mutational sequence space cannot be performed in this manner.

A great deal of sequence data exist for TCS proteins, reflecting a sequence space that has been well sampled by evolution. Because TCS signaling partners are often adjacent to one another on the genome, e.g., cognate pairs from the same operon, a number of studies (11, 13–20) have applied statistical methods to collections of cognate pairs to identify the evolutionarily conserved interactions between HK and RR signaling partners from their multiple-sequence alignments (MSA). These studies extend upon early work using statistical methods to infer protein–protein interactions (21, 22) from coevolutionary data. The recent development of a global statistical inference method called direct coupling analysis (DCA) (17, 18, 23) has advanced the study of sequence coevolution by pruning out the contributions from indirect couplings (i.e., statistical couplings through third party residues or phylogenetic effects) and thus quantifying the direct couplings between coevolving residues with greater accuracy. DCA has successfully been used to identify intradomain (23–27) and interdomain (16, 17, 23, 28) contacts in proteins, including the prediction of a transient HK/RR complex that is within crystallographic accuracy of the experimentally determined structure (6). Other recent statistical methods have also been applied to sequence coevolution to explore a diverse range of topics ranging from protein structure and function (29–35) to the evolutionary fitness of HIV (36). Extending the predictive power of DCA beyond structure prediction, a recent study by Procaccini et al. (37) demonstrated that the direct couplings inferred from DCA can be used to quantify interaction specificity among HK and RR proteins. The mutually coevolved interface between HK/RR signaling partners is evolutionarily conserved to maintain the interaction between them and is, thus, captured by the statistical model of DCA. Using a DCA-derived metric, they were able to correctly predict known signaling partners and “cross-talkers” in two model bacterial systems as well as correctly predict the interaction partner of a number of orphan signaling proteins, which are not adjacent to a signaling partner on the genome.

Motivated by the notion that the molecular determinants of interaction specificity can be found within the sequence data of signaling partners, we characterize the predictive power of DCA in quantifying changes in the interaction between signaling proteins through site-directed mutations. We adopt the recently developed mean field formulation of DCA (23), which allows us to explore significantly larger sets of sequence data than previous implementations of DCA. Because signaling partners are constrained by evolutionary forces to maintain their ability to bind and transfer a phosphoryl group, we use DCA to probe the mutual sequence coevolution between partners to infer the effect of sequence mutations on their functional interaction. To accomplish this, we introduce a DCA-derived metric closely related to direct information (DI) (17, 23) and compare its predictions directly to those of a number of experimental mutagenesis studies that examine the effect of mutation on phosphotransfer between HK/RR partners. We demonstrate that our metric correlates accurately with these experimental studies, suggesting that there is a direct relation between the predictions of our metric and the ability of the mutant HK/RR pair to bind and transfer phosphoryl groups. Furthermore, by subtracting from our metric an appropriate null model corresponding to conserved features that are common among HK/RR pairs, we can focus on mutations associated with variable residues among TCS signaling proteins such as interprotein residues responsible for binding and recognition. These findings open the door for the potential rational redesign of TCS systems from abundant sequence data as well as a system-level approach to study the interaction of TCS signaling proteins. Our methodology can easily be extrapolated to other sequence-rich systems for which the protein–protein interaction and recognition are still uncharacterized.

Results

Quantifying Mutational Changes in HK/RR Interactions, Using Genomic Data.

We characterize the mutational changes in the functional interaction between HK/RR proteins through evolutionarily conserved interactions between the HK dimerization and histidine phosphotransfer (DHp) domain and the RR receiver (REC) domain of its cognate partner (Fig. 1A) because the primary interactions between HK and RR proteins occur between these two domains. Taking advantage of the abundant sequence data, we construct a multiple-sequence alignment (MSA) with 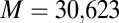cognate pairs as our input set (Materials and Methods).

Fig. 1.

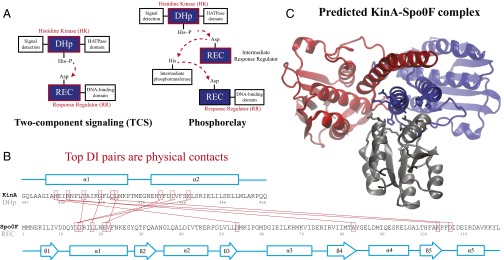
(A) A schematic of two-component signaling (TCS) and phosphorelay signaling. In TCS, a phosphoryl group is transferred from a conserved His residue on the HK DHp domain to a conserved Asp residue on the RR REC domain. Phosphorelay signaling involves an additional intermediate RR REC domain and intermediate phosphotransferase. In our study, we focus only on the interactions between the DHp domain and the REC domain, which are highlighted in red. (B) Sequence of the KinA DHp domain and its signaling partner Spo0F, where the top 10 interprotein DI pairs computed for our input set of 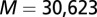cognate pairs are shown in red (excluding DI pairs involving gaps in the MSA). These top pairs reflect evolutionarily covarying interprotein residue pairs that tend to be physical contacts. (C) The predicted structure of the KinA/Spo0F (HK/RR) complex, using the top 20 DI pairs as physical contacts for docking (Materials and Methods). The top 10 DI pairs shown in B form physical contacts (<8 Å separation) in our predicted complex with the exception of R408/A83. Two KinA monomers (red and blue, respectively) form the KinA homodimer whereas Spo0F (dark gray) is shown bound to the DHp domain of one of the KinA proteins. The residues involved in the top 10 DI pairs are shown in stick representation.

Using our cognate pair MSAs, we compute direct couplings (for a detailed derivation, refer to ref. 23) between HK/RR interprotein residue pairs that arise from the mutual coevolution of interprotein residues that allows for signaling partners to maintain their ability to transfer signal. As previously discussed (37), the magnitude and sign of the position-averaged direct couplings between amino acids correlate well with their physical interaction type (e.g., electrostatic, hydrophobic, etc.) with high statistical significance. Furthermore, mutational changes in the direct couplings have been shown to correlate well with the experimental mutational changes in the free energy for individual proteins (38). We formulate a metric called the direct information score (DIS) from the direct couplings (Eqs. 1 and 2) in a manner closely related to that of the DI (17, 23). A value of this metric can be computed for a given concatenated MSA sequence of an HK and RR protein, 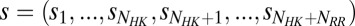, where the HK positions span from 1 to 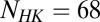whereas the RR positions span from 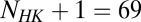to 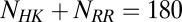. Furthermore, mutational changes in 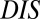for a particular mutant sequence can be computed with respect to a wild-type sequence as 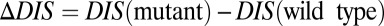. Positive 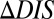is interpreted as mutational changes associated with a net increase in the direct couplings between an HK and an RR protein and thus reflects enhancements in their interaction (e.g., enhanced phosphotransfer). Likewise, negative 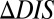is interpreted as a net decrease in the direct couplings that reflects deleterious effects to the HK/RR interaction (e.g., reduced phosphotransfer).

DIS Qualitatively Captures in Vivo Phenotypes of Experimental Mutagenesis.

A closely related extension of TCS called the phosphorelay (3) has evolved to contain an additional intermediate RR, which lacks a DNA-binding domain, and an intermediate phosphotransferase protein (Fig. 1A). One of the most well-known examples of such a signaling motif is the sporulation phosphorelay of Bacillus subtilis (39), which controls the process in which the detection of environmental stress results in sporulation, i.e., the formation of spores and the death of the mother cell.

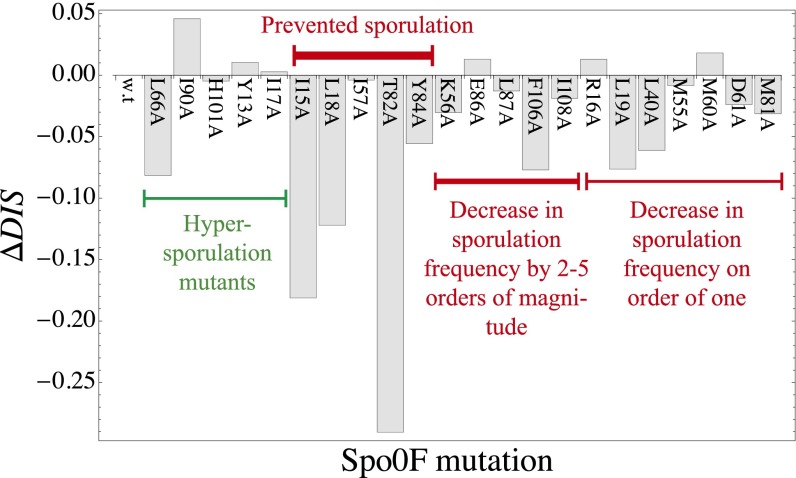
In a study by Tzeng and Hoch (10), single-residue alanine-scanning mutagenesis was performed on the loop and helical regions of the intermediate RR protein, sporulation initiation phosphotransferase F (Spo0F), of the sporulation phosphorelay. By expressing the mutant Spo0F in B. subtilis, they were able to observe 22 notable sporulation phenotypes (see Fig. S1A and Table S1 for mutational positions with basic information about conservation). The resultant mutants had altered protein–protein interactions that either improved or impaired phosphotransfer through the phosphorelay, resulting in “hypersporulation” or sporulation-deficient phenotypes, respectively. The mutations could affect the interactions between Spo0F and the five sporulation kinases (i.e., sporulation kinase A–E abbreviated as KinA–KinE), the intermediate phosphotransferase after Spo0F in the relay (i.e., Spo0B), and the Rap phosphatases (40–42) as well as proteins whose interaction with Spo0F has yet to be identified. In total, they observed 5 hypersporulation mutants, 10 sporulation-deficient mutants, and 7 mutants with decreased sporulation frequency on the order of one.

Considering only the KinA/Spo0F HK/RR interaction, we use the DIS metric (Eq. 1) to compute a score for the 22 Spo0F mutants with distinct phenotypes as well as a score for the wild-type KinA/Spo0F interaction. A plot of the mutational change in DIS with respect to the wild type, i.e., 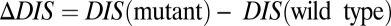, is shown in Fig. 2. We find that mutational changes in DIS reflecting the altered interaction between KinA and Spo0F appear to reproduce the global phenotypic details observed in the in vivo experiment. For instance, 3 of 5 of the hypersporulation mutants had a positive 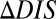whereas the sporulation-deficient mutants tended to have the most negative 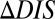. The metric also roughly captured the magnitude differences for the sporulation-deficient mutants (red labels in Fig. 2). Capturing these coarse details by considering the KinA/Spo0F interaction is supported by the suggestion that KinA serves as the primary source of phosphoryl groups for Spo0F under stress conditions (43).

Fig. 2.

The 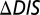was computed for the interaction of KinA with each of the 22 Spo0F mutants explored by Tzeng and Hoch (10) that resulted in notable sporulation phenotypes. By definition, 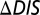for the wild-type KinA/Spo0F interaction is 0. We observe that 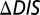appeared to capture qualitative details associated with the sporulation phenotypes despite considering only the KinA/Spo0F interaction.

To better understand how the mutations could affect the KinA/Spo0F interaction, we computationally predict the structure of the wild-type KinA/Spo0F complex (Fig. 1C) (Materials and Methods and ref. 16). Consistent with an experimentally determined HK/RR complex (6), the majority of the contacts between Spo0F and the KinA DHp domain are formed by the 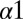helix, 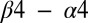loop, and 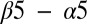loop regions of Spo0F (Fig. 1B). Most of the alanine mutations that resulted in notable phenotypes are in regions that form interfacial contacts with the KinA DHp domain in the wild-type complex. There are, however, some exceptions such as the positions L40, L66, H101, I90, and L87. The L66, H101, and I90 positions are, respectively, buried on the 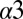helix, the 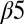sheet, and the 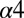helix, which do not appear to be in contact with KinA in the predicted complex, although it has been suggested that the hypersporulation phenotypes associated with these mutants arise through the conformational stabilization of an active Spo0F structure (44, 45) rather than directly forming stabilizing contacts with KinA. Likewise, the L87 position located on the C-terminal end of the 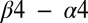loop may influence the orientation the 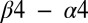loop, which forms key contacts with the DHp domain.

The agreement between our predictions for the in vivo phenotypes served as a first step to assess the capabilities of our metric to characterize pairwise HK/RR recognition and phosphotransfer. Although it is feasible to improve the genomic predictions of the sporulation phenotypes by incorporating additional HK/RR interactions (e.g., KinB–KinE) or interactions with non-HK protein families (e.g., Spo0B, Rap phosphatases) in an additive manner, an analysis of protein interaction systems is outside the scope of this paper. To further test the predictive power of DIS, we turn to a series of in vitro studies where pairwise HK/RR phosphotransfer is evaluated.

DIS Quantitatively Agrees with in Vitro Phosphotransfer Measurements of Response Regulator Mutagenesis.

Extending upon their phenotypic study of Spo0F mutants, Tzeng and Hoch (10) selected a set of sporulation-deficient mutants for in vitro phosphotransfer experiments. The rate of phosphotransfer from phosphorylated KinA to Spo0F was measured as a function of KinA substrate concentration, 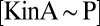, and the data were fitted to a Michaelis–Menten saturation curve of the form 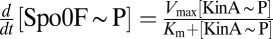, where 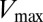is the maximum velocity at substrate saturation and 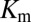is the dissociation constant of Spo0F from KinA. To this end, Tzeng and Hoch measured the mutational change in 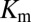, , 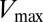and 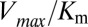with respect to the kinetic parameters corresponding to the wild-type Michaelis–Menten curve.

For comparison of our DIS predictions with the experimental changes in 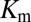and 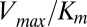, we restrict the computation of DIS (Eq. 2) to include only residue pairs within a cutoff distance from one another in our predicted KinA/Spo0F complex (e.g., interfacial residues). Considering only interfacial residues in DIS to predict properties governed by the transient binding and unbinding makes intuitive sense. When comparing the predictions of Eq. 2 using a 12-Å cutoff with the experimentally reported changes in 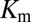and 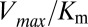(Fig. 3 A and B), we find significant agreement (Pearson correlation of −0.66) and quantitative agreement (Pearson correlation of –0.83), respectively. Here, a correlation coefficient of −1 represents perfect correlation. The remarkable agreement with 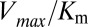is of particular interest because the rate of phosphorylated Spo0F formation predicted by Michaelis–Menten is proportional to 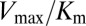under physiological conditions where the concentration of KinA is small compared with 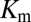(10). We have chosen a fairly relaxed cutoff definition of 12 Å in Fig. 3 A and B such that it can be applied to other HK/RR systems, accommodating subtle structural/conformational differences in those systems. By removing distal interprotein pairs from the computation, the overall quality of the predictions for 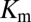and 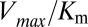is improved and we find that these predictions are fairly insensitive to the particular value of the cutoff distance used to define a contact (Fig. S2).

Fig. 3.

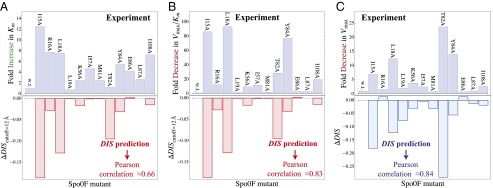
Direct comparison of our DIS metric with in vitro phosphotransfer measurements between KinA and the Spo0F mutant by Tzeng and Hoch (10). Comparison of 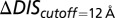(Eq. 2) with (A) the experimentally measured fold increase in the dissociation constant, 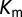, and (B) the experimental fold decrease in 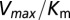yields Pearson correlation coefficients of −0.66 and −0.83, respectively. (C) Comparison of 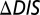(Eq. 1) with the experimental fold decrease in 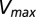yields a Pearson correlation of −0.84.

We observe a remarkable agreement between our DIS metric and the experimentally reported change in 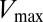(Fig. 3C) when we include all possible interprotein pairs regardless of separation in the predicted complex, using Eq. 1. Our prediction in Fig. 3C exhibits a Pearson correlation of −0.84 with the experimental data, where −1 represents perfect correlation. We find a steady improvement in our prediction of 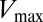as the cutoff distance is increased such that more and more interprotein pairs are included (Fig. S2). A possible explanation is that mutations in residues that are catalytically important, hence affecting 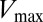, could require compensatory mutations in both the interfacial and the noninterfacial residues of their signaling partner to maintain their interaction. In such a case, the coevolution between distal interprotein residues would be meaningful. Further validation of this notion with biochemical data would certainly be necessary to elucidate the role of noninterfacial residues in relation to the catalytic activity of signal transfer. However, following this potential reasoning, the inclusion of the direct couplings between all interprotein pairs would thus be needed to reflect the large deleterious change in the DIS resulting from mutating a catalytically important residue. An example of such a case is the interfacial T82 residue located on the 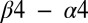loop that is found to be present in 73% of RR receiver domains in our cognate pair alignment and has been implicated as being one of the catalytically important residues in RR proteins (1, 46). The DIS metric quantifies the T82A mutation as having the largest decrease with respect to the wild type among the mutants. Fig. 3C (Lower) shows how this change coincides with the largest fold decrease in 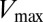that was observed experimentally (Fig. 3C, Upper). Significant decreases in DIS are also observed when other catalytically important residues in Spo0F (e.g., D10, D11, D54, K104) are mutated to alanine.

DIS Quantitatively Agrees with in Vitro Phosphotransfer Measurements of Histidine Kinase Mutagenesis.

In a recent experimental study, Capra et al. (11) performed single-residue alanine-scanning mutagenesis of the HK protein EnvZ of Escherichia coli that is the signaling partner of the RR protein OmpR. Of the 30 total mutations distributed over the 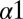and 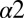helices of the EnvZ DHp domain, 29 corresponded to alanine mutations whereas 1 mutation corresponded to a threonine mutation on 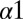(i.e., A255T). See Fig. S1B and Table S2 for mutational positions with basic information about conservation. Their study explored the effect of the EnvZ mutations on the in vitro phosphatase activity from OmpR∼P to EnvZ as well as the phosphotransfer from EnvZ∼P to OmpR.

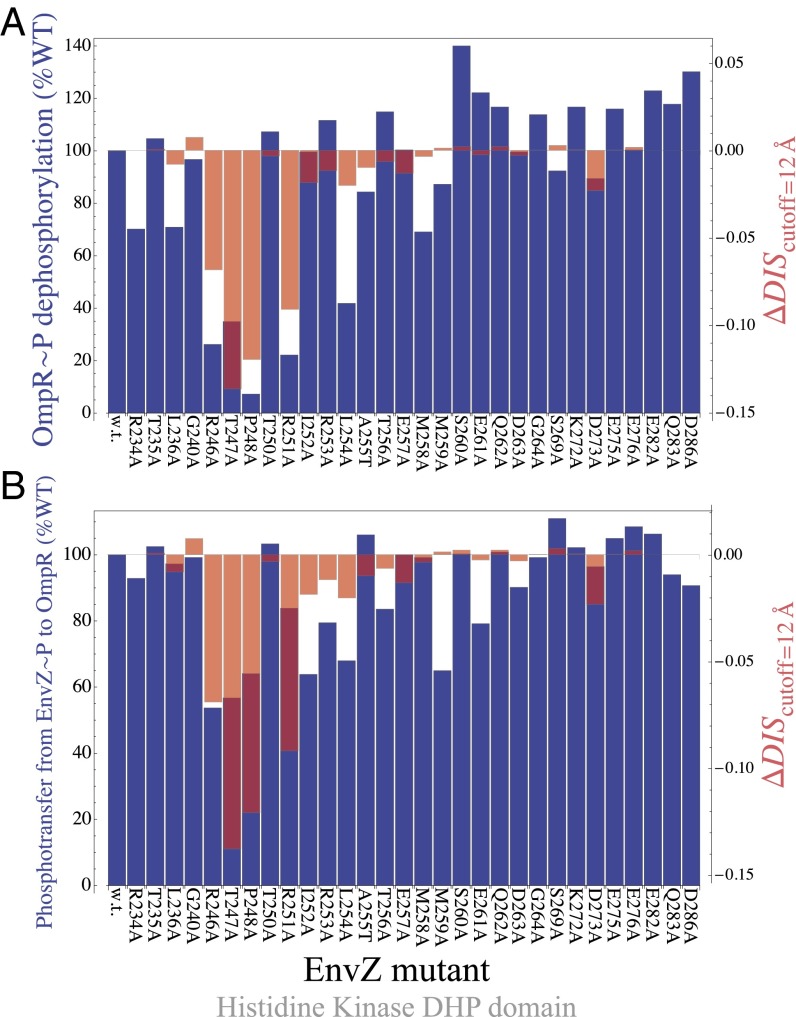
To better understand the mutations explored by Capra et al., we first computationally predict the structure of the wild-type EnvZ/OmpR complex (Materials and Methods), which we find to be consistent with that of an experimentally determined HK/RR complex (6), similar to our predicted KinA/Spo0F complex. We find strong quantitative agreement between the mutational change in phosphatase activity of the mutant EnvZ and our DIS metric (Eq. 2) with a Pearson correlation of 0.80 when only interfacial residues are considered (Fig. 4A). Using the same set of predictions, we also find agreement with experimental phosphotransfer from EnvZ∼P to OmpR (Fig. 4B) with a Pearson correlation of 0.66. For the experimental comparisons in Fig. 4 A and B, a relaxed cutoff definition of 12 Å was used in Eq. 2, similar to the experimental comparison in the previous section. Consistent with the findings of Capra et al., our metric predicts that the most deleterious mutations to the EnvZ/OmpR interaction are located on the 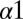helix of EnvZ in a region that forms contacts with OmpR in our predicted wild-type complex. The agreement of our genomic predictions with two different measurements can be explained by the similarities in the two processes—e.g., many of the same residues on EnvZ are involved in both phosphotransfer and phosphatase activity.

Fig. 4.

Direct comparison of our DIS metric with in vitro phosphotransfer measurements between the EnvZ mutant and OmpR by Capra et al. (11). The 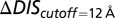(Eq. 2) is directly compared with (A) the experimentally measured phosphatase activity of OmpR∼P by EnvZ and (B) the experimentally measured phosphotransfer from EnvZ∼P to OmpR. Our prediction exhibited Pearson correlations of 0.80 and 0.66 with the experimental data shown in A and B, respectively. The dark purple color is due to the overlap between the bars representing the experimental data (dark blue) and the bars representing the predictions of our metric (light red).

Similarly, we find for a closely related experiment by Qin et al. (12) involving cysteine-scanning mutagenesis of EnvZ that our predictions (Fig. S3) are able to capture the deleterious effects of mutations to a region of 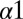that forms contacts with OmpR in our predicted complex. However, our predictions are unable to capture the strong experimentally observed effects of cysteine mutations to the N-terminal end of the 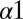helix or to the 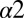helix. A possible explanation is that cysteine mutations may influence the stability of the DHp domain through intradomain effects, which are not considered in our study, as well as potentially form disulfide bonds with OmpR.

Construction of a DIS Null Model.

To distinguish between mutational changes in our DIS metric associated with binding and recognition and generic properties that are common among HK/RR, we first compute a null model by eliminating the cognate pair assumption (Materials and Methods). The resulting null model reflects the direct couplings between conserved features in both HK and RR, respectively. In accordance with this interpretation, we find that the top 10 ranked DI pairs for the scrambled HK/RR alignment are generally between highly conserved catalytic residues (Fig. 5A). Projecting the top DI pairs on the KinA/Spo0F sequences, we find that the DI pair with the highest rank for our null model corresponds to the His phosphorylation site on the DHp domain (H405) and the Asp phosphorylation site on the REC domain (D54). Another DHp residue involved in the top 10 pairings is the conserved P410 that is responsible for a structural kink in the 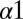helix (47), possibly involved in a phosphorylation-induced conformational change. On the REC domain, D11, T82, and K104 have been implicated as catalytically conserved residues (1, 46) whereas G62 has been suggested to play an important role in the flexibility of the 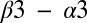loop (48) that contains the Asp phosphorylation site. Although distant from the Spo0F active site, G97 is also highly conserved among RR proteins.

Fig. 5.

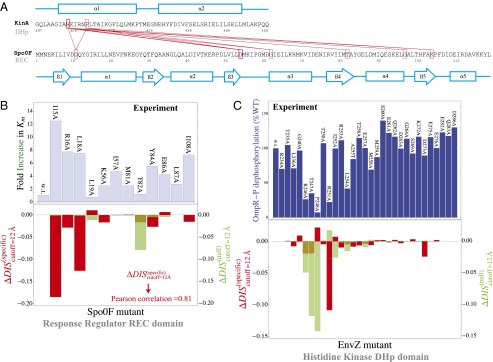
(A) Top 10 interprotein DI pairs of the scrambled HK/RR input set (Materials and Methods) are plotted on the KinA/Spo0F sequences in red. The top DI pairs of the null model are generally between conserved catalytic residues. (B) Applying Eq. 3b to 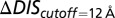in Fig. 3A to obtain 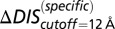(red) from 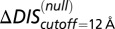(green). The agreement of 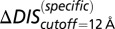with the experimental fold increase in 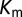(10) has an improved Pearson correlation of −0.81. (C) Applying Eq. 3b to 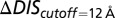in Fig. 4A, we find that the 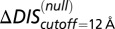(green) metric is able to distinguish the deleterious effect of mutating the conserved EnvZ residues R246, T247, and P248 to alanine observed experimentally (11). A direct comparison of 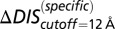or 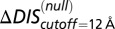with the experimental data in Fig. 4A was not performed because the experimental measurement does not distinguish between mutational changes that affect the molecular determinants of binding and recognition and mutations that affect conserved residues. In both B and C, the overlap between the red and green bars has a light brown color.

Computing DCA using the scrambled HK/RR MSAs instead of the cognate pair sequences, Eqs. 1 and 2 can be used to obtain a “null” score—i.e., 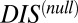(Materials and Methods). A metric dealing with nonconserved interprotein residue pairs can then be obtained by subtracting 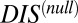from the original DIS to obtain 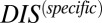(Eq. 3). Using this idea, we are able to separate our DIS metric into 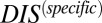, which we interpret as containing the determinants of specificity and recognition for HK/RR proteins, and 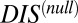, which we interpret as being associated to very generic, conserved features of HK/RR signaling. Hence, HK/RR signaling partners tend to have higher values of 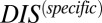than nonpartners due to their mutually coevolved interface. We are able to validate this interpretation by computing 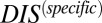for the collection of HK and RR proteins in B. subtilis and E. coli and correctly identifying cognate pairs that have the highest 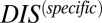, in accordance with the methodology of Procaccini et al. (37), with the exception of RstB/RstA from E. coli. We are able to further validate our interpretation of 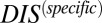by subdividing the input set into a new input set of 15,623 cognate pairs from which we compute a corresponding 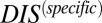. When we apply 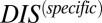of our new input set to the remaining 15,000 cognate HK/RRs not present in the input as well as to 15,000 scrambled HK/RRs not present in the input (Fig. S4), we see a clear distinction between the distributions of the cognate and scrambled sets. The origin of the long tail corresponding to cognate pairs with low specificity can potentially be attributed to a relaxed requirement of molecular specificity for signaling partners that obtain specificity through other means (e.g., cellular localization).

When we revisit the experimental results in Fig. 3A and apply our separation procedure, we find that 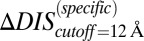(Fig. 5B) better predicts the fold increase in 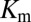with an improved Pearson correlation of −0.81 from the previous correlation of −0.66. This supports the notion that a metric associated with the mutually coevolved interface of HK/RR cognate pairs is a better predictor of mutational changes in the experimental dissociation constant. This improvement occurs as a result of subtracting the null background, 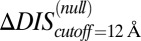, which captures the mutation of the catalytic residue T82 (Fig. 5B). Likewise, 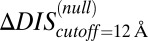(Fig. 5B) exhibits a correlation of −0.78 with the experimental fold decrease in shown in Fig. 3C, which is comparable to the prediction in Fig. 3C using DIS with all interprotein pairs (Eq. 1). Although it should be noted that the agreement of 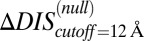is almost entirely due to the decrease associated with the T82A mutation.

When we revisit our predictions for the DHp mutational study in Fig. 4A and apply the separation procedure (Fig. 5C), we find that 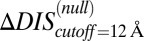is better at quantifying the deleterious mutational change associated with mutating the conserved R246, T247, and P248 residues. These three residues located on the 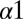helix of the DHp domain are common among many histidine kinase proteins and play an important role in phosphatase activity as well as phosphotransfer to its RR partner (11). Furthermore, the conserved P248 residue has been implicated with the structural kink in the 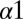helix (47), which has been suggested to play a role in the functional state of HK proteins.

Although we are able to show that 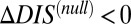captures the deleterious effects associated with mutating important conserved residues, a number of important questions remain regarding the interpretation of 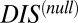and its relation to catalytic activity. Is 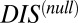a sufficient proxy for catalytic activity or does the DIS metric (Eqs. 1 and 2) contain additional coevolutionary information necessary to describe catalytic activity? Future work in this area is necessary to fully explore these concepts and to understand the differences between Eqs. 1 and 2 and the null model metric in predicting quantities such as .

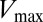Addressing Specificity and Recognition in Cognate Pairs and Hybrid TCS Proteins.

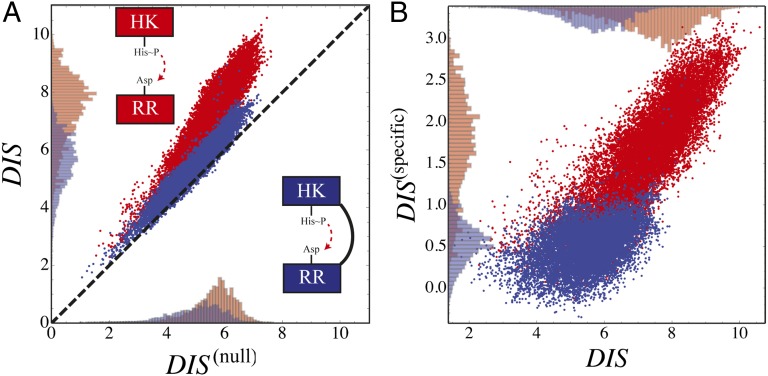
A recent study by Townsend et al. (49) demonstrated that hybrid TCS proteins, which are single proteins that contain both an HK and an RR joined by a linker, exhibit a relaxed molecular specificity in contrast to their nonhybrid counterparts. In other words, the HK and RR domains of a hybrid protein do not need to maintain their interaction specificity by having a highly coevolved interface because their mutual tethering significantly increases their encounter rate. When we plot 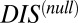vs. 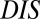for hybrid TCS proteins and nonhybrid cognate pairs (Fig. 6A), we find that hybrid proteins tend to fall along the line 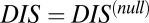whereas cognate pairs tend toward higher values of DIS (i.e., 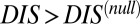). Recalling that 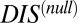reflects generic properties of scrambled HK/RR proteins, our findings are consistent with those of Townsend et al. that hybrid pairs tend to have lower specificity. This can be further demonstrated by plotting the distributions of cognate and hybrid pairs as a function of 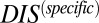(Fig. 6B), which shows that the cognate pair distribution is shifted toward higher values of 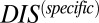. These results cannot be attributed to sampling bias due to the hybrid proteins being absent from our input set while cognate pairs are present. We demonstrate this by obtaining direct couplings from an input set of 15,623 cognate pairs and applying them to 15,000 cognate pairs and 15,000 hybrid proteins, neither of which are in the input set (Fig. S5). Also plotted in Fig. 6B are the cognate and hybrid distributions as a function of DIS for direct comparison with 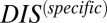. It is interesting to note that if 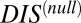does in fact reflect catalytic activity, a possible evolutionary explanation for why DIS tends toward even higher values for increasing 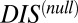would be to reduce the deleterious effects of a cross-talk by a catalytically effective phosphotransferer/receiver.

Fig. 6.

(A) Plot of 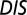vs. 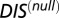for 30,623 cognate pairs (red) and 17,413 hybrid proteins (blue) that we could identify from available sequence data. Noting that 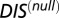captures generic features that are common among HK/RR proteins, we find that hybrid proteins generally fall along 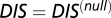(dashed line) whereas cognate proteins tend toward 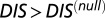especially as 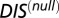increases. 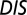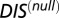Histograms of the cognate pairs and hybrid proteins are projected along the axis representing and , respectively. (B) Plot of 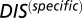vs. 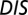for all cognate pairs and hybrids demonstrates that 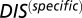is able to discern between the cognate pairs, which generally feature a highly coevolved interface, and hybrid proteins, for which the requirement for high specificity is relaxed.

Discussion

Although DCA has previously been associated with protein structure prediction, recent work by Procaccini et al. (37) applied the message-passing formulation of DCA to study TCS signaling partners, suggesting that the determinants of their interaction are conserved by evolution in their sequence data. Here, we have applied the interprotein direct couplings inferred by mean field DCA from abundant sequence data (30,623 cognate pair sequences) for cognate pairs to characterize the effects of mutational changes on the functional interaction between HK and RR signaling proteins. TCS signaling partners undergo sequence coevolution because they are under selective pressure to maintain their ability to bind and transfer phosphoryl groups (i.e., signal). Hence, mutations to the binding interface of one TCS protein require compensatory mutations in the binding interface of its partner. We take advantage of this coevolution with DCA to infer the effect of mutations on the phosphotransfer ability. We have provided strong evidence that we can predict mutational changes in phosphotransfer ability between HK/RR proteins by using our DIS, suggesting that 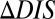can be used to predict mutations that desirably tune the strength of signal transfer between TCS proteins. Our DIS metric can further be used to focus on nonconserved features of HK/RR signaling, such as the variable residues responsible for binding and recognition, by subtracting an appropriate null model corresponding to pairwise conservative features of HK/RR signaling partners. Although recent stimulating work (11, 15) has demonstrated the rewiring of HK/RR signaling in vitro, our methodology could potentially afford us additional flexibility in exploring sequence space for mutations that can be used to preferentially switch the interaction of a TCS protein toward a nonpartner by using 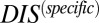. One strategy would be to simply look for mutations that increase DIS between, for example, an RR and a nonpartner HK.

Our methodology also potentially forms a starting foundation for the system-level study of protein–protein interactions in TCS systems as well as other signaling systems and regulatory proteins, such as the toxin–antitoxin (TA) proteins (50), provided that there are enough sequences of interacting proteins (>1,000). We provide further evidence that hybrid TCS proteins exhibit a reduced molecular specificity (considering 17,413 hybrid sequences), in agreement with recent experimental work by Townsend et al. (49). Furthermore, we have demonstrated that 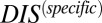can be used as a proxy for interaction specificity among signaling proteins because higher values tend toward a more mutually coevolved interface. Although we have considered only pairwise interactions between the REC domain of an RR and the DHp domain of an HK, future work could extend our methodology to systems of multiple interacting domains such as networks of potentially interacting TCS systems in model bacterial organisms. In particular, we could explore the role of cellular localization and negative selection (51) in limiting cross-talk in TCS networks. Understanding these concepts would likely be necessary to make phenotype-level predictions in model bacteria based on site-directed amino acid mutations in protein sequences.

Materials and Methods

Construction of Cognate Pair Input Set.

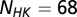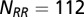We obtained MSAs from Pfam (52) for HisKA (PF00512), the dimerization domain of the HK, and Response_reg (PF00072), the receiver domain of the RR. All residue inserts were removed from the respective Pfam databases such that each MSA entry for the HK and the RR has lengths of and , respectively. Using the Uniprot (53) protein database, we extracted the genomic locations (i.e., loci index) for HK and RR proteins obtained from Pfam. Similar to a number of studies (11, 13–18), we assume that HK and RR that are adjacent to one another on the genome tend to be cognate pairs that interact with high specificity with one another as signaling partners. Furthermore, we excluded hybrid proteins because they feature a relaxed specificity (49). We concatenated the MSAs of each nonhybrid cognate pair to have a combined sequence, 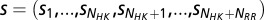, where the HK positions span from 1 to 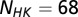whereas the RR positions span from 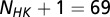to 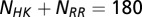. We were able to construct an input set of 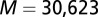nonhybrid cognate pairs in this manner.

DIS.

We introduce a metric for quantifying the interaction (e.g., specificity and phosphotransfer activity) between the dimerization domain of an HK and the receiver domain of an RR. This metric is defined as a summation of the direct information values between all interprotein residue pairs for a particular sequence ,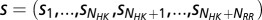

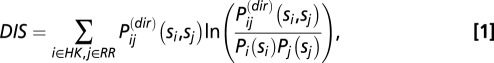where 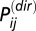is the amino acid pair distribution associated with the direct couplings inferred from DCA and 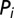is the amino acid marginal distribution of a position i in the concatenated MSA. This metric is closely related to the definition of DI (17, 23), which focused on the mutual information associated with the direct couplings between particular positions i and j for all possible combinations of amino acids at those positions. It should be noted that computation of Eq. 1 from a given MSA sequence 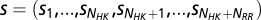would include the contribution of gaps located in the MSA. We generally find that the contribution of gaps is negligible for sequences consisting of only a small fraction of gaps.

The number of terms in the summation of Eq. 1 can be further reduced by considering only interprotein residue pairs that are within a cutoff distance in an available 3D structure of an HK/RR complex. Eq. 1 can thus be reduced to

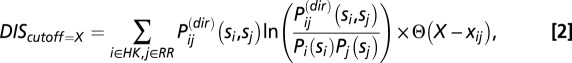where 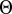denotes the Heaviside step function, 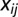denotes the minimum distance between the interprotein residues given by positions i and j, and X is the cutoff distance. For a given HK/RR MSA sequence, the positions corresponding to gaps are excluded from Eq. 2 because MSA gaps are not defined in the structure.

Null DIS and Specific DIS.

We performed random permutations on the HK/RR pairings from the cognate pair MSA discussed earlier to generate an alignment of randomized HK/RR pairings. This procedure was performed 25 times to obtain 25 randomized HK/RR databases each with 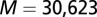entries. Using these null model MSAs, we computed pairwise interprotein direct couplings using DCA and averaged these couplings for all 25 databases. We also obtained the associated direct pair distribution of DCA, , corresponding to our null model. Substituting directly into Eqs. 1 and 2, we were similarly able to compute a DIS corresponding to our null model, which we denote as 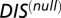. This null model score captures very generic properties of HK/RR proteins and the highly correlated interprotein residue pairs tend to be highly conserved residues related to function/catalytic activity.

One can obtain a DIS-related metric that focuses on interprotein residue pairs that are highly variable (i.e., not conserved) among HK/RR signaling partners, such as the residues that give rise to specificity and recognition. This specific score can be obtained by subtracting 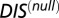from Eq. 1:

Similarly, if a complex structure is used to reduce the number of interprotein pairs using Eq. 2,

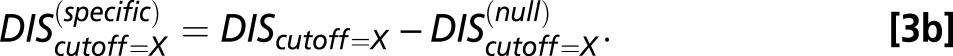The same cutoff distance is applied to both 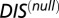and 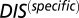in Eq. 3b such that their sum always recovers Eq. 2.

Prediction of Unknown HK/RR Complex: KinA/Spo0F and EnvZ/OmpR.

Because no structural data exist for the KinA/Spo0F complex or the EnvZ/OmpR complex, we predict their 3D structures using genomics-aided complex prediction (16) that combines DCA-derived (23) contacts in structure-based models (SBM) (54, 55) for docking. Although other relevant methods for docking proteins exist (56–58), genomics-aided complex prediction has successfully been used to predict the HK/RR complex of TM0853/TM0468 within crystallographic accuracy of its experimentally determined structure (6) as well as to predict the active conformation of an HK in the act of autophosphorylation (28). SBMs of the uncomplexed wild-type proteins were constructed using homology modeling with I-TASSER (59, 60). The N-terminal sensor domains of KinA and EnvZ as well as the C-terminal DNA-binding domain of OmpR were excluded from their respective SBMs. Using the input MSAs of HK/RR cognate pairs described earlier in Materials and Methods, the ranked DI was computed for all interprotein pairs. The top 20 DI pairs excluding pairs corresponding to gaps in the MSA were treated as physical contacts in SBM docking. The docked complexes were then relaxed using the CHARMM27 (61, 62) force field with TIP3P water/counter ions (63) on the GROMACS software package (64) to remove artifacts, resulting in reliable complex structures. The predicted complexes for KinA/Spo0F and EnvZ/OmpR are included in PDB format as Dataset S1 and Dataset S2, respectively.