Programmed Allee effect in bacteria causes a tradeoff between population spread and survival

Significance

Understanding how species spread and survive is important in many biological contexts. The ability to disperse has been shown to enhance spread in some species but detract in others. Theoretical studies have predicted that these observations may be due to the Allee effect. To test this theory, we engineered Escherichia coli to have an Allee effect. Using these bacteria, we found that if dispersal is too fast or too slow, a population cannot spread. By manipulating the number of patches, we uncovered tradeoffs that control spread and survival. Finally, we demonstrate that fluctuations in growth may serve to determine if spread occurs. Our results may be useful in controlling invasive species and the spread of infectious diseases.

Abstract

Dispersal is necessary for spread into new habitats, but it has also been shown to inhibit spread. Theoretical studies have suggested that the presence of a strong Allee effect may account for these counterintuitive observations. Experimental demonstration of this notion is lacking due to the difficulty in quantitative analysis of such phenomena in a natural setting. We engineered Escherichia coli to exhibit a strong Allee effect and examined how the Allee effect would affect the spread of the engineered bacteria. We showed that the Allee effect led to a biphasic dependence of bacterial spread on the dispersal rate: spread is promoted for intermediate dispersal rates but inhibited at low or high dispersal rates. The shape of this dependence is contingent upon the initial density of the source population. Moreover, the Allee effect led to a tradeoff between effectiveness of population spread and survival: increasing the number of target patches during dispersal allows more effective spread, but it simultaneously increases the risk of failing to invade or of going extinct. We also observed that total population growth is transiently maximized at an intermediate number of target patches. Finally, we demonstrate that fluctuations in cell growth may contribute to the paradoxical relationship between dispersal and spread. Our results provide direct experimental evidence that the Allee effect can explain the apparently paradoxical effects of dispersal on spread and have implications for guiding the spread of cooperative organisms.

A fundamental question in biology is how the spread and survival of an organism is influenced by various factors (1), including population density (2), dispersal rate (3), and habitat configuration (4). Addressing this question has implications for understanding and controlling biological invasions caused by the introduction of a new species into an established ecosystem (1), the spread of infectious diseases, or the emergence of new pathogens (5).

Dispersal has been recognized as being particularly critical in promoting successful spread (e.g., ref. 1; additional examples in SI Text). However, dispersal has also been shown to reduce spread (e.g., ref. 6; additional examples in SI Text). Theoretical studies have proposed that this paradoxical observation can be explained by the Allee effect, which is defined as a positive relationship between individual fitness and the total density of the population (7, 8). In the extreme case, called a strong Allee effect, the population will display a negative fitness, which can be manifested as a negative growth rate, when its initial density is below a critical threshold. Often, a strong Allee effect can be due to the inability to initiate a cooperative behavior at low density (7). This dynamic is observed in several contexts of biology including invasive species, reintroduction biology, epidemiology, the infection of an individual host by microbial pathogens, and quorum sensing (SI Text).

By assuming a strong Allee effect, theoretical studies have predicted that dispersal can have a dual effect on population survival and spread. Slow dispersal can prevent the colonization of new territories because the number of individuals arriving in a new area is insufficient to establish a new population (e.g., ref. 9; additional examples in SI Text). Fast dispersal can act as a drain on a source population, which can become too small to be maintained (e.g., ref. 10; additional examples in SI Text). These predictions have been invoked previously to explain the failure of organisms to expand their ranges or to become established (SI Text and Table S1).

Although this theoretical explanation is plausible, its experimental demonstration is lacking. This is particularly difficult to verify experimentally in a natural setting because such settings are subject to numerous confounding factors that can obscure the contribution of individual components to the outcome of successful spread. Along this line, it has been suggested that environmental and demographic stochasticity may contribute to population extinction, even in species without an Allee effect (SI Text). The role of a strong Allee effect is further complicated by the limited number of empirical studies that demonstrate the existence of an Allee effect (11), in part due to difficulty in quantifying and studying small populations.

To overcome these difficulties, we engineered a gene circuit to confer a strong Allee effect in Escherichia coli and examined its impact on spread and survival. Synthetic biology involves creating novel behaviors in biological systems using gene circuits. These synthetic systems have resulted in numerous novel behaviors including spatial patterning (12) and modulation of fitness (13). Synthetic systems have several advantages over both field and theoretical studies (14). These systems provide a well-defined system to focus on the key, fundamental parameters in a more definitive manner, and they allow direct mapping between modeling and experiments. Although modeling is often used as a driving force in such studies, the ability to confirm the model predictions in a living system serves as a critical proof-of-principle for the plausibility of these predictions. The use of synthetic gene circuits can be thought of as an extension to the use of microbes as model systems to examine questions in evolution and ecology (e.g., ref. 15).

Results

Programming a Strong Allee Effect in E. coli.

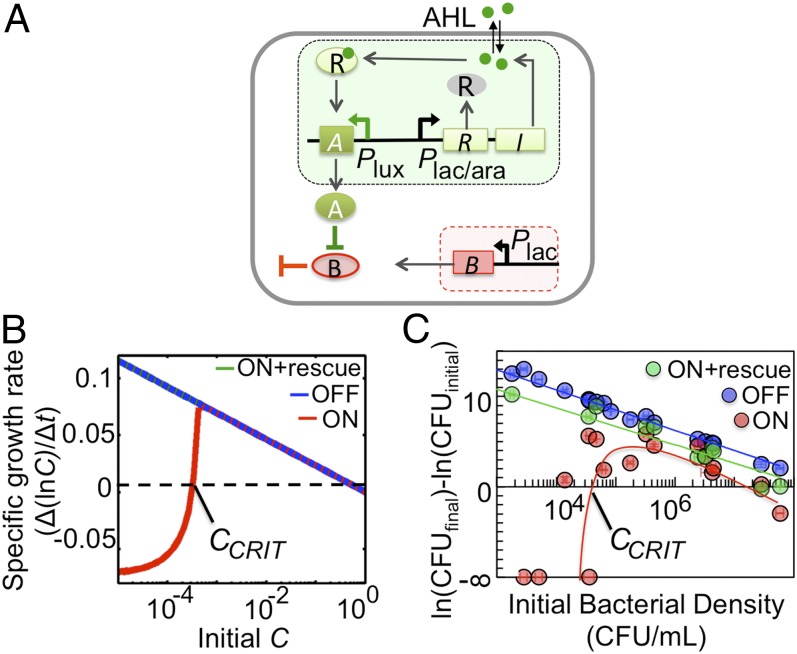
The fundamental property of a strong Allee effect is a population that has a negative fitness level below a density threshold (SI Text); the population can only grow when its initial density is above a threshold density, C_CRIT. As such, the strong Allee effect represents a form of bistable growth (16). To realize this property, we used the LuxR/LuxI quorum-sensing (QS) system from Vibrio fischeri (17) and the CcdA/CcdB toxin–antitoxin module to control population survival (Fig. 1A and Fig. S1A). Induction of our circuit by isopropyl β-d-1-thiogalactopyranoside (IPTG; 1 mM) activates expression of the LuxR/LuxI system and CcdB. CcdB causes cell death by inhibiting DNA replication (18). CcdB can be inhibited by CcdA, which is controlled by the QS module. LuxI leads to synthesis of acyl-homoserine lactone (AHL). Because AHL can diffuse across the cell wall, its concentration increases with bacterial density. At a sufficiently high concentration, AHL activates LuxR, which drives the expression of CcdA. CcdA then inhibits CcdB, thus rescuing the population. Our circuit logic mimics the generation of the Allee effect due to environmental conditioning, where a group of cooperative organisms modifies the environment to grow (Table S2).

Fig. 1.

Programming a strong Allee effect in E. coli. (A) The circuit consists of a killing module (red shaded) and a rescue module (green shaded). The killing module consists of the P_lac promoter driving expression of ccdB (indicated by B). The rescue module consists of the luxR(R)/luxI(I) quorum sensing (QS) system under the control the P_lac/ara promoter and ccdA (indicated by A) under the control of the P_lux promoter_. Green circles, 3-oxohexanoyl-homoserine lactone (AHL). (B) Specific growth rates of the engineered bacterial population. With the circuit OFF or ON + rescue (directly behind blue line, initial rescue [A] = 0.1 μM), the specific growth rate is predicted to decrease with increasing initial C (bacterial density). With the circuit ON, a strong Allee effect is observed; the specific growth rate is negative if the initial C is below the Allee threshold (C_CRIT). Specific growth rate [Δ(lnC)/Δt] at t = 100 h. (C) Experimental verification of a strong Allee effect. With the circuit OFF (−IPTG) or ON + rescue (+IPTG/AHL), cfus decreased with increasing initial bacterial densities. With the circuit ON (+IPTG), a strong Allee effect was conferred to the population, where cfus decreased below an initial bacterial density of ∼10⁴ cfu/mL. Change in cfu/mL was calculated using ln(cfu_final) − ln(cfu_initial) at 28 h. When cfu_final was 0, a result of negative infinity was obtained. SD from three replicates. Lines drawn as a guide.

In a natural setting, spread occurs when an organism travels from an initial area to a separate, geographically distinct area. Spread by such organisms often displays a central area of growth (i.e., source patch) surrounded by several separate areas of growth (i.e., target patch) indicative of between-patch or multipatch (i.e., multitarget or stratified) dispersal (e.g., ref. 19; additional examples in SI Text). These patches are often only connected by dispersal and are therefore physically separated. It has been suggested that failing to account for between-patch dispersal has led to the inability to accurately predict spread rates (20) and that an understanding of these dynamics is required to understand population spread (21).

To understand how between-patch dispersal and a strong Allee effect interact to control spread, we established a theoretical and experimental framework (SI Text). We initially consider two discrete patches (a source and a target patch) that are connected via one-way dispersal (from source to target). Both populations at the source and target populations are well mixed, and we do not account for any measure of distance between the patches. This two-patch system with discrete dispersal has been used extensively in the past to model the spread of species (SI Text). Experimentally, we emulated dispersal by discretely transferring bacteria from a source patch to a target patch and measured optical density (OD) in both patches over 28 h. Our discrete transfer protocol follows similar techniques that have been used to simulate dispersal using synthetic systems (e.g., ref. 22). Finally, our protocol may be amenable for the study of Allee effects in natural systems, including Drosophila melanogaster (Table S2). One could disperse an established population of flies to new medium in a separate culture and examine reproductive success.

The circuit can be modeled by two equations (Eqs. 1 and 2, Materials and Methods, SI Text, and Table S3). With the circuit OFF or ON + rescue (i.e., medium supplemented with 0.1 μM AHL), the model predicts that the bacterial density (C) will increase regardless of initial C (Fig. S1B). With the circuit ON, the model predicts that the population will only grow when starting from a sufficiently high initial C (Fig. S1B). To test these predictions, we inoculated the engineered bacteria at varying initial densities and grew them under three conditions in a microplate reader: no IPTG (circuit OFF), 1 mM IPTG (circuit ON), and 1 mM IPTG and 0.1 μM AHL (circuit ON + rescue). For each culture, we measured its density using OD (measured at 600 nm) every 20 min for 50 h. When the circuit was OFF or ON + rescue, the cultures grew regardless of their initial densities (Fig. S1C). When the circuit was ON, the cultures starting from a high initial density (∼10⁸ cfu/mL) grew to a high density (OD = ∼0.4) after ∼25 h, whereas those starting from a low initial density (∼10⁴ cfu/mL) did not grow over 70 h (Fig. S1C).

The OD measurements were consistent with viable cell counts measured by cfus. With the circuit OFF or ON + rescue, our model reduces to a logistic equation where the specific growth rate [Δ(lnC)/Δt] is expected to decrease with initial C (Fig. 1B, blue and green lines, respectively). This was confirmed by experiment (Fig. 1C, blue and green circles/lines). When the circuit is ON, the specific growth rate is predicted to be negative for an initial C below a threshold, C_CRIT (Fig. 1B, red line). Above C_CRIT, the specific growth rate first increases and then decreases with increasing initial C, while going through a maximum at an intermediate initial C. This prediction was confirmed by experiment (Fig. 1C, red circles/lines, and Fig. S1D). When our engineered bacteria were grown with the circuit ON and from a low initial density (<∼10⁴ cfu/mL), the number of cfus decreased over 28 h. Cultures starting with an initial density above ∼10⁴ cfu/mL grew during the same time period. The net change in culture density increased with the initial density until the latter reached ∼10⁵ cfu/mL. Beyond this point, the net change in culture density declined with further increases in the initial density.

C_CRIT is readily tunable in our system. Decreasing the degradation rate constant of AHL (k_dA) is predicted to increase C_CRIT (Fig. S2A): with faster AHL degradation, a higher bacterial density is required to induce sufficient CcdA expression to rescue the population. One method to decrease AHL stability is to increase the pH of the medium (23). We observed that C_CRIT increased by ∼100-fold when our engineered bacteria were grown at pH 7.5 (compared with pH 7.0; Fig. S2 B–F). Inclusion of leaky gene expression, a metabolic burden, nonlinear activation of ccdA, or stochastic dynamics in our model still leads to a strong Allee effect (Fig. S2 G–J), which suggests that our simple model (Eqs. 1 and 2) is sufficient to capture the dynamics of our synthetic circuit.

A Biphasic Dependence of Population Spread on Dispersal.

To guide our dispersal experiments, we modified our model (Eqs. 1 and 2) to account for the discrete transfer of bacteria from a source patch to a target patch (Eqs. S20 and S21 and Fig. S3A). The modified model also accounts for death of dispersing individuals (Eq. S21 and SI Text) as dispersing individuals have increased rates of mortality (24). The discrete transfer of bacteria mimicked group dispersal, which has been observed in cooperative species (Table S4). Spread is assumed to have occurred when robust growth (an increase in OD greater than 0 as determine by a t test; SI Text) occurs at both the source and target patches (1, 25).

We first examined dispersal where only one target patch is present (n = 1, where n represents the number of target patches; Fig. S3A). With the circuit OFF or ON + rescue, our model predicts that spread would occur for all dispersal rates (initial C = 0.05; Fig. 2A, Left and Right, respectively). With the circuit ON, our model predicts a biphasic dependence of the total growth (summed between the source and the target patches) on the dispersal rate (Fig. 2A, Center). Total growth first increases and then decreases with the dispersal rate. In the presence of a strong Allee effect, growth at either the source or the target patches increases with the initial C at the corresponding patch (after dispersal). Thus, growth at the source patch will decrease with dispersal rate (Fig. 2A, Center, black line) but growth at the target will increase with dispersal rate (Fig. 2A, Center, green line). When combined, total growth is maximized at intermediate dispersal rates, resulting in an optimal dispersal rate, which leads to the greatest amount of total growth.

Fig. 2.

A strong Allee effect causes a biphasic dependence of spread on the dispersal rate. (A) Bacterial densities (C) of a population containing our synthetic circuit with increasing α (dispersal rate). When the circuit is OFF (Left) or ON + rescue (initial rescue [A] = 0.1 μM; Right), spread (i.e., growth at the source and target patch) is predicted to occur regardless of α. When the circuit is ON (Center), spread is predicted to occur within a small range of α, leading to a biphasic trend. Outside this range, growth is reduced at either the source or the target patch. Total C is the summed densities between both patches. Initial C = 0.05, t (simulation time) = 28 h. y axis scale is the same for each panel. (B) Density of bacterial populations containing our synthetic circuit with increasing dispersal rates. With the circuit OFF (−IPTG) or ON + rescue (+IPTG/AHL), our engineered bacteria underwent spread regardless of the dispersal rate (Left and Right, respectively). With the circuit ON (+IPTG; Center), our engineered bacteria had a small range of dispersal rates that led to spread. Outside this range, growth was reduced at either the target or the source patch. The lowest and highest dispersal rates that led to spread were 0.975 (P ≤ 0.04) and 0.025 (P ≤ 0.015, two-tailed t test; SI Text). SD from at least four replicates. Initial density = 5.8 ± 1.2 × 10⁶ cfu/mL. OD at 28 h. y axis scale is the same for each panel.

To test these predictions, we emulated dispersal by transferring a fixed volume of bacteria from one well of a 96-well plate (i.e., a source well) to a second well (i.e., a target well) after an initial period of growth (SI Text). We chose an initial density in the source well that was above C_CRIT (5.8 ± 1.2 ×10⁶ cfu/mL), such that bacteria would grow for all circuit states (OFF, ON, or ON + rescue) in the absence of dispersal. Our experimental system validated these predictions: with the circuit ON (Fig. 2B, Center, and Fig. S3 B and C), increasing dispersal rates promoted growth at the target (green line) but reduced growth at the source (i.e., dispersal rates of 0.995 and 0.975; black line), leading to a biphasic dependence of the total growth on dispersal rate (red line). An optimal dispersal rate was observed at a dispersal rate of 0.375 where the highest amount of total growth was observed. In the OFF and ON + rescue conditions, growth occurred at all dispersal rates (Fig. 2B, Left and Right). Inclusion of a death term of nondispersing individuals, the implementation of continuous dispersal, or stochastic dynamics in our model (Eqs. S22 and S23) produce the same qualitative predictions of the biphasic dependence of total growth on dispersal rate (Fig. S3 D–F and SI Text).

This biphasic dependence demonstrates that presence of a strong Allee effect can indeed account for the paradoxical observations on dispersal and successful spread. Our experimental system thus provides support for two key previous theoretical predictions that have yet to be demonstrated experimentally: slow dispersal can lead to insufficient growth at the target, but fast dispersal serves as a drain at the source (SI Text).

Initial Source Density Determines the Range of Dispersal Rates That Allow Spread.

A prominent observation in several species is that as the number of individuals released in a new area declines, so does establishment and spread success (e.g., ref. 2). Intuitively, populations with initial densities below C_CRIT may be more likely to go extinct. However, it remains unclear as to how the Allee effect and dispersal control spread when the initial density at the source patch increases above C_CRIT.

Our model predicts that with the circuit ON, increasing the initial C of the source population expands the range of dispersal rates that allow spread (Fig. 3A). At a low initial C (0.007), spread only occurs within a very small range of intermediate dispersal rates (Fig. 3B, Left). Here total growth is the highest at low dispersal rates where growth is reduced at the target but occurs at the source. At an intermediate initial C (0.05), a larger range of intermediate dispersal rates are predicted to promote spread (Fig. 3B, Center), and the total growth is the highest within this range. The range of intermediate dispersal rates that promote spread is greatly expanded for a high initial C (0.3; Fig. 3B, Right). In contrast, when the circuit is OFF, our model predicts that spread occurs regardless of the initial density or the dispersal rate (Fig. S3 G and H).

Fig. 3.

Dispersal rates allowing spread depend on the initial density at the source patch. (A) Spread landscape in the presence of a strong Allee effect. Increasing the initial bacterial density (C) at the source patch expands the range of dispersal rates (α) allowing spread (i.e., growth at the source and target patches). Total C is the summed densities at the source and target patches. t (simulation time) = 28 h. (B) Slices of the spread landscape along the x axis with different initial C. Low initial C = 0.007, intermediate initial C = 0.05, and high initial C = 0.3. (C) Density of bacterial populations that exhibit a strong Allee effect with varying initial densities. With the circuit ON (+IPTG), increasing the initial source density by ∼100-fold increased the range of dispersal rates allowing spread. The highest and lowest dispersal rates that led to spread were 0.75 [P ≤ 0.005, two-tailed t test (SI Text)] and 0.125 (P ≤ 0.043) for low initial density, 0.975 (P ≤ 0.04) and 0.025 (P ≤ 0.015) for intermediate initial density, and 0.995 (P ≤ 0.006) and 0.005 (P < 0.001) for high initial density. SD from six replicates. Low initial density = 6.1 ± 1.1 × 10⁵ cfu/mL, intermediate initial density = 5.8 ± 1.2 × 10⁶ cfu/mL, and high initial density = 5.5 ± 1.4 × 10⁷ cfu/mL. OD measured at 28 h.

Our experimental results validated these predictions (Fig. 3C). When cultures were grown with the circuit ON, spread only occurred in a small range of dispersal rates when the source well contained a low initial density of bacteria (6.1 ± 1.1 × 10⁵ cfu/mL; Fig. 3C, Left). As predicted, the most amount of growth occurred at lower dispersal rates, where spread did not occur. With a 10-fold increase in the initial density (intermediate initial density, 5.8 ± 1.2 × 10⁶ cfu/mL; Fig. 3C, Center), intermediate dispersal rates led to spread. Here total growth is highest within the range of dispersal rates that lead to spread. The range of permissible dispersal rates was drastically expanded when the initial density at the source well was increased by another 10-fold (high initial density, 5.5 ± 1.4 × 10⁷ cfu/mL; Fig. 3C, Right). In contrast, with the circuit OFF, bacteria grew at both the source and the target wells regardless of the dispersal rate or the initial density of the source population (Fig. S3I).

These results suggest that species with a strong Allee effect may have two different growth patterns when arriving in a new territory with a population density slightly above C_CRIT. One one hand, species that disperse at a low rate will maximize their density at the source population but fail to establish a population at the target patch. On the other hand, species that disperse at a high rate may spread; however, they face the added risk of detracting from population growth should the dispersal rate not fall within the biphasic growth area. As such, although high dispersal rates would lead to successful spread when the initial density is sufficiently above C_CRIT, here it may serve to detract from spread success, and population growth, when the initial density is close to C_CRIT.

A Tradeoff Between Effectiveness of Spread and Survival.

A key prediction of multitarget dispersal (in the absence of an Allee effect) is that population growth increases with increasing patches colonized making spread more prolific (20, 26). In the presence of a strong Allee effect, however, simultaneous dispersal of a small amount of bacteria to each target patch (n) may be insufficient to establish growth in the target patch but collectively can detract too much from the population at the source patch, which could lead to suppression of spread. This reasoning suggests a tradeoff between efficiency and robustness of spread and that increasing the number of target patches does not necessarily guarantee more effective total spread.

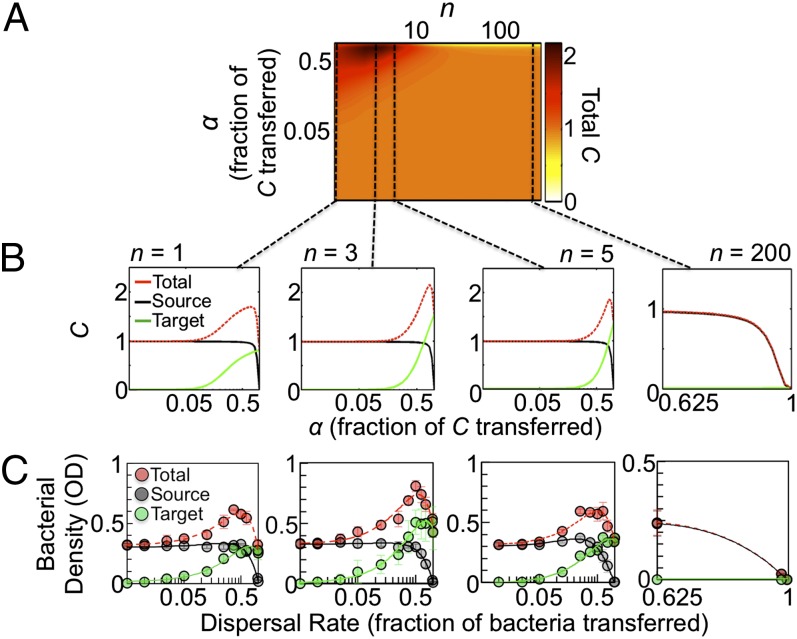
Our model predicts that with the circuit ON, the biphasic dependence of total C on dispersal rate is maintained when n > 1. Moreover, increasing n from 1 to 3 can increase the maximum total C for the overall population (Fig. 4 A and B). However, this contracts the range of dispersal rates that allows spread, indicating a tradeoff between efficiency and robustness of spread. Our model predicts that a further increase in the number of targets (n = 5) not only shrinks the range of dispersal rates that allow spread but also reduces total C (Fig. 4B, Right Center). In other words, for a given dispersal rate, spread also has a biphasic dependence on n. We note that this biphasic dependence is transient because at the steady state, bacteria in all target patches would grow to carrying capacity (Fig. S4D). However, the contraction of dispersal rates allowing spread observed as n increases is still observed at steady state. Furthermore, our model predicts that at n = 200, high dispersal rates cause complete population extinction, whereas low dispersal rates allow growth at the source patch only (Fig. 4B, Right). In contrast, with the circuit OFF, our model predicts the population will undergo spread regardless of the number of target patches (Fig. S4 A and B), and total C always increases with increasing n. This result is observed transiently and at the steady state (Fig. S4E).

Fig. 4.

A tradeoff between efficiency and robustness of spread in multitarget dispersal. (A) Spread landscape for multitarget dispersal in the presence of a strong Allee effect. Increasing n (number of target patches) can lead to an increase in the number of target patches colonized where maximum total C is highest at an intermediate n. As n increases, the range of dispersal rates allowing spread contracts. Total C is the summed densities of the source and target patches. α represents the dispersal rate. Initial C = 0.05, t (simulation time) = 28 h. (B) Slices of the spread landscape along the x axis with increasing values of n. (C) Density of bacterial populations with increasing dispersal rate and number of target wells. With the circuit ON (+IPTG), when the number of target wells was increased from one to three, the maximum total growth increased (P = 0.01; SI Text), but the range of dispersal rates allowing spread was reduced. For five target wells, the range of dispersal rates allowing spread further contracted, and total growth was reduced (P = 0.03). For 200 target wells, growth was observed in the source well at low dispersal rates. At high dispersal rates, growth was not observed. The highest and lowest dispersal rates that led to spread were 0.975 (P ≤ 0.04, two-tailed t test; SI Text) and 0.025 (P ≤ 0.015) for n = 1, 0.975 (P < 0.001) and 0.05 (P ≤ 0.008) for n = 3, and 0.75 (P ≤ 0.003) and 0.125 (P ≤ 0.003) for n = 5. SD from six replicates. Experiments initiated from an initial density of 5.8 ± 1.2 × 10⁶ cfu/mL. OD at 28 h. See SI Text and Fig. S4 for OD calculation.

Our experimental results validated these predictions (Fig. 4C and Fig. S4 C and F–J). Experimentally, we assumed that transfer to one target well could be used as a surrogate of transfer to multiple wells (SI Text and Fig. S4J). We transferred the same total amount of medium out of the source well but only transferred a fraction of the amount into a target well [calculated relative to the number of target wells (e.g., five target wells: 125 µL out of the source patch, 25 µL into a target patch, and the remaining 100 µL was discarded)]. We then multiplied the final bacterial density (OD) at 28 h by the total number of target wells in the system (Fig. 4C). When cultures were grown with the circuit ON and when the number of target wells was increased from one to three, the range of dispersal rates allowing spread contracted, and the maximum total growth (i.e., source well + all target wells) increased (Fig. 4C, Left Center). With five target wells, dispersal rates allowing spread further contracted (Fig. 4C, Right Center), and total growth decreased. With 200 target wells, growth was not detected in either the source or target wells at a high dispersal rate (Fig. 4C, Right). At low dispersal rates, growth occurred in the source well only. When the circuit was OFF, bacteria grew at all dispersal rates in both source and target wells (Fig. S4). Our analysis demonstrated that a strong Allee effect creates a tradeoff between efficient spread and survival: dispersing to multiple patches allows more efficient spread but increases the risk of failing to spread or of going extinct.

Theoretical (27) and experimental analyses (28) have demonstrated that as a population approaches a bifurcation point (e.g., C_CRIT), fluctuations in growth increase. Such fluctuations may serve as early indicators of catastrophic population collapse (28). Given the importance of such fluctuations toward predicting population dynamics, particularly in species with an Allee effect, we analyzed fluctuations in growth in target patches during multitarget dispersal. Our stochastic model (Eqs. S22 and S23) predicts that as α per n decreases, the distribution of lnC widens (Fig. S5A), and coefficient of variance (CV) (Fig. S5B) increases in the target patch. CV is predicted to be the lowest at dispersal rates that lead to the greatest amount of growth in the target patches. In contrast, with the circuit OFF, our stochastic model predicts that the fluctuations do not change with α per n (Fig. S5 A and B).

To test these predictions, we dispersed our engineered bacteria to one, three, or five target wells and quantified OD in the target wells. We observed that as dispersal rate per target patch increased, the distribution of lnOD widened (Fig. S5C), and CV increased (Fig. S5D) in the target patch. As predicted, CV was the lowest at dispersal rates that led to the greatest amount of growth in the target patches. In contrast, with the circuit OFF, the distribution of lnOD (Fig. S5C) and the CV (Fig. S5D) in the target well did not change significantly with dispersal rate per patch or the number of target wells. Similar trends were observed in the source well (SI Text). Our analysis indicates that fluctuations at low dispersal rates may offer an additional explanation as to why in some cases slow dispersal appears to lead to spread but in other cases it fails to result in spread.

Discussion

Our analysis has provided experimental evidence validating previous theoretical predictions that a strong Allee effect can resolve the opposite roles that dispersal has on spread success. As reflected by our results in Figs. 3 and 4, the overall outcome of spread critically depends on several environmental factors, including the initial cell density in the source population, the presence of absence of Allee effect, the dispersal rate, the number of target sites, and the time window of the growth. Each of these factors has direct relevance to variables that are considered critical in studies of invasive species. Our modeling analysis shows that continuous dispersal (Fig. S3E) can also lead to a biphasic dependence of the population spread on the dispersal rate, suggesting that our conclusions are applicable in the absence of group dispersal. Although our experimental framework accounts for dispersal and different patches, it does not include additional aspects of the environment (e.g., environmental heterogeneity and evolution). Exclusion of these factors has allowed to us draw more definitive conclusions on the contribution of dispersal and habitat configuration to population spread.

Our results also reveal tradeoffs between spread and survival for a cooperative species exhibiting a strong Allee effect. High dispersal rates have been proposed to facilitate the spread process (e.g., ref. 29 and SI Text). However, our experimental results demonstrate that a high dispersal rate can detract from successful spread. Furthermore, we have demonstrated that the initial release size and dispersal influence spread success (Fig. 3). We observed that populations with initial densities just above C_CRIT maximize their total growth at low dispersal rates, where spread does not occur. Thus, fast dispersal could serve to limit population growth and may not always be favored as previously suggested. This tradeoff may explain why, during biological invasions, spread is initially slow but tends to increase over time (30). Species must achieve a minimum density in the source population before spread will occur for a particular dispersal rate. Our results may aid in guiding release sizes for reintroduced species (31) and echo previous literature that cautions against estimating the spread rate when a population is small (30).

Our results have also revealed that increasing the number of target patches presents two tradeoffs (Fig. 4). First, increasing the number of target patches decreases the range of dispersal rates that allow for spread. As such, cooperative species with an Allee effect face a tradeoff: increasing the number of target patches can result in a more prolific spread but simultaneously increases the risk of failing to spread or going extinct. Second, dispersing to an intermediate number of target patches leads to the highest population density in the short term. This result contrasts with theoretical studies that suggest that increasing the number of target patches colonized increases the total population monotonically (20). Therefore, cooperative species with a strong Allee effect follow unique spread dynamics, which may be dictated by the environment (i.e., number of target patches). This may offer an additional explanation to the highly variable spread rates observed during spread.

Our analysis has shown that as the dispersal rate per target patch decreases, fluctuations in cell growth increase (Fig. S5). This observation is in line with previous studies that have found that as a species approaches a survival threshold, an increase in fluctuations in cell growth occurs (28). Our results serve to further extend this notion to between-patch dispersal, where fluctuations may serve as an indicator of population collapse in the target patches, and may offer an additional explanation to account for the paradoxical relationship between dispersal and spread.

These results have implications for intervention programs that aim to limit control spread of a cooperative species. It has been suggested that reducing dispersal between patches can reduce or stop species from spreading (e.g., ref. 32). Intervention strategies that can reduce or prevent dispersal into different areas of the environment include a barrier zone (33), modification of the habitat to reduce dispersal (32), or the regulation of dispersal vectors (34). Our results may suggest that reduction of dispersal rate may be counterproductive, and this may push a cooperative species into a range of dispersal rates that allow optimal spread or increases total growth. Furthermore, limiting the number of target patches to which a cooperative species is dispersing to may serve to increase the total population density.

Materials and Methods

Model Development.

Our circuit can be modeled by two delayed differential equations (Eqs. 1 and 2 or Eqs. S10 and S11):

where C represents the bacterial density, [A] represents the concentration of AHL (μM), µ represents the maximum specific growth rate (h⁻¹), k_A represents the synthesis rate constant of AHL (μM h⁻¹), k_dA represents the degradation rate constant of AHL (h⁻¹), τ represents the time delay of the activation of gene expression by the LuxR–AHL complex (h), t represents simulation time (h), γ is a lumped term that represents the killing rate of CcdB (μM h⁻¹), and β is a lumped term that represents the amount of CcdA leading to half-maximal killing rate of CcdB (μM). In Eq. 1, growth is modeled by logistic kinetics, and the AHL-mediated rescue is modeled as a Michaelis–Menten–type equation. See SI Text for derivation of these equations.

Strains, Growth Conditions, and Circuit Characterization.

We implemented the circuit in E. coli strain DH5αPRO. Single colonies were grown overnight in LB medium supplemented with chloramphenicol and kanamycin at 37 °C. Cultures were diluted in M9 medium supplemented with 2% casamino acids and 0.5% thiamine and buffered to pH 7.0 with 100 mM Mops. The circuit was induced (i.e., circuit ON) by 1 mM of IPTG. To “rescue” a population with circuit turned ON, 0.1 μM of 3-oxohexanoyl-homoserine lactone (AHL) was added. For dispersal experiments, 200-µL cultures were grown in a 96-well plate at 37 °C in a VICTOR 3 microplate reader. cfu counts were performed on LB solid medium supplemented with chloramphenicol, kanamycin, 1 mM IPTG, and 0.1 μM AHL. See SI Text.