Hydrodynamics and collective behavior of the tethered bacterium Thiovulum majus

Significance

In this paper we examine the dynamics underlying a form of collective behavior exhibited by bacteria. In a nutrient gradient, Thiovulum majus cells aggregate into a community in which cells attach to one another using mucus tethers. As tethered cells beat their flagella, they pull nutrient-laden water through the community. The flow of water created by many cells gives rise to variations in the nutrient concentration. As cells reorganize in response to these nutrient gradients, they change the flow of water. We show that the coupling between the motion of water, nutrients, and cells generates large-scale flows that dramatically increase the rate at which nutrients are pulled to the cells.

Abstract

The ecology and dynamics of many microbial systems, particularly in mats and soils, are shaped by how bacteria respond to evolving nutrient gradients and microenvironments. Here we show how the response of the sulfur-oxidizing bacterium Thiovulum majus to changing oxygen gradients causes cells to organize into large-scale fronts. To study this phenomenon, we develop a technique to isolate and enrich these bacteria from the environment. Using this enrichment culture, we observe the formation and dynamics of T. majus fronts in oxygen gradients. We show that these dynamics can be understood as occurring in two steps. First, chemotactic cells moving up the oxygen gradient form a front that propagates with constant velocity. We then show, through observation and mathematical analysis, that this front becomes unstable to changes in cell density. Random perturbations in cell density create oxygen gradients. The response of cells magnifies these gradients and leads to the formation of millimeter-scale fluid flows that actively pull oxygenated water through the front. We argue that this flow results from a nonlinear instability excited by stochastic fluctuations in the density of cells. Finally, we show that the dynamics by which these modes interact can be understood from the chemotactic response of cells. These results provide a mathematically tractable example of how collective phenomena in ecological systems can arise from the individual response of cells to a shared resource.

The ecology of microbial mats and soils is, in large part, controlled by the formation and dynamics of nutrient gradients and microenvironments (1). An understanding of how bacteria respond to nutrient gradients has important consequences for microbial ecology (2, 3) and nutrients cycles (4, 5). The challenges of living in nutrient gradients have driven many sulfur-oxidizing bacteria to evolve remarkable morphologies (6–9) and behaviors such as magnetotaxis (10) and symbioses (11, 12). Here we show how the response of the bacterium Thiovulum majus (13–16) to nutrient gradients leads to the formation of a bacterial front that efficiently draws nutrient-rich water from its surroundings.

T. majus exploits collective hydrodynamic effects to change its natural environment (17, 18). Cells in a T. majus community generate millimeter-scale convective flows that pull nutrient-rich water to cells (17). Despite interest in the ecology (19, 20), motility (21–23), physiology (14, 15), and community morphology (24–26) of these bacteria, relatively little is understood about how the dynamics of T. majus cells give rise to collective phenomena. Past studies have been hampered by the difficulty in enriching T. majus from environmental samples. Using techniques described in this article, we have maintained an enrichment culture for over 2 y. We use this culture to show how the chemotactic response of these bacteria causes them to form a propagating front. We then show how the behavior of bacteria in the front gives rise to an instability that generates large-scale convective flows that pull nutrients through the front.

T. majus is a member of the sulfur-oxidizing bacteria (15). This phylogenetically diverse group of bacteria uses the energy released by the oxidation of reduced sulfur species, often sulfide, to support primary production (27, 28). The metabolism of these bacteria requires access to both reduced sulfur and a terminal electron acceptor (often oxygen). Many sulfur-oxidizing bacteria live in coastal sediments (27). At the sediment–water interface, reduced sulfur species—produced from the decay of organic material in anoxic sediment—diffuse into the overlaying water. Oxygen from the water diffuses into the sediment. Within these gradients, nutrients are transported through the relatively slow process of chemical diffusion. The metabolic rates of cells living in this environment become diffusion limited (18). Because many sulfur-oxidizing bacteria, including T. majus, store a reserve of sulfur in intercellular granules (15, 29), the bacteria become limited by the flow of oxygen.

T. majus has evolved a remarkable adaptation that allows it to overcome diffusion limitation. A T. majus cell produces a tether that attaches the cell to a surface (30). Very little is known about the nature of this tether other than it is sticky, attaches to the cell on the posterior end of the cell, and is likely produced on the surface of the cell (20, 31). By beating their flagella—which cover the cell surface (20)—while tethered, cells pull nutrient-laden water through the diffusive boundary layer (17, 18). Because the tether resists the force exerted by the beating flagella, the cell remains roughly stationary. The use of flagella to pull water to a cell (32), rather than the cell through water, has been observed in a small number of other microbes, including both bacteria (33–35) and eukaryotes (36–39). A single tethered cell is shown in Fig. 1A, and Movie S1 shows this bacterium pulling water toward it. The typical length of a tether is 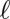∼ 50−100 μm. Cells have a typical length a = 5−20 μm. T. majus cells are among the fastest bacteria known (21). When untethered, cells swim at speeds up to U_s ∼ 600 μm⋅s⁻¹ (30), implying a flagellar force of 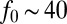pN. The resulting Reynolds number 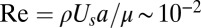, where ρ and μ are the density and viscosity of water.

Fig. 1.

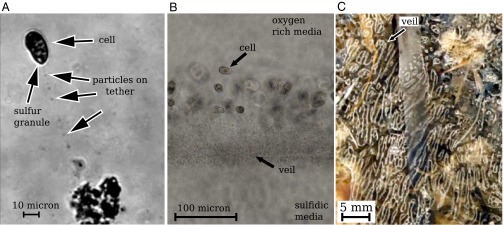
Three images of Thiovulum majus cells and veils. (A) An individual cell from an environmental sample tethered to a mote of dirt. The cell generates a flow of water toward the mote. Movie S1 shows the advection of particles past the cell. (B) As the density of cells increases, the tethers become entangled to form a cohesive matrix to which cells attach. Cells make veils in sulfide–oxygen gradients (30). Movie S2 shows this veil. (C) A naturally occurring T. majus veil in a salt marsh. The veil has a white coloration. Tethered cells pull water toward the veil. Because cells are concentrated on the thin white lines, water flows into the veil at the white lines and out through the transparent holes. These convective cycles stir the diffusive boundary layer (17).

T. majus cells also use tethers to construct new surfaces. At high cell density, mucus tethers become entangled to form a matrix upon which T. majus cells attach (30). This matrix—called a veil—can extend over centimeters. Throughout this paper we refer to the ensemble of bacteria as a “community” or “front” and reserve the term “veil” for the matrix to which cells are attached. A photograph of cells attached to a veil and a naturally occurring centimeter-scale veil in a salt marsh are shown in Fig. 1 B and C and Fig. S1. Movies S2 and S3 show cells forming and attaching to a veil. When attached to a veil, the spacing between cells is only several body lengths, giving a typical density of 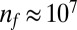cells⋅cm⁻³.

To quantify the effectiveness of a cell or community at transporting oxygen through the diffusive boundary layer, it is useful to define the Péclet number Pe (40). This dimensionless number compares the rate at which nutrients are transported by fluid flow and the rate at which nutrients are transported by diffusion. We take 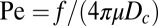, where 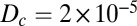cm²⋅s⁻¹ is the diffusion coefficient of oxygen in water.

The flow created by T. majus cells becomes more efficient as the cells form a veil. An individual cell exerting a force of 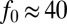pN experiences a Péclet number of 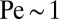. However, when cells tether to a veil, variations in cell density drive large-scale flows that stir the environment (17, 26). Remarkably, natural veils are observed to generate millimeter-scale flows that pull oxygen through the water with Péclet number 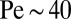(17). This paper is about how this collective behavior arises out of the dynamics of individual cells.

By observing the formation and dynamics of T. majus communities and comparing these observations to a simple model, we find that the dynamics by which cells generate macroscopic flows can be broken into two parts. First, chemotactic cells swimming up an oxygen gradient form a sharply defined front. As cells in the front swim past one another, the tethers begin to intertwine into a cohesive matrix, thus forming a veil. In the second stage, the flow of water created by cells tethered to the veil begins to pull oxygenated water through the community. We show that these currents destabilize the front. The resulting fluctuations in the density of the cells drive macroscopic fluid flows. These fluctuations appear in the front as millimeter-scale indentations, which interact and coalesce with one another. We show that the interactions between indentations result from the motion of individual cells in response to the local oxygen concentration. Thus, both the transition of a swarm of cells into a front and the generation of large-scale convective flows result from the coupling between the flow of oxygen and the response of cells.

Materials and Methods

The bacteria used in this study were enriched from inundated mud taken from School Street Marsh in Woods Hole, MA. T. majus veils were most readily enriched from mud in which the smell of sulfide was pungent. The following materials are useful in building and maintaining an enrichment culture: modified artificial seawater media described in ref. 41 (no silica or vitamins, 5 mM Tris), anoxic 2% agar with 1 mM H₂S, 15-mL falcon tubes, 50-mL falcon tubes, 50-μL glass sterile capillary tubes, autoclaved sand, and a 150-mL sterile serum bottle. We have used these techniques twice to generate a stable enrichment culture from environmental samples.

Step i: Generating a Bloom.

The first step in the enrichment of a T. majus culture is to create conditions in which T. majus cells in the pore space of the mud leave to form a veil. Following past work (14, 15, 20, 42), we do so by placing the inoculum over a sulfide source. As the inoculum becomes sulfidic and anoxic, sulfide-oxidizing bacteria move to the surface. To create these conditions, first pour 20 mL of liquid sulfidic agar into a serum bottle and let it solidify into a plug. Once it is hard, add a layer of mud (∼10 mL) onto the agar. Cover the mud with a layer of clean sand. The layer of sand ensures that the mud does not get mixed in when media are added. Finally, pour in seawater media until the serum bottle is about half full. Seal the top of the bottle with parafilm. The serum bottle prevents the water from mixing due to air currents. Alternatively, an aquarium pump can be used to lightly bubble the media. After several days, a veil will form at the surface of the sand. We have had greater success with the still culture, although both methods are recommended. An alternate method to generate a bloom is to simply nearly fill a 50-mL container with 30 mL environmental mud and 10 mL seawater and 10 mL head space. Tightly seal the container. As organics in the mud decay, the media become sulfidic, leaving the head space as the only oxygen source. After several days a T. majus veil can often be found at the surface. Whichever method is used to generate a bloom, collect the veil with a 1-mL pipette. Lightly vortex (2–3 s) the 1 mL of fluid to break up the veil before reinoculating.

Step ii: Maintaining a Culture.

To maintain a T. majus culture, place the cells in an environment with a slowly evolving sulfide–oxygen gradient. It is common for this step to fail for poorly enriched cultures. Making many replicates is recommended. It typically takes several hundred replicates (1–2 mo) before a reliable enrichment culture can be maintained in these tubes. Because the greatest difficulty in the enrichment process is isolating T. majus cells, which do not grow on plates, this process could be improved substantially by using a cell sorter. In a 15-mL falcon tube, pour in 1 mL of sulfidic agar solution and let it harden. Once it is hard, add 100 μL of inoculum from step i. Add clean sand up to a level where the walls are dry. Finally, add saltwater media until the tube is about two-thirds full. Have at least 4 cm of water above the surface of the sand. Close the tube. In 12 h (for well-enriched cultures) to 5 d (for poorly enriched cultures) a veil will form in the tube. Collect 1 mL of fluid from the veil. Lightly vortex (2–3 s) the 1 mL of fluid to break up the veil. One can either repeat this procedure to maintain the enrichment or enrich the culture as described in the next section. At the early stages of enrichment, veils left in one of these tubes typically stay potent for about 1 wk before becoming overrun with contaminants. For a well-enriched or pure culture, cells can survive in these tubes for ∼6 mo.

Step iii: Enrichment.

In a 50-mL falcon tube, pour in 30 mL of seawater. Take the cap of the falcon tube and poke three to five holes in it the same diameter as the capillary tubes. Bubble the medium for 5–7 min with nitrogen to deplete, but not completely remove, oxygen. Add 1 mL inoculum from step ii. Take one capillary tube and dip it into fresh oxygenated medium. Put the capillary through one of the holes in the falcon tube cap so that the bottom of the capillary is in the anoxic medium. Repeat for each of the three to five holes in the top. Wait 1–2 h (shorter times if the inoculum is rich in bacteria). Look at the capillary under the microscope and ensure that there is at least one cell (typically we observe between one and three). With a 100-μL pipette, pull the medium from the capillary. Inoculate into the tubes described in step ii.

Results

Constitutive Equations.

We begin by discussing how cells move in response to nutrient gradients and how the distribution of cells changes these gradients.

When T. majus cells are free swimming, they move through a combination of chemotaxis and diffusion (14–16, 22, 30). Notably, these cells show a strong chemotactic response toward a specific concentration of oxygen, 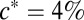(22, 30) atmospheric. Thus, T. majus cells tend to aggregate where the oxygen concentration 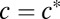(30). A chemotactic response to sulfide has not been observed (15, 30). Motivated by these observations, the concentration n of cells changes in time t as

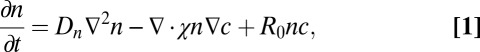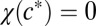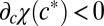where D_n is the diffusion coefficient of cells, the function χ(c) determines the speed with which cells swim up in an oxygen gradient, and R₀ is the rate per unit oxygen concentration at which cells reproduce. To account for the behavior of cells to swim toward a particular oxygen concentration, we require that and . Observations by Thar and Kühl (23) have demonstrated that, given typical conditions, the diffusive component of cell motion is very small relative to the chemotactic component.

To understand how the cells move, we must also characterize how the concentration of oxygen changes in time. We require that the oxygen evolves through a combination of diffusion, advection by moving water, and consumption by cells. Thus,

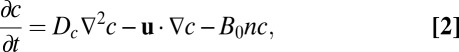where 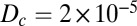cm²⋅s⁻¹ is the diffusion coefficient of oxygen, u is the velocity of water, and B₀ is the rate per unit cell density at which cells consume oxygen.

The model presented in this section represents a modified version of the Kolmogorov–Petrovskii–Piskunov (KPP) equation (43), also called the Fisher equation (44). The KPP equation was originally used to understand the motion of nonchemotactic bacteria (i.e., 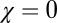) in an evolving nutrient gradient. The formulation has since been used to gain insight into a wide range of phenomena (40, 45). The important difference between this model and the original KPP equation is the inclusion of chemotaxis to a particular oxygen concentration. As we shall show, this behavior leads the cells to form a sharply defined front.

Formation of a Front.

To understand how the T. majus cells aggregate and form a veil, we design an experiment that allows us to reproducibly generate and observe the formation of veils. A T. majus community requires competing gradients of oxygen and sulfide. We construct these gradients in a test tube. As illustrated in Fig. 2A and Fig. S2, a plug of sulfidic agar (1 mL of 1.5% agar, 1 mM sulfide) at the tube base acts as the sulfide source. T. majus cells (∼10⁴ cells) are inoculated into a 0.7-cm layer of sand covering the agar plug. Finally, 8 mL of artificial seawater media in equilibrium with the atmosphere is added. To visualize the growing community, we illuminate from above by a light-emitting diode. The scattered light from the cells provides a clear image of the density of cells in the test tube. We periodically image the system with a Nikon D5000 DSLR camera with a 55-mm lens.

Fig. 2.

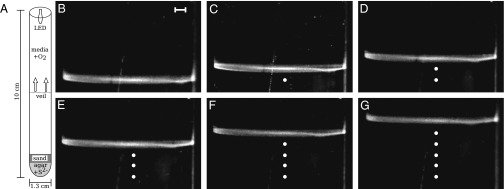
Thiovulum majus cells aggregate into a front that propagates up the oxygen gradient. (A) A schematic of the experiment. Bacteria are inoculated above a sulfide source at the base of a test tube. As cells consume oxygen, the front moves up the test tube. (B–G) Images of the front at 15-min intervals. The front is shown in profile. White dots show the position of the front in the preceding stills. (Scale bar, 1 mm.)

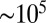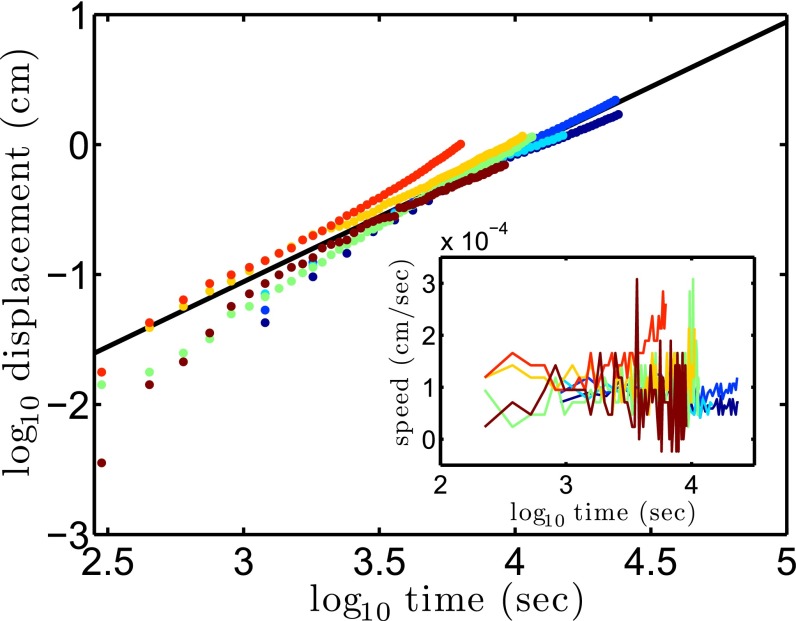
Eighteen to 36 h after inoculation, the population has grown to a size sufficient ( cells) to form a clearly visible front. Similar fronts have been previously observed in T. majus communities (21, 30). From this time lag we estimate a doubling time of 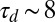h. This front, shown in profile in Fig. 2 B–G and Movies S4–S6, moves up the oxygen gradient. It fills the cross-sectional area of the test tube. As shown in Fig. 3, the front moves up the oxygen gradient with a constant velocity of 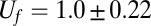μm⋅s⁻¹.

Fig. 3.

T. majus fronts move up oxygen gradients at a constant velocity. The front shows displacement linearly with time. The black line shows constant velocity. (Inset) The mean speed of the veil up the oxygen gradient is 10⁻⁴ cm⋅s⁻¹. The corresponding oxygen flux into the front 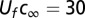pmol⋅cm⁻²⋅s⁻¹ is consistent with past estimates in natural veils (19).

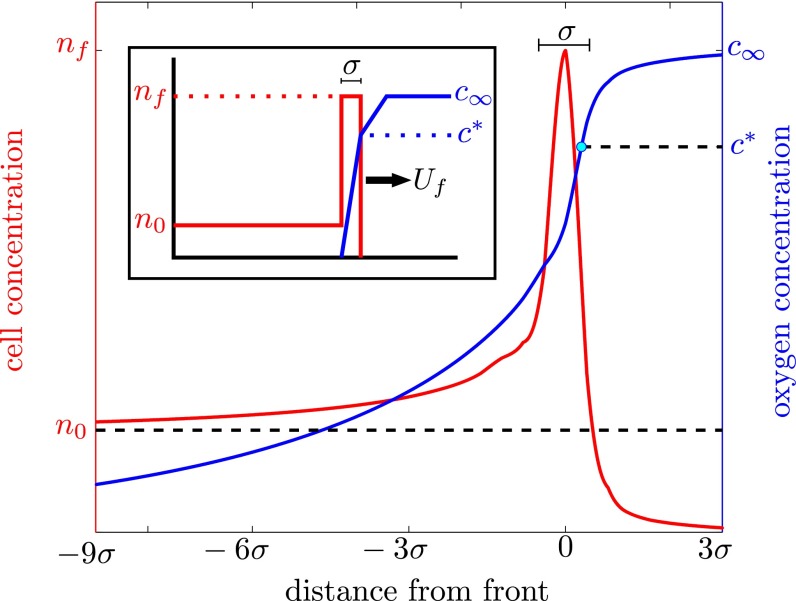
To understand how a swarm of free-swimming cells forms into a front, we analyze the motion of free-swimming bacteria in response to a one-dimensional oxygen gradient in the absence of fluid flow. We numerically integrate Eqs. 1 and 2 in one dimension, assuming a linear relation (Movie S7) for 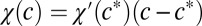. As shown in SI Text, Estimates of Cell Parameters from Front Dynamics, the initial distribution of cells quickly converges to a solution with a sharp front that travels at a constant velocity up the oxygen gradient. Fig. 4 shows the form of the translating bacterial front (in red) and the oxygen field (in blue). Traveling-wave solutions are a typical feature of the KPP equation (45). The front shown in Fig. 4 differs from the usual traveling-wave solution by virtue of a prominent rise in cell concentration at the front. This feature forms as cells aggregate at a particular concentration of oxygen (23, 30).

Fig. 4.

Numerical integration of Eqs. 1 and 2 shows that T. majus cells aggregate into the front with a constant translating form. As cells consume oxygen, the front moves in the direction of increasing oxygen concentration (blue). In this simulation, we chose 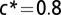to accentuate the leading edge of the front and a small chemotactic coefficient so that the tail of the front can be clearly seen. (Inset) The geometry of this front can be understood by analyzing an idealized front.

To understand the generic features of this front, it is useful to consider the geometrically simple front shown in Fig. 4, Inset. According to this idealization, the concentration of cells is divided into two parts, a sharp front of width σ, in which the oxygen is consumed, and a long tail. The densities of cells in the front and tail are n_f and n₀, respectively. The motion of free-swimming cells in gradients is typically dominated by chemotaxis (23); the position of the bacterial front is therefore close to the point where the concentration of oxygen c = c*.

We constrain this idealization by requiring conservation of oxygen and cell number as well as flux balances between the moving front and the tail. The four resulting scalings (SI Text, Estimates of Cell Parameters from Front Dynamics) relate the characteristics of the front to the behavior of individual cells in gradients. We take the front velocity 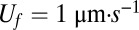, width 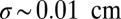, reproductive rate 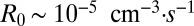, and density 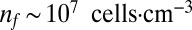. From these values we estimate four parameters, of which only two are used in the results presented in the second half of this paper. The metabolic rate per cell density 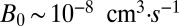and the cell density 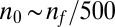. The other two values, both of which are consistent with past observations of T. majus, are provided in SI Text, Estimates of Cell Parameters from Front Dynamics.

We have shown how the tendency of T. majus cells to form a sharp front that propagates up an oxygen gradient results from the fact that cells are chemotactic toward a particular concentration of oxygen, as was previously suggested (30). This analysis also elucidates how a swarm of T. majus cells weave their tethers into a veil. Tethers are woven into a veil as a result of collisions between cells (30). Because the rate at which cells collide scales with the square of density, the rate at which tethers are woven into a single cohesive veil is enriched by a factor of 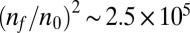in the front relative to the tail. Movie S3 shows microscope images of a sharp front of T. majus cells producing a veil.

Observations of Moving Fronts.

To better understand how a front of bacteria begins to generate macroscopic flows, we return to the experimental observations. As a T. majus front moves up an oxygen gradient, it shows remarkable dynamics. Fig. 5 shows that an initially flat veil generates millimeter-scale indentations that persist for ∼1 h. We call these indentations “dimples”. Similar features in other T. majus veils have been attributed to bioconvection (21). Below each dimple, there is an opaque plume that intensifies when dimples form or two merge (Fig. 5F). This plume appears to be composed of dispersed veil material. When there are multiple dimples in the veil, they move toward one another.

Fig. 5.

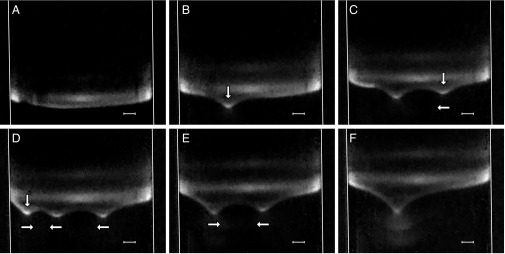
The evolution of a T. majus veil in a sulfide–oxygen gradient shows the spontaneous formation of persistent and interacting dimples. (A–F) The veil moves upward as a deformed 2D sheet that curves upward near tube walls (white lines). (F) Opaque plume is clearly visible. Vertical arrows show the position of a new dimple. Horizontal arrows show the direction of lateral motion, if any. (Scale bar, 1 mm.) Images are separated by 15 min. Movies S4–S6 and S8–S11 show veil evolution.

These dynamics bear a loose similarity to another application of the KPP equation, the dynamics of a flame front in a tube (40). Flames, like a veil, also move up an oxygen gradient. Oxygen is consumed at the front and transported by a fluid flow that is engendered by the front. According to the Darrieus–Landau instability, flame fronts can develop into “cellular flames” (40, 46), which bear a qualitative similarity to dimples.

Motivated by this analogy, we now investigate the stability of the front to perturbations.

Dynamics of a Front with Veil.

As a front of cells develops a veil, tethered cells beating their flagella pull oxygenated water to the front. Thus, the dynamics of a front arise out of the coupling of three fields: the density of cells, the flow of water, and the concentration of oxygen. In this section, we begin by showing how the motion of cells on the veil is modified by the formation of tethers. We then relate the flow of water around the veil to the distribution of cells tethered to the front. Finally, we show that the flow of oxygen changes quasistatically as the cells move over the front.

Consider the motion of cells close to the veil. Because the chemotactic response of cells causes them to remain near the veil, the dynamics of cell motion are confined to the 2D front. Consequently, the formation of a front reduces the dimensionality of the dynamics. As shown in Fig. 4, the front forms at an oxygen concentration just below c*. Cells detaching from the veil swim a short distance before the oxygen concentration rises above c*. At this point, the chemotactic response causes cells to reverse direction and return to the veil. This qualitative prediction is confirmed by the observations of Fenchel (30) and Thar and Kühl (23), who suggested that this behavior is a chemotactic response. They observe that when the tether breaks, a cell swims away from the veil in a random direction. The cell typically swims for 0.5−2.0 s before turning back toward the veil. It returns to the front a distance 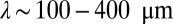from where it began (23).

The process of constantly breaking and remaking tethers causes a cell to perform a random walk over the surface of the veil. The flux of cells is given by the diffusion equation (47). The effective diffusion coefficient 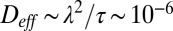cm²⋅s⁻¹, where 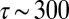is the length of time a tether lasts before breaking. Observations by Fenchel (30) have shown that cells swim faster and are tethered for shorter periods of time where the oxygen concentration is very high. To account for these observations, we allow D_eff to be a function of the oxygen concentration that takes a minimum where c = c*. The front dynamics are therefore described by the coupling between diffusion of cells over the surface of the veil and the flow of oxygen around the veil:

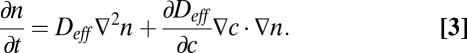Because the concentration of cells in the front is fixed by the dynamics of front motion, reproduction does not change the concentration of cells.

To characterize the flow of water around a veil, we solve the Stokes equations subject to the boundary condition that cells on the veil exert a force of the surrounding fluid and the velocity u vanishes on the walls of the test tube. This system of equations is quite difficult to solve in the geometry imposed by the experiments. Consequently, we move to the simpler, 2D geometry of a Hele-Shaw chamber (40). We consider the 2D flow of water around a veil in an infinite strip of width w. A straight front of cells stretches in the 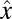direction from 0 to w and moves up the oxygen gradient in the 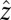direction. To account for the test tube walls, we include impenetrable boundaries along the lines x = 0 and x = w (Fig. S3). As shown in SI Text, Flow in a Hele-Shaw Chamber, the velocity field due to cells is

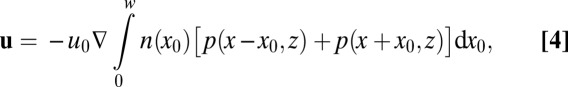where coefficient 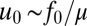, 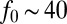pN is the force exerted by a single cell, and μ is the dynamic viscosity of water. The harmonic dimensionless pressure field

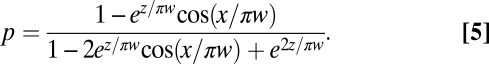Fig. 6A shows the velocity field around the front (gray line). In this numerical solution, the front moves upwards (i.e., in the 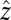direction) with the observed front velocity 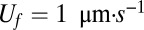; i.e., 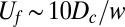. The distribution of cells in this example, shown in Fig. 6B, is uniform with a Gaussian perturbation composed of 1.25% of the cells.

Fig. 6.

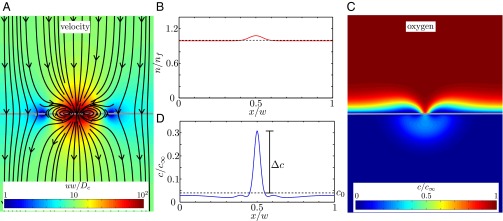
The flow of water and oxygen around a T. majus front is determined by the distribution of cells. (A) Cells, tethered to the veil (gray line), beat their flagella to pull water through the front. The velocity field is given in Eq. 4. (B) The distribution of cells in the one-dimensional front is a Gaussian perturbation composed of 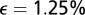of the total number of cells in the front. The dashed line shows average cell density. (C) The concentration field around the front (gray line) is a solution to Eq. 6, using the velocity field shown in A. (D) The concentration of oxygen on the front. The flow created by the cells pulls oxygen toward the most concentrated cells, creating a local maximum of amplitude c. The dashed line shows the concentration c₀ in the absence of a density fluctuation.

The third field that controls the motion of cells is the flow of oxygen. Because cells are tethered to a veil, the concentration of oxygen relaxes to steady state much faster than cells diffuse within the front. Given the scale of oxygen gradients, the diffusion coefficient of oxygen, and the effective diffusion coefficient of tethered cells, the concentration of oxygen relaxes to equilibrium ∼400 times faster than the concentration of tethered cells. The flow of oxygen into a veil therefore evolves quasistatically as cells rearrange; we therefore neglect the explicit time dependence in Eq. 2. Moving to the reference frame of the propagating front, the oxygen concentration evolves as

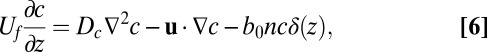where 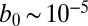cm²⋅s⁻¹ is the metabolic rate of cells normalized by the surface density of cells in the front. The Dirac delta function 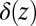requires that oxygen be consumed only within a one-dimensional front positioned at z = 0.

We solve Eq. 6 numerically, using the finite-element method as implemented by FreeFem++ (48). We approximate the infinite strip as a rectangle with a length 400 times larger than the typical size of oxygen gradients, 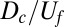. We account for the singular consumption of oxygen by taking the front to be part of the boundary. The boundary condition on the front equates the discontinuity in the oxygen flux with the metabolism of the bacteria, .

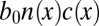Fig. 6C shows the concentration of oxygen around the front (gray line) associated with the velocity field shown in Fig. 6A and the distribution of cells shown in Fig. 6B. Fig. 6D shows the concentration of oxygen in the front (i.e., along the gray line in Fig. 6C). Oxygen levels are higher where the cells are more dense because the cells pull oxygenated water from their surroundings.

The physical basis for the positive feedback by which dimples form can be understood from Fig. 6. As cells break and remake their tethers, they move, on average, in response to gradients both in the concentration of cells and in that of oxygen. According to the first term of Eq. 3, locally concentrated cells tend to move apart. According to the second term, cells remain longer where the oxygen concentration is closer to c*. As we showed in Formation of a Front, the front forms at an oxygen concentration just below c*. Thus, for small oxygen gradients, cells moving over the veil tend to concentrate where the oxygen level is higher. As cells pull oxygen-rich water toward the veil, the oxygen level rises, causing neighboring cells to join the perturbation faster than cell diffusion smoothes gradients.

Linear Stability of the Front.

Cells diffuse over the surface of the front with a diffusion coefficient that varies with the concentration of oxygen. However, the concentration of oxygen is coupled to the distribution of cells through metabolism and the flow of water; thus c is a function of n. Consequently, Eq. 3 is a nonlinear diffusion equation. In this section, we investigate how this nonlinearity influences the distribution of cells in the front.

We consider the growth of a small perturbation to an otherwise uniform distribution of cells. Using standard methods (49), it is straightforward to show that a uniform distribution of cells is linearly stable to all perturbations. This fact can be seen directly from Eq. 3. The uniform front lacks gradients of both cell density and oxygen. If the fraction of cells in the perturbation is 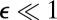, the term proportional to must be proportional to 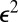. Thus, oxygen gradients provide a negligible contribution to the motion of cells. The random motion of cells over the veil smoothes out all small perturbations.

This result is in agreement with the observed formation of dimples (Fig. 5 and SI Text, Movies S8–S11). Dimples are relatively small compared with the diameter of the test tube and they form in a series of isolated events. If dimples formed due to a linear instability, one would expect to see sinusoidal perturbations growing into dimples. No such evolution is observed.

In this analysis, we explicitly assumed that the typical amplitude of random fluctuations is sufficiently small to justify a linearized model. Because the linearized model cannot explain the observed formation of dimples, we must reevaluate this assumption. According to the central limit theorem (50), the number of cells N in an area 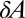is normally distributed with mean 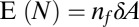and variance 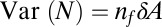. Taking 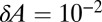cm² as the area of a dimple, the typical size of fluctuations is 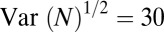cells. We numerically integrate Eqs. 4 and 6 to determine the influence of a perturbation of composed of 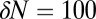cells. Remarkably, the resulting flow is sufficient to increase the local concentration of oxygen by 70%. As shown in SI Text, Cell Density Fluctuations, cells moving randomly over the surface of the veil generate density fluctuations of this size at a rate 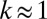h⁻¹. The observed nucleation rate of dimples is 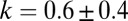h⁻¹. The similarity of these timescales leads us to propose that the purely stochastic fluctuations in the concentration of cells are sufficient to generate large oxygen gradients in the front. In the language of dynamical systems, the uniform propagating front is a stable fixed point. However, random fluctuations periodically push the front outside of the basin of attraction.

Growth of Nonlinear Modes.

We now investigate the growth of small, but finite, cell density fluctuations. We begin by characterizing the size of oxygen gradients produced by cells. The flow of oxygen is coupled to the distribution of cells through metabolism and the fluid flow they create. Two biological characteristics define this coupling. The first, 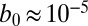cm²⋅s⁻¹, appearing in Eq. 6, is the metabolic rate per unit cell density. The second important parameter 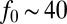pN is the force a cell exerts on the water, which has dynamics viscosity μ. Taking the ratio of these coefficients, we define the dimensionless efficiency 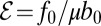of bacteria in pulling oxygen to the veil. If 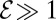, tethered cells pull water through the veil much faster than they consume oxygen, thus increasing the concentration of oxygen in the front. If 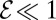, metabolism dominates and the concentration of oxygen decreases. Given our estimates of f₀ and b₀, we find 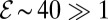. Thus, even small perturbations in the density of cells create large oxygen gradients.

From Eq. 3, a perturbation in the density of cells pulls enough oxygen to overcome diffusion when

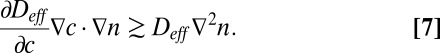From this equation, we find that a localized perturbation grows if

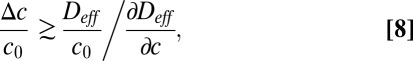where c₀ is the original concentration of oxygen and Δc is the change in oxygen concentration due to the additional flow created by locally concentrating cells.

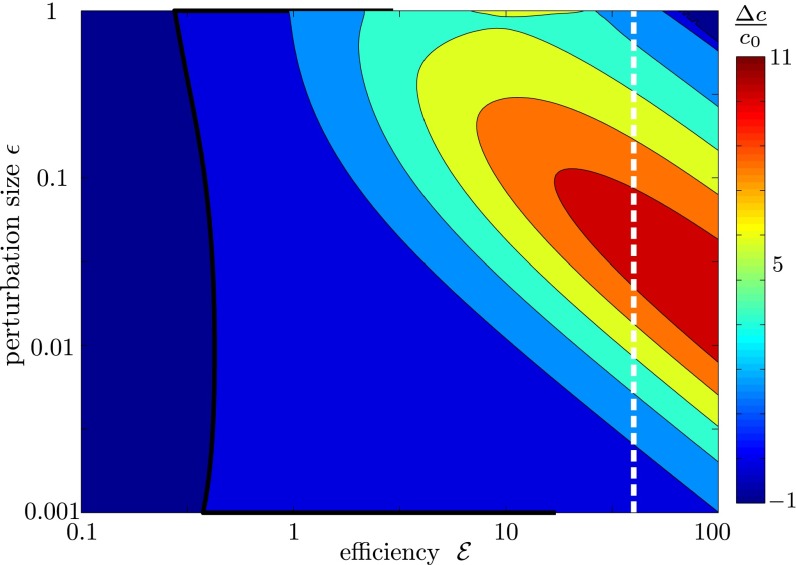
We numerically integrate Eqs. 4 and 6 to determine how different density fluctuations change the concentration of oxygen. As shown in Fig. 6B, we use a Gaussian perturbation to an otherwise uniform, 1-cm front. The perturbation includes a fraction ε of the total number of bacteria in the front. The width of the Gaussian 0.1 cm is chosen to match the observed size of the dimples (Fig. 5). Fig. 7 shows how the change in oxygen concentration 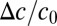varies with both the efficiency 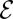, by changing f₀, and the size ε of the perturbation. Notably, there is a minimum efficiency required for the perturbation, regardless of size, to pull more oxygen than it consumes. Because the estimated efficiency 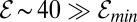, we conclude that even a small number of cells are sufficiently powerful to create substantial oxygen gradients. According to Eq. 8, these oxygen gradients excite a nonlinear positive feedback by which perturbations in the cell density grow. In this way, the front begins to generate a macroscopic flow that stirs the surrounding water.

Fig. 7.

The fractional change in oxygen concentration as one varies both the size of the density perturbation ε and the efficiency 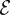of cells. 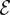is defined as the rate at which cells pull water toward the front compared with the rate they consume oxygen. Points to the left of the solid black line correspond to perturbations that consume more oxygen than they draw. The dashed white line shows the estimated efficiency of T. majus cells.

Dynamics of Nonlinear Modes.

As a front generates dimples, the dimples move toward one another and coalesce. This process is shown in Fig. 5 and in SI Text, Movies S8–S11. In this final section, we show that this behavior is consistent with interactions mediated by the flow of oxygen. To understand this phenomenon, we consider the case of two dimples in an infinite, 2D front. This approximation is valid provided the distance between dimples is small compared with the size of the dimples.

Dimples pull oxygenated water toward the front. Because these structures are localized, the oxygen flux decreases with distance. This gradient in oxygen flux gives rise to a gradient in the concentration of oxygen. Oxygen is highest near the dimple and decreases with distance. Thus, if two dimples are close together, they create oxygen gradients over one another. Cells within the dimples move in response to these oxygen gradients.

The typical size of oxygen gradients over the surface of the front is determined by the decay of the velocity field around a dimple. Because the front does not accelerate, any force exerted by the cells must be balanced by drag on the veil. Consequently, the leading-order influence of a dimple is that of a force dipole of magnitude Q_d. The resulting velocity field u_v over the veil scales as 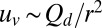, where r is the distance to the dimple. The increase in the oxygen flux 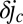to the front is 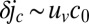, where c₀ is the oxygen concentration at the front. All of the oxygen transported by u_v is consumed by the cells in the front. Balancing the increase in metabolic rate with the flux of oxygen, we find that the perturbation to the oxygen concentration δc away from a dimple decreases as

If the motion of dimples toward one another is driven by oxygen gradients, then, according to Eq. 3, the velocity of dimples is proportional to the oxygen gradient. From Eq. 9, the typical magnitude of oxygen gradients decreases as 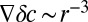, yeilding an inverse cube attraction.

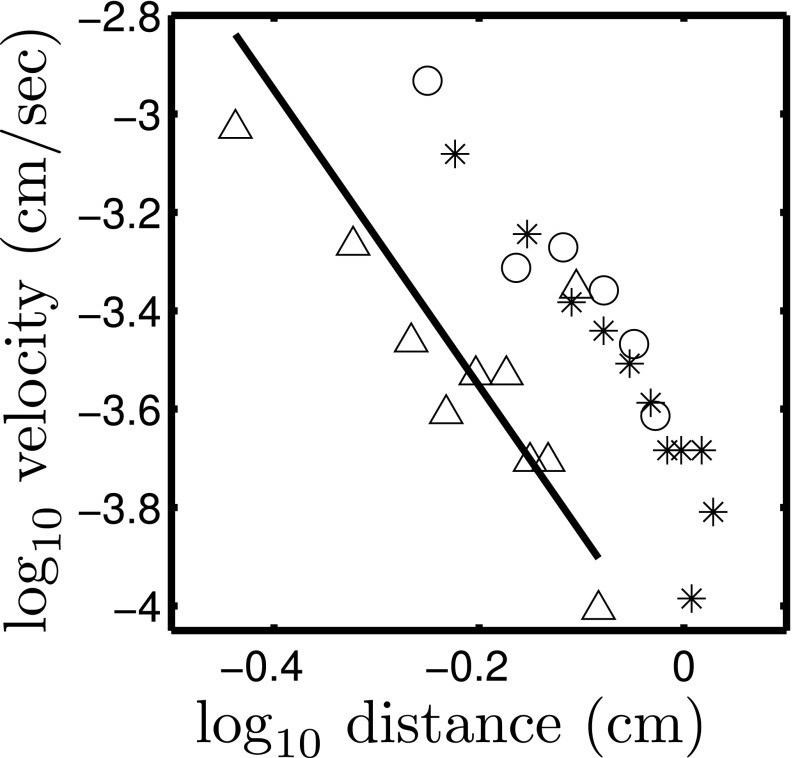
As shown in Fig. 8, the measured velocity v of dimples toward one another decreases with their separation as 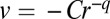. The average exponent 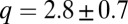(95% confidence interval) is consistent with an inverse cube attraction. This leads us to conclude that interactions between dimples are mediated by oxygen gradients.

Fig. 8.

Dimples in the veil move toward one another with a velocity that is a decreasing function of separation. Dimples move together with a power-law attraction. The measured exponents are (stars), 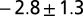(circles), and 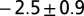(triangles). The solid line has slope −3. Only the component of velocity and distance normal to the camera can be measured, leading to an ambiguity in the measurement of the scaling coefficient. Different symbols correspond to different experiments. Movies S9–S11 show different experiments.

Discussion

We have found that the collective dynamics by which a T. majus community stirs its environment arise from the chemotactic response of cells to oxygen. Because cells are chemotactic toward a particular concentration of oxygen, they tend to aggregate into a dense front. As cells consume oxygen, the front moves up the oxygen gradient to remain at the constant oxygen concentration. As cells in the front produce a veil, tethered cells begin to pull oxygenated water through the front. The resulting flow of oxygen destabilizes the front. The chemotactic response causes cells to aggregate together and produce large-scale fluid flows.

This model differs substantially from a previous model of T. majus dynamics proposed by Cogan and Wolgemuth (24, 26). In their model, interactions between cells are mediated by the flow of water. As tethered cells pull water toward the veil, they also pull free-swimming cells. According to our model, all interactions between T. majus cells are mediated by the flow of oxygen. The relative importance of chemotaxis and hydrodynamic interactions is determined by the ratio of the swimming speed 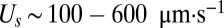and the velocity v of the flow created by the veil. When 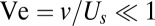, the flow created by the veil only weakly perturbs the motion of swimming cells. When 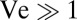—as implicitly assumed in past models—untethered cells are passively carried by the flow. Because all flow through a veil is generated by variations in the density of cells, a uniform veil drives no flow; consequently 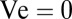. Natural veils generate flows with a typical velocity 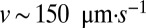(17), corresponding to 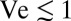. Thus, chemotaxis alone is sufficient to understand the early development of a veil, whereas both chemotaxis and hydrodynamics determine the eventual patterns that emerge.

Although the details of these dynamics (e.g., production of a tether) are specific to a small number of microbes, their behavior is characteristic of a more general phenomenon. It is the average response of individual T. majus cells to a shared resource that leads them to form communities capable of stirring the environment. These dynamics provide an example of how baroque collective behavior arises out of the independent responses of cells to a shared resource. Because diffusively driven nutrient gradients are a generic feature of many microbial mats and the pore spaces of sediments, we expect that this type of analysis can help elucidate the ecological dynamics of these systems.