Empirical prediction of genomic susceptibilities for multiple cancer classes

Significance

It is widely assumed that human genomic variations are associated with an individual’s susceptibility to complex diseases such as cancers and autoimmune diseases. However, extensive genome-wide association studies thus far had limited success because the results have low predictive value of practical utility to individuals. We present a prediction process where two machine-learning analysis methods are applied to two different descriptors of each individual’s common genomic variations to predict an individual’s susceptibility to eight major cancer traits. The accuracy of the prediction ranges from 33% to 57% depending on cancer type, which is significantly better than 11% for a random prediction, with probability estimates that may be useful for making practical health decisions for individuals or for a population.

Abstract

An empirical approach is presented for predicting the genomic susceptibility of an individual to the most likely one among nine traits, consisting of eight major cancer classes plus a healthy trait. We use four prediction methods by applying two supervised learning algorithms to two different descriptors of common genomic variations (the profiles of genotypes of SNPs and SNP syntaxes with low P values or low frequencies) of each individual genome from normal cells. All four methods made correct predictions substantially better than random predictions for most cancer classes, but not for some others. A combination of the four results using Bayesian inference better predicted overall than any individual method. The multiclass accuracy of the combined prediction ranges from 33% to 56% depending on cancer classes of testing sets, compared with 11% for a random prediction among nine traits. Despite limited SNP data available and the absence of rare SNPs in public databases, at present, the results suggest that the framework of this approach or its improvement can predict cancer susceptibility with probability estimates useful for making health decisions for individuals or for a population.

Whole genome (WG) sequence information of individuals is revolutionizing our understanding of the content and organization of genomic variations in human genomes (1). Most regions of untransformed human genomes have been found to have the same sequences, but a small fraction, spread throughout the genome, have variations among a population, such as SNPs, insertion-deletions of various lengths, copy number variations, and repeats or inversions of various lengths (2). Of these, SNPs account for the largest number of variations and have been identified at more than 3 million genomic tag positions at a minor allele frequency (MAF) greater than 5% (3, 4) of the population, and many more have been identified at a lower minor allele frequency (5).

It has been widely assumed that these genomic variations of normal (untransformed) cells contain one or more sets of variations that render an individual susceptible to a given disease or phenotype, usually in combination with nongenomic factors. One of the hopes from genome-wide association studies (GWASs) (6) has been to predict the genomic component of the susceptibility of individuals to complex diseases such as cancers, autoimmune diseases, neurological diseases, infectious diseases, and others. Intensive and extensive studies to find the association between SNP genotypes and the susceptibility for various cancer classes have resulted in discovery of more than 100 genomic association loci for the susceptibility of more than 16 cancer classes thus far (7), but no more than a fraction of the specific prediction loci has been found (8). Moreover, some criticized that GWAS-identified loci do not explain, in most cases, the high familial risk of most cancers (9). Thus, the results from the current analysis methods and interpretation of them for predicting the genomic susceptibility for cancer based on GWAS-confirmed SNPs from normal cells are thought to have had limited predictive value of practical utility for making health-related decisions at an individual or population level without information of family histories.

GWASs revealed that the odds ratios of most SNPs between cases and controls for a given complex disease such as cancer are usually close to 1.0. Even for most of the GWAS-identified and disease-associated SNPs, their odds ratios are rarely very far from 1.0, and their predictive value has been low. These observations, combined with recent experimental observations of heterogeneity in cancer cells with different somatic mutations not only among different cancer subtypes in a given cancer class but also even in a single tumor (10, 11), suggest the following possibilities for cancer susceptibility: (i) there are many more undiscovered susceptibility alleles for a given cancer than those confirmed by GWASs thus far; (ii) there may be many known and unknown interactions among the alleles; (iii) a specific combination of many of the susceptibility alleles may render an individual susceptible to the cancer of a specific class (the polyallelic model); and (iv) there may be multiple sets of such allele combinations in a population, and each set (with mostly different alleles assorted from a large pool of the susceptibility alleles) renders an individual susceptible to the same class cancer (the model of multiple assortment of genomic alleles).

These complex possibilities prompted us to take an empirical approach of predicting cancer susceptibility using multiple supervised learning methods applied to multiple descriptors of genomic variations. We also recognize that the susceptibility alleles and causal alleles of cancer may or may not be the same or easily correlated.

Approach

The objective of this work is not to test any existing models for cancer causation or cancer susceptibility but to find a framework of methods that can produce cancer susceptibility information with predictive value of practical utility. Thus, we take the approach of classification by supervised learning, where we first empirically optimize various parameters in selecting the groups of SNP variations as descriptor variables and use supervised learning algorithms suitable for these descriptor variables to obtain the best outcome on susceptibility prediction without being encumbered by any existing specific assumptions. We then let the results suggest any possible model or models, if any, for cancer susceptibility prediction.

It has been widely acknowledged that no single classifier performs better than all others consistently in all applications. Thus, we recognize that a complex system such as genomic variations can be described in more than one way and that there is more than one analysis algorithm to extract a complex property, such as susceptibility for cancer, from genomic variations of individuals. We also recognize that one descriptor/analysis combination suitable for one cancer may not be suitable for other cancers. Thus, to test whether more predictive information can be derived from WG tag SNPs (for simplicity, SNPs from here on) of nontransformed cells, we explore four different methods: two supervised learning analysis algorithms applied to two different descriptors of individual genomic variations. We also test combining the results of the four methods. Also, because all cancer cells have a common property of unregulated proliferation, we estimate multiclass cancer susceptibility, i.e., susceptibility for one cancer in the context of other cancers. Such multiclass prediction has more practical value for individuals or a given population rather than the susceptibility prediction for a single cancer class in the absence of other competing cancer classes.

We chose two types of descriptors of an individual genomic variations: (i) the profile of ordered SNP genotypes, where each SNP genotype is assumed to be independent of those of its neighbors, and (ii) the profile of SNP syntaxes (SNP-Ss), where an SNP-S is defined as a string of connected, ordered SNP genotypes of a given length. All of the SNP-Ss are generated by sliding a window of a given length along the entire length of the WG SNPs. The use of SNP-S as the descriptor element is to accommodate the observations that each SNP haplotype is not independent, but is linked to its neighbors to varying extents and degrees (linkage disequilibrium of SNPs) (3, 4), and the use of coded genotypes (Table S1), rather than haplotypes, is due to the observed unreliability of computationally inferred haplotypes (12), especially for low-frequency SNPs or SNP-Ss of unrelated individuals (13), on which two of our methods are primarily built (see below). In addition, we select all descriptor elements at loci with P values or the occurrence frequency among study population below respective optimal cutoff values depending on the analysis algorithm used, where the optimal cutoff values are obtained by the supervised learning from the samples of known phenotypes. This selection is to include as many susceptibility allele candidates as possible beyond the small number of GWAS-confirmed SNPs for each cancer class and to accommodate broad models including the polyallelic and the multiple assortment of genomic alleles models for cancer susceptibility.

Two very different analysis algorithms suitable for the two descriptors mentioned above are used: (i) the k-nearest neighbor (kNN) algorithm (14) and (ii) the support vector machine (SVM) algorithm (15). These two algorithms do not depend on good clustering of the samples of each cancer class in a multidimensional space. The kNN algorithm is to search for the kNNs of a test individual (in terms of genome variations) among the study population and assign the most common trait among the neighbors as the predicted trait for the test individual (In case of more than one most common trait, see the kNN/SNP-S method in Materials and Methods). Here, we calculate all pairwise distances between the descriptor of a test individual and that of each of all individuals in the study population, and then we select the top kNNs. The SVM algorithm is a discriminatory classification method to identify the most likely class (group) to which the test individual is likely to belong. Here, we train SVM to recognize the correct trait group for an individual in each of all binary trait group pairs. We then predict that the individual is likely to be susceptible to the trait with the maximum vote of all pairwise classifications by SVM (Materials and Methods). A combined prediction of the susceptibility for each test individual is estimated based on Bayesian inference (SI Text) from the four predictions.

For female individuals, the multiclass susceptibilities are predicted for nine classes (eight common cancer classes plus one healthy trait), and for male individuals, the predictions are made for six classes, excluding the three female-specific or female-dominant cancer classes.

Results

Data Source, Selection, and Sampling.

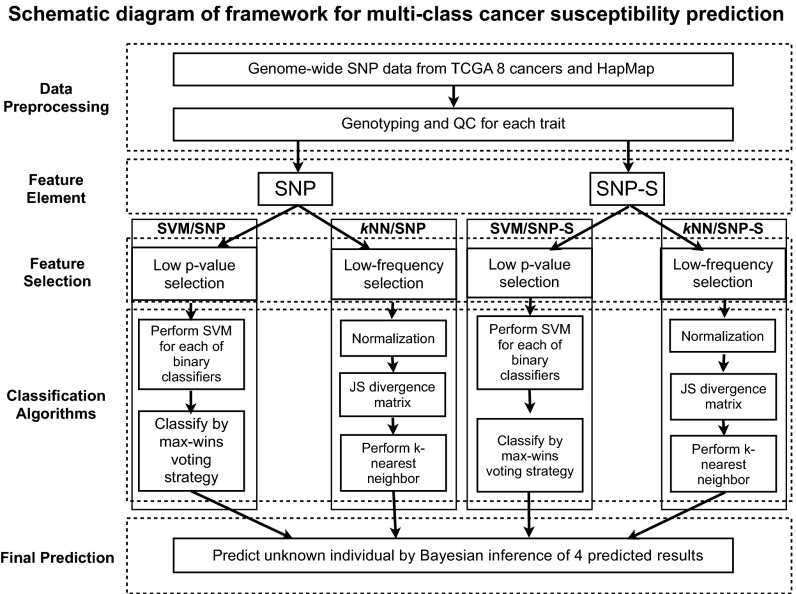
All of the data used in this study are obtained from public databases, The Cancer Genome Atlas (TCGA) with permissions, and HapMap. The details of data selection, sampling method, quality control processes applied, and other details are described in Materials and Methods and Table S2. Fig. 1 shows the workflow of this study.

Fig. 1.

Schematic diagram of workflow for a process of estimating genomic susceptibility for eight major cancers: a framework. The workflow is divided into a series of steps from SNP data preprocessing such as quality control screening and genotype encoding, selection of descriptor elements with low P values or rare SNP syntaxes, applying two different algorithms, and final prediction by combining the results from the four methods.

Optimization of Parameters Using a Training Set.

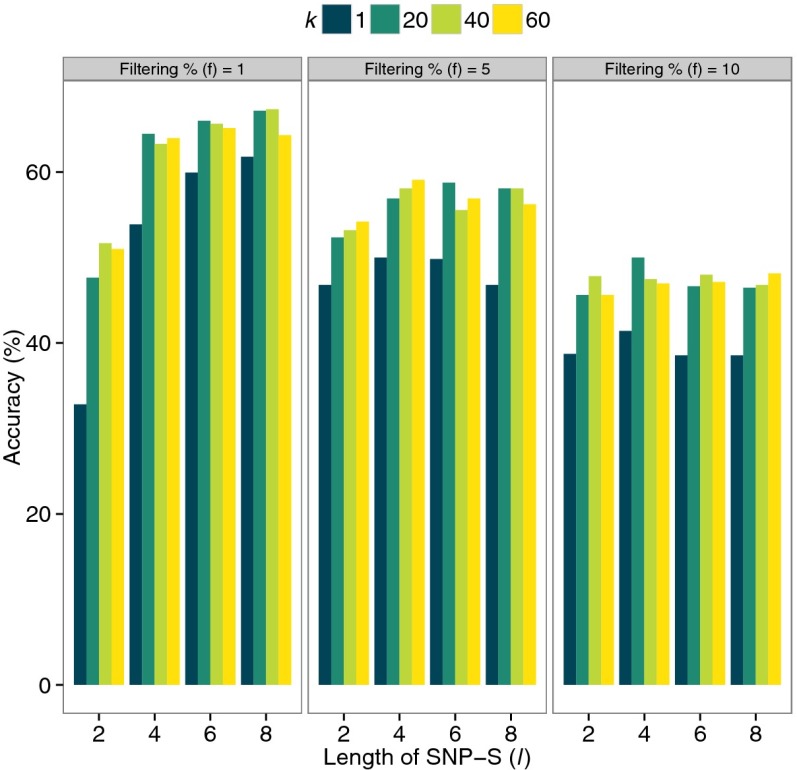
The training set consists of 594 samples: 66 randomly selected individuals from each of nine trait groups (the cohort of 66 individuals is the smallest sample size among the nine trait groups in the two databases). Fig. 2 shows the results of the optimization of the parameters in the kNN/SNP-S method (kNN analysis algorithm applied to the SNP-S descriptor): the optimized parameters for the method are l (the length of SNP-S), k (the number of nearest neighbors having similar descriptor profiles to that of testing individuals), and f (the percentage cutoff value for selecting low frequency SNP-Ss), and they are 8%, 20%, and 1%, respectively, for the method. The optimizations of the parameters for the remaining three methods are shown in Fig. S1 A–C.

Fig. 2.

Optimization of parameters for the process of applying the kNN algorithm to the profiles of SNP-syntaxes. kNN algorithm to SNP-S profiles has three parameters: (i) filtering percentage for selecting rare features below specified frequency threshold. For example, for 1% filtering, the features below 1% frequency among study population are selected for analysis; (ii) the length of SNP-S; and (iii) k for selecting number of nearest neighbors of a test individual. The training accuracies of the method were measured for several different settings of the three variables and the optimal setting was found for the best accuracy. The accuracy is defined as (TP + TN)/(TP + TN + FP + FN), where TP, TN, FP, and FN denote the number of true positives, true negatives, false positives, and false negatives, respectively.

Accuracies of Multiclass Prediction for a Training Set.

To estimate the statistical accuracies of susceptibility prediction for each trait, each test individual is taken out from the 594 training population. Table 1 shows the results from the kNN/SNP-S method as a contingency table. The tables for the remaining three methods are in Tables S3–S5. The summary of the four tables for the correct susceptibility predictions is shown in Table 2. It is clear from the tables that (i) in each of the four methods, the correct trait was predicted for the largest number of individuals as manifested by the large diagonal elements of Table 1 and Tables S3–S5; (ii) in all four methods, the correct predictions are made with significantly higher accuracies than random predictions. (e.g., with the kNN/SNP-S method shown in Table 1, the true-positive rate is 66% and the false-positive rate is 33%); (iii) no single method out of the four methods is the best in predicting the susceptibility for all traits; and (iv) no false positives were found for the healthy trait group: there were a few cancer individuals who were identified to belong to the healthy group, but no individual in the healthy group was found in any cancer group (see Discussion for this possible artefact).

Table 1.

Training performance of kNN algorithm applied to profiles of SNP-Ss

	Predicted trait
Actual trait	BRCA	COAD	HNSC	KIRC	LGG	OV	READ	UCEC	CEU	Sample size	Accuracy (%)
BRCA	32	2	10	0	5	11	5	1	0	66	48.5%
COAD	4	30	5	2	6	7	6	1	5	66	45.5%
HNSC	2	1	55	2	1	0	1	2	2	66	83.3%
KIRC	3	3	7	30	6	4	9	2	2	66	45.5%
LGG	1	5	3	1	52	0	1	0	3	66	78.8%
OV	5	1	2	1	2	50	1	1	3	66	75.8%
READ	0	4	2	2	4	1	52	0	1	66	78.8%
UCEC	3	5	7	1	2	11	7	25	5	66	37.9%
CEU	0	0	0	0	0	0	0	0	66	66	100%
										Sum 594	Overall 66.0%

BRCA, breast invasive carcinoma; CEU, Caucasians from Utah; COAD, colon adenocarcinoma; HapMap, Haplotype Map Project; HNSC, head and neck squamous cell carcinoma; KIRC, kidney renal clear cell carcinoma; LGG, brain lower grade glioma; OV, ovarian serous cystadenocarcinoma; READ, rectum adenocarcinoma; UCEC, uterine corpus endometrioid carcinoma.

Table 2.

Correct prediction ratios for training set by four methods for each of nine traits

	Predicted trait
Method	BRCA	COAD	HNSC	KIRC	LGG	OV	READ	UCEC	CEU	Total	Selected features
kNN/SNP	3.0%	40.9%	54.5%	10.6%	13.6%	68.2%	19.7%	22.7%	100%	37.0%	236,107
kNN/SNP-S	48.5%	45.5%	83.3%	45.5%	78.8%	75.8%	78.8%	37.9%	100%	66.0%	16,333,627
SVM/SNP	53.0%	50.0%	78.8%	68.2%	86.4%	36.4%	42.4%	62.1%	100%	64.1%	9,838
SVM/SNP-S	47.0%	16.7%	59.1%	47.0%	56.1%	47.0%	34.8%	51.5%	100%	51.0%	1,597

Multiclass Prediction Accuracies and Confidence Levels for Multiple Testing Sets.

The construction of a testing set for all nine traits was not achievable due to the small sample size of some cancers in our data set from TCGA. Thus, we used 100 randomly selected new samples (not used in the training set) from only three groups [breast invasive carcinoma (BRCA), ovarian serous cystadenocarcinoma (OV), and uterine corpus endometrioid carcinoma (UCEC)], for which more public data are available for multiple sampling. We calculated the multiclass accuracy for the test individuals using the same set of parameters as optimized in the training set for each method. Resampling of 50 individuals (randomly selected within the 100 test samples) was repeated 10 times for each of the three cancer classes. Fig. 3 shows the results of the four methods with statistical spreads from multiple sampling. The results of the testing set can be summarized as follows: (i) for each cancer class, three of four methods make correct predictions for the testing set with accuracies significantly better than random prediction; (ii) the individual genomic variations (strictly speaking, the descriptors of SNPs or SNP-Ss) of BRCA and OV are more closely related to each other than to any other remaining cancer classes by three of the four methods; and (iii) there is also a similar relationship between the descriptors of OV and UCEC, but to a lesser extent.

Fig. 3.

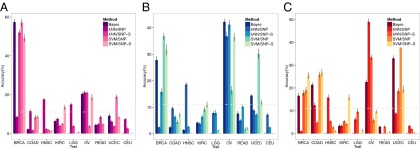
Nine-class prediction accuracy of a testing set of 50 individuals for each of three cancer classes of (A) BRCA, (B) OV, and (C) UCEC. Nine-class prediction accuracies of four methods and the combined prediction by Bayesian inference for 50 test individuals for each of three cancer classes are depicted. Dotted lines show random prediction accuracy and the tick mark on each bar in the figure shows SEs of the predictions measured by resampling method. kNN/SNP, kNN algorithm on individual’s SNP profiles; kNN/SNP-S, kNN algorithm on SNP syntax profiles; SVM/SNP, SVM algorithm on individual’s SNP profiles; SVM/SNP-S, SVM algorithm on SNP syntax profiles.

Because none of the four methods performed poorly in a consistent way, we calculated the combined predictions using Bayesian inference (see SI Text for details) of the results of the four methods applied to the three testing groups as also shown in Fig. 3. The combined results show that, similar to the summary of the testing performances of individual methods listed in the previous paragraph, (i) the accuracies of the combined predictions for the three classes are significantly higher than the 11% for random prediction; (ii) the testing accuracies of the combined method are better than or comparable to any of the individual methods; (iii) the individual genomic variations (specifically, SNPs and SN-Ss) of BRCA and those of OV are more related or similar to each other than to any other cancer classes; and (iv) there is also a similar relationship between the descriptors of OV and UCEC, but to a lesser extent.

It is interesting to note that the observation iii is consistent with a recent experimental study that showed a GWAS in BRCA1 mutation carriers revealed novel loci associated with breast and ovarian cancer risk (16). Perhaps, more interesting is that observations iii and iv, revealing the relationships between variations of untransformed cell genomes of BRCA and OV individuals and also between those of OV and UCEC individuals, suggest that the related variations may be correlated with the shared somatic mutational profiles of tumor cell genomes across three cancer classes of BRCA, OV, and UCEC, as observed in another recent experiment (17).

For each test individual, the confidence of the prediction by the combined method can be estimated by the posterior probability of Bayes inference. The results for the three test classes (Fig. S2) indicate that all predictions are made with posterior probabilities higher than 0.3 compared with the 0.11 (i.e., 1/9) expected for random probability. Furthermore, for example, 30% of BRCA test individuals had high confidence calls, defined as test individuals having the highest posterior probability ≥0.9, and these calls had an accuracy of 83.3% (Fig. S2), which is a 25.3% increase from the overall accuracy of BRCA of 58% (Fig. 3A).

Multiple Assortments of Susceptibility Alleles.

With kNN/SNP-S, one of the three better performing methods, all pairwise Jensen–Shannon distances among all individual descriptor profiles were calculated, and the distance matrix was assembled for the study population. Using the matrix, we applied multidimensional scaling (18) to inquire how well the members of a given cancer class form an exclusive cluster, which is separated from the clusters of other cancer classes. We found that, for each cancer group, no clear exclusive clustering was evident (data not shown), suggesting that there is no overwhelming collection of descriptor elements that are common to all members of the cancer class. The fact that, despite the poor clustering, the kNN and SVM methods make good cancer susceptibility predictions suggests that many different assortments from a select collection of descriptors (susceptibility alleles) render individuals susceptible to the same cancer class, supporting the model of the multiple assortment of genomic alleles for cancer susceptibility.

Overall Conclusions.

The multiclass accuracy of the predictions for cancer susceptibility based on a combination of the results of the four methods (two supervised learning algorithms applied to two descriptors consisting of low P value SNPs or low-frequency SNP-Ss of common genomic variations) is several folds better than random predictions and is better than those of individual methods.

The number of the descriptor elements, which can be considered as cancer susceptibility alleles, is far greater (order of magnitude or more) than the limited associations confirmed by GWASs thus far.

Our results are supportive of the model of the multiple assortment of genomic alleles for the susceptibility to a given cancer class, where multiple different selections from the susceptibility alleles render a population susceptible to the same cancer class.

Despite the limited SNP data available in public databases at present, the results suggest that the framework of this or its improvement can predict the susceptibility for the eight major cancer classes, with probability estimates useful for making health decisions at an individual or population level. Such predictions are achievable by the profiles of selected groups of SNPs and SNP-Ss consisting of common SNPs with a MAF >1%.

The genomic variations of individuals with BRCA are more similar to those with OV than to any other cancers studied. The same is true for those with OV to UCEC to a lesser extent.

Discussion

Comparison with Other Studies.

There are no prior publications to compare with our studies that address the multiclass susceptibility prediction of several cancers or any other group of related diseases. However, there are a few published papers on risk prediction of a single disease by various methods. Of these, the work of Wei et al. (19) is most relevant to our study: they applied the SVM algorithm to SNPs to predict the susceptibility of one disease: type 1 diabetes (T1D). Their results suggest that improved disease risk for T1D can be predicted by using the SVM algorithm on a subpopulation of SNPs with low P values as descriptor variables. Furthermore, they showed that SVM performed far better than the logistic regression (LR) algorithm. This preference of SVM over LR suggests that (i) SMV takes into account many possible significant interactions among the SNP markers, whereas LR assumes they are independent; and (ii) unlike most regression-based methods, SVM allows more input features, such as SNPs, than samples, so it is particularly useful in classifying high-dimensional data in their study and ours. One of the four methods in our study took the same approach where we applied the SVM algorithm on SNPs with P < 10⁻⁵, not just for one trait but for all nine traits separately, and then took the trait with the maximum votes.

Sample Population and Control Group.

As described previously, no false positives were found for the healthy group from Caucasians from Utah (CEU) during the training step. However, there were a few cancer individuals whose genomes suggest they are predicted to belong to the healthy group, but no individuals in the healthy group showed genomic susceptibility to any cancer group. Several factors may have contributed to this apparent artefact. For this framework study, (i) the true control group should consist of a combination of a healthy group plus representative individuals with each of all cancers except the eight major cancer classes in the study. However, we used healthy individuals in the HapMap database as the control group of this study, because a true control group is impractical to assemble. (ii) The artificial segregation between cancer groups and the healthy group may be caused by the two separate databases typed from different laboratories (20).

Limits and False Predictions.

The susceptibility (risk) prediction will improve as the sample size and diversity increases for a given cancer type, as the number of different cancer classes increases, and as better descriptor/algorithm combinations are discovered. However, the accuracies will not reach 100% even under the best circumstances, because not all of the genomic susceptibility for a given cancer leads to the initiation of cancer, but, in most cases, it requires one or more initiating events that are nongenomic. Furthermore, susceptibility alleles may or may not be directly related to causal alleles. Also, false predictions, although relatively small in numbers, may also be due to several factors such as (i) systemic errors arising from incorrect genotype calls due to experimental or computational biases (21); (ii) population substratification (22); (iii) errors in human reference genome sequences (23); and (iv) batch differences (21, 24).

Practicality of Information.

On a population or personal level, our method may provide information for practical use: quantitative estimation of the size of a population with high genomic susceptibility for cancer can be a part of the information useful for planning cancer prevention policies and cost management strategies for the population. Similarly, such estimates for an individual can provide motivation for prevention and for proactive early diagnostic tests to initiate early intervention.

Possible Improvement of the Framework of This Approach.

There are many ways our approach can be improved by incorporating additional information, such as the following. (i) Improved databases: larger and more diverse populations and cancer classes in future databases. (ii) Rare SNPs: the public databases we used contain common SNPs with MAF >1%. We expect that future public databases that include rare SNPs with MAF <1% may improve the prediction performance of our approach. (iii) Population stratification: the relative frequencies of cancers vary depending on many factors such as ethnicity, age, diet, lifestyle, environment, and others. Inclusion of such information may also improve prediction accuracy. (iv) Other genomic variations: although SNPs account for the largest number of genomic variations, other variations, such as insertion-deletions of various lengths, copy number variations, and repeats or inversions of various lengths, can be codified and included in a more comprehensive descriptor of genomic variations of an individual. (v) Other descriptor/algorithm pairs: additional descriptor/algorithm pairs can be added and their results combined after attrition of the results from those pairs that perform worse than others consistently or most of the time. (vi) Important SNPs and SNP-Ss: our starting point is not designed to find one or a few important features (SNPs or SNP-Ss) unique to a given cancer class. In fact, our optimization processes result in a large number of features as useful for multiclass prediction. However, it is theoretically possible, although high in computational burden, to identify a smaller set of more important features that most downgrade the overall performance when removed from the selected features (19). Using such important features with higher weights may improve the prediction.

Other Potential Applications.

This framework of analysis can be applied, with appropriate modifications, for other purposes such as (i) for multiclass prediction of genomic susceptibility to member diseases of other common and complex disease groups such as autoimmune diseases, neurodegenerative diseases, and others; (ii) for pharmacogenomics application to assess susceptibility of a patient for the most beneficial or serious adverse drug or therapy among multiple options; and (iii) for clinical trials to select trial candidates who are likely to respond positively in a clinical trial for a drug or therapy.

Materials and Methods

Samples and Genotyping.

We downloaded a total of 2,192 SNP array results and related clinical information from the TCGA of the National Institute of Health (NIH) website (cancergenome.nih.gov) from April 2, 2012 to April 4, 2012 with the approval of National Center for Biotechnology Information database of Genotypes and Phenotypes (general research use approval). We downloaded SNP genotype data of those patients’ blood, carefully called and tested at the Broad Institute. The patients were mostly white American individuals with European ancestries. A few outliers from different ancestries were removed in the quality control step. All markers were typed on Affymetrix 6.0 SNP chips. For the healthy population, CEU data from the HapMap project were used, because it is believed to be the best representation of overall healthy white individuals available at present. Only females were included in our training and testing datasets for BRCA, OV, and UCEC. To reduce loss of SNP information arising from merging of two datasets with different marker sets, we downloaded 165 SNP array results of CEU, typed on an Affymetrix 6.0 chip from the HapMap ftp website. We genotyped the data using Affymetrix Power Tools with default parameter settings and discarded samples that had been reported to have low quality from the website (see Table S2 for study sample information).

Quality Control.

The dataset used in this study was derived using PLINK (25) with the following conditions: considering that the platform we used is designed to type high polymorphic sites, SNPs having minor allele frequency at 1% or below were assumed to be noise and thus removed, and the Hardy–Weinberg equilibrium tests were applied to each marker in CEU individuals only (P > 10⁻⁶). Furthermore, we applied the plate-effect test by assessing the association test (P > 10⁻⁸) between a plate and the others for every plate (having more than 30 samples) within each cancer trait (24). For those SNPs who passed quality control, we extracted self-reported Caucasian individuals in the United States for TCGA data and performed a genetic relatedness test (PI_HAT < 0.2) (26). In addition, all related individuals in CEU were removed using pedigree information. For example, we removed two individuals of trios and one of duos. Finally, by merging samples and having joint SNPs across post–quality control trait datasets, we obtained genotypes for 714,649 nonredundant SNPs of autosomal chromosomes for 1,741 individuals (see Table 2 for more information).

Encoding of Descriptor Elements.

Two types of encodings are used: (i) to compare genotypes of two individuals at a SNP locus, it is sufficient to compare the number of minor alleles at the locus, because the identities of the major and minor alleles of the locus are known in the databases we used. Thus, each SNP genotype (as a descriptor element) is converted to the numeric value of 0, 1, or 2, depending on the count of minor alleles in the genotype, i.e., 0 for homozygous in major allele, 1 for heterozygous, and 2 for homozygous in minor allele; (ii) to compare two SNP-Ss, we need to compare the genotype of each SNP allele in the SNP-Ss. Thus, each SNP in a SNP-S descriptor elements is convert to 1 of 10 alphabets representing 10 possible SNP genotypes (Table S1).

Optimal Length of SNP-Ss.

Because the number of SNP-Ss of all possible lengths is gigantic (∼10¹² for an SNP string of length of 10⁶ positions), and because mathematical operations needed for comparing the profiles of SNP-Ss of such size is prohibitive, we use only the SNP-Ss with an optimal length. Practical utility for using the optimal length to drastically reduce computational burden has been shown in our previous works (27, 28).

Four Methods.

Fig. 1 shows the workflow of the four methods.

kNN/SNP-S method: kNN algorithm on SNP-Ss.

The format of the descriptor for this method is a large vector consisting of all SNP-S alleles that are present in the training population. The descriptor of each member of the training set is constructed by filling up the format with those encoded SNP-S alleles present in the member’s genome. Then, we select low-frequency SNP-Ss by removing all SNP-S loci where the SNP-S allele is present among more than a given percentage of the training population and calculate the frequencies of distinct SNP-S alleles. Finally, we construct a Jensen–Shannon (JS) divergence matrix of the frequency profiles between all member pairs. [JS divergence (29) for measuring distances of the descriptors was selected because it showed better predictive capacity over other conventional methods such as allele sharing]. For each test individual, we select k individuals of known traits with the shortest JS divergence to the frequency profile of the test individual. We then assign the most common trait among them as the likely trait the test individual is susceptible to. In case of a tie, we pick the class of having the shortest average JD distance to the test individual. The length of SNP-S, i, the f parameter for low-frequency selection, and the parameter k are optimized for the best accuracy of estimating cancer susceptibility on the training data set. The optimal parameter values came out to be 8, 1%, and 40 for i, f, and k, respectively (Fig. 2 and Table 1).

In the testing step for prediction accuracy, for each test individual, we profile features of testing individuals filtered at 1%, followed by normalization. Then we measure the JS distance vector between the test individual and the training samples. The traits of the test individuals are predicted by the same voting scheme as in training phase with the optimal k parameter.

kNN/SNP method: kNN algorithm on SNPs.

The kNN algorithm is the same as above but applied to the descriptor profile of SNPs instead of SNP-Ss. The format of the descriptor for this method is a large vector consisting of all SNP loci, and the descriptor of an individual is constructed by filling up the vector with ordered, encoded SNP alleles of the individual’s genome. In this method, we optimize the f and k parameters (Fig. S1A and Table S3). Optimized values for f and k are 15% and 200, respectively.

SVM/SNP method: SVM on SNPs.

SVM was originally designed for classifying a data set into two classes. It was later extended for the multiclass prediction problem by various approaches. Of these, we use the one-versus-one (OVO) scheme because it is empirically known to outperform other approaches (30). The OVO method generates n(n − 1)/2 class-pairs from n classes and takes the trait with the highest votes from n(n − 1)/2 predictions as the most likely trait a test individual is susceptible to [for implementation of the OVO SVM method, we used LIBSVM by Chang et al. (31)]. Radial basis function (RBF) is selected for the kernel function, because it is known to perform better than other major functions in general. In building a binary class-pair of the SNP descriptor, we select SNPs associated between the two classes by filtering out SNPs over a predefined P value threshold. To find the optimal cutoff, we vary its range from 10⁻³ to 10⁻⁶ (32). At cutoff values less than 10⁻⁶, some classifiers had no SNPs left after filtering by association tests. During the training phase, we evaluate the performance of the OVO SVM prediction by leave-one-out cross-validation in a dataset of having 66 samples for each cancer (a total of 594 individuals). For this, the prediction performance of the method was tested on a random sample based on the parameters trained from the rest of the dataset by leave-one-out cross-validation. This procedure was iterated for all cases, and the test results of class (cancer type) assignment were collected and tabulated in the contingency matrix (Table S4). In cases of ambiguous predictions, that is, multiple highest votes, we repeat the poll within the set of classes having the highest votes until the tie breaks. The one exception is that when all traits have an equal number of votes, we choose one arbitrarily. The occurrence rate of such a case is extremely low (less than 1% of total predictions). The results of definitive predictions by OVO SVM perform best when the P value cutoff value is 1 × 10⁻⁵ (Fig. S1B).

SVM/SNP-S: Support vector machine on SNP-Ss.

This procedure is the same as above except the SNPs are replaced by SNP-Ss. One additional parameter of the optimal length of SNP-S needs to be optimized using the training set (Fig. S1C and Table S5). The optimized values for the P value cutoff and optimal length for SNP-S are 10⁻⁵ and 2, respectively.