Abstract
Objective
Research on ethnic health disparities requires the use of psychometrically sound instruments that are appropriate when applied to ethnically diverse populations. The Short Inventory of Problems (SIP) assesses alcohol-related consequences and is often used as a measure to evaluate intervention effectiveness in alcohol research; however, whether the psychometric properties of this instrument are comparable across language and ethnicity remains unclear.
Method
Multi-group Confirmatory Factor Analysis (MGCFA) was used to test for the invariance of the measurement structure of the SIP across White Non-Hispanic English speaking (N=642), Hispanic English speaking (N=275), and Hispanic Spanish speaking (N=220) groups.
Results
The MGCFA model in which factor loadings, measurement intercepts, and item residuals were constrained to be equal between English speakers and Spanish speakers exhibited a reasonable fit to the data, χ2(221)=1089.612 p<.001, TLI=.926; CFI=.922, RMSEA=.059 (90%CI=.055–.062). The ΔCFI supported strict factorial invariance, ΔCFI=.01, across groups; no significant group differences were found between factor loadings, measurement intercepts, or item residuals between English speakers and Spanish speakers.
Conclusions
This study extends the existing confirmatory factor analysis results of the SIP by providing additional data to inform the utility of the SIP among Hispanics. Strict factorial invariance between Spanish and English speakers is necessary to: conclude the underlying constructs have the same meaning across groups; test for group differences in the latent variables across groups; and presume group differences are attributable only to true differences between groups. Thus, the SIP is strongly supported for evaluating the effectiveness of alcohol treatment among Hispanics.
1. Introduction
1.1 Ethnic differences in alcohol consumption and consequences
Over the next three decades, racial and ethnic minority groups are estimated to represent half the US population (Centers for Disease Control and Prevention [CDC], 2011). Hispanics are currently the largest minority group in the U.S, representing 16.3%, an increase of 43% since 2000 (Ennis, Ríos-Vargas & Albert, 2011). In southwestern states, the proportion of Hispanics is already at this higher level: Texas, 38%; New Mexico, 46%; Arizona, 30%; and California, 38% Hispanic (Ennis et al., 2011). Mexican Americans constitute about 60% of the US Hispanic population and are currently the largest Hispanic subgroup. Differences in alcohol consumption and alcohol-related problems currently exist between ethnically diverse populations (Galvan & Caetano, 2003). Compared to Caucasians, Hispanics tend to consume alcohol in higher quantities per occasion, are approximately twice as likely to die from cirrhosis of the liver, are more likely to report social consequences of drinking, and more likely to report two or more dependence symptoms (Stinson, Grant & Dufour, 2001; Mulia, Ye, Greenfield & Zemore, 2009). Caetano and Clark (1998) found that the proportion of Caucasian and Black men reporting one, two, or three or more alcohol related consequences remained stable between 1984 and 1995 while the proportion of Hispanic men reporting three or more alcohol related consequences increased from 9% to 16% during this time period. Given the growth of the Hispanic population in the US and their increased risk for alcohol-related problems, evaluating the effectiveness of interventions in this population is essential to effectively addressing this health disparity (Bernal & Sharro-del-Rio, 2001; Atkinson, Bui & Mori, 2001). However, evidence on the effectiveness of treatments among ethnic minority groups is limited, in part, because of the necessity to use psychometrically sound instruments that are appropriate when applied to ethnically diverse populations.
1.2 Purpose
The Short Inventory of Alcohol Problems (SIP) is a measure often used to evaluate intervention effectiveness in alcohol research (Soderstrom et al., 2007; Walters, Bennett & Miller, 2000) The main goal of the SIP is to evaluate a person’s drinking-related consequences independent from consumption, alcohol dependence, and help seeking behavior. Originally, developed out of the 45-item DrInC, the 15-item SIP is particularly useful in time-limited settings like emergency rooms, trauma care settings, and primary care (Soderstrom et al., 2007; Forcehimes, Tonigan, Miller, Kenna & Baer, 2007; Longabaugh et al., 2001). Findings of prior exploratory and confirmatory factor analyses on the SIP are somewhat mixed. Feinn, Tennan and Kranzler (2003) suggest using a second-order five-factor model rather than a first-order one factor or first-order five-factor model. However, Feinn et al. (2003) did report high correlations among the factors. Kenna et al. (2005) suggest that a first-order five-factor model showed no significant improvement in fit over the one-factor model, and therefore concluded that the first-order one factor model may be most appropriate. The first-order one factor model is also supported in drug consequence studies using the SIP (Blanchard, Morgenstern, Morgan, Labouvies & Bux, 2003; Tonigan and Miller, 2002). Thus, one limitation of the SIP is the lack of consistent evidence regarding its factor structure. A second limitation of the SIP is whether scores on the instrument can be compared across language and ethnicity. In order to test and look for difference in intervention effectiveness for minority groups, it is vital that researchers utilize valid instruments that have established measurement invariance across groups. In other words, the observed scores reflect the true mean score on the latent construct being measured and the scores are being measured similarly across groups (Stewart & Napoles-Springer, 2003). Thus, the goals of the present study were to 1) further investigate the measurement structure of the SIP and 2) inform the assessment and utility of the SIP across language and ethnicity.
2. Material and method
2.1 Participants
This study included 642 self-identified White Non-Hispanic English speaking patients, 275 Hispanic English speaking patients, and 220 Hispanic Spanish speaking patients (N=1137) who agreed to participate in a randomized clinical trial conducted in a Level-1 trauma department. All participants had suffered a traumatic injury, screened positive for high-risk drinking, and were admitted to a Level I Trauma Center in the South. See Field, Caetano, Harris, Frankowski and Roudsari (2009) for a thorough description of study methods, recruitment, and interventions.
Demographic information collected on study participants includes age, gender, personal income, education level, employment status, percent of lifetime in the U.S., Glasgow Coma Scale (GCS) level, and insurance status. While not the focus of this study, significant differences across gender, age, income, employment status, and insurance status existed between the three groups. Tukey’s post-hoc tests revealed that Hispanic Spanish speakers were significantly younger, had lower income levels, received less formal education, and had spent less time in the U.S. compared to both Hispanic English Speakers and White English speakers. See Table 1 for a summary of demographic results. Authors note that it is important to consider these potential differences when interpreting multi-group analysis, particularly when a measurement does not hold up across groups.
Table 1.
SIP demographics
| Variable | White Non-Hispanic English Speakers (642) |
Hispanic English Speakers (275) |
Hispanic Spanish Speakers (220) |
Total (1137) |
Group Difference Tests |
|---|---|---|---|---|---|
| Age | M=34.51, SD=11.61 | M=34.49, SD=12.58 | M=29.25, SD=8.55** | M=33.48, SD=11.51 | F(2, 1134)=22.175, p=.000 |
| Gender | X2(2, A=1137)=19.720, p=<0.001 | ||||
| Male | n=504 | n=220 | n=202 | N=926 | |
| Female | n=138 | n=55 | n=18 | N=211 | |
| Personal Income” | M= 2.29, SD=3.80 | M=2.25, SD=3.83 | M=1.32, SD=3.15** | M=2.09, SD=3.71 | F(2,1133)=5.173, p=0.006 |
| Education Level b | M=3.20, SD=1.24 | M=3.19, SD=1.31 | M=1.98, SD=1.20** | M=2.96, SD=1.34 | F(2,1134)=84.396, p<0.001 |
| Employment Status | X2(2, N=1137)=58.019, p<0.001 | ||||
| Employed | n=411 | n=183 | n=192 | N=786 | |
| Unemployed | n=146 | n=67 | n=25 | N=238 | |
| Student | n=30 | n=4 | n=3 | N=37 | |
| Retired | n=7 | n=7 | n=0 | N=14 | |
| Other | n=48 | n=14 | n=0 | N=62 | |
| Percent of lifetime in the US | M=97.20%, SD=12.52% | M=98.00%, SD=9.16% | M=40.60%, SD=36.34%** | 86.5%, SD=29.40% | F(2,1130)=368.921, p<0.001 |
| GCS Level | M=14.73, SD=1.52 | M=14.64, SD=1.98 | M=14.62, SD=1.99 | M=14.69, SD=1.72 | F(2, 732)=368.921, p=0.737 |
| Insurance | X2(2, N=1137)=33.567, p=0.000 | ||||
| No Insurance | n=387 | n=160 | n=77 | N=724 | |
| Insurance | n=255 | n=145 | n=43 | N=413 |
0=No Income, 1=Less than 10,001, 2=10,001-20,000, 3=20,001-30,000, 4=30,001-40,000, 5=40,001-50,000, 6=50,001-75,000, 7=75,001-100,000, 8=100,001 or more
1=Less then High School, 2=Some High School, 3=High School Diploma or GED, 4=Some College (1-3 years) 5=Vocational or Associate's Degree, 6=Bachelor's Degree, 7=Graduate Degree
Tukey’s post hoc test revealed that Hispanic Spanish Speakers were significantly different (p<.05) than Hispanic English Speakers and White Non-Hispanic English Speakers
2.2 Measures
The SIP was developed as a short form of the Drinker Inventory of Consequences (DrInC; Miller et al., 1995), a 45-item measure created to assess alcohol-related consequences independent from consumption, dependence, and help seeking behavior. The DrInC assesses alcohol-related consequences across five domains: physical, interpersonal, intrapersonal, social responsibility, and impulse control. The SIP uses the top three items that are most highly correlated with their corresponding subscale totals and combines them to form a 15-item short form of the DRINC (Miller, Tonigan & Longabaugh, 1995). Compared to the DrInC, the SIP performs well in assessing overall levels of alcohol-related consequences with its total scores being strongly related to the corresponding DrInC scores (Alterman, Cacciola, Ivey, Habling & Lynch, 2009; Forcehimes et al., 2007). However, there is some discrepancy as to whether or not the SIP yields subscale scores that reflect the presence of distinct subscales (Forcehimes et al., 2007; Feinn et al., 2003; Blanchard et al., 2003; Tonigan & Miller, 2002).
3. Data analytic strategy
3.1 Reliability
The reliability of the SIP instrument in this study was examined by calculating Chronbach’s α coefficients using the White Non-Hispanic English speakers, Hispanic English speakers, Hispanic Spanish speakers, and the total sample.
3.2 Construct validity
Confirmatory Factor Analysis (CFA) was used to estimate predicted first-order one-factor, first-order five-factor, and second-order five-factor models using AMOS (Analysis of Moment Structures, version 18.0), a software commonly used to estimate structural equation models for manifest and latent variables. The three models were evaluated and compared, and the most appropriate model was selected based on the following fit indices: comparative fit index (CFI), Tucker-Lewis Index (TLI), root-mean-square error of approximation (RMSEA), 90% confidence intervals (CI) for the RMSEA, the Standardized Root Mean Square Residual (SRMR; Bentler, 1995), and the chi square test statistic for overall model fit.
3.3 Measurement invariance across groups
Multi-group Confirmatory Factor Analysis (MGCFA) was used to test for the invariance of the measurement structure of the SIP across White Non-Hispanic English speaking (N=642), Hispanic English speaking (N=275), and Hispanic Spanish speaking (N=220) groups. In order to conduct MGCFA, adequate sample size is necessary. Bentler and Chou (1987) recommend at least the 5:1 ratio of participants to parameters with a preference of a 10:1 ratio. This study met sample size recommendations having a ratio of 24:1 participants to parameters.
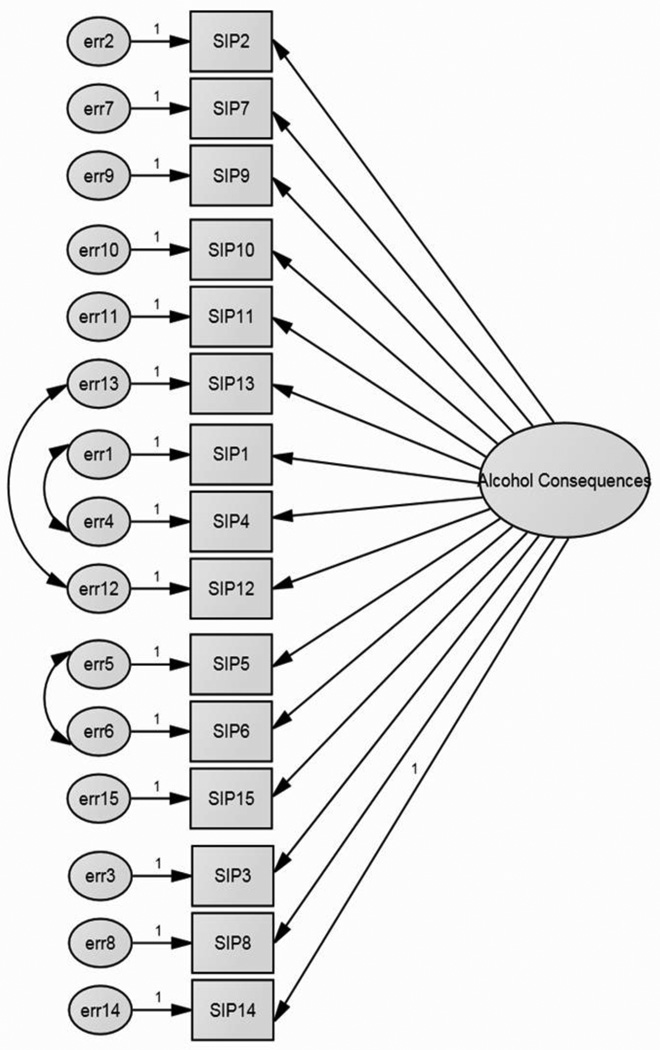
In MGCFA, measurement invariance tests are used to examine the relationship between latent constructs and measured variables across groups. In this study, four common models were used to test for configural, weak, strong, and strict factorial invariance. See Figure 1 to view the hypothesized model under test.
Figure 1.
Hypothesized first-order one factor model, unconstrained
3.3.1 Configural invariance
In the first step of testing measurement invariance, it is customary to establish a baseline model (Byrne, 2001) by examining configural invariance across each group (i.e., a pattern of free factor loadings across groups without equality constraints). In this study, individual CFAs were run for each individual group to determine if the basic model structure of the SIP appeared to be the same for each group. Next, a MGCFA constraining the factor loadings across groups without equality constraints was run to establish a baseline model, which served as the comparison standard for subsequent tests.
3.3.2 Weak factorial invariance (pattern invariance)
To test for weak factorial invariance (pattern invariance), the factor loadings are constrained to be equal without imposing additional equality constraints. This model was used to determine if groups responded to the items and underlying constructs in a similar way. If supported, the measurement of the latent variable can be assumed equivalent across groups.
3.3.3 Strong factorial invariance (scalar invariance)
To test for strong factorial invariance (scalar invariance), factor loadings and intercepts were constrained to be equal across groups. In addition to implying no difference in measurement of latent variables across groups, strong factorial invariance allows for the testing of mean differences in the latent variable across groups. In other words, scores can be compared across groups when individuals who have the same score on the latent construct also have the same score on the observed variables regardless of group membership.
3.3.4 Strict factorial invariance
After establishing strong factorial invariance, strict factorial invariance would be tested by constraining factor loadings, intercepts, and item residuals to be equal across groups (Drasgow, 1984; Byrne, Shavelson & Muthén, 1989). Under strict factorial invariance, group differences in the relationship of manifest variables, or measured variables, are attributable only to differences across groups in common factor means and dispersion matrices (Meredith & Teresi, 2006).
3.3.5 Comparison of models
At each level, model fit was assessed using Worthington and Whittaker’s (2006) proposed criteria for model fit: chi square test, Root Mean Square Error of Approximation (RMSEA; Steiger & Lind, 1980) with corresponding 90% confidence intervals (RMSEA< .08), Comparative Fit Index (CFI; Bentler, 1990) (CFI> .90), Tucker Lewis Index (TLI; Tucker & Lewis, 1973) (TLI> .90), and Standardized Root Mean Square Residual (SRMR; Bentler, 1995) (SRMR< .10).
To test for invariance across all three groups, Byrne (2001) suggests determining if two of the three groups are invariant first. If measurement invariance is supported across the two groups, then these groups can be combined and tested against the third group. Initially, White Non-Hispanic English speakers & Hispanic English speakers were grouped together. Grouping order was based on the fact that the two English-speaking groups were more similar demographically. If the two groups differ, invariance across all three groups could not be supported; however, each English-speaking group could then be tested individually against the Spanish-speaking group to evaluate if invariance is supported between any two groups.
For the first model, parameters from the two English-speaking groups were constrained to be equal to test whether a significant drop in fit occurred when estimating a more constrained model. To reject the null hypothesis of measurement invariance and conclude that a significant drop in fit occurred, two criteria had to be met: Δχ2 significant at p < .05 (Byrne, 2001) and ΔCFI > .01 (Cheung & Rensvold, 2002). If measurement invariance was supported across the two English speaking groups, then these groups could be combined and tested against the Spanish speakers. Testing for invariance on the four levels could then be repeated to determine if measurement invariance is supported across all three groups.
4. Results
4.1 Reliability
Internal consistency estimates as calculated by Chronbach’s alpha were excellent for all subgroups; White Non-Hispanic English Speakers=.939, Hispanic English Speakers=.954, Hispanic Spanish Speakers=.937, and total sample=.943.
4.2 Construct validity
CFA allowing for all parameters to be freely estimated showed a reasonably good fit of the data to the predicted first-order one-factor, first-order five-factor, and second-order five-factor models (See Table 2). The fit indices suggest the first-order five-factor and the second-order five-factor model fit the data similarly to the first-order one factor model. However, the factors in both the first-order five-factor and second-order five-factor model were highly correlated (range r=.79–1.07) and negative variances were present indicating that one underlying factor may be explaining the majority of the systematic variance (Byrne, 2001). Therefore, the first-order one-factor solution was determined to be the preferred factor structure for the SIP.
Table 2.
Comparison of model fit between three competing SIP models
| Model | Factor model |
X2 | df | TLI | CFI | RMSEA |
|---|---|---|---|---|---|---|
| 1 | One Factor | 1059.134 | 261 | 0.915 | 0.930 | 0.052 (0.049–0.055) |
| 2 | Five Factor | 952.220 | 237 | 0.916 | 0.937 | 0.052 (0.048–0.055) |
| 3 | Five Factor Second Order | 984.450 | 252 | 0.920 | 0.936 | 0.051 (0.047–0.054) |
4.3 Measurement invariance
4.3.1 SIP descriptive statistics
SIP Total scores for the Caucasian-English speakers ranged from 0 to 56 with a mean score of 6.19 (SD=9.94). Total scores for Hispanic-English speakers ranged from 0 to 56 with a mean score of 6.6 (SD=11.58). Total scores for Hispanic-Spanish speakers ranged from 0 to 48 with a mean score of 6.77 (SD=9.32). Individual means, standard deviations, and factor loadings for each SIP item by subgroup are reported in Table 3. Item 15 had the lowest factor loadings of all items and ranged from .28 among White, Non-Hispanic English speakers to .52 among Hispanic Spanish speakers. With the exception of item 15, factor loadings from .56 to .81 among White, Non-Hispanic English speakers, from .70 to .85 among Hispanic English speakers and from .61–.81 among Hispanic Spanish speakers.
Table 3.
Descriptive statistics and standardized factor loadings of the SIP
|
White Non- Hispanic English |
Hispanic English | Hispanic Spanish | ||||
|---|---|---|---|---|---|---|
| SIP Item | Factor Loading |
M(SD) | Factor Loading |
M(SD) | Factor Loading |
M(SD) |
| 1. I have been unhappy because of my drinking. | 0.77 | 0.60(1.11) | 0.82 | 0.55(1.18) | 0.73 | 0.44(0.87) |
| 2. Because of my drinking, I have not eaten properly. | 0.67 | 0.72(1.22) | 0.76 | 0.62(1.16) | 0.69 | 0.79(1.16) |
| 3. I have failed to do what is expected of me because of my drinking. | 0.81 | 0.40(0.90) | 0.83 | 0.51(1.09) | 0.77 | 0.40(0.85) |
| 4. I have felt guilty or ashamed because of my drinking | 0.80 | 0.59(1.06) | 0.82 | 0.63(1.18) | 0.67 | 0.82(1.06) |
| 5. I have taken foolish risks when I have been drinking | 0.68 | 0.60(0.97) | 0.74 | 0.60(1.08) | 0.70 | 0.75(0.99) |
| 6. When drinking, I have done impulsive things that I regretted later. | 0.72 | 0.53(0.91) | 0.80 | 0.64(1.09) | 0.75 | 0.50(0.91) |
| 7. My physical health has been harmed by my drinking. | 0.56 | 0.30(0.82) | 0.70 | 0.28(0.81) | 0.73 | 0.33(0.73) |
| 8. I have had money problems because of my drinking. | 0.74 | 0.36(0.95) | 0.84 | .042(1.01) | 0.81 | 0.44(0.89) |
| 9. My physical appearance has been harmed by my drinking, | 0.69 | 0.31(0.82) | 0.73 | 0.36(0.91) | 0.74 | 0.34(0.73) |
| 10. My family has been hurt by my drinking. | 0.79 | 0.37(0.91) | 0.77 | 0.45(1.04) | 0.61 | 0.28(0.74) |
| 11. A friendship or close relationship has been damaged by my drinking. | 0.74 | 0.27(0.70) | 0.73 | 0.30(0.81) | 0.73 | 0.23(0.62) |
| 12. My drinking has gotten in the way of my growth as a person. | 0.80 | 0.34(0.87) | 0.85 | 0.32(0.96) | 0.72 | 0.43(0.92) |
| 13. My drinking has damaged my social life, popularity or reputation. | 0.76 | 0.25(0.72) | 0.75 | 0.33(0.95) | 0.78 | 0.37(0.76) |
| 14. I have spent too much or lost a lot of money because of my drinking. | 0.79 | 0.45(0.92) | 0.81 | 0.56(1.08) | 0.78 | 0.72(1.13) |
| 15. I have had an accident while drinking or intoxicated. | 0.28 | 0.13(0.35) | 0.43 | 0.15(0.41) | 0.52 | 0.11(0.33) |
Note: All factor loadings are statistically significant at the .01 level.
4.3.2 Configural invariance
MGCFA allowing for all parameters to be freely estimated showed a reasonably good fit of the data to the predicted first order one-factor model. The chi square test for overall fit was statistically significant, χ2(261)=1059.134, p<.001, which was expected due to the large sample size. The RMSEA value (.052, 90% CI=.049–.055) and value of SRMR (.038) indicated good fit. The TLI (.915) and CFI (.930) also supported reasonable fit. Thus, when examining the basic model structure of three groups individually, findings were consistent across the groups.
Large correlated errors between items 1 and 4, items 12 and 13, and items 5 and 6 existed across the groups. Lewis (1987) proposed that individuals who experience shame are prone to depression. This correlation could explain why errors from item 1 (I have been unhappy because of my drinking) and item 4 (I have felt guilty or ashamed because of my drinking) are significantly correlated in this measure. The error terms for items 5 and 6 (I have taken foolish risks when I have been drinking and when drinking, I have done impulsive things I have regretted later) may be highly correlated because of the order of these items. The individual may be more likely to consider how impulsive they were in situations specifically around foolish risks. Similarly, correlated error terms on items 12 (my drinking has gotten in the way of my growth as a person) and item 13 (my drinking has damaged my social life, popularity, or reputation) may also be influenced by order of items. Immediately after considering how drinking impacts interpersonal growth, a person may be more likely to endorse item 13. Based on this justification, these three correlated errors were included as free parameters in the model.
4.3.3 English speakers
A hypothesized model with no constraints was first estimated between White Non-Hispanic and Hispanic English speakers. Weak, strong, and strict invariance was tested by constraining factor loadings, intercepts, and item residuals. MGCFA models that included factor loadings and measurement intercepts constrained to be equal between White Non-Hispanic English speaking and Hispanic English speaking subgroups resulted in reasonable model-data fit, χ2(203)=840.39, p<.01, TLI=.93; CFI= .932, RMSEA=.059 (90% CI= .055–.063). Results supported strong factorial invariance in that no significant group differences were found between factor loadings or measurement intercepts for the Caucasian and Hispanic English speakers, ΔCFI<.01; therefore, English speakers were combined into one group to be compared to Spanish speakers (See Table 4).
Table 4.
MGCFA model comparisons
| Step | Model Description | Groups | Comparative Model |
X2 | df | AX2 | Adf | Statistical Significance |
CFI | ACFI |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Model 1: Unconstrained | White Non-Hispanic English Speakers/ Hispanic English Speakers/ |
-- | 1059.134 | 261 | -- | -- | -- | .0930 | -- |
| 2 | Model 1: Fully Constrained | White Non-Hispanic English Speakers/ Hispanic English Speakers/ |
Model 1 | 1375.767 | 332 | 316.632 | 71 | 0.000 | 0.908 | 0.022 |
| 3 | Model 1(a): Unconstrained | White Non-Hispanic English Speakers/ Hispanic English |
-- | 797.174 | 174 | -- | -- | -- | 0.933 | -- |
| 4 | Model 1(a): Factor Loadings | White Non-Hispanic English Speakers/ Hispanic English |
Model 1a | 812.353 | 188 | 15.179 | 14 | 0.366* | 0.933 | 0.000* |
| 5 | Model 1(a): Factor Loadings, Measurement Intercepts | White Non-Hispanic English Speakers/ Hispanic English |
Model 1a | 840.439 | 203 | 28.063 | 15 | 0.021 | 0.932 | 0.001* |
| 6 | Model 1(a): Factor Loadings, Measurement Intercepts, Item Residuals | White Non-Hispanic English Speakers/ Hispanic English Speakers |
Model 1a | 963.121 | 221 | 122.682 | 18 | 0.000 | 0.921 | 0.011 |
| 7 | Model 1(b): Unconstrained | English Speakers/ Spanish Speakers |
-- | 815.061 | 174 | -- | -- | -- | 0.943 | -- |
| 8 | Model 1(b): Factor Loadings | English Speakers/ Spanish Speakers |
Model 1b | 881.596 | 188 | 66.534 | 14 | 0.000 | 0.938 | 0.005* |
| 9 | Model 1(b): Factor Loadings, Measurement Intercepts | English Speakers/ Spanish Speakers |
Model 1b | 963.230 | 203 | 81.634 | 15 | 0.000 | 0.932 | 0.006* |
| 10 | Model 1(b): Factor Loadings, Measurement Intercepts, Item | English Speakers/ Spanish Speakers |
Model 1b | 1089.612 | 221 | 126.382 | 18 | 0.000 | 0.922 | 0.010* |
Meets one of two criteria to establish invariance: AX2>.05 or ACFI<.01.
4.3.4 English speakers vs. Spanish speakers
After finding support for strong invariance in factor structure of the English speakers, the remaining analyses treated these two groups as one to be compared with Spanish speakers’ results. The MGCFA model that constrained factor loadings to be equal between English speakers and Spanish speakers resulted in a reasonable fit to the data, χ2(203)=840.39, p<.01, TLI=.93; CFI= .932, RMSEA=.059 (90% CI= .055–.063). The ΔCFI supported strict factorial invariance, ΔCFI=.01; no significant group differences were found between the groups’ factor loadings, measurement intercepts, and item residuals (See Table 4).
5. Discussion
The findings extend the existing confirmatory factor analysis results of the SIP by providing additional data to inform the assessment and utility of the SIP. Internal consistency of the SIP was high and analogous with previous reports (Kenna et al., 2005; Bender, Griffin, Gallop & Weiss, 2007).
Results from the CFA indicated the first-order five-factor and the second-order five-factor model fit the data similarly to the first-order one factor model. Aside from being more parsimonious, the presence of highly correlated factors and negative variances among the five factor and second order five factor model indicate that one underlying factor may be explaining the majority of the systematic variance (Byrne, 2001). Therefore, the first-order one-factor solution was determined to be the preferred factor structure for the SIP, a finding consistent with most prior exploratory and confirmatory factor analyses on the SIP and its variations (Kenna et al., 2003; Alterman et al., 2006; Bender et al., 2007; Blanchard et al., 2003; Tonigan & Miller, 2002).
While not the focus of this study, it is worth noting that the factor loadings on item 15 of the SIP were low across all three groups. These factor loadings suggest the measure could potentially be shortened; however, removal of this item would require additional replication across populations, other settings, and treatment-seeking patients before such a recommendation is definitively made.
This MGCFA study extends the current psychometric property information for the SIP by providing evidence of SIP scores’ measurement invariance across language and ethnicity. Given the scores measure the latent variable (alcohol consequences) similarly across language and ethnicities (Stewart & Napoles-Springer, 2003), the SIP may be a useful tool in evaluating intervention effectiveness and alcohol consequences among Hispanic minority groups. Results of the MGCFA analyses indicate the presence of strict factorial invariance (or residual invariance) across English and Spanish speakers. The invariance of the factor loadings allows for meaningful comparisons based on the observed or manifest variables, the testing for group differences in the latent variables across groups, and the attribution of group differences in the relationship of manifest variables to differences across groups in common factor means and dispersion matrices.
Overall, findings from this study support the utilization of the SIP across both Non-Hispanic and Hispanic English and Spanish speaking individuals. One limitation to this study is that only White and Hispanic populations were examined. Future studies should explore the use of this measure across additional ethnic populations including Blacks and Asians. A second limitation to the study is that all participants were injured, non-treatment seeking individuals recruited in a trauma center. It is unclear whether this measure will hold up across a more generalized population or treatment seeking populations outside a medical setting. Thirdly, the Hispanic population in this study comprised predominately of Mexican American males. Future research should include a more diverse Hispanic population and include a larger percentage of women. Regardless, the current research strongly supports the use of the SIP when evaluating the effectiveness of alcohol treatment in Hispanics and Spanish speaking Hispanics. To further encourage the investigation of health disparities, similar studies should be conducted with other commonly used measures in alcohol outcomes research.
Highlights.
We assess the utility of the SIP across language and ethnicity in a trauma setting
We investigate the preferred factor structure of the SIP
We examine the measurement structure of this SIP among Hispanics
Data supports the first-order one-factor SIP model as the preferred factor structure
Findings support the use of the SIP across ethnicity and language
Acknowledgments
Role of Funding Sources
Funding of this study was provided to the University of Texas School of Public Health by the National Institute on Alcohol Abuse and Alcoholism (NIAAA) Grant RO1-AA013642 (PI: Raul Caetano). The NIAAA had no role in the study design, collection, analysis or interpretation of the data, writing the manuscript, or the decision to submit the paper for publication.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributors
All authors contributed to and have approved the final manuscript. Field and Caetano designed the study, wrote the protocol, and secured the funding to collect the data. Marra conducted literature searches and created the first draft of the manuscript. Marra conducted the statistical analysis, consulting with Field and Von Sternberg.
Conflict of Interest
All authors ensure that they have no conflicts of interest.
Contributor Information
L.B. Marra, Email: laura.marra@austin.utexas.edu.
C.A. Field, Email: craig.field@austin.utexas.edu.
R. Caetano, Email: raul.caetano@uth.tmc.edu.
K. von Sternberg, Email: vonsternberg@mail.utexas.edu.
References
- Alterman AI, Cacciola JS, Ivey MA, Habling B, Lynch KG. Reliability and validity of the alcohol short index of problems and a newly constructed drug short index of problems. Journal of Studies on Alcohol and Drugs. 2009;70:304–307. doi: 10.15288/jsad.2009.70.304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atkinson DR, Bui U, Mori S. Multicultural sensitive empirically supported treatments-An oxymoron? In: Ponterotto J, Casas JM, Suzuki LA, Alexander CM, editors. Handbook of multicultural counseling. Thousand Oaks, CA: Sage; 2001. pp. 542–574. [Google Scholar]
- Bender BA, Griffin ML, Gallop RJ, Weiss RD. Assessing negative consequences in patients with substance use and bipolar disorder: Psychometric properties of the short inventor of problems (SIP) The American Journal of Addictions. 2007;16:503–509. doi: 10.1080/10550490701641058. [DOI] [PubMed] [Google Scholar]
- Bentler PM, Chou CP. Practical issues in structural modeling. Sociological Methods & Research. 1987;16:78–117. [Google Scholar]
- Bentler PM. Comparative fit indexes in structural models. Psychological Bulletin. 1990;107:238–246. doi: 10.1037/0033-2909.107.2.238. [DOI] [PubMed] [Google Scholar]
- Bentler PM. EQS: Structural equations program manual. Encino, CA: Multivariate Software; 1995. [Google Scholar]
- Bernal G, Scharro-del-Rio MR. Are empirically supported treatments valid for ethnic minorities? Towards an alternative approach for treatment research. Cultural Diversity & Ethnic Minority Psychology. 2001;7:328–342. doi: 10.1037/1099-9809.7.4.328. [DOI] [PubMed] [Google Scholar]
- Blanchard KA, Morgenstern J, Morgan TJ, Labouvies EW, Bux DA. Assessing consequences of substance use: Psychometric properties of the inventory of drug use consequences. Psychology of Addictive Behaviors. 2003;17:328–331. doi: 10.1037/0893-164X.17.4.328. [DOI] [PubMed] [Google Scholar]
- Byrne BM, Shavelson RJ, Muthén B. Testing for the equivalence of factor covariance and mean structures: The issue of partial measurement invariance. Psychological Bulletin. 1989;105:456–466. [Google Scholar]
- Byrne BM. Structural equation modeling: Basic concepts, applications, and programming. Mahwah, NJ: Lawrence Erlbaum Associates, Inc.; 2001. [Google Scholar]
- Caetano R, Clark CL. Trends in alcohol related problems among whites, blacks, and Hispanics: 1984–1995. Alcoholism: Clinical and Experimental Research. 1998;22:534–538. [PubMed] [Google Scholar]
- Centers for Disease Control and Prevention (CDC) Injury prevention & control: Injury response. 2011 Retrieved November 4, 2011 from http://www.cdc.gov/injuryresponse/alcohol-screening/index.html.
- Cheung GW, Rensvold RB. Evaluating goodness-of-fit indexes for testing measurement invariance. Structural Equation Modeling. 2002;9:233–255. [Google Scholar]
- Drasgow F. Scrutinizing psychological tests: Measurement equivalence and equivalent relations with external variables are the central issues. Psychological Bulletin. 1984;95:134–135. [Google Scholar]
- Ennis SR, Ríos-Vargas M, Albert NG. The Hispanic population: 2010. (U.S. Census Bureau No. C2010BR-04) 2011 Retrieved November 4, 2011 from http://www.census.gov/prod/cen2010/briefs/c2010br-04.pdf.
- Field CA, Caetano R, Harris TR, Frankowski R, Roudsari B. Ethnic differences in drinking outcomes following a brief intervention in the trauma care setting. Addiction. 2009;105:62–73. doi: 10.1111/j.1360-0443.2009.02737.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feinn R, Tennen H, Kranzler HR. Psychometric properties of the short index of problems as a measure of recent alcohol-related problems. Alcoholism: Clinical and Experimental Research. 2003;27:1436–1441. doi: 10.1097/01.ALC.0000087582.44674.AF. [DOI] [PubMed] [Google Scholar]
- Forcehimes AA, Tonigan S, Miller WR, Kenna GA, Baer JS. Psychometrics of the drinker inventory of consequences (DrInC) Addictive Behaviors. 2007;32:1699–1704. doi: 10.1016/j.addbeh.2006.11.009. [DOI] [PubMed] [Google Scholar]
- Galvan FH, Caetano R. Alcohol use and related problems using ethnic minorities in the United States. Alcohol Research and Health. 2003;27:87–94. [PMC free article] [PubMed] [Google Scholar]
- Hu L, Bentler PM. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling. 1999;6:1–55. [Google Scholar]
- Kenna GA, Longabaugh R, Gogineni A, Woolard RH, Nirenberg TD, Becker B, Minugh PA, Caarty K, Clifford PR, Karolczuk K. Can the short index of problems (SIP) be improved? Validity and reliability of the three-month SIP in an emergency department sample. Journal of Studies on Alcohol. 2005;66:433–437. doi: 10.15288/jsa.2005.66.433. [DOI] [PubMed] [Google Scholar]
- Longabaugh R, Woolard RF, Nirenberg TD, Minugh AP, Becker B, Clifford PR, et al. Evaluating the effects of a brief motivational intervention for injured drinkers in the emergency department. Journal of Studies on Alcohol. 2001;62:806–816. doi: 10.15288/jsa.2001.62.806. [DOI] [PubMed] [Google Scholar]
- Meredith W, Teresi JA. An essay on measurement and factorial invariance. Medical Care. 2006;44:569–577. doi: 10.1097/01.mlr.0000245438.73837.89. [DOI] [PubMed] [Google Scholar]
- Miller WR, Tonigan JS, Longabaugh R. The drinker inventory of consequences (DrInC): An instrument for assessing adverse consequences of alcohol abuse. (Project MATCH Monograph Series) (Vol. 4) (NIH Publication No. 95-3911) Rockville, MD: National Institute on Alcohol Abuse and Alcoholism; 1995. [Google Scholar]
- Mulia N, Ye Y, Greenfield TK, Zemore SE. Disparities in alcohol-related problems among white, black, and hispanic americans. Alcoholism: Clinical and Experimental Research. 2009;33:654–662. doi: 10.1111/j.1530-0277.2008.00880.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soderstrom CA, DiClemente CC, Dischinger PC, Hebel R, McDuff DR, Auman KM, Kufera JA. A controlled trial of brief intervention versus brief advice for atrisk drinking trauma center patients. Journal of Trauma, Injury, Infection, and Critical Care. 2007;62:1102–1112. doi: 10.1097/TA.0b013e31804bdb26. [DOI] [PubMed] [Google Scholar]
- Steiger JH, Lind JC. Statistically based tests for the number of factors; Presented at the annual spring meeting of the Psychometric Society; Iowa City, IA. 1980. [Google Scholar]
- Stewart AL, Napoles-Springer AM. Advancing health disparities research: Can we afford to ignore measurement issues? Medical Care. 2003;41:1207–1220. doi: 10.1097/01.MLR.0000093420.27745.48. [DOI] [PubMed] [Google Scholar]
- Stinson F, Grant B, Dufour M. The critical dimension of ethnicity in liver cirrhosis mortality statistics. Alcoholism: Clinical and Experimental Research. 2001;25:1181–1187. [PubMed] [Google Scholar]
- Tonigan JS, Miller WR. The Inventory of Drug Use Consequences (InDUC): Test-retest stability and sensitivity to detect change. Psychology of Addictive Behaviors. 2002;16:165–168. [PubMed] [Google Scholar]
- Tucker LR, Lewis C. A reliability coefficient for maximum likelihood factor analysis. Psychometrica. 1973;38:1–10. [Google Scholar]
- Walters ST, Bennett ME, Miller JE. Reducing alcohol use in college students: A controlled trial of two brief interventions. Journal of Drug Education. 2000;30:361–372. doi: 10.2190/JHML-0JPD-YE7L-14CT. [DOI] [PubMed] [Google Scholar]
- Worthington RL, Whittaker TA. Scale development research: A content analysis and recommendations for best practices. The Counseling Psychologist. 2006;34:806–838. [Google Scholar]