Pointing with the ankle: the speed-accuracy trade-off

Abstract

This study investigated the trade-off between speed and accuracy in pointing movements with the ankle during goal-directed movements in dorsal–plantar (DP) and inversion–eversion (IE). Nine subjects completed a series of discrete pointing movements with the ankle between spatial targets of varying difficulty. Six different target sets were presented, with a range of task difficulty between 2.2 and 3.8 bits of information. Our results demonstrated that for visually evoked, visually guided discrete DP and IE ankle pointing movements, performance can be described by a linear function, as predicted by Fitts’ law. These results support our ongoing effort to develop an adaptive algorithm employing the speed-accuracy trade-off concept to control our pediatric anklebot while delivering therapy for children with cerebral palsy.

Introduction

Fitts’ law has been widely used for more than half a century to quantify the human motor system (Fitts 1954; Fitts and Peterson 1964). Fitts’ law models the speed-accuracy tradeoff in untrained movements by establishing the existence of a linear relationship between (a) the time, MT, required to complete a discrete movement over different distances, D, to targets of different size, W, and (b) the difficulty of the task, measured by the index of difficulty, ID, in bits as a logarithmic ratio of D to W. Traditionally, Fitts’ law is formulated as follows:

$$\text{MT}=a+b(\text{ID}),\text{where}\text{ID}={log}_2\left(\frac{2D}{W}\right),$$

where a and b are empirical constants that depend on the conditions under which movement is made. The intercept, a, can be thought of as an indicator of the reaction time and the slope, b, as the sensitivity of the motor system to a change in difficulty of the task. Although Fitts’ law was originally used to describe human forearm movement, numerous studies have established that it is a reliable predictor of MT in psychomotor studies involving a variety of limb and muscle groups, including the upper limbs (Leisman 1989; Bootsma et al. 1994), head (Jagacinski and Monk 1985), and trunk (Kim et al. 1996) movements in children, adults (Kerr 1975; Hay 1981), and the elderly (Temprado et al. 2013).

Not only Fitts’ law, per se, but also its disturbances in upper limb movements have been extensively studied in neurodegenerative and neurodevelopmental disorders. Slowly moving Parkinson’s disease patients have a reduced capability to initiate and regulate force (Weiss et al. 1996) perhaps because of a weakened implicit “motor motivation” signal sent from the substantia nigra to the striatum (Mazzoni et al. 2007). Children with developmental coordination disorder are found to have an impaired ability to process efferent copy signals, and their movements do not conform to Fitts’ law (Maruff et al. 1999; Wilson et al. 2001). In childhood dystonia, reaching movements are significantly slower regardless of the target size, and movement speed is more sensitive to changes in target size when compared to movements executed by unimpaired subjects (Sanger et al. 2005). A few studies have given us ambiguous results in cerebral palsy (CP). Despite obvious limitations in fine motor control, children with congenital spastic hemiplegia—which is a common symptom in CP—are found to obey Fitts’ law (Smits-Engelsman et al. 2007), whereas data analyses from two other studies in adults with CP yielded no significant adherence to the speed-accuracy trade-off (Bravo et al. 1993; Gump et al. 2002).

Despite the ambiguous results with arm movements in CP, the robustness of Fitts’ law in a wide range of neural disorders led us to place the speed-accuracy trade-off at the core of our adaptive assist-as-needed robotic therapy delivered to both upper and the lower limbs of CP children (Krebs et al. 2003, 2011). Twenty years after the early studies for neurorehabilitation with the MIT-Manus (Krebs et al. 1998), we are focusing our research on what constitutes an ideal therapy intervention and on how to tailor therapy to a particular patient’s needs (Krebs and Hogan 2012), including children with CP (Fasoli et al. 2012). We had introduced and tested extensively the concept of adaptive assist-as-needed controller for upper extremities (Krebs et al. 2003). We are now extending the concept of performance-based progressive robotic therapy to meet the needs and special characteristics of the lower extremities in children with CP (Michmizos and Krebs 2012a). Briefly, our algorithm identifies the ability of the youngster to move and point with the ankle in visually guided, visually evoked games (Michmizos and Krebs 2012b) and then independently adjusts the speed of the gameplay and the size of the target (Michmizos and Krebs 2012a). To our knowledge, no study has examined the ankle’s sensorimotor control in terms of obeying (or not) Fitts’ law. Establishing a speed-accuracy trade-off in human ankle movement could be coupled with the metrics anticipated to quantify separately the ability to move fast and accurately. This would allow us to (a) assess the level of motor-related impairment in CP and (b) provide targeted therapy driven by one’s inability to move fast or accurately. Here, we describe the experimental protocol employing our adult anklebot (Roy et al. 2009) to test the presence of the speed-accuracy trade-off in ankle movements of healthy young adults.

Ankle joints and muscles

Although widely viewed as a single joint, the ankle actually consists of a series of joints highly integrated with each other. The most important joints are the talocrural joint (upper ankle joint), the subtalar joint (lower ankle joint), and the inferior tibiofibular joint (Moore et al. 2010). The boney architecture of the ankle consists of three bones, namely the ankle bone (talus), the lower leg bone (tibia), and the calf bone (fibula). The upper ankle joint is a synovial hinge joint that connects the distal ends of the tibia and the fibula with the proximal end of the talus. This joint articulates along a single axis (monoaxial) and permits two movements that raise or lower the foot: (a) plantar flexion, in which the ankle and the foot are moved away from the tibia and (b) dorsal flexion in which the top of the ankle and foot are moved toward the anterior tibia bone. Dorsal flexion is a more limited movement (typical maximum range 18°) than plantar flexion (typical maximum range 48°) (Boone and Azen 1979). The lower ankle joint is the articulation located between the talus and the heel bone (calcaneus). It permits (a) eversion, the turning of the ankle and foot outward, i.e., away from the midline, and (b) inversion, the turning of the ankle and foot inward, i.e., toward the midline. Eversion of the foot is more limited movement (typical range 18°) compared to the inversion of the foot (typical range 33°) (Boone and Azen 1979).

Several strong muscles are attached to the ankle. These muscles allow ankle movements, including pointing, flexing, and circling the foot. There are 11 ankle and foot muscles that produce more than one ankle movement (Table 1). In this paper, we test whether the two main ankle joint movements obey Fitts’ law. The experimental results build support for using the speed-accuracy tradeoff as a key element in lower limb robotic adaptive therapy to help CP children grow and develop to their maximum capabilities.

Table 1.

Ankle and foot muscles acting on ankle movements in sagittal and coronal planes

Muscle	Plantar flexion	Dorsal flexion	Eversion	Inversion
Gastrocnemius—(TA)	+
Soleus—(TA)	+
Tibialis posterior—(TA)	+			+
Flexor digitorum longus—(EDL)	+			+
Flexor hallucis longus—(EHL)	+			+
Peroneus longus—(TA)	+		+
Peroneus brevis	+		+
Tibialis anterior—(Gastro, Sol, PL, TP)		+		+
Extensor digitorum longus—(FDL, PB)		+	(Weak)
Extensor hallucis longus—(FHL, PB)		+		(Weak)
Peroneus tertius		(Weak)	+

Muscles are ordered with respect to typical volumes, from largest to smallest. Acronyms inside the parentheses denote the most common antagonists. Weak contribution to a movement is noted

Methods

Subjects

Nine unimpaired human subjects (7 male, 2 female) were recruited for this study. Average biometric data were 28 ± 5 years of age, 1.75 ± 0.07 m in height, and 70 ± 10 kg in mass (mean ± SD). All subjects had normal or corrected-to-normal vision and were right-foot dominant according to their preferential use of the foot during daily activities such as kicking a ball. Subjects had no reported history of traumas or neuropathies to the lower limbs. All subjects were naive to the task upon enrollment and gave written informed consent according to the procedure approved by the Massachusetts Institute of Technology Committee on the Use of Humans as Experimental Subjects.

Experimental apparatus

The speed-accuracy trade-off was measured for dorsal–plantar (DP) and inversion–eversion (IE) ankle pointing movements using a highly back-drivable wearable robot, Anklebot (Interactive Motion Technologies, Watertown, MA). It allows the maximum range of motion required for the typical gait of healthy or pathological subjects (Perry 1992). Subjects wore a modified shoe and a knee brace, to which the robot was connected. Subjects were seated, and the knee brace was securely fastened to the chair to fully support the weight of the robot and to ensure that measurements were made in a repeatable posture (Fig. 1). The chair was placed 1.5 m away from a 60-inch 1080p (Full HD) 120 Hz 1,024 × 768 Liquid Crystal TV (Sharp LC60L, Sharp Electronics Corporation) that was positioned at eye level. For this study, the robot acted as a passive device and recorded simultaneously the DP and IE positions. Ankle position kinematics, with respect to the zero angle (neutral position, defined below), were recorded at 200 Hz sampling frequency (Roy et al. 2009) and were converted to screen pixels for visualization purposes.

Fig. 1.

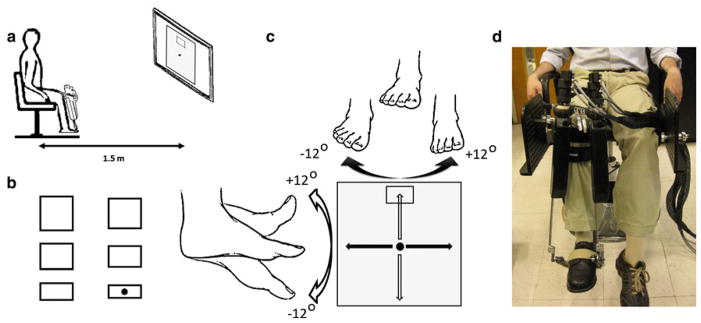
a Schematic showing experimental setup with the subject wearing the anklebot in a seated position, facing a 60-inch monitor; b representation of 6 different target sizes presented randomly to the subjects relative to the circular cursor (black dot); c a schematic showing control of the cursor (black dot in the middle of the screen) using the ankle in two directions as well as range of motion; d subject wearing anklebot in a seated condition. Right leg is in the anatomically neutral position. The weight of the anklebot is supported by the chair through the screw bolt

Experimental protocol

Subjects were instructed to control with their ankle a circular cursor moving vertically (for DP motion) or horizontally (for IE motion). Participants were asked to move a cursor between two defined targets “as fast and accurately as possible” by dorsi-/plantar flexing or inverting/everting their ankle. They were getting an online visual feedback of their performance by a cursor moving toward the onscreen target. The same IDs (movement amplitudes and target widths) and the same feedback display were used in the DP and IE experiments. Due to the visual feedback being exactly equal for both experiments, we ensured the same feedback resolution across both joint movements.

The experiment was divided into two independent orthogonal dimension tasks where the targets and the cursor were constrained to horizontal or vertical movements. Subjects were first asked to place the moving dot at the center of the screen that was equivalent to positioning their ankle in the neutral position, defined as the sole being at a right angle to the tibia. Next, a rectangular target was shown up (right) or down (left), for the DP (IE) experiment, and subjects made an outbound movement, i.e., they moved their ankle away from the neutral position. Outbound targets were presented in a random order, so that the subject could not anticipate movements. The maximum ankle angle with respect to the neutral position, for any movement, was 0.2 rads (12°). For the movement to be considered as discrete, the moving dot had to land inside the rectangular target (i.e., not touching any of its borders) and its instantaneous speed had to be lower than 0.001 rad/s. When both criteria were met, the outbound target disappeared, and after a dwell time randomly ranging between 800 and 1,200 ms, a new target appeared. The completion of an outbound movement was followed by an inbound target, i.e., a target centered around the central position for which the subject had to move his/her ankle near to its neutral position. Each experimental session consisted of 180 movements; the diameter of the moving dot was 0.015 rads (23 pixels), and the target width, in the direction of the movement, was randomly selected between 0.03 rads (45 pixels) and 0.08 rads (120 pixels), with a step increment of 0.01 rad (15 pixels). For each of the 6 different target widths, 30 targets (15 inbound and 15 outbound) were presented in a random order. Random presentation of differently sized targets and short overall duration of the experiment (<3.5 min) ensured that no fatigue could happen during a session. Each subject participated in one DP and one IE session.

Kinematic analysis

Although various approaches have been followed to measure MT in Fitts’ tasks (e.g., Smits-Engelsman et al. 2002), most of the recent experiments on Fitts’ law track the velocity trace (Buchanan et al. 2003, 2006). We measured MT backward from the point of peak velocity until movement velocity fell below 5 % of the maximum of peak speed; movement termination was measured forward from peak speed using the same threshold. MT was then defined as the temporal difference between the start, t_start, and end, t_end, of the movement. Movement amplitude, D, was estimated as the actual distance on the direction of the movement at times t_start and t_end. For the purpose of the present work, only outbound movements were analyzed.

Outbound movements that did not conform to the definition of success were excluded from the analysis. For each subject, we excluded movements with MTs that were very short in duration (<200 ms) and distance (<0.05 rads); these movements were produced by the subjects in anticipation of the target. We also excluded movements with MTs very long in duration (>3.5 s); these movements were usually influenced by circumstances exogenous to the experimental factors, such as loss of attention. We also removed non-discrete movements, i.e., those in which the ankle velocity at the onset of the target was larger than 0.001 rad/s. We finally removed any DP (IE) movement during which the maximum IE (DP) angle exceeded 0.1 rad (6°) that ensured both ankle joints operating inside their normal range.

Statistical analysis

For each of the 4 outbound directions, we estimated the MT, the peak speed, V_peak, the mean speed, V_avg, and the D. We grouped MTs against IDs for each movement separately—dorsiflexion, plantar flexion, inversion, and eversion. There were enough data points for each ID ( $\text{ID}(\overline{n_{\text{ID}}}=107>30\text{samples})$ to estimate the mean MT for each ID,μ_MT,ID, and its 95 % confidence interval as $2\times \sigma /\sqrt{n_{\text{ID}}}$, n_ID being the number of data observations per ID, and σ their standard deviation. The average predicted MT was then estimated from the regression analysis. For the average experimental results, we fit two models, a linear and a quadratic model, using the linear least-square regression method. To compensate for the different number of parameters of those models, we estimated the adjusted R² value, which is defined as follows:

$$R_{\text{adj}}^2=1-\left(\frac{{SS}_{\text{resid}}}{{SS}_{\text{total}}}\right)\times \left(\frac{n-1}{n-d-1}\right),$$

where SS_resid is the residual sum of squares, SS_total is the total sum of squares of the data observations, n is the number of data observations, and d is the degree of the polynomial. Same analysis was done for V_avg as well as inbound movements; results for the latter are not shown here and will not be addressed in this paper.

The mean MTs and V_avg, as predicted from the regression analysis, were fed into repeated-measures analysis of variance (ANOVA) as the dependent variables. To explore significant effects, we used post hoc pairwise comparisons with Bonferroni correction to compensate for multiple comparisons. To compare the mean MT and V_avg over IDs for the same movement and between movements, a 1-way unbalanced ANOVA and a Student’s t test were used, respectively. A significance level of p < 0.05 was used for the t test and $p<\frac{0.05}{6}=0.008\overline{3}$ for the ANOVA.

Results

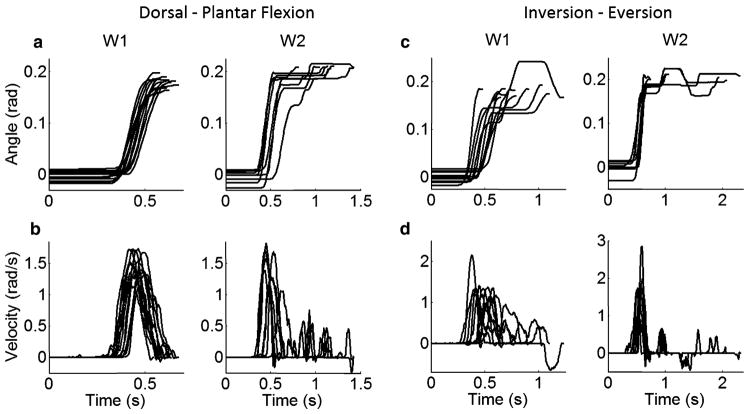
All subjects performed the task successfully. Figure 2 shows the kinematic profile of the cursor movement in DP directions by a representative subject (Subject 4) in conditions {W1; target width equal to 0.08 rads} and {W2; target width equal to 0.03 rads}. For the lower IDs, kinematic profiles were consistent across subjects. For the higher IDs (ID > 3.5), velocity fluctuations, indicative of corrective submovements, were present near the end of some of the movements. Most of these fluctuations were very short in duration, and since they are not of primary interest in this paper, we will not fully address them here. Corrective movements were present consistently across subjects in IE movements not only in higher but also in lower IDs (Fig. 2c, d). On average, the subjects slightly overshot the target in plantar flexion and undershot the target in dorsiflexion, whereas no clear trend was identified in the inversion/eversion movements (Fig. 3). The ID, averaged across subjects, increased from 2.17 to 3.77. For DP (IE) movements, the mean ID ± the coefficient of variation was 2.17 ± 0.02 (0.04), 2.40 ± 0.01 (0.03), 2.66 ± 0.02 (0.02), 2.96 ± 0.01 (0.03), 3.32 ± 0.02 (0.03), and 3.77 ± 0.01 (0.02), for the six different target widths, respectively.

Fig. 2.

The time profiles of (a, c) ankle movement position (angle) with respect to neutral position, and (b, d) its velocity profile for widths W1 = 0.08 rads (ID = 2.3) and W2 = 0.03 rads (ID = 3.8) is presented for the series of trials performed within each of the two conditions by a representative subject for DP (a, b) and IE (c, d) movements (Subject 4). The trials were aligned by the onset of the visual target (t = 0). Please note forms of corrective actions that are consistent with secondary adjustive movements (Fig. 2, Brown and Slater-Hammel 1949)

Fig. 3.

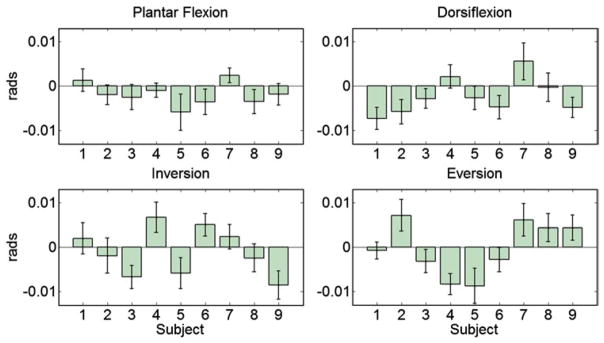
Average accuracy estimated by the difference in rads between the final position of the cursor minus the center of the target, across all outbound discrete movements, per subject. Error bars correspond to 95 % uncertainty

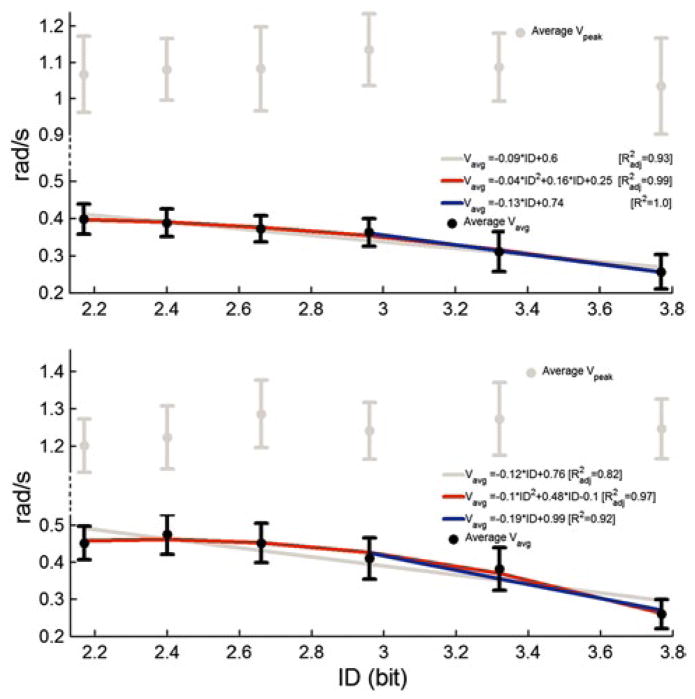
The relationship between ID and MT for 1D horizontal and vertical cursor movements is shown in Figs. 4 and 5, respectively. Regression models averaged across subjects for each 1D direction are shown in each graph. For dorsiflexion (plantar flexion) movement, a quadratic model, with $R_{\text{adj}}^2=0.98(0.98)$, fit the data better than a linear one $R_{\text{adj}}^2=0.88(0.87)$. Hence, for DP outbound movements with ID < 2.96, ID had no significant effect on MT. With ID = 2.96, ID had a significant effect on MT. A line fitted to the dorsiflexion (plantar flexion) data points with ID = 2.96 resulted in R² = 0.99 (0.94). No statistical differences were found between the slopes of those regression lines (p < 0.05). For both IE outbound movements, the linear model fit the data better than the quadratic model ( $\mathrm{\Delta }{R}_{\text{adj}}^2>0.1$ for both directions). Hence, the data for each direction were fitted with Fitts’ law equation for the entire ID range (R² = 0.97 and 0.96 for inversion and eversion, respectively).

Fig. 4.

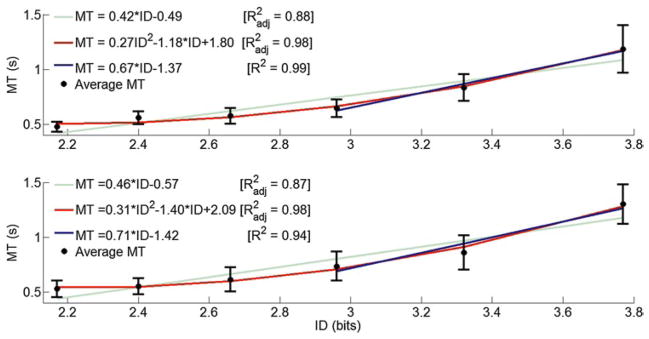
Movement time as dependent of Fitts’ index of difficulty, averaged across subjects for dorsiflexion (up) and plantar flexion (bottom) ankle movements. Error bars correspond to 95 % precision uncertainty values

Fig. 5.

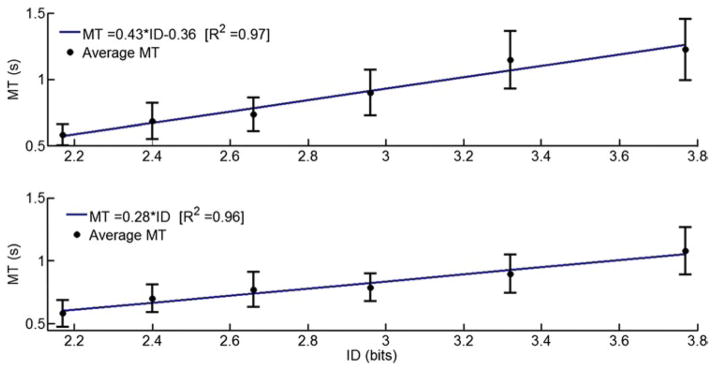
Movement time as dependent of Fitts’ index of difficulty, averaged across subjects for inversion (up) and eversion (bottom) ankle movements. Error bars correspond to 95 % precision uncertainty values

For DP movements, the pairwise comparisons revealed that the different IDs resulted in significantly different MT values (p < 0.05) between ID = 2.17 and ID = 2.96, 3.32, 3.77; ID = 2.4 and ID = 3.32, 3.77; ID = 2.66 and 3.32, 3.77; ID = 2.96 and 3.32 (only for dorsiflexion), 3.77; and ID = 3.32 and 3.77. For IE movements, the different IDs resulted in significantly different MT values (p < 0.05) between ID = 2.17 and ID = {3.32, 3.77}; ID = 2.4 and ID = {3.32, 3.77}; ID = 2.66 and ID = {3.32, 3.77}; ID = 2.96 and ID = {3.32 (only for eversion), 3.77}. We did not find any significant difference in MTs between dorsiflexion (inversion) and plantar flexion (eversion) for the same ID (p < 0.05). Yet, in cross-movement comparisons, MTs were statistically different between dorsiflexion and inversion (eversion) for ID = {2.4, 2.66, 2.96} (ID = {2.17, 2.66, 2.96, 3.32}) and between plantar flexion and eversion (inversion) for ID = 3.32 (ID = 2.4).

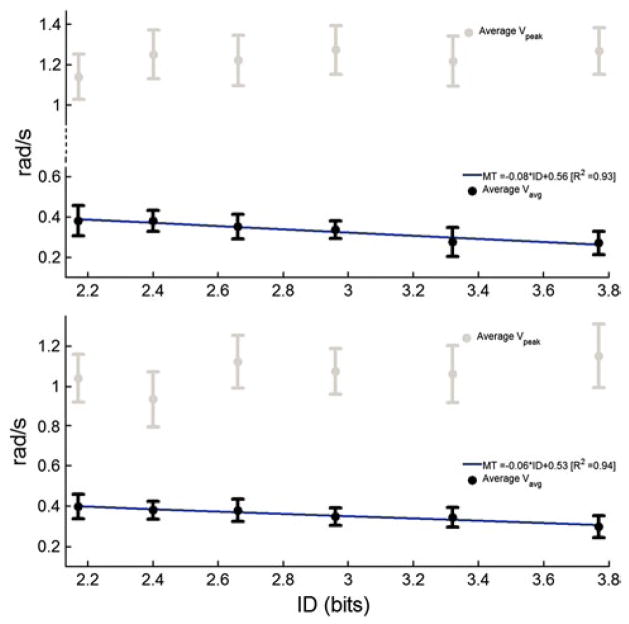
The same statistical analysis was conducted on the regression curves of the average speed profiles for DP and IE movements. We examined the peak speed, V_peak, and the mean speed, V_avg, or DP movements (Fig. 6) and IE movements (Fig. 7). Peak speeds were found neither to be significantly different nor to follow a straight-line trajectory (R² < 0.35) in the ID range (p < 0.05) for all 4 movements. However, V_avg followed a line with a negative slope as the ID increased (R² > 0.94 for all 4 movements) indicating a decrease in the average speed. The V_avg decrease was significantly different in dorsiflexion for ID = {2.17, 2.4, 2.66, 2.96} and ID = 3.77 and in plantar flexion for ID = {2.17, 2.4, 2.66, 2.96, 3.32} and ID = 3.77. Comparing same joint movements, we found that V_avg was significantly different between plantar flexion and dorsiflexion only for IDs = {2.4, 2.66} and between eversion and inversion only for ID = {2.4, 3.77}. In cross-movement comparisons, V_avg was statistically different between plantar flexion and eversion (inversion) for ID = {2.4, 2.66, 2.96, 3.32} (ID = 2.4).

Fig. 6.

Peak velocity (V_peak) and mean velocity (V_avg) as dependent of Fitts’ index of difficulty, averaged across subjects for dorsiflexion (up) and plantar flexion (bottom) ankle movements. Error bars correspond to 95 % precision uncertainty values

Fig. 7.

Peak velocity (V_peak) and mean velocity (V_avg) as dependent of Fitts’ index of difficulty, averaged across subjects for inversion (up) and eversion (bottom) ankle movements. Error bars correspond to 95 % precision uncertainty values

Discussion

In terms of the present work, we were interested primarily in the MT–ID relationship in the upper and lower ankle joints but also whether there were indications that the control processes changed between the two joints. As expected from Fitts’ law, average MT was highly correlated with the task difficulty for each 1D movement direction in both IE and DP movements. In addition, although V_peak remained virtually unchanged in the ID range, V_avg decreased linearly with the increase in accuracy demand. Differences in average MTs and V_avg were not found to be significant between movements of the same joint in the tested ID range; however, significant differences in MTs were found between DP and IE movements. As the visual gain was the same for DP and IE experiments, the findings may serve as an indication of a difference in control capability between upper and lower ankle joints.

The visual gain, although kept constant across the experiments, may still have influenced the speed-accuracy performance. Manipulation of the visual gain might account for breaking the linearity typically found in Fitts’ tasks both at high IDs (ID > 4.5) (Fernandez and Bootsma 2008; Kovacs et al. 2008) and low IDs (ID < 3) (Gan and Hoffmann 1988). In Fig. 4, the average MT for DP movements deviated from a straight line at low IDs (ID < 2.96). In these movements, subjects seemed to ignore the constraint of the endpoint accuracy. This is further supported by the clear tendency that subjects showed to either overshoot or undershoot the targets (Fig. 2), especially in low ID tasks, hence not using the entire range of the target width but only an “effective” portion of it (Schmidt et al. 1979). To speculate further, DP movements in low ID were no longer visually controlled but rather ballistic in nature, and their MT was not a function of the ID (i.e., the target width did not affect MT) but of the amplitude of the movement, as described by the ballistic equation (Hoffmann 1981; Gan and Hoffmann 1988; Lin and Drury 2011). In fact, Gan and Hoffmann have determined that the critical ID value beyond which discrete arm movements are considered to be under visual control is at less than about 3 bits (Gan and Hoffmann 1988), which is consistent with our result (ID = 2.96) for the DP movement of the ankle. For large ID values, it was necessary for the subjects to use visual control to successfully place the cursor within the target that established the linearity between MT and higher IDs (Figs. 4, 6). Interestingly, for IE movements, linearity was not violated in terms of the best-fit model over the tested ID range. Two possible explanations include (a) a wider uncertainty range for the average MT values that might have hidden their saturation at around 0.5 s, and (b) submovements were present even in small ID tasks for the IE direction (Fig. 2c) that resulted in the significant increase in MT. We speculate on whether larger muscle volumes (see Table 1) might have offered a better control in low IDs for the upper ankle joint, compared to the lower ankle joint.

Not only MT but also the whole kinematic pattern changed with ID. The existence of submovements following an initial ballistic movement was revealed by the analysis of the kinematic data for large ID target acquisitions in both DP and IE directions. A single, smooth submovement covered most of the total displacement and was usually followed by subsequently smaller and slower ankle movements that corrected with any undershoot or overshoot of the initial movement (Fig. 2, W2). This was reflected in the regression analysis of the velocity profiles (Figs. 6, 7): Changing the ID did not affect the average amplitude of the initial, open-loop, ballistic impulse movement as measured by V_peak; on the other hand, V_avg decreased with the ID as the result of the presence of corrective, visually controlled, slower submovements. Submovements, such as the ones we report here, might be of diagnostic importance as they have been recently used to quantify performance gains in a large movement study with autistic kids (Torres et al. 2013). Our findings are supported by Woodworth’s venerable model that entails both a central and a (feedback-based) current-control component (Woodworth 1899, p. 41) as well as models able to approximate Fitts’ law at a high level, such as the stochastic optimized-submovement model (Meyer et al. 1988), and several other empirical and theoretical studies (Crossman and Goodeve 1983; Novak et al. 2000; Elliott et al. 2001). However, Fitts’ law has been shown to hold in tasks where no visual feedback of the target and the moving limb was available; this excludes visual corrective mechanisms (Wu et al. 2010).

Whether Fitts’ law emerges at the level of motor planning or at that of movement correction is an ongoing research question. As we have removed the reaction time, it seems reasonable to state that the scaling of MT with ID yields a significant contribution at the level of corrections during the movement. However, a interplay of the feed-forward (motor planning) and feedback mechanisms might produce Fitts’ law with the relative importance of the two mechanisms dependent on particular features of the task including the joint mechanics.

The comparison of how different joints perform in Fitts’ tasks has given ambiguous results. In line with Fitts’ original prediction of effector-specific hierarchical systems (Fitts 1954), a commonly cited study has claimed the processing of finger and wrist movements to be more efficient compared to when done on the arm (Langolf et al. 1976). However, a newer study suggested that the three effectors were similar in terms of processing (in bits/s) and movement time (Balakrishnan and MacKenzie 1997). In the present experiment, we evaluated the performance of two joints that work together, using the same Fitts’ tasks. The findings across the experiments provide strong evidence for performance differences between upper and lower ankle joints. Analysis of the kinematic profiles revealed the presence of submovements in low ID values for IE movements. This resulted in increased MTs for IE movements compared to DP. The differences should be seen from the perspective of the specific movement amplitude (0.2 rads), gain in the visual display, and after removing the reaction time from the measurement of MT (please see Methods). This finding is most probably a function of the increased control capability of the DP movement and the ankle mechanics.

Normalized versions of our kinematic parameters could be informative in motor learning studies and in comparisons across different limbs, groups of subjects, and apparatus. For example, the percentage of MT relative to the total duration of a movement, MT_rel, could be understood as reentrant sensory information in the motor system (Torres and Andersen 2006) and hence used to assess the effects of sensorimotor training. As our experiment was very short in duration, it was no surprise that MT_rel did not change between the first and last 30 movements in both directions and for each subject (p < 0.05). Nevertheless, MT_rel can describe the learning progressions governing the upper and lower ankle limb—and any difference between them. Another common normalization used in analyses of anthropological data is that of dividing V_peak by the sum of V_peak and V_avg for each trial (Torres 2013). This metric could be useful in comparing upper and lower limbs or groups of subjects with intrinsically different movement speeds (such as kids and young adults or healthy and impaired subjects). Other normalized metrics include movement variability, latency before V_peak, and reaction time. Analyzing these metrics goes beyond the scope of this paper and will not be addressed further.

To summarize, the microscopic details of how neural information flow is integrated into discrete, goal-directed movements is an important theoretical question for which the macroscopic answer is Fitts’ law. Previous studies on upper limbs concluded that biomechanical constraints at the level of the effector are independent of informational constraints at the level of the task during upper limb movement (Fernandez and Bootsma 2004). Identifying the fundamental characteristics of the changes in ankle kinematic patterns with task difficulty can provide interesting routes into understanding motor-related neural diseases and harnessing new therapeutic methods for locomotion.

Implications for robotic neurorehabilitation

Much current robotic research on neurorehabilitation focuses on adapting the behavioral intervention to each patient’s special needs and abilities. Notwithstanding our early work toward this goal (Krebs et al. 2003), there are still many milestones to accomplish (Krebs and Hogan 2012). “An underlying, activity-dependent neural plasticity is probably a key mechanism through which robotic therapy produces clinical results” (Hogan et al. 2006). Given the importance of active participation during therapy (Ferraro et al. 2003) and the need for specificity in therapeutic tasks that resemble (if not exploit) motor learning, Fitts’ law shows a great potential to empower new therapeutic protocols that adapt to and challenge patients according to their ability to move their limbs fast and/or accurately.

Rehabilitation games based on the speed-accuracy tradeoff can be used as a tool for rehabilitation while at the same time challenging the individual to do his/her best in movement planning and execution (Michmizos and Krebs 2012a, b). This study demonstrated the appropriateness of Fitts’ law to model ankle pointing movements, thus supporting the idea that Fitts’ law parameters can be incorporated into our present development of adaptive, assist-as-needed therapeutic intervention for the lower limbs. Furthermore, Fitts’ law may serve as an effective tool for comparing motor abilities across subjects, modalities, and rehabilitation tasks. This study also has implications for enhancing understanding of brain plasticity and neurocognitive networks involved in motor planning and control: If there are changes in the kinematic profiles of ankle movements due to robotic sensorimotor therapy, there may be implications for rehabilitation in people with motor disabilities.

It remains a question for further research to determine whether kinematics of movements differ between upper and lower ankle joints in a wider range of IDs and for different movement amplitudes, factors that would need to be ruled out before all differences are definitely attributed to central mechanisms. As robotic therapy continues to expand and address motor impairments of children with CP or stroke (Fasoli et al. 2008; Frascarelli et al. 2009; Krebs et al. 2009), it will be increasingly important to understand and quantify neuroplasticity both at the neural and system level. A robotic controller incorporating concepts derived from a Fitts’ law model could predict the performance of a subject, assess his/her current performance, and continue to adapt to guide neurodevelopment and sustain attention. This would greatly impact the field of neurorehabilitation and make headway toward realizing the goal of providing a customized “assist-as-needed” therapy in humans.

Conclusion

The results from this study demonstrate the adequacy of Fitts’ law to describe four major ankle joint pointing movements and support the use of linear models to predict the ankle performance in DP and IE directions. As we continue to move away from the misperception that the brain is static and hardwired and explore the potential of plasticity as a fundamental property of the human brain, it is necessary to test and confirm basic models such as the speed-accuracy trade-off so that we can properly strengthen existing or create new neural pathways.