Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2015 Jan 1.
Published in final edited form as: Neuroimage. 2013 Sep 8;84:554–561. doi: 10.1016/j.neuroimage.2013.08.066

Alternative Thresholding Methods for FMRI Data Optimized for Surgical Planning

William L Gross a,1, Jeffrey R Binder a
PMCID: PMC3919165  NIHMSID: NIHMS530740  PMID: 24021837

Abstract

Current methods for thresholding functional magnetic resonance imaging (fMRI) maps are based on the well-known hypothesis-test framework, optimal for addressing novel theoretical claims. However, these methods as typically practiced have a strong bias toward protecting the null hypothesis, and thus may not provide an optimal balance between specificity and sensitivity in forming activation maps for surgical planning. Maps based on hypothesis-test thresholds are also highly sensitive to sample size and signal-to-noise ratio, whereas many clinical applications require methods that are robust to these effects. We propose a new thresholding method, optimized for surgical planning, based on normalized amplitude thresholding. We show that this method produces activation maps that are more reproducible and more predictive of postoperative cognitive outcome than maps produced with current standard thresholding methods.

Keywords: Functional MRI, Thresholding, Statistical Testing, Preoperative Mapping

1. Introduction

Despite extensive research exploring potential clinical applications of fMRI, many clinicians remain skeptical of brain mapping as a clinical tool. Clinicians frequently fault current fMRI methods for their perceived variability and questionable accuracy. Although studies using large groups of subjects generally produce consistent results (Frost et al., 1999; Thirion et al., 2007), similar stability is not always obtained in individual subject maps with the variable data quality found under common clinical conditions (Detre, 2006; Machielsen, Rombouts, Barkhof, Scheltens, & Witter, 2000). In applications where reliable results are required for individual subjects under conditions of variable data quality (e.g., presurgical mapping), the measurement variability in current imaging methods may lead to hesitancy in adopting these methods.

The validity of the fMRI signal and its coupling to neural activity (by way of blood oxygen-level dependent, or BOLD, contrast) are now well established (Logothetis & Pfeuffer, 2004). However, many factors can influence the location and magnitude of the underlying neural activity, some of which are difficult to adequately control (e.g., cognitive strategy, level of effort, and noise sources like degree of head motion). Variation in these factors often leads to a high degree of variability observed within and across individual subject maps, even when noise from hardware and vascular systems are held constant. Because fMRI is a relatively new modality and the data produced are complex, analytical techniques to handle these data are still maturing (Logan, Geliazkova, & Rowe, 2008; Turner, Howseman, Rees, Josephs, & Friston, 1998). While some de facto standards of data analysis exist, there is no strong consensus on the most valid and powerful statistical thresholding methods. This ambivalence within the field contributes to a lack of confidence in fMRI results. Here we propose a new method of thresholding data for surgical planning based on statistical theory, combined with a consideration of the specific goals of presurgical functional mapping. We then compare this method with two other approaches, using reproducibility and clinical predictive value as metrics for comparison.

1.1. Current thresholding methods

Current methods of statistical thresholding for functional images are based on a direct analogue from traditional hypothesis-testing, applying a fixed p-value cutoff to each voxel (Friston, Frith, Liddle, & Frackowiak, 1991). Because this test is applied repeatedly to thousands of voxels, it must be adjusted for multiple comparisons using family-wise error correction. Several correction methods exist, each having trade-offs in sensitivity and specificity. The Bonferroni correction, which treats each statistical test as independent, is the most strict and straightforward method (Locascio, Jennings, Moore, & Corkin, 1997). However, threshold values derived from this method are overly conservative for most imaging applications because the information contained in adjacent voxels is not independent (Petersson, Nichols, Poline, & Holmes, 1999). While there are a large number of comparisons performed (proportional to the number of voxels), the actual information content of the image is relatively much smaller.

The most common method currently used in fMRI research combines the traditional p-value threshold with a required minimum number of contiguous voxels (commonly referred to as a “cluster size threshold”). This latter requirement is based on the assumption, borne out by many observations, that functional imaging data are spatially correlated, and true positive activation tends to occur in clusters of contiguous voxels (Forman et al., 1995). Several methods can be used to derive threshold cluster sizes, including Monte Carlo procedures or Gaussian random field theory (Petersson et al., 1999), to produce maps with an acceptable global alpha level.

1.2. Limitations of the hypothesis-testing framework in clinical fMRI

Traditional hypothesis-testing is based on a test statistic, such as the t- or F-value, that depends not only on the size of the effect but also on the variance associated with its measurement (i.e., degree of random noise) and the number of measurements. Consequently, even relatively large effects can fail to reach significance when noise levels are high. Noise in fMRI is the result primarily of head motion and non-neural physiological (cardiac and respiratory) activity. Averaging of data both within and across subjects is used to suppress the effect of these random signals, but the success of this approach is highly dependent on sample size (Voyvodic, Petrella, & Friedman, 2009; Voyvodic, 2006). In the case of research studies involving averaging a group of subjects, there is usually an opportunity to increase statistical power by adding more subjects. In single-subject clinical applications, the stability of activations – particularly the activation border – is critical (Voyvodic, 2006), yet increasing the sample size (i.e., number of images averaged) is limited by many practical factors, such as patient comfort. These differences in application require a different approach when creating maps for presurgical applications.

The hypothesis-testing framework is also problematic for clinical fMRI because of its inherently conservative nature (Daniel, 1998; Shaver, 1993). A test against the null hypothesis tacitly assumes that no effect is present unless there is overwhelming evidence proving that there is. This logic works well for directing progress in basic research, where the null hypothesis is a conservative, safe choice (i.e., not believing anything until it has been thoroughly tested). In the context of surgical planning, however, “null” may not be a safe default. Declaring a region of the brain to be inactive may support the decision of a surgeon to resect it. On the other hand, declaring a region active may lead to the preservation of potentially disease-causing tissue (e.g., cancer or epileptogenic tissue). In this context, bias in either direction is problematic. Rather than a conservative test that assumes a null hypothesis, a direct measure of the response magnitude may be the most useful information in this situation.

Finally, it is important to note a common fallacy of interpretation in hypothesis-testing, i.e., that significance implies importance (Keppel & Zedeck, 1989). Because of the relationship between sample size, variability, and significance levels, even trivially small effects can become extremely “significant”, given a sufficiently large number of samples or sufficiently low variability (Chow, 1988; Daniel, 1998). While such effects are “significant” according to a standard hypothesis-test, they may be so small that they are not practically relevant. To avoid such misinterpretation, statisticians recommend always reporting effect size measurements along with p-values (Levin, 1993; McLean & Ernest, 1998), allowing the reader to subjectively judge the importance of an effect. On the other hand, as noted above, even large effects can be declared “non-significant” because of an insufficient sample size relative to measurement variability (i.e., a Type II error due to lack of power).

1.3. Alternative thresholding methods

Many authors have discussed alternative methods for thresholding brain activation maps within the traditional hypothesis-testing framework, usually with a focus on maximizing detection power while controlling family-wise error (Fadili & Bullmore, 2004; Friston & Penny, 2003; Hartvig & Jensen, 2000). Only one method has been discussed as an alternative to the traditional framework (Voyvodic et al., 2009; Voyvodic, 2006, 2012). This approach, named “activation mapping as a percentage of local excitation” (AMPLE), normalizes t-value maps by the peak t-value in a specified region of interest (ROI). This normalization produces unit-less ratios, which are then thresholded at a predetermined level. Voyvodic and colleagues found that applying this technique to motor cortex activation maps produced stable maps across different scan durations, whereas traditional p-value thresholding created maps that were strongly scan-time (i.e., sample size) dependent (Voyvodic et al., 2009). Voyvodic (2012) also applied this analysis to a language-mapping paradigm, showing that several metrics derived from AMPLE-thresholded maps – including laterality index (LI), spatial extent, and location of activation clusters – were more consistent than those derived from t-value thresholded maps.

While the AMPLE approach is promising, several potential problems need to be considered. A significant limitation of the previously mentioned studies is that the thresholds used were chosen arbitrarily and were not equated on levels of strictness. As discussed in the Methods below, differences in strictness can induce large differences in reliability, confounding the conclusions of these studies that AMPLE is more reliable. Additionally, a ratio of t-values is an unfamiliar statistic, with no obvious meaning or commonly known distribution. A t-value is a combination of amplitude (x), sample standard deviation (s), and sample size (n). If all voxels of interest have similar standard deviations, the ratio of their t-values will effectively be a measure of percent signal (see Equation 1). When the standard deviations are unequal (e.g., the standard deviation of an individual voxel is much greater than the peak voxel standard deviation), the final value will be weighted by their ratio (see Equation 2). When the peak voxel has a relatively low standard deviation, this has the effect of minimizing activation from voxels with a large standard deviation. Although the AMPLE method allows blending of these two statistics, if percent signal and standard deviation are the metrics of interest, using them directly might be more informative and adaptable.

Equation 1.

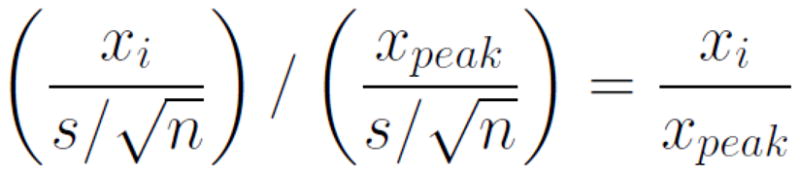
Equation 1

Open in a new tab

AMPLE method, assuming equal variance among voxels. The left side of the equation simplifies to percent signal of peak voxel

Equation 2.

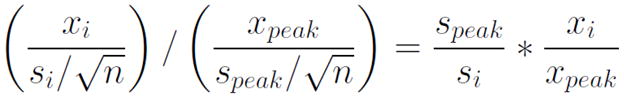
Equation 2

Open in a new tab

AMPLE method, not assuming equal variance among voxels. The equation simplifies to percent signal, weighted by the ratio of standard deviation differences among the peak and current voxels.

An additional problem with the AMPLE method is that normalizing by the peak t-value from the ROI confounds the normalization procedure with the activation observed. For example, if a region of activation maintains a similar spatial extent, but doubles in magnitude, the activation would appear identical before and after this change (and surrounding activations will actually decrease). The AMPLE method is correctly insensitive to changes in signal noise and sample size, but is also insensitive to overall magnitude changes.

1.4. Amplitude-based thresholding

Hypothesis-test statistics indicate the size of a measurement relative to the measurement error, thus they capture the degree of confidence in the measurement (Keppel & Zedeck, 1989). In contrast, parameter estimates of the sample (e.g., mean amplitude) are defined as the most likely value for a given parameter (Keppel & Zedeck, 1989), and are independent of sample size and measurement variability. To illustrate this difference, consider that quadrupling the number of measurements in a sample will double its t-value, while the mean value will be similar (assuming the original estimate was relatively accurate). While noise and sample size have strong effects on the confidence in the data, they do not change the estimate of the data.

We propose that, within certain limits, the estimate of fMRI response amplitude is more relevant for neurosurgical applications than is the degree of confidence that the response is present. Mean response amplitude is roughly proportional to neural activation (Logothetis, 2003; Rees, Friston, & Koch, 2000), thus maps representing mean response amplitude provide a more direct representation of the degree of involvement of a brain region in an activity than a map of p-values. This should come as no surprise, as mean amplitude is the primary metric used for visual presentation of data in all fields of study. When creating bar graphs, for example, the value typically graphed is the mean, not the t-statistic. Other statistics are annotated on the graph (e.g., with error bars and asterisks), but the primary visual representation of the data is the mean value, rather than the statistic. Values that fail to reach significance are not displayed as “zero,” rather they are displayed at their best-estimated value, along with appropriate qualifiers. In contrast, graphing t-values would provide a representation of the confidence that the mean values in question are reliable, but no information about the actual magnitude of the means.

Based on these considerations, we hypothesized that an amplitude-based thresholding method will provide more informative maps for surgical applications. We compared amplitude-based thresholding, standard p-value thresholding, and the AMPLE method on two clinically relevant measures: test-retest reliability and prediction of clinical outcome. Optimally, under conditions where the underlying neural activity is stable, a thresholding method should produce values with minimal additional variability. For the reliability metric, we used Dice’s coefficient of similarity (Dice, 1945) to measure the similarity between two independently thresholded fMRI maps obtained from the same individual. For outcome prediction, we compared maps produced using these methods on their ability to predict postsurgical cognitive outcome, using previously collected patient data. These data previously revealed significant correlations between activation-based metrics and patient outcomes in epilepsy surgery (Binder et al., 2008; Sabsevitz et al., 2003). We re-analyzed these data using all three thresholding methods. The strongest correlation was achieved using amplitude-based thresholding, supporting the hypothesis that this method more reliably identifies activation that is functionally relevant, which is the principal goal of presurgical mapping.

2. Methods

2.1. Subjects

Data from a series of 71 healthy control subjects who underwent fMRI language mapping using a semantic decision task (Binder et al., 1997) were used to test the reliability of each thresholding method. The sample included 30 men and 41 women. Their average age was 35.6 years. All were right-handed and spoke English as a first language.

Data for the outcome analysis were taken from a previous study by Binder et al. (2008). In this study, 60 epilepsy patients were studied with the same semantic decision fMRI protocol prior to left temporal lobe resection, and underwent pre- and postoperative neuropsychological testing to assess change in cognitive abilities. Of these, 51 had sufficiently complete data to be entered into a multivariate prediction analysis and were included in the present study. This sample included 23 men and 28 women. Their average age was 37.3 years. Of these patients, 39 were right-handed, 11 left-handed, and one was ambidextrous.

2.2. FMRI methods

The fMRI methods employed here were described in detail previously (Binder et al., 1997; Binder et al., 2008; Frost et al., 1999). In brief, the task protocol consisted of alternating 24-sec blocks of a semantic decision task and a tone decision task. In the semantic decision task, individuals listened to animal names and were instructed to press a button if the animal was both found in the United States and used by humans. In the tone decision task, individuals listened to brief sequences of high (750 Hz) and low (500 Hz) tones and were instructed to press a button if they heard a sequence containing two high tones. The contrast of the semantic decision task with the tone decision task isolates speech perception and semantic language processes while controlling for attention, working memory, auditory, and motor processes. This contrast produces left-lateralized language activation in frontal, temporal, and parietal areas in healthy right-handed controls (Binder et al., 1997; Binder et al., 2008; Frost et al., 1999).

As described elsewhere (Binder et al., 1997; Frost et al., 1999), imaging was conducted on commercial 1.5T and 3T GE MRI scanners. High-resolution, T1-weighted anatomic reference images were obtained using a three-dimensional spoiled-gradient-echo sequence. Functional imaging used a gradient-echo T2*-weighted echoplanar sequence. Echoplanar image volumes were acquired as contiguous sagittal or axial slices covering the whole brain. Scanning parameters, including in-plane voxel size and slice thickness, varied slightly across both samples. Slice number varied from 36 to 47 slices (average: 39.2, SD: 2.6). This variability further tested the robustness of the thresholding methods.

Image processing and statistical analyses were performed using AFNI software (Cox, 1996). All analyses were performed at the individual subject level. Volumetric image registration was used to reduce the effects of head movement. Task-related changes in MRI signal were identified using a multivariable general linear regression model. The predicted task effect was modeled by convolving a gamma function with a time series of impulses representing each task trial. Movement vectors (computed during image registration) and a second-order linear trend were included as covariates of no interest. The results of the regression analysis include a map of amplitude values (beta coefficients), which represent the estimated mean difference in BOLD signal amplitude between the semantic decision and tone decision tasks at each voxel, and a map of t-values, which represent the statistical reliability of this task effect at each voxel.

2.3. Thresholding procedures

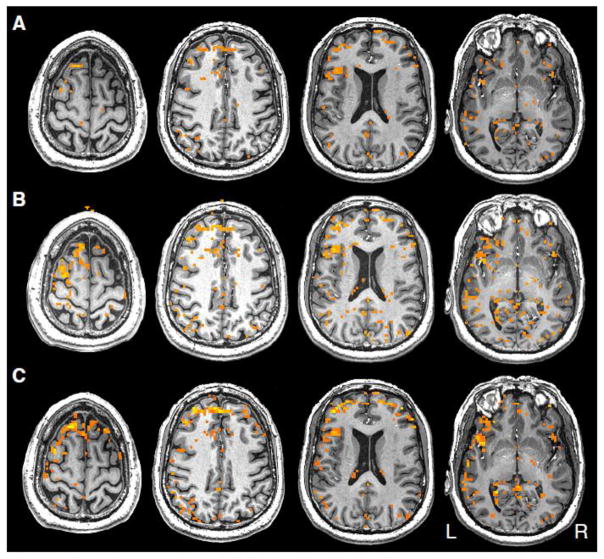
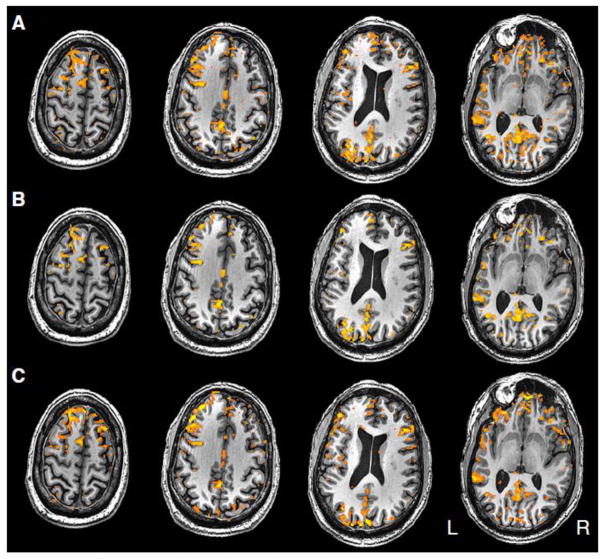
Example activation maps from individual subjects, thresholded using each of the following three methods, are shown in Figures 1 and 2 to demonstrate representative patterns. Although particular regions may have more or less activation in certain thresholding methods, the thresholds were set such that the total number of voxels declared active in each method, averaged across subjects, was equal.

Figure 1.

Figure 1

Open in a new tab

Example from a single subject of the three thresholding methods compared in this paper: A) p-value B) AMPLE and C) n-signal.

Figure 2.

Figure 2

Open in a new tab

Second example from another representative single subject of the three thresholding methods compared in this paper: A) p-value B) AMPLE and C) n-signal.

2.3.1. Amplitude thresholding

The maps of mean difference in BOLD signal amplitude between task conditions were used for amplitude-based thresholding. Because MRI signal values use an arbitrary scale that can vary due to many factors (including temperature and hardware gain), raw amplitude values were converted to a percentage of the average signal within a whole brain mask, on a per-subject basis. Commonly used percent signal methods use the local voxel-wise baseline signal value, however these methods are subject to large artifacts from misalignment and heterogeneity in baseline values. This is particularly seen along the edges of structures where small amounts of motion can shift voxels from one baseline value to another and dramatically change their percent value. We theorized that using a baseline signal average across the whole brain would result in more stable values. Because this is not the standard method of computing percent signal, we refer to this method as normalized signal (n-signal). The method used to select a threshold for n-signal is described below in the section “Threshold calibration”.

2.3.2. Hypothesis-test thresholding

Maps of t-values calculated from the task contrast were used for this analysis. A t-value threshold was calculated based on the p-value target of p < 0.001.

2.3.3. AMPLE

The AMPLE method was applied to the t-value maps using a slight modification of the published methods (Voyvodic, 2006). Instead of normalizing the t-values to the single peak t-value in a hand-drawn ROI as in the original method, the t-value maps were divided by the 98th percentile value in each individual map, within a whole brain mask. The 98th percentile was chosen over the peak value to be more robust to outliers. These t-value ratio maps were then thresholded at the calculated value described in the next section.

2.4. Threshold calibration

To avoid artifactual differences in the comparison metrics due to differences in threshold strictness, threshold levels were set to produce a similar spatial extent of activation (i.e., similar number of voxels surviving the threshold) for each method. The similarity of activated areas across maps is related to the threshold level used and follows a roughly parabolic function. At very lenient thresholds (e.g., p < 1.0), nearly all voxels will be selected, thus all maps will be highly consistent. Conversely, at very strict thresholds (e.g., p = 0.0), no voxels will be selected, again resulting in artificially high levels of consistency. Because of this relationship, a procedure to equate the three thresholding methods on their absolute strictness is required. To accomplish this, threshold strictness was quantified as the average, across all subjects, of the percentage of a whole brain mask that was declared activated. For example, a fairly strict threshold level may correspond to an average of 5% of the brain being declared as active, whereas a lenient threshold may correspond to 30% of the brain declared active. Because this is not a commonly used metric, Figure 3 shows examples of different threshold levels in terms of percent of brain active.

Figure 3.

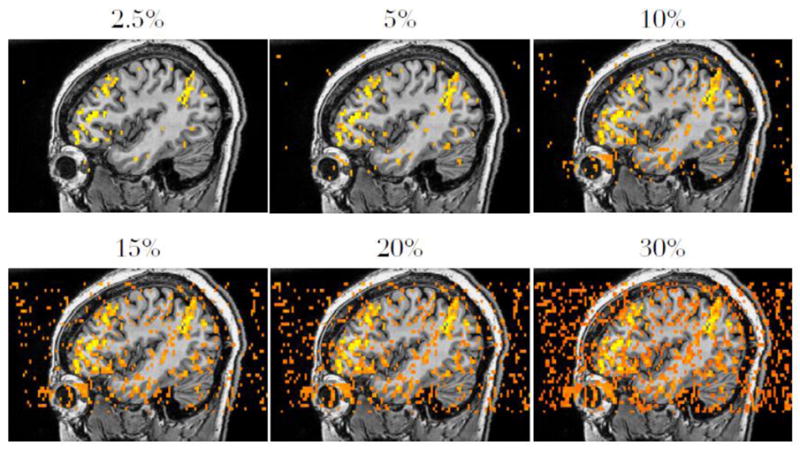
Figure 3

Open in a new tab

Examples of average percent brain activation. This figure is not meant to represent any particular thresholding method, but to orient the reader to the novel metric of percent brain activation.

For the following tests, thresholds resulting in 5.79% active voxels were used. This is the mean percentage of the brain volume activated across the sample of control subjects after thresholding each subject’s t-value map at a p-value of 0.001, a threshold often used in functional imaging studies. A simple non-linear optimization method was then used to find the closest threshold for the n-signal and AMPLE methods that corresponded to 5.79% brain activity. Thresholds were repetitively chosen and then applied to the data in each subject. The mean percent brain activity across the entire sample was then measured, the threshold was updated, and the process continued until the mean percent brain activity was within 0.01% of 5.79% (i.e., an absolute difference of < 0.000579%). The final derived threshold for the AMPLE method was 0.425 (corresponding to 42.5% of the per-subject 98th percentile t-value). For the n-signal threshold, the final value used was 0.92% (i.e., a signal change equal to 0.92% of the per-subject average intraparenchymal raw signal value).

2.5. Split-half reliability assessment

The first metric used to compare the thresholding methods assesses intra-subject variability in fMRI maps. Data from individual subjects were randomly split into two data sets and analyzed separately. These results were then compared using Dice’s coefficient of similarity (Dice, 1945), which measures the amount of consistency between two sets of items. Coefficients can range from 0.0 to 1.0, with 1.0 indicating identical sets. Thresholding methods that produce consistent results should produce high values for this metric.

To split the data into two halves with the least amount of bias, a single raw fMRI time series was divided randomly, volume-by-volume, in a temporally noncontiguous fashion. This was done using the censor feature of the AFNI program “3dDeconvolve” to remove individual data points, while preserving global timing information. Each pair of results for a given subject was created by first randomly selecting 50% of the data points from the subject’s time series, analyzing them, and then analyzing their complement independently. The same threshold was applied to both resultant maps, and a Dice coefficient was calculated (Equation 3) to quantify their degree of overlap. These values were then averaged across subjects to yield a mean coefficient for each threshold value. This procedure was repeated for 50 iterations, selecting a new random sample of data points on each subject and threshold method, to create a distribution of reliability coefficients for each thresholding method.

Equation 3.

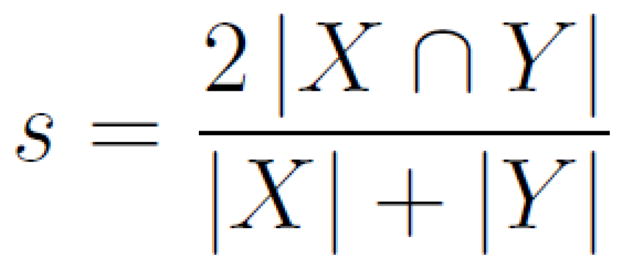
Equation 3

Open in a new tab

Dice coefficient for quantifying the overlap in two data sets, X and Y. |X| refers to the number of activated voxels in the first split-half dataset, |Y| refers to the activated voxels in the second split-half dataset. |X ∩ Y| refers to the number of voxels that are activated in the same location in both split-half datasets.

2.6. Correlation with patient outcome

The second metric used to compare the thresholding methods assessed their ability to predict verbal memory outcome after left anterior temporal lobectomy. As in the original study by Binder et al. (2008), voxels that passed the threshold were counted in right and left homologous ROIs, then a language LI was computed for each patient using the normalized ratio shown in Equation 4 (Binder et al., 1996). The method that was found previously to be most predictive used an ROI that encompassed the majority of the lateral cortex of the frontal, temporal, and parietal lobes (Binder et al., 2008). LIs in the original study were derived by applying an uncorrected p-value threshold of p < 0.001. For the present study, LIs were recalculated for the 51 subjects using the original p-value method, and then calculated again using the n-signal and AMPLE thresholds.

Equation 4.

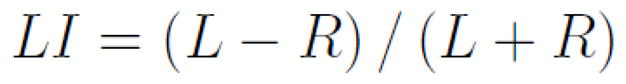
Equation 4

Open in a new tab

Laterality index (LI) used to predict memory outcomes based on distribution of fMRI activation. L refers to the number of voxels above threshold in the left-sided ROI and R refers to the number of voxels on the right.

Verbal memory was measured before and 6 months after surgery using two measures from the Selective Reminding Test (Buschke & Fuld, 1974): consistent long term recall (CLTR) and long term storage (LTS). A change score on each measure was computed for each patient by subtracting the preoperative from the postoperative score. Prediction was done using a step-wise linear regression model. The first step always entered age of onset of epilepsy and preoperative memory score, because these values are easily obtainable and were previously shown to predict outcome (Binder et al., 2008). FMRI LI values derived from each threshold method were then added to the regression model, and the change in R2 was measured and tested for significance.

3. Results

3.1. Split-half reliability

Results of the split-half reliability assessments are shown in Table 1. The mean Dice coefficient was significantly different between the thresholding methods (F(2,225) = 6.447, p < 0.002), being driven primarily by the simple effects of n-signal being more reliable than p-value thresholds (coefficient difference = 0.054; t(225) = 2.643, p < 0.009) and AMPLE (coefficient difference = 0.070; t(225) = 3.426, p < 0.001) thresholding. The standard p-value threshold was not significantly more reliable than AMPLE (coefficient difference = 0.016; t(225) = 0.783, p = 0.435).

Table 1.

Split-half reliability results. Dice coefficients quantifying the similarity of randomly split data sets for each thresholding method.

Threshold Method Average Dice Coefficient
p-Value 0.335
AMPLE 0.321
n-Signal 0.391
Open in a new tab

Simple correlations between LIs derived from each thresholding method and outcome variables (Table 2) revealed stronger correlations using n-signal and AMPLE thresholding than using p-value thresholding. This finding was confirmed in the multivariate regression model, where each thresholding method produced results that could predict outcome significantly more accurately than the baseline model (age of onset and preoperative score), with the exception of p-value thresholding for the LTS score (see Table 3). Across both CLTR and LTS outcome measures, n-signal thresholding produced the most predictive model. In addition, LIs derived from p-value thresholds did not significantly improve the n-signal based models, nor did they improve the AMPLE models, whereas adding n-signal LIs significantly improved prediction accuracy relative to a model that already included standard p-value LIs. The increase in R2 of each thresholding model over baseline is depicted in Figure 4.

Table 2.

Simple correlations of laterality indices (LIs) derived using each thresholding method with outcome variables.

Threshold Method
p-value AMPLE n-signal
CLTR 0.294 0.330 * 0.405 *
LTS 0.332 * 0.446 ** 0.461 **
Open in a new tab
*

p < 0.05

**

p < 0.01

Table 3.

Results of multiple regression prediction model. Baseline R2 was calculated using age of onset and preoperative score. Subsequent models were derived in a step-wise manner, adding LIs derived from each thresholding method, calculating the new R2, and testing if the increase in R2 was significant.

CLTR LTS
R2 p R2 p
Age of Onset & Preoperative Score 0.542 0.000 0.345 0.000
graphic file with name nihms530740t1.jpg 0.599 0.031 0.402 0.072
0.659 0.018 0.509 0.009
0.617 0.203 0.486 0.023
0.658 0.001 0.502 0.002
0.659 0.829 0.509 0.503
0.666 0.385 0.502 0.893
0.617 0.012 0.470 0.006
0.617 0.966 0.486 0.304
0.666 0.030 0.502 0.138
Open in a new tab

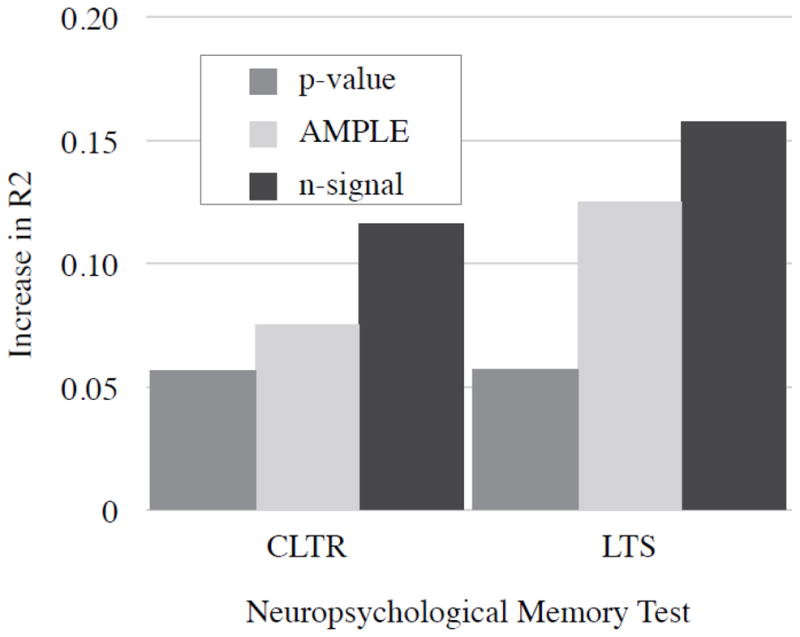
Figure 4.

Figure 4

Open in a new tab

Increase in R2 after adding LIs derived from each thresholding method to multiple regression model for each memory test

4. Discussion

Using both the reliability of maps as well as prediction of clinical data, n-signal thresholded data yielded superior results relative to the traditional p-value and the proposed AMPLE method. Although this approach is distinctly different from the hypothesis-testing approach that emphasizes a conservative evaluation of novel hypotheses, it is well motivated by the theoretical and pragmatic arguments presented above. Several significant challenges could arise from the proposed methodology, which will need to be addressed in order to apply this method routinely. However, the current data suggest that results of this method, if properly implemented, would be superior relative to current methodology for the purposes of presurgical mapping.

Considering the classic interpretation of each of these statistical values, it is understandable that thresholding based on n-signal would yield the best results for identifying functionally relevant brain activity. The statistical mean is defined as the most likely estimate of a value, thus it is the logical choice to quantify a change in magnitude of activity associated with a task. Other statistics can complement this estimate by showing how confident one should be in the estimate (in the form of a p-value, for example). However, we propose that in the context of creating surgical maps, it is more important to know how large an effect is, rather than how confident we are in it. Selecting voxels based solely on a high degree of confidence produces a map that is strongly biased toward missing large-amplitude responses when the data happen to contain a large amount of noise.

Traditional p-value thresholding and the AMPLE method produced similar results in the reliability analysis. This is consistent with the theoretical argument above, because AMPLE removes variability due to sample size (which was held constant) but maintains sensitivity to noise. The insensitivity of AMPLE to sample size limitations was seen in the outcome analysis, where the models using AMPLE were slightly more predictive than those using p-value thresholding.

When evaluating these metrics based on their reliability, it is important to recognize the underlying variability of the neural activity that is being measured. Variability in a measurement reflecting neural activity does not imply poor reliability if the underlying neural activity itself is not stable. The reliability analyses here assume that the neural activity was optimally stabilized using strong experimental methodology (e.g., designing tasks that minimize off-task processing and matching attentional and perceptual demands of tasks) and random sampling from within the same scanning session. Within this context, differences in reliability among different analyses can be construed as variation resulting from the analysis. Residual variability common to all of the analyses may be attributed to other noise sources, for example the measurement, or signal itself.

While the p-value is not the best estimate of amplitude, it provides a complementary measure of confidence in the measurement. Confidence measures are necessary for quality assurance and are useful for determining when data are grossly unreliable. However, after reaching a degree of confidence, relying on the p-value to filter data can lead to biased results. The data used in the present analyses were tacitly assumed to have sufficient signal-to-noise quality and sample size to provide good estimates of response amplitude. In future applications of amplitude-based thresholding, those requirements for data quality will need to be formalized. One possible method of assuring data integrity without biasing the results is to create a complementary confidence map, which would display areas with unreliable data estimates. This is analogous to the error bars and annotations added to a bar graph to inform the reader of more or less reliable values. However, in contrast to current methodology, the criterion for data quality would be relatively liberal, and voxels with marginal p-values would not be labeled as “inactive” if they also passed the response amplitude threshold.

One significant limitation to the n-signal method is the lack of a standard threshold value. The values used here were chosen to match the standard p-value in strictness and were applied uniformly across the brain and across subjects. However, it is possible that the function relating neural activation to BOLD signal change or the underlying reactivity of the vascular supply varies across the brain (Bandettini & Wong, 1997; Rostrup et al., 2000) and across subjects. To appropriately categorize an area as “activated” or “not activated” one would need a priori knowledge of the distribution of n-signal changes within this region (the prior distribution, using Bayesian terminology). Future work could create an atlas of prior distributions by region that could then be used to derive region-specific thresholds. Alternatively, thresholds could be derived on a per-experiment or per-subject basis using standardized or physiologic stimuli (e.g., breath-holding).

Another limitation of the current study is the lack of an assessment of reliability across multiple scanning sessions. The reliability metrics above demonstrated the relative reliability of the different methods within a single scanning session. Comparing scans between different scanning sessions, potentially on different scanner hardware, would introduce more variability and further test the robustness of each method. Future studies on this topic may integrate multiple scanning sessions into their designs to test these paradigms.

In summary, the results demonstrated here are consistent with theoretical predictions that amplitude-based thresholding methods can provide more reliable and predictive functional imaging results than standard thresholding methods. In clinical applications such as presurgical mapping, where reliability is required across varying conditions of noise and sample size, thresholding based mainly on response amplitude may provide an optimal approach.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Bandettini PA, Wong EC. A hypercapnia-based normalization method for improved spatial localization of human brain activation with fMRI. NMR in biomedicine. 1997;10(4–5):197–203. doi: 10.1002/(sici)1099-1492(199706/08)10:4/5<197::aid-nbm466>3.0.co;2-s. [DOI] [PubMed] [Google Scholar]
  2. Binder JR, Frost JA, Hammeke TA, Cox RW, Rao SM, Prieto T. Human brain language areas identified by functional magnetic resonance imaging. The Journal of neuroscience: the official journal of the Society for Neuroscience. 1997;17(1):353–362. doi: 10.1523/JNEUROSCI.17-01-00353.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Binder JR, Swanson SJ, Hammeke TA, Morris GL, Mueller WM, Fischer M, Haughton VM. Determination of language dominance using functional MRI: a comparison with the Wada test. Neurology. 1996;46(4):978–984. doi: 10.1212/wnl.46.4.978. [DOI] [PubMed] [Google Scholar]
  4. Binder JR, Sabsevitz DS, Swanson SJ, Hammeke TA, Raghavan M, Mueller WM. Use of preoperative functional MRI to predict verbal memory decline after temporal lobe epilepsy surgery. Epilepsia. 2008;49(8):1377–1394. doi: 10.1111/j.1528-1167.2008.01625.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Buschke H, Fuld PA. Evaluating storage, retention, and retrieval in disordered memory and learning. Neurology. 1974;24(11):1019–1025. doi: 10.1212/wnl.24.11.1019. [DOI] [PubMed] [Google Scholar]
  6. Chow SL. Significance test or effect size? Psychological Bulletin. 1988;103(1):105–110. [Google Scholar]
  7. Cox RW. AFNI: software for analysis and visualization of functional magnetic resonance neuroimages. Computers and biomedical research, an international journal. 1996;29(3):162–173. doi: 10.1006/cbmr.1996.0014. [DOI] [PubMed] [Google Scholar]
  8. Daniel LG. Statistical Significance Testing: A Historical Overview of Misuse and Misinterpretation with Implications for the Editorial Policies of Educational Journals. Research in the Schools. 1998;5(2):23–32. [Google Scholar]
  9. Detre JA. Clinical applicability of functional MRI. Journal of magnetic resonance imaging: JMRI. 2006;23(6):808–815. doi: 10.1002/jmri.20585. [DOI] [PubMed] [Google Scholar]
  10. Dice LR. Measures of the Amount of Ecologic Association Between Species. Ecology. 1945;26(3):297. [Google Scholar]
  11. Fadili MJ, Bullmore ET. A comparative evaluation of wavelet-based methods for hypothesis testing of brain activation maps. NeuroImage. 2004;23(3):1112–1128. doi: 10.1016/j.neuroimage.2004.07.034. [DOI] [PubMed] [Google Scholar]
  12. Forman SD, Cohen JD, Fitzgerald M, Eddy WF, Mintun MA, Noll DC. Improved assessment of significant activation in functional magnetic resonance imaging (fMRI): use of a cluster-size threshold. Magnetic resonance in medicine: official journal of the Society of Magnetic Resonance in Medicine/Society of Magnetic Resonance in Medicine. 1995;33(5):636–647. doi: 10.1002/mrm.1910330508. [DOI] [PubMed] [Google Scholar]
  13. Friston KJ, Frith CD, Liddle PF, Frackowiak RS. Comparing functional (PET) images: the assessment of significant change. Journal of cerebral blood flow and metabolism: official journal of the International Society of Cerebral Blood Flow and Metabolism. 1991;11(4):690–699. doi: 10.1038/jcbfm.1991.122. [DOI] [PubMed] [Google Scholar]
  14. Friston KJ, Penny W. Posterior probability maps and SPMs. NeuroImage. 2003;19(3):1240–1249. doi: 10.1016/s1053-8119(03)00144-7. [DOI] [PubMed] [Google Scholar]
  15. Frost JA, Binder JR, Springer JA, Hammeke TA, Bellgowan PS, Rao SM, Cox RW. Language processing is strongly left lateralized in both sexes. Evidence from functional MRI. Brain: a journal of neurology. 1999;122(Pt 2):199–208. doi: 10.1093/brain/122.2.199. [DOI] [PubMed] [Google Scholar]
  16. Hartvig NV, Jensen JL. Spatial mixture modeling of fMRI data. Human brain mapping. 2000;11(4):233–248. doi: 10.1002/1097-0193(200012)11:4&#x0003c;233::AID-HBM10&#x0003e;3.0.CO;2-F. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Keppel G, Zedeck S. Data analysis for research designs: analysis of variance and multiple regression, correlation approaches. Worth Publishers; 1989. [Google Scholar]
  18. Levin JR. Statistical Significance Testing from Three Perspectives and Interpreting Statistical Significance and Nonsignificance and the Role of Statistics in Research. Journal of Experimental Education. 1993;61(4):378–93. [Google Scholar]
  19. Locascio JJ, Jennings PJ, Moore CI, Corkin S. Time series analysis in the time domain and resampling methods for studies of functional magnetic resonance brain imaging. Human brain mapping. 1997;5(3):168–193. doi: 10.1002/(SICI)1097-0193(1997)5:3<168::AID-HBM3>3.0.CO;2-1. [DOI] [PubMed] [Google Scholar]
  20. Logan BR, Geliazkova MP, Rowe DB. An evaluation of spatial thresholding techniques in fMRI analysis. Human brain mapping. 2008;29(12):1379–1389. doi: 10.1002/hbm.20471. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Logothetis NK. The Underpinnings of the BOLD Functional Magnetic Resonance Imaging Signal. The Journal of Neuroscience. 2003;23(10):3963–3971. doi: 10.1523/JNEUROSCI.23-10-03963.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Logothetis NK, Pfeuffer J. On the nature of the BOLD fMRI contrast mechanism. Magnetic resonance imaging. 2004;22(10):1517–1531. doi: 10.1016/j.mri.2004.10.018. [DOI] [PubMed] [Google Scholar]
  23. Machielsen WC, Rombouts SA, Barkhof F, Scheltens P, Witter MP. FMRI of visual encoding: reproducibility of activation. Human brain mapping. 2000;9(3):156–164. doi: 10.1002/(SICI)1097-0193(200003)9:3&#x0003c;156::AID-HBM4&#x0003e;3.0.CO;2-Q. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. McLean JE, Ernest JM. The Role of Statistical Significance Testing in Educational Research. Research in the Schools. 1998;5(2):15–22. [Google Scholar]
  25. Petersson KM, Nichols TE, Poline JB, Holmes AP. Statistical limitations in functional neuroimaging. II. Signal detection and statistical inference. Philosophical transactions of the Royal Society of London Series B, Biological sciences. 1999;354(1387):1261–1281. doi: 10.1098/rstb.1999.0478. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Rees G, Friston K, Koch C. A direct quantitative relationship between the functional properties of human and macaque V5. Nature Neuroscience. 2000;3(7):716–723. doi: 10.1038/76673. [DOI] [PubMed] [Google Scholar]
  27. Rostrup E, Law I, Blinkenberg M, Larsson HB, Born AP, Holm S, Paulson OB. Regional differences in the CBF and BOLD responses to hypercapnia: a combined PET and fMRI study. NeuroImage. 2000;11(2):87–97. doi: 10.1006/nimg.1999.0526. [DOI] [PubMed] [Google Scholar]
  28. Sabsevitz DS, Swanson SJ, Hammeke TA, Spanaki MV, Possing ET, Morris GL, Binder JR. Use of preoperative functional neuroimaging to predict language deficits from epilepsy surgery. Neurology. 2003;60(11):1788–1792. doi: 10.1212/01.wnl.0000068022.05644.01. [DOI] [PubMed] [Google Scholar]
  29. Shaver JP. What Statistical Significance Testing Is, and What It Is Not. Journal of Experimental Education. 1993;61(4):293–316. [Google Scholar]
  30. Thirion B, Pinel P, Mériaux S, Roche A, Dehaene S, Poline JB. Analysis of a large fMRI cohort: Statistical and methodological issues for group analyses. NeuroImage. 2007;35(1):105–120. doi: 10.1016/j.neuroimage.2006.11.054. [DOI] [PubMed] [Google Scholar]
  31. Turner R, Howseman A, Rees GE, Josephs O, Friston K. Functional magnetic resonance imaging of the human brain: data acquisition and analysis. Experimental brain research. Experimentelle Hirnforschung Expérimentation cérébrale. 1998;123(1–2):5–12. doi: 10.1007/s002210050538. [DOI] [PubMed] [Google Scholar]
  32. Voyvodic JT. Activation mapping as a percentage of local excitation: fMRI stability within scans, between scans and across field strengths. Magnetic resonance imaging. 2006;24(9):1249–1261. doi: 10.1016/j.mri.2006.04.020. [DOI] [PubMed] [Google Scholar]
  33. Voyvodic JT, Petrella JR, Friedman AH. fMRI activation mapping as a percentage of local excitation: consistent presurgical motor maps without threshold adjustment. Journal of magnetic resonance imaging: JMRI. 2009;29(4):751–759. doi: 10.1002/jmri.21716. [DOI] [PubMed] [Google Scholar]
  34. Voyvodic JT. Reproducibility of single-subject fMRI language mapping with AMPLE normalization. Journal of magnetic resonance imaging: JMRI. 2012;36(3):569–580. doi: 10.1002/jmri.23686. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES