Abstract
DNA is subject to oxidative damage due to radiation or by-products of cellular metabolism, thereby creating electron holes that migrate along the DNA stacks. A systematic computational analysis of the dependence of the electronic properties of nucleobase stacks on sequence and conformation was performed here, on the basis of single- and double-stranded homo-nucleobase stacks of 1–10 bases or 1–8 base pairs in standard A-, B-, and Z-conformation. First, several levels of theory were tested for calculating the vertical ionization potentials of individual nucleobases; the M06-2X/6-31G* hybrid density functional theory method was selected by comparison with experimental data. Next, the vertical ionization potential, and the Mulliken charge and spin density distributions were calculated and considered on all nucleobase stacks. We found that (1) the ionization potential decreases with the number of bases, the lowest being reached by Gua≡Cyt tracts; (2) the association of two single strands into a double-stranded tract lowers the ionization potential significantly (3) differences in ionization potential due to sequence variation are roughly three times larger than those due to conformational modifications. The charge and spin density distributions were found (1) to be located toward the 5′-end for single-stranded Gua-stacks and toward the 3′-end for Cyt-stacks and basically delocalized over all bases for Ade- and Thy-stacks; (2) the association into double-stranded tracts empties the Cyt- and Thy-strands of most of the charge and all the spin density and concentrates them on the Gua- and Ade-strands. The possible biological implications of these results for transcription are discussed.
Keywords: quantum chemistry calculations, hybrid density functional theory, DNA stacks, homo-nucleobase stacks, radical cations, electron holes, charge distribution, spin density distribution, vertical ionization potential, oxidative damage, charge transfer
Introduction
Nucleic acids, DNA and RNA, are the building blocks of all living organisms, from plants and animals to bacteria and viruses. The basic chemical unit of a nucleic acid, the nucleotide, consists of a sugar bound on one side to a phosphate group and on the other side to a nucleobase (Saenger, 1984). Although the chemical nature of nucleic acids is well established, the study of the electronic properties of nucleic acid bases is still an area of intense research and continuing progress (Barnett, Cleveland, Joy, Landman, & Schuster, 2001; Chakraborty, 2007; Kumar & Sevilla, 2011; Šponer & Hobza, 1999; Šponer, Riley, & Hobza, 2008). Such electronic properties, in particular the charge transport resulting from oxidized DNA sites, are expected to play an important role in many biological processes (Genereux, Boal, & Barton, 2010; Heller, 2000; Merino, Boal, & Barton, 2008). In particular, DNA or RNA conformations with particular electronic properties are found in many sites known to be biologically important (Rooman, Cauët, Liévin, & Wintjens, 2011). Recently, a statistical correlation between the occurrence of mutations in disease-related genes and the DNA electronic properties has been reported, thereby suggesting that the change in DNA electronic structure induced by mutations strongly alters fundamental biological processes (Shih, Wells, Hsu, Cheng, & Römer, 2012).
Oxidative DNA damage, triggered by exposure either to high-energy radiations or to reactive oxygen species generated as by-products of cellular metabolism, is inherent to the biochemistry of the cells, resulting in a variety of physical and chemical changes in DNA (Cerón-Carrasco & Jacquemin, 2012; Kumar & Sevilla, 2010; Schuster, 2009; Zhang & Eriksson, 2007). An important feature of such damage is the ionization of DNA and thus the production of electron holes and ground-state cation radicals (DNA·+). Guanines, which have the lowest ionization potentials of the four nucleobases, tend to trap the electron hole after a base-to-base charge transfer process through the stacked nucleobases, resulting from coupling between the overlapping π-orbitals (Giese, 2002). However, direct experimental measurements of long-distance hole transfer in DNA remain the subject of intense debate mainly due to the challenging experimental requirement of working at the nanoscale (Triberis & Dimakogianni, 2009).
Several theoretical models of hole transport in DNA have been proposed. The simplest one is defined by an effective one-dimensional Hückel-Hamiltonian for charge transfer through the highest occupied molecular orbital (HOMO) states of the nucleobases (Chakraborty, 2007). The most often used models describe the dynamics of hole migration in terms of tunneling or hopping mechanisms (Giese, 2000; Boon & Barton, 2002). For most of the charge-transfer modeling, a correct determination of vertical ionization potentials (vIPs) is of great importance. Over the last two decades, there have been numerous studies to calculate vIP of isolated bases and DNA base pair stacks (Cauët, Dehareng, & Liévin, 2006; Close, 2003; Close, 2004; Close & Øhman, 2008; Colson, Besler, & Sevilla, 1993; Colson & Sevilla, 1995; Crespo-Hernández et al., 2004; Fernando, Papadantonakis, Kim, & LeBreton, 1998; Paukku & Hill, 2011; Prat, Houk, & Foote, 1998; Roca-Sanjuán, Rubio, Merchán, & Serrano-Andrés, 2006; Sevilla, Besler, & Colson, 1995; Šponer & Hobza, 1994; Šponer, Leszczynski, & Hobza 1996).
In contrast, reports on ab initio vIP calculations of long-sequence DNA stacks (more than two stacked bases) are much less numerous. In a series of articles (Saito, Takayama, Sugiyama, & Nakatani, 1995; Saito et al., 1998; Sugiyama & Saito, 1996), vIPs of DNA trimer and pentamer stacks in B-form with various nucleobase sequences were computed using Koopmans’ theorem (Koopmans, 1934), at HF/6-31G* calculation level. It has been shown that calculated vIPs of different B-form DNA sequences are correlated with the experimentally observed relative reactivity toward photo-induced one-electron oxidation. This indicates that the vIP values represent a simple way to estimate how different DNA sequences impinge to the reactivity of one-electron oxidation.
Later, molecular dynamics simulations of long base pair duplexes have been performed in the context of charge migration (Barnett et al., 2001; Bongiorno, 2009). In the tetrameric base pair duplex 5′-Gua-Ade-Gua-Gua-3′, the hole distribution was estimated to be of 20% on Gua1 (the first Gua), 5% on Ade2, and 40% on the Gua3-Gua4 pair (Barnett et al., 2001). Simulation of a B-DNA 5′-Ade-Gua-Gua-Ade-3′ duplex indicated that the hole delocalizes over the two central guanines (Bongiorno, 2009). A mixed quantum-mechanical /molecular mechanics (MD) simulation on a fully hydrated 38-base pair B-DNA showed that the electron hole is localized on the three proximal guanines 5′-Gua-Gua-Gua … −3’ with a density peak on the central Gua2 (Gervasio, Boero, & Parrinello, 2006). Pentameric Ade stacks in B-conformation have also been studied by mixed MD and density functional theory (DFT) calculations (Improta, 2008) and showed that the HOMO of the cationic species is delocalized over the three central adenines. The ionization potential of B-form Gua = Cyt duplexes consisting of up to 6 nucleotide pairs was evaluated in gas phase and water using semi-empirical AM1 calculations (Yokojima, Yoshiki, Yanoi, & Okada, 2009). It was shown to decrease with increasing duplex length in gas phase, but this decrease is reduced in water. The major part of the hole's charge was found localized on a particular Gua that depends on duplex length, both in gas and in aqueous phases.
More recently, vIPs and hole delocalization were investigated using the M06-2X/6-31G* level of theory in one-electron oxidized single-stranded Ade stacks from dimer to octamer, and of Gua stacks from dimer to trimer (Kumar & Sevilla, 2011). In the latter report, the hole in the multimeric Ade stacks was found largely localized on Ade2, whereas, as experimentally established (Hall, Holmlin, & Barton, 1996; Saito et al., 1995; Saito et al., 1998), it was preferentially located on Gua1 in the Gua-Gua-Gua trimer.
The present study focuses on the theoretical evaluation of the vIPs, and of the charge and spin density distributions, of single- and double-stranded homo-nucleobase stacks with up to 10 stacked bases or 8 stacked base pairs, in the three standard DNA conformations A, B, and Z. Although several reports have already been published on calculations of these features on single nucleobases or short stacks, calculations on such long single- and double-stranded nucleobase stacks have, to the best of our knowledge, not yet been extensively and systematically performed. Moreover, the effects of DNA conformation on these features had not been thoroughly analyzed either. These calculations allowed us to demonstrate consistent and interesting findings and trends, which could not be seen on shorter molecules.
Computational methods
In a first stage, the four nucleobases Ade, Cyt, Gua, and Thy were considered separately. Their sugar cycle and phosphate group were omitted, and the glycosidic bond was replaced by a hydrogen atom. Their initial geometries were taken from the molecular-modeling program package Insight 2000 (Accelrys Inc.). These geometries were then optimized at different levels of calculation: Hartree-Fock (HF) (Roothaan, 1951), second-order Møller-Plesset perturbation theory (MP2) (Møller & Plesset, 1934), and three different hybrid DFT methods, named BLYP (for Becke-Lee-Yang-Parr) (Becke, 1988; Miehlich, Savin, Stoll, & Preuss, 1989), B3LYP (for Becke, 3-parameter, Lee-Yang-Parr) (Lee, Yang, & Parr, 1988), and M06-2X (Zhao & Truhlar, 2008). In conjunction with these methods, several basis sets for atomic orbitals were used: the split-valence polarized basis sets 6-31G* and 6-31G** (Ditchfield, Hehre, & Pople, 1971; Hariharan & Pople, 1973), as well as 6-311++G** that has in addition double diffuse functions (Clark, Chandrasekhar, Spitznagel, & Schleyer, 1983; Frisch, Pople, & Binkley, 1984). The Gaussian 09 program suite (Frisch et al., 2010) was used for these, and all subsequent, calculations. The energy in gas phase of all these optimized geometries was then computed, both for the neutral species and for the radical cationic species, with one missing electron, that adopts the same geometry as the neutral molecule. All calculations on cationic molecules were performed with restricted open-shell procedures, which prevent spin contamination problems. Note that the indicator of the quality of treatment of this problem, that is, the total spin-squared operator 〈S2〉, was systematically checked in all calculations on DNA·+ cation radicals. The values of 〈S2〉 turned out to be always equal to the expected value of 0.75.
To compute the vIP in gas phase of the four individual nucleobases, we used two methods. The first calculates the vIP as the difference between the energy of the radical cationic species and of the neutral species, both adopting the optimized geometry of the neutral molecule. The second estimates the vIP as minus the energy of the HOMO level of the neutral closed-shell molecule, calculated at HF level of theory, according to Koopman's theorem (Koopmans, 1934). We also tested the equivalent approximation with the MP2 and DFT levels of theory, which include electron correlation effects (Maksic & Vianello, 2002; Politzer & Abu-Awwad, 1998; Salzner & Baer, 2009; Stowasser & Hoffmann, 1999).
In a second stage, we considered the four types of single-stranded homo-nucleobase stacks, that is, poly-Ade, poly-Cyt, poly-Gua, and poly-Thy, from dimer to decamer in standard A- and B-conformation. We also considered the corresponding double-stranded homo-nucleobase stacks, poly-Ade = Thy, and poly-Gua ≡ Cyt, from dimer to octamer. Single-stranded and double-stranded nucleobase stacks with alternating Gua and Cyt bases, that is, poly-Gua/Cyt and poly-Gua ≡ Cyt/Cyt ≡ Gua, in standard Z-DNA conformations, were also analyzed; like for the A- and B- conformations, dimers to decamers were considered for single-stranded stacks and dimers to octamers for double-stranded stacks. The energy calculations were performed with the method and basis set that gave the best results on the individual nucleobases and provide the best compromise between accuracy and time consumption, that is, M06-2X and 6-31G*, as discussed in the results section.
The geometries of the nucleobase stacks were built with Insight 2000 (Accelrys Inc.); they are based on early fiber X-ray diffraction studies by Arnott and co-workers (Arnott, 1970; Arnott, Hukins, Rubin, Brennan, & Sundaralingam, 1972; Arnott et al., 1972). The global geometry of these stacks was not optimized, but rather, the isolated nucleobases, individually optimized at the M06-2X/6-31G* level, were superimposed onto the original bases forming the stacks, so as to minimize their root mean square deviation of atomic positions using the U3BEST algorithm (Kabsch, 1976). These optimized bases were hence taken to replace the original nonoptimized ones in the stacks. The Cartesian coordinates of the structures so obtained are given as PDB files (Berman et al., 2000) in the Supporting Information section.
The gas phase energies of the single-stranded and double-stranded stacks of optimized nucleobases, for the neutral and radical cationic species, were calculated at the M06-2X level with the 6-31G* basis set, using the same geometry for both species. Convergence problems of energy calculations were observed for the cationic state of some of the longer single-stranded and double-stranded nucleobase stacks. To avoid these problems, we used the wave function obtained for the neutral species, stored in the checkpoint file, as initial guess for the cationic state wave function. Moreover, we performed the energy calculations on the cationic species in two steps: first, we applied the simple 6-31G basis set and then used the resulting wave function as initial guess for a refined calculation using the 6-31G* set.
To calculate the vIP in gas phase of all considered nucleobase stacks, we used the method that works best for the individual nucleobases, which consists of considering the difference between the energy of the radical cationic species and of the neutral species, both adopting the (partially) optimized geometry of the neutral molecule. Finally, the charge distribution on the cationic molecules was estimated from the Mulliken population analysis (Mulliken, 1955). Similarly, the spin density, defined as the density difference of electrons of α-spins and β-spins, was also estimated from the Mulliken population analysis.
The omission of the sugar-phosphate backbone in all our calculations is primarily justified by the fact that their inclusion would require so much additional computer time and computer memory that the calculations on the long molecules considered here would be basically impossible. Besides this pragmatic reason, we have more fundamental justifications. In particular, calculations on Cyt and Thy indicated that the ionization energy is strongly affected by the presence of the sugar and phosphate moieties in gas phase, but much less upon bulk hydration, due to the screening ability of the aqueous solvent (Slavíček, Winter, Faubel, Bradforth, & Jungwirth, 2009). Moreover, ab initio calculations and experimental data showed that the lowest ionization pathway originates from the nucleobase rather than sugar-phosphate backbone (Fernando et al., 1998; Slavíček et al., 2009).
We also chose to disregard the solvent and to perform all calculations in gas phase, although solvation is described as impacting the electronic properties of DNA molecules (Cerón-Carrasco, Requena, Perpète, Michaux, & Jacquemin, 2010). We made this choice primarily to reduce computing requirements, but also because gas phase calculations appear suitable for comparing the vIP values of various nucleobase stack sequences and conformations. Indeed, calculations on individual nucleobases highlighted the effect of the solvent in lowering the vIP values while maintaining the relative ordering between the bases (Cauët, Valiev, & Weare, 2010; Close, 2004). Moreover, as discussed above, dropping both the sugar-phosphate backbone and the solvent have opposite effects that tend to cancel out (Slavíček et al., 2009).
Results and discussion
VIP of individual nucleobases
We first proceeded to the identification of an appropriate level of theory to properly compute the vIPs of isolated nucleobases, for which experimental data are available. Figure 1a shows the vIPs of the four nucleobases, computed as the energy difference between neutral and radical-cationic species with the same geometry, at different levels of calculation and with different basis sets. These results are compared with the experimental vIP ranges taken from the literature (Dougherty & McGlynn, 1977; Dougherty, Wittel, Meeks, & McGlynn, 1976; Dougherty, Younathan, Voll, Abdulnur, & McGlynn, 1978; Hush & Cheung, 1975; Lauer, Schäfer, & Schweig, 1975; Lias et al., 1988; Lin et al., 1980a; Lin et al., 1980b; Orlov, Smirnov, & Varshavsky, 1976; Padva, O'Donnell, & LeBreton, 1976; Roca-Sanjuán et al., 2006; Urano, Yang, & LeBreton, 1989; Yu, Peng, Akiyama, Lin, & LeBreton, 1978).
Figure 1.
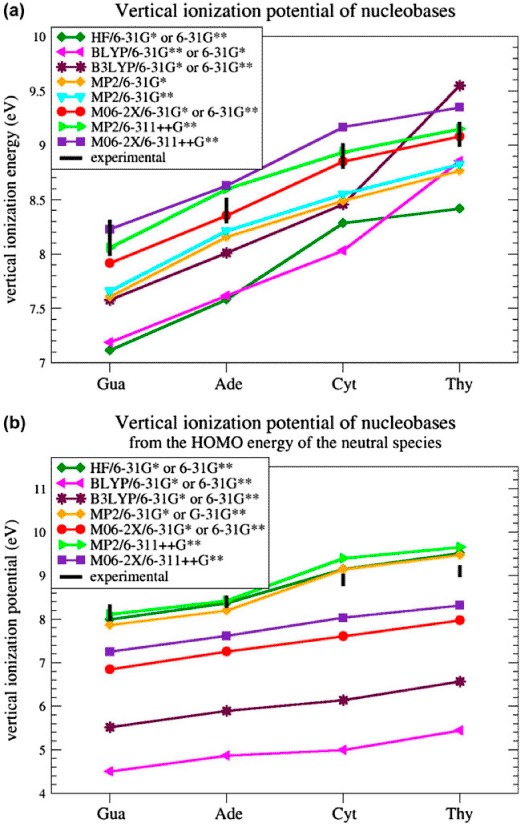
Vertical ionization potential computed (a) as the difference between the energies of the radical-cationic and neutral species in the same geometry and (b) as minus the HOMO energy of the neutral species, at different levels of theory and with different basis sets.
HF and BLYP calculations with a medium-size basis set (6-31G* and 6-31G**) were found to underestimate vIP values by about 1 eV on average, in accordance with previous works (Cauët et al., 2006; Crespo-Hernández et al., 2004; Roca-Sanjuán et al., 2006). MP2 and B3LYP with the same basis sets also gave underestimated vIP values, by about 0.5 eV. When adding diffuse functions to the basis set, in particular when using 6-311++G**, calculations at the MP2 and M06-2X levels gave better results but now slightly overestimate the vIPs: such overestimation occurs for two of the four nucleobases with MP2, and for three with M06-2X. The best results were obtained with M06-2X coupled to the medium-size basis sets 6-31G* or 6-31G**. Indeed, the vIPs of Ade, Cyt, and Thy are in the range of experimental vIPs and the vIP of Gua is underestimated by 0.1 eV only. Basically, no difference is observed between the basis sets 6-31G* and 6-31G** combined with M06-2X.
We thus use in all subsequent calculations the hybrid DFT method M06-2X with the simplest of the two basis sets, 6-31G*. Note that this result is in agreement with previous findings demonstrating that the M06-2X method, a DFT method with 54% HF exchange contribution, is effective for accurately estimating energies of stacked DNA base pairs (Gus, Wang, Leszczynski, Xie, & Schaefer, 2008; Hohenstein, Chill, & Sherrill, 2008; Kumar & Sevilla, 2011), as well as electron affinities and ionization potentials for DNA bases (Paukku & Hill, 2011).
Not only is M06-2X/6-31G* the best of the methods tested for our purposes, it is also less computer time- and memory consuming than MP2. This advantage is not clear for individual nucleobases, but it becomes obvious when considering large DNA stacks in various conformations, for which MP2 calculations are unable to converge on our computer cluster.
Finally, we also tested the approximation of calculating the vIPs as minus the HOMO energy of the (closed-shell) neutral species. The results are given in Figure 1b. Not any of the hybrid DFT calculations give satisfactory results; they all strongly underestimate the vIPs, in agreement with previous tests (Maksic & Vianello, 2002; Politzer & Abu-Awwad, 1998; Salzner & Baer, 2009; Stowasser & Hoffmann, 1999). MP2/6-31G* and MP2/6-31G** calculations do better but are not in the experimental range (Maksic & Vianello, 2002). MP2/6-311++G** calculations fall in the experimental range for two of the four nucleobases, and so do HF/6-31G*, and HF/6-31G** calculations. The HOMO-based approach with MP2/6-311++G**, HF/6-31G* and HF/6-31G** calculations performs thus well for estimating vIPs, but not as well as the straightforward method described above, consisting of computing the difference between the energies of the cationic and neutral species with M06-2X/6-31G*. Note, however, that the HOMO-based method has the advantage of being much faster – it does not require computing the energy of the radical cationic species. In spite of this advantage, and given that the cationic state calculations are in any case necessary to study the charge and spin density distributions, we continue to estimate the vIPs as the energy difference between cationic and neutral species, using M06-2X/6-31G*. This choice is, moreover, also motivated by the fact that HF calculations are known to be inadequate for estimating dispersion energies and hence stacking interactions (Hobza, Šponer, & Polasek, 1995). This is an obvious shortcoming for our purposes, which cannot be detected from calculations on individual bases, and definitely disqualifies HF.
VIP of poly-nucleobase stacks
The vIPs for single-stranded poly-Ade, poly-Gua, poly-Cyt, poly-Thy and poly-Gua/Cyt stacks, consisting of one to ten stacked nucleobases, were computed at the
M06-2X level using the basis set 6-31G*. The results are given in Figure 2a and Table S1 of Supporting Information. Clearly, nucleobase stacking significantly lowers the vIP values in all the modeled stacks. The vIP decreases as the length of the stacks increases, but the decrease is strongest for shorter stacks, in agreement with previous calculations (Kumar & Sevilla, 2011; Saito et al., 1995; Saito et al., 1998; Sugiyama & Saito, 1996). The Gua-stacks reach by far the lowest vIPs (6.3 eV for the decamer in A-form), followed by Ade-stacks (7.1 eV for the decamer in both forms), Cyt-stacks (7.3 eV for the decamer in B-form), and Thy-stacks (7.6 eV for the decamer in A-form). For Gua- and Thy-stacks, the A-forms reach lower vIPs than the B-forms. For Ade-stacks, both forms yield the same vIPs, whereas for Cyt-stacks, the B-form yields lower vIPs than the A-form. The Gua/Cyt-stacks, in Z-conformation, yield vIPs in the same range as Ade-stacks for short strands, and as Cyt-stacks for longer strands. Here, the vIP's decrease with length is less pronounced: it decreases when a Gua base is added, and remains almost constant when a Cyt base is added.
Figure 2.
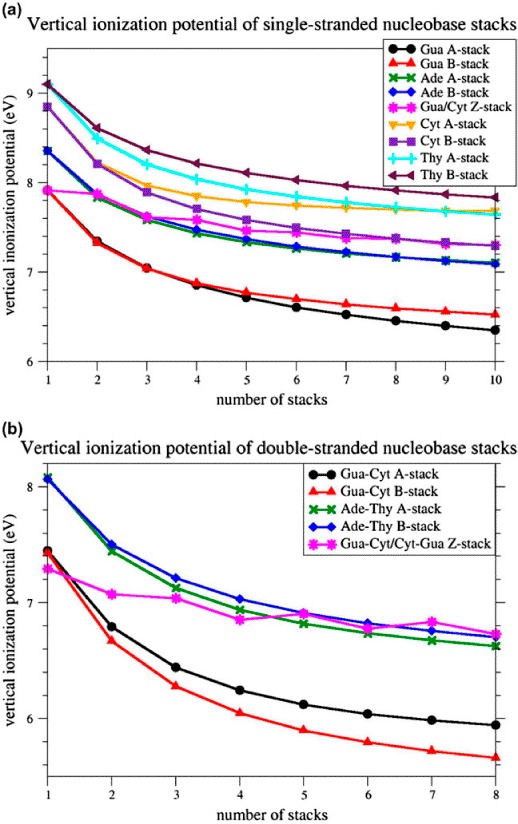
Vertical ionization potential for homo-nucleobase stacks in standard A-, and B-conformation, and for alternating Gua/Cyt nucleobase stacks in standard Z-conformation, computed at M06-2X/6-31G* level of theory. (a) single-stranded nucleobase stacks from monomer to decamer; (b) double-stranded nucleobase tracts from monomer to octamer.
Both the nucleobase sequence and conformation are thus found to affect the vIPs. However, the vIP variation due to sequence changes are larger than those due to conformational changes, at least for the sequences and conformations tested. Indeed, the largest vIP difference observed between two sequences is equal to 1.3 eV and occurs between decameric poly-Gua and poly-Thy stacks, whereas the largest vIP differences observed between two conformations is 0.4 eV and occurs between decameric poly-Cyt stacks in A- and B-form. The conformation can thus roughly be estimated to influence vIPs three times less than the sequence. Note that a previous computational study had reported a smaller vIP difference (0.04 eV instead of 0.12eV) between A- and B-form for a di-nucleobase pair Gua ≡ Cyt stack, using HF level of theory and Koopman's theorem (Sugiyama & Saito, 1996). Here, on the basis of an exhaustive analysis on much longer nucleobase stacks, and with an appropriate level of theory for studying stacking interactions, we highlighted a significant effect of DNA conformation.
The vIPs for double-stranded poly Ade = Thy, poly Gua ≡ Cyt and poly Gua ≡ Cyt/Cyt ≡ Gua tracts, containing one up to 8 stacked nucleobase pairs, are depicted in Figure 2b and given in Table S2. The decrease in the vIP with the number of stacked bases is similar to that for the single-stranded stacks: it is quite pronounced for all stacks except for the Z-form Gua ≡ Cyt/Cyt ≡ Gua tracts. B-form Gua ≡ Cyt tracts reach the lowest vIPs (5.7 eV for the octamer), followed by A-form Gua ≡ Cyt tracts (5.9 eV), A-form Ade = Thy tracts (6.6 eV), and B-form Ade = Thy tracts (6.7 eV). In Z-conformation, the Gua ≡ Cyt base pair has the lowest vIP of all individual base pairs (7.3 eV), and the octameric Gua ≡ Cyt/ Cyt ≡ Gua tract reaches ex æquo the highest vIP (6.7 eV).
Clearly, two single-stranded DNA stacks have separately higher vIPs than when they are associated to form a double-stranded tract. For example, a Gua-stack and a Cyt-stack of 5 nucleobases each, in B-form, have vIPs equal to 6.8 and 7.6 eV, respectively, whereas the corresponding double-stranded B-form Gua ≡ Cyt tract has a vIP of 5.9 eV. Even a single-stranded Gua stack of 10 bases has a higher vIP (6.5 eV) than a Gua ≡ Cyt tract of 5 base pairs (5.9 eV). So, the association of two single-stranded stacks into a double-stranded tract significantly lowers the vIP
We observe, thus, a double effect in double-stranded nucleobase tracts, consisting of the vIP lowering both by base stacking and by H-bonding to the complementary strand. The relative strength of these effects can be estimated from individual nucleobases: the vIP values of Gua and Cyt bases are equal to 7.9 and 8.8 eV, respectively, of a Gua ≡ Cyt pair to 7.4 eV, and of a Gua/Gua and Cyt/Cyt stack to 7.3 and 8.2 eV. Hence, we can estimate the stacking effect to decrease the vIP by 0.6 eV, and the H-bonding effect to decrease the lowest of the two bases’ vIP by 0.5 eV. These estimations depend slightly on the type of sequence and conformation and diminish with the number of nucleobases involved. We can, thus, conclude that the effects of stacking and H-bonding on the vIP's decrease are of the same order of magnitude.
Mulliken charge and spin density distributions on nucleobase stacks
The charge distribution on all the radical-cationic single- and double-stranded nucleobase stacks was estimated from the Mulliken population analysis. The spin density, representing the distribution of unpaired electrons, was estimated in a similar way.
For single-stranded stacks, the results are given in Figures 3 and 4a, Table S3 and Figure S1. The charge distribution basically coincides with the spin density distribution, up to a few percent at most. It differs according to both sequence and structure, but larger variations are observed according to sequence. The charge is more localized at the 5′-terminus for Gua-stacks and at the 3′-end for Cyt-stacks. This tendency is more pronounced for A-form than for B-form stacks. For Ade- and Thy-stacks, the charge is quite delocalized over all nucleobases, with a smaller amount on the terminal bases, especially the 5′ base. For Z-DNA, the partial charges are essentially located on the Gua bases, with a larger fraction on the 5′-end Gua.
Figure 3.
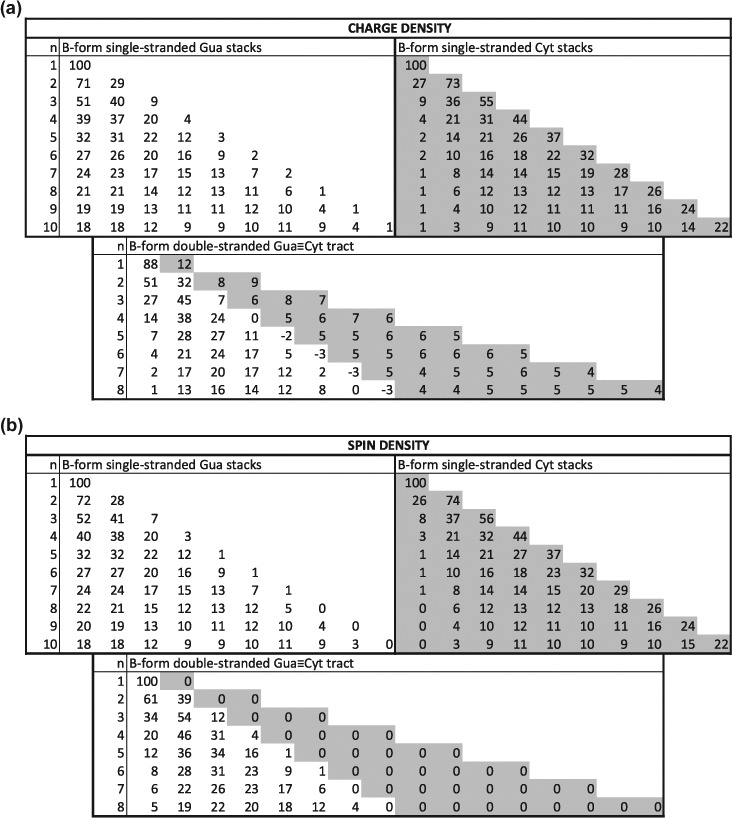
Mulliken charge and spin density distribution (in %) of B-form single-stranded homo-Gua and Cyt stacks, from one to 10 bases, and of B-form double-stranded Gua ≡ Cyt tracts, from one to 8 base pairs, calculated at M06-2X level of theory with 6-31G* basis set; n indicates the number of successive bases for single strands and of base pairs for double strands; for double strands, the densities are given for the first strand, from 5′ to 3′, on white background, and then for the second strand, from 5′ to 3′, on gray background. (a) Charge density; (b) Spin density.
Figure 4.
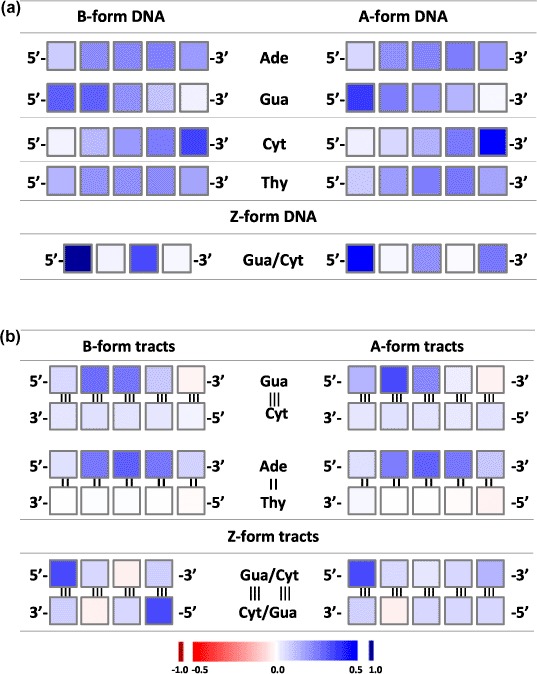
Mulliken charge distribution per nucleobase for homo-5-nucleobase stacks in standard A-, and B-conformation, and for alternating Gua/Cyt 4- and 5-nucleobase stacks in standard Z-conformation, computed at M06-2X/6-31G* level of theory. (a) single-stranded DNA; (b) double-stranded DNA. The color ramp is given at the bottom of the figure.
For double-stranded stacks, the charge and spin density distributions are given in Figures 3 and 4b, Table S4 and Figure S2. They appeared to be very different from the distributions on single strands. For Ade = Thy tracts, the charge is essentially distributed over the whole Adestrand, with a smaller amount on the 3′-Ade and even less on the 5′-Ade. On the Thy-strand, the bases carry a very small positive, vanishing, or even negative charge. For Gua ≡ Cyt tracts, a small but non-negligible fraction of the positive charge is distributed almost evenly on the Cyt-strand. Yet, the vast majority of the charge is on the Gua strand, mostly toward the 5′-end. The maximum of the distribution is on the first Gua for the dimer, on the second Gua from trimer to pentamer, and on the third Gua from hexamer to octamer in B-form tracts; for A-form tracts, the maximum remains on the second Gua. The Gua base at the 3′-end even carry a slightly negative partial charge for the longer stacks. Note finally that the charge delocalization is somewhat more pronounced on the B-form than on the A-form for Gua ≡ Cyt tracts and that the opposite is observed for the Ade = Thy tracts.
For the double-stranded Z-form nucleobase tracts, the charge is essentially localized on the two 5′-terminal Gua bases for tracts with an even number of nucleobase pairs, and on the 5′-terminal Gua and somewhat on the 3′-terminal Gua for tracts with an uneven number of base pairs. Some bases, mostly cytosines but sometimes guanines, carry a small negative partial charge.
The spin density distribution is significantly different from the charge distribution in double-stranded tracts, in contrast to what is observed for single-stranded stacks. Indeed, although both strands carry a – although uneven – part of the charge, only one of the strands carries the spin density, for homo-base pair stacks. More precisely, the spin density is basically exactly zero on the Thy-strand of all the considered Ade = Thy tracts, and on the Cyt-strand of all the Gua ≡ Cyt tracts in A- and B-form. Hence, according to our calculations, only the Ade- and Gua-strands show chemical reactivity. In the Z-form tracts, there is also an important difference between charge and spin density distributions: both are distributed over the two strands, but exclusively on Gua bases for the spin and with some small part on the Cyt bases for the charge.
The delocalized nature of the electron hole distribution is supported by numerous experimental and theoretical works (Barnett et al., 2001; Blancafort & Voityuk, 2006; Bravaya, Kostko, Ahmed, & Krylov, 2010; Conwell & Basko, 2001; Conwell, 2005; Golubeva & Krylov, 2009; Henderson, Jones, Hampikian, Kan, & Schuster, 1999; Improta, 2008; Kubar & Elstner, 2009; Kumar & Sevilla, 2011; Kurnikov, Tong, Madrid, & Beratan, 2002; Lange & Herbert, 2009; Lewis, Cheatham, Starikov, Wang, & Sankey, 2003; Santoro, Barone, & Improta, 2009; Schuster, 2009; Shao, Augustyn, & Barton, 2005; Steinbrecher, Koslowski, & Case, 2008; Voityuk, 2005). Being the most easily oxidized base, Gua-stacks have been the most studied. In a double-stranded Gua ≡ Cyt tract of two base pairs, it is experimentally established that the hole is mainly localized on the 5′-Gua (Hall et al., 1996; Sugiyama & Saito, 1998), in agreement with our calculations. Electron spin resonance experiments at 77 K on Gua = Cyt tracts of three base pairs also located preferentially the hole at the 5′-Gua, but with significant amounts on the middle and the 3′-end guanines (Adhikary, Khanduri, & Sevilla, 2009). Our results slightly deviate from the latter findings: in Gua ≡ Cyt tracts of three base pairs, the positive charge is essentially located on the first two Gua's, with a maximum on the second. These discrepancies might partly be attributed to differences in nucleobase stack conformations.
Furthermore, a previous computational results on optimized single-stranded Ade-stacks of 1 to 8 bases showed a preferential localization of the hole on the second Ade base from 5′-end (Kumar & Sevilla, 2011), whereas we found it rather evenly distributed over the whole length of the stack except the terminal bases. The difference can be attributed to the fact that these authors use optimized B-form stacks and, moreover, optimize both the neutral and cationic species; this interpretation is again consistent with our findings that the charge distribution varies according to the conformation of the stacks.
We also analyzed the charge distribution on the different atoms that constitute the nucleobases. Figure 5 and S3 show the difference in charge distribution between the charged and neutral molecular species. In double-stranded Gua ≡ Cyt tracts, the additional positive charge carried by the cationic species is mostly located on the H-atom attached to C8 of Gua, on the O-atom linked to C6 and on N2 and N3. Some differences are visible according to whether DNA is in A- or B- or Z-conformation, or according to the position in the stack. For example, the N7 and/or C5 atoms carry an extra positive partial charge on the nucleobases that carry such a charge and carry a negative partial charge otherwise instead of being neutral like other atoms. In double-stranded tracts, the Cyt bases carry no charge, but in single-stranded stacks, they carry the extra positive charge on the extracyclic O- and H-atoms except those linked to N4-C4, and on the N3 atom and sometimes the N1 and C5 atoms of the cycle.
Figure 5.
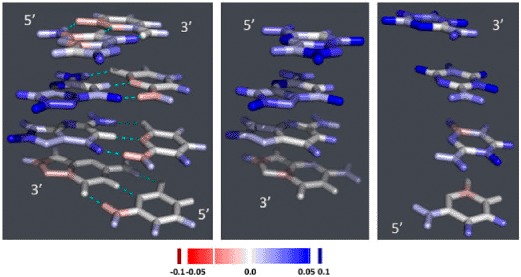
Difference in charge distribution between the radical-cationic nucleobase stacks and the corresponding neutral stacks: 4-nucleobase stacks in B-conformation. The figures are drawn using PYMOL (DeLano, 2002). Left: double-stranded Gua≡Cyt tract; middle: single-stranded Gua-stack; right: single-stranded Cyt-stack. The color ramp used is depicted at the bottom of the figure.
Finally, note that most of our results are in agreement with existing experimental data and previous calculations and those that are not may be attributed – at least in part – to different calculation levels or to the fact that the studied conformations are not identical, which, as we have shown, may entail significant variations of the electronic properties.
Concluding remarks
We found that the M06-2X hybrid density functional theory with the 6-31G* basis set is particularly suitable for the calculation of the properties resulting from one-electron oxidation, as previously noted (Paukku & Hill, 2011). This level of theory allows obtaining reliable vIP values, as compared to experimental values obtained for individual nucleobases, in a relatively short computational time. All the molecules we consider are built from individual nucleobases whose structures are optimized at M06-2X/6-31G* level of theory. In contrast, we chose not to optimize the stacks themselves, but to use the stacks modeled in standard conformations. Indeed, the optimization of stacks in the absence of the sugar-phosphate backbone and the solvent are likely to lead to unphysical structures that may be very different from the standard conformations. Note that another approach developed to select relevant geometries and to monitor their fluctuations is based on molecular dynamics simulations (Svozil, Hobza, & Šponer, 2010).
Our main conclusion is that the vIPs are not only extremely sensitive to the nucleobase sequence, but also depend significantly on the conformation. For single-stranded stacks, differences of 0.2 eV are observed between A- and B-forms Gua- or Thy-stacks of 10 bases, and of 0.4 eV for 10-base Cyt-stacks. For double-stranded tracts, the difference between A- and B-forms is of 0.3 eV for 8-base pair Gua ≡ Cyt tracts, and of 0.1 eV for Ade = Thy tracts. We must emphasize, however, that the vIPs depend less crucially on conformation than on sequence. Indeed, differences of 1.3 eV are observed between single-stranded 10-base Gua- and Thy-stacks, and of 1.0 eV between double-stranded 8-base pair Gua ≡ Cyt and Ade = Thy tracts.
Similarly, the charge and spin density distributions on the cationic species vary with both sequence and structure. For single-stranded stacks, the charge is highest at the 5′-terminus for Gua-stacks, and at the 3′-terminus for Cyt-stacks. For Ade- and Thy-stacks, it is basically distributed over all bases. Variations of these trends are observed between the A- and B-forms. For Z-form Gua/Cyt stacks, the densities are essentially localized on Gua bases, with a preference for those positioned near the 5′-end. For double-stranded tracts, the charge is almost completely distributed on the Gua strand for Gua ≡ Cyt tracts, and on the Ade strand for Ade = Thy tracts; the Thy strand is even slightly negatively charged. For Z-form tracts, it is preferentially located on the Gua bases situated at the 3′-end and especially at the 5′-end. The distributions of charge and spin densities are very similar for single-stranded stacks, but display significant differences for double-stranded tracts. For example, the spin density is equal to zero on the Thy- and Cyt-strand of Ade = Thy and Gua ≡ Cyt tracts, both in B- and in A-form, and on the Cyt-bases of the Z-form tracts, which is not the case for the charge density. The localization is thus much more clear-cut for spin density – and thus for chemical reactivity – than for charge.
In conclusion, our results show that the vIP, charge and spin density distributions change along DNA strands or duplexes as a function of the nucleobase sequence, in agreement with earlier findings. This may be viewed as a spatial dependence: given a DNA molecule with a specific sequence – for example, a genome – the vIP, charge and spin density vary as a function of the position along it. The novel result is that, in addition, the vIP, charge and spin density vary at each position of the DNA molecule according to the conformation – even though this variation is roughly three times smaller. This may be viewed as a time dependence: the flexibility of the DNA molecule, or at least of some regions, entail conformational variations and thus continuous changes in vIP, charge and spin density. This time dependence may have biological implications. Indeed, many transcription factors modify the conformation of DNA upon binding and thus its electronic properties. On the other hand, many transcription factors bind DNA through positively charged amino acids, often forming cation-π interactions with the nucleobases (Rooman, Liévin, Buisine, & Wintjens, 2002; Wintjens, Liévin, Rooman, & Buisine, 2000); as a consequence, the protein/DNA-binding affinities are affected by the time-varying electronic properties of DNA.
Associated content
Supporting Information
Detailed values of the vIP, the charge density and the spin density, for all single- and double-stranded nucleobase stacks considered in this study, as well as the structures (in PDB format (Berman et al., 2000)) of A-, B- and Z-form decameric double-stranded nucleobase tracts.
Supplementary material
The supplementary material for this paper is available online at http://dx.doi.10.1080/07391102.2013.783508.
Acknowlegments
MR and RW are Research Director and Research Associate, respectively, at the National Fund for Scientific Research FNRS-FRS (Belgium), which is gratefully acknowledged for support. We also thank Jean Marc Kwasigroch for computer assistance.
References
- Adhikary A., Khanduri D., Sevilla M. D. Direct observation of the hole protonation state and hole localization site in DNA-oligomers. Journal of the American Chemical Society. 2009;131:8614–8619. doi: 10.1021/ja9014869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arnott S. The geometry of nucleic acids. Progress in Biophysics and Molecular Biology. 1970;21:265–319. doi: 10.1016/0079-6107(70)90027-1. [DOI] [PubMed] [Google Scholar]
- Arnott S., Hukins D. W. L. Optimised parameters for A-DNA and B-DNA. Biochemical and Biophysical Research Communications. 1972;47:1504–1509. doi: 10.1016/0006-291x(72)90243-4. [DOI] [PubMed] [Google Scholar]
- Arnott S., Hukins D. W. L., Rubin J., Brennan J., Sundaralingam M. Nucleotide conformations. Science. 1972;177:451–452. doi: 10.1126/science.177.4047.451. [DOI] [PubMed] [Google Scholar]
- Barnett R. N., Cleveland C. L., Joy A., Landman U., Schuster G. B. Charge migration in DNA: Iongated transport. Science. 2001;294:567–571. doi: 10.1126/science.1062864. [DOI] [PubMed] [Google Scholar]
- Becke A. D. Density-functional exchange-energy approximation with correct asymptotic behavior. Physical Review A. 1988;38:3098–3100. doi: 10.1103/physreva.38.3098. [DOI] [PubMed] [Google Scholar]
- Berman H. M., Westbrook J., Feng Z., Gilliland G., Bhat T. N., Weissig H., Bourne P. E. The protein data bank. Nucleic Acids Research. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blancafort L., Voityuk A. A. CASSCF/CAS-PT2 study of hole transfer in stacked DNA. Journal of Physical Chemistry A. 2006;110:6426–6432. doi: 10.1021/jp061184s. [DOI] [PubMed] [Google Scholar]
- Bongiorno A. Energy landscape of an electron hole in hydrated DNA. Journal of Physical Chemistry B. 2009;112:13945–13950. doi: 10.1021/jp801872e. [DOI] [PubMed] [Google Scholar]
- Boon E. M., Barton J. K. Charge transport in DNA. Current Opinion in Structural Biology. 2002;12:320–329. doi: 10.1016/s0959-440x(02)00327-5. [DOI] [PubMed] [Google Scholar]
- Bravaya K. B., Kostko O., Ahmed M., Krylov A. I. The effect of π-stacking, h-bonding, and electrostatic interactions on the ionization energies of nucleic acid bases: Adenine-adenine, thymine-thymine and adenine-thymine dimmers. Physical Chemistry Chemical Physics: PCCP. 2010;12:2292–2307. doi: 10.1039/b919930f. [DOI] [PubMed] [Google Scholar]
- Cauët E., Dehareng D., Liévin J. Ab initio study of the ionization of the DNA bases: Ionization potentials and excited states of the cations. Journal of Physical Chemistry A. 2006;110:9200–9211. doi: 10.1021/jp0617625. [DOI] [PubMed] [Google Scholar]
- Cauët E., Valiev M., Weare J. H. Vertical ionization potentials of nucleobases in a fully solvated DNA environment. Journal of Physical Chemistry B. 2010;114:5886–5894. doi: 10.1021/jp9120723. [DOI] [PubMed] [Google Scholar]
- Cerón-Carrasco J. P., Jacquemin D. Interplay between hydroxyl radical attack and H-bond stability in guanine-cytosine. RSC Advances. 2012;2:11867–11875. [Google Scholar]
- Cerón-Carrasco J. P., Requena A., Perpète E. A., Michaux C., Jacquemin D. Theoretical study of the tau-tomerism in the one-electron oxidized guanine-cytosine base pair. Journal of Physical Chemistry B. 2010;114:13439–13445. doi: 10.1021/jp101711z. [DOI] [PubMed] [Google Scholar]
- Chakraborty T. Charge migration in DNA: Perspectives from physics, chemistry and biology. Berlin: Springer Verlag; 2007. [Google Scholar]
- Clark T., Chandrasekhar J., Spitznagel G. W., Schleyer P. V. R. Efficient diffuse function-augmented basissets for anion calculations. 3. The 3–21+G basis set for the 1st-row elements, Li-F. Journal of Computational Chemistry. 1983;4:294–301. [Google Scholar]
- Close D. M. Oxidative damage to cytosine: Implication for the study of radiation-induced damage to DNA. Journal of Physical Chemistry B. 2003;107:864–867. [Google Scholar]
- Close D. M. Calculation of the ionization potentials of the DNA bases in aqueous medium. Journal of Physical Chemistry A. 2004;108:10376–10379. [Google Scholar]
- Close D. M., Øhman K. T. Ionization energies of the nucleotides. Journal of Physical Chemistry A. 2008;112:11207–11212. doi: 10.1021/jp805308p. [DOI] [PubMed] [Google Scholar]
- Colson A.-O., Besler B., Sevilla M. D. Ab initio molecular orbital calculations on DNA base pair radical ions: Effect of base pairing on proton-transfer energies, electron affinities, and ionization potentials. Journal of Physical Chemistry. 1993;97:13852–13859. [Google Scholar]
- Colson A.-O., Sevilla M. D. Elucidation of primary radiation damage in DNA through application of ab initio molecular orbital theory. International Journal of Radiation Biology. 1995;67:627–645. doi: 10.1080/09553009514550751. [DOI] [PubMed] [Google Scholar]
- Conwell E. M. Charge transport in DNA: The role of polarons. Proceedings of the National academy of Sciences of the USA. 2005;102:8795–8799. doi: 10.1073/pnas.0501406102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conwell E. M., Basko D. M. Hole traps in DNA. Journal of the American Chemical Society. 2001;123:11441–11445. doi: 10.1021/ja015947v. [DOI] [PubMed] [Google Scholar]
- Crespo-Hernández C. E., Arce R., Ishikawa Y., Gorb L., Leszczynski J., Close D. M. Ab initio ionization energy thresholds of DNA and RNA bases in gas phase and in aqueous solution. Journal of Physical Chemistry A. 2004;108:6373–6377. [Google Scholar]
- DeLano W. L. The PyMOL molecular graphics system, delano scientific. 2002. San Carlos, CA. Retrieved from http://www.pymol.org.
- Ditchfield R., Hehre W. J., Pople J. A. Self-consistent molecular orbital methods. 9. Extended Gaussian-type basis for molecular orbital studies of organic molecules. Journal of Chemical Physics. 1971;54:724–728. [Google Scholar]
- Dougherty D., McGlynn S. P. Photoelectron spectroscopy of carbonyls. Biological molecules. Journal of Chemical Physics. 1977;67:1289–1290. [Google Scholar]
- Dougherty D., Wittel K., Meeks J., McGlynn S. P. Photoelectron spectroscopy of carbonyls. Ureas, uracils and thymine. Journal of the American Chemical Society. 1976;98:3815–3820. doi: 10.1021/ja00429a013. [DOI] [PubMed] [Google Scholar]
- Dougherty D., Younathan E. S., Voll R., Abdulnur S., McGlynn S. P. Photoelectron spectroscopy of some biological molecules. Journal of Electron Spectroscopy and related Phenomena. 1978;13:379–393. [Google Scholar]
- Fernando H., Papadantonakis G. A., Kim N. S., LeBreton P. R. Conduction-band-edge ionization thresholds of DNA components in aqueous solution. Proceedings of the National academy of Sciences of the USA. 1998;95:5550–5555. doi: 10.1073/pnas.95.10.5550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frisch M. J., Trucks G. W., Schlegel H. B., Scuseria G. E., Robb M. A., Cheeseman J. R., Fox D.J. Gaussian 09, Revision B.01. Wallingford, CT: Gaussian, Inc; 2010. [Google Scholar]
- Frisch M. J., Pople J. A., Binkley J. S. Self-consistent molecular orbital methods. 25. Supplementary functions for Gaussian basis sets. Journal of Chemical Physics. 1984;80:3265–3269. [Google Scholar]
- Genereux J., Boal A., Barton J. DNA-mediated charge transport in redox sensing and signaling. Journal of the American Chemical Society. 2010;132:891–905. doi: 10.1021/ja907669c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gervasio F. L., Boero M., Parrinello M. Double proton coupled charge transfer in DNA. Angewandte Chemie International Edition. 2006;45:5606–5609. doi: 10.1002/anie.200602106. [DOI] [PubMed] [Google Scholar]
- Giese B. Long-distance transport in DNA: The hopping mechanism. Accounts of Chemical Research. 2000;33:631–636. doi: 10.1021/ar990040b. [DOI] [PubMed] [Google Scholar]
- Giese B. Long-distance electron transfer through DNA. Annual Review of Biochemistry. 2002;71:51–70. doi: 10.1146/annurev.biochem.71.083101.134037. [DOI] [PubMed] [Google Scholar]
- Golubeva A. A., Krylov A. I. The effect of -stacking and H-bonding on ionization energies of a nucleobase: Uracil dimer cation. Physical Chemistry Chemical Physics: PCCP. 2009;11:1303–1311. doi: 10.1039/b817284f. [DOI] [PubMed] [Google Scholar]
- Gus J. D., Wang J., Leszczynski J., Xie Y. M., Schaefer H. F. To stack or not to stack: Performance of a new density functional for the uracil and thymine dimers. Chemical Physics Letters. 2008;458:164–166. [Google Scholar]
- Hall D. B., Holmlin R. E., Barton J. Oxidative DNA damage through long-range electron transfer. Nature. 1996;382:731–735. doi: 10.1038/382731a0. [DOI] [PubMed] [Google Scholar]
- Hariharan P. C., Pople J. A. Influence of polarization functions on MO hydrogenation energies. Theoretica Chimica Acta. 1973;28:213–222. [Google Scholar]
- Heller A. On the hypothesis of cathodic protection of genes. Faraday Discussions. 2000;116:1–13. doi: 10.1039/b006196o. [DOI] [PubMed] [Google Scholar]
- Henderson P. T., Jones D., Hampikian G., Kan Y. Z., Schuster G. B. Long-distance charge transport in duplex DNA: The phonon-assisted polaron-like hopping mechanism. Proceedings of the National Academy of Sciences of the USA. 1999;96:8353–8358. doi: 10.1073/pnas.96.15.8353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hobza P., Šponer J., Polasek M. H-bonded and stacked base pairs: Cytosine dimer. An ab initio second Moller-Plesset study. Journal of the American Chemical Society. 1995;117:792–798. [Google Scholar]
- Hohenstein E. G., Chill S. T., Sherrill C. D. Assessment of the performance of the M05-2X and M06-2X exchange-correlation functional for noncovalent interactions in biomolecules. Journal of Chemical Theory and Computation. 2008;4:1996–2000. doi: 10.1021/ct800308k. [DOI] [PubMed] [Google Scholar]
- Hush N. S., Cheung A. S. Ionization potentials and donor properties of nucleic acid bases and related compounds. Chemical Physics Letters. 1975;34:11–13. [Google Scholar]
- Improta R. The excited states of π-stacked 9-methyladenine oligomers: A TD-DFT study in aqueous solution. Physical Chemistry Chemical Physics: PCCP. 2008;10:2656–2664. doi: 10.1039/b718562f. [DOI] [PubMed] [Google Scholar]
- Kabsch W. A solution for the best rotation to relate two sets of vectors. Acta Crystallographica A. 1976;32:922–923. [Google Scholar]
- Koopmans T. Uber die Zuordnung von wellenfunktionen und eigen-werten zu den einzelnen elektronen eines atom. Physica. 1934;1:104–113. [Google Scholar]
- Kubar T., Elstner M. Solvent reorganization energy of hole transfer in DNA. Journal of Physical Chemistry B. 2009;113:5653–5656. doi: 10.1021/jp901888r. [DOI] [PubMed] [Google Scholar]
- Kumar A., Sevilla M. D. Proton-coupled electron transfer in DNA on formation of radiation-produced ion radicals. Chemical Reviews. 2010;110:7002–7023. doi: 10.1021/cr100023g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar A., Sevilla M. D. Density functional theory studies of the extent of the hole delocalization in one-electron oxidized adenine and guanine base stacks. Journal of Physical Chemistry B. 2011;115:4990–5000. doi: 10.1021/jp200537t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kurnikov I. V., Tong G. S. M., Madrid M., Beratan D. N. Hole size and energetics in double helical DNA: Competition between quantum delocalization and solvation localization. Journal of Physical Chemistry B. 2002;106:2381–2392. [Google Scholar]
- Lange A. W., Herbert J. M. Both intra- and inter-strand charge-transfer excited states in aqueous B-DNA are present at energies comparable to, or just above, the 1ππ* excitonic bright state. Journal of the American Chemical Society. 2009;131:3913–3922. doi: 10.1021/ja808998q. [DOI] [PubMed] [Google Scholar]
- Lauer G., Schäfer W., Schweig A. Functional sub-units in the nucleic acid bases uracil and thymine. Tetrahedron Letters. 1975;45:3939–3942. [Google Scholar]
- Lee C., Yang W., Parr R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Physical Review B. 1988;37:785–789. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- Lewis J. P., Cheatham T. E., Starikov E. B., Wang H., Sankey O. F. Dynamically amorphous character of electronic states in poly(dA)-poly(dT) DNA. Journal of Physical Chemistry B. 2003;107:2581–2587. [Google Scholar]
- Lias S. G., Bartmess J. E., Liebman J. F., Holmes J. L., Levin R. D., Mallard W. G. Gas-phase ion and neutral thermochemistry. Journal of Physical and Chemical Reference Data. 1988;17(Suppl. 1):1–861. [Google Scholar]
- Lin J., Yu C., Peng S., Akiyama I., Li K., Lee L. K., Lebreton P. R. Ultraviolet photoelectron studies of the ground-state electronic structure and gas-phase tau-tomerism of purine and adenine. Journal of the American Chemical Society. 1980a;102:4627–4631. [Google Scholar]
- Lin J., Yu C., Peng S., Akiyama I., Li K., Lee L. K., Lebreton P. R. Ultraviolet photoelectron studies of the ground-state electronic structure and gas-phase tau-tomerism of hypoxanthine and guanine. Journal of Physical Chemistry. 1980b;84:1006–1012. [Google Scholar]
- Maksic Z. B., Vianello R. How good is Koopman's approximation? G2(MP2) study of the vertical and adiabatic ionization potentials od some small molecules. Journal of Physical Chemistry A. 2002;106:6515–6520. [Google Scholar]
- Merino E. J., Boal A. K., Barton J. K. Biological contexts for DNA charge transport chemistry. Current Opinion in Chemical Biology. 2008;12:229–237. doi: 10.1016/j.cbpa.2008.01.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miehlich B., Savin A., Stoll H., Preuss H. Results obtained with the correlation-energy density functionals of Becke and Lee, Yang and Parr. Chemical Physics Letters. 1989;157:200–206. [Google Scholar]
- Møller C., Plesset M. S. Note on an approximation treatment for many-electron systems. Physical Review. 1934;46:618–622. [Google Scholar]
- Mulliken R. S. Electronic population analysis on LCAO-MO molecular wave functions. I. Journal of Chemical Physics. 1955;23:1833–1840. [Google Scholar]
- Orlov V. M., Smirnov A. N., Varshavsky Y. M. Ionization potentials and electron-donor ability of nucleic acid bases and their analogues. Tetrahedron Letters. 1976;17:4315–4395. [Google Scholar]
- Padva A., O'Donnell T. J., LeBreton P. R. UV photoelectron studies of biological pyrimidines: The valence electronic structure of methyl substituted uracils. Chemical Physics Letters. 1976;41:278–282. [Google Scholar]
- Paukku Y., Hill G. Theoritical determination of one-electron redox potentials for DNA bases, base pairs, and stacks. Journal of Physical Chemistry A. 2011;115:4804–4810. doi: 10.1021/jp201281t. [DOI] [PubMed] [Google Scholar]
- Politzer P., Abu-Awwad F. A comparative analysis of Hartree-Fock and Kohn-Sham orbital energies. Theoretical Chemistry Accounts. 1998;99:83–87. [Google Scholar]
- Prat F., Houk K. N., Foote C. S. Effect of guanine stacking on the oxidation of 8-oxoguanine in B-DNA. Journal of the American Chemical Society. 1998;120:845–846. [Google Scholar]
- Roca-Sanjuán D., Rubio M., Merchán M., Serrano-Andrés L. An initio determination of the ionization potentials of DNA and RNA nucleobases. Journal of Chemical Physics. 2006;125:084302. doi: 10.1063/1.2336217. [DOI] [PubMed] [Google Scholar]
- Rooman M., Cauët E., Liévin J., Wintjens R. Conformations consistent with charge migration observed in DNA and RNA X-ray structures. Journal of Biomolecular Structure & Dynamics. 2011;28:949–953. doi: 10.1080/073911011010524985. [DOI] [PubMed] [Google Scholar]
- Rooman M., Liévin J., Buisine E., Wintjens R. Cation-/H-bond stair motifs at protein-DNA interface. Journal of Molecular Biology. 2002;319:67–76. doi: 10.1016/s0022-2836(02)00263-2. [DOI] [PubMed] [Google Scholar]
- Roothaan C. C. J. New developments in molecular orbital theory. Reviews of Modern Physics, 23, 69–89. 1951.
- Saenger W. Principles of nucleic acid structure. New-York, NY: Springer-Verlag; 1984. [Google Scholar]
- Saito I., Nakamura T., Nakatani K., Yoshioka Y., Yamaguchi K., Sugiyama H. Mapping of the hot spots for DNA damage by one-electron oxidation: Efficacy of GG doublets and GGG triplets as a trap in long-range hole migration. Journal of the American Chemical Society. 1998;120:12686–12687. [Google Scholar]
- Saito I., Takayama M., Sugiyama H., Nakatani K. Photoinduced DNA cleavage via electron transfer: Demonstration that guanine residues located 5’ to guanine are the most electron-donating sites. Journal of the American Chemical Society. 1995;117:6406–6407. [Google Scholar]
- Salzner U., Baer R. Koopman's springs to life. Journal of Chemical Physics, 131, 231101-231104. 2009. [DOI] [PubMed]
- Santoro F., Barone V., Improta R. The excited states decay of the A-T DNA: A PCM/TD-DFT study in acqueous solution of the (9-methyl-adenine)2(1-methyl-thymine)2 stacked tetramer. Journal of the American Chemical Society. 2009;131:15232–15245. doi: 10.1021/ja904777h. [DOI] [PubMed] [Google Scholar]
- Schuster G. B. One-electron oxidation of DNA: Mechanism and consequences. Nucleic Acids Symposium Series. 2009;53:85–86. doi: 10.1093/nass/nrp043. [DOI] [PubMed] [Google Scholar]
- Sevilla M. D., Besler B., Colson A.-O. Ab initio molecular orbital calculations of DNA radical ions. 5. Scaling of calculated electron affinities and ionization potentials to experimental values. Journal of Physical Chemistry. 1995;99:1060–1063. [Google Scholar]
- Shao F., Augustyn K., Barton J. K. Sequence dependence of charge transport through DNA domains. Journal of the American Chemical Society. 2005;127:17445–17452. doi: 10.1021/ja0563399. [DOI] [PubMed] [Google Scholar]
- Shih C.-T., Wells S. A., Hsu C.-L., Cheng Y.-Y., Römer R. A. The interplay of mutations and electronic properties in disease-related genes. Science Reports. 2012;2:272. doi: 10.1038/srep00272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slavíček P., Winter B., Faubel M., Bradforth S., Jungwirth P. Ionization energies of aqueous nucleic acids: Photoelectron spectroscopy of pyrimidine nucleosides and ab initio calculations. Journal of the American Chemi cal Society. 2009;131:6460–6467. doi: 10.1021/ja8091246. [DOI] [PubMed] [Google Scholar]
- Šponer J., Hobza P. Bifurcated hydrogen bonds in DNA crystal structure. An ab initio quantum-chemical study. Journal of the American Chemical Society. 1994;116:709–714. [Google Scholar]
- Šponer J., Hobza P. Structure, energetic and dynamics of the nucleic acid base pairs: Nonempirical ab initio calculations. Chemical Reviews. 1999;99:3247–3276. doi: 10.1021/cr9800255. [DOI] [PubMed] [Google Scholar]
- Šponer J., Leszczynski J., Hobza P. Nature of nucleic acid-base stacking: Nonempirical ab initio and empirical potential characterization of 10 stacked base dimers. Comparison of stacked and H-bonded base pairs. Journal of Physical Chemistry. 1996;100:5590–5596. [Google Scholar]
- Šponer J., Riley K. E., Hobza P. Nature and magnitude of aromatic stacking of nucleic acid bases. Physical Chemistry Chemical Physics: PCCP. 2008;10:2595–2610. doi: 10.1039/b719370j. [DOI] [PubMed] [Google Scholar]
- Steinbrecher T., Koslowski T., Case D. A. Direct simulation of electron transfer reactions in DNA radical cations. Journal of Physical Chemistry B. 2008;112:16935–16944. doi: 10.1021/jp8076134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stowasser R., Hoffmann R. What do the Kohn-Sham orbitals and eigenvalues mean? Journal of the American Chemical Society. 1999;121:3414–3420. [Google Scholar]
- Sugiyama H., Saito I. Theoretical studies of GG-specific photocleavage of DNA via electron transfer: Significant lowering of ionization potential and 5’-localization of HOMO of stacked GG bases in B-form DNA. Journal of the American Chemical Society. 1996;118:7063–7068. [Google Scholar]
- Svozil D., Hobza P., Šponer J. Comparison of intrinsic stacking energies of ten unique dinucleotide steps in A-RNA and B-DNA duplexes. Can we determine correct order of stability by quantum-chemical calculations? Journal of Physical Chemistry B. 2010;114:1191–1203. doi: 10.1021/jp910788e. [DOI] [PubMed] [Google Scholar]
- Triberis G. P., Dimakogianni M. DNA in the material world: Electrical properties and nano-applications. Recent Patents on Nanotechnology. 2009;3:135–153. doi: 10.2174/187221009788490040. [DOI] [PubMed] [Google Scholar]
- Urano S., Yang X., LeBreton P. R. UV photoelectron and quantum mechanical characterization of DNA and RNA bases: Valence electronic structures of adenine, 1-9-dimethylguanine, 1-methylcytosine, thymine, and uracil. Journal of Molecular Structure. 1989;214:315–328. [Google Scholar]
- Voityuk A. A. Are radical cation states delocalized over GG and GGG hole traps in DNA? Journal of Physical Chemistry B. 2005;109:10793–10796. doi: 10.1021/jp050985c. [DOI] [PubMed] [Google Scholar]
- Wintjens R., Liévin J., Rooman M., Buisine E. Contribution of cation- interactions to the stability of protein-DNA complexes. Journal of Molecular Biology. 2000;302:393–408. doi: 10.1006/jmbi.2000.4040. [DOI] [PubMed] [Google Scholar]
- Yokojima S., Yoshiki N., Yanoi W., Okada A. Solvent effects on ionization potentials of guanine runs and chemically modified guanine in duplex DNA: Effect of electrostatic interaction and its reduction due to solvent. Journal of Physical Chemistry B. 2009;113:16384–16392. doi: 10.1021/jp9054582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu C., Peng S., Akiyama I., Lin J., LeBreton P. R. Ultraviolet photoelectron studies of biological pyrimidines. The valence electronic structure of cytosine. Journal of the American Chemical Society. 1978;100:2303–2307. [Google Scholar]
- Zhang R. B., Eriksson L. A. Effects of OH radical addition on proton transfer in the guanine-cytosine base pair. Journal of Physical Chemistry B. 2007;111:6571–6576. doi: 10.1021/jp071772l. [DOI] [PubMed] [Google Scholar]
- Zhao Y., Truhlar D. G. The M06 suite of density functional for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, a, d transition elements: Two new functional and systematic testing of four M06-class functional and 12 other functional. Theoretical Chemistry Accounts. 2008;120:215–241. [Google Scholar]


