Moving Difference (MDIFF) Non-adiabatic rapid sweep (NARS) EPR of copper(II)

Abstract

Non Adiabatic Rapid Sweep (NARS) EPR spectroscopy has been introduced for application to nitroxide-labeled biological samples (AW Kittell et al, (2011)). Displays are pure absorption, and are built up by acquiring data in spectral segments that are concatenated. In this paper we extend the method to frozen solutions of copper-imidazole, a square planar copper complex with four in-plane nitrogen ligands. Pure absorption spectra are created from concatenation of 170 5-gauss segments spanning 850 G at 1.9 GHz. These spectra, however, are not directly useful since nitrogen superhyperfine couplings are barely visible. Application of the moving difference (MDIFF) algorithm to the digitized NARS pure absorption spectrum is used to produce spectra that are analogous to the first harmonic EPR. The signal intensity is about 4 times higher than when using conventional 100 kHz field modulation, depending on line shape. MDIFF not only filters the spectrum, but also the noise, resulting in further improvement of the SNR for the same signal acquisition time. The MDIFF amplitude can be optimized retrospectively, different spectral regions can be examined at different amplitudes, and an amplitude can be used that is substantially greater than the upper limit of the field modulation amplitude of a conventional EPR spectrometer, which improves the signal-to-noise ratio of broad lines.

1. Introduction

Non-adiabatic rapid sweep (NARS) EPR spectroscopy was proposed by Kittell et al. [1] as a general purpose method for acquisition of continuous wave (CW) EPR spectra. The phase-sensitive detector was eliminated, and the normal 100 kHz sinusoidal field modulation was changed to triangular field modulation at an audio frequency. Data were directly digitized and signal averaged using an Agilent/Acqiris model AP-240 ADC/Averager PCI card. Nitroxide radical spin-label spectra were acquired in 10 G segments using a 28.2 G peak-to-peak triangular waveform and a sweep frequency of 5.2 kHz. For two adjacent segments, there was 18.2 G of overlap. The complete spectrum was constructed by fitting the overlapping regions of the segments. Pure absorption spectra were obtained, which could be transformed to first harmonic spectra if desired using the technique known as pseudomodulation [2], which convolutes the spectrum with a sinusoid.

Klein and Barton [3] pointed out that signal averaging of n spectra each acquired in time T would have no benefit over acquisition of a single spectrum in time nT if the noise were white and the bandwidths were inversely proportional to the acquisition times. These authors also observed that the signal-averaging method is an effective way to improve the signal-to-noise ratio (SNR) in cases where the noise exhibits a 1/f character. In NARS detection of a spectral segment, 1/f-type noise also is suppressed relative to a single slow sweep with very long integrating time constant. This is a fundamental benefit of NARS methodology.

Ernst [4] analyzed the method of Klein and Barton, which he labeled “The Method of Time Averaging.” He arrived at a five-point conclusion: (1) Time Averaging and single scan measurements within the same total time give the same SNR if the noise has a white power spectrum. (2) In a wide range of circumstances where noise power increases at low frequencies, including a 1/f dependence, the SNR exhibits an n^1/2 dependence favoring Time Averaging over single scan measurement. (3) Departures from the n^1/2 law can be found that depend on the actual shape of the noise power spectrum, but were not judged to be significant. (4) Specifically, the n^1/2 law was obeyed within 2^1/2 for noise with an exponential correlation time. For the important case that the noise power is a linear combination of white noise and 1/f noise, the n^1/2 law was found to be fulfilled exactly. (5) An exception to these rules occurs if a noise peak exists at the repetition frequency. Ernst concludes that the n^1/2 law is a reasonable assumption when applying the method of Time Averaging. His paper provides the theoretical basis for the work reported here. The Ernst analysis was carried out in the context of sufficiently slow sweep that passage effects were avoided. Ernst and Anderson considered these effects in a second paper [5].

The rationale for use of 100 kHz field modulation when it was introduced more than 50 years ago was that this frequency was sufficiently high that 1/f noise contributions from both the microwave detector diode and the irradiating CW microwave source could be avoided. In addition, environmental microphonic noise is a less serious problem at 100 kHz than at lower field modulation frequencies. In the intervening years, this rationale has shifted. Use of low noise microwave amplifiers (LNAs) reduces 1/f noise in the receiver, and use of loop-gap resonators (LGRs) decreases the impact of microwave source noise. There are two reasons for the reduced source noise problem when using LGRs: at constant H₁ at the sample, the incident power is lower and, in addition, the Q-value is lower. Nevertheless, 1/f noise may be encountered, in which case the method of Time Averaging can be applied to phase-sensitive detected EPR data following Klein and Barton [3].

Experiments presented here support the hypothesis that acquisition and signal averaging of many thousands of spectral segments effectively suppresses 1/f noise, although the parameter space is large and the studies are still incomplete. It is apparent that we are engaged in the development of a general purpose approach to CW EPR spectroscopy using modern technology that will eventually replace the phase-sensitive detector.

Experimental data reported here are from frozen solutions at L-band (ca. 2 GHz) of the square planar Cu(II) complex that is formed by four in-plane imidazole ligands (Fig. 1). It serves as a model system with an overall spectral width of about 800 G. In our previous paper, the spectral width of the spin label (about 100 G) was covered in 10 segments; in the present study, the number of segments was much higher.

Figure 1.

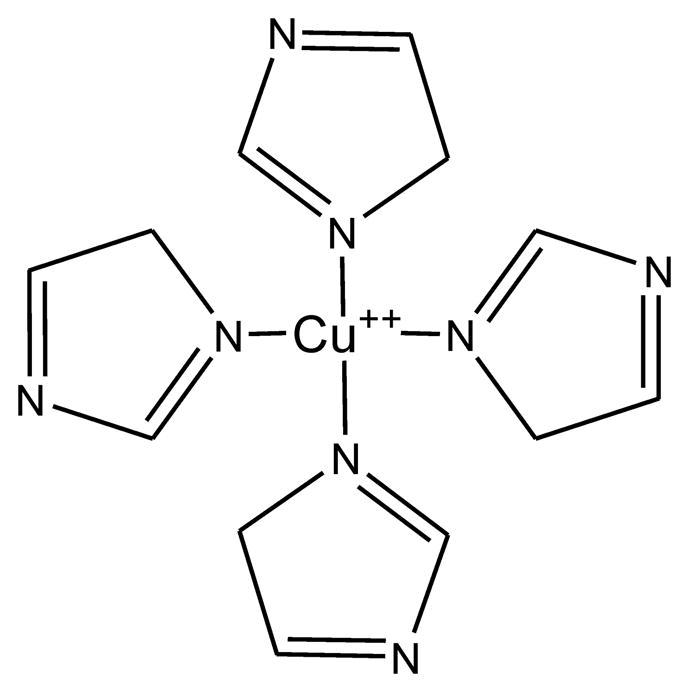
The schematic shows CuIm, the equatorial coordination of Cu(II) by imidazole. One or more axially coordinated water or imidazole moieties may also be present, but are not shown.

Absorption spectra of this complex are best observed in the first harmonic display. Some features are narrow and others are broad. Since NARS spectroscopy produces pure absorption spectra, the desired spectral display can be computed using pseudomodulation [2].

Although pseudomodulation is a technique that we originated and used in all of our early studies of NARS, we have come to prefer the method of moving difference (MDIFF): Two discrete values of the spectrum at the beginning of the sweep are selected, Δx apart. These values are continuously subtracted as they are swept through the spectrum. In this paper, we focus on this method, which we call MDIFF NARS. It seems not to have been used previously in the context of EPR spectroscopy.

The primary purpose of the MDIFF or pseudomodulation algorithms when applied to a pure absorption NARS spectrum is to increase the relative signal intensities of narrow spectral features relative to broad features. It is not to obtain a mathematical derivative, which generally is of little interest to the EPR spectroscopist. These algorithms can also be applied to theoretical simulations. Comparison of theoretical models with data is an important spectroscopic goal. For both algorithms, there is a compromise between line shape and signal intensity. A certain level of spectral distortion is acceptable in order to obtain adequate signal intensity. The same spectral distortion occurs in the theoretical model.

The complex studied here, Cu(II)-tetrakis(imidazole) (CuIm) (Fig. 1), has been previously studied [6–8]. CuIm is a model for Type II copper-binding proteins of biomedical interest, including prion protein [9], β-amyloid [10], α-synuclein [11,12], and ceruloplasmin [13]. CuIm exhibits superhyperfine structure (shfs) arising from coordinating ¹⁴N nuclei as well as M_I-dependent Cu hyperfine features in the EPR spectrum at 1.9 GHz that provide a stringent test of NARS. We demonstrate that the spectral segmentation NARS method can be applied effectively to broad spectra. We compare the NARS data with traditional 100 kHz field modulation spectra and with calculated spectra.

2. Materials and methods

2.1. Sample preparation

The ⁶³CuIm sample (2mM ⁶³Cu(II), 40 mM imidazole, pH 8.0) was prepared as described in earlier work [6,7].

2.2. EPR spectroscopy

NARS EPR and 100 kHz field modulation EPR were carried out at 1.9 GHz and 110 K using an octave-bandwidth 1–2 GHz spectrometer previously described [1]. It was equipped with a 1.9 GHz one-loop–one-gap resonator and a liquid nitrogen flow system and temperature controller (Research Specialties, Cedar Grove, WI). The same resonator and microwave elements (bridge, low-noise amplifier, detector) were used for both 100 kHz EPR and NARS. The automatic frequency control system was of conventional design based on 70 kHz FM of the microwave source that was incident on the resonator.

We were concerned in this work with the possibility that triangular sweeps of the current through the magnetic field sweep coils might not result in ideal triangular sweeps of the magnetic field across the sample because of differing eddy current patterns among the harmonics of the sweep waveform. See Appendix 2. An experimental method was devised to test this concern. A triangular sweep amplitude of 45 G was applied – i.e., ± 22.5G -, and the static field was progressively swept in 5 G segments. Thus, for each 5 G step of the static field, nine 5 G spectral intervals of data were acquired, saved, and labeled, for later analysis. Typically, multiple representations of the same segment were combined by averaging point-by-point.

One could expect a number of benefits of this procedure. (1) If signal averaging of the nine available copies of each segment (noting that each copy is itself the result of signal-averaging of thousands of sweeps) did not result in spectral blurring, but did result in improvement of S/N by a factor of 9^1/2 = 3, then eddy current effects are negligible for this particular sample, and the available time could be used in this way. (2) If the same procedure were to be applied for both sweeps of the magnetic field up and down, then an additional 2^1/2 in the use of time would be gained. If some segments, for example those acquired at the ends of the sweep, result in blurring, they could be deleted (i.e., censored). (3) Information is available that could be useful in least-squares concatenation of segments. (4) One might choose to increase the sweep frequency and decrease the sweep amplitude while holding the sweep rate constant. (It is observed that even though the n^1/2 law applies, it could be useful to reduce the amount of 1/f noise present in the data acquisition, which would favor a higher Time-Averaging spectral sweep frequency.)

In summary, NARS data were collected using a 45 G field sweep with a 234 kG s⁻¹ (23.4 T s⁻¹) sweep rate (i.e., 2.6 kHz triangular frequency, 45 G peak to peak). The polarizing magnet was stepped manually in 170 increments of 5 G across the spectral envelope. The total acquisition time was of the order of two hours. The actual time for data collection was of the order of 7/9 of one hour, since the back sweep time as well as 2/9 of the forward sweep time near the apices was lost. Other parameters were as in earlier work [1]. Data were collected under non-saturating conditions [i.e., intensity ∝ (microwave power)^1/2] as described earlier [7].

A preconditioning filter is used in NARS acquisitions, which is inserted after the microwave detector and before the A/D converter [1]. The Signal Recovery (Oakridge, TN) model 5114 preamplifier preconditioning filter was set at 1 to 300 kHz with a 6 dB/decade roll off. The lower edge is determined by the triangular sweep frequency and the upper edge by the number of EPR spectral features that are expected in a spectral segment. The lower bound of this filter was determined to show no EPR signal distortion on narrow lines.

2.3. Data processing

pplication of the MDIFF algorithm to pure NARS data replicates the spectral waveform that would be obtained if ideal square wave magnetic field modulation and broadband phase sensitive detection were experimentally feasible. The MDIFF algorithm is a filter of low frequency noise when applied to pure absorption NARS data because of the finite element derivative character. See Figure 9 in Appendix 1.

Figure 9.

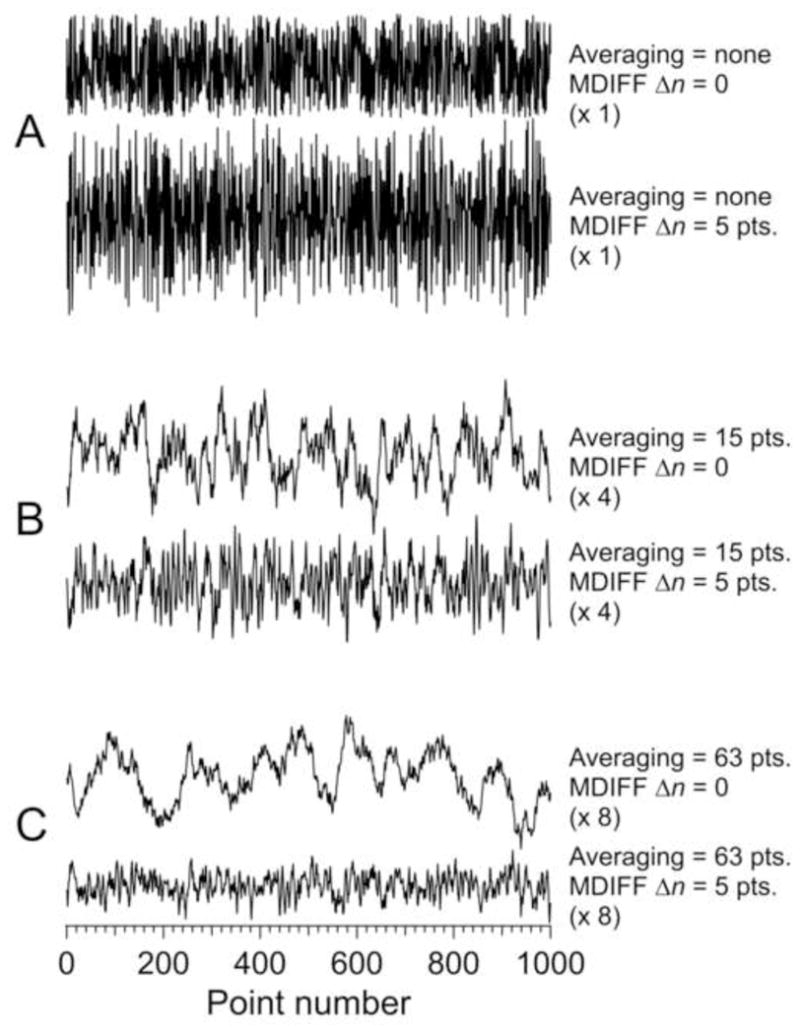
Effect of MDIFF on raw and averaged simulated noise. The upper of the A traces shows simulated noise and the lower shows noise after application of the MDIFF algorithm. Traces B show the effect of 15 point smoothing on traces A. Similarly, traces C show the effect of 63 point smoothing on traces A. Some traces were scaled relative to the raw noise. The multiplication factor is shown in parentheses.

In an early data-processing strategy, the first and last 20 G portions of each NARS segment were discarded. Spectra were constructed by concatenating the remaining 5 G segments using Mathematica v. 8.0.1 (Wolfram Research, Champaign, IL). In other post–processing studies, portions of the discarded segments of various lengths were included. Steps remained at 5 G, and the SNR improved because of increased spectral overlap. These studies allowed us to probe possible nonlinearity in field sweep.

Spectra were reduced from ~60,000 data points to 4096 data points using symmetrical 14 point averaging (IGORPro v. 6.22A, Wavemetrics, Lake Oswego, OR), effectively applying 0.2 G smoothing. The 4096 point spectra were converted to Bruker OS9 binary format (WinEPR, Bruker Biospin), and a second-order polynomial background was determined by least-squares fitting to the baseline signal surrounding the spectral envelope and subtracted (Xepr, Bruker Biospin). Fourier transformation was carried out in Xepr. Theoretical spectra were calculated using XSophe (Bruker Biospin) [14,15] using the spin Hamiltonian parameters given in earlier work [7]. Code for NARS MDIFF was self-written.

In our papers in which we applied NARS to spin labels, we compared the conventional method directly with the pure absorption display of NARS in order to overcome the line-height – line-shape compromise. This comparison was central to detection of weak dipole-dipole broadening [16]. The problem that we address in the present paper is a different one. The features of principal interest in the Cu²⁺ spectrum, namely the superhyperfine couplings to ligand nuclei, can hardly be seen in the pure absorption. First harmonic displays seems essential. They suppress the Zeeman and copper hyperfine interactions, which are very broad. This paper revolves around differences between two methods to produce first harmonic displays: conventional field modulation with phase sensitive detection and MDIFF NARS with digital detection and Time Averaging.

3. Results

3.1. Fourier filtering

The NARS spectrum of a frozen solution of ⁶³CuIm at 1.9 GHz is shown as Figure 2A. The resonances due to the outer M_I = ±3/2 g_|| manifolds are distinct from the more complex central region of the spectrum that contains resonances due to the M_I = ±1/2 g_|| manifolds, the g_⊥ transitions, and the extra absorption (EA) lines that result from the orientation dependencies of Zeeman and hyperfine interactions [17]. Superhyperfine structure (shfs) with a splitting of about 13 G is evident and is assignable to directly coordinated ¹⁴N. It was anticipated that additional spurious periodicity may arise from imperfect alignment of the NARS segments when constructing the spectrum, and the segment size of 5 G was chosen to avoid misinterpretation of this type of periodicity as shfs. Features exhibiting 5 G periodicity were indeed observed (see the inset of Fig. 2) and gave rise to a distinct feature in the Fourier transform (FT) at 0.2 G⁻¹ and a harmonic at 0.4 G⁻¹. These features were well separated from the characteristic pattern centered at 0.07 G⁻¹ that is due to the ¹⁴N shfs. They were censored, and the reverse FT (Trace B and lower trace of the inset of Fig. 2) was calculated. The Fourier-filtered spectrum was the basis of all subsequent data processing. Elimination of segment-step artifacts through use of segments that are narrower than known spectral features combined with the FT filter described here may be useful in future NARS studies.

Figure 2.

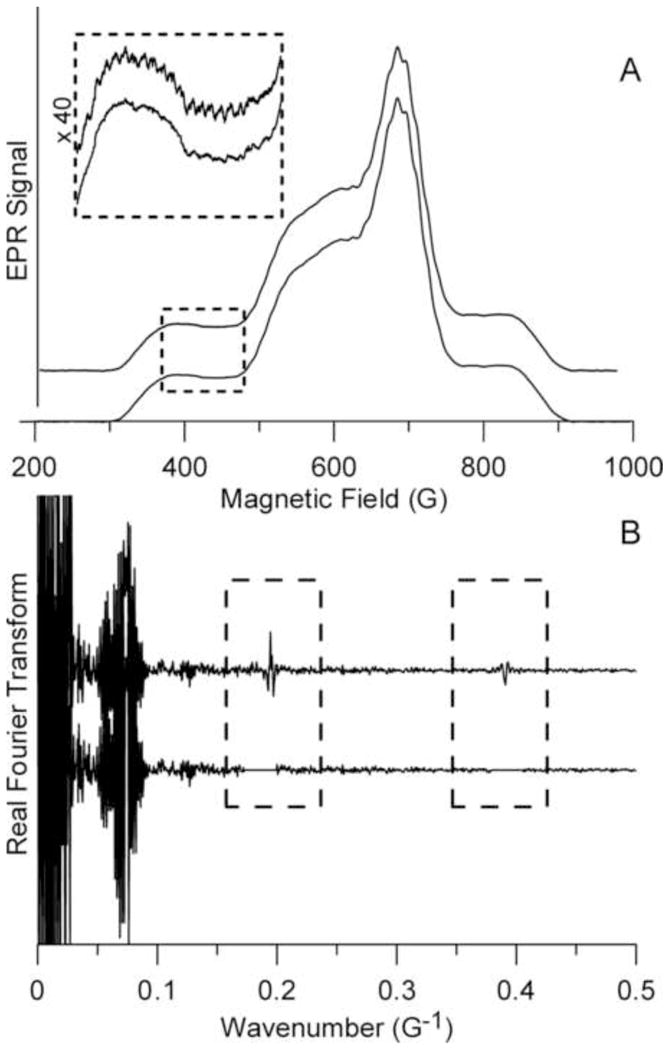
NARS-EPR spectra of CuIm. Trace A (upper) is the raw NARS spectrum, and Trace B (upper) is the Fourier transform. Trace B (lower) is the Fourier-filtered NARS spectrum, generated by editing the FT as indicated. The dashed box of A shows a low-field region of the raw (upper trace) and Fourier-filtered (lower trace) spectra expanded for clarity. The MDIFF algorithm was applied to Trace A, lower, to produce Figures 3, 4, 5A, 6, and 7.

Segment size is an experimental parameter that can be varied as a control. Shift of all segment acquisitions by an offset field is another experimental parameter. It is apparent that there are many patterns for variation of the triangular sweep amplitude, the segment size and the field setting at which the segmental acquisition begins.

3.2. Sweep width

Nonlinearity in the field sweep could arise from eddy currents induced in the resonator and shield. The triangular incident waveform of the NARS field sweep can be expressed as a Fourier series in which each term interacts differently with the resonator and shield. This phenomenon could compromise the linearity of the triangular sweep, particularly around the apices of the waveform.

In order to gauge the extent to which we could utilize more of the data and improve the signal-to-noise ratio (SNR), we explored a strategy of overlapping progressively larger portions of the 45 G sweep in multiples of 5 G, from 10 to 35 G. The polarizing magnetic field was stepped in 5 G intervals. Concatenation artifacts remained outside the region of the shfs spectral information and allowed Fourier filtering. Fourier-filtered MDIFF spectra are shown that were constructed from NARS segments of 5, 15, 25, and 35 G (Fig. 3). The spectra are remarkably alike. There is clear identification of a shfs line at 760 G with a 25 or 35 G NARS segment size that is not evident with a 5 or 15 G segment size.

Figure 3.

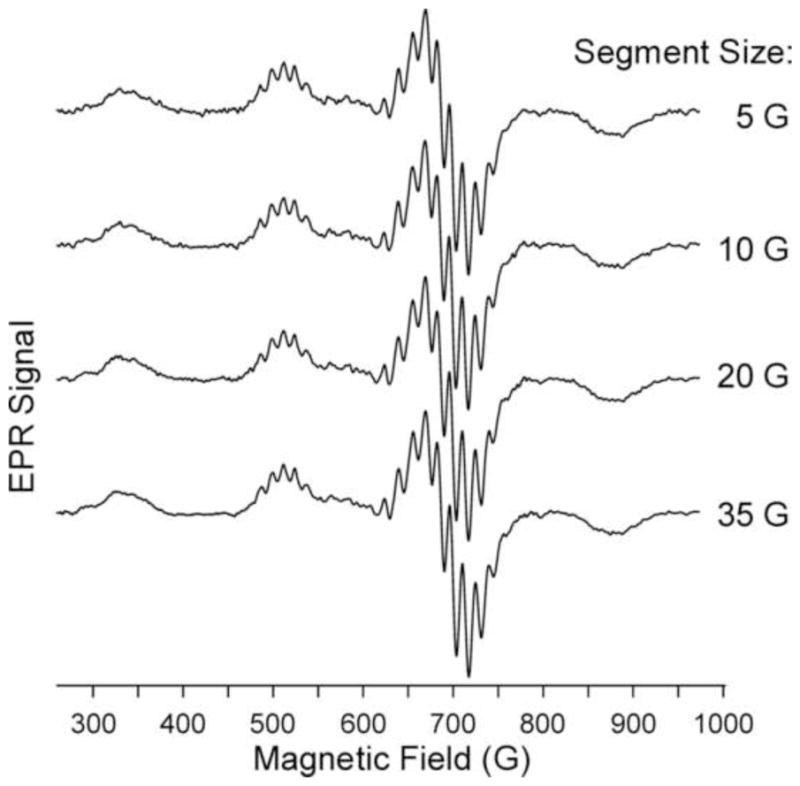
Three G-MDIFF NARS spectra of CuIm. The segment size used to generate these spectra is indicated. MDIFF NARS was applied to the baseline-subtracted and Fourier-filtered data of Figure 2.

Using an alternative strategy (data not shown), we constructed a NARS spectrum from three individual spectra, each itself constructed using 5 G segments of the 45 G sweep, one from 17.5 to 22.5 G, a second from 22.5 to 27.5 G, and a third from 27.5 to 32.5 G. These spectra remained amenable to Fourier filtering to remove concatenation artifacts. As with the overlapping 15 G spectrum of Figure 3, this composite spectrum formed by averaging of these three spectra exhibited the expected √3 increase in SNR, with no detectable loss of resolution compared to a single 5 G spectrum. Considerable flexibility exists for optimization of processing strategies for the extraction of discrete pieces of information from a single NARS data set.

3.3. Comparison of MDIFF NARS and 100 kHz spectra

The adiabatic condition is very often violated when using 100 kHz magnetic field modulation in a conventional EPR spectrometer. Use of sinusoidal field modulation gives rise to modulation sidebands and also to intermodulation sidebands [18]. Spectral broadening can occur and phenomena associated with microwave power saturation can be altered relative to continuous wave solutions to the Bloch equations. Passage effects at 100 kHz field can be probed in several ways including comparison with NARS data. NARS is, in general, a more conservative way to acquire EPR spectra under conditions that are unaffected by residual passage effects.

The MDIFF algorithm was applied to the NARS spectrum, Figure 2, using the central 5 G from the complete data set for comparison with the 100 kHz spectrum. See Figure 4 A,B. The circled points have been found useful for comparison of resolution, which appears similar comparing Figures 4A and 4B. From the theory of Appendix 1, the MDIFF NARS is expected to exhibit higher signal-to-noise ratio than the conventional 100 kHz EPR spectrum with phase-sensitive detection. Data appear consistent with this expectation. Figure 4C illustrates extension of the MDIFF algorithm to achieve the equivalent of a second harmonic display [19,20].

Figure 4.

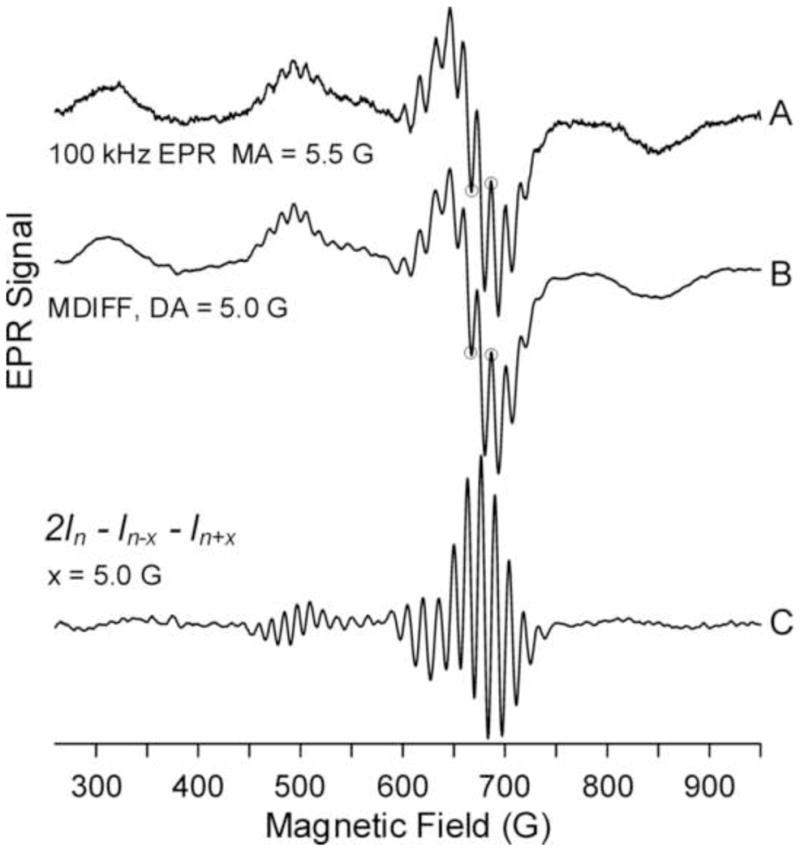
Comparison of NARS and 100 kHz EPR spectra of CuIm. (A) 100 kHz field modulation with PSD. (B) MDIFF NARS. (C) Second finite element derivative.

The NARS method has some fundamental advantages with respect to noise. The bandwidth can be retrospectively adjusted to reduce high frequency noise. Data are acquired at high bandwidth, and, retrospectively, the bandwidth can be narrowed by smoothing. Spectra with alternative filtering are readily compared. As shown in Appendix 1, at a fixed acquisition time, MDIFF NARS yields higher SNR than the use of field modulation followed by phase-sensitive detection by a factor that can be as much as 10 times.

The NARS spectrum that is acquired is pure absorption, and application of the MDIFF algorithm is a signal-processing step that also alters noise. In the Fourier domain, high frequencies are increased by 2^1/2 since subtraction and addition have the same effect. In contrast, low frequencies are diminished by subtraction. The noise is no longer white. In contrast, the noise in the field-modulation display remains white unless a decision is made to apply an ad hoc filter. Noise is analyzed in Appendix 1.

Experimental problems are intrinsic to conventional phase-sensitive detection methods. Trial-and-error methods are customarily used to select the field modulation amplitude and time constant. If one is overly conservative in selection of these experimental parameters, the SNR is lowered, which can require another experiment at a longer acquisition time. Experimental settings are determined asymptotically by repeated acquisitions. Retrospective analysis of MDIFF NARS spectra overcomes these intrinsic problems of conventional EPR methods.

3.4. The M_I = −1/2 g_|| turning point of square planar Cu²⁺ complexes

When using field modulation, the M_I = −1/2 g_|| turning point resembles a pure absorption rather than a first harmonic line shape. In the presence of nitrogen ligation, this feature often shows multiple overlapping lines. The number of lines depends on the number of nitrogen ligands of the square-planar copper complex, with 1,3,5,7 and 9 lines corresponding, respectively to 0,1,2,3, and 4 nitrogens with relative intensities in the case of four nitrogens of 1:4:10:16:19:16:10:4:1. These are called superhyperfine lines. The general theory of this spectral feature was developed independently by Weil and Hecht [21] and by Hubbell and McConnell [22].

According to the theory, all four copper g_|| features should exhibit this superhyperfine pattern independent of the microwave frequency at which experiments are carried out. In fact, this pattern is seen only on the two low field turning points: M_I = −1/2, and M_I = −3/2, and the resolution depends on microwave frequency. Froncisz and Hyde discovered that this behavior arose from g- and A-strain broadening, and were able to replicate the observed experimental behavior by assuming that g-strain and A-strain distributions were correlated [23]. A- and g-strains tended to cancel for the two low-field turning points, with the degree of cancellation dependent on the microwave frequency.

Distinguishing between three and four nitrogen ligands presents an experimental challenge. The outside lines for four nitrogens are weak and the central three lines for three and four nitrogens have nearly the same relative intensities. Information on the number of nitrogens depends on the ratio of the third line from the center to the second, and the second to the first. This approach was refined by Hyde et al [24].

Problems in counting nitrogens remain. Figure 5, dashed lines, show the theoretical pattern at a microwave frequency of 1.9 GHz. A feature is seen at 545 gauss that is confirmed experimentally and does not appear at a mirrored position on the low frequency side of the spectrum. This feature may arise from overlap with a feature in the perpendicular region of the spectrum. The NARS spectrum fits well with the theoretical spectrum except for a broad spectral feature in the range of 510 to 535 G. It is possible that another conformation of CuIm is present in the sample at low concentration. The outside lines with 19 times lower concentration is difficult to assign. The fit to the NARS data is consistently better than the fit to the 100 kHz data. Figure 5 leads to the suggestion that the low frequency side of the pattern is more reliable than the high frequency side at this particular microwave frequency.

Figure 5.

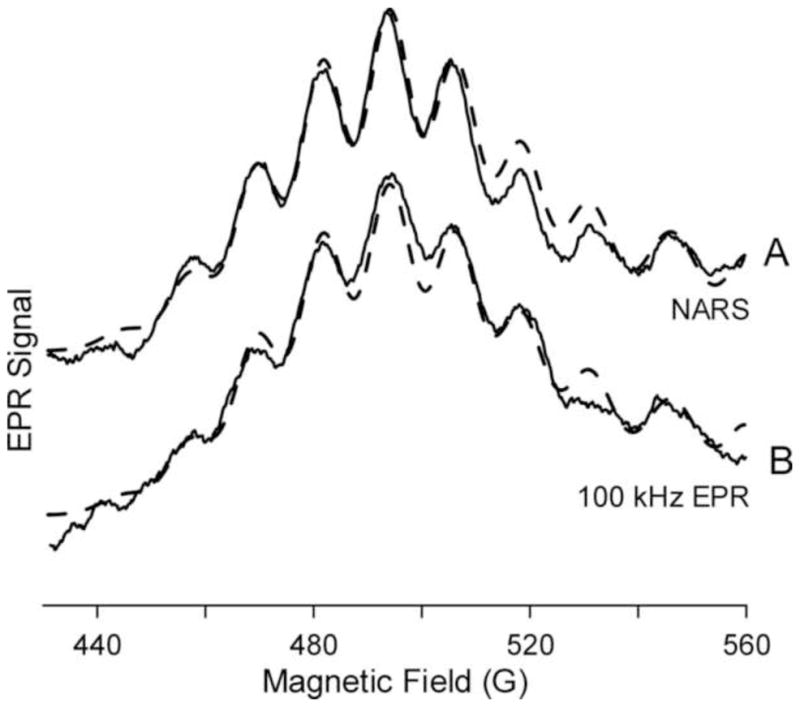
The M_I = −1/2 g_|| resonance of CuIm. The solid traces are the 5 G-MDIFF NARS spectrum (A) and the 5 G-field modulated 100 kHz spectrum of CuIm (B). Overlaid upon each is a portion of a complete simulation assuming four equivalent equatorially coordinated nitrogen atoms (dashed traces).

3.5. Strain broadening of the M_I = ± 3/2 features

MDIFF NARS spectra produced by a difference amplitude up to 32 G results in improved SNR of the M_I = +3/2 g_|| line (Fig. 6). These spectra were produced by MDIFF NARS and then divided by the digital difference. The flexibility of the application of MDIFF to NARS presents the opportunity retrospectively to determine the amplitude that maximizes the signal intensity without introducing noticeable broadening.

Figure 6.

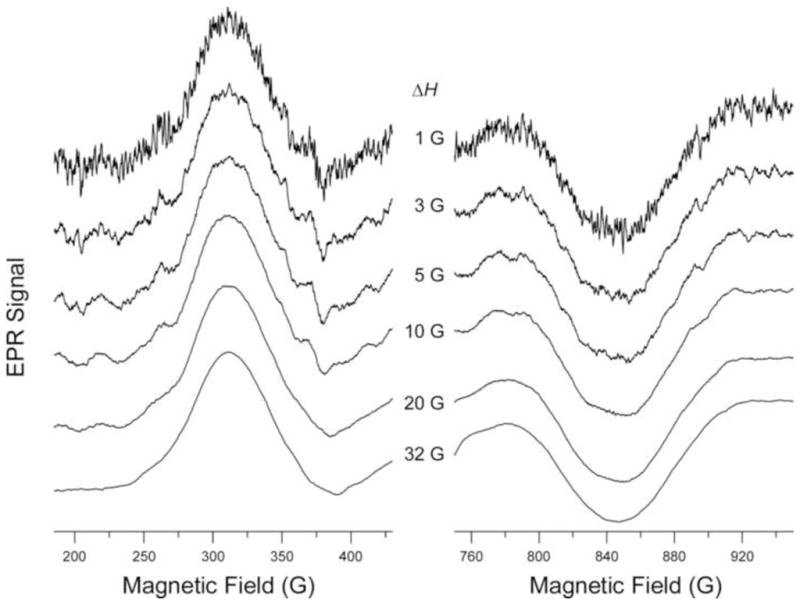
The M_I = −3/2 and M_I = +3/2 g_|| resonances of CuIm. Traces for the low and high field M_I = −3/2 and M_I = +3/2 features are shown on the left and right, respectively. MDIFF NARS spectra of CuIm with various MDIFF amplitudes, ΔH, are shown. Spectra were divided by the digital difference.

The spectra of Figure 6 (left), which depend on imperfect cancellation of strain that is nevertheless highly correlated, and of Figure 6 (right), which depend on addition of highly correlated g- and A-strain, were obtained from the same experimental NARS acquisition (Fig. 2). Thus, these spectra were obtained under truly identical conditions. This is a new experimental capability that can be expected to advance the study of strain broadening as a way to probe the environment of metal complexes, which is expected to be an important direction for future research.

3.6. The g_⊥ region

In another study, the NARS spectrum in the g_⊥ region was studied by the application of MDIFF with amplitudes of 0.1–12 G (Fig. 7). As in Figure 6, these spectra were produced by MDIFF NARS and then divided by the digital difference. For values of ΔH up to 2.4 G, loss of resolution because of use of a digital difference that is too wide is not visible. This is a convenient visual display for setting the value of ΔH. Above 3 G, however, the spectra become less and less sharp with increasing difference amplitude, but with improved SNR. An analogous determination of the optimum field modulation amplitude value using 100 kHz EPR would require multiple acquisitions of spectra.

Figure 7.

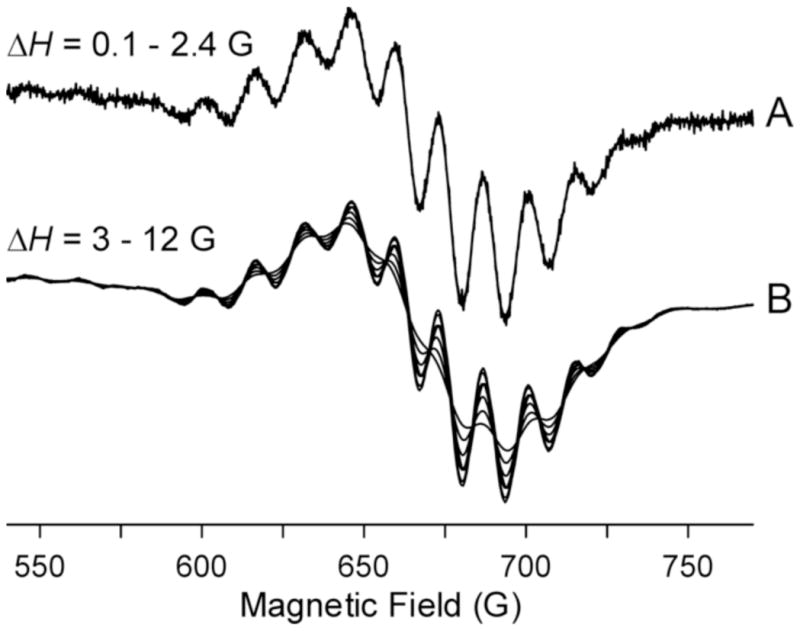
MDIFF NARS spectra on the perpendicular region of CuIm with variable MDIFF amplitudes, ΔH. The figure shows the effect of the difference amplitude on the spectra. Spectra were divided by the digital difference.

4. Discussion

4.1. Noise

In NARS spectroscopy, one can acquire and signal average any number of spectral segments. This is a temporal filter. One can also smooth any desired spectral region within a segment, which is a spectral filter. Temporal and spectral filtering are separate and independent processes in NARS, whereas these processes are combined in the RC filter at the output of the phase sensitive detector in conventional EPR. Temporal and spectral decoupling is a fundamental benefit in cases where the temporal aspect, such as signal decay, is of interest.

The upper limit of the magnetic field sweep rate that is consistent with the assumption of non-adiabatic sweep is determined by the Bloch equations. If this rate is held constant, there is a tradeoff between triangular sweep frequency and triangular sweep amplitude. For example, at higher sweep frequency, the sweep amplitude must be reduced to hold the sweep rate constant. See Eq. (4), Appendix 2. If one wanted to reduce the possible impact of 1/f noise, one could increase the sweep frequency, reduce the sweep amplitude, and reset the lower limit of the conditioning filter to a higher value. See Appendix 2.

The size and timing of the magnetic field step, which defines the beginning of the acquisition of a new segment and the end of temporal filtering of the previous segment, enters the analysis of noise in NARS spectroscopy. Since the step size and the triangular sweep amplitude are independent, the acquired spectral region can be divided into two parts: a new segment and a portion that overlaps with other spectral segments. Within the parameter space of sweep frequency, sweep amplitude, magnetic field step size, spectral filter, and temporal filter, we make the hypothesis that if the noise is white, only the total time of acquisition at the output of the spectral filter determines the spectral noise. But in the presence of 1/f noise, increase of sweep frequency will reduce the spectral noise. This is a generalization of the theorem of Klein and Barton [3].

There seem to be two types of 1/f noise: that which originates in the spectrometer such as phase noise from the microwave source, and that which originates in the environment such as microphonics. For microphonic noise to be significant, it must mix with the microwave carrier. Moreover, after microwave detection, it must be of sufficiently high frequency that it can pass the conditioning filter. Mixing between microwave source, triangular magnetic field sweep, and low frequency microphonics is a possible source of this type of noise. For example, the eddy currents at the various sinusoidal components of the triangular field sweep can give rise to Lorentz forces on the metallic components of the resonator, resulting in a mixing with the microwave carrier, and this mixing can additionally be modulated by microphonics.

4.2. Signal processing

Not much can be learned about CuIm from a visual inspection of the pure absorption NARS spectrum of Figure 2. Yet the SNR is exceptionally high. Application of the MDIFF algorithm picked out subtle inflections in the spectrum of Figure 2A that led to Figures 3 through 7. The MDIFF algorithm is a key aspect of NARS spectroscopy. Benefits relative to conventional field modulation include exact knowledge of the digital difference; use of high digital differences that are not experimentally feasible; perfect homogeneity over the sample; retrospective application with any desired accuracy; access by a Hilbert transform to the dispersion; no eddy current effects; no adiabatic rapid passage effects; and no sample or resonator heating. Most significantly, there is a fundamental gain in SNR as shown in Appendix 1.

4.3. Strain broadening

Two GHz is a particularly informative microwave frequency for EPR of Cu(II) [25]. Three of the four g_|| turning points are well resolved: the lower field M_I = −3/2 and M_I = −1/2 lines, and the highest field M_I = +3/2 line. Objective characterization of the lineshapes and linewidths of these three features at more than one frequency can provide reliable numerical values for the strains in A_|| and g_||, the strain distributions σA_|| and σg_||, respectively, as well as the correlation between g- and A-strain distributions, εσg_||σA_||. The M_I = +1/2 line overlaps with other features at frequencies ≤ 6 GHz, and the linewidth and shape may be difficult to determine unambiguously [25]. Characterization of an additional spectrum at ~4 GHz allows unambiguous determination of the sign of εσg_||σA_|| through the relative resolutions of the M_I = +3/2 and M_I = −3/2 lines. Analyses of strains provide information on the distributions of bonding parameters.

Froncisz and Hyde [23] developed a molecular orbital-derived general description of coupled distributions of the spin Hamiltonian parameters for tetragonal Cu(II) that accounts for the frequency-dependent cancellation of strain broadening on the low-field M_I = −3/2 and M_I = −1/2 lines. This strain broadening was described as being due to random statistical fluctuations in g and A [25]. The use of NARS at L-band coupled with computer simulations allows for sensitive analysis of the phenomenological strain parameters σg and σA. The high strains for CuIm may reflect tetrahedral distortion and may provide a measure of that distortion for CuIm and related square planar biological copper sites. Tetrahedral distortion will change the degree of covalency of the bonding between copper and imidazole, with attendant changes in magnetic parameters.

4.4. Resonators for NARS

The nitroxide experiment was carried out at both L- and X-bands [1]. The X-band LGR was made from silver plated MACOR (Corning Incorporated, Corning, NY). The plating was sufficiently thin that 100 kHz field modulation penetrated with little attenuation. The L-band LGR was made from solid silver with slots cut to allow penetration of field modulation. The MACOR resonator was found to be superior to the slotted resonator with respect to eddy currents.

5. Conclusion

The EPR spectrum of Cu²⁺ in frozen solution can be predicted from the spin Hamiltonian, which includes superhyperfine interactions with nitrogen ligands, hyperfine interactions with the copper nucleus, and Zeeman interactions. Each of these interactions tends to be axial with small rhombic distortion. Sensitivity Analysis involving partial derivatives of the synthesized spectrum indicates complicated variation across the spectrum of the sensitivity to each of the input parameters [26]. The EPR spectrum is strongly sensitive to the Zeeman interaction and changes markedly with the applied magnetic field. Non-linear aspects of Cu²⁺ EPR spectroscopy include electron spin lattice relaxation, and the transverse relaxation of nitrogen and copper nuclei which gives rise to connectivity between selected spectral regions.

Ordinary magnetic field modulation has a major weakness in that it combines data from a spectral region of width that depends on the field modulation amplitude. In general, the weighting of the sensitivity of the various terms in the spin Hamiltonian will vary across that region and will be blurred when field modulation is applied. We introduce the Moving Difference (MDIFF) method in this paper, which is the difference between two points of any selected separation swept across the spectrum. It is, in fact, the numerator of the finite element derivative, and division by the separation of points results in a finite element derivative. We are of the opinion that the MDIFF algorithm is particularly appropriate in formation of derivative-like displays in the context of the complexity of the spin Hamiltonian since data at only two points are combined to form one point in the spectrum. It is possible that three dimensional displays of intensity, magnetic field position and MDIFF amplitude will reveal aspects of the spectral complexity.

For magnetic field modulation, the sinusoidal EPR signal rides on the microwave carrier. Noise is added to this carrier at the low noise amplifier. For MDIFF NARS, the pure NARS absorption rides on the microwave carrier and noise also is added at the low noise amplifier. Application of the MDIFF algorithm to the NARS signal occurs after the addition of noise, and the subtraction process strongly filters low frequency noise. This is a fundamental benefit of MDIFF NARS. Although the field modulation amplitude and the MDIFF amplitude play similar roles in determining the amplitude of the EPR signal, field modulation does not filter noise while noise filtering is a major function of application of the MDIFF algorithm.

Appendix 1 shows that at constant noise level, the MDIFF NARS signal amplitude is four times higher than the field modulation amplitude for Lorentzian or Gaussian lineshapes. This result follows in an obvious manner from the early analysis of Berger and Gunthart [27]. See also Wilson [28] which is summarized by Poole [29]. Appendix 1 also considers the noise in order to estimate the SNR ratio of MDIFF NARS relative to field modulation methods. It is shown that application of a smoothing filter removes high frequency noise from the field modulation signal and the MDIFF NARS signal in a similar manner, and that the low frequency noise level of MDIFF NARS is strongly suppressed. It is shown in the Appendix that the MDIFF NARS noise can be at least two to three times lower. Combining this factor with the factor of 4 benefit in signal amplitude results in a total improvement of a factor of about 10 times. The factor must, however, be reduced in the present work because only 7/18 of the available time was used in data accumulation, resulting in lowering of SNR improvement to a factor of 6. This large factor is the principal result of the paper. It opens numerous opportunities for the further study of metallo-proteins using EPR spectroscopy.

From Appendix 2, it is recognized that triangular magnetic field sweep is an alternative to sinusoidal magnetic field sweep. Both rely on transfer of modulation to the microwave carrier to achieve good baseline stability. Using modern analogue to digital converters and signal averagers, it is possible to bypass the conventional phase sensitive detector and to collect EPR data directly. The advantage of the linear sweep of the triangular waveform is that the segment of the spectrum that is collected is faithfully represented, whereas the convolution of a sinusoidal magnetic field sweep with the spectrum is a more complicated process. In addition, our work has established that linear segments of the spectrum can be concatenated to yield the pure NARS spectrum. The digitized NARS waveform is a replica of the initial true waveform.

In our first two NARS papers we emphasized the benefit of pure absorption displays over first harmonic field modulation displays. In the present paper we show that MDIFF NARS, which has the appearance of a first harmonic spectrum, also exhibits a number of favorable features including improved display of nitrogen superhyperfine interactions of square planar copper complexes.

Highlights.

• Non adiabatic rapid sweep (NARS) EPR spectroscopy is applied to copper imidazole.

• Spectra are acquired in 170 segments of 5 G across 850 G at 1.9 GHz.

• MDIFF displays are analogous to first harmonic EPR spectra.

• The SNR is 10 times higher than with phase-sensitive detection.

• The digital difference can be optimized retrospectively for each spectral region.

Appendix 1: The Moving Difference Function (MDIFF) in EPR Spectroscopy

In EPR spectroscopy as it is usually practiced, a phase sensitive detector (PSD) is used. Sinusoidal magnetic field modulation at frequency ω_m/2π produces a sinusoidal EPR signal that rides on the microwave carrier. The purpose of field modulation is to improve stability of the spectrometer. The rationale is “transfer of modulation” to the microwave carrier when the condition for magnetic resonance is satisfied. After microwave detection followed by capacitive AC coupling, the signal incident on the PSD can be described as f(t)cos ω_m t. As the magnetic field is swept, the output of the PSD, f(t), varies monotonically, and constitutes the EPR spectrum, which is called the first harmonic display. It swings back and forth across the baseline and integrates to zero as the main magnetic field is swept.

In his general consideration of sensitivity enhancement in magnetic resonance, Ernst found it useful to distinguish between “filtering” and “transformation” of spectra, although he observed that the distinction is arbitrary and only justified by the different purposes [30]. His approach is followed here. We consider transformation of the MDIFF operator on the theoretical pure absorption EPR spectrum and on white noise separately and combine the results linearly. Transformation plus filtering is visualized as a moving average repeated about each point in the combined “spectrum + noise” voltage.

For a Lorentzian EPR line of full width at half height ΔH and unit peak intensity, the maximum possible signal is obtained when using magnetic field peak-to-peak modulation of amplitude 2ΔH. See Refs. [27–29]. This signal amplitude has a maximum numerical value of ¼. Since the first harmonic line shape can swing both positive and negative, the peak-to-peak height of f(t) is ½.

In the analysis of these citations, the convolution of sinusoidal field modulation with the Lorentzian line shape is expressed as a series of harmonics of the field-modulation frequency. The relative amplitudes of the terms in this series depend on the ratio of the field-modulation amplitude to the Lorentzian linewidth. The largest term is at zero frequency and to the best of the authors’ knowledge has never been detected experimentally.

This loss of a factor of two is recovered in the NARS method [1]. If two copies of the NARS spectrum are made, one shifted from the other, and they are subtracted, a spectrum is produced that resembles the first harmonic spectrum f(t). In the asymptotic limit of large shift, the peak-to-peak signal height is 2, in comparison with ½ for the ordinary field modulation signal height, for a net gain in transformation of a factor of 4.

The comparison is developed in Figure 8. Consider a function of x, f(x), and let ΔX be defined as a distance. Then MDIFF(x, ΔX) = [f(x − ΔX/2) – f(x + ΔX/2)]. If f(x) consists of a series of discrete values, f(x_n), with the points separated by δ, then the discrete MDIFF(x_n, Nδ) = [f(x ₋ Nδ/2) – f(x + Nδ/2)]. Comparing the discrete and continuous formulations, Nδ and ΔX are equivalent and are differences along the x-axis. This formulation can be termed the “centered” MDIFF. If the discrete MDIFF is divided by the value of Nδ, one arrives at the finite difference derivative [31].

Figure 8.

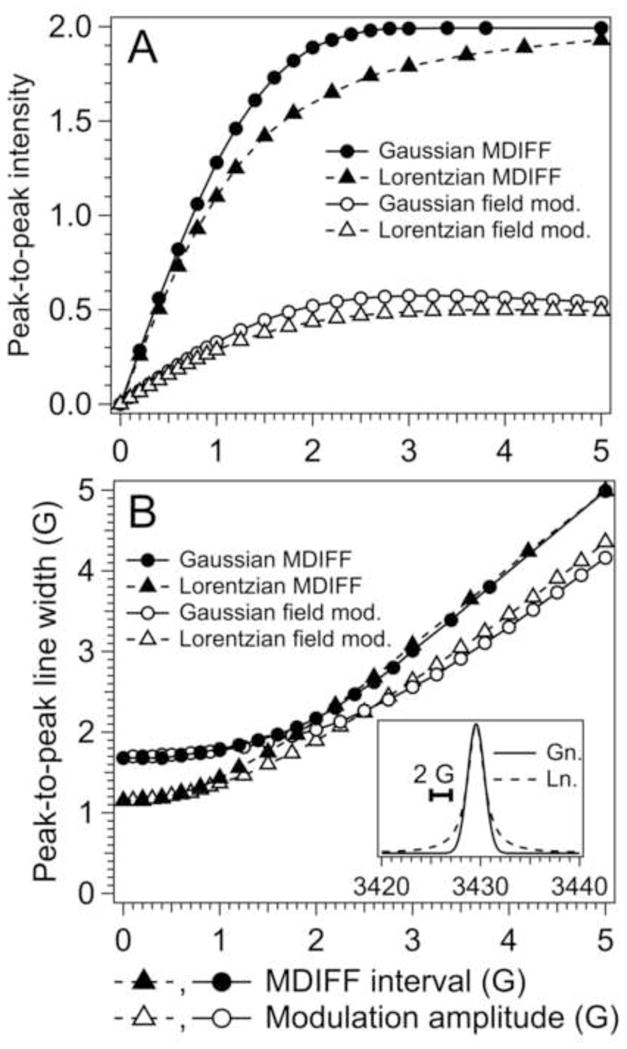
Computer simulation of EPR lines as a function of modulation or difference amplitudes. See the insert in B. (A) intensities, (B) line widths. Triangles are Lorentzian and circles are Gaussian lines, each of unit height and unit half-width at half-height. Filled points are MDIFF and open points are field modulation.

Calculations for of the convolution of magnetic field modulation with Lorentzian and Gaussian lineshapes for the first harmonic have previously been published [27–29] and are reproduced for convenience in Figure 8, open triangles and open circles. Figure 8A shows signal heights and Figure 8B shows spectrum linewidths. The so-called line-height—line-shape compromise is illustrated. As the field modulation amplitude increases, the signal height increases, which is desirable, but the line width increases, which is undesirable. Ernst reflected on this compromise in a section of [30] entitled “Sensitivity improvement with restricted line distortion.”

Parallel calculations for MDIFF are shown in Figure 8, closed triangles and circles. It is apparent that the line-height—line-shape compromise must still be made but that MDIFF has some advantage. At 5 G modulation amplitude, a four times increase in signal height is obtained when using MDIFF but the increase in linewidth relative to the field modulation method is only 20%. There is a further advantage: at high modulation amplitude, the leading and trailing edges of the MDIFF display are identically undistorted pure absorption leading and trailing sides of the Lorentzian and Gaussian lineshapes. Thus the MDIFF display appears to have some advantage by achieving sensitivity improvement with restricted distortion of the outer portions of the line.

Figure 8 completes our consideration of transformation, and we next consider filters. One imagines that a microwave EPR bridge is set up with a low noise microwave amplifier (LNA) in place that determines the system noise level for both conventional detection and NARS detection. Across a combination of digitizing, time-averaging and smoothing, gains and bandwidths are assumed to be identical, resulting in identical noise levels for identical total acquisition times. Under these assumptions, the pure NARS signal is of unit intensity, and the benefit of MDIFF with respect to signal intensity is apparent: a factor of 4. However, an analysis of noise is required to arrive at the ratio of SNR values comparing NARS MDIFF with conventional EPR. Results of noise analysis are given in Figure 9.

The top trace is the noise level before signal processing. It was generated with a Mersenne twister pseudorandom number generator that returns a random value from a uniform distribution over a fixed range for each point [32]. Noise is assumed to be the same for both pure ordinary EPR and NARS. Klein and Barton have argued convincingly that if the same time is used to collect NARS and PSD spectra at the same bandwidth, and noise is white, noise levels will be the same [3]. Application of the MDIFF algorithm to the upper of the A traces results in the second of the A traces, Figure 9. The noise power at high frequencies doubles and the noise voltage increases by a factor of 2^1/2.

The two B traces of Figure 9 illustrate the application of a running-average smoothing filter to the two A traces, respectively. High frequency noise is strongly filtered and the peak-to-peak values of the B traces are similar. However, the noise characteristics are different. It is apparent that the MDIFF algorithm has reduced low frequency noise as expected since it yields a “derivative-like” display. The two C traces have been calculated by increasing the width of the smoothing filter from 15 points to 63 points. The eye of the spectroscopist is greatly bothered by the low frequency noise of the ordinary EPR signal (trace C, upper). The noise of trace C, lower, which is the MDIFF NARS trace, is between two and three times lower.

In a continuous wave EPR spectrometer that utilizes physical modulation of the magnetic field, a first harmonic signal is produced that rides on a microwave carrier. In modern spectrometers, the microwave carrier is amplified by a low noise microwave amplifier (LNA), and detected, resulting in white noise that arises in the amplifier and is superimposed on the first harmonic signal. The signal is reduced to baseband by a phase sensitive detector. An RC time constant, time averaging and spectral smoothing can be employed as desired. An important difference between the NARS—MDIFF method and physical field modulation is that the former achieves the desired first-harmonic—like display by post processing, which is also a filter, and the latter does not automatically incorporate noise filtering. This is because noise from the LNA is added after the first harmonic signal has been created. Thus, the upper trace of Figure 9 is a reasonable model for noise in a continuous wave EPR spectrometer and the lower trace for MDIFF—NARS. This is a benefit of a factor of two or three. It arises because of the filtering of low frequency noise of the MDIFF algorithm.

In this example, where SNR values of MDIFF NARS and conventional EPR are modeled under comparable conditions, the SNR of the MDIFF NARS is about 10 times higher. The signal-processing step for formation of the first harmonic display intrinsically filters low frequency noise. In addition, the algorithm permits separation of broad spectral features from narrow inflections, which is desirable in the EPR spectroscopy of square planar copper complexes.

This analysis is considered to be a rigorous theoretical argument. In practice, there would be some additional loss because of our failure to use all of the available time – namely a factor of 7/9 in the triangular sweep, thereby deleting the apices, as well as the return sweep time of the triangular waveform. Our failure to use the return sweep time is a technical detail that will soon be corrected. There may always be some loss near the apices because of the discontinuity of the magnetic field sweep rate.

Figure 10 is a demonstration of improved SNR of the central line of a spin label at L-band using the methodology of this paper. This line has a shape that is closely approximated as Gaussian. The left and right spectra (A and C) are from Ref. [16], and were obtained under carefully controlled conditions. The NARS pure absorption spectrum was found to exhibit a factor of 4 to 5 higher SNR. The comparison was considered representative, although it does depend on assumptions made concerning the line-height—line-shape compromise. Figure 10B was produced from Figure 10A by the MDIFF method. An identical running-average filter was applied to all three spectra in Figure 10 in order to ensure a fair comparison. This figure shows a factor of 4 to 5 benefit of MDIFF—NARS over conventional field modulation. It is hypothesized that the predicted factor of 10 can be obtained by refinement of filters and further consideration of the line-height—line-shape compromise.

Figure 10.

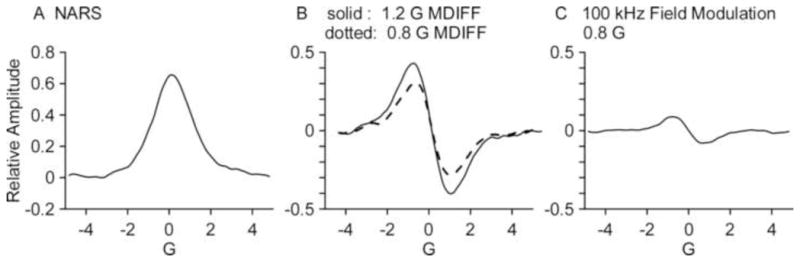
Comparison of physical field modulation EPR of the central line of a nitroxide at L-band using 0.8 G modulation amplitude (C) with the NARS spectrum (A) and MDIFF spectra using 0.8 and 1.2 G modulation amplitude (B). Data for A and C are from Ref. [16], but have been further filtered at high frequencies following Figure 9C.

Hyde et al [2] introduced the post processing algorithm known as pseudomodulation and studied its transformation and filter properties. The signal input parameter is any well behaved monotonically changing function of magnetic field normalized to the peak value. The convolution of sinusoidally varying magnetic field modulation of any desired amplitude with the function is calculated and displayed as a series of harmonics of the modulation frequency. Application of this algorithm to Figure 10A with an input parameter of 0.8 G results in a line shape that is the same, except for noise, as Figure 10C. In addition, low frequency noise is reduced relative to that of Figure 10C in a similar manner as application of the MDIFF filter to Figure 10A. In work in progress, signal-to-noise ratios and the line-height—line-shape compromise of MDIFF and pseudomodulation are being compared. Although the transformation properties of MDIFF are superior to pseudomodulation, it is possible that the filter properties of pseudomodulation are better.

Appendix 2: Triangular field sweeps

The Fourier series for a triangular wave is given by Eq. (1) as a function of the magnetic field H during triangular magnetic field sweep from −H_m/2 to +H_m/2.

$$f(H)=H_m\left(\frac{4}{{\pi }^2}\right)\left[sin\left(\pi \frac{H}{H_m}\right)+\frac{1}{9}sin\left(\frac{\pi 3H}{H_m}\right)+\frac{1}{25}sin\left(\frac{\pi 5H}{H_m}\right)+\dots +\right]$$ (1)

Thus, the third harmonic is only 1/9 as intense as the first and similarly for higher harmonic ratios in the series. Equation (1) can also be expressed as a temporal waveform.

$$f(t)=H_m\left(\frac{4}{{\pi }^2}\right)\left[sin{\omega }_{m}t+\frac{1}{9}sin3{\omega }_{m}t+\frac{1}{25}sin5{\omega }_{m}t+\dots +\right]$$ (2)

Here, ω_m = 2πυ_m, where υ_m is the frequency of the waveform.

From Faraday’s law, eddy currents are proportional to the frequency and also to the modulation amplitude H_m. Since Lorentz forces are proportional to eddy currents, the forces on the third harmonic eddy currents are 1/3 as great as they are on the first harmonic eddy current, and similarly for higher harmonics in the series. For the experiments described in this paper, the repetition frequency was reduced to 2600 Hz, a factor of two from that used in our first NARS paper [1]. Sensitivity to nonlinear sweeps in NARS spectroscopy also depends on the linewidths of the EPR sample. The characteristic linewidth for Cu(II) square-planar complexes that exhibit nitrogen superhyperfine structure is 13 G, which is greater than for the nitroxide spectra examined in Ref. [1], and, therefore, eddy current effects are less apparent.

A definition for a figure of merit for the linearity of the magnetic field at the sample is provided in Eq. (3):

$${\phi }^2=\underset{-H_m/4}{\overset{+H_m/4}{\int }}{(H^{\prime }-H)}^{2}dH,$$ (3)

where H′ is an experimental rather than a theoretical expression for the triangular waveform. The equation is a measure of difference between the desired linear magnetic field sweep and the actual magnetic field sweep. It can be evaluated from data obtained by sweep of the static field across the triangular-swept field while observing the spectrum of a sample having a narrow line.

From Eq. (2), the rate of change of the triangular waveform can be written as:

$$df(t)/dt=H_m{\omega }_m\frac{4}{{\pi }^2}\left[cos{\omega }_{m}t+\frac{1}{3}cos3{\omega }_{m}t+\frac{1}{5}cos5{\omega }_{m}t+\dots +\right]$$ (4)

From Eq. (4), it can be seen that df (t) /dt is proportional to H_mω_m. The term in square brackets in Eq. (4) is the Fourier series of a square wave. If we let υ_m be the triangular frequency, the triangular frequency sweep rate is proportional to H_mυ_m and the magnitude is constant both for up and for down sweeps. Rate of sweep is important in satisfying the non-adiabatic condition.