A Personalized Biomechanical Model for Respiratory Motion Prediction

Abstract

Time-resolved imaging of the thorax or abdominal area is affected by respiratory motion. Nowadays, one-dimensional respiratory surrogates are used to estimate the current state of the lung during its cycle, but with rather poor results. This paper presents a framework to predict the 3D lung motion based on a patient-specific finite element model of respiratory mechanics estimated from two CT images at end of inspiration (EI) and end of expiration (EE). We first segment the lung, thorax and sub-diaphragm organs automatically using a machine learning algorithm. Then, a biomechanical model of the lung, thorax and sub-diaphragm is employed to compute the 3D respiratory motion. Our model is driven by thoracic pressures, estimated automatically from the EE and EI images using a trust-region approach. Finally, lung motion is predicted by modulating the thoracic pressures. The effectiveness of our approach is evaluated by predicting lung deformation during exhale on five DIR-Lab datasets. Several personalization strategies are tested, showing that an average error of 3.88 ± 1.54mm in predicted landmark positions can be achieved. Since our approach is generative, it may constitute a 3D surrogate information for more accurate medical image reconstruction and patient respiratory analysis.

1 Introduction

Respiratory motion is a source of artifacts in medical image acquisition, which is the basis for disease monitoring, therapy planning and intervention guidance. Currently, signals from devices such as spirometers, abdominal pressure belts or external markers are used as surrogates of respiratory motion. However, the one-dimensional nature of these signals makes it difficult to estimate the 3D lung deformation accurately. There is therefore a need for methods to predict the 3D lung deformation during regular and irregular breathing cycles.

Two categories of methods for patient-specific estimation of respiratory movements can be distinguished: image-based and biomechanical methods. On the one hand, image-based methods commonly estimate the lung deformations between two or more phases of the respiratory cycle using non-linear image registration.

The idea is to create a lung-motion atlas, which is subsequently adapted to the patient [4]. Advanced image registration techniques have been developed to that end, relying in particular on advanced spatial regularization terms that allow sliding [8, 10]. Recent results are promising, but image-based methods are usually restricted to normal breathing patterns [13], with lower predictive power and versatility in patients. On the other hand, biomechanical approaches compute lung biomechanics, often using finite element methods (FEM), to simulate the physiological deformations during respiration cycles [1, 12]. The anatomical model is created from patient images and then deformed according to lung tissue properties and non-physiological driving forces defined from the difference between two volumetric objects [1, 12]. As a result, these approaches still rely on 4D image data, which makes it difficult to predict respiratory motion when unexpected changes in breathing patterns appear [9, 11].

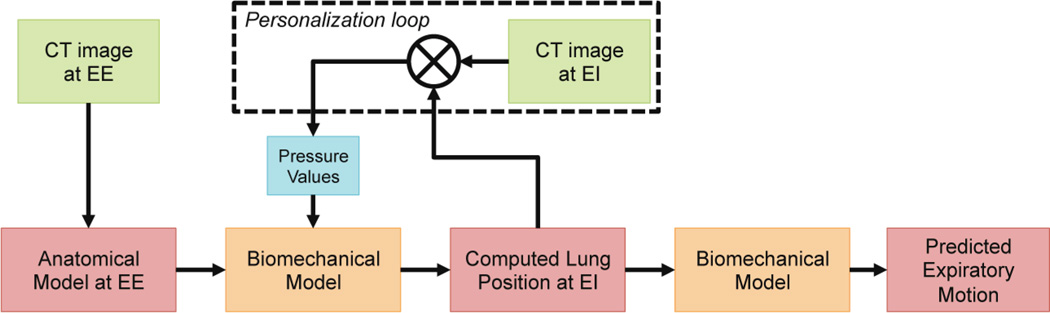
As a first step towards the prediction of respiratory motion given 1D surrogate signals of the thorax displacements, we propose a generative biomechanical model of the respiratory system driven by patient-specific thoracic and diaphragmatic pressures (Sec. 2). Contrary to previous approaches, our framework is not directly driven by image forces but by a novel thorax/diaphragm/lung interaction model. Deformation is not limited by a secondary geometry or based on image data. As illustrated in Fig. 1, the framework first estimates a comprehensive anatomical model from an image at end of exhale (EE). If not available, the thoracic and diaphragmatic pressures necessary to load the lung till end of inhale (EI) are estimated automatically using a trust region optimizer. Lung deformation is then predicted throughout the respiratory cycle by modulating the thoracic pressures. The prediction power of our model is evaluated by predicting exhale deformations in five DIR-Lab datasets (Sec. 3). We further investigate the need of including information about the deformation into personalization and show in experiments that an average error of 3.88 ± 1.54mm in predicted landmark positions can be achieved. Sec. 4 concludes the paper.

Fig 1.

Pipeline of the proposed motion model. See text for details

2 Methods

The motion model consists of two main components: i) a detailed anatomical model of the respiratory system comprising the lungs, thorax, and a sub diaphragm region grouping abdominal organs including the diaphragm(Sec. 2.1); and ii) a generative biomechanical model that computes lung deformations according to tissue properties and pressures generated by the thorax and the diaphragm (Sec. 2.2). The pressure parameters of the model are estimated automatically from two EE and EI CT images (Sec. 2.3).

2.1 Anatomical Model of Respiratory System

Thorax dynamics are complex, involving several interacting organs. In particular, the lung is deformed indirectly through expansion and contraction of the rib cage and diaphragm. During this process, the lung slides along the thoracic surface of the rib cage and diaphragm. The diaphragm is fixed along the rib cage and is curved towards the lung, and in some patients it slides along the rib cage as well. To capture these interactions, we create an anatomical model that consists of four independent components: the two lungs, the thorax, and a lumped component, called sub-diaphragm region, which includes the diaphragm and other abdominal organs. The two lungs and patient’s skin, which defines the outer layer of the thorax, are automatically segmented from 3D CT images using a machine learning approach combined with level-set optimization, as described in [5] (Fig. 2, left panel). The sub-diaphragm region is computed automatically from the skin and the lung segmentations by casting the lung downwards (Fig. 2).

Fig 2.

a): The coronal CT slice is overlaid by the skin segmentation (blue) and intersects in 3D with the left lung (pink) and the sub-diaphragm mesh (green). b): The thorax (front face removed) with different coloring for each pressure patch for the left lung. Below the lung lays the sub-diaphragm mesh (brown; one pressure patch visible in red) comprising the diaphragm and the abdominal organs. For more realistic deformations, this mesh is separated from the thorax.

Each component is meshed with tetrahedra using CGAL (www.cgal.org). To capture the heterogeneous muscle forces, thoracic and diaphragmatic pressures are estimated regionally. The inner surface of the thorax and the diaphragmatic interface are sub-divided into uniform patches (Fig. 2 right panel). The number of patches is set experimentally; in areas with lung interaction 9 evenly distributed thoracic patches (incl. mediastinum), and two on the diaphragm.

2.2 Biomechanical Model of Respiratory System

During respiration, the muscles apply forces, which are then transferred to the lungs. We thus deform the lung by solving simultaneously the dynamics equations for the lungs (l), thorax (t) and sub-diaphragm region (d):

$$\{\begin{array}{c}{M}^l{\ddot{U}}^l+C^l{\dot{U}}^l+K^l{U}^l=F_c^{t\to l}+F_c^{d\to l}\hfill \\ M^t{\ddot{U}}^t+C^t{\dot{U}}^t+K^t{U}^t=F_c^{l\to t}+F_c^{d\to t}+F_p^t\hfill \\ M^d{\ddot{U}}^d+C^d{\dot{U}}^d+K^d{U}^d=F_c^{l\to d}+F_c^{t\to d}+F_p^d\hfill \end{array}$$ (1)

In the following, the superscripts are omitted if not necessary. The vectors Ü, U̇ and U gather the accelerations, velocities and positions of the free nodes of each simulated object. M is the (lumped) mass matrix (mass densities: ρ^l = 1.05 g/mL, ρ^{t,d} = 1.50 g/mL). K is the stiffness matrix of the internal elastic forces. C is a damping matrix. Here, Rayleigh damping is chosen, with coefficients 0.1 for both mass and stiffness. As described below, lungs, thorax and subdiaphragm are each subject to interaction forces F_c, which model the sliding interactions between two organs, and pressure forces F_p, which represents the physiological force driving the respiratory motion.

Passive Material Properties

Lungs, thorax and diaphragm are non-linear, heterogeneous materials [9, 11]. Because we want to estimate the driving pressures and lung stiffness, fast simulations are necessary to reduce computation time.

We thus chose to use a linear elastic model [1], whose stiffness is set by the Young’s modulus E and compressibility by Poisson’s ratio ν. Co-rotational linear tetrahedra are employed to cope with large deformations [6]. The parameters are set using values reported in the literature [1]: E^l = 900Pa, E^{t,d} = 7800Pa, ν^l = 0.4 and ν^{t,d} = 0.43.

Respiratory Forces

Breathing relies on the contraction of surrounding muscles, which expand the lungs during contraction. In our model, we apply the negative pressure as force on each element of the thoracic surface of the thorax and diaphragm: ${\mathit{f}}_{\mathit{p}}^{\mathit{i}}=p^i$ n dS, where pⁱ is the pressure of the i-th patch and n is the normal of the surface element dS.

Collision and Sliding Interaction

Between lung and thorax lies the pleura, which is filled with a serous fluid allowing nearly friction-free movement between the lungs and thoracic cavity. During respiration, the lungs stay attached with the thoracic surface of the rib cage and diaphragm, the change of pleural volume being minimal. To model this behavior, a collision model has been implemented as a penalty force to prevent interpenetration, allow tangential sliding movement, and attract objects to each other to ensure they stay connected. The collision detection, based on proximity detection, is provided by the SOFA framework1.

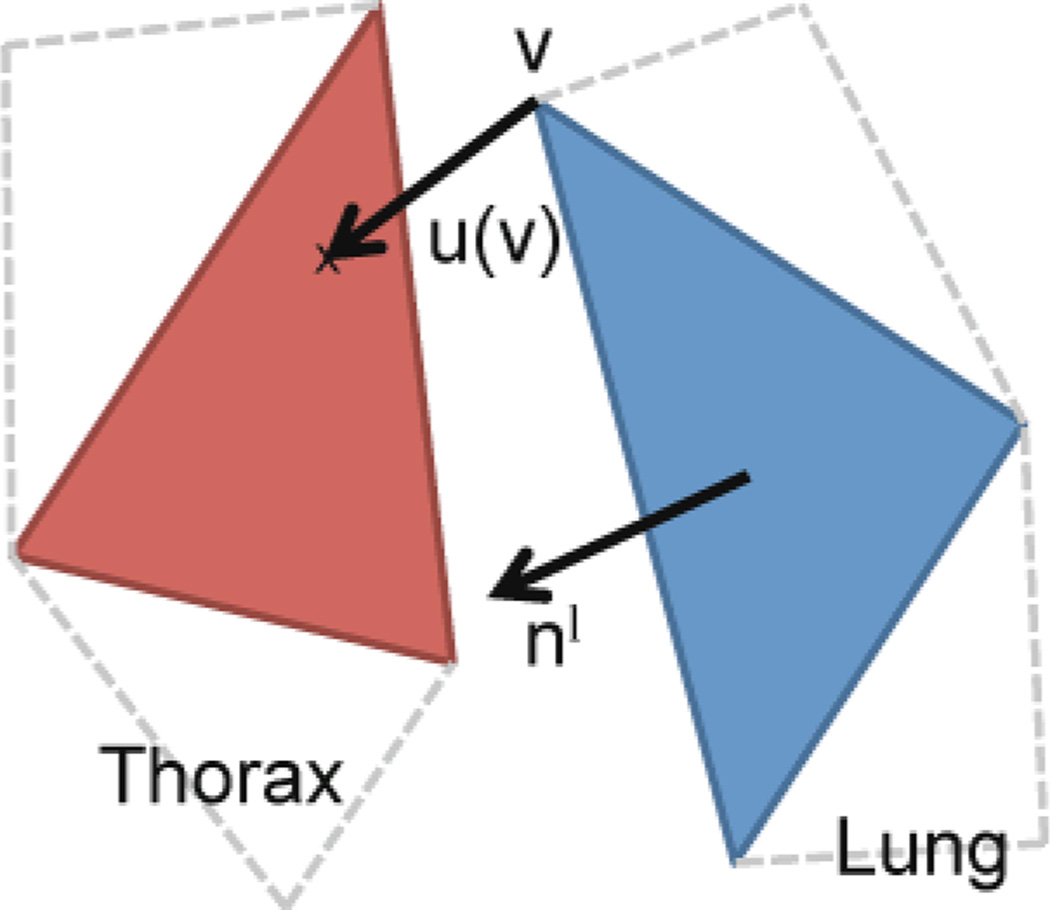
Once a collision is detected, the proposed penalty force is applied automatically whenever the distance between a vertex of one object and a triangle of another object is lower than an alarm distance da. Exemplarily for all interactions between lungs, thorax and diaphragm the force generated by the thorax on a vertex v of the lung can be written as (Fig. 3):

$$\{\begin{array}{c}{\mathrm{F}}_c^{t\to 1}(\mathrm{v})=0,\text{if}\Vert \mathbf{u}(\mathbf{v})\Vert =0\text{or}\Vert \mathbf{u}(\mathbf{v})\Vert >d_a\hfill \\ {\mathrm{F}}_c^{t\to 1}(\mathrm{v})=-{\mathrm{n}}^l{k}_s(\mathbf{u}(\mathbf{v})·{\mathbf{n}}^l)\text{otherwise}\hfill \end{array}$$

where u is the vector between the lung vertex vwhich belongs to the triangle T^l, and the corresponding collision point on the thorax. n^l is the normal of the triangle T^l. k_s is the penalty force stiffness coefficient, set to 0.1 N/m in this study. The interactions F_c between all three objects are defined in a similar way.

Fig 3.

Drawing of the collision force. By design, that force does not restrict sliding but only penalizes inter-penetration of the thorax and lung.

Implementation

The biomechanical model is implemented based on SOFA framework1. Eq. 1 is solved using a semi-implicit Euler solver with a time step of 1ms.

2.3 Model Personalization

Model personalization is achieved by optimizing the patch-wise pressure values. We estimate the pressure necessary to load the lung from EE to EI by minimizing a multi variate cost function using Powell’s NEWUOA algorithm [7], a trust region method that does not explicitly calculate cost function gradients.

The cost function is defined by C = D_S + D_LM, where D_S is the mean Hausdorff surface-to-surface distance between the deformed EE lung surface at system equilibrium and the segmented lung surface at EI. D_LM is the average Euclidian distance between landmarks at EI and their corresponding EE landmarks moved according to the internal deformation provided by the biomechanical models.

3 Experiments and Results

Two different sets of experiments were carried out to evaluate our approach and assess the importance of considering internal deformation during personalization. Tab. 1 summarizes the different protocols. All configurations were validated by predicting full exhale (EI to EE), without any image information.

Table 1.

Experiment protocols. See text for details.

Personalization (Optimization Parameters)	Cost Function
Experiment 1 (E1): Personalization based on surface distance
14 pressure values	C = DS
Experiment 2 (E2): Personalization based on surface and landmark distances
14 pressure values	C = DS + DLM

Data Sets and Pre-Processing

We used EI and EE images from DIR Lab data sets [2] for which the thorax is entirely visible (cases 6 to 10, image resolution of 0.97 × 0.97 × 2.50mm). For these sets landmarks were available. We automatically segmented the lungs and skin surface and meshed the thorax, lung, and diaphragm including abdominal organs with 25351, 2650 and 2754 tetrahedra on average. In the following we report results for the left lung only, but due to the anatomical separation, our method can easily be extended to both lungs.

Personalization

The pressure estimation was based on a cost function (see Tab. 1), which compared the current state of the simulation with the ground truth at EI. The NEWUOA optimizer converged after an average of 109 iterations for pressure estimation (≈ 15h single threaded system with 2.93GHz and 6GB memory; improvements expected by use of multi threading and collision detection on GPU, such as in [3]). The obtained landmark errors at EI (Tab. 2) were of the same order of magnitude as values reported in the literature [10,12], although our model is not directly driven by image forces.

Table 2.

Mean errors between simulation and ground truth. Setup details in Tab 1.

Case	6	7	8	9	10	Mean
E1: C = DS
EI surface error (mm)	4.66	3.73	4.43	3.09	2.95	3.77 ± 0.89
EI landmark error (mm)	4.68	7.32	11.17	5.25	2.85	6.26 ± 4.92
Mean landmark error during prediction (mm)	3.96	4.67	6.35	3.29	2.83	4.22 ± 2.13
E2: C = DS + DLM
EI surface error (mm)	4.08	3.66	4.35	3.17	3.04	3.66 ± 0.69
EI landmark error (mm)	4.53	6.86	8.63	4.53	2.32	5.37 ± 3.26
Mean landmark error during prediction (mm)	3.67	4.55	5.41	3.18	2.56	3.88 ± 1.54

Validation

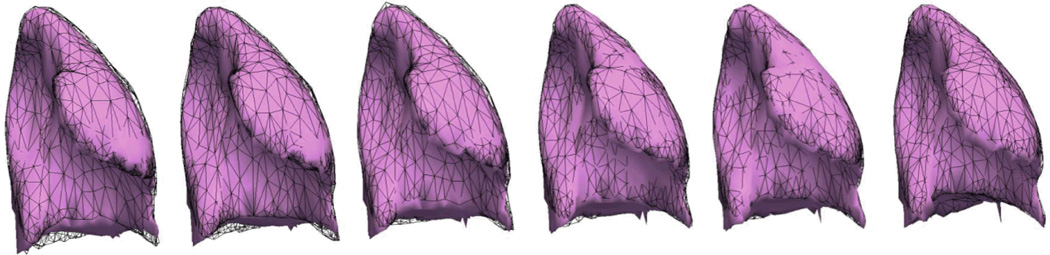
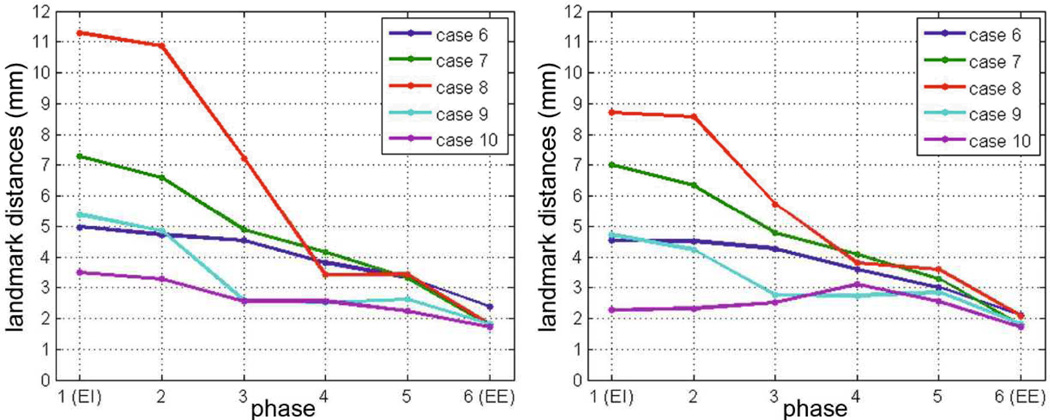
The quality of the model’s exhale prediction was evaluated by comparing the simulated landmark positions with the landmarks of each intermediate phase during exhale, which were not used during personalization. The exhale was performed by turning off the personalized thoracic pressures just after reaching the EI equilibrium (Fig 4). To reproduce a real-case scenario we synchronized the simulated lung with the 4D CT images by means of the lung volume. Despite the simplifications of our model, we obtained promising predicted lung motion, with an average landmark error of 3.88 ± 1.54mm (Tab. 2, Fig. 5). The experiments showed that the predictive power of the model can be improved by considering the landmarks as information of internal deformation into the cost function; surface matching is not enough. Analysis based on the distances of each landmark using a paired t-test showed that the improvements of the model’s exhale prediction obtained in E2 were significant for cases 6 to 9 (p-value < 0.05). Error in case 10 was already of the order of magnitude of the slice thickness, therefore a significant improvement was not expected.

Fig 4.

A simulated lung during exhale (pink). The ground truth (in black wireframe) and the simulation (in pink) are showed for each 4D CT phase.

Fig 5.

Average landmark error during exhale simulation for the two experiment scenarios: estimation of patch-wise pressure values using the surface distance (left) or the surface plus landmark distance (right) as cost function. The simulation starts at the mechanical no-load phase EE, the lung is loaded using the personalized pressure, and recoils to the no-load phase (plotted exhale). Therefore the errors near EE are smaller.

4 Discussion and Future Works

In this study we have presented a novel approach to predict patient respiratory motion, including the estimation of the thoracic pressure values. To the best of our knowledge, our generative model is the first to simulate the lung, thorax and diaphragm interactions without being explicitly driven by image forces. Personalized from two CT images, the model is generative and can predict respiratory motion throughout the entire cycle. The obtained results were of the same order of magnitude as state-of-the-art respiratory motion models, encouraging further work in this direction. Tethering the lungs to the airways, estimating spatial varying tissue properties, using hyperelastic material, refining the anatomical model, and reducing the uncertainties in the FEM simulation could reduce the simulation error. In a step towards the clinical application, we plan to investigate the correlation between the 1D surrogate and personalized pressure force field. In conclusion, our method, being generative, may constitute a 4D surrogate model to improve prediction of respiratory motion for image reconstruction.