An Investigation of Ion-Pairing of Alkali Metal Halides in Aqueous Solutions Using the Electrical Conductivity and the Monte Carlo Computer Simulation Methods

Abstract

The ion pairing is, in very dilute aqueous solutions, of rather small importance for solutions’ properties, which renders its precise quantification quite a laborious task. Here we studied the ion pairing of alkali halides in water by using the precise electric conductivity measurements in dilute solutions, and in a wide temperature range. The low-concentration chemical model was used to analyze the results, and to estimate the association constant of different alkali halide salts. It has been shown that the association constant is related to the solubility of salts in water and produces a ’volcano relationship’, when plotted against the difference between the free energy of hydration of the corresponding individual ions. The computer simulation, using the simple MB+dipole water model, were used to interprete the results, to find a microscopic basis for Collins’ law of matching water affinities.

1. Introduction

Aqueous solutions of salts are ubiquitous, and solvated ions greatly influence many naturally occurring processes, such as the protein folding and the conformational changes of nucleic acids [1], the permeability, conductance, and electrostatic potential of cell membranes [2, 3], the micellization of surfactants and hydrophobic effect (also Hofmeister effects) [4, 5]. Ions are often cofactors of enzymes, or have some other properties (e.g. acid-base properties), that influence activity of biomolecules [1]. Charged species also affect the mechanism, and thus kinetics, of chemical reactions [6, 7]; the mechanism of ion-exchange [8]; the sol-gel transition [9]; and many other phenomenons. Solvated ions were, thus not surprisingly, subject of many experimental [10–16] and theoretical [17–37] studies.

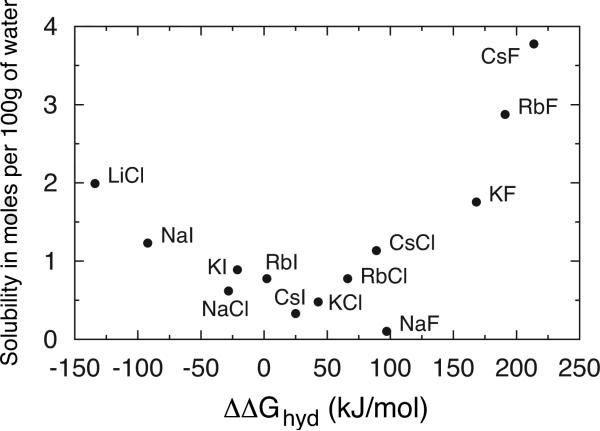
In this work we are particularly interested in systematic investigation of the interactions between oppositely charged ions in aqueous solutions of simple alkali halide salts. These salts have been extensively studied in the past, experimentally [11, 12, 14–16] as well as theoretically [27–29, 31–37]. Properties, such as osmotic coefficients and enthalpies of dilution, of these solutions show a strong correlation with the chaotropic or kosmotropic character of the ions [38, 39]. The osmotic coefficient of aqueous solutions of salts with kosmotropic cation (such as sodium or potassium) increases with increasing anion size, whereas for salts with chaotropic cation like caesium, this order is reversed. On the other hand, for salts with common anion, osmotic coefficient of their aqueous solutions decreases with increasing cation chaotropicity [40]. Enthalpies of dilution of salts with common small ion (e.g. sodium salts or chlorides) do not change much with increasing chaotropicity of counterion, whereas for salts with common larger ion (e.g. caesium salts or iodides) the dilution becomes more endothermic with increasing the size of the counterion [39]. The property that was of particular interest for us was the solubility of these salts. It is well known, that certain salts, such as LiF, which involve two small ions, are poorly soluble in water. Salts such as CsI, which involve both a large anion and cation, also have limited solubilities. However, in contrast, salts like CsF, in which one ion is large and the other is small, are highly soluble in water [41]. Interestingly, if plotted against the difference of the Gibbs free enthalpy of hydration between cation and anion, the results for the solubility show the inverse Collins’ pyramid-like correlation [42], as it is presented in Fig. 1.

Figure 1.

The solubility of alkali halides at 25°C [41] as a function of the difference between Gibbs’ free enthalpies of hydration of single ions [43].

It has been already shown theoretically [36, 37], that these differences can be explained following the idea of Collins’ matching water affinities [42], with different ion-pairing tendency. However, due to the lack of appropriate experimental data and inconsistencies within different forcefield models a thorough analysis is still lacking.

Experimental quantification of weak association is not a trivial task. It has been reported, that even the conductivity measurements, as one of the most established techniques, yields only a rough estimation for the association constant, $K_{\mathrm{A}}^{\circ }\le 10$ [44]. Despite the fact that there is plenty of precise conductivity data for alkali metal halides in water [45–51], they are, in general, limited to 298.15 K and do not cover the diluted solutions in sufficient detail. The appropriate analysis of existing conductivity data is therefore not reliable.

Here we decided to carry out precise conductometric measurements on diluted aqueous solutions (c~<0.005 mol · L^–1) of all alkali metal chlorides and three iodides (NaI, KI, and CsI) over the broad temperature range. To obtain the association constants, $K_{\mathrm{A}}^{\circ }\left(T\right)$, and limiting molar conductivities at infinite dilution, Λ^∞(T), the experimental data were analyzed using Barthel's low-concentration chemical model (lcCM) [52]. Due to the hydrolysis of fluoride ion in water, fluoride salts were not included in our investigation.

To explain the obtained results of $K_{\mathrm{A}}^{\circ }$ on a microscopic scale, we used a simple 2D water model, that was parametrized to qualitatively reproduce the association tendency.

The paper is organized as follows. After this brief introduction, the experimental method is outlined, followed by the description of the model used to analyze the results. Next, the results are summarized and discussed; the conclusions are given at the end.

2. Experimental

2.1. Materials

Lithium chloride (LiCl, Merck, Darmstadt, Germany, suprapur), potassium chloride (KCl, Aldrich, USA, 99.999 %), rubidium chloride (RbCl, Merck, Darmstadt, Germany, suprapur), caesium chloride (CsCl, Aldrich, USA, 99.999 % (sample I) and CsCl, Sigma-Aldrich, USA, 99.9 % (sample II)), sodium iodide (NaI, Aldrich, 99.999 %), potassium iodide (KI, Aldrich, 9.999 %) and caesium iodide (CsI, Aldrich, 99.999 %) were used as received. All salts were were dried for 24 h at T ≈ 400 K with a vacuum line (p < 0.01 Pa) and stored in a desiccator over P₂O₅ before use.

Stock solutions were prepared by mass from the pure compounds and demineralized distilled water. Demineralized water was distilled two times in a quartz bidestillation apparatus (Destamat Bi 18E, Heraeus). The final product with specific conductivity κ < 6 · 10^–7 S·cm^–1 was distilled into a flask permitting storage and transfer of water into the measuring cell under an atmosphere of nitrogen.

2.2. Conductivity Measurements

Conductivity measurements were performed with a three-electrode flow cell (cell constant C = (0.81143±0.00005) cm^–1 at 298.15 K) connected to a mixing chamber and mounted in a lid for immersion in a temperature bath [53, 54]. The cell was calibrated with potassium chloride solutions [55]. The computer-controlled measurement system, based on a high-precision thermostat (Lauda UB 40J, WK 1400) and an impedance analyzer (Agilent 4284A), was described previously [56]. This system allows automatic setting of each temperature between T= 278.15 K and 313.15 K, with a reproducibility better than 0.005 K.

At the beginning of each measurement cycle, the cell was filled under nitrogen atmosphere with a known mass of water. After measurement of the water conductivity, κ′(ν), as a function of frequency, ν, in the range of (200 to 10 000) Hz in steps of 200 Hz for all chosen temperatures of the program, known masses of stock solution were subsequently added with a gas-tight syringe and the temperature program repeated.

Conductivity of KI solutions was measured at 298.15 K only, because it turned out to be unstable in a longer time period as it is usually demanded for covering whole temperature range. We also encountered unexpected problems when investigating CsCl in extremely diluted solutions (c~<0.002 mol · L ^–1), so measurements done on CsCl solutions were repeated with different sample. Results are presented in the SI in Figure S6.

The measurement procedure, which included correction for lead resistance and extrapolation of the recorded frequency-dependent conductivities, κ′(ν), to 1/ν = 0 in order to eliminate electrode polarization effects, was described in detail elsewhere [56]. The corrected conductivities, κ = lim_1/ν→0 κ′(ν), of all investigated systems, converted to molar conductivities, Λ = κ/c, are given in Table S4 in the SI as a function of electrolyte molality, m. The latter relates to the corresponding (temperature-dependent) molar concentration, c, via c = md/(1 + M₂m) where M₂ is the molar mass of the salt and d is the density of solution.

A linear change of density with temperature, T, was observed, d = d_s + b · m, where d_s is the density of water at the given temperature, taken from the literature (see Table S3 in the SI). The density coefficients b were determined from density measurements of the stock solution and the final solution in the conductivity cell by the method of Kratky et al. [57] using Anton Paar density meter DMA 5000 (Anton Paar, Graz, Austria) with a declared precision of the measurements ±0.01 kg m^–3. They are assumed to be independent of temperature and are included in the Table S3 in the SI.

Taking into account the sources of error (calibration, measurements, impurities) the values of k and L are certain within 0.05 %.

2.3. Data Analysis

The presented molar conductivities, Λ(c) (Table S4 in the SI, Fig. 2 and Fig. 3), were analyzed in the framework of the low-concentration chemical model (lcCM) of Barthel [52]. This approach uses the set of equations

$$\frac{\Lambda }{\alpha }={\Lambda }^{\infty }-S\sqrt{\alpha c}+E\alpha c\ln \left(\alpha c\right)+J_1\alpha c-J_2{\left(\alpha c\right)}^{\frac{3}{2}}$$ (1)

$$K_{\mathrm{A}}^{\circ }=\frac{1-\alpha }{{\alpha }^{2}c{\left(y_{\pm }^{\prime }\right)}^2};y_{\pm }^{\prime }=\exp (-\frac{{\kappa }_{\mathrm{D}}q}{1+{\kappa }_{\mathrm{D}}R});{\kappa }_{\mathrm{D}}^2=16\pi N_{\mathrm{A}}q\alpha c;q=\frac{e^2}{8\pi {\epsilon }_0\epsilon k_{\mathrm{B}}T}$$ (2)

and

$$K_{\mathrm{A}}^{\circ }=4\pi N_{\mathrm{A}}{\int }_a^R{r}^2\exp \left[\frac{2q}{r}-\frac{W_{\pm }^{\ast }}{k_{\mathrm{B}}T}\right]\mathrm{d}r$$ (3)

where Λ^∞ is the molar conductivity at infinite dilution, (1–α) is the fraction of oppositely charged ions bound in ion pairs, and $K_{\mathrm{A}}^{\circ }$ is the standard-state association constant. The activity coefficients of the free cations, $y_{+}^{\prime }$, and anions, $y_{-}^{\prime }$, define ${\left(y_{\pm }^{\prime }\right)}^2=y_{+}^{\prime }{y}_{-}^{\prime }$; κ_D is the Debye parameter, e the proton charge, ε is the relative permittivity of the solvent, ε₀ is the permittivity of vacuum, and T is the Kelvin temperature; k_B and N_A are the Boltzmann and Avogadro constants, respectively. The lcCM model counts two oppositely charged ions as an ion pair if their mutual distance, r, is within the limits a ≤ r ≤ R. Expressions for the coefficients S, E, J₁ and J₂ of eq. 1 are given by Barthel et al [45, 52]. The limiting slope, S, and the parameter E are fully defined by the known data [45] for the density, d_s, viscosity, η and relative permittivity, ε, of the water (Table S3 in the SI). The coefficients J₁ and J₂ are functions of the distance parameter, R, representing the distance up to which oppositely charged ions can approach as freely moving particles in the solution. With eq. 3 it is assumed that the potential of mean force between cations and anions can be split into a Coulomb contribution and non-coulombic interactions, $W_{\pm }^{\ast }$, of maximum range R.

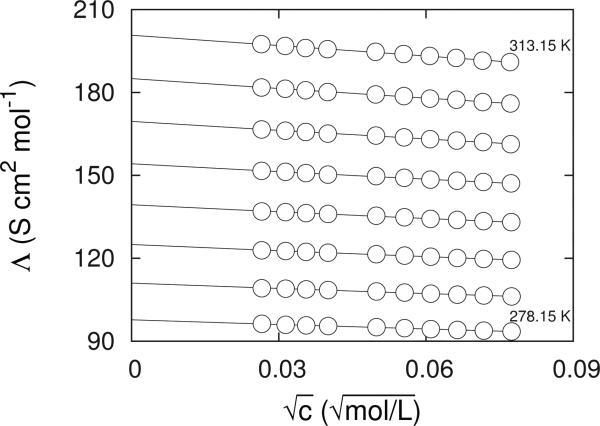
Figure 2.

Molar conductivities, Λ; ○, of RbCl in water from T = (278.15 to 313.15) K in steps of 5 K and in the concentration range 0.7 · 10^–3 < c/mol · L^–1 < 0.006. Lines show the results of the lcCM calculations.

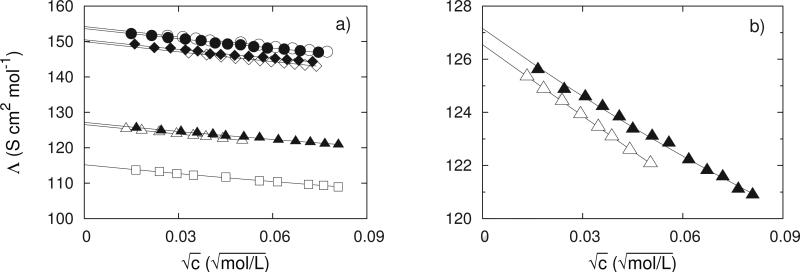
Figure 3.

Molar conductivities, Λ of LiCl, □; NaCl, △; KCl,◇; RbCl, ○; NaI, ▲; KI, ◆; and CsI, ●, at 298.15 K. The lines show the results of the lcCM calculations. Values for CsCl are not drawn due to the coincidence with RbCl data. Data for NaCl were taken from the literature [58].

For associated electrolytes, data analysis is carried out by a non-linear least squares fit with coefficients S, E, J₁ of eq. (1) preset to their calculated values and with Λ^∞, $K_{\mathrm{A}}^{\circ }$ and J₂ as the adjustable parameters [45, 52]. A three-parameter evaluation is reduced to a two-parameter procedure for very weak associating electrolytes where usually coefficient J₂ is also fixed [52]. The input data for the calculation of the coefficients are the known solvent properties (see Table S3 in the SI) and the distance parameter R. The lower limit, a, of the association integral is the distance of closest approach (contact distance) of cation and anion, a = a₊ + a₋, calculated from the ionic radius of anions and cations. Values of a₋ = 0.181 nm and 0.220 nm for the Cl⁻ and I⁻ anion and a₊ = 0.078,0.098,0.133,0.149, and 0.165 nm for Li⁺, Na⁺, K⁺, Rb⁺, and Cs⁺ cations were used, respectively [52].

Thus, a is assumed to be the the mean distance of closest approach between the centers of charge of the cation and anion. From extended investigations of electrolyte solutions in different solvents, it was found [52] that the upper limit of association is given by an expression of the type R = a + n · s, where s is the length of an orientated solvent molecule and n an integer number. For water, value of s = 0.28 nm was taken from the literature [58]. Assuming the possible existence of contact (CIP) and solvent-shared (SSIP) ion pairs in the solution, n = 1 was used throughout in the data analysis.

3. Theoretical

Several models at different levels of approximation [27–37, 40, 59–65] were used in the past to study ion-pairing of alkali halides in water theoretically. Although different models lead to somehow different results for the potential of mean force (pmf) between the cation and anion in question, they more or less agree on the description of ions hydration shells. To interpret our experimental results we therefore used a simple MB + dipole water model [20] that is easy to visualize, and is, at the same time, proven to correctly predict the microscopic structure of the ionic solvation shell [20, 65, 66]. A detailed description of the model is given in references [20, 66], and is therefore not repeated here. A brief overview of the MB + dipole model, together with the definition of the reduced units used in the text, is presented in the SI.

The model was studied using the isobaric-isothermal Monte Carlo computer simulations [67] in a systems with 60 MB+dipole water molecules and single ion or ion pair. Reduced temperature, T*, and pressure, p*, of the systems were 0.20 and 0.19 respectively. Initial configuration was chosen randomly and then equilibrated in 10⁷ cycles long simulation. Statistics was then collected over 10⁸ cycles long production run, which started from equilibrated configuration. In one cycle all water molecules were either rotated or displaced (equal probability for rotation or displacement). Maximal displacement and rotation were adjusted throughout the simulation, so that approximately one half of Monte Carlo moves were accepted.

Displacement of water molecules was followed by displacement of present ions (if they were not fixed). Ions were displaced in the same way as water molecules and their maximal displacements were also adjusted to achieve the acceptance ratio of one half. Finally, the change of the volume of the simulation was attempted where the maximal change was adjusted in the same way as maximal displacement. For the water molecules, the periodic boundary conditions with the minimum image convention were used to reduce the surface effects.

4. Results and discussion

4.1. The molar conductivities and the standard-state association constants

The molar conductivities were analyzed with the procedure described above. Best values of the $K_{\mathrm{A}}^{\circ }$ and Λ^∞ were obtained by minimizing the standard deviation σ_Λ

$${\sigma }_{\Lambda }={\left[\sum _{j=1}^{N_{\mathrm{p}}}{({\Lambda }_{j,\mathrm{fit}}-{\Lambda }_j)}^2∕(N_{\mathrm{p}}-3)\right]}^{1∕2}$$ (4)

defined by the differences between experimental, Λ_j, and calculated, Λ_j,fit, values of N_p data points j. As an example of temperature dependence of the molar conductivity, the molar conductivities of the aqueous RbCl solutions are shown in Fig. 2. The symbols represent the experimental data, while the lines represent the results of the lcCM model, eqs. 1 - 3. In the range of concentrations studied, the lcCM model represents a perfect fit to the experimental data at all the temperatures considered.

The derived molar conductivities at infinite dilution, Λ^∞, standard-state association constants, $K_{\mathrm{A}}^{\circ }$, together with the applied radii, R, are summarized in table 1. For comparison, values of Λ^∞ as calculated from ionic contributions reported by Harned and Owen [46] are also presented. Evidently, mostly an excellent agreement was obtained confirming the accuracy of our experiment. The experimental (symbols) and calculated values (lines) of molar conductivities at 298.15 K for all the salts investigated, with the exception of CsCl, are presented in Fig. 3a.

Table 1.

Limiting molar conductivities, Λ^∞, and association constants, $K_{\mathrm{A}}^{\circ }$ of investigated alkali metal halides in water. The assumed upper limit of association, R, is indicated.

T	Λ ∞	$K_{\mathrm{A}}^{\circ }$	Λ ∞	$K_{\mathrm{A}}^{\circ }$	Λ ∞	$K_{\mathrm{A}}^{\circ }$	Λ ∞	$K_{\mathrm{A}}^{\circ }$
K	S · cm2 · mol−1	mol−1 ·dm3	S · cm2 · mol−1	mol−1 ·dm3	S · cm2 · mol−1	mol−1 ·dm3	S · cm2 · mol−1	mol−1 ·dm3
	LiCl, R/nm=0.538		NaCl,a R/nm=0.559		KC1, R/nm=0.594		RbCl, R/nm=0.610
278.15	70.49±0.03	0.71 ±0.16	77.75±0.02	1.33±0.22	94.33±0.03	1.66±0.13	97.76±0.03	1.24±0.12
	70.27b		77.80b		94.23b		97.62b
283.15	80.98±0.05	0.90±0.20	89.16±0.02	1.58±0.22	107.45±0.04	1.62±0.13	111.03±0.05	1.06±0.17
	80.67b		89.21b		107.36b		110.97b
288.15	91.69±0.06	0.10±0.23	101.11±0.01	1.62±0.13	121.10±0.04	1.57±0.13	124.97±0.05	1.17±0.13
	91.63b		101.14b		121.03b		124.88b
293.15	103.21±0.06	0.32±0.20	113.58±0.02	1.70±0.15	135.27±0.05	1.49±0.13	139.37±0.06	1.23±0.16
	103.07b		113.58b		135.21b		139.28b
298.15	115.21±0.06	0.44±0.17	126.55±0.01	1.58±0.07	149.94±0.04	1.47±0.10	154.21±0.06	1.26±0.15
	114.99b		126.50b		149.85b		154.16b
303.15	127.61 ±0.05	0.56±0.13	139.96±0.01	1.65±0.08	164.96±0.04	1.41±0.10	168.51±0.07	1.50±0.16
	127.36b		139.89b		164.93b		169.46b
308.15	140.39±0.03	0.61±0.08	153.79±0.02	1.59±0.10	180.49±0.09	1.77±0.18	185.02±0.08	1.60±0.16
	140.16b		153.73b		180.40b		185.15b
313.15	153.40±0.05	1.45±0.10			196.13±0.09	2.53±0.17	200.72±0.11	2.09±0.20
	153.37b				196.25b		201.17b

	CsCl, R/nm=0.626		Nal, R/nm=0.598		Csl, R/nm=0.665		KI, R/nm=0.633
278.15	97.74±0.04	1.69±0.14	79.07±0.05	0.79±0.24	98.53±0.05	1.53±0.21
	97.50b		78.92b		98.62b
283.15	110.62±0.05	0.76±0.14	90.30±0.04	0.58±0.15	111.46±0.04	1.47±0.17
	110.80b		90.18b		111.78b
288.15	124.42±0.06	0.86±0.14	102.11±0.04	0.060±0.14	125.03±0.05	1.39±0.16
	124.61b		101.98b		125.44b
293.15	138.69±0.06	0.88±0.14	114.44±0.08	0.53±0.22	138.98±0.08	0.97±0.24
	138.88b		114.27b		139.58b
298.15	153.47±0.07	1.00±0.15	127.16±0.06	0.34±0.15	153.64±0.05	1.33±0.13	150.50±0.09	0.71±0.26
	153.61b		127.05b		154.16b	150.40*
303.15	168.57±0.07	0.96±0.13	140.33±0.09	0.43±0.22	168.45±0.07	1.30±0.19
	168.76b		140.28b		169.15b
308.15	183.89±0.07	0.76±0.14	153.91±0.12	0.68±0.28	183.59±0.08	1.30±0.18
	184.31b		153.94b		184.51b
313.15	199.45±0.08	1.19±0.15	167.63±0.12	1.27±0.24	198.83±0.09	1.87±0.20
	200.23b		168.0b1		200.23b

^aReevaluated form the literature data [58]

^bHarned Owen

For CsCl solutions an unusual behavior was observed. The data for CsCl in aqueous solutions at 298.15 K are shown in Figure S6 in the SI together with the available literature data in this concentration range. It is evident, that at contractions below ~ 0.002 mol/L, CsCl exhibits quite unusual and unexpected behavior which has been detected in both runs of experiments with different origin of sample. In the data analysis the values in the concentration range ~ 0.002 <c ~ 0.005 mol/L from second run were taken into account. The results of fitting procedure are represented with line.

The unusual behavior of the CsCl aqueous solutions has been previously observed by the diffraction experiment [68]. However, further investigation of this phenomena would be needed.

An inspection of Table 1 reveals that the molar conductivity at infinite dilution strongly depends on the nature of cation (they are the lowest in the case of lithium salts and larger in the case of caesium and rubidium salts). On the other hand, the substitution of iodide for chloride affects the molar conductivity to much smaller extent. They are, however, in all the studied cases slightly larger for iodide salts, compared to the chloride ones.

The quantity of the greatest interest for us was the derived standard-state association constants, $K_{\mathrm{A}}^{\circ }$. Despite the fact, that small $K_{\mathrm{A}}^{\circ }$ values could be regarded as a rough approximation, the difference in their magnitude obtained at all temperatures can not be overlooked. An important observation is that $K_{\mathrm{A}}^{\circ }$ is much more sensitive to the nature of the anion: although the difference in molar conductivity between NaI and NaCl solutions, for example, is relatively small (Fig. 3b.), this difference is reflected in the change of the association constant from a value of 0.34 for NaI to the value of 1.58 for NaCl at 298.15 K. This indicates the importance of the temperature and concentration dependence for determining the results. It must be mentioned, that the absolute values of $K_{\mathrm{A}}^{\circ }$ depend on the model applied in analysis of conductivity data. Relative values, however, are model independent.

As it has been already mentioned in the Introduction, the molar conductivities of alkali halide salts in water have been studied before [45–51, 53]. Although the reported data are accurate, the measurements were performed at higher salt concentrations (in many of these, the lowest salt concentration studied is actually the highest concentration in our study). Nevertheless, we re-evaluated the available literature data [47–51] by means of lcCM model. Despite some difficulties with convergence in fitting procedure $K_{\mathrm{A}}^{\circ }=0.2\pm 0.7,0.2\pm 0.6,0.7\pm 0.5,0.2\pm 0.7,0.7\pm 1.5$, for LiCl, NaCl, KCl, RbCl, and CsCl at 298.15 K were obtained. As already mentioned in the Introduction, to the best of our knowledge, there are no data available at other temperatures. Thus here no explicit dependence on the structure of salt can be assumed. As indicated above, we ascribe this to the fact that all the measurements reported in the literature were done for the concentrations above ~ 0.005 mol/L, while the ion specific effects play a major role at low concentrations.

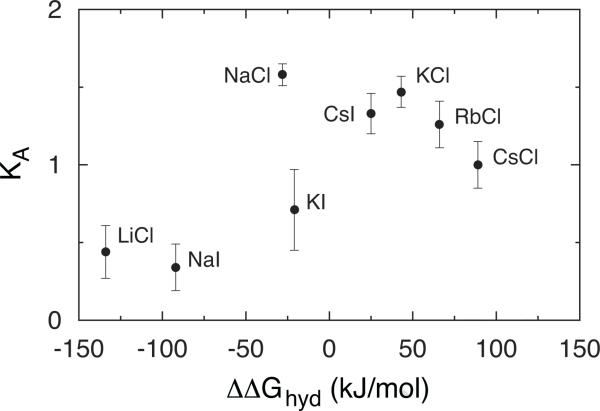
To test the idea of Collins matching water affinities, we plotted the standard-state association constant in the same manner as the solubilities are plotted in Fig. 1, this is against the difference in Gibbs free energy of cation and anion hydration in Fig. 4. An approximately inverse picture to that in Fig. 1 emerges, which is expected, due to the general understanding of the salt solubility: The ions that are strongly associated (high association constant) should have low solubility and vice versa. Evidently, our results confirm this view.

Figure 4.

Dependence of association constants, $K_{\mathrm{A}}^{\circ }$ of investigated salts obtained by lcCM from conductivity data on difference of Gibbs free energy of ion hydration, Δ(ΔG_hydr).

4.2. Microscopic view of the ion-pairing

The microscopic structure of the alkali halide ion pairs has been extensively studied by Fennel et al. [36, 37] who have evaluated the pmfs for different alkali metal halide ion pairs. In this work we have chosen a simpler, two-dimensional model to analyze the water structure in the systems studied. The structure of the system was studied using several distribution/correlation functions which were calculated as ensemble averages [67].

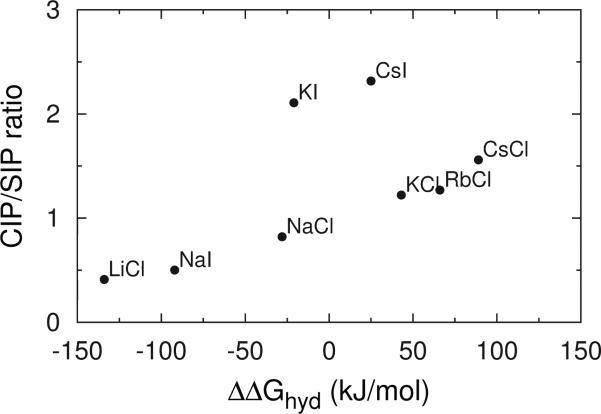
The pmfs for different ion pairs are, for the comparison with the results of more sophisticate models, given in the SI. As already explained above, a good qualitative agreement is obtained with previous results [36, 37, 62, 63]. The pmfs for different ion pairs differ in the relative depth of the first and the second minimum in the function, the first one corresponding to the two ions being in contact (contact ion pair, CIP), and the second minimum correspond to the situation, where the two ions are separated by one water molecule (solvent separated pair, SIP). These observations can be presented as a CIP/SIP ration, which is, for our model, as a function of the difference in Gibbs free energy of cation and anion hydration, shown in Fig. 5.

Figure 5.

CIP/SIP ratio as a function of the difference between Gibbs’ free enthalpies of hydration of single ions [43].

By comparing the figures 1, 4, and 5, one can clearly see the correlation. The greater is CIP/SIP ratio, the larger is the association constant, and less soluble is the salt. The ion pairs with more similar free energy of hydration (similar size) are more likely to be found in the CIP configuration, and have therefore the largest association constant. On the contrary, the ions with large difference in free energy of hydration (different ion size) are more likely to allow a water molecule to come in-between them (SIP). This consequently lowers the association constant. The observation is in agreement with Collins’ idea of matching affinities. Similar findings were previously reported in the literature [36, 37].

The association constant is high when the two ions are similar in size and low otherwise. According to Collins [42, 69–71], two small oppositely charged ions (both kosmotropes) will associate, because interaction between them is stronger than interaction between small ion and larger water molecule. When having large oppositely charged ions (both chaotropes), water-water interaction is stronger than interaction between water and ion, which is larger than water molecule; as a result two chaotropes also associate. On the other hand, chaotrope and kosmotrope will tend to dissociate as interaction between smaller ion and water molecule is stronger than interaction with oppositely charged large ions. To see the microscopic origin of this general, well established, view we performed a thorough analysis of the strucure of hydration water from computer simulation.

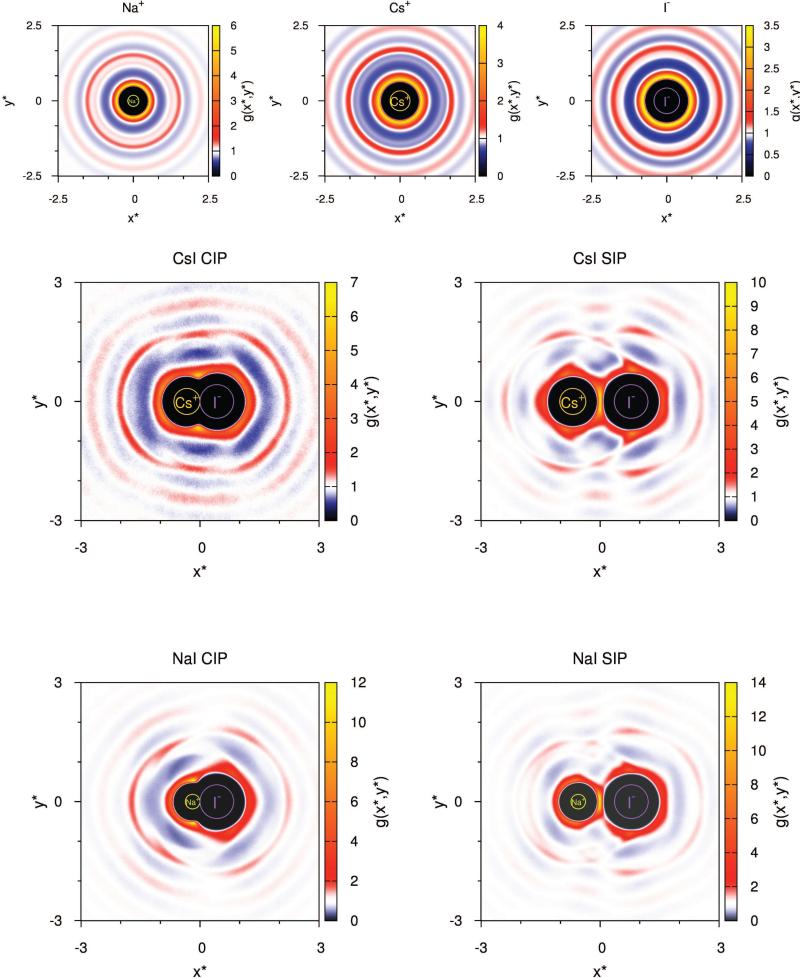
Fig. 6 shows the relative density of water molecules around single ions, as well as around ion pairs when in CIP and SIP state, for two cases with very different association constant (CsI and NaI). The middle part of the Fig. 6 shows the case for CsI, where both ions are large, and the association constant is above 1 (1.33 at 298 K). The bottom part of the Fig. 6, on the other hand, is showing the relative density of water molecules around NaI ion pair, where cation and anion largely differ in size; the association constant for this case at 298 K was determined to be only 0.34.

Figure 6.

Planar distribution functions for water molecules around single ions (Na⁺, Cs⁺ and I⁻), CsI and NaI. In case of ion pairs both ions lie on abscissa axis, and ther x-coordinate is given by equations given in the SI. White color corresponds to g(x*,y*) = 1.

In both cases, for contact ion pair configuration, the water molecules will most likely be found as close as possible to both ions. It is also obvious that in SIP state ions are separated by one water molecule as water density peak lies in the midpoint of line segment joining ion centres. The relative water density in-between the two ions increases compared to the water density around a single ion which is in agreement with the findings of Fennel et al. [36, 37]. It the case of ions with large difference in size, and therefore also in the affinity for water, circularly symmetric hydration shells of larger ion (ion with lower water affinity) gets distorted (see Fig. 6, NaI). The affinity of smaller ion (sodium in Fig. 6) for water is so strong, that we can observe its ring corresponding to the first minimum in ion-water distribution function even in the vicinity of the larger ion (iodine in the Fig. 6). We can also notice that it looks like part of the first hydration shell of the iodide is missing. When both ions have comparable affinity to water (CsI, for example, Fig. 6), the above described effect can be noticed for both ions (CsI SIP). For CIP state ion pairs, we can observe that hydration shells of the same order fuses and can be seen as “elliptical ring”.

The number of water molecules and number of first hydration shell hydrogen bonds around single ions and ion pairs is given in Table 2. We can see, that number of hydrogen bonds in first hydration shell around ion pair in CIP state is smaller than the sum of hydrogen bonds for relevant single ions. This could imply that forming contact ion pair is entropy-driven process.

Table 2.

Number of water molecules in the first hydration shell around an ion pair (n_water) and number of hydrogen bonds between molecules in the first hydration shell (n_H-bonds) for investigated salts.

Ion pair	nwaters	nH-bonds
LiCl CIP	4.59 ± 0.01	2.25 ± 0.01
LiCl SIP	6.82 ± 0.01	2.50 ± 0.01
NaCl CIP	4.82 ± 0.01	2.33 ± 0.01
NaCl SIP	6.87 ± 0.01	2.42 ± 0.01
KCl CIP	5.05 ± 0.01	2.37 ± 0.01
KCl SIP	7.01 ± 0.02	2.65 ± 0.01
RbCl CIP	5.16 ± 0.01	2.41 ± 0.01
RbCl SIP	7.13 ± 0.01	2.85 ± 0.01
CsCl CIP	5.36 ± 0.01	2.48 ± 0.02
CsCl SIP	7.40 ± 0.01	3.21 ± 0.01
NaI CIP	5.39 ± 0.01	2.86 ± 0.02
NaI SIP	7.39 ± 0.01	3.10 ± 0.01
KI CIP	5.51 ± 0.01	2.70 ± 0.02
KI SIP	7.47 ± 0.01	3.40 ± 0.02
CsI CIP	5.68 ± 0.01	2.53 ± 0.01
CsI SIP	7.77 ± 0.01	3.95 ± 0.02

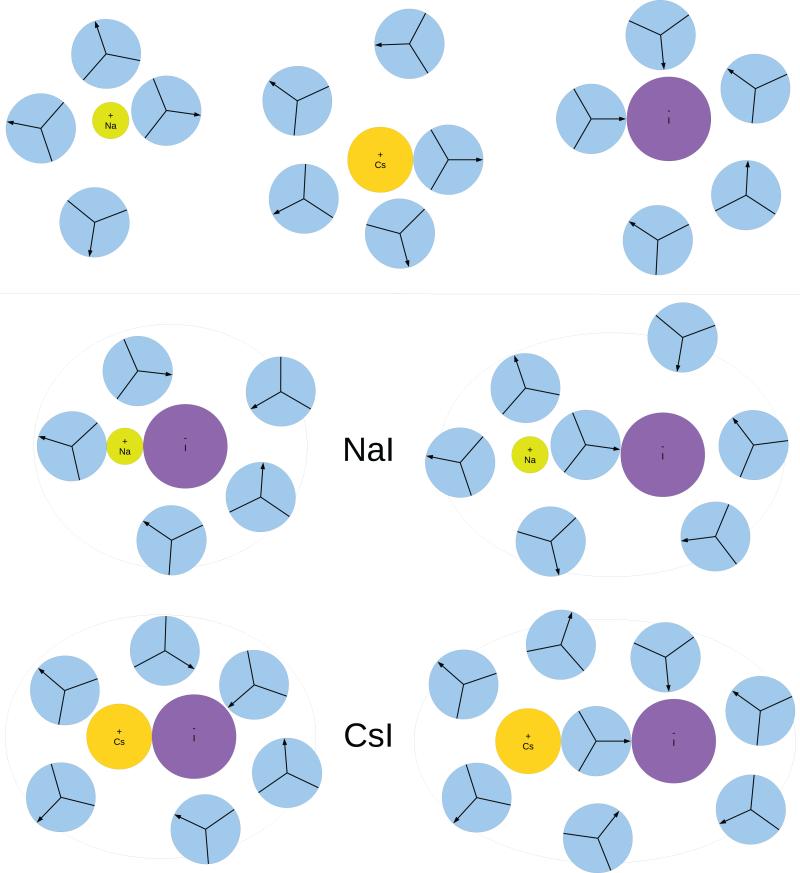
To analyze the influence of each separate ion on the hydration shell of the ion pair, the orientation of water molecules in the hydration shell was determined. During the simulation the angle distribution function for waters in first hydration shell and the ion-water correlation function were calculated and used to construct the most probable configuration of water molecules in the first hydration shells of CIP and SIP states of different ion pairs. These “snapshots” of the most typical ion pairs, i.e. CsI and NaI, are shown in Fig. 7.

Figure 7.

Snapshots of water molecules in the first hydration shell of single ions (Na⁺,Cs⁺ and I⁻) and ion pairs (NaI and CsI) in their most probable configuration and orientation, as suggested by pair correlation and angular distribution functions. Area of first hydration shell is enclosed by drawn ellpise; arrow is used to label arm bearing positive charge.

In CIP state angular distribution functions of water molecules for anion's and cation's region slightly differ from angular distribution functions for single ions [20]. However, the water between ions (formally this is is part of ellipse where x_c < x < x_a, see the SI) in CIP state have distinctive preferential orientation. On average there was one water molecule in described region and preferred angle that this molecule makes with cation was between 70° and 95° for cation (see the SI).

In SIP state the closest distance between ion edges was roughly σ_LJ, which equals to diameter of MB water molecule. In the region between the ions there were 3–4 water molecules, of which one was (with its centre) almost in the line joining both ion centres; it was in electrostatically most favorable orientation (see SIP state ion pairs in Fig. 7). Angular distribution functions for waters in first hydration shell are the same as for single ions [20]. On the basis of this observation, we can conclude that ordering of the MB waters is favorable for both ions considered. Collins [42, 69–71] states that water around ion is ordered via hydrogen bond formation and electrostatic interactions with ions. In case of cations these processes are cooperative, however, the electrostatic mechanism opposes hydrogen bond formation in case of anions. In the constructed snapshots we can see that around cations there are more MB waters with favorable orientation for the formation of the hydrogen bond.

5. Conclusions

Molar conductivities, L, were determined as a function of temperature for dilute solutions, m ~≤ 0.005 mol·L^–1, of the eight metal halides in water. The data were analyzed with Barthel's low-concentration chemical model. [52] When plotted against the difference in ion free energy of hydration, a ’volcano relationship’ was obtained; ions with large difference in the hydration free energy (large difference in size) have relative low association constant compared to those who have similar hydration free energy and tend to associate in water. The microscopic structure was obtained with Monte Carlo computer simulations, using a simple two-dimensional water model. It has been shown that in all cases, the relative water density in-between the two ions increases, compared to the relative water density around two separate ions. In case of two small ions, the two are associated due to the strong electrostatic interaction (in agreement with the Collins’ ’law of matching water affinities’ ), while in the case of two large ions, we attribute the pairing to entropic reasons. The number of waters, as well as the number of hydrogen bonds in the first hydration shell of an ion pair is reduced compared to the single ions. On the other hand, in the case of two ions with very different water affinity, the small ion would be strongly hydrated and not releasing its water upon pairing, the process leading to a small association constant.

Highlights.

1. We report precise conductance data and Ka for alkali halides that can be used to evaluate theoretical models.

2. Graph of Ka vs difference in \Delta G of hydration of the corresponding individual ions produces a ‘volcano relationship’.

3. Association constant is interpreted using a simple solution model.