Skip to main content
PMC home page
International Journal of Experimental Pathology logoLink to International Journal of Experimental Pathology
. 2013 Dec 20;95(1):1–7. doi: 10.1111/iep.12062

A mathematical model of the colon crypt capturing compositional dynamic interactions between cell types

Kieran Smallbone *, Bernard M Corfe *,†,‡
PMCID: PMC3919643  PMID: 24354351

Abstract

Models of the development and early progression of colorectal cancer are based upon understanding the cycle of stem cell turnover, proliferation, differentiation and death. Existing crypt compartmental models feature a linear pathway of cell types, with little regulatory mechanism. Previous work has shown that there are perturbations in the enteroendocrine cell population of macroscopically normal crypts, a compartment not included in existing models. We show that existing models do not adequately recapitulate the dynamics of cell fate pathways in the crypt. We report the progressive development, iterative testing and fitting of a developed compartmental model with additional cell types, and which includes feedback mechanisms and cross-regulatory mechanisms between cell types. The fitting of the model to existing data sets suggests a need to invoke cross-talk between cell types as a feature of colon crypt cycle models.

Keywords: apoptosis, cancer, cell cycle, cell–cell signalling, colon crypt, differentiation, mathematical model

The colon (and small intestine) is lined by many millions of crypts, which serve to increase the surface area of the gut for absorptive and secretory functions, which provide a mechanism for replenishment of cells lost through sloughing and which act in sensing and signalling capacity to monitor luminal contents. The crypt has a slow-dividing, long-lived stem cell compartment at the base, which populates a more actively dividing transit-amplifying compartment, from which cells exit by differentiating into one of the secretory lineages. A further subclass of cells is the enteroendocrine (EEC) compartment, which comprises a small number of cells, but whose role may be significant: for example, most of the postprandial GLP-1 release driving cessation of eating comes from the colon (Anini et al. 1999). Likewise, not only other gut hormones (Gunawardene et al. 2011) but molecules known to be involved in apoptotic signalling, such as VEGF and VEGF-receptor (Gulubova & Vlaykova 2008) and Nrp-1 (Yu et al. 2011), are expressed in cells of the EEC lineage.

The crypt is therefore a microcosmic model of stem cell differentiation, amplification, differentiation and death. The crypt is thought to be under exquisite regulation in order to maintain a reasonably steady state, but nonetheless retains the ability to shrink or grow in conditions of starvation and to respond to alterations in the large bowel content (Sakata & von Engelhardt 1983; Sakata 1987; Inagaki & Sakata 2005). Changes in crypt composition have been noted in large bowel pathologies; numbers of proliferating cells per crypt are elevated in the macroscopically normal tissues in pericancerous and peri-adenomatous fields (Humphries & Wright 2008); likewise, perturbations in rates of apoptosis may contribute to breakdown of epithelia associated with forms of colitis, or failure to shed in hyperplasia. Our group have previously shown that there are changes in the EEC compartment in peri-adenomatous fields (Yu et al. 2011). The mechanisms underlying this perturbation of crypt dynamics are unclear, but work using xenograft models of colorectal cancer has also shown that there is a change in EEC numbers in the gut mucosa, suggesting a diffusible factor may contribute (Cho et al. 2008).

It is logical that small changes in crypt dynamics may, over large amounts of time, lead to the types of macroscopic abnormalities associated with early stages of colorectal disease; however, such changes are not readily identified or captured by empirical methods. Mathematical modelling offers the chance to identify and compute interactions based on observable data and to explore where interactions may be influenced to lead to pathologies. The colonic crypt has previously been subject to a number of modelling efforts, notably the compartmental model from Tomlinson and Bodmer (1995), which has been subject to iterations and adaptations (Johnston et al. 2007a). Other models exist and have been reviewed (Johnston et al. 2007b; De Matteis et al. 2013). The compartmental model has a number of useful features – in particular the compartmental concept relates closely to observable biology and provides a set of semantic terms that are measurable, specifically the model divides the crypt into stem cells (N0), transit-amplifying cells (N1) and differentiated cells (N2) each of which has a rate of apoptosis, and in the case of N0 and N1 a rate of exit and replenishment.

However, the model also has limitations, including a term for saturating feedback with no obvious biological meaning. Furthermore, the model does not include an EEC compartment, which we have shown is both biologically important and subject to alteration in proximity to neoplasia. Finally, in common with the majority of models, this is built to approach a numerical steady-state derived from averaged observations. In reality, there will be dynamic relationships between cell types, which exist to maintain the global steady state. Whilst independent observations are made, for example, on changes in numbers or proportions of proliferating cells, of EEC, or of goblet cells (Bernstein et al. 2000), few studies have addressed large numbers of endpoints within the same data series. We therefore formally hypothesize that the relationships between cell types in colon crypt compartments will not be constant in strength or direction and that the incorporation of measurements into a crypt model will potentially reveal novel or key regulatory decision points in the crypt cell fate pathway.

Model development

The general workflow for development of the revised model is presented in the supplementary online material, Figure S1. Briefly, we used a pre-existing base model and established goodness of fit to our in vivo observed data. We developed a score for fit and then undertook a series of iterative revisions until a model was yielded, which fairly represented the dynamic interactions between cell types in the colon crypt.

The models developed below are made available in Systems Biology Markup Language (SBML, Hucka et al. 2003), an exchange format for computer models of biological processes that is understood by a wide range of software tools. The models are available from the BioModels.net database (Li et al. 2010):

Version 0: http://identifiers.org/biomodels.db/MODEL1306190000

Version 1: http://identifiers.org/biomodels.db/MODEL1306190001

Version 2: http://identifiers.org/biomodels.db/MODEL1306190002

Version 3: http://identifiers.org/biomodels.db/MODEL1306190003

Parameter values used are presented in Table 1. Simulations and analysis were performed using COPASI (Hoops et al. 2006, available from http://copasi.org/).

Table 1.

Terms included in successive iterations of the model and their semantic meaning. Parameters used in version 0 derived from Johnston et al. (2007a)

Parameter v0 v1 v2 v3 Units Semantic
a0 0.1 Per day
a1 0.24 Per day
b0 0.22 Per day
b1 0.55 Per day
c0 1 Per day
c1 1 Per day
m0 2.9 Cell
m1 29 Cell
d0 0.10 0.10 0.20 0.02 Per day Rate of apoptosis from N0
d1 0.26 0.42 0.84 0.55 Per day Rate of apoptosis from N1
d2 1.8 1.1 2.2 1.9 Per day Rate of apoptosis from N2
d3 0.038 0.168 Per day Rate of apoptosis from N3
K 120 120 106 Cell Crypt capacity
r0 1.8 2.0 2.0 Cell per day Rate of stem cell cycle
r1 5.9 6.1 10.6 Cell per day Rate of proliferating cell cycle
p01 0.86 0.82 0.63 1 Rate of exit from stem cell
p12 0.83 0.83 0.81 1 Rate of entry into terminal differentiation
q03 0.094 0.935 1 Maximum probability of N0 to N3 division
K03 1.60 0.78 Cell Maximum probability of N0 to N3 division
K0X 1.60 0.15 Cell N3 level at which N0 apoptosis is half-maximal
K1X 1.6 15.4 Cell N3 level at which N1 apoptosis is half-maximal
K2X 1.6 2.7 Cell N3 level at which N2 apoptosis is half-maximal
Open in a new tab

NOTE: until publication the models are available from

http://www.ebi.ac.uk/biomodels/reviews/MODEL1306190000-3/

Base model

As a base model (version 0), we follow the ‘saturating feedback’ model of Johnston et al. (2007a) (other parameterizations of the same model are described in Johnston et al. 2007b). The model describes cell population dynamics in the colonic crypt. Let N0, N1 and N2 denote the numbers of stem, semidifferentiated (transit-amplifying) and fully differentiated cells respectively. Their evolutions are defined by the system

graphic file with name iep0095-0001-mu1.jpg
graphic file with name iep0095-0001-mu2.jpg
graphic file with name iep0095-0001-mu3.jpg

where Rii denotes the rate of symmetric division Ni → 2Ni, Rij denotes the rate of asymmetric division Ni → Ni + Nj, and RiX denotes the rate of cell death Ni →∅.

Reaction rates are defined by Johnston et al. as

graphic file with name iep0095-0001-mu4.jpg
graphic file with name iep0095-0001-mu5.jpg
graphic file with name iep0095-0001-mu6.jpg

Note that most available data from formalin-fixed, paraffin-embedded (FFPE) tissue are based on scores established per hemicrypt in section. These measures are one-dimensional (per crypt length) rather than three-dimensional (per crypt volume). Consequently, the base model has been rescaled so that the cellularity T = Σ Ni (the total number of cells per hemicrypt) equals 74, rather than 250. It should be noted, however, that there is no explicit spatial dependence defined in the model.

Capacity constraints

The model of Johnston et al. suffers from a number of problems. Whilst described as ‘saturating feedback’, it in fact contains no feedback mechanism: the dynamics of stem cells N0 are independent of the levels of N1 and N2, for example. Assessment of this model indicated that it could grow or shrink beyond biologically observed sizes through perturbation of a1 – the cell cycle rate of N1 (Supplementary online information Figure S2). Furthermore, in a series of stochastic simulations of compartment cellularity, the model frequently lost its stem cell compartment but did not become extinct (Supplementary online data).

The most natural way to incorporate feedback is via capacity constraints. We define the rates of N0 and N1 division as fi = ri Ni (1 – T/K) where K is the carrying capacity of the crypt, estimated as the largest observed crypt size. This division can then be symmetric (Rii = pii fi) or asymmetric (Rij = pij fi) where p00 + p01 = 1 and p11 + p12 = 1. Capacity constraints are typical in biological models. A carrying capacity is used in logistic growth; this is often extended to development of multiple cells or species via the competitive Lotka–Volterra equations.

Parameter values for this model (version 1) are calculated using measured cell counts Ni and assuming transition rates as per the base model. The model improves on the base model by constraining the size of the crypt to within biologically feasible bounds.

Enteroendocrine population

Our previous studies have shown that perturbations in the enteroendocrine cell (EEC) population occur in the macroscopically normal mucosa of subjects with a colorectal lesion, in proximity to the lesion. It has previously been reported that in mice with xenografted colorectal tumours, there is a similar depression of EEC numbers in the colorectal mucosa (Cho et al. 2008). These data suggest that there is potentially an important compositional change in the cell types of the crypt, with EEC being, at the very least, a barometer of such effect. EECs are associated with the expression of receptors, environmental sensors, signalling molecules and receptors such as the apoptosis regulator NRP-1 (Gunawardene et al. 2011). Thus, we add a new compartment N3 to the model (version 2, see Figure 1). We initially estimate – based on observed frequency data (see Table 2) – that 1% of stem cell divisions are used to produce EEC cells.

Figure 1.

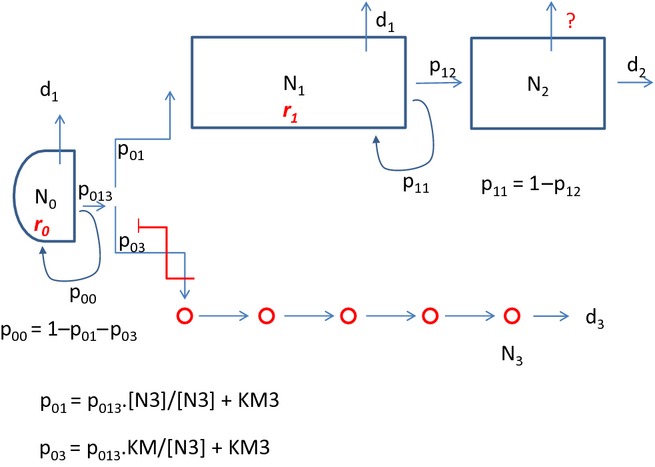
Figure 1

Open in a new tab

Summary of relationships described in the model, including feedback loops. Parameters are detailed in Table 1 and are an extension of the terms used previously. Briefly, main cell compartments are identified as N0 (stem cell), N1 (transit-amplifying cells), N2 (differentiated cells) and N3 (enteroendocrine cells). All cell compartments have a rate of apoptotic death (d0–d3 respectively), and N0 and N1 have rates of cell cycle (r0 and r1, respectively). N1 cells may exit into a differentiation pathway with rate p12, or may replenish at rate p11, which sum to unity as the ‘usual’ fates of N1 cells. N0 cells may likewise replenish at rate p00 or enter a differentiation path at rate p013, which are reciprocal events. Entry into N1 or N3 lineages are alternative pathways from p013, and the numbers of N3 cells feedback to control this fate determination point.

Table 2.

Assessment of root mean square fit of model to experimentally derived parameters

OBS v0 v1 v2 v3
N1 27 44 27 28 30.3
N2 46 27 46 46 47.9
N3 1.6 1.7 1.2
fit 0.71 0.58 0.05 0.14
N2 v N1 −0.24 1.00 0.08 1.00 −0.31
N3 v N1 0.04 1.00 0.04
N3 v N2 0.26 1.00 0.00
N1 v T 0.80 1.00 0.95 1.00 0.90
N2 v T 0.11 1.00 0.03 1.00 0.13
N3 v T 0.06 1.00 0.11
fit 5.73 0.88 13.30 0.60
Open in a new tab

Top half of table shows predicted number of cells at steady state for successive modifications to the model, and a comparison to experimentally observed average numbers. The bottom half shows predicted correlations between compartment sizes and experimentally observed correlations. In both cases, a comparison is made using the root mean square fit. Observed data (OBS) were reference values from the normal group in a cross-sectional study (Corfe et al. 2009). In all 41 subjects, data were used to determine mean values and Spearman's correlation coefficients.

We define p03 = q03 K03/(N3 + K03) so that N3 cells inhibit their own production. Michaelis constants are typically found to be the same order as their substrates (Smallbone & Mendes 2013); thus, as an initial estimate, K03 is set to be of the same order as the number of N3 cells.

The EEC may play a variety of signalling functions in the crypt. For the purposes of this model, we consider that their primary role is the inhibition of apoptosis, and thus, redefine RiX = di Ai Ni where the apoptosis rate Ai is given by Ai = KiX/(N3 + KiX). Again, KiX is assumed to be of the same order as N3. The model extends the base model by including a small, but biologically important, compartment of EEC, but estimated parameters are improved upon in the next section.

Development of assessment criteria

We have acquired data from the macroscopically normal mucosa of patients with and without neoplasia under an ongoing research project (Corfe et al. 2009). In total, 41 subjects were free from pathology. Histology had been undertaken, and numbers of proliferating cells were determined by Ki67 staining (defined as N1), cellularity (T) by H&E staining and EEC by enterochromaffin staining (N3).

As the crypt is a dynamic entity with variation in compartment size and cellularity over time, we were able to establish by correlation that some (but not all) compartments had strong positive or negative inter-relationships (Table 2). The strength and direction of these relationships formed a set of assessment criteria for the fit of models to experimental data. We hypothesize that, to capture the dynamic relationship between cell types, it is informative to model their correlation, as well as their average values, as the latter would only lead to a steady-state representation.

A theoretical sample of crypts may be obtained by iteratively allowing independent parameter values to vary by a small proportion δ, calculating the compartmental steady state, then comparing the theoretical correlations obtained with those observed experimentally. In the limit as δ→0, the effect of changing one parameter on a compartment is given by its scaled sensitivity coefficient. Thus, the theoretical correlation is given by the correlation between each compartment's scaled sensitivity coefficients.

In Table 2, we see that, although steady-state modelling indicated that version 2 of the model was stable, achieved predicted numbers of cells in each compartment and became extinct on loss of stem cells, the strength and direction of relationships was a poor fit to the assessment criteria. Thus, we allow the parameters to vary around their initial estimates, to minimize the distance between the experimental and theoretical correlations, whilst maintaining similar values for compartment size. This was performed in COPASI using its inbuilt Hooke and Jeeves algorithm. We see that the fit (version 3) is much improved.

A summary of the model and its internal relationships is shown in Figure 1.

Example applications

Identifying principal potential mechanism of action of butyrate

To test the value of the model in identification of novel potential mechanisms of action, we sought to identify parameters whose alteration may recapitulate the observed effects of butyrate on crypt composition. Butyrate is a fermentation product of the luminal microbiome, which is implicated as a metabolite of the colon epithelium, as a regulator of cell cycle, of differentiation and of cell death (Hamer et al. 2008). Several in vivo models have shown that butyrate appears to stimulate proliferation. We surveyed the literature and found that the majority of reports from human studies find a weak and non-significant relationship between the numbers of observed proliferating cells and the faecal butyrate concentration (Bowles & Corfe, in preparation). Our group have recently reported a stronger negative correlation between the enteroendocrine population and faecal butyrate.

We used sensitivity analysis to identify parameters whose variation would confer these relationships at these relative magnitudes (oppositional with greater magnitude per unit change for N3 than for N1). Sensitivity analysis suggested p01, q03 and K03 all had potential to modify N1 and N3 with the opposite directionality and greater magnitude for N3 (Supplementary Online Information Figure S3). We therefore undertook a parameter scan, within biologically sensible limits (in stepwise increments −15% to +15). Endpoint data from timecourses are shown in Figure 2a and suggest variation in p01 – the rate of exit from the stem cell compartment – may best recapitulate the effects of butyrate. Such predictions cannot exclude the likely pleiotropic effects of butyrate, but fit well with a substantive literature suggesting that butyrate affects the cell cycle.

Figure 2.

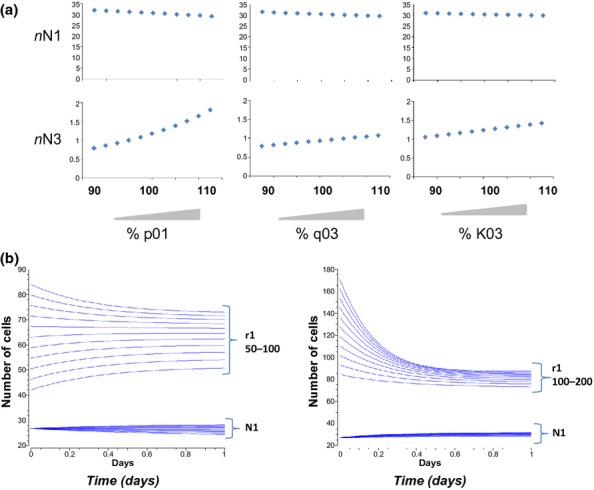
Figure 2

Open in a new tab

Sample applications of the model. (a) The variations aim to mimic the effects of butyrate upon crypt composition as observed in vivo. Predictive outputs consequential to parameter sweeping p01 and q03 and K03 from −10% to +10% of their value were established for output parameters N1 and N3. (b) The effect of varying cell cycle time (r1) upon numbers of proliferating cells (N1) and cellularity (T). Left panel shows progressive 10% decreases in r1 from 100 to 50%. Right panel shows progressive 10% increases in r1 from 100 to 200%. Variation of r1 has little effect on N1.

Effect of varying cell cycle rate on numbers of observed proliferating cells

Changes in the number of proliferating cells in crypts have been observed associated with the presence of a lesion (Sandler et al. 2000) and in response to the microenvironment (Holt et al. 1996). Such measurements are usually made (in human tissues at least) through classical immunohistochemical approaches. Butyrate has been shown to reduce cell cycle rates in vitro in colorectal cancer cell lines and to drive an increase in the number of N1 cells in normal tissue. It has been induced from this observation that the in vivo observation represents an increase in proliferation, which is opposite to the effect on cancer cells in vitro and that this apparently paradoxical effect may be a mechanism of chemopreventive action on transformed cells (Gibson et al. 1992; Scheppach et al. 1995; Hague et al. 1997). We hypothesized that a decrease in cell cycle rate may equally lead to an increase in apparent number of proliferative cells as it may, for example, be the number of cycles, rather than rate, which determines N1 composition. Such arguments are precedented.

We used our model to undertake a parameter scan of cell cycle rate (r1) and to measure its effect on numbers of cells in the N1 compartment (Figure 2b). r1 was varied between half and double its baseline value. There was no effect of alteration on the N1 compartment. These data suggest that the cell cycle rate may not be a principle determinant of size of the N1 compartment in the crypt.

Discussion

The colonic crypt is an attractive target for modelling for a number of reasons – it encapsulates a cycle from stem cell through proliferation, differentiation and death, it is highly regulated, and perturbations in this regulatory process are at the root of early colorectal carcinogenesis, a major cause of cancer mortality.

We have shown that an established model of the colon crypt was unsuited to the analysis and interpretation of our data sets as follows: (i) the absence of a cell subtype (enteroendocrine cells) which we have previously shown to become deranged in proximity to a colorectal lesion (ii) the model was not size-limited and (iii) the direction of relationships between cell types did not mimic those observed in vivo. We sought to use the features of the base model, notably compartmental organization, and then cell fate decisions from each compartment, and to evolve this to our purpose. By exploring the direction and strength of relationships between cell compartment types in an existing data set, as opposed to using global data, we have identified oppositional relationships that needed to be incorporated into the model. It should be noted that the model is built around data generated in one dimension (hemicrypt scores). This is usual for histopathology, and our model is therefore compatible with raw data from human samples; however, this limitation should be noted when comparing against established spatially, rather than histopathologically, motivated 2-d and 3-d models of the crypt (see, for example, Buske et al. 2011; Dunn et al. 2012; Mirams et al. 2012; Pin et al. 2012).

We have deliberately sought throughout the developmental steps in modelling to ensure semantic clarity of terms. This allows incorporation into hypermodels or linking of this model to other models (Fishwick 2012), which is to the benefit of the modelling community and ensures that the model has biological meaning and that it is useable and manipulable by biologists.

Two applications of the model have been shown – in the identification of parameters which may account for the observed compositional impact of butyrate upon crypt cell types and for the effects of variation of cell cycle rate. These approaches allow deduction about effects of microenvironmental factors, for example that the assumption that increased proliferation observed in response to butyrate is indicative of an increase in cell cycle rate in normal cells, which would be oppositional to the effect seen in vitro in cancer cells (Scheppach et al. 1995), is not supported by this model. As such this revised model offers enlarged scope for application in identification of the biological basis of crypt compositional perturbation in early neoplasia, in response to the physiological microenvironment and leading to epithelial breakdown in inflammatory disease.

Author contributions

KS wrote successive iterations of the model, undertook model fitting to experimental data and wrote the paper; BMC generated relationships between cell types, evaluated iterations of the model and applications and wrote the paper. The authors declare no conflict of interest.

Acknowledgments

KS is grateful for the financial support of the EU FP7 (KBBE) Grant 289434 ‘BioPreDyn: New Bioinformatics Methods and Tools for Data-Driven Predictive Dynamic Modelling in Biotechnological Applications’. BMC undertook this work as a visiting researcher to MCISB.

Supporting information

Additional Supporting Information may be found in the online version of this article:

Figure S1. Observational data from our ongoing and previously published work were used to establish a set of assessment criteria (relevant compartments, capacity of crypts and direction and strength of relationships between compartments) by which any revision of the model could be objectively assessed.

Figure S2. Lack of fit of existing model to observed data.

Figure S3. Sensitivity Analysis of model v3.

iep0095-0001-sd1.pptx (2MB, pptx)

References

  1. Anini Y, Fu-Cheng XM, Cuber JC, Kervran A, Chariot J, Roze C. Comparison of the postprandial release of peptide YY and proglucagon-derived peptides in the rat. Pflugers Arch. 1999;438:299–306. doi: 10.1007/s004240050913. [DOI] [PubMed] [Google Scholar]
  2. Bernstein C, Bernstein H, Payne CM, Garewal H. Field defects in progression to adenocarcinoma of the colon and esophagous. Electron. J. Biotech. 2000;3:3. [Google Scholar]
  3. Buske P, Galle J, Barker N, Aust G, Clevers H, Loeffler M. On the biomechanics of stem cell niche formation in the gut–modelling growing organoids. PLoS Comput. Biol. 2011;7:e1001045. [Google Scholar]
  4. Cho K-H, Lee H-S, Ku S-K. Decrease in intestinal endocrine cells in Balb/c mice with CT-26 carcinoma cells. J. Vet. Sci. 2008;9:9–14. doi: 10.4142/jvs.2008.9.1.9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Corfe BM, Williams EA, Bury JP, et al. A study protocol to investigate the relationship between dietary fibre intake and fermentation, colon cell turnover, global protein acetylation and early carcinogenesis: the FACT study. BMC Cancer. 2009;9:332. doi: 10.1186/1471-2407-9-332. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. De Matteis G, Graudenzi A, Antoniotti M. A review of spatial computational models for multi-cellular systems, with regard to intestinal crypts and colorectal cancer development. J. Math. Biol. 2013;66:1409–1462. doi: 10.1007/s00285-012-0539-4. [DOI] [PubMed] [Google Scholar]
  7. Dunn SJ, Appleton PL, Nelson SA, Näthke IS, Gavaghan DJ, Osborne JM. A two-dimensional model of the colonic crypt accounting for the role of the basement membrane and pericryptal fibroblast sheath. PLoS Comput. Biol. 2012;8:e1002515. doi: 10.1371/journal.pcbi.1002515. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Fishwick PA. Hypermodelling: an integrated approach to dynamic system modelling. J. Simul. 2012;6:2–8. [Google Scholar]
  9. Gibson PR, Moeller I, Kagelari O, Folino M, Young GP. Contrasting effects of butyrate on the expression of phenotypic markers of differentiation in neoplastic and nonneoplastic colonic epithelial-cells in vitro. J. Gastroenterol. Hepatol. 1992;7:165–172. doi: 10.1111/j.1440-1746.1992.tb00956.x. [DOI] [PubMed] [Google Scholar]
  10. Gulubova M, Vlaykova T. Chromogranin A-, serotonin-, synaptophysin-and vascular endothelial growth factor-positive endocrine cells and the prognosis of colorectal cancer: an immunohistochemical and ultrastructural study. J. Gastroenterol. Hepatol. 2008;23:1574–1585. doi: 10.1111/j.1440-1746.2008.05560.x. [DOI] [PubMed] [Google Scholar]
  11. Gunawardene AR, Corfe BM, Staton CA. Classification and functions of enteroendocrine cells of the lower gastrointestinal tract. Int. J. Exp. Pathol. 2011;92:219–231. doi: 10.1111/j.1365-2613.2011.00767.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Hague A, Singh B, Paraskeva C. Butyrate acts as a survival factor for colonic epithelial cells: further fuel for the in vivo versus in vitro debate. Gastroenterology. 1997;112:1036–1040. doi: 10.1053/gast.1997.v112.agast971036. [DOI] [PubMed] [Google Scholar]
  13. Hamer HM, Jonkers D, Venema K, Vanhoutvin S, Troost FJ, Brummer RJ. Review article: the role of butyrate on colonic function. Aliment. Pharmacol. Ther. 2008;27:104–119. doi: 10.1111/j.1365-2036.2007.03562.x. [DOI] [PubMed] [Google Scholar]
  14. Holt PR, Atillasoy E, Lindenbaum J, et al. Effects of acarbose on fecal nutrients, colonic pH, and short-chain fatty acids and rectal proliferative indices. Metabolism. 1996;45:1179–1187. doi: 10.1016/s0026-0495(96)90020-7. [DOI] [PubMed] [Google Scholar]
  15. Hoops S, Sahle S, Gauges R, et al. COPASI – a COmplex PAthway SImulator. Bioinformatics. 2006;22:3067–3074. doi: 10.1093/bioinformatics/btl485. [DOI] [PubMed] [Google Scholar]
  16. Hucka M, Finney A, Sauro HM, et al. The systems biology markup language (SBML): a medium for representation and exchange of biochemical network models. Bioinformatics. 2003;19:524–531. doi: 10.1093/bioinformatics/btg015. [DOI] [PubMed] [Google Scholar]
  17. Humphries A, Wright NA. Colonic crypt organization and tumorigenesis. Nat. Rev. Cancer. 2008;8:415–424. doi: 10.1038/nrc2392. [DOI] [PubMed] [Google Scholar]
  18. Inagaki A, Sakata T. Dose-dependent stimulatory and inhibitory effects of luminal and serosal n-butyric acid on epithelial cell proliferation of pig distal colonic mucosa. J. Nutr. Sci. Vitaminol. 2005;51:156–160. doi: 10.3177/jnsv.51.156. [DOI] [PubMed] [Google Scholar]
  19. Johnston MD, Edwards CM, Bodmer WF, Maini PK, Chapman SJ. Mathematical modeling of cell population dynamics in the colonic crypt and in colorectal cancer. Proc. Natl. Acad. Sci. U S A. 2007a;104:4008–4013. doi: 10.1073/pnas.0611179104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Johnston MD, Edwards CM, Bodmer WF, Maini PK, Chapman SJ. Examples of mathematical modeling – tales from the crypt. Cell Cycle. 2007b;6:2106–2112. doi: 10.4161/cc.6.17.4649. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Li C, Donizelli M, Rodriguez N, et al. BioModels Database: an enhanced, curated and annotated resource for published quantitative kinetic models. BMC Syst. Biol. 2010;4:92. doi: 10.1186/1752-0509-4-92. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Mirams GR, Fletcher AG, Maini PK, Byrne HM. A theoretical investigation of the effect of proliferation and adhesion on monoclonal conversion in the colonic crypt. J. Theor. Biol. 2012;312:143–156. doi: 10.1016/j.jtbi.2012.08.002. [DOI] [PubMed] [Google Scholar]
  23. Pin C, Watson AJ, Carding SR. Modelling the spatio-temporal cell dynamics reveals novel insights on cell differentiation and proliferation in the small intestinal crypt. PLoS ONE. 2012;7:e37115. doi: 10.1371/journal.pone.0037115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Sakata T. Stimulatory effect of short chain fatty-acids on the epithelial-cell proliferation in rat intestine – a possible explanation for trophic effects of fermentable fiber, gut microbes and luminal trophic factors. Br. J. Nutr. 1987;58:95–103. doi: 10.1079/bjn19870073. [DOI] [PubMed] [Google Scholar]
  25. Sakata T, von Engelhardt W. Stimulatory effect of short chain fatty-acids on the epithelial-cell proliferation in rat large-intestine. Comp. Biochem. Physiol. A Comp Physiol. 1983;74:459–462. doi: 10.1016/0300-9629(83)90631-x. [DOI] [PubMed] [Google Scholar]
  26. Sandler RS, Baron JA, Tosteson TD, Mandel JS, Haile RW. Rectal mucosal proliferation and risk of colorectal adenomas: results from a randomized controlled trial. Cancer Epidemiol. Biomarkers Prev. 2000;9:653–656. [PubMed] [Google Scholar]
  27. Scheppach W, Bartram HP, Richter F. Role of short-chain fatty acids in the prevention of colorectal cancer. Eur. J. Cancer. 1995;31A:1077–1080. doi: 10.1016/0959-8049(95)00165-f. [DOI] [PubMed] [Google Scholar]
  28. Smallbone K, Mendes P. Large-scale metabolic models: from reconstruction to differential equations. Ind. Biotechnol. 2013;9:179–184. [Google Scholar]
  29. Tomlinson IPM, Bodmer WF. Failure of programmed cell-death and differentiation as causes of tumors – some simple mathematical models. Proc. Natl Acad. Sci. USA. 1995;92:11130–11134. doi: 10.1073/pnas.92.24.11130. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Yu DC, Bury JP, Tiernan J, Waby JS, Staton CA, Corfe BM. Short-chain fatty acid level and field cancerization show opposing associations with enteroendocrine cell number and neuropilin expression in patients with colorectal adenoma. Mol. Cancer. 2011;10:27. doi: 10.1186/1476-4598-10-27. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Figure S1. Observational data from our ongoing and previously published work were used to establish a set of assessment criteria (relevant compartments, capacity of crypts and direction and strength of relationships between compartments) by which any revision of the model could be objectively assessed.

Figure S2. Lack of fit of existing model to observed data.

Figure S3. Sensitivity Analysis of model v3.

iep0095-0001-sd1.pptx (2MB, pptx)

Articles from International Journal of Experimental Pathology are provided here courtesy of Wiley

RESOURCES