Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Feb 11;4:4055. doi: 10.1038/srep04055

Unraveling wetting transition through surface textures with X-rays: Liquid meniscus penetration phenomena

C Antonini 1,5, J B Lee 2,5, T Maitra 1,5, S Irvine 3, D Derome 4,a, Manish K Tiwari 1,b, J Carmeliet 2,4, D Poulikakos 1,c
PMCID: PMC3920273  PMID: 24514762

Abstract

In this report we show that synchrotron X-ray radiography is a powerful method to study liquid-air interface penetration through opaque microtextured surface roughness, leading to wetting transition. We investigate this wetting phenomenon in the context of sessile drop evaporation, and establish that liquid interface sinking into the surface texture is indeed dictated by the balance of capillary and Laplace pressures, where the intrinsically three-dimensional nature of the meniscus must be accounted for. Air bubble entrapment in the texture underneath impacting water drops is also visualized and the mechanisms of post-impact drop evaporation are discussed.

A sessile drop on a superhydrophobic surface has an almost spherical shape and can easily roll off the surface upon even a gentle nudging. This is due to the presence of an air-liquid-solid interface under the drop, where air pockets prevent full surface wetting. A drop with such behavior is referred to be in the Cassie-Baxter state1. The macroscopic manifestation of this state is that the drop contact angle can reach values higher than 150°. Additionally, the contact angle hysteresis (difference between advancing and receding contact angles), which provides an indication of drop stickiness on the surface, can be lower than 10°. Such high water repellency is useful in a variety of applications2, such as self-cleaning surfaces3, liquid transport4, heat transfer enhancement due to dropwise condensation5,6, realization of heat transfer devices7 and in anti-icing8,9,10,11.

To promote the Cassie-Baxter state, a combination of surface topography, i.e. roughness, and surface chemistry, i.e. low surface energy, comes to play. The opposite scenario of drop behavior is the complete penetration through the surface asperities, reaching the so-called Wenzel state12. In the Wenzel state, although high contact angles may still be observed, the contact angle hysteresis is significantly enhanced. Consequently, the water drop loses its mobility on the surface and becomes ‘sticky’. The transition from Cassie-Baxter to Wenzel states can be caused by a variety of factors, such as drop impact13,14,15,16, drop evaporation17,18,19,20, pressure rise in the liquid20, mechanical vibration21, electrowetting etc.22,23. Such a transition on surfaces designed to be superhydrophobic is not desirable, since its reversal is possible only in special situations23. Different tools have been developed to visualize this transition and to observe the related complex wetting phenomena. Most of these techniques employ optical methods such as observation of the overall drop shape17,19,21, visualization of the drop from the top18 or from the bottom24 (on transparent solid surfaces), or in some cases even by means of high-resolution microscope imaging20. Recently a variety of advanced techniques, such as environmental scanning electron microscopy (ESEM)25 and confocal scanning microscopy26, has also been explored; such techniques offer significantly better spatial resolution of the liquid meniscus. Papadoupolos et al.26 proposed a confocal microscopy based technique, which allowed three-dimensional (3D) reconstruction of the liquid meniscus on superhydrophobic surfaces consisting of micropillars, with a time resolution of ~1 s. Reflection interference contrast microscopy (RICM) was used by Moulinet and Bartolo27 to visualize the air-water meniscus penetration into a microtextured surface (with typical pillar pitch of 50 μm) of a transparent PDMS surface. Interferometry measurements can also be used to study dynamic events, as recently shown by Bouwhuis et al.28, who investigated bubble entrainment upon drop impact on a transparent glass substrate. Typically, optical techniques for visualizing the meniscus between the texture asperities are limited by either time resolution, or substrate transparency, or both.

X-rays offer a unique alternative to optical and ESEM based visualization. Lee et al.29 used ultrafast X-ray phase-contrast imaging to visualize the formation and evolution of a bubble underneath a drop impacting on a smooth solid surface. Here, we show that X-ray projection imaging, which we performed at the TOMCAT beamline at the Swiss Light Source, Paul Scherrer Institute, Villigen, Switzerland, can be used to visualize liquid meniscus penetration into the microtexture of superhydrophobic surfaces, consisting of a micropillar array with inter-pillar spacing of ~5 μm, and to analyze the pertinent meniscus dynamics. First, the details of the imaging technique are explained, and second, two specific case studies, used to illustrate the technique capabilities, are presented. Specifically, we show how X-ray imaging can be used to investigate the meniscus shape and dynamics of two important physical phenomena occurring on a microstructured superhydrophobic surface, i.e the evaporation of sessile water drops with transition from the Cassie-Baxter to the Wenzel state and the entrapment of a gas bubble upon impact.

Our results clearly establish the feasibility of the X-ray method to penetrate through superhydrophobic micropillar forests, with an unprecedented combined time and spatial resolution. In addition, liquid meniscus transition during drop evaporation is explained by means of a force balance approach. Although this approach has been recently brought into question19,30 and alternative energy based approaches have been proposed, here we show that a force balance approach is valid, if the appropriate three dimensional geometry of the meniscus is accounted for.

Results and discussion

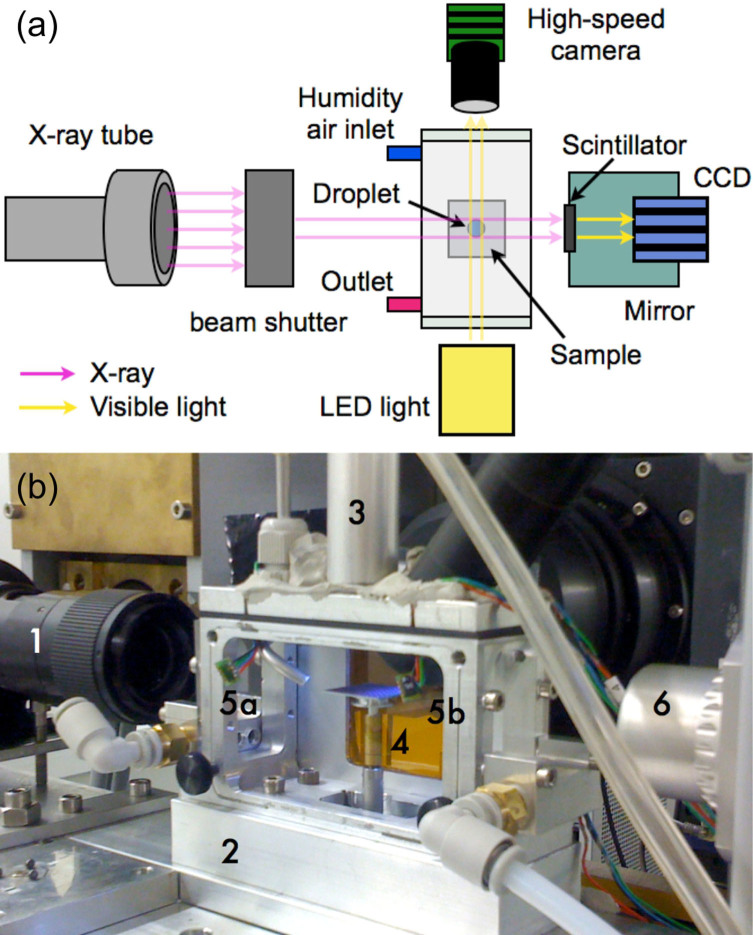
Figure 1a and b include a schematic and a picture of the setup, respectively. The X-ray beam, passing through the superhydrophobic surface and the drop, is converted by scintillator (LAG:Ce 20 μm) into visible light, which is captured by the 20× objective lens fitted to a CCD camera (pco.edge, PCO), as shown in Figure 1a. Simultaneous observation by means of an optical high-speed camera was also performed. A detailed description of the setup, together with details on the process for superhydrophobic surface fabrication, is provided in the Methods and Materials section.

Figure 1. Experimental setup.

Figure 1

Open in a new tab

(a) schematic top view with main components and (b) picture of (1) the optical lens, (2) the environmental chamber, (3) the falling drop guide tube, (4) the sample on the translation and tilting stage, (5a,b) the relative humidity sensors and (6) the LED illuminator.

The projection image sequence shown in Figure 2a–d captures the four stages of drop evaporation. The corresponding evolution of drop radius, R, drop contact radius, RC, and the contact angle, θ, are shown in Figure 3. At the beginning, i.e. during stage 1 (Figure 2a), the drop was sitting on top of the micropillars in the Cassie-Baxter state. The contact angle in stage 1 essentially corresponded to the receding contact angle, i.e. 140°. During stage 1, the contact line retracted, in a stepwise manner, due to local pinning and depinning at the pillar edges (see also Supplementary Video 1). Our experimental data are well fitted by R ∝ (t0 − t)0.5 (see Figure 3d), in particular during stage 1, suggesting that evaporation is diffusion-dominated31. This is also in agreement with the findings from a recent study on drops evaporating on superhydrophobic surfaces32. During stage 2 (Figure 2b, Supplementary Video 2), the contact line was pinned and the contact angle decreased, while the drop volume decreased due to evaporation. In stage 3 (Figure 2c, Supplementary Video 3), liquid penetration between pillars occurred: this phenomenon, known as impalement, essentially marks a transition from Cassie-Baxter to Wenzel state. The transition is due to the continuous increase of pressure inside the drop. With a decrease in drop volume and radius, the pressure inside the drop increases due to Laplace pressure difference, ΔpL = 2σlg/R, between the drop interior and the surroundings. The symbols σlg and R denote the water surface tension and drop radius of curvature, respectively. For a large drop radius, the liquid penetration can be avoided, if the force driving the sinking into the texture due to Laplace pressure difference is counterbalanced by the resisting capillary force13, the correct formulation of which will be discussed in the sequel. When the pressure inside the drop overcomes the capillary pressure, the liquid meniscus will penetrate through the pillar forest. Interestingly, during stage 3 an increase in the contact radius by ~20% was noticed. This is a consequence of drop volume conservation: since the contact angle decreased rapidly during this stage, the contact radius had to increase26. Finally, during stage 4 (Figure 2d, Supplementary Video 4) the liquid film among the pillars evaporated completely.

Figure 2. (a–d) X-ray image sequence showing the four stages of a sessile drop evaporation on a pillar-like microtextured surface, and (e) SEM image of the superhydrophobic surface micropillars.

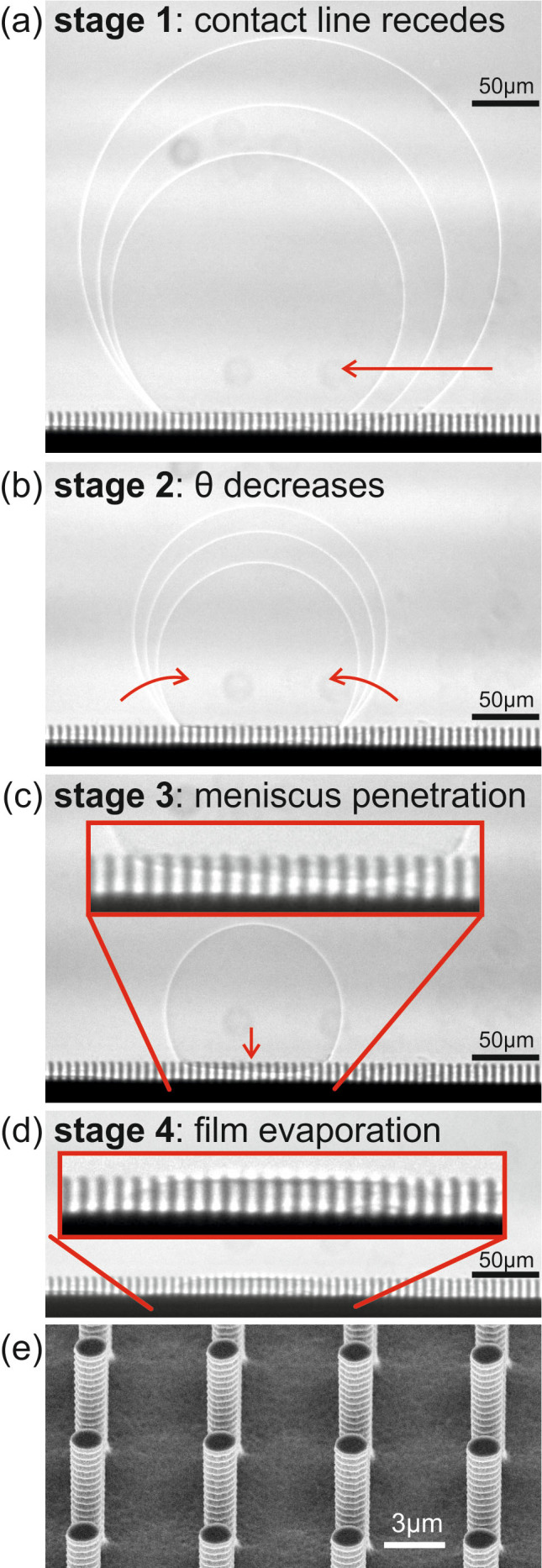
Figure 2

Open in a new tab

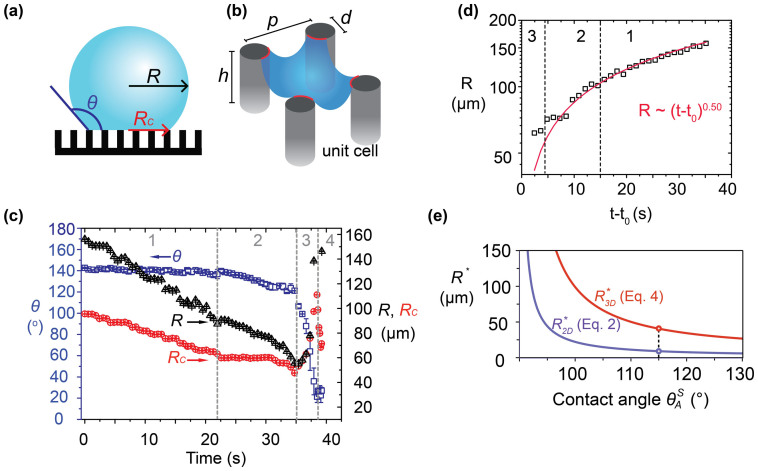
Figure 3.

Figure 3

Open in a new tab

(a) Schematic of evaporating drop. (b) Schematic of liquid meniscus (blue surface) and contact line (red line) in a unit cell of the surface microtexture. (c) Time evolution of drop radius, R, drop contact radius, RC, and apparent contact angle, θ, for an evaporating drop. The four stages of evaporation, as observed in Figure 2, are also indicated. Definition of initial time t = 0 s is arbitrary. A repeat measurement is also shown in Supplementary Figure 1. (d) Experimental data compared to the law for diffusion-dominated evaporation, R ∝ (t0 − t)0.5. (e) Critical drop radius as function of 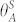Inline graphic, i.e. the advancing contact angle measured on the corresponding smooth surface.

Understanding Cassie-Baxter to Wenzel state transition is fundamental to design surfaces, usually aiming at avoidance or delay of such transition. Two main mechanisms have been identified in the literature to predict the critical drop radius, R*, at which the transition occurs: the “touch-down” and the “sliding”13 (alternatively called “pinning instability”19) mechanisms. In the touch-down mechanism, the meniscus remains pinned at the top of the pillar and deforms by the increase in pressure inside the drop. Eventually, if the pillars are not too tall, the transition can occur by the meniscus touching the bottom of pillars. As can be seen from Figure 2c, this was not the impalement mechanism in our case. Rather, in our experiment the penetration occurred via meniscus de-pinning from the top of the pillars and eventual penetration of the gaps between them. In this mechanism, the meniscus should start to sink into the texture when the Laplace pressure, ΔpL, overcomes the resisting capillary pressure. Here below we show that the radius at which transition will occur can be determined on the basis of mechanical equilibrium principle, using the Laplace-capillary pressure balance. Complete thermodynamic equilibrium in the general sense implies the absence of all gradients causing fluxes, in this case, pressure, species and temperature gradients33. The drop evaporation process is practically isothermal, so that thermal non-equilibrium effects on droplet motion from vaporization are negligible34. Also, no chemical gradients affecting the droplet motion are present. Hence, the drop motion in the direction normal to the surface is driven by pressure gradients and is effectively initiated when the related forces are not in mechanical equilibrium.

For a square array of micropillars, using a simplistic two-dimensional (2D) approach, the force balance (per unit length) in a unit cell of the pillars can be expressed as:

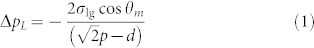graphic file with name srep04055-m1.jpg

where 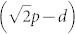Inline graphic is the maximum distance between two pillars in a unit cell and θm is the contact angle of the meniscus. In Eq. 1, the right hand side quantifies the capillary pressure, pC. The diagonal separation between the pillars is used, since that would correspond to the weakest capillary pressure. Eq. 1 is used quite commonly in the literature19,26,35. However, as we will show in the sequence, it disregards the three-dimensional (3D) shape of the meniscus and, hence, although useful for intuitive understanding, it is quantitatively incorrect. In Eq. 1, θm can vary, within a limit, to accommodate the increase in ΔpL with the decrease in drop radius. The meniscus is in equilibrium until 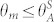Inline graphic, where 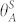Inline graphic is the advancing contact angle that can be macroscopically measured on the corresponding smooth surface. At the moment of transition 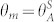Inline graphic, using the expression for Laplace pressure, ΔpL = 2σlg/R, the critical drop radius can be calculated as:

graphic file with name srep04055-m2.jpg

The correct expression for the Laplace-capillary force balance has to be formulated taking into account the inherent 3D geometry of the meniscus in the unit cell13, as:

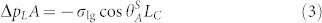graphic file with name srep04055-m3.jpg

where 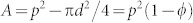Inline graphic is the projected planar area of the meniscus and LC = πd is the total length of the contact line, where capillary force is acting (see schematic in Figure 3b). The resulting drop radius at the moment of transition is:

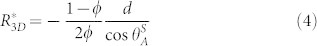graphic file with name srep04055-m4.jpg

The predictions from Eqs. 2 and 4 are plotted in Figure 2b as function of 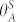Inline graphic. The difference between the predictions becomes relevant especially for surfaces with very low values of the solid fraction, as is typical for superhydrophobic surfaces and, in particular, for the surface tested in the present study, having ϕ = 4.2%. The validity of the force balance approach for meniscus penetration is still a debated topic in the recent literature, where it has been proposed that only energy-based approaches are able to explain meniscus penetration19,30. However, our data show that the force balance approach works well, if the correct formulation, as expressed in Eq. 4, is used. 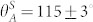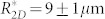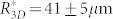Indeed, as the Figure 3e shows, for the measured value of Inline graphic, the corresponding critical drop radii are Inline graphic and Inline graphic, respectively. 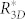Inline graphic is thus rather close to the measured value of 59 ± 5 μm despite the fact that no fitting parameter is employed to obtain it. On the other hand, 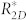Inline graphic is significantly lower than the experimentally measured value, implying that use of a 2D approach for force balance calculation, expressed in Eq. 1, is incorrect and should not be used on pillar-like microtextures. Note that the measured critical radius of 59 ± 5 μm, from Eq. 4, corresponds to a 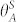Inline graphic value of 107 ± 2°, which is close to the measured value of 115 ± 3°. Therefore, from both these metrics our experiments underpin the validity of the force balance approach. As an additional note, the prediction from Eq. 4 should be considered as the minimum radius for observing meniscus penetration. Simple variations such as deposition of dust from room air on the surface may change the local contact angle, and thus engender impalement even at higher radii, as already reported36.

Another interesting set of drop interface penetration dynamics involves impact of drops on textured surfaces. Here, evaporation and dynamic features of drops impacted on microtextured surfaces were investigated. Due to a concomitant need for high spatial resolution (having to visualize the inter-pillar gap of ~5 μm), the X-ray radiography setup had a time resolution of ~30 ms. Thus, events with a characteristic convective time scale of ~1 ms or lower14, could not be visualized. However, our time resolution was sufficient for investigating the post-impact drop state and dynamics. Due to the kinetic energy of the impact, the liquid can locally penetrate into the surface texture, with a portion of the drop remaining on the surface after impact. In fact, due to meniscus penetration, the drop is not capable to fully bounce off from the surface after impact, as typically observed for low speed water drop impact on superhydrophobic surfaces and on some hydrophobic surfaces37. This was also observed by high-speed optical camera (see Figure 4a and Supplementary Video 5). Analysis of this remnant drop yielded useful information regarding the drop impact process. Figure 4c shows the remnant drop on the surface after impact, at two different magnifications: water wetted the pillars under most of the drop, except in the central region, where a trapped air bubble was visible. Although most of the drop interface was in the Wenzel state, a Cassie-Baxter “island” persisted. This is consistent with previous experimental observations38,39 as well numerical simulations40. A bubble can be entrapped either at the interface, at the moment of impact, or when the rim collapses, during the drop recoiling phase41. The origin of bubble entrapment has been attributed to drop deformation and dimple formation prior to drop impact, due to gas compressibility effects42. The bubble entrapment can be easily observed during the drop impact event with a high-speed camera viewing from the top. The latter allowed the identification of an air bubble (bright spot in Figure 4b and Supplementary Video 6) trapped within a ring-like region, where transition to Wenzel state had occurred (dark grey ring in the center).

Figure 4. Evaporation of a miniature drop remaining on the surface after impact of a ~1 mm radius drop (impact speed V = 2 m/s).

Figure 4

Open in a new tab

(a) The original drop only partially rebounded after impact, with a portion remaining attached to the surface. (b) Top view optical image of an impacting drop, captured during drop spreading, showing a trapped air bubble (bright spot in the center) underneath the drop. (c) Side view of the miniature remnant drop and magnified view into the microstructure, showing a trapped air bubble. (d) and (e) Release of the trapped bubble upon the receding motion of the contact line. (f) and (g) The corresponding schematic of the drop shape.

With drop evaporation, the contact line receded, moving in the direction of the trapped bubble. Before reaching the bubble, the contact line remained circular (see Figure 4d). However, after reaching the bubble, the contact line rapidly receded above the bubble. The contact line took a locally concave shape, which appeared as multiple apparent contours with multiple contact angles in the projection image shown in Figure 4e (see also the Supplementary Video 7). Figure 4f and g show schematics of the drop state, before and after the bubble release. In Figure 4g the contours, visible in Figure 4e, have been highlighted for clarity. Overall, the sequence establishes the ability of X-ray radiography to capture liquid meniscus dynamics and the related inter-pillar events.

Conclusions

In conclusion, we presented an X-ray radiography based visualization method to directly observe the intricate wetting phenomena on textured surfaces. The high spatial and temporal resolution of the technique allowed visualization of Cassie-Baxter to Wenzel state transitions during drop evaporation on micro-pillared superhydrophobic surfaces. A force balance accounting for the three dimensional shape of the meniscus matched well with experimental observations on meniscus penetration into the microtexture. Furthermore, entrapment and release of an air bubble, underneath an evaporating drop after impact on the micro-pillared surface, was captured through a post-impact visualization, thereby also illustrating the dynamics of the receding contact line. Our work clearly demonstrates that use of X-rays can be a powerful approach for investigating complex wetting and multiphase flow physics on opaque textured surfaces.

Methods

X-ray projection imaging

The TOMCAT beamline exploits a 2.9 T magnetic dipole, corresponding to a critical energy of 11.1 keV, generating a closely bundled and highly brilliant X-ray beam. A fixed-exit double crystal multilayer monochromator (DCMM) is set up to obtain a central X-ray photon energy of 30 keV. The X-ray beam passing through the sample setup is converted by scintillator (LAG:Ce 20 μm) into visible light, which is captured by the 20× objective lens fitted to a CCD camera (pco.edge, PCO), as shown in Figure 1a. The synchrotron X-ray radiography images were recorded at 33 fps, with an exposure time of 20 ms, and at ~0.33 μm pixel resolution, providing high temporal and spatial accuracy. The spatial resolution is set by the microscope system of TOMCAT beamline, where the camera pixel size is 6.5 μm and the magnification of objective lens is 20×. Simultaneously, for control reasons, an optical high-speed camera recorded the impinging drops at 5000 Hz in shadowgraphy mode, perpendicular to the X-ray beam (see Figure 1). Drops of ~1 mm radius were generated by hand for sessile drop experiments, and by a syringe pump, for the drop impact tests. For impact tests, droplets were released from heights of 20 cm and 40 cm. The drops fell through a tube to prevent deviations by air drafts and reached the superhydrophobic surfaces in a chamber maintained at ~31°C temperature and ~22% relative humidity (see Figure 1b).

The use of X-ray visualization technique can be in general extended to liquids other than water, with the requirement of relative transparency of the liquid with respect to the wavelength of the X-Rays. This defines the range of liquids that can be used for experiments similar to those presented in the report. Of course different combinations of substrates and liquids can be used, yielding a visible drop surface at all times. Refractive effects at the surface will reduce sharpness of the image.

Superhydrophobic surface fabrication

To fabricate the superhydrophobic surface, a p-type (100) silicon wafer was used. The wafer was photolithographically patterned using Karl Suss MA6 mask aligner and AZ1505 positive photoresist. The patterned photoresist film was used as mask to etch silicon in a SF6 and C4F4 plasma (Bosch process in Alcatel AMS 200 machine) and form the micropillars. Then, the photoresist film was stripped and the wafer was diced into 2 × 2 cm size chips. After standard cleaning, the chips were wet functionalized by 1H,1H,2H,2H-Perfluorodecyltrichlorosilane (FDTS) (96% Alfa Aesar) in n-hexane solution. The fabricated surface had pillar diameter d = 1.5 μm, pillar center-to-center distance p = 6.5 μm, height h = 13 μm, and a corresponding solid fraction ϕ = 4.2%. The measured advancing and receding contact angles were equal to 155 ± 4° and 140 ± 4°, respectively.

Author Contributions

D.P., M.K.T. and D.D. conceived the problem and designed research. C.A. and T.M. were responsible for superhydrophobic surface fabrication. J.B.L. was responsible for experimental setup preparation. C.A., T.M., J.B.L. and S.I. performed the experiments under direct supervision of D.D. and M.K.T. Analysis of results and theoretical modeling were performed by C.A., M.K.T., T.M. and J.B.L. under supervision of D.P., D.D. and J.C. All authors participated in paper writing and commenting.

Supplementary Material

Supplementary Information

Supplementary Video 1

Download video file (10.7MB, avi)
Supplementary Information

Supplementary Video 2

Download video file (4.1MB, avi)
Supplementary Information

Supplementary Video 3

Download video file (3.9MB, avi)
Supplementary Information

Supplementary Video 4

Download video file (1.2MB, avi)
Supplementary Information

Supplementary Video 5

Download video file (3.3MB, avi)
Supplementary Information

Supplementary Video 6

Download video file (3.2MB, avi)
Supplementary Information

Supplementary Video 7

Download video file (2.1MB, avi)
Supplementary Information

Supplementary Information

srep04055-s8.doc (1.1MB, doc)

Acknowledgments

We thank Rajmund Mokso at the TOMCAT beamline of the Swiss Light Source, PSI, Villigen, for his efforts to make these experiments possible. Support from PSI through the proposal 20121103 is acknowledged. Partial support for this work came from the Swiss National Science Foundation (SNF) grant 200021_135479. C.A. acknowledges funding through a Marie Curie Intra-European Fellowship within the 7thFP of European Community (ICE2, 301174).

References

  1. Quéré D. Non-sticking drops. Rep Prog Phys 68, 2495–2532 (2005). [Google Scholar]
  2. Marengo M., Antonini C., Roisman I. V. & Tropea C. Drop collisions with simple and complex surfaces. Curr Opin Colloid and Interface Sci 16, 292–302 (2011). [Google Scholar]
  3. Roach P., Shirtcliffe N. J. & Newton M. I. Progess in superhydrophobic surface development. Soft Matter 4, 224–240 (2008). [DOI] [PubMed] [Google Scholar]
  4. Schutzius T. M., Elsharkawy M., Tiwari M. K. & Megaridis C. M. Surface tension confined (STC) tracks for capillary-driven transport of low surface tension liquids. Lab Chip 12, 5237–5242 (2012). [DOI] [PubMed] [Google Scholar]
  5. Dietz C., Rykaczewski K., Fedorov A. G. & Joshi Y. Visualization of droplet departure on a superhydrophobic surface and implications to heat transfer enhancement during dropwise condensation. Appl Phys Lett 97, 033104 (2010). [Google Scholar]
  6. Torresin D., Tiwari M. K., Del Col D. & Poulikakos D. Flow Condensation on Copper-Based Nanotextured Superhydrophobic Surfaces. Langmuir 29, 840–848 (2013). [DOI] [PubMed] [Google Scholar]
  7. Boreyko J. B., Zhao Y. & Chen C.-H. Planar jumping-drop thermal diodes. Appl Phys Lett 99, 234105 (2011). [Google Scholar]
  8. Antonini C., Innocenti M., Horn T., Marengo M. & Amirfazli A. Understanding the effect of superhydrophobic coatings on energy reduction in anti-icing systems. Cold Reg Sci Technol 67, 58–67 (2011). [Google Scholar]
  9. Jung S., Dorrestijn M., Raps D., Das A., Megaridis C. M. & Poulikakos D. Are Superhydrophobic Surfaces Best for Icephobicity? Langmuir 27, 3059–3066 (2011). [DOI] [PubMed] [Google Scholar]
  10. Meuler A. J., Smith J. D., Varanasi K. K., Mabry J. M., McKiney G. H. & Cohen R. E. Relationships between Water Wettability and Ice Adhesion. ACS Appl Mat Interfaces 2, 3100–3110 (2010). [DOI] [PubMed] [Google Scholar]
  11. Tarquini S., Antonini C., Amirfazli A., Marengo M. & Palacios J. Investigation of Ice Shedding Properties of Superhydrophobic Coatings on Helicopter Blades. Cold Reg Sci Technol 100, 50–58 (2014). [Google Scholar]
  12. Lafuma A. & Quéré D. Superhydrophobic states. Nat Mater 2, 457–460 (2003). [DOI] [PubMed] [Google Scholar]
  13. Bartolo D., Bouamrirene F., Verneuil E., Buguin A., Silberzan P. & Moulinet S. Bouncing or sticky droplets: Impalement transitions on superhydrophobic micropatterned surfaces. Europhys Lett 74, 299–305 (2006). [Google Scholar]
  14. Reyssat M., Pepin A., Marty F., Chen Y. & Quéré D. Bouncing transitions on microtextured materials. Europhys Lett 74, 306–312 (2006). [Google Scholar]
  15. Antonini C., Villa F., Bernagozzi I., Amirfazli A. & Marengo M. Drop Rebound after Impact: The Role of the Receding Contact Angle. Langmuir 29, 16045–16050 (2013). [DOI] [PubMed] [Google Scholar]
  16. Antonini C., Amirfazli A. & Marengo M. Drop impact and wettability: From hydrophilic to superhydrophobic surfaces. Phys Fluids 24, 102104 (2012). [Google Scholar]
  17. McHale G., Aqil S., Shirtcliffe N. J., Newton M. I. & Erbil H. Y. Analysis of droplet evaporation on a superhydrophobic surface. Langmuir 21, 11053–11060 (2005). [DOI] [PubMed] [Google Scholar]
  18. Peters A. M., Pirat C., Sbragaglia M., Borkent B. M., Wessling M., Lohse D. & Lammertink R. G. H. Cassie-Baxter to Wenzel state wetting transition: Scaling of the front velocity. Eur Phys J E 29, 391–397 (2009). [DOI] [PubMed] [Google Scholar]
  19. Tsai P., Lammertink R. G. H., Wessling M. & Lohse D. Evaporation-Triggered Wetting Transition for Water Droplets upon Hydrophobic Microstructures. Phys Rev Lett 104, 116102 (2010). [DOI] [PubMed] [Google Scholar]
  20. Luo C., Xiang M., Liu X. & Wang H. Transition from Cassie-Baxter to Wenzel States on microline-formed PDMS surfaces induced by evaporation or pressing of water droplets. Microfluid Nanofluid 10, 831–842 (2011). [Google Scholar]
  21. Bormashenko E., Pogreb R., Whyman G., Bormashenko Y. & Erlich M. Vibration-induced Cassie-Wenzel wetting transition on rough surfaces. Appl Phys Lett 90, 201917 (2007). [Google Scholar]
  22. Mugele F. & Baret J. C. Electrowetting: From basics to applications. J Phys-Condens Mat 17, R705–R774 (2005). [Google Scholar]
  23. Han Z., Tay B., Tan C., Shakerzadeh M. & Ostrikov K. Electrowetting Control of Cassie-to-Wenzel Transitions in Superhydrophobic Carbon Nanotube-Based Nanocomposites. ACS Nano 3, 3031–3036 (2009). [DOI] [PubMed] [Google Scholar]
  24. Xu W. & Choi C. H. From Sticky to Slippery Droplets: Dynamics of Contact Line Depinning on Superhydrophobic Surfaces. Phys Rev Lett 109, 024504 (2012). [DOI] [PubMed] [Google Scholar]
  25. Paxson A. T. & Varanasi K. K. Self-similarity of contact line depinning from textured surfaces. Nat Commun 4, 1492 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Papadopoulos P., Mammen L., Deng X., Vollmer D. & Butt H.-J. How superhydrophobicity breaks down. Proc Natl Acad Sci USA 110, 3254–3258 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Moulinet S. & Bartolo D. Life and death of a fakir droplet: Impalement transitions on superhydrophobic surfaces. Eur Phys J E 24, 251–260 (2007). [DOI] [PubMed] [Google Scholar]
  28. Bouwhuis W., van der Veen R. C. A., Tran T., Keij D. L., Winkels K. G., Peters I. R., van der Meer D., Sun C., Snoeijer J. H. & Lohse D. Maximal Air Bubble Entrainment at Liquid-Drop Impact. Phys Rev Lett 109, 264501 (2012). [DOI] [PubMed] [Google Scholar]
  29. Ji San L., Byung Mook W., Jung Ho J. & Fezzaa K. How Does an Air Film Evolve into a Bubble During Drop Impact? Phys Rev Lett 109, 204501 (2012). [DOI] [PubMed] [Google Scholar]
  30. Chen X. M., Ma R. Y., Li J. T., Hao C. L., Guo W., Luk B. L., Li S. C., Yao S. H. & Wang Z. K. Evaporation of Droplets on Superhydrophobic Surfaces: Surface Roughness and Small Droplet Size Effects (vol 109, 116101, 2012). Phys Rev Lett 109, 116101 (2012). [DOI] [PubMed] [Google Scholar]
  31. Shahidzadeh-Bonn N., Rafai S., Azouni A. & Bonn D. Evaporating droplets. J Fluid Mech 549, 307–313 (2006). [Google Scholar]
  32. Dash S. & Garimella S. V. Droplet Evaporation Dynamics on a Superhydrophobic Surface with Negligible Hysteresis. Langmuir 29, 10785–10795 (2013). [DOI] [PubMed] [Google Scholar]
  33. Bonn D., Eggers J., Indekeu J., Meunier J. & Rolley E. Wetting and spreading. Rev Mod Phys 81, 739–805 (2009). [Google Scholar]
  34. Jung S., Tiwari M. K., Doan N. V. & Poulikakos D. Mechanism of supercooled droplet freezing on surfaces. Nat Commun 3, 615 (2012). [DOI] [PubMed] [Google Scholar]
  35. Deng T., Varanasi K. K., Hsu M., Bhate N., Keimel C., Stein J. & Blohm M. Nonwetting of impinging droplets on textured surfaces. Appl Phys Lett 94, 133109 (2009). [Google Scholar]
  36. Reyssat M., Yeomans J. M. & Quéré D. Impalement of fakir drops. Epl-Europhys Lett 81, 26006 (2008). [Google Scholar]
  37. Bartolo D., Josserand C. & Bonn D. Retraction dynamics of aqueous drops upon impact on non-wetting surfaces. J Fluid Mech 545, 329–338 (2005). [Google Scholar]
  38. Tsai P. C., Hendrix M. H. W., Dijkstra R. R. M., Shui L. L. & Lohse D. Microscopic structure influencing macroscopic splash at high Weber number. Soft Matter 7, 11325–11333 (2011). [Google Scholar]
  39. Maitra T., Tiwari M. K., Antonini C., Schoch P., Jung S., Eberle P. & Poulikakos D. On the Nanoengineering of Superhydrophobic and Impalement Resistant Surface Textures below the Freezing Temperature. Nano Lett 14, 172–182 (2014). [DOI] [PubMed] [Google Scholar]
  40. Mehdi-Nejad V., Mostaghimi J. & Chandra S. Air bubble entrapment under an impacting droplet. Phys Fluids 15, 173–183 (2003). [Google Scholar]
  41. Bartolo D., Josserand C. & Bonn D. Singular jets and bubbles in drop impact. Phys Rev Lett 96, 124501 (2006). [DOI] [PubMed] [Google Scholar]
  42. Mandre S. & Brenner M. P. The mechanism of a splash on a dry solid surface. J Fluid Mech 690, 148–172 (2012). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Video 1

Download video file (10.7MB, avi)
Supplementary Information

Supplementary Video 2

Download video file (4.1MB, avi)
Supplementary Information

Supplementary Video 3

Download video file (3.9MB, avi)
Supplementary Information

Supplementary Video 4

Download video file (1.2MB, avi)
Supplementary Information

Supplementary Video 5

Download video file (3.3MB, avi)
Supplementary Information

Supplementary Video 6

Download video file (3.2MB, avi)
Supplementary Information

Supplementary Video 7

Download video file (2.1MB, avi)
Supplementary Information

Supplementary Information

srep04055-s8.doc (1.1MB, doc)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES