Importance of Accurate Charges in Molecular Docking: Quantum Mechanical/Molecular Mechanical (QM/MM) Approach

Abstract

The extent to which accuracy of electric charges plays a role in protein-ligand docking is investigated through development of a docking algorithm, which incorporates quantum mechanical/molecular mechanical (QM/MM) calculations. In this algorithm, fixed charges of ligands obtained from force field parameterization are replaced by QM/MM calculations in the protein environment, treating only the ligands as the quantum region. The algorithm is tested on a set of 40 cocrystallized structures taken from the Protein Data Bank (PDB) and provides strong evidence that use of nonfixed charges is important. An algorithm, dubbed “Survival of the Fittest” (SOF) algorithm, is implemented to incorporate QM/MM charge calculations without any prior knowledge of native structures of the complexes. Using an iterative protocol, this algorithm is able in many cases to converge to a nativelike structure in systems where redocking of the ligand using a standard fixed charge force field exhibits nontrivial errors. The results demonstrate that polarization effects can play a significant role in determining the structures of protein-ligand complexes, and provide a promising start towards the development of more accurate docking methods for lead optimization applications.

Introduction

High throughput docking of small molecule ligands into high-resolution protein structures has become a standard component of computational approaches to drug discovery.^1–3 In typical pharmaceutical applications, the receptor structure is kept fixed, while the optimal location and conformation of the ligand (which is allowed to remain flexible) are sought using a variety of sampling algorithms. A number of software packages, including FlexX,⁴ DOCK,⁵ GOLD,⁶ and GLIDE,^7,8 are now widely used in the pharmaceutical industry, and are capable of screening libraries of ligands consisting of millions of compounds. Redocking of a ligand into its native cocrystallized structure is frequently performed with reasonably high accuracy by many of the programs cited above, whereas “cross docking”—docking of a ligand into a non-native conformation (for that ligand)—is often far more difficult. However, even native redocking fails a nontrivial fraction of the time; no currently available docking program has as of yet achieved complete robustness in this regard.

The most accurate docking programs, such as the GLIDE program developed in our laboratory, employ an approximate physical chemistry-based representation of protein-ligand interactions. Among the most important components of the energy model are the electronic charges that are assigned to the atoms of the ligand. In high-throughput docking calculations, where millions of ligands must be docked in a relatively short time frame, the charges are typically obtained from a molecular mechanics force-field such as OPLS.⁹ However, in a lead optimization context, it is reasonable to expend additional effort to produce high quality charges. The question is whether improvement of the charge model will lead to superior accuracy in docking, despite the fact that other aspects of the energy model, including solvation effects and the presence of explicit waters, are often either ignored or treated in a highly approximate fashion.

In the present article, we address this question via the use of mixed quantum mechanical/molecular mechanics (QM/MM) methods^10–12 to compute the ligand charge distribution. By using an ab initio quantum chemical approach (DFT) to determine the ligand charges, we avoid the problem of the quality of the force-field charge model for a wide range of medicinal chemistry compounds. Furthermore, employment of QM/MM techniques enables the charge calculations for the ligand to be performed in the protein environment, thus incorporating polarization effects in a natural (and accurate) fashion; the QM model is able to reliably reproduce, for arbitrary ligand chemistry, the response to an external electric field. Because the protein and ligand are not covalently attached, definition of the QM/MM interface is straightforward, and the computational cost of evaluating the charges (requiring only a single point calculation, as opposed to geometry optimization) is reasonable, particularly in a lead optimization context where hundreds or thousands, as opposed to millions, of ligands are to be studied.

As the present article represents an initial effort to investigate this topic, we confine our studies to native redocking, as opposed to cross docking (which will be investigated in a subsequent publication). Within this restricted regime, we address two fundamental questions:

1. If the ligand charges are optimized for the cocrystallized structure via a QM/MM calculation on the native complex, will subsequent redocking of the ligand yield superior structures as compared to the use of force-field based charges, which do not include polarization? Clearly if this objective is not satisfied, further investigation of the use of more accurate charges in the context of current rigid receptor docking models is unlikely to be profitable.

2. Is it possible, starting with no knowledge of the cocrystallized ligand geometry, to improve binding mode prediction by multiple cycles of docking, recomputation of charges, and redocking, selecting at the end of the process the lowest energy structure (taking into account the charge polarization)? Our algorithmic approach to this problem is rather primitive, and could almost certainly be quantitatively improved, but even with a first generation methodology, in which only one iterative cycle of docking, charge recomputation, and redocking, is employed, dramatic improvements in the prediction of ligand binding modes are obtained.

The article is organized as follows. We first briefly review our underlying docking methodology (implemented in the GLIDE program) and QM/MM approach (implemented in the QSITE program), and discuss how we have coupled these two programs together to develop a methodology in which docking and charge computation can, in principle, be iterated to convergence (although the effects of only a single iteration are examined in the present article). We then examine three relatively simple test suites for trypsin cocrystals, t-RNA, and for sugar-binding proteins. For these test cases, GLIDE performs reasonably well using force-field charges; charge recomputation is shown to increase robustness and accuracy with remarkable consistency. Finally, we examine 40 diverse PDB complexes, which exhibit a range of errors in standard GLIDE docking, with many cases in the intermediate range of 1.0–3.0 Å RMSD from the experimental crystal structure. For errors of this magnitude (which make up a substantial fraction of the errors in GLIDE native redocking), it is reasonable to hope that the initial guess for the geometry is good enough to allow an iterative protocol to succeed, assuming that improved charge distributions can in fact yield that result. Our results for this statistically significant test suite demonstrate definitively that generation of more accurate charges, which take polarization into account, is a highly promising approach to improving docking accuracy. Finally, in the conclusion, we outline future directions.

Methods

Docking Method

We employed the GLIDE¹³ program as our primary docking engine. The docking algorithm in GLIDE utilizes a hierarchical search protocol, in which the final step is minimization of a flexible ligand in the field of the Coulomb and van der Waals potential of the protein, as represented by the OPLS-AA molecular mechanics potential energy function. Selection of the final ligand pose is primarily determined by the total Coulomb-van der Waals energy (Ecvdw), with the Coulomb energy screened by a distance-dependent dielectric constant. The scoring function, called GLIDE score, for computing binding affinity is an extension of an empirically based Chem-Score function of Eldridge et al.¹⁴ The ligand structures and the corresponding receptor protein structures were prepared using utilities provided in the Schrödinger's First Discovery suite. All the test cases in this article we started from the raw PDB files. After separating ligands from proteins, we set the right bond orders and used MAESTRO's¹⁵ hydrogen treatment option to obtain the correct protonation state. The total charges of the ligands were assigned according to pK_a values. For protein receptors, protonation states were determined by templates provided in MAESTRO's hydrogen treatment module. Structural waters were deleted in all cases, except for 1bkm, in which a water molecule inside the binding pocket plays a crucial role of mediating a hydrogen bond. A part of this preparation procedure involves minimization with the OPLS-AA force-field, which gave us the reference structures. We calculated the root mean square distance (RMSD) of the resulting ligand configurations to these reference structures as an indicator for accuracy of the results. As we generated ligand poses, we discarded those that were within 0.6 Å of RMSD values to any previously accepted poses. We kept 10,000 poses for each ligand docking from initial generation for refinement. After the refinement we kept 1000 poses for minimization using grids during which a maximum of 100 steps were imposed. Finally, we scored 100 poses and ranked them after minimizations.

Subsequent Minimizations

When further minimization with the molecular mechanics force-field was needed, we employed IMPACT's¹⁶ force-field-based conjugate gradient minimizations routine. This procedure should give us a more precise minimization than GLIDE alone does, because GLIDE uses a grid-based algorithm. We cannot make direct comparison of energy values of GLIDE and IMPACT because of the empirical parameters of the GLIDE scoring function. However, relative energy changes can be calculated and this procedure was performed to both compare with the QM/MM result and further refine the structure with QM/MM charges. We set the maximum number of steps in minimizations to be 100 for efficiency.

QM/MM Methodology

For QM/MM calculations, we employed the QSITE program,¹⁷ which was constructed through a tight coupling of JAGUAR suite¹⁸ for QM region and the IMPACT molecular modeling code for MM region. When there are covalent connections between the QM and MM regions, QSITE uses frozen localized molecular orbitals along the covalent bonds to construct an interface between the two regions. However, for the protein-ligand complexes investigated in this article, the interactions between ligand and protein are exclusively noncovalent; by defining the ligand as the QM region, and the protein as the MM region, construction of the interface in essence becomes trivial (although significant parameterization of the van der Waals radii in the QM region is required to obtain accurate results for hydrogen bond interactions between the QM and MM regions). Further details concerning the QSITE methodology and implementation can be found in refs. 10–12.

Ab initio density functional theory (DFT) methods were used to represent the QM region, as a reasonable compromise between accuracy and efficiency. The 6-31G* basis set of Pople and coworkers, and hybrid DFT functional B3LYP,^19–21 which has been shown to yield excellent results for atomization energies and transition states in a wide range of chemical systems,^22–24 were used. At each configuration, a single point energy calculation was performed and the output was used for further computation. The optimization of the QM wave-function was performed incorporating coupling of the surrounding MM point charges; it is the effect of these point charges that leads to polarization of the ligand charge distribution. The DFT-based methodology used here is capable of representing this polarization with a reasonable degree of accuracy; almost certainly, other approximations that are being made (e.g., neglect or highly approximate treatment of solvation effects) make larger contributions to any observed errors in the binding mode prediction.

Charge Replacement

Once the DFT calculation was performed for the ligand, we needed to utilize the resulting wave-function to alter the charges on the ligand atoms. One possible way to do this is to use Mulliken population analysis, which is implemented in our QM software. However, atomic charges based on Mulliken population analysis vary erratically with the basis set used for the calculation. The optimal way to get reasonable atomic charges is by first calculating the molecular electrostatic potential (MEP) and fitting atomic charges to it. MEP is a rather well-defined quantity, and therefore, getting electric charges from it is a better choice than using a population-based method such as Mulliken analysis. This atomic charge assignment is made employing electrostatic potential (ESP) fitting, and it was the choice for our charge calculations. It is known that ESP charges can be troublesome for QM/MM calculations because of the interface of QM and MM regions. However, in our cases where no explicit bonds existed between the ligands and proteins, ESP charges were a good representative of actual atomic charges. Appropriate options (ip442=2 for print option and mulken=1 for postprocessing) that are specified in input files force the program to calculate and print ESP charge value for each atom of the ligand in the output files. We substituted the charge values in the structure files for ligands with these values and forced GLIDE to use them in the subsequent calculations.

Results and Discussion

Examples for illustration of the method are grouped in four classes: trypsin inhibitors, sugar binding proteins, t-RNA synthetases, and 40 selected cocrystals. This variety of cases encompasses ligands of all sizes and characters such as sugars, small peptides, amino acids, and other small organic molecules. Others are a selected subset of the GLIDE test suite,²⁵ and many are in the range for which the ordinary GLIDE calculation yields results of moderate accuracy, giving RMSD values in the range of 1.0–3.0 Å. These cases are clearly beyond the range of experimental error, yet are hopefully close enough to the correct answer that a simple iterative protocol has a good chance of converging; in subsequent work, we will examine more challenging cases in which larger RMSD deviations from experiment of the initial GLIDE calculation are observed. All of the examples were downloaded from protein data bank (PDB). Utilities of First Discovery suite were used for preparation of these cocrystal structures. RMSD values between the resulting structures, which are used as reference structures, and the initial PDB structures are in the range of 0.2 ≈ 0.4 Å.

Validation Studies Using Ligand Charges Derived from the Cocrystallized Complex Coordinates

Our initial investigations were aimed at determining whether charges obtained from the QM/MM calculation using the native (cocrystallized) structure would give docking results that are superior to those obtained from docking using the default force-field charges. For this study we performed the QM/MM calculation on the reference structures, which are the best approximations to the native structures in our force-field-based modeling, to obtain atomic charges on ligand atoms. These calculated charges are, in our description, presumed to represent with reasonable accuracy the ligand atom charges that are polarized by the surrounding atoms of the receptor molecule within the binding sites. If accurate charges on ligand atoms matter at all, this substitution should give better result upon docking.

Details of the procedure are as follows. We consider the reference structure of a given cocrystal obtained from cleaning and preparing the raw PDB file. We run GLIDE to dock the separated ligand back into the receptor with regular force-field charges and record the top scoring structure for comparison. Next, setting the ligand only as the QM region, we run QM/MM calculation on the reference structure to obtain new atomic charges on the ligand atoms. Once we substitute charge values in the ligand file with these new charge values, we perform another GLIDE run, forcing the program to use the new charge values. Again we record the top scoring structure and compare it with the one from the regular GLIDE run. To enable comparisons of the energies obtained from each protocol, we list Ecvdw values for each complex. GLIDE predominantly uses the aforementioned scoring function for ranking the final structures, although there is a small admixture of the empirical scoring terms as well. However, there is a high correlation between these two values and we are interested in the charge effect on the energy; hence the report of Ecvdw. We also report the change in charge values by root-mean-square value of charge difference between force-field and QM calculation.

In developing the original function in GLIDE for selecting the correct binding mode, we found (as mentioned above) that results overall were improved by mixing in a small component of the empirical scoring terms (e.g., hydrophobic contact term, hydrogen bonding terms) with the Ecvdw. However, it is possible that when properly polarized charges are employed, the Ecvdw becomes a more robust descriptor in selecting the correct ligand pose. This hypothesis will be investigated in some detail in what follows.

Trypsin Inhibitors

There are eight cocrystals for trypsin inhibitors^26,27 currently in PDB. Trypsin is rather a rigid protein and the binding site does not change appreciably for different ligands; thus we have selected it as an “easy” test case in which the charge model could be a dominant source of error, to the extent that error is observed. Table 1 shows the result of both a regular GLIDE run (FF Dock) and a GLIDE run with QM/MM modified charges (QM Dock). One can see that with QM Dock one always obtains better or equally good values of RMSD; in fact, the error using the QM Dock model is uniformly less than 0.4 Å and averages to about 0.2 Å, within experimental error (whereas default docking yields an average error of 0.8 Å, a good result but clearly inferior to what is obtained with QM Dock).

Table 1.

Validation Study Results for Trypsin Inhibitors.

		Ecvdw	RMSD	RMS charge
1pph	FF Dock	–52.8	0.83	0.42
	QM Dock	–67.9	0.41
1tng	FF Dock	–22.4	0.22	0.07
	QM Dock	–24.4	0.22
1tni	FF Dock	–27.9	2.32	0.09
	QM Dock	–29.7	0.34
1tnj	FF Dock	–29.3	0.23	0.13
	QM Dock	–31.6	0.23
1tnk	FF Dock	–27.1	0.93	0.11
	QM Dock	–31.9	0.41
1tnl	FF Dock	–25.4	0.63	0.15
	QM Dock	–33.2	0.25
1tpp	FF Dock	–32.4	0.93	0.10
	QM Dock	–37.4	0.24
3ptb	FF Dock	–29.3	0.17	0.05
	QM Dock	–31.3	0.18

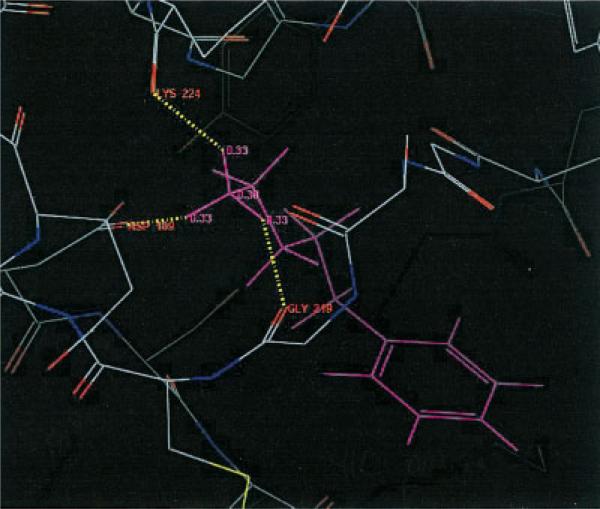
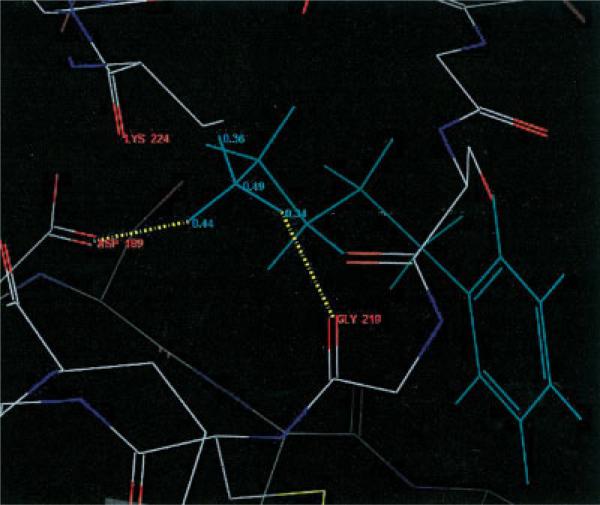
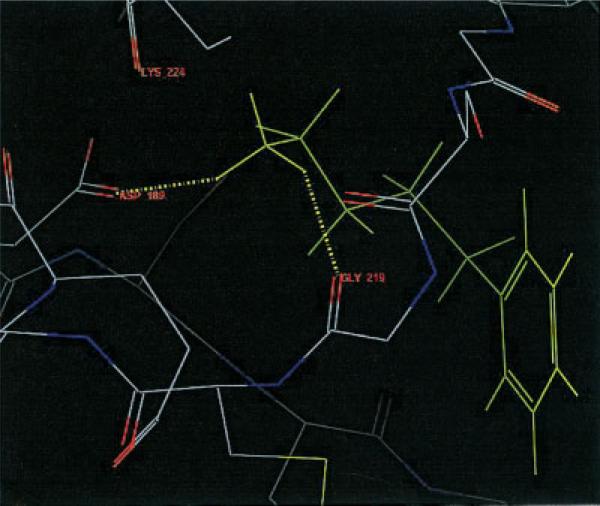
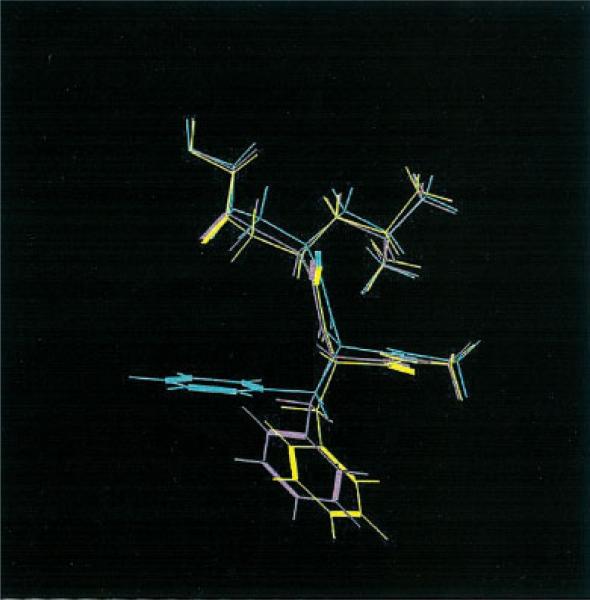
Let us focus on 1tni case, in which QM Dock improved the RMSD value rather dramatically. Figure 1 shows the top scoring structure of 1tni generated by FF Dock. The three hydrogen atoms of the amine group at the tail of the ligand that form hydrogen bonds with the receptor atoms each have a charge value of 0.33, which is a fixed charge value obtained from OPLS-AA force-field parameters. Notice that they are bonded to GLY 219, LYS 224, and ASP 189. However, in Figure 2, the three hydrogen atoms have charge values of 0.34, 0.36, and 0.44, and only two of them are bonded to GLY 219 and ASP 189. The geometry in Figure 2 is favorable in QM Dock because the energy contribution from hydrogen bonding is greater due to the larger charge of one of the hydrogen atoms, which is bonded to ASP 189 and polarized by the negative charge of that residue. Figure 3 shows the docking geometry of the native structure of 1tni, which has the same hydrogen bonds as in QM Dock.

Figure 1.

Not-so-good conformation of 1tni by FF Dock.

Figure 2.

Good conformation of 1tni by QM Dock.

Figure 3.

Native structure of 1tni.

Finally, note that cases such as 1tng and 3ptb yield very little change in charge and consequently QM Dock and FF Dock do not give appreciably different results. For some fraction of test cases, the force-field charges will be relatively close to the QM charges, and minimal improvement can be expected (although the results will not, of course, become worse).

Sugar Binding Proteins

We consider nine cocrystal structures of sugar binding proteins.^28–30 The ligands in these cases are rather small (20 ≈ 24 atoms) and regular GLIDE performs very well in obtaining low RMSD (below 1 Å) structures as top scoring ones. This is again an “easy” case, with a rigid active site; QM Dock nevertheless provides small but noticeable improvements for a number of the test cases, while harming none of them (Table 2).

Table 2.

Validation Study Results for Sugar Binding Proteins.

		Ecvdw	RMSD	RMS charge
1abe	FF Dock	–45.8	0.42	0.08
	QM Dock	–49.5	0.16
1abf	FF Dock	–44.7	0.21	0.16
	QM Dock	–50.4	0.26
1apb	FF Dock	–46.6	0.35	0.14
	QM Dock	–51.6	0.12
1bap	FF Dock	–45.9	0.47	0.08
	QM Dock	–48.3	0.23
5abp	FF Dock	–40.7	0.28	0.15
	QM Dock	–53.6	0.21
6abp	FF Dock	–46.4	0.43	0.08
	QM Dock	–48.7	0.10
7abp	FF Dock	–48.2	0.26	0.13
	QM Dock	–52.5	0.26
8abp	FF Dock	–40.1	0.38	0.11
	QM Dock	–50.6	0.29
9abp	FF Dock	–39.2	0.45	0.15
	QM Dock	–51.3	0.22

tRNA Synthetases

Transfer RNA (tRNA) is the “adaptor” molecule that enables the genetic code contained in the nucleotide sequence of a messenger RNA (mRNA) molecule to be translated into the amino acid sequence of a polypeptide chain. The key to this process lies in the specific recognition of the correct tRNA molecule by an amino-acyl-tRNA synthetase enzyme, which attaches the correct amino acid for the tRNA to the acceptor stem. We consider seven of these complexes. Unlike the previous two cases, we have various proteins as receptors and the ligands are amino acids. The results are depicted in Table 3. Except for 1f4l, QM Dock produces lower or equal RMSDs for the top scoring structures. In the case of 1f4l, the reason QM Dock does not perform any better is quite clear. The docking in this case is driven by hydrophobicity and electric charge does not play an important role.

Table 3.

Validation Study Results for tRNA Synthetases.

		Ecvdw	RMSD	RMS charge
1adj	FF Dock	–31.6	0.65	0.12
	QM Dock	–34.3	0.45
1b70	FF Dock	–34.2	0.49	0.23
	QM Dock	–36.7	0.35
1bs2	FF Dock	–35.7	0.62	0.10
	QM Dock	–39.7	0.20
1c0a	FF Dock	–63.2	0.36	0.31
	QM Dock	–77.1	0.11
1f4l	FF Dock	–30.1	0.20	0.15
	QM Dock	–29.7	0.24
3ts1	FF Dock	–60.3	0.13	0.32
	QM Dock	–56.3	0.13
4ts1	FF Dock	–36.0	0.27	0.19
	QM Dock	–38.1	0.25

Forty Diverse Complexes Where GLIDE Performance Is in Many Cases Lacking in Quantitative Accuracy

GLIDE has been tested on an extensive set of 282 publicly available cocrystallized complexes.²⁵ Among these 282 complexes we selected 40 cases which, when the GLIDE docking algorithm is applied, are reported in the GLIDE user manual to yield 1.5 ≈ 3.0 Å RMSD deviations from the crystal structure; these are considered in the docking community as “intermediate” results. We have run GLIDE v. 2.5 on these complexes; the results are presented in Table 4. In some cases, our results are somewhat different from those in the user manual; such differences can arise from, for example, the use of different input geometries for the ligands. (GLIDE uses the input geometry to construct a torsional profile around each bond, and this affects the subsequent docking; no memory of the actual torsion angles is retained by the program. Also, different versions of the program might have had a role.) The test suite still contains a significant number of cases with errors in the 1.0 ≈ 3.0 Å range (and, in fact, a few of the test cases have even larger errors), providing a challenging test for the QM Dock methodology.

Table 4.

Validation Study Results for 40 Randomly Selected Complexes.

		Ecvdw	RMSD	RMS charge			Ecvdw	RMSD	RMS charge
121p	FF Dock	–145.9	1.83	0.26	1dog	FF Dock	–36.9	0.23	0.14
	QM Dock	–156.7	0.07			QM Dock	–44.6	0.29
1aaq	FF Dock	–57.6	3.67	0.17	1eap	FF Dock	–55.8	0.72	0.17
	QM Dock	–80.0	0.23			QM Dock	–54.8	0.65
1azm	FF Dock	–54.9	1.52	0.27	1ela	FF Dock	–37.3	5.82	0.26
	QM Dock	–77.4	0.21			QM Dock	–46.8	0.41
1b6j	FF Dock	–67.8	2.18	0.19	1ele	FF Dock	–47.1	0.36	0.48
	QM Dock	–102.2	0.41			QM Dock	–47.5	0.45
1b6k	FF Dock	–81.1	1.10	0.17	1epb	FF Dock	–40.1	0.74	0.19
	QM Dock	–88.4	0.21			QM Dock	–45.2	0.73
1b6l	FF Dock	–60.9	0.59	0.17	1eta	FF Dock	–20.1	1.85	0.39
	QM Dock	–79.5	0.16			QM Dock	–23.1	0.52
1b6m	FF Dock	–67.0	1.19	0.19	1ezq	FF Dock	–67.0	0.52	0.17
	QM Dock	–81.7	0.21			QM Dock	–68.5	0.17
1bkm	FF Dock	–56.0	1.98	0.15	1f0s	FF Dock	–50.0	2.00	0.18
	QM Dock	–67.6	0.10			QM Dock	–59.4	0.62
1cbs	FF Dock	–38.3	1.97	0.21	1f0u	FF Dock	–61.4	0.42	0.14
	QM Dock	–42.9	0.18			QM Dock	–65.0	0.29
1cde	FF Dock	–55.0	1.95	0.15	1fki	FF Dock	–27.7	5.70	0.13
	QM Dock	–63.4	0.14			QM Dock	–48.4	0.22
1cil	FF Dock	–60.9	0.74	0.24	1hbv	FF Dock	–70.8	3.14	0.19
	QM Dock	–85.5	0.29			QM Dock	–73.4	0.47
1com	FF Dock	–38.6	1.10	0.24	1hfc	FF Dock	–82.4	2.53	0.24
	QM Dock	–40.5	0.84			QM Dock	–107.7	0.13
1cps	FF Dock	–68.2	3.55	0.24	1hri	FF Dock	–41.6	1.97	0.17
	QM Dock	–100.5	0.55			QM Dock	–44.7	0.14
1ctr	FF Dock	–37.2	1.15	0.17	1hvr	FF Dock	–89.9	0.23	0.17
	QM Dock	–39.5	0.42			QM Dock	–102.4	0.09
1d3d	FF Dock	–67.7	2.59	0.17	1icn	FF Dock	–34.2	1.60	0.11
	QM Dock	–68.1	0.80			QM Dock	–34.5	0.41
1d3p	FF Dock	–67.6	2.58	0.16	1ivc	FF Dock	–45.3	2.01	0.15
	QM Dock	–68.1	0.72			QM Dock	–46.2	1.69
1d8f	FF Dock	–87.7	2.73	0.22	1ive	FF Dock	–30.6	3.44	0.19
	QM Dock	–101.4	0.35			QM Dock	–33.1	0.23
1dbm	FF Dock	–50.8	2.09	0.13	1lcp	FF Dock	–104.1	1.00	0.29
	QM Dock	–52.6	2.00			QM Dock	–129.6	0.82
1dds	FF Dock	–57.1	1.93	0.17	1mbi	FF Dock	–25.2	0.30	0.25
	QM Dock	–64.0	0.20			QM Dock	–35.6	0.25
1did	FF Dock	–37.6	0.58	0.13	1mnc	FF Dock	–83.0	0.70	0.26
	QM Dock	–47.9	0.24			QM Dock	–112.3	0.46

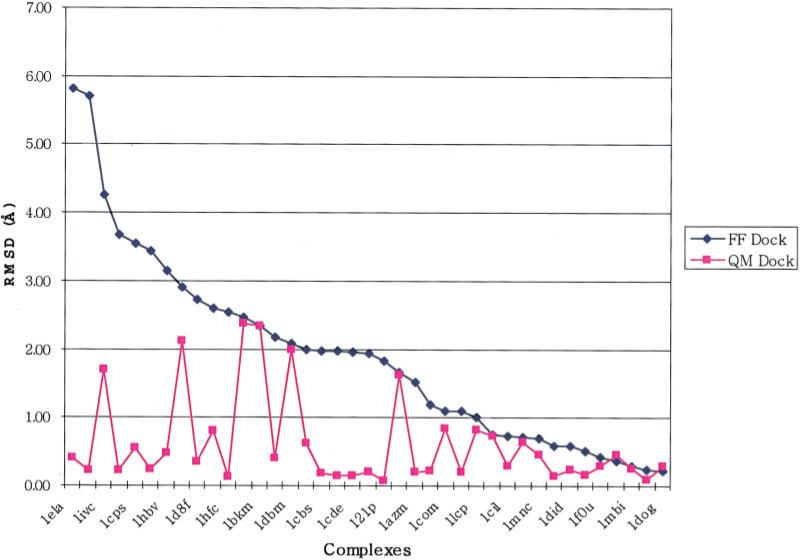
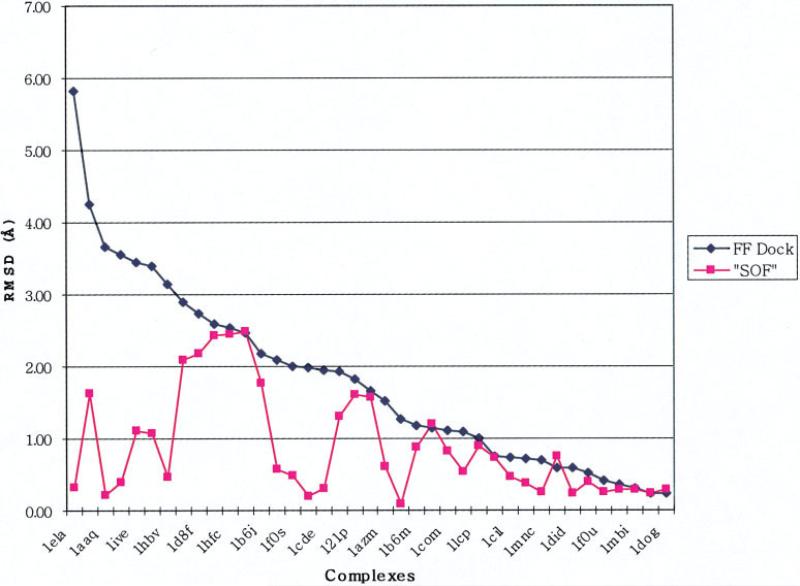
The results obtained from the QM Dock protocol described in the section “Validation Studies Using Ligand Charges Derived from the Cocrystallized Complex Coordinates” are depicted in graphical form in Figure 4; RMSD values are presented in Table 4. It can be seen that, in many cases, the QM Dock protocol yields dramatic improvements as compared to the original GLIDE results, with the improvements often greater than 1.5 Å RMSD. The maximum error is reduced from 5.7 to 2.0 Å and the average RMSD from 1.81 to 0.43 Å. Some improvement is obtained in the vast majority of cases where there was a sizeable initial discrepancy from the experimental structure, and there are no instances where the results are significantly worse.

Figure 4.

RMSD changes from FF Dock to QM Dock as in Table 4.

While these results are highly encouraging, the use of the native complex to generate the ligand charges is obviously not an unbiased procedure. There are two sources of uncertainty as to whether the present approach can be applied to a problem where the answer is not known a priori:

1. The charges computed by the QM Dock protocol are, by construction, designed to optimize the interaction of the ligand with the protein in the native conformation. It is possible that a different structure of the complex would induce very different charges, optimized to that structure, which could have a lower total energy than those reported in Table 4. If that is indeed the case, an exhaustive, unbiased sampling protocol, in which all ligand poses were sampled and the appropriate QM charges were evaluated for each pose, would not select the native structure as its prediction (assuming of course that the total Ecvdw remained as the primary determinant of pose selection).

2. Even if the native complex is lowest in Ecvdw in the phase space search defined in (1), there is no guarantee that it could be located in a reasonable amount of CPU time without prior knowledge of the native structure. While it is reasonable to expend considerably more time per ligand in docking for purposes of lead optimization (lead docking) than in virtual screening for lead discovery, there has to be some limit, and the cost of carrying out, for example, thousands of QM/MM computations of the ligand charges would be prohibitive.

To address these two issues, we have developed an iterative QM/MM-based protocol that does not require prior knowledge of the correct ligand pose. We apply this protocol to the 40 complexes discussed in the present section; a description of the methodology, and the results, are presented below.

A brief comment is in order on the use of the total Ecvdw to select the correct pose from among dockings generated by differently polarized ligand charge sets. The use of charges obtained in conformation A to compute the total energy in conformation B represents an approximation to what would be obtained in a fully quantum chemical calculation; iteration of the polarization of the charge distribution to convergence, via multiple cycles of docking and iteration, would address this issue. For now, we simply employ the approximation in the hope that the errors are relatively small. Secondly, there is some reorganization energy of the ligand associated with polarization of its charge distribution from the gas phase; this term is ignored in what follows as well. In future work, we will address both of these problems in more detail; however, as is shown below, the present approximations are sufficient to establish that the methodology represents a very substantial improvement upon the use of gas phase charges.

Iterative Algorithms

The above studies assume that we have native structures at hand, which means that we know how the polarization of the ligand atoms should be before attempting the docking. This amounts to feeding the answer back into our procedure by doing QM/MM calculation with native structures. However, in a realistic drug discovery problem where prediction of the binding mode of a novel ligand is desired, one does not have the luxury of knowing the native structures and must find a way to figure out how the charge substitution can be adopted to improve docking. One way could be by performing QM/MM calculations iteratively.

Iterative Minimization

The simplest iterative protocol that can be defined, invoking multiple cycles of minimization, is as follows: (1) start with standard GLIDE docking to obtain a top scoring structure. (2) Perform QM/MM calculation and replace the charge values. (3) Using the new set of charge values, perform MM minimization. (4) Repeat steps (2) and (3) until change in charge values drops below a prescribed value. We have applied this algorithm to 1tni case, where we know that FF Dock does not give a good structure whereas QM Dock does (Table 5). The key point here is that after step (2), one should be able to hop over to a different local minimum from the one that has been found in the previous iteration. After the initial docking, switching to new set of charges calculated by QM/MM method certainly gives a noticeable dip in energy and RMSD. However, just after the first iteration, we cannot escape from the new local minimum and quickly arrive at the termination condition. The basic problem with this approach is that there are multiple local minima into which the ligand can dock, and one is dependent upon the initial guess for the charges as to where the top-scoring pose winds up. If the initially obtained pose is too far away from the native structure, the subsequently recalculated charges will not represent an improvement upon the initial force-field charges, and the protocol has no chance to converge to the correct nativelike pose (even if such a pose were to have the lowest overall Ecvdw).

Table 5.

Iterative Minimization on 1tni.

	Relative energy	RMSD	RMS charge
Initial structure	0.00	2.32	0.00
1st iteration	–12.33	1.45	0.12
2nd iteration	–2.15	1.44	0.02
3rd iteration	–0.03	1.44	0.00

Iterative Docking

A different iterative algorithm, in which instead of minimizations docking is performed, is considered. In this algorithm, after the initial FF Dock is performed, QM/MM calculation is imposed on the top scoring structure to obtain a new set of charge values. With this new charge set, we do another docking. These two steps can be repeated to improve the result further. This algorithm was tested on the 40 complexes of the section “Forty Diverse Complexes Where GLIDE Performance Is in Many Cases Lacking in Quantitative Accuracy”. Table 6 shows the result. In this table, we report Emodel (E) and GLIDE score (GS). Only the first iterations were done for all 40 complexes and the results are named before and after to denote the initial FF Dock and subsequent QM Dock. Among the 40 complexes, iterative docking made a substantial improvement in 12 cases (>0.5 Å) and some improvement in 12 cases (<0.5 Å). However, in 10 cases, the iterative docking gave somewhat worse results than the initial FF Dock. In six cases, QM Dock actually “blew up” the RMSD values. There are a few observations that can be made from this study. First of all, QM Dock on a relatively good structure most likely will give a good result. In the case of the initial structures being below 1 Å, the QM Dock always gave results that were below 1 Å. Some of the intermediate FF Dock results (>1.0 and <3.0 Å) turned into “excellent” results (<0.5 Å) by QM Dock. But in other cases, QM Dock made the results worse. The interpretation of these observations is as follows. RMSD is a function of multidimensional variables and cannot be taken as a simple metric. Although in past studies³¹ it was shown that most structures that are below a small value of RMSD (e.g., 0.6 Å) to the native structure can be minimized to virtually the same structure, structures that have slightly larger RMSD (1.0 ≈ 2.0 Å) can have quite different geometry, which in turn will give a different set of charges with QM/MM calculations. It must be emphasized that the charge calculations with QM/MM in our algorithms depend solely on the geometry of the structure. Structures with similar values of RMSD can have vastly different (qualitative) geometries, which explains varying QM Dock results from intermediate initial FF Dock results. This conclusion suggests yet another strategy for QM/MM docking without the native structures.

Table 6.

Iterative Docking on 40 Complexes.

	E before	E after	RMSD bf	RMSD af	GS before	GS after
121p	–290.7	–312.3	1.83	1.02	–10.64	–14.19
1aaq	–100.8	–153.4	1.30	1.46	–9.32	–11.07
1azm	–73.7	–110.0	1.52	1.07	–7.15	–8.13
1b6j	–128.4	–108.7	2.18	10.52	–10.86	–8.09
1b6k	–149.4	–125.9	1.10	0.92	–12.56	–9.77
1b6l	–106.6	–134.8	1.06	0.67	–10.81	–12.23
1b6m	–140.1	–68.3	1.19	10.70	–10.75	–9.21
1bkm	–106.3	–124.3	2.33	2.41	–10.81	–10.71
1cbs	–55.8	–67.9	1.97	0.19	–8.02	–8.49
1cde	–93.4	–103.9	1.95	2.81	–10.49	–8.88
1cil	–74.1	–122.1	0.74	0.69	–9.31	–9.23
1com	–58.8	–68.1	0.80	0.86	–7.30	–7.42
1cps	–102.8	–158.9	3.55	3.59	–8.36	–6.56
1ctr	–50.1	–54.6	1.15	5.31	–6.80	–3.97
1d3d	–118.2	–120.2	2.59	1.46	–11.68	–11.52
1d3p	–115.0	–118.6	2.47	2.38	–10.89	–11.13
1d8f	–141.0	–186.1	2.73	2.62	–10.82	–12.53
1dbm	–81.3	–87.0	2.09	2.02	–10.33	–11.71
1dds	–98.2	–109.2	1.93	1.87	–8.84	–8.61
1did	–61.0	–72.5	2.66	0.23	–5.59	–7.32
1dog	–62.3	–82.9	3.74	0.30	–7.47	–7.87
1eap	–95.6	–98.9	0.72	0.83	–11.25	–12.05
1ela	–71.5	–147.3	6.11	9.72	–6.59	–6.07
1ele	–71.8	–101.2	0.36	0.77	–8.29	–8.00
1epb	–57.4	–76.3	2.12	0.72	–9.16	–10.08
1eta	–49.4	–34.1	1.67	1.66	–4.09	–4.79
1ezq	–147.4	–163.9	0.52	0.18	–12.14	–12.01
1f0s	–57.1	–91.8	2.00	0.47	–8.65	–9.48
1f0u	–131.0	–154.0	0.69	0.48	–9.42	–10.37
1fki	–35.8	–40.6	5.70	5.97	–6.05	–4.75
1hbv	–117.1	–99.3	3.14	4.90	–11.09	–9.69
1hfc	–140.0	–206.9	2.53	2.45	–10.13	–10.87
1hri	–59.9	–65.7	1.97	0.52	–8.59	–9.37
1hvr	–181.6	–224.3	0.22	0.18	–15.74	–16.58
1icn	–45.1	–47.2	2.90	8.88	–7.82	–7.79
1ivc	–55.3	–46.4	4.26	2.22	–5.49	–5.92
1ive	–37.3	–48.0	5.35	1.90	–5.63	–5.48
1lcp	–124.5	–166.8	1.00	1.14	–7.79	–8.71
1mbi	–29.0	–60.6	2.08	0.12	–4.76	–4.00
1mnc	–142.7	–220.5	0.70	2.09	–11.93	–13.63

“Survival of the Fittest” (SOF) Algorithm

Inspection of the list of output structures from FF Dock reveals that there are some good structures with low RMSD (<1 Å) somewhere in the list in most cases. Even in the case in which none of the top scoring structures has RMSD smaller than 1 Å, almost certainly are there structures in the intermediate range of RMSD. Therefore, it is natural to ask whether the results can be improved if we go down the list of structures that FF Dock generates and perform QM Dock on multiple charge sets generated from different initial poses. It could be computationally demanding, but at the same time inherently parallelizable, much like Monte Carlo sampling. The idea is that among the many structures generated by FF Dock one should be able to find something close enough to the right geometry that will give a substantially improved set of charges, and these in turn will enable finding and scoring the good structures through QM Dock procedure on subsequent iterations. As we saw in earlier examples, our scoring with QM/MM-generated charge sets, based on comparison of the total Ecvdw, should be able to distinguish the correct ligand poses from among the second generation of docked structures. Our proposed algorithm for the implementation of this idea is rather simple. After generating a set of structures with FF Dock, we simply go down the list and perform QM/MM calculations to attain new sets of charges. With these new charges, we run QM Dock to generate a second generation of structures, from which the new scoring will pick the overall winner. We name this algorithm “survival of the fittest” (SOF) algorithm for the similarity to the biological evolution process. Because QM/MM calculations and the subsequent QM Dock on different structures are completely independent procedures, after the initial generation of docked structures, the algorithm is “embarrassingly parallel”. The bulk of total computation time is devoted to this latter stage of the algorithm and hence the algorithm scales very well.

We have tested the foregoing algorithm using the 40 complexes in our initial test set (although, as is explained below, technical problems were encountered for one complex, so final results were obtained only for 39 of the 40 initial test cases). Starting from the lists of structures that are sorted by energies (GLIDE score) from initial FF Dock, we pick the first five structures and perform QM Dock on all of them. The cutoff value of five structures was motivated based on the following observations. In the initial GLIDE docking, we find that there are 19 out of 40 complexes that contain a structure with RMSD below 1.0 Å within the top five ranked structures. If one scans further through the top 10, the number would be 21 out of 40. Similarly, 31 out of the 40 test cases contain a structure within the top five structures with an RMSD less than 2.0 Å, whereas 33 test cases exhibit such a structure within the top 10 structures. Thus, the enrichment of low RMSD structures going from five to 10 retained poses is relatively small. Furthermore, restricting the number of poses retained to five keeps the computational effort to a reasonable level (as opposed, for example, to retaining hundreds of poses that would each require a QM/MM calculation). We have omitted 1fki among the 40 complexes of previous sections from the report here because QM/MM calculations failed to converge in all but one structure. As with all of our docking with GLIDE, we impose clustering condition of 0.6 Å, thus none of these poses from initial FF Dock will be closer to each other than 0.6 Å; this prescription ensures that the structures in the QM Dock ensemble are not clustered around a single basin of attraction, which would negate the point of the exercise, namely exploration of charge distributions emerging from qualitatively differing poses and hence differing hydrogen bonding patterns.

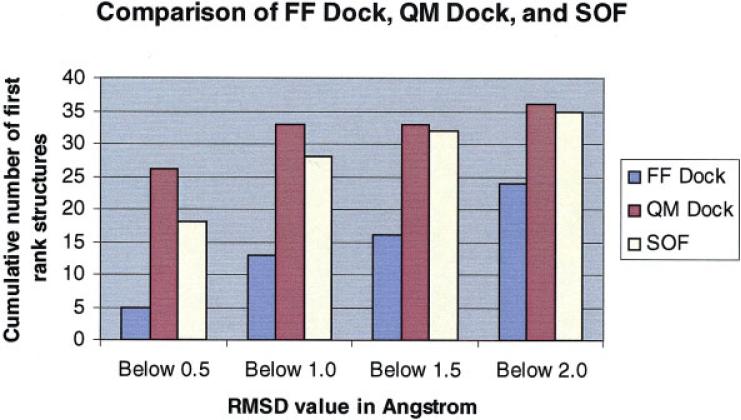
The raw data for the five redockings with QM charges are shown in Table 7. The final pose selection for the SOF algorithm is performed by choosing the pose with the lowest total Ecvdw (given in Table 7 for each pose). Figure 5 plots the RMSD of the lowest energy pose (by the criterion defined in the previous sentence) for the 39 complexes investigated. These results can be compared with those in Figure 4, which is a similar plot for the RMSD obtained using the charge distribution calculated from the reference poses, discussed above (which presumably represents the best result obtainable for each complex by optimizing the charge distribution to the native structures). The quality of results displayed in Figure 5 is remarkable. The maximum error is reduced from 6 Å to slightly more than 2 Å, the average RMSD is reduced from 1.77 to 0.88 Å, and large numbers of test cases experience dramatic improvement in the accuracy of the pose, with many more at the limit of experimental error than in the original FF docking. Based on these results, questions (1) and (2) posed above in “Forty Diverse Complexes Where GLIDE Performance Is in Many Cases Lacking in Quantitative Accuracy” can be answered affirmatively; Ecvdw of the complex can be used to select the correct answer from a range of charge distributions and resultant structures, and the sampling problem can be attacked in a tractable fashion with existing computational resources and tools. The comparison of FF Dock, QM Dock, and SOF is depicted in Figure 6, in which the numbers of first ranked structures that are below 0.5, 1.0, 1.5, and 2.0 Å out of 40 complexes are represented by bars.

Table 7.

Results of SOF Algorithm on 40 Complexes.

Complex	Values		Rank 1	Rank 2	Rank 3	Rank 4	Rank 5
121p	FF Dock	RMSD	1.67	2.03	1.94	1.22	1.32
		Ecvdw	–144.0	–135.7	–105.6	–113.8	–105.5
	QM Dock	RMSD	0.89	1.46	1.45	1.79	1.61
		Ecvdw	–141.7	–151.8	–157.7	–161.8	–166.4
	RMS charge		0.26	0.33	0.30	0.28	0.30
1aaq	FF Dock	RMSD	3.67	3.56	6.86	3.71	3.72
		Ecvdw	–57.6	–49.2	–59.4	–51.9	–52.5
	QM Dock	RMSD	0.22	0.22	6.83	3.38	3.35
		Ecvdw	–84.2	–84.3	–68.5	–76.5	–71.5
	RMS charge		0.15	0.18	0.17	0.15	0.17
1azm	FF Dock	RMSD	1.67	1.93	0.98	1.52	2.11
		Ecvdw	–49.7	–51.1	–51.0	–54.9	–52.5
	QM Dock	RMSD	1.03	1.94	0.62	1.03	0.31
		Ecvdw	–73.1	–64.6	–80.7	–73.1	–76.7
	RMS charge		0.24	0.23	0.29	0.24	0.26
1b6j	FF Dock	RMSD	2.18	11.53	11.90	1.40	1.28
		Ecvdw	–67.8	–76.2	–69.6	–44.4	–32.7
	QM Dock	RMSD	5.86	4.66	1.11	5.89	4.66
		Ecvdw	–63.5	–56.0	–74.5	–52.3	–64.2
	RMS charge		0.26	0.36	0.36	0.33	0.26
1b6k	FF Dock	RMSD	1.10	0.63	3.06	3.09	3.06
		Ecvdw	–81.1	–78.6	–11.0	–8.4	–8.3
	QM Dock	RMSD	1.16	0.53	0.96	0.39	0.85
		Ecvdw	–73.4	–83.9	–65.4	–82.2	–78.0
	RMS charge		0.27	0.26	0.28	0.28	0.28
1b6l	FF Dock	RMSD	0.59	0.66	1.23	0.97	1.16
		Ecvdw	–60.9	–53.7	–49.3	–48.3	–44.4
	QM Dock	RMSD	0.75	0.53	1.02	1.11	1.22
		Ecvdw	–78.0	–76.5	–70.8	–62.8	–20.7
	RMS charge		0.26	0.25	0.23	0.26	0.25
1b6m	FF Dock	RMSD	1.19	1.68	1.57	10.44	11.22
		Ecvdw	–67.0	–53.7	–52.4	–50.0	–36.2
	QM Dock	RMSD	1.87	0.88	4.22	9.18	N/A
		Ecvdw	–74.6	–77.4	–58.4	–52.3	N/A
	RMS charge		0.32	0.34	0.35	0.28	N/A
1bkm	FF Dock	RMSD	1.26	1.48	1.44	1.46	1.56
		Ecvdw	–55.5	–53.9	–54.8	–50.1	–50.0
	QM Dock	RMSD	0.09	0.10	0.09	0.09	0.09
		Ecvdw	–66.4	–66.1	–66.5	–66.1	–65.7
	RMS charge		0.17	0.17	0.14	0.16	0.18
1cbs	FF Dock	RMSD	1.97	1.12	0.47	2.08	1.57
		Ecvdw	–38.3	–36.5	–36.5	–35.3	–30.0
	QM Dock	RMSD	0.19	0.20	0.19	0.21	0.21
		Ecvdw	–43.7	–44.3	–43.7	–44.7	–41.9
	RMS charge		0.22	0.21	0.21	0.21	0.21
1cde	FF Dock	RMSD	1.95	2.50	9.82	3.25	9.92
		Ecvdw	–55.0	–62.5	–51.1	–53.3	–45.9
	QM Dock	RMSD	0.14	9.75	2.90	0.30	2.92
		Ecvdw	–54.7	–52.3	–54.0	–64.2	–56.7
	RMS charge		0.14	0.15	0.17	0.18	0.16
1cil	FF Dock	RMSD	0.74	0.19	0.99	1.32	1.36
		Ecvdw	–60.9	–62.6	–53.8	–55.2	–54.4
	QM Dock	RMSD	3.31	0.46	1.66	1.33	2.25
		Ecvdw	–67.6	–81.8	–66.5	–69.4	–73.7
	RMS charge		0.25	0.24	0.19	0.16	0.18
1com	FF Dock	RMSD	0.80	1.10	1.34	1.20	2.49
		Ecvdw	–36.3	–38.6	–34.2	–31.7	–32.5
	QM Dock	RMSD	0.82	1.09	0.79	0.84	1.08
		Ecvdw	–38.0	–37.1	–36.7	–35.6	–36.1
	RMS charge		0.22	0.22	0.19	0.17	0.16
1cps	FF Dock	RMSD	3.55	3.11	6.85	2.85	2.18
		Ecvdw	–68.2	–57.7	–50.4	–58.5	–44.5
	QM Dock	RMSD	3.00	3.90	0.39	3.74	3.52
		Ecvdw	–55.7	–67.8	–68.5	–67.3	–64.8
	RMS charge		0.38	0.39	0.29	0.25	0.33
1ctr	FF Dock	RMSD	1.15	1.13	7.64	7.68	6.70
		Ecvdw	–37.2	–36.0	–31.6	–30.7	–23.7
	QM Dock	RMSD	1.19	N/A	7.67	2.94	7.09
		Ecvdw	–36.5	N/A	–34.2	–32.5	–31.7
	RMS charge		0.17	N/A	0.19	0.20	0.18
1d3d	FF Dock	RMSD	2.59	2.26	2.46	1.69	2.32
		Ecvdw	–67.7	–60.9	–67.2	–63.3	–59.7
	QM Dock	RMSD	2.56	2.05	2.43	2.04	2.74
		Ecvdw	–70.5	–68.3	–72.3	–70.7	–70.1
	RMS charge		0.15	0.14	0.16	0.16	0.18
1d3p	FF Dock	RMSD	2.75	2.83	2.47	1.21	2.41
		Ecvdw	–61.6	–60.2	–63.2	–63.9	–65.3
	QM Dock	RMSD	1.93	1.89	2.34	1.94	2.48
		Ecvdw	–62.9	–67.3	–70.0	–64.4	–70.9
	RMS charge		0.17	0.17	0.16	0.15	0.17
1d8f	FF Dock	RMSD	2.41	2.54	9.17	2.73	2.71
		Ecvdw	–76.9	–83.9	–64.4	–87.7	–86.0
	QM Dock	RMSD	1.51	2.17	0.64	2.67	2.75
		Ecvdw	–84.3	–87.5	–85.7	–87.2	–81.2
	RMS charge		0.20	0.21	0.23	0.21	0.21
1dbm	FF Dock	RMSD	2.04	2.09	2.42	1.94	0.54
		Ecvdw	–49.6	–50.8	–48.2	–46.7	–48.3
	QM Dock	RMSD	0.95	0.55	0.58	0.70	0.50
		Ecvdw	–48.1	–50.1	–58.8	–50.5	–49.4
	RMS charge		0.13	0.13	0.13	0.13	0.15
1dds	FF Dock	RMSD	11.11	2.28	1.93	1.64	2.32
		Ecvdw	–57.8	–48.2	–57.1	–54.4	–51.8
	QM Dock	RMSD	N/A	1.30	1.78	1.83	1.35
		Ecvdw	N/A	–64.7	–53.9	–60.9	–64.6
	RMS charge		N/A	0.17	0.17	0.19	0.16
1did	FF Dock	RMSD	0.90	0.58	3.23	3.07	3.51
		Ecvdw	–28.3	–37.6	–25.4	–22.9	–33.1
	QM Dock	RMSD	0.23	0.87	0.57	0.98	0.27
		Ecvdw	–51.0	–43.6	–40.6	–41.0	–50.5
	RMS charge		0.09	0.07	0.09	0.11	0.11
1dog	FF Dock	RMSD	0.23	0.66	0.72	0.41	3.68
		Ecvdw	–36.9	–31.2	–24.7	–27.9	–18.2
	QM Dock	RMSD	0.23	0.29	0.31	0.29	0.32
		Ecvdw	–36.9	–37.7	–37.5	–37.0	–37.6
	RMS charge		0.12	0.09	0.09	0.18	0.11
1eap	FF Dock	RMSD	0.36	0.72	0.77	2.10	0.87
		Ecvdw	–55.4	–55.8	–54.1	–51.7	–53.2
	QM Dock	RMSD	0.37	0.38	0.81	0.72	0.73
		Ecvdw	–55.7	–55.3	–52.8	–55.7	–54.4
	RMS charge		0.18	0.17	0.18	0.17	0.17
1ela	FF Dock	RMSD	6.11	7.36	5.80	5.82	6.60
		Ecvdw	–36.2	–34.6	–37.2	–37.3	–32.8
	QM Dock	RMSD	0.33	0.32	4.75	5.96	2.69
		Ecvdw	–53.6	–55.9	–34.6	–37.1	–37.4
	RMS charge		0.37	0.37	0.36	0.37	0.35
1ele	FF Dock	RMSD	0.34	0.36	0.34	6.22	3.14
		Ecvdw	–46.9	–47.1	–45.9	–28.6	–30.5
	QM Dock	RMSD	1.52	0.29	3.04	0.27	2.67
		Ecvdw	–26.7	–47.7	–34.5	–46.3	–34.2
	RMS charge		0.46	0.45	0.47	0.34	0.42
1epb	FF Dock	RMSD	0.74	2.41	2.12	2.00	2.09
		Ecvdw	–40.1	–35.3	–37.1	–36.3	–37.6
	QM Dock	RMSD	0.74	0.72	0.72	0.73	0.74
		Ecvdw	–45.8	–43.6	–45.0	–44.8	–42.4
	RMS charge		0.21	0.20	0.19	0.18	0.19
1eta	FF Dock	RMSD	1.47	8.70	8.43	1.85	1.47
		Ecvdw	–18.1	–20.6	–13.3	–20.1	–20.0
	QM Dock	RMSD	1.62	1.99	2.01	1.76	1.35
		Ecvdw	–21.8	–21.1	–21.3	–20.7	–25.5
	RMS charge		0.15	0.14	0.17	0.15	0.18
1ezq	FF Dock	RMSD	0.52	0.54	2.67	1.54	3.59
		Ecvdw	–67.0	–67.2	–31.5	–59.1	–39.3
	QM Dock	RMSD	0.52	0.58	0.39	0.54	0.61
		Ecvdw	–67.0	–64.0	–67.4	–66.8	–64.1
	RMS charge		0.17	0.17	0.15	0.13	0.13
1f0s	FF Dock	RMSD	2.00	1.28	2.14	2.26	2.13
		Ecvdw	–50.0	–54.0	–51.5	–47.1	–43.7
	QM Dock	RMSD	0.50	0.53	0.48	0.49	0.45
		Ecvdw	–54.7	–55.6	–55.5	–56.4	–55.9
	RMS charge		0.18	0.15	0.19	0.17	0.17
1f0u	FF Dock	RMSD	0.42	0.26	0.49	0.69	0.62
		Ecvdw	–61.4	–63.0	–59.9	–57.9	–58.3
	QM Dock	RMSD	0.26	0.42	0.24	0.28	0.29
		Ecvdw	–63.1	–61.5	–62.8	–63.0	–63.0
	RMS charge		0.16	0.14	0.16	0.15	0.15
1hbv	FF Dock	RMSD	3.14	4.98	3.15	5.04	3.24
		Ecvdw	–70.8	–62.2	–68.2	–62.2	–58.2
	QM Dock	RMSD	0.46	0.46	0.47	3.54	5.11
		Ecvdw	–72.4	–69.4	–72.4	–66.1	–64.6
	RMS charge		0.18	0.17	0.20	0.19	0.20
1hfc	FF Dock	RMSD	2.85	2.58	2.53	0.45	0.41
		Ecvdw	–78.1	–77.9	–82.4	–81.4	–81.1
	QM Dock	RMSD	2.52	2.38	2.44	0.49	2.52
		Ecvdw	–111.4	–104.3	–125.0	–109.4	–109.0
	RMS charge		0.27	0.25	0.31	0.25	0.23
1hri	FF Dock	RMSD	1.12	4.61	1.97	10.07	3.40
		Ecvdw	–37.8	–33.3	–41.6	–29.6	–43.0
	QM Dock	RMSD	0.79	1.08	3.17	3.48	1.15
		Ecvdw	–44.0	–44.8	–44.2	–44.5	–43.9
	RMS charge		0.09	0.11	0.09	0.08	0.18
1hvr	FF Dock	RMSD	0.23	0.28	0.30	0.53	0.22
		Ecvdw	–89.9	–89.2	–88.9	–88.9	–89.8
	QM Dock	RMSD	0.23	0.28	0.33	0.23	0.35
		Ecvdw	–90.3	–90.3	–90.2	–90.3	–90.0
	RMS charge		0.17	0.16	0.16	0.18	0.17
1icn	FF Dock	RMSD	2.90	2.13	2.57	2.32	1.91
		Ecvdw	–33.3	–37.8	–36.3	–27.1	–31.3
	QM Dock	RMSD	1.99	2.12	2.55	2.08	2.34
		Ecvdw	–37.3	–37.8	–35.4	–37.8	–39.2
	RMS charge		0.09	0.15	0.11	0.10	0.10
1ivc	FF Dock	RMSD	4.26	4.74	5.38	3.89	5.33
		Ecvdw	–32.1	–26.5	–26.9	–26.7	–29.5
	QM Dock	RMSD	4.11	5.09	3.79	4.14	1.62
		Ecvdw	–31.4	–31.3	–28.3	–31.8	–32.9
	RMS charge		0.13	0.17	0.13	0.14	0.14
1ive	FF Dock	RMSD	5.35	5.33	5.45	3.91	5.53
		Ecvdw	–22.7	–23.2	–29.2	–19.9	–25.5
	QM Dock	RMSD	3.58	3.87	1.10	3.96	3.36
		Ecvdw	–29.7	–29.3	–31.1	–30.3	–29.0
	RMS charge		0.14	0.15	0.12	0.20	0.14
1lcp	FF Dock	RMSD	0.26	1.79	0.97	1.00	2.04
		Ecvdw	–101.8	–82.5	–85.3	–104.1	–78.5
	QM Dock	RMSD	0.30	0.82	0.86	0.89	0.28
		Ecvdw	–128.0	–132.7	–128.0	–137.1	–112.6
	RMS charge		0.28	0.22	0.21	0.26	0.11
1mbi	FF Dock	RMSD	1.66	1.66	1.66	1.66	1.66
		Ecvdw	–15.8	–15.8	–15.9	–15.9	–15.9
	QM Dock	RMSD	0.28	0.31	0.28	0.30	0.23
		Ecvdw	–25.6	–25.6	–25.6	–25.5	–26.4
	RMS charge		0.09	0.09	0.09	0.09	0.11
1mnc	FF Dock	RMSD	0.70	2.47	6.82	6.79	6.62
		Ecvdw	–83.0	–81.4	–67.9	–62.6	–69.4
	QM Dock	RMSD	0.76	0.65	6.55	2.61	0.26
		Ecvdw	–82.6	–83.9	–83.6	–76.6	–86.4
	RMS charge		0.29	0.28	0.24	0.26	0.38

Figure 5.

Changes in RMSD values from FF Dock to SOF algorithm.

Figure 6.

Comparison of different methods in terms of number of first-ranked structures obtained that are under 0.5, 1.0, 1.5, and 2.0 Å.

Particularly noteworthy is the ability of the methodology to locate dramatically improved poses for ligands with a large number of rotatable bonds, where the sampling problem would be anticipated to pose a considerable challenge. Examples include 1aaq and 1hbv, which have 23 and 17 rotatable bonds, respectively. In both cases, the RMSD obtained with FF docking is high (3 ≈ 4 Å), whereas the SOF results are 0.22 and 0.46 Å, respectively. Clearly what is happening here is that there are alternative hydrogen bond patterns available to the two ligands, and that incorporation of polarization via the QM/MM calculations enables the correct hydrogen bond pattern to be decisively selected (large energy gaps as compared to the incorrect poses are seen in both cases).

If the number of poses retained from the initial docking is increased from 5 to 10, only one test case, 1d8f, is materially improved, from an RMSD of 2.17 to 0.78 Å. While our current view is that this improvement would not justify the doubling (approximately) of the CPU time, one might want to employ enhanced parameters of this type if accuracy was a much more important objective than computational performance. However, the algorithm needs to be tested on an expanded set of self-docking test cases, and also on cross docking problems where the ranking of the correct pose may be inferior to what we have seen to date. Given that the results presented here are intended as preliminary, we view the data reported above as confirming the cutoff of five retained structures as a reasonable compromise between speed and accuracy.

There are a small number of other cases where SOF yields results that are significantly worse than those obtained from QM Dock. Of these, only one can be attributed exclusively to sampling (1ctr); for this case, the QM Dock Ecvdw is lower than any of the results obtained by SOF. For the remaining cases (1d3d, 1d3p, 1dds, 1eta, 1hfc, 1icn), the Ecvdw of the best scoring pose in SOF is lower than that attained via QM Dock; this is a scoring problem, because even if the native structure could be located, it would not be selected by the protocol in place at present. Given the approximations currently being used, the existence of scoring problems at this level is unsurprising, and it will require a more sophisticated approach to obtain greater robustness.

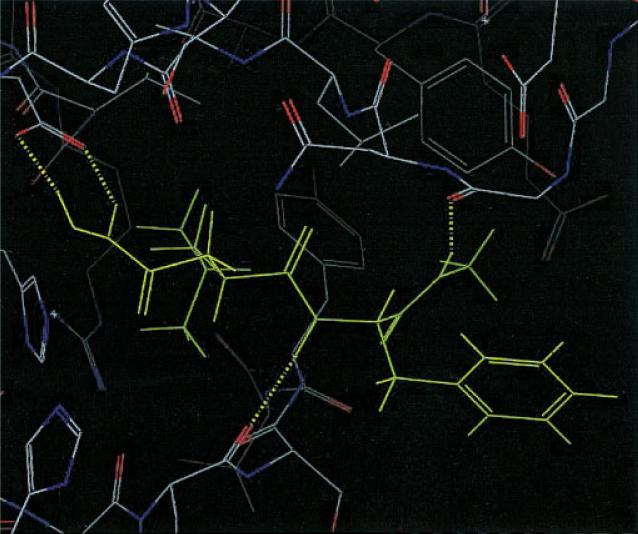
Most of the scoring errors cited above are relatively small, typically a few kcal/mole. However, one case, 1hfc, displays a scoring error of 17 kcal/mol, an order of magnitude larger than the remaining cases. This ligand has a significant piece projecting into solution, and a reasonable hypothesis is that solvation effects are critical in stabilizing the experimental binding mode. We have performed a preliminary investigation of this system by carrying out minimization using a generalized Born implicit solvation model³² for the five candidate structures obtained; the results are presented in Table 8. It can be seen that the solvation term does indeed make up the gap between the correct and incorrect structures (Fig. 7), and that in fact the correct structure would now be selected by the total energy including solvation. Figure 8 shows that except for the part in the solution, the correct and incorrect structures have the same hydrogen bond pattern as in the native structure; hence the importance of solvation calculations. General application of a solvation model across a wide range of complexes will require a more detailed investigation, including refinement of the structures; we are currently pursuing efforts in this direction, and will report the results in a future publication. The result for 1hfc, while anecdotal, can be regarded as encouraging.

Table 8.

Surface Generalized Born Implicit Solvent Method Energy Calculations for 1hfc QM Dock Structures.

1hfc		Rank 1	Rank 2	Rank 3	Rank 4	Rank 5
QM Dock	RMSD	2.52	2.38	2.44	0.49	2.52
	Ecvdw	–111.4	–104.3	–125.0	–109.4	–109.0
	Solvation	–988.6	–992.8	–994.3	–1012.1	–993.0
	Total	–1100.0	–1097.1	–1119.3	–1121.5	–1102.0

Figure 7.

Overlap of native (yellow), third (green), and fourth (purple) QM Dock structures of 1hfc from Table 8.

Figure 8.

Hydrogen bonds of native, third QM Dock, and fourth QM Dock structures of 1hfc within the binding site.

QM Charges of Free Ligands

A final control experiment is to use QM methods to calculate ligand charges in the gas phase, and then dock the ligands with these charges. In performing this experiment, we put the ligand in the same conformation as in the cocrystallized complex; thus what is being tested is the importance of the influence of the protein environment in engendering accurate docked poses. The comparison between QM charges and QM/MM charges will tell us how much the environment within the binding pocket will effect the polarizations of ligand atoms.

Table 9 shows that there are substantial differences between force-field charges and QM charges. In some cases, QM/MM charges and QM charges are not much different, which means that there is little polarization within the binding pockets. 1icn is such a case, and indeed neither QM Dock with charges calculated from the native structure nor the SOF algorithm improves the FF Dock result. However, in many other cases, the polarization effects are substantial, and the QM/MM charges are quite different from gas phase QM results.

Table 9.

Root-Mean-Square Differences between Force-Field Charges and Quantum Mechanical Charges (FF – QM) and between Quantum Mechanical Charges and QM/MM Charge (QM – QM/MM).

	FF – QM	QM – QM/MM
121p	0.24	0.15
1aaq	0.16	0.04
1azm	0.24	0.21
1b6j	0.17	0.05
1b6k	0.15	0.05
1b6l	0.16	0.04
1b6m	0.17	0.05
1bkm	0.14	0.05
1cbs	0.18	0.05
1cde	0.13	0.06
1cil	0.17	0.17
1com	0.14	0.20
1cps	0.21	0.18
1ctr	0.16	0.07
1d3d	0.16	0.04
1d3p	0.13	0.09
1d8f	0.18	0.21
1dbm	0.13	0.05
1dds	0.16	0.06
1did	0.09	0.08
1dog	0.12	0.06
1eap	0.16	0.07
1ela	0.12	0.27
1ele	0.16	0.53
1epb	0.17	0.04
1eta	0.38	0.04
1ezq	0.14	0.06
1f0s	0.17	0.06
1f0u	0.14	0.06
1fki	0.14	0.03
1hbv	0.18	0.06
1hfc	0.15	0.21
1hri	0.17	0.02
1hvr	0.19	0.08
1icn	0.11	0.02
1ivc	0.14	0.13
1ive	0.11	0.13
1lcp	0.27	0.21
1mbi	0.23	0.19
1mnc	0.17	0.22

We have performed docking on our standard 40 complex test suite with charges obtained from free ligand QM calculations (Free-QM Dock). The results are shown in Table 10. In general, these results are better than FF Dock but not as good as QM Dock (with QM/MM charges), yielding 1.35 Å of average RMSD values. Except for a few cases, the energy values of Free-QM Dock are in between those of FF Dock and QM Dock. While the RMSD cited above reflects some improvement as compared to docking with FF charges (unsurprising, given that the estimation of charges in the FF model is in many cases highly approximate), the improvement due to inclusion of polarization is qualitatively much larger. Thus, this result confirms the central importance of polarization effects in determining the observed hydrogen bonding patterns in protein-ligand complexes.

Table 10.

Results of Free-QM Dock on 40 Complexes.

	Ecvdw	RMSD
121p	–124.3	1.50
1aaq	–78.0	1.33
1azm	–44.2	1.99
1b6j	–98.0	0.44
1b6k	–83.2	1.01
1b6l	–74.6	0.16
1b6m	–69.6	1.32
1bkm	–58.9	2.05
1cbs	–39.9	1.99
1cde	–55.6	2.63
1cil	–57.3	0.19
1com	–38.7	1.21
1cps	–83.3	0.54
1ctr	–39.2	3.53
1d3d	–66.2	1.74
1d3p	–67.3	2.50
1d8f	–73.7	3.45
1dbm	–61.5	2.01
1dds	–62.8	1.38
1did	–36.9	0.22
1dog	–40.3	0.25
1eap	–51.2	0.74
1ela	–53.0	0.37
1ele	–50.3	0.16
1epb	–42.1	0.72
1eta	–15.5	4.86
1ezq	–70.0	0.45
1f0s	–58.4	0.39
1f0u	–62.7	0.42
1fki	–52.7	0.17
1hbv	–68.4	0.46
1hfc	–68.1	2.66
1hri	–44.9	3.47
1hvr	–94.2	0.15
1icn	–36.3	1.57
1ivc	–34.9	2.27
1ive	–29.6	1.92
1lcp	–80.7	0.93
1mbi	–25.7	0.29
1mnc	–74.8	0.64

Conclusions and Future Work

The results presented above definitively demonstrate that the use of accurate charges, and environmental polarization effects, leads to, in many cases, dramatic improvements in docking accuracy for a wide range of PDB complexes. Furthermore, this improvement is (predominantly) recoverable via a simple iterative algorithm starting with no knowledge of the native complex, which can be executed in a reasonable amount of CPU time. Based on these results, we believe that the SOF version of the QM Dock algorithm as described herein (or with minor modifications) can be deployed profitably in “lead docking” applications where highly accurate structures are desired. The principal uncertainty at this point is whether performance in cross docking (as opposed to self docking) can be similarly improved; investigation of this question is currently ongoing in our laboratory.

An alternative approach to the use of QM/MM methods to incorporate polarization effects on charges is to employ a polarizable force-field. Such an approach would not only reduce CPU times, it would also allow, in principle, modified charges to be used for key active site residues in the protein as well as for the ligand. Assuming that the polarizable force-field is capable of accurately reproducing QM charge distributions and polarization effects, it should deliver very similar results to those presented in this article. We are currently initiating an investigation in this direction as well.

Finally, the models and algorithms employed in this article can be improved on in some obvious ways, for example by continuing to iterating the SOF protocol for several more rounds, development of a more sophisticated scoring function for selecting the final pose that includes solvation effects, and so forth. Such development should improve robustness and at the same time reduce CPU requirements to a minimum. We believe that the first step should be to expand our set of test cases (particularly those involving cross docking); however, assuming the methodology is successful on such an expanded test set, development of a next generation version should be straightforward.

A more general question is whether there are similar problems associated with the use of fixed charge force-fields in explicit solvent molecular dynamics and Monte Carlo simulations. The energy model considered here, as was discussed above, essentially ignores solvation effects. This appears to work reasonably well in predicting protein-ligand binding affinities, possibly because the key components of the ligand (i.e., those making the crucial hydrogen bonded contacts with the protein) are buried in the protein active site, with little solvent exposure. Nevertheless, the profound effects seen here, for a substantial number of test cases, suggest that it will be very interesting to investigate similar predictions of structural motifs with polarizable and fixed charge force-fields in explicit solvent simulations.