Abstract
Doppler OCT (DOCT) can provide blood flow velocity information which is valuable for investigation of microvascular structure and function. However, DOCT is only sensitive to motion parallel with the imaging beam, so that knowledge of flow direction is needed for absolute velocity determination. Here, absolute volumetric flow is calculated by integrating velocity components perpendicular to the B-scan plane. These components are acquired using two illumination beams with a predetermined angular separation, produced by a delay encoded technique. This technology enables rapid pulsatile flow measurement from single B-scans without the need for 3-D volumetric data or knowledge of blood vessel orientation.
OCIS codes: (110.4500) Optical coherence tomography, (170.3880) Medical and biological imaging
1. Introduction
Blood flow is a critical factor that regulates developmental programs during cardiogenesis. During early embryonic development, deviations from the normal blood flow pattern have been shown to lead to congenital heart defects including septal defects and outflow tract anomalies [1–6]. Blood flow and its resulting hemodynamic forces may alter gene expression in the surrounding cells and thereby influence developing cardiovascular form and function [7–11]. To better understand the role flow plays during cardiovascular development precise tools are needed to rapidly calculate and monitor blood flow.
Volumetric flow rate in a vessel can be defined as the volume of blood that passes a given cross section of that vessel per unit time. The flow rate can be calculated if the cross sectional area of the vessel of interest and the absolute velocity vector everywhere on cross section are known. In cultured avian embryos, which are useful models of heart development that we use regularly [12–15], vessel cross sectional area is easily measured using optical coherence tomography (OCT) imaging [16]. At the same time, Doppler OCT (DOCT) can provide depth-resolved velocity information with high spatial resolution [17–20]. DOCT has been used to measure blood velocity and the resulting hemodynamic forces on the vessel wall [13, 15, 21, 22], as well as to estimate total flow [23, 24]. However, DOCT is only sensitive to motion parallel to the imaging beam, so additional information is needed to obtain the absolute velocity vector in order to calculate absolute flow. This additional information has required volumetric imaging or increased system complexity.
Two major strategies have been employed to overcome this limitation and obtain the absolute velocity vector. One method is to determine the vessel orientation as an estimate of the Doppler angle and use it to correct the measured velocity. The Doppler angle (α) is the angle between the imaging beam and the absolute velocity vector of the blood (Fig. 2(c)). If it is assumed that the flow is parallel with the vessel’s orientation, the direction of the velocity vector can be estimated by acquiring a 3-D structural OCT volume of the vessel and measuring the vessel orientation [25, 26]. However, the orientation can sometimes be difficult to determine in smaller blood vessels that are usually more tortuous and with borders that are difficult to discern. Around the optic nerve head, the vessel angle has been estimated by recording two concentric circumpapillary scans at slightly different radii and using the two corresponding cross sections of each vessel to determine the vessel orientation [27–29]. This method is faster than acquiring a 3-D volume, but is also more susceptible to error in estimating the vessel orientation. An error in estimating the flow direction leads to an error in the corresponding velocity and flow measurement, which becomes particularly significant when the OCT beam is nearly perpendicular to the flow (Fig. 1 ).
Fig. 1.
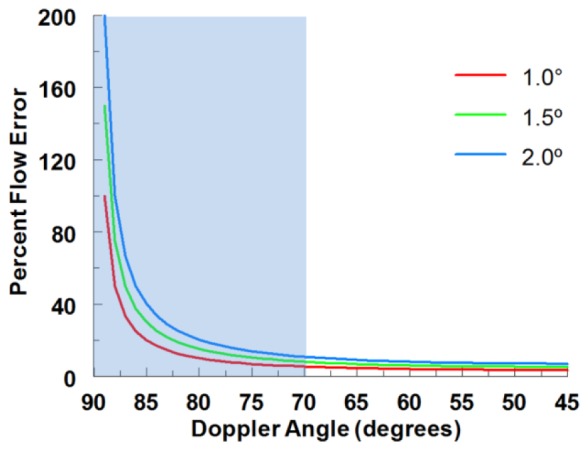
Theoretical flow percentage error from vessel angle estimation inaccuracies as a function of Doppler angle. The typical inter-user variability we observe when measuring vessel orientation in 3D volumes is around 1.0° which can result in flow error greater than 20% when the Doppler angle is at 85°. The blue box represents the typical vessel angles for the quail embryonic vascular network.
Alternatively, the absolute velocity vector can be determined by imaging the same location using multiple imaging beams at different angles of incidence [30–35]. This has been accomplished by utilizing polarization multiplexing [30, 34], delay multiplexing [31, 32], and through the use of additional OCT interferometers [33, 35]. To completely determine the velocity vector with no additional information, at least three different measurements are necessary [32]. This can't be done with polarization multiplexing, requires significant range for delay encoding, and increases system and alignment complexity when adding OCT interferometer channels. The velocity vector can be calculated using only two imaging beams if the angle between the vessel and the incident plane supported by the two illumination beams is aligned to zero, or is known or measured [34, 35].
Recently it has been recognized that flow can be calculated with no knowledge of the orientation of the vessel or absolute velocity vectors. This calculation only requires measurement of the velocity components normal to the imaging plane. To satisfy this condition a 3-D volume of the vessel is acquired with DOCT and the flow is calculated from an en face section, which is naturally perpendicular to the acquired velocities and illumination beam [13, 24, 36–38]. The flow calculation does not suffer from the angle error described previously because vessel orientation is not needed. However, acquiring a 3-D volume can be time consuming, so measuring pulsatile flow using this technique would require either gating data over several heart cycles [38–40] or imaging a small enough region of interest to acquire volumes in real time [37].
To enable pulsatile flow calculations without the need for 3-D volume acquisition we have extended the en face cross section method to the B-scan plane. To measure velocity perpendicular to the B-scan plane with a minimally-modified OCT instrument, we generate imaging beams at two different effective incidence angles using delay encoding [31]. The beams are precisely aligned so that the plane of the two angled beams is perpendicular to the B-scan direction. The perpendicular velocities can then be calculated over the cross sectional area to determine the flow. With this technique, flow rates can be calculated from individual B-scan images which allows for the measurement of pulsatile flows with high temporal resolution throughout the heart cycle.
To validate this technique, a capillary tube flow phantom was imaged at various orientations and at various flow rates provided by a syringe pump. The technique was validated for in vivo blood flow measurement by imaging quail embryo yolk sac vessels. The measurements were compared with the conventional 3-D technique. Vessels were measured at separated positions to determine the consistency of the measurement along the vessel length. Bifurcated vessels were also imaged before and after the bifurcation to confirm that the two smaller measured flow rates equaled the parent vessel’s flow rate.
2. Methods
2.1 Velocity measurement by delay encoding
Flow (F) in a vessel may be calculated from a single cross-sectional B-scan as the product of the pixel area (ΔS) and the sum of the velocity perpendicular to the imaging plane () at each pixel in the cross-section area S, as
| (1) |
To determine , at least two Doppler measurements must be taken at different angles of incidence and the plane of those two vectors should be orthogonal to the B-scan imaging plane. To accomplish this, we used a delay-encoded method that we have previously demonstrated [31]. This method requires only a single OCT channel (i.e. one interferometer and detector) and is readily implemented by adding a single optical element to an OCT scanner. Briefly, a glass plate was placed to half-intersect the imaging beam in the OCT scanner before the scanning elements and objective lens as illustrated in Fig. 2(a) (for simplicity, the scanning elements are not depicted in the figure). The separation angle 2θ between the two beams is determined by [31] where ro is the 1/e radius of the Gaussian beam and f is the focal length of the lens (Fig. 2(c)). In this work, the total angle difference 2θ was measured as 8.4 degrees in air and 6.1 degrees in tissue. The introduction of the glass divides the imaging beam into two components with one half of the light delayed. This results in the generation of 3 delay-encoded images as shown in Fig. 2(b) from the 4 different paths the light can take. The top image (AA) results from light taking path A twice, which experiences no optical delay. The bottom image (BB) results from light taking path B twice and being optically delayed twice. The middle image (AB/BA) results from light taking either path A forward and path B back or vice versa, and thus being delayed once. The glass is inserted into the imaging beam so that the plane formed by the two components is perpendicular to the B-scan direction. The orientation of the two planes can be verified by ensuring that the three generated images are aligned vertically with one another (Fig. 2(b)). The three images result from beams with different effective angles of incidence on the sample which therefore experience different Doppler shifts when imaging flow, as is evident in the three Doppler OCT images in Fig. 2(b). The information in the two images AA and BB is sufficient to determine the transverse velocities.
Fig. 2.
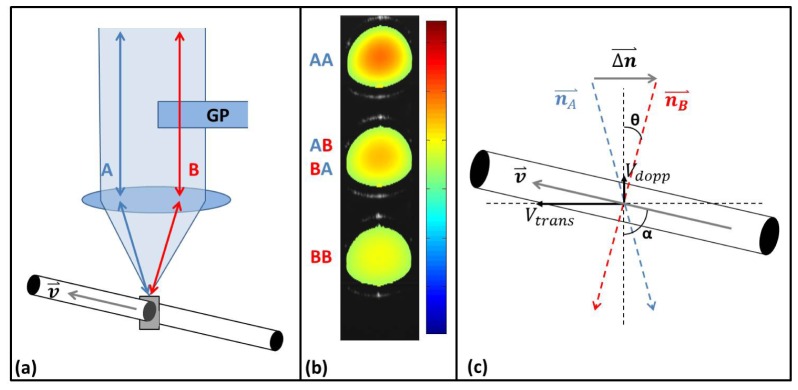
(a) Principle of operation: A glass plate (GP) was introduced into the imaging beam and the resulting two imaging sub-beams (A, B) are incident on a capillary tube. (b) OCT Doppler overlay image generated from the plane cross-sectioning the capillary tube showing the three sub-images (AA, BB, AB/BA) generated from the two delay-encoded sub-beam paths (A, B). The illuminating sub-beams have different effective angles of incidence resulting in different Doppler images. (c) Diagram defining the vectors, angles and velocities used for absolute flow calculation (see description in text).
2.2 Calculation of absolute flow
When velocity components measured in image AA are subtracted from velocity components measured in image BB, the common axial velocity component is eliminated, leaving only the velocity components perpendicular to the B-scan plane. Referring to Fig. 2(c),
| (2) |
and, so
| (3) |
| (4) |
| (5) |
where represents a velocity measured in image AA and represents a velocity measured in image BB. The calculated transverse velocity values can then be input to Eq. (1) to determine the flow. In practice, the cross-section areas in image AA and image BB (SA and SB respectively) do not correspond pixel-by-pixel, so one may integrate the velocity profiles before calculating the velocity difference:
| (6) |
This straightforward analysis assumes that the two image slices are interrogating the identical cross-section, i.e. SA = SB. However, due to the angular separation between the two beams this is never quite the case. This discrepancy results in two potential problems: that the cross sectional areas SA and SB are different, and that the two slices are not necessarily interrogating exactly the same locations in the vessel. The effect of this error on the flow measurement was examined by computer-simulation (Matlab). Flow velocity data in a cylindrical channel with a perfect parabolic flow profile was generated, and then artificially sectioned at two different angles of incidence. The Doppler velocities in the two cross sections were found, simulating the physical two-beam imaging measurement, and the flow was calculated based on Eq. (6). This simulation was repeated at various angles of orientation between the flow and the image planes, from −30° to 30°. The results of the simulation are represented as the solid line in Fig. 3(a) and show an overestimation in the flow as the angle increases. Furthermore, the overestimation is independent of beam separation angle θ, and of the diameter of the flow channel.
Fig. 3.
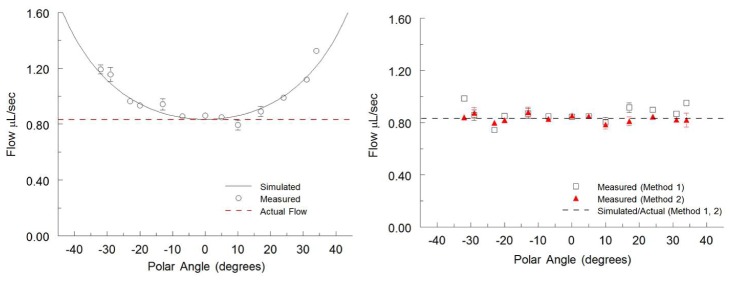
Simulated and measured flow rates in a capillary tube plotted against varying polar angles. A syringe pump perfused the capillary tube at a constant flow rate of 0.83uL/sec represented by the dotted line in both panels. (a) Flow rates calculated from the straightforward analysis utilizing Eq. (6) showing the increasing overestimation at larger polar angles. The results generated from the simulated data are represented by the solid black line. (b) Flow rates calculated using methods 1 and 2 showing unbiased flow measurement at all angles measured. The simulated data are identical to the constant flow rate line so they are both represented by a single black dotted line. All measured flow rates are represented as mean ± S.D. over 80 imaging frames.
We investigated two methods for compensating for the flow error caused by the difference between the two cross-sections.
Method 1
The first method is to use the difference between the mean velocities in the two cross-sections to obtain the mean transverse velocity . Then, can be multiplied by the “true” cross-section area, S, which we obtain from image AB/BA. This effectively projects the velocity components measured at the two angles onto a single cross-section, which is orthogonal to the calculated transverse velocity, and eliminates the inaccuracies that result from the differences in cross sectional area between the two slices. Under the assumptions that all flow in the tube is in the same direction, and that the tube is rigid within the sampling region, the flow equation can be rewritten as:
| (7) |
where is the average perpendicular velocity over the cross-section area, S, and and are the mean velocities in the two cross sectional areas SA and SB. In case of other two beam methods that do not produce this middle image, the average of the two images’ cross sectional area could be used instead, which is only slightly less accurate.
Method 2
Calculating the mean velocity over a cross-section requires dividing by the cross-section area, estimated by segmentation. This step is prone to error. Therefore, we decided to approach the flow measurement from a different direction which does not assume the two slices are interrogating identical points, and does not require dividing by an estimated area. The transverse velocity () is readily obtained from the measured Doppler velocity () when the Doppler angle α is known (Fig. 2(c)). Under the assumption that the flow in the tube is all in the same direction, at angle α, Eq. (1) can then be rewritten as:
| (8) |
For each of the two beams generated by delay encoding, the flow rate at each cross section can be expressed:
| (9) |
and
| (10) |
Therefore,
| (11) |
and
| (12) |
Under the assumption that the portion of the vessel being imaged is rigid the total flow across these planes will be equal to one another () so that Eq. (11) and (12) can be rearranged to eliminate α using the identity:
| (13) |
Solving for F results in a quadratic equation
| (14) |
Solving this equation enables determination of the flow without any prior knowledge of the Doppler angle α and does not require dividing by an estimated cross-section area. Equation (14) will result in the two solutions
| (15) |
where
| (16) |
and
| (17) |
However, in most applications, where the vessels are oriented nearly perpendicular to the imaging beam, it is simple to determine the correct solution by choosing the one corresponding to the larger angle α. In situations where the correct angle is ambiguous (α ~45°) method 1 could be used, or the correct solution could be determined from a priori information.
2.3 Data acquisition and processing
The 2.5mm glass plate was inserted into a quasi-telecentric OCT scanner [41] in a Fourier domain OCT system [42]. A superluminescent diode centered at 1310nm with a FWHM of 75nm was used as the light source. A linear-in-wavenumber spectrometer [42] was used to project interference fringes onto a 1024-pixel InGaAs line-scan camera with a line rate of approximately 47 kHz. The system has an axial and lateral resolution of ~10 µm in tissue, depth range of 4.3 mm in air, and a roll-off of 6dB over 1.7 mm [42]. Doppler shifts were calculated from phase differences between subsequent A-scans and a mean filter was applied in the complex domain to reduce noise.
2.4 Validation experiments
To compare the analysis methods over various Doppler angles, a capillary tube flow phantom with an outer diameter of 0.4 mm and an inner diameter of 0.3 mm was perfused with a 2% lipid suspension solution (Intralipid, Clayton, NC) using a syringe pump (NE-300 from New Era Pump Systems, Inc, Farmingdale NY) and imaged using the OCT system described above. The syringe pump perfused the tube at a constant flow rate of 0.83 μL/sec and B-scan images were acquired at various Doppler angles. For convenience, we plot by polar angle (90−α). The experimental results were furthermore compared with simulated results which were generated as described above. After comparing analysis methods, method 2 was selected for further experimental validation. The technique was validated using the capillary phantom and in vivo.
Using the capillary and pump system described above, the absolute flow was measured at various flow rates set by the syringe pump ranging from 0.04 μL/sec to 1.50 μL/sec. Next, the capillary tube was rotated to various azimuthal and polar angles to verify that the flow rate measurement was orientation-independent. At each position, a 3-D structural image set was obtained in order to validate the capillary tube’s orientation.
To validate the technique for measuring blood flow in vivo, stage HH18 quail embryos’ yolk blood vessels were also imaged to measure absolute flow at a variety of locations in the vascular network. These vessels were chosen because they all reside on the surface of the yolk sac with no moving tissue underneath and hence we were able to avoid any potential tissue overlap between the three images. Embryos were cultured using a shell-less culture method and placed in an environmental OCT imaging chamber with controlled temperature (38°C) and humidity to reproduce physiological conditions [14]. 714 B-scan images were acquired over the duration of approximately 8 seconds or approximately 30 heartbeats. Vessels were imaged at two different positions along their length to determine whether the flow measurement was consistent over the entire vessel. 3-D structural volumes were also acquired to compare the new absolute flow measurement technique to the traditional flow measurement, correction by measuring the vessel orientation using the 3-D image. Finally, vessels were imaged before and after bifurcations to verify that the combined smaller vessels’ flow after bifurcation equaled the parent vessel’s flow. For each vessel measurement, heart rates were roughly calculated using the FFT of the pulsatile flow measurement. The average flow was calculated over the course of the full 30 heart beats.
3. Results
To compare the accuracy of the methods presented here, simulated data were generated at various polar angles and the values were input to Eq. (6), Eq. (7), and Eq. (15). These simulated results were then confirmed by imaging a capillary tube phantom with a constant flow rate at various polar angles. Flow rates were calculated from the phantom measurements using all methods and plotted together with the simulation results. As shown in Fig. 3(a), the straightforward analysis using Eq. (6) is accurate near α = 90, but significantly overestimates the flow as the angle deviates from perpendicular. Methods 1 and 2 consistently measure the correct flow without bias, with method 1 and 2 deviating from the actual flow rate by an average of 6.4% and 2.7% respectively. Having determined that analysis method 2 results in a more precise measurement, the balance of the validation experiments were analyzed using this method.
The capillary tube flow phantom experiment for various flow rates was repeated three times and the means and standard deviations were obtained from the combined results (Fig. 4(a) ). The linear fit to the data had a slope of 1.001 and a y-intercept of 0.008 indicating that the OCT measurements are consistent with flow rates set by the syringe pump. The measured flow rates varied from the actual flow rates by an average of 3.1%. The capillary tube phantom was then imaged under a constant flow rate of 0.83μL/sec at various azimuthal and polar angles of the tube. For each of these experiments, the angle was confirmed by obtaining a 3-D structural volume of the capillary tube at each position. The means and standard deviations of these experiments are shown in Fig. 4(b)-4(c). Both sets of data generate a trendline with negligible slope (<0.0001) and y-intercept of approximately 0.83 indicating a consistent flow measurement of 0.83μL/sec over the range of angles measured. The measured flow rates varied from the actual rate by an average of 1.7% and 2.4% for the azimuthal data sets and polar data sets respectively.
Fig. 4.
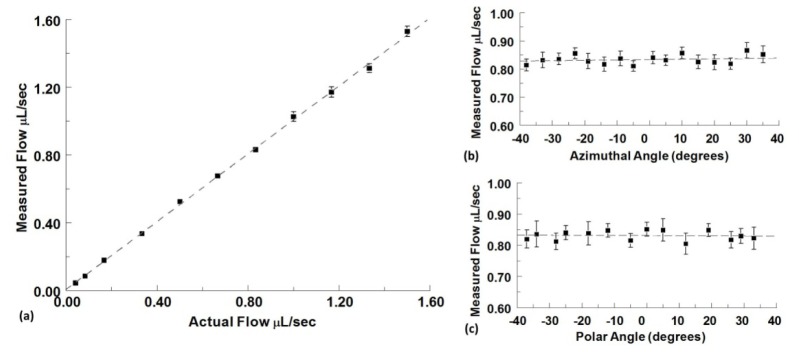
(a) Measured absolute flow in a capillary tube plotted vs actual syringe pump flow rates. Flow rates are represented as mean ± S.D. using the combined results from three independent experiments with 80 imaging frames at each angle. (b) Constant absolute flow measured at different azimuthal angle orientations of the capillary tube phantom at a polar angle of 3°. (c) Constant absolute flow measured at different polar angle orientations of the capillary tube phantom at an azimuthal angle of 5° (the actual syringe pump flow rate is set at 0.83 µl/sec for both angle variation experiments). Flow rates are represented as mean ± S.D. over 80 imaging frames.
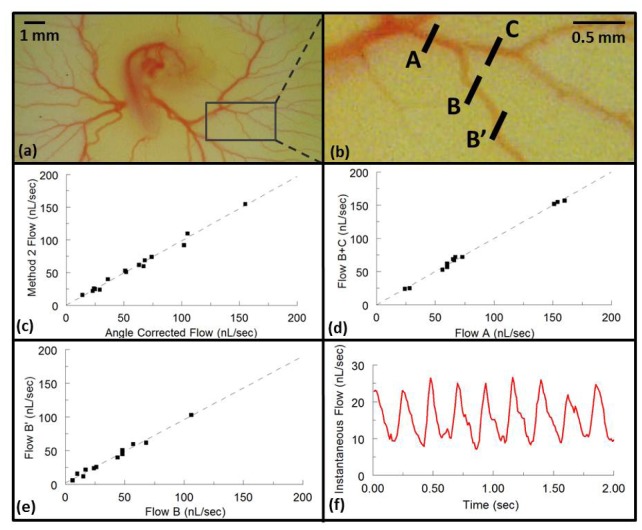
To validate the technique for measuring blood flow in vivo, yolk sac blood vessels from 9 quail embryos at the cardiac looping stage (Fig. 5(a) ) were imaged and the time-averaged flow rates were calculated over 30 heart beats using analysis method 2. These measurements were compared with those obtained by the conventional technique of compensation by measuring vessel orientation from 3-D image volumes. 15 vessels were measured and compared using a scatter plot and a linear regression analysis was performed resulting in a slope of 0.98 (95% confidence intervals 0.92-1.05, R2 = 0.989) (Fig. 5(c)). The majority of the Doppler angles of the selected vessels were around 10-15 degrees so when measured using the conventional 3-D method they did not suffer significantly from the uncertainties described in Fig. 1, so that they could be used as the gold standard for comparison.
Fig. 5.
(a) A representative stage HH18 quail embryo in shell-less culture was removed from the incubator and photographed with a microscope (Dino-Lite, AnMo Electronics Corporation, Torrance, CA) for documentation purposes. (b) Enlarged image marked by a box in (a) of representative imaged vessels. B-scan OCT images were obtained and the resulting data processed to calculate flow using analysis method 2 and by correcting for the Doppler angle measured via 3-D structural volumes for the same cross section. The resulting time-averaged flows are plotted against each other in panel c. B-scan OCT images were also obtained at A, B, and C to measure the time-averaged absolute flow before and after bifurcations. The corresponding flows are shown in panel d. Finally, vessels were imaged at two different positions (B and B’) to confirm consistent time-averaged flow measurements at different vessel positions and orientations. The resulting flows are represented in panel e. (f) A representative pulsatile flow rate is plotted over 8 heart cycles.
Next, 11 embryonic vessels were imaged before and after bifurcations as shown in Fig. 5(b). The sum of the time-averaged flow in the two branch vessels (e.g. position B and C) were plotted against the time-averaged flow in the parent vessel (position A) resulting in a slope of 1.00 (95% confidence intervals 0.96-1.04, R2 = 0.997) (Fig. 5(d)). Fifteen vessels were imaged at two different positions along their length to determine if the time-averaged flow measurement was consistent at different vessel positions and orientations (e.g. Figure 5(b), position B and B’). The linear regression of the comparison resulted in a slope of 0.94 (95% confidence intervals 0.86-1.02, R2 = 0.985) (Fig. 5(e)). The variance observed in these three experiments can be explained by small biological variability, such as heart rate, during the imaging session. In addition to determining the average flow rate, the pulsatile flow rate profile can be obtained with high temporal resolution across the duration of multiple heart beats (Fig. 5(f)). Due to the fact that only a single B-scan is needed to measure the flow, the instantaneous flow rate can be determined at any point during the heart cycle allowing for the observation of systolic and diastolic dynamics without the need for real-time volumetric imaging.
4. Discussion
To generate two beams at different angles of incidence we utilized delay encoding. Delay encoding is a simple technique that can be applied to almost any free-space OCT scanner with little difficulty, simply by adding one optical element. This technique also ensures the two sub-beams are perfectly aligned at the focus, greatly simplifying alignment compared to other dual-beam approaches. However, this method does have some potential draw backs, one of which is ensuring that the OCT system has enough axial imaging range to be capable of capturing all three images simultaneously. The pathlength delay caused by a glass plate of thickness D and index n produces the three images spaced by a distance D(n-1)/2. This limitation becomes more serious if a vascular network over a range of depth is imaged, requiring longer separation between sub-images. The insertion of the glass plate could potentially generate a dispersion mismatch between the three sub-beams. However, the OCT system used did not have an exceptionally wide bandwidth and by our observation, the dispersion of the glass did not significantly influence the three images. Another limitation of delay encoding is the loss of sensitivity. The light is being broken into four different paths. The top and bottom satellite images, as shown in Fig. 2(b), are each resulting from 25% of the original incident light, while the center image results from 50% of the incident light. Less light results in less sensitivity and less depth penetration for each slice. This could be compensated by increasing the total light, however for some applications, such as retinal imaging, maximum exposure limits cannot be exceeded. Alternatively, other techniques which generate two imaging beams simultaneously could be used to calculate flow with less loss of light (50% instead of 25%). The analysis presented here could readily be applied to any technique that generates two properly-aligned illumination beams. It should be noted that even low-SNR OCT images can provide reasonably strong Doppler OCT signals, so this is not a strong limitation. Decreased SNR will increase phase noise which may decrease the precision of the flow measurements at larger angles where the phase difference becomes smaller, but this should not introduce bias, affecting accuracy.
Two methods for calculating instantaneous flow rates were presented here. The straightforward analysis expressed in Eq. (6) assumes a pixel by pixel correspondence of the two acquired images. However, this relies on the assumption that the two cross sectional images are interrogating exactly the same slice of the vessel, which is not true because of the angular separation between the probe beams. Two potential problems arise from this difference. The first is that the cross sectional area of the two slices can be different sizes. Secondly, the locations being interrogated are not necessarily identical between the two slices. The error these differences introduce is negligible at small Doppler angles, but quickly causes large overestimations of flow at larger angles as shown in Fig. 3(a). In addition, simulation results indicate that this overestimation is independent of the beam separation or the size of the vessel, therefore reducing the dual beam angle separation or imaging smaller vessels will not solve the problem.
The first way we overcame this error (Method 1) was to compensate for the influence of the different cross sectional areas on the flow by finding the mean velocities and projecting them onto a single cross-sectional area. This method assumes that the flow in the tube is in a single direction and that the tube is rigid. This method proved to be accurate over a wide range of Doppler angles in the flow phantom, and it may work reasonable well even when these conditions are not strictly met.
Although method 1 was shown to be accurate and reasonably precise, its reliance on the mean velocity is susceptible to segmentation errors, which decreases its precision (6.4% error in the phantom) compared with method 2 (2.7% error in the phantom). It can be seen in Fig. 3(b) that the error in method 1 is higher than method 2, and the errors are worse at higher angles. A small change the apparent area of either cross section, as measured by segmentation, will directly influence the mean velocities and . Since the mean velocities are already close to one another, small errors will strongly propagate to the final flow calculation. For example, under a typical polar angle of 20°, a small segmentation inaccuracy around the vessel border (1% size change of the segmented area) can result in a 3.2% error in flow measurement. This inaccuracy increases with higher polar angles such that at an angle of 40 degrees the flow measurement could have an estimated error of up to 7.4%. This susceptibility to segmentation errors could become problematic for biological applications where the vessel boundary is more difficult to discern, and therefore difficult to measure by automated segmentation.
Method 2 approaches the flow measurement from a different direction. It does not require the assumption that the two measured images interrogate the identical slice, nor does it involve dividing by a measured cross-section area. This analysis is equally accurate as the other method and is very resistant to segmentation errors and therefore was used for the majority of validation work presented here. With method 2, a 1% area segmentation inaccuracy only results in a 0.1% error in the flow calculation. This resistance to segmentation errors originates from method 2 utilizing the summed velocities to determine the flow rather than the mean velocity. Segmentation errors tend to occur at the boundary of the vessel affecting the pixels with the smallest velocities. This segmentation error therefore has minimum impact on the summed velocities. The resistance of analysis method 2 to segmentation errors may allow the use of less computationally expensive segmentation approaches.
The primary limitation of method 2 is that is generates two solutions for a given measurement. For most cases it is straightforward to determine which of the solutions represents the correct flow measurement. The two flow rate solutions each also have an associated Doppler angle solution, and the two angles sum to 90°. Most applications of OCT blood flow imaging involve imaging vascular networks near tissue surfaces, which are nearly perpendicular to the imaging beam. Therefore, the solution with the larger angle will nearly always be the correct one. When the vessel being imaged approaches 45°, the two solutions and angles become very close to each other to the point that it becomes difficult to determine the correct one. In these cases, method 2 could be used to determine the flow, or a priori information may be obtainable to resolve the ambiguity. Occasionally, at angles near 45°, the solutions can be complex values due to noise in the measurements. This is due to the fact that when the two solutions are close to one another, the discriminant becomes very small, and therefore more susceptible to noise. In these rare occurrences we found that using the real component of the complex solution was a reasonable estimate.
Both methods rely on the assumptions that the vessel is rigid and that flow in the vessel is in one direction. The rigidity assumption guarantees that the flow is constant across both imaging planes, and the single-direction assumption is implicit when velocities are averaged in method 1, and is assumed in the formulation of method 2. However, these assumptions cannot always be met in biological applications where vessels can be tortuous. In these situations, the parallel assumption will be violated and will result in a small error for both methods. Using our simulated data, under a typical Doppler angle with a 3cm radius of curvature, the error resulting from the curvature is usually no more than 2% for both methods. The solution to minimize such errors is to keep the vessel of interest at the focus, thus minimizing the physical separation of the two imaging planes and the curvature between the two planes. The assumption that the vessel is rigid is generally valid on the time-scale and spatial scale of OCT imaging.
An additional assumption for the method presented here is that the plane formed by the two imaging beams is orthogonal to the B-scan direction. This orientation can easily be ensured by adjusting the position of the glass plate in the imaging beam when raster scanning patterns are used. Alternative scanning patterns such as circular or helical scanning are more challenging to ensure the two planes remain orthogonal to one another. A potential solution could involve rotating the glass within the sample arm in synchronization with the rotation of the B-scan, as has been previously demonstrated with a rotational Dove prism [35].
The method presented here relies on accurate calculation of the transverse velocity by the difference of two slightly angled Doppler images. This difference decreases with both increasing polar and azimuthal angles. The increasing angle results in a larger cross sectional area of the vessel, and therefore requiring a larger field of view. Additionally, the decreasing difference between the two Doppler images brings the value closer to the phase noise at higher angles. At larger polar angles where these issues become problematic, the original en-face method [36] would be a valid alternative for the determination of absolute flow. At larger azimuthal angles if the difference between the two sub-images approaches the phase noise, the scanning direction can be rotated 90 degrees to eliminate this problem.
Recently, Blatter et al have independently demonstrated an angle-independent method for measurement of absolute flow in retinal blood vessels using a very similar dual-angle Doppler OCT system [43]. That approach made use of two parallel beams that are focused on the same spot on the retina with a known angular separation, and are interrogated by two parallel interferometers. These two interferometers generate two separate images with different Doppler shifts that are used to calculate flow using a method equivalent to what we described here as method 1. The measurements were validated by use of a capillary tube phantom perfused at a constant flow rate by a syringe pump. The velocity and flow were measured at various capillary tube orientations demonstrating the angle independence of the measurements. Measurements of velocity and flow were also demonstrated in vivo by measuring blood flow in a retinal artery. The measurements were averaged over one cardiac cycle and resulted in consistent flow measurements at various locations along the length of the artery at different vessel orientations. The technology presented by Blatter et al is very similar to the technology presented here, and results in an equivalent measurement. Both studies found the measurements to be valid and repeatable and provide strong support for the feasibility of orientation-independent measurement of absolute flow in small vessels using dual-angle Doppler OCT systems.
While this work made use of a spectral-domain OCT (SDOCT) system, the technique is equally applicable to swept-source (SSOCT) or time-domain OCT (TDOCT). In fact SSOCT and TDOCT are less limited by the significant axial range needed for delay encoding. The instrument used in this work was configured such that the sub-image separation distance was 0.625 mm. While sufficient for some applications, other target tissues may require a longer separation. In any particular case, the axial range of the OCT system must be long enough to accommodate the three sub-images. If the third sub-image is attenuated significantly by roll-off, then the phase noise will not be the same as the first sub-image. Additionally, in the case of inadequate separation distances, the static tissue from one of the three sub-images may overlap with the vessel cross section of another sub-image. Both the attenuation caused by the roll-off and the image overlap would be expected to increase noise, but not necessarily to bias the velocity or flow measurement. The technique is also not limited by choice of Doppler OCT processing algorithm. Any method that produces an accurate estimation of Doppler shift is sufficient.
The results of the validation experiments indicate that our proposed technique of orientation-independent absolute blood flow measurement using dual-angle Doppler OCT is accurate and robust. The measurement errors determined by the phantom experiments are very low compared to biological variability, so the technique is very applicable to in vivo experimentation. In vivo validation results indicate that accurate absolute flow can be obtained rapidly from single B-scans of microvasculature, including flow pulsatility. This technique will enable us to objectively assay hemodynamics in experimental models of congenital heart disease. Measurement of flow rates with high temporal resolution over multiple heartbeats will allow for the examination of beat to beat differences that may result from arrhythmias.
The technology presented here could also be applied to OCT imaging of retinal vasculature. OCT is already an important clinical tool for diagnosing retinal disease [44, 45]. Decreased retinal and choroidal blood flow has been shown to correlate with age related macular degeneration [46–48]. Glaucoma and diabetic macular edema have been shown to correlate with alterations to blood flow as well [49–52]. Incorporation of the flow measurement technique described here will allow for more precise real-time measurement of retinal blood flow.
In conclusion, we have demonstrated a Doppler OCT technique for absolute blood flow measurement that eliminates the need for volumetric data acquisition or vessel angle knowledge, allowing for rapid flow measurements from single B-scans. The rapid nature of this technique allows for visualization and measurement of pulsatile flow throughout the heart beat without the need for gating techniques or real-time volumetric imaging. The rapid nature and relative ease of implementation of the technique presented here may prove to be a powerful tool for future investigations of the role of blood flow in a variety of vascular models.
Acknowledgments
This research is supported in part by the National Institutes of Health (RO1HL083048, R01HL095717, R21-HL115373), the Ohio Wright Center of Innovation and Biomedical Research and Technology Transfer award: “The Biomedical Structure, Functional and Molecular Imaging Enterprise,” and the Interdisciplinary Biomedical Imaging Training Program NIH T32EB007509. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Heart, Lung, and Blood Institute or the National Institutes of Health.
References and links
- 1.Hogers B., DeRuiter M. C., Gittenberger-de Groot A. C., Poelmann R. E., “Extraembryonic venous obstructions lead to cardiovascular malformations and can be embryolethal,” Cardiovasc. Res. 41(1), 87–99 (1999). 10.1016/S0008-6363(98)00218-1 [DOI] [PubMed] [Google Scholar]
- 2.Broekhuizen M. L. A., Hogers B., DeRuiter M. C., Poelmann R. E., Gittenberger-de Groot A. C., Wladimiroff J. W., “Altered hemodynamics in chick embryos after extraembryonic venous obstruction,” Ultrasound Obstet. Gynecol. 13(6), 437–445 (1999). 10.1046/j.1469-0705.1999.13060437.x [DOI] [PubMed] [Google Scholar]
- 3.Hove J. R., Köster R. W., Forouhar A. S., Acevedo-Bolton G., Fraser S. E., Gharib M., “Intracardiac fluid forces are an essential epigenetic factor for embryonic cardiogenesis,” Nature 421(6919), 172–177 (2003). 10.1038/nature01282 [DOI] [PubMed] [Google Scholar]
- 4.Reckova M., Rosengarten C., deAlmeida A., Stanley C. P., Wessels A., Gourdie R. G., Thompson R. P., Sedmera D., “Hemodynamics is a key epigenetic factor in development of the cardiac conduction system,” Circ. Res. 93(1), 77–85 (2003). 10.1161/01.RES.0000079488.91342.B7 [DOI] [PubMed] [Google Scholar]
- 5.Hove J. R., Köster R. W., Forouhar A. S., Acevedo-Bolton G., Fraser S. E., Gharib M., “Intracardiac fluid forces are an essential epigenetic factor for embryonic cardiogenesis,” Nature 421(6919), 172–177 (2003). 10.1038/nature01282 [DOI] [PubMed] [Google Scholar]
- 6.Groenendijk B. C. W., Hierck B. P., Vrolijk J., Baiker M., Pourquie M. J. B. M., Gittenberger-de Groot A. C., Poelmann R. E., “Changes in Shear Stress-Related Gene Expression After Experimentally Altered Venous Return in the Chicken Embryo,” Circ. Res. 96(12), 1291–1298 (2005). 10.1161/01.RES.0000171901.40952.0d [DOI] [PubMed] [Google Scholar]
- 7.Azuma N., Duzgun S. A., Ikeda M., Kito H., Akasaka N., Sasajima T., Sumpio B. E., “Endothelial cell response to different mechanical forces,” J. Vasc. Surg. 32(4), 789–794 (2000). 10.1067/mva.2000.107989 [DOI] [PubMed] [Google Scholar]
- 8.Dekker R. J., van Soest S., Fontijn R. D., Salamanca S., de Groot P. G., VanBavel E., Pannekoek H., Horrevoets A. J. G., “Prolonged fluid shear stress induces a distinct set of endothelial cell genes, most specifically lung Krüppel-like factor (KLF2),” Blood 100(5), 1689–1698 (2002). 10.1182/blood-2002-01-0046 [DOI] [PubMed] [Google Scholar]
- 9.Yashiro K., Shiratori H., Hamada H., “Haemodynamics determined by a genetic programme govern asymmetric development of the aortic arch,” Nature 450(7167), 285–288 (2007). 10.1038/nature06254 [DOI] [PubMed] [Google Scholar]
- 10.Poelmann R. E., Gittenberger-de Groot A. C., Hierck B. P., “The development of the heart and microcirculation: role of shear stress,” Med. Biol. Eng. Comput. 46(5), 479–484 (2008). 10.1007/s11517-008-0304-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Vermot J., Forouhar A. S., Liebling M., Wu D., Plummer D., Gharib M., Fraser S. E., “Reversing Blood Flows Act Through Klf2a to Ensure Normal Valvulogenesis in the Developing Heart,” PLoS Biol. 7(11), e1000246 (2009). 10.1371/journal.pbio.1000246 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Jenkins M. W., Adler D. C., Gargesha M., Huber R., Rothenberg F., Belding J., Watanabe M., Wilson D. L., Fujimoto J. G., Rollins A. M., “Ultrahigh-speed optical coherence tomography imaging and visualization of the embryonic avian heart using a buffered Fourier Domain Mode Locked laser,” Opt. Express 15(10), 6251–6267 (2007). 10.1364/OE.15.006251 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Jenkins M. W., Peterson L., Gu S., Gargesha M., Wilson D. L., Watanabe M., Rollins A. M., “Measuring hemodynamics in the developing heart tube with four-dimensional gated Doppler optical coherence tomography,” J. Biomed. Opt. 15(6), 066022 (2010). 10.1117/1.3509382 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Jenkins M. W., Watanabe M., Rollins A. M., “Longitudinal Imaging of Heart Development With Optical Coherence Tomography,” IEEE J. Sel. Top. Quantum Electron. 18(3), 1166–1175 (2012). 10.1109/JSTQE.2011.2166060 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Peterson L. M., Jenkins M. W., Gu S., Barwick L., Watanabe M., Rollins A. M., “4D shear stress maps of the developing heart using Doppler optical coherence tomography,” Biomed. Opt. Express 3(11), 3022–3032 (2012). 10.1364/BOE.3.003022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Liu A., Yin X., Shi L., Li P., Thornburg K. L., Wang R., Rugonyi S., “Biomechanics of the Chick Embryonic Heart Outflow Tract at HH18 Using 4D Optical Coherence Tomography Imaging and Computational Modeling,” PLoS ONE 7(7), e40869 (2012). 10.1371/journal.pone.0040869 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Chen Z., Milner T. E., Srinivas S., Wang X., Malekafzali A., van Gemert M. J. C., Nelson J. S., “Noninvasive imaging of in vivo blood flow velocity using optical Doppler tomography,” Opt. Lett. 22(14), 1119–1121 (1997). 10.1364/OL.22.001119 [DOI] [PubMed] [Google Scholar]
- 18.Izatt J. A., Kulkarni M. D., Yazdanfar S., Barton J. K., Welch A. J., “In vivo bidirectional color Doppler flow imaging of picoliter blood volumes using optical coherence tomography,” Opt. Lett. 22(18), 1439–1441 (1997). 10.1364/OL.22.001439 [DOI] [PubMed] [Google Scholar]
- 19.Yazdanfar S., Rollins A. M., Izatt J. A., “Imaging and velocimetry of the human retinal circulation with color Doppler optical coherence tomography,” Opt. Lett. 25(19), 1448–1450 (2000). 10.1364/OL.25.001448 [DOI] [PubMed] [Google Scholar]
- 20.Liu G., Lin A. J., Tromberg B. J., Chen Z., “A comparison of Doppler optical coherence tomography methods,” Biomed. Opt. Express 3(10), 2669–2680 (2012). 10.1364/BOE.3.002669 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Davis A., Izatt J., Rothenberg F., “Quantitative Measurement of Blood Flow Dynamics in Embryonic Vasculature Using Spectral Doppler Velocimetry,” Anat. Rec. (Hoboken) 292(3), 311–319 (2009). 10.1002/ar.20808 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Li P., Yin X., Shi L., Rugonyi S., Wang R. K., “In vivo functional imaging of blood flow and wall strain rate in outflow tract of embryonic chick heart using ultrafast spectral domain optical coherence tomography,” J. Biomed. Opt. 17(9), 096006 (2012). 10.1117/1.JBO.17.9.096006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wang Y., Bower B. A., Izatt J. A., Tan O., Huang D., “In vivo total retinal blood flow measurement by Fourier domain Doppler optical coherence tomography,” J. Biomed. Opt. 12(4), 041215 (2007). 10.1117/1.2772871 [DOI] [PubMed] [Google Scholar]
- 24.Baumann B., Potsaid B., Kraus M. F., Liu J. J., Huang D., Hornegger J., Cable A. E., Duker J. S., Fujimoto J. G., “Total retinal blood flow measurement with ultrahigh speed swept source/Fourier domain OCT,” Biomed. Opt. Express 2(6), 1539–1552 (2011). 10.1364/BOE.2.001539 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Michaely R., Bachmann A. H., Villiger M. L., Blatter C., Lasser T., Leitgeb R. A., “Vectorial reconstruction of retinal blood flow in three dimensions measured with high resolution resonant Doppler Fourier domain optical coherence tomography,” J. Biomed. Opt. 12(4), 041213 (2007). 10.1117/1.2771553 [DOI] [PubMed] [Google Scholar]
- 26.Makita S., Fabritius T., Yasuno Y., “Quantitative retinal-blood flow measurement with three-dimensional vessel geometry determination using ultrahigh-resolution Doppler optical coherence angiography,” Opt. Lett. 33(8), 836–838 (2008). 10.1364/OL.33.000836 [DOI] [PubMed] [Google Scholar]
- 27.Wang Y., Bower B. A., Izatt J. A., Tan O., Huang D., “Retinal blood flow measurement by circumpapillary Fourier domain Doppler optical coherence tomography,” J. Biomed. Opt. 13(6), 064003 (2008). 10.1117/1.2998480 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wang Y., Lu A., Gil-Flamer J., Tan O., Izatt J. A., Huang D., “Measurement of total blood flow in the normal human retina using Doppler Fourier-domain optical coherence tomography,” Br. J. Ophthalmol. 93(5), 634–637 (2009). 10.1136/bjo.2008.150276 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hwang J. C., Konduru R., Zhang X., Tan O., Francis B. A., Varma R., Sehi M., Greenfield D. S., Sadda S. R., Huang D., “Relationship among Visual Field, Blood Flow, and Neural Structure Measurements in Glaucoma,” Invest. Ophthalmol. Vis. Sci. 53(6), 3020–3026 (2012). 10.1167/iovs.11-8552 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Davé D. P., Milner T. E., “Doppler-angle measurement in highly scattering media,” Opt. Lett. 25(20), 1523–1525 (2000). 10.1364/OL.25.001523 [DOI] [PubMed] [Google Scholar]
- 31.Pedersen C. J., Huang D., Shure M. A., Rollins A. M., “Measurement of absolute flow velocity vector using dual-angle, delay-encoded Doppler optical coherence tomography,” Opt. Lett. 32(5), 506–508 (2007). 10.1364/OL.32.000506 [DOI] [PubMed] [Google Scholar]
- 32.Ahn Y.-C., Jung W., Chen Z., “Quantification of a three-dimensional velocity vector using spectral-domain Doppler optical coherence tomography,” Opt. Lett. 32(11), 1587–1589 (2007). 10.1364/OL.32.001587 [DOI] [PubMed] [Google Scholar]
- 33.Iftimia N. V., Hammer D. X., Ferguson R. D., Mujat M., Vu D., Ferrante A. A., “Dual-beam Fourier domain optical Doppler tomography of zebrafish,” Opt. Express 16(18), 13624–13636 (2008). 10.1364/OE.16.013624 [DOI] [PubMed] [Google Scholar]
- 34.Werkmeister R. M., Dragostinoff N., Pircher M., Götzinger E., Hitzenberger C. K., Leitgeb R. A., Schmetterer L., “Bidirectional Doppler Fourier-domain optical coherence tomography for measurement of absolute flow velocities in human retinal vessels,” Opt. Lett. 33(24), 2967–2969 (2008). 10.1364/OL.33.002967 [DOI] [PubMed] [Google Scholar]
- 35.Blatter C., Coquoz S., Grajciar B., Singh A. S. G., Bonesi M., Werkmeister R. M., Schmetterer L., Leitgeb R. A., “Dove prism based rotating dual beam bidirectional Doppler OCT,” Biomed. Opt. Express 4(7), 1188–1203 (2013). 10.1364/BOE.4.001188 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Srinivasan V. J., Sakadzić S., Gorczynska I., Ruvinskaya S., Wu W., Fujimoto J. G., Boas D. A., “Quantitative cerebral blood flow with Optical Coherence Tomography,” Opt. Express 18(3), 2477–2494 (2010). 10.1364/OE.18.002477 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Choi W., Baumann B., Liu J. J., Clermont A. C., Feener E. P., Duker J. S., Fujimoto J. G., “Measurement of pulsatile total blood flow in the human and rat retina with ultrahigh speed spectral/Fourier domain OCT,” Biomed. Opt. Express 3(5), 1047–1061 (2012). 10.1364/BOE.3.001047 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Schmoll T., Leitgeb R. A., “Heart-beat-phase-coherent Doppler optical coherence tomography for measuring pulsatile ocular blood flow,” J. Biophotonics 6(3), 275–282 (2013). 10.1002/jbio.201200029 [DOI] [PubMed] [Google Scholar]
- 39.Gargesha M., Jenkins M. W., Wilson D. L., Rollins A. M., “High temporal resolution OCT using image-based retrospective gating,” Opt. Express 17(13), 10786–10799 (2009). 10.1364/OE.17.010786 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Miura M., Makita S., Iwasaki T., Yasuno Y., “An Approach to Measure Blood Flow in Single Choroidal Vessel Using Doppler Optical Coherence Tomography,” Invest. Ophthalmol. Vis. Sci. 53(11), 7137–7141 (2012). 10.1167/iovs.12-10666 [DOI] [PubMed] [Google Scholar]
- 41.Hu Z., Rollins A., “Quasi-telecentric optical design of a microscope-compatible OCT scanner,” Opt. Express 13(17), 6407–6415 (2005). 10.1364/OPEX.13.006407 [DOI] [PubMed] [Google Scholar]
- 42.Hu Z., Rollins A. M., “Fourier domain optical coherence tomography with a linear-in-wavenumber spectrometer,” Opt. Lett. 32(24), 3525–3527 (2007). 10.1364/OL.32.003525 [DOI] [PubMed] [Google Scholar]
- 43.Blatter C., Grajciar B., Schmetterer L., Leitgeb R. A., “Angle independent flow assessment with bidirectional Doppler optical coherence tomography,” Opt. Lett. 38(21), 4433–4436 (2013). 10.1364/OL.38.004433 [DOI] [PubMed] [Google Scholar]
- 44.Jaffe G. J., Caprioli J., “Optical coherence tomography to detect and manage retinal disease and glaucoma,” Am. J. Ophthalmol. 137(1), 156–169 (2004). 10.1016/S0002-9394(03)00792-X [DOI] [PubMed] [Google Scholar]
- 45.Jindahra P., Hedges T. R., Mendoza-Santiesteban C. E., Plant G. T., “Optical coherence tomography of the retina: applications in neurology,” Curr. Opin. Neurol. 23(1), 16–23 (2010). 10.1097/WCO.0b013e328334e99b [DOI] [PubMed] [Google Scholar]
- 46.Friedman E., Krupsky S., Lane A. M., Oak S. S., Friedman E. S., Egan K., Gragoudas E. S., “Ocular Blood Flow Velocity in Age-Related Macular Degeneration,” Ophthalmology 102(4), 640–646 (1995). 10.1016/S0161-6420(95)30974-8 [DOI] [PubMed] [Google Scholar]
- 47.Remsch H., Spraul C. W., Lang G. K., Lang G. E., “Changes of retinal capillary blood flow in age-related maculopathy,” Graefes Arch. Clin. Exp. Ophthalmol. 238(12), 960–964 (2000). 10.1007/s004170000202 [DOI] [PubMed] [Google Scholar]
- 48.Boltz A., Luksch A., Wimpissinger B., Maar N., Weigert G., Frantal S., Brannath W., Garhöfer G., Ergun E., Stur M., Schmetterer L., “Choroidal Blood Flow and Progression of Age-Related Macular Degeneration in the Fellow Eye in Patients with Unilateral Choroidal Neovascularization,” Invest. Ophthalmol. Vis. Sci. 51(8), 4220–4225 (2010). 10.1167/iovs.09-4968 [DOI] [PubMed] [Google Scholar]
- 49.Flammer J., “The vascular concept of glaucoma,” Surv. Ophthalmol. 38(Suppl), S3–S6 (1994). 10.1016/0039-6257(94)90041-8 [DOI] [PubMed] [Google Scholar]
- 50.Flammer J., Orgül S., Costa V. P., Orzalesi N., Krieglstein G. K., Serra L. M., Renard J.-P., Stefánsson E., “The impact of ocular blood flow in glaucoma,” Prog. Retin. Eye Res. 21(4), 359–393 (2002). 10.1016/S1350-9462(02)00008-3 [DOI] [PubMed] [Google Scholar]
- 51.Sakata K., Funatsu H., Harino S., Noma H., Hori S., “Relationship between Macular Microcirculation and Progression of Diabetic Macular Edema,” Ophthalmology 113(8), 1385–1391 (2006). 10.1016/j.ophtha.2006.04.023 [DOI] [PubMed] [Google Scholar]
- 52.Landa G., Amde W., Haileselassie Y., Rosen R. B., “Cilioretinal Arteries in Diabetic Eyes Are Associated With Increased Retinal Blood Flow Velocity and Occurrence of Diabetic Macular Edema,” Retina 31(2), 304–311 (2011). 10.1097/IAE.0b013e3181e91108 [DOI] [PubMed] [Google Scholar]