Measurement of the total retinal blood flow using dual beam Fourier-domain Doppler optical coherence tomography with orthogonal detection planes

Abstract

We present a system capable of measuring the total retinal blood flow using a combination of dual beam Fourier-domain Doppler optical coherence tomography with orthogonal detection planes and a fundus camera-based retinal vessel analyzer. Our results show a high degree of conformity of venous and arterial flows, which corroborates the validity of the measurements. In accordance with Murray’s law, the log-log regression coefficient between vessel diameter and blood flow was found to be ~3. The blood’s velocity scaled linearly with the vessel diameter at higher diameters (> 60 µm), but showed a clear divergence from the linear dependence at lower diameters. Good agreement with literature data and the large range and high measurement sensitivity point to a high potential for further investigations.

1. Introduction

The research on non-invasive methods to quantify the total retinal blood flow has seen increased attention in the last years. As a number of common causes of blindness, such as diabetic retinopathy, glaucoma, and macular degeneration, go hand in hand with abnormalities of the retinal perfusion, advances in this field are eagerly awaited [1, 2].

Besides methods such as laser Doppler flowmetry, laser Doppler velocimetry and fluorescence angiography, Doppler optical coherence tomography (OCT) has found firm footing as suitable, non-invasive approach to measuring the total retinal blood flow. Doppler OCT uses the phase shift between reference- and sample-beam of a low-coherence interferometer to gain information on the flow velocities and to achieve high-resolution cross-sectional images.

Extending the method to Fourier domain OCT (FD-OCT) allows measuring a full depth profile at once, without having to change the reference arm length. Among the first to use Doppler FD-OCT for measuring blood flow were Leitgeb et al.; they used a single-beam color Doppler Fourier domain OCT (FD-OCT) system to measure in vitro velocity profiles for human blood flowing through glass capillaries [3] and to determine velocity profiles in human retinal vessels in vivo [4].

The drawback of single-beam systems is that they are dependent on the, usually unknown, Doppler angle, i.e. the angle between measurement beam and vessel. This issue can be addressed by several different methods. One approach is to divide a single OCT beam into two components which illuminate the vessel under different angles. By delaying a part of the beam with a glass plate (e.g. Pedersen et al. [5]), the two components with different angles can be detected individually. By aligning the incidence plane with the blood vessel, absolute velocity values can be achieved. Another approach, also using one beam, is to determine the vessels’ angle from two separate cross-sectional scans at different but close positions along the vessel. This was done e.g. by Wang et al. [6], who measured total venous blood flow in the human retina by scanning around the optic nerve head (ONH) in two concentric circles. An alternative method that avoids acquiring two scans was suggested by Singh et al by tracking circular scans within a reference volume [7]. In principle, the vessel orientations could be extracted in post processing from recorded volumes [8, 9]. However, these methods are calculation intensive and suffer from angle errors that critically affect the precision of velocity determination especially for large Doppler angles. A further method to avoid dependence on the Doppler angle was proposed by Srinivasan et al. [10]: although the velocity was measured only in direction of a fixed single beam, the authors were able to calculate the flow by integrating the velocity over the vessels’ en-face cross section. As the latter scales with the Doppler angle oppositely to the velocity, the dependence cancels itself out and the total flow can be determined. Baumann et al. [11] applied this method to the determination of the total retinal blood flow in the human retina using an ultrahigh speed swept source Doppler FD-OCT. Schmoll and Leitgeb [12] later extended the method to reconstruct heart-beat-phase-coherent volumes and, thus, carry out quantitative time-resolved flow analysis by implementing a pulse oximeter. The drawback of this method, however, is that the velocity cannot be measured when the beam is perpendicular to the vessel, which is the case in most parts of the retina (with exception of the ONH).

A different approach to eliminating the dependence on the Doppler angle is the introduction of a second beam, i.e. a dual beam system: by focusing both beams onto one point in the sample, the measurement’s dependence on the unknown angle in the plane of the beams is eliminated. A second advantage of dual-beam systems is that at least one beam is not perpendicular to the vessel: if a single beam falls perpendicularly onto a vessel, the velocity component in beam direction is zero and the velocity cannot be determined. With the two distinct angles of a dual beam system, at least one velocity component is always non-zero. Among the first to use dual beam Doppler FD-OCT for blood flow measurements were Iftimia et al. [13], who measured blood flow and structure of zebrafish larvae. Werkmeister et al. [14] were the first to demonstrate the capability of measuring absolute flow velocities in vivo in the human retina using a dual-beam Doppler FD-OCT system.

Although bidirectional Doppler OCT is not dependent on the Doppler angle, it still depends on the en-face angle. In a recent paper, Blatter et al. [15] presented a dual beam swept-source Doppler OCT system with a rotating scanning scheme using a dove prism, which allows for a rapid absolute velocity extraction of the major vessels around the ONH. In this case, the en-face angle was assumed to be neglectable, as vessels are almost radially oriented in proximity of the optic nerve head, and the circular scanning pattern thus allowed them to be crossed perpendicularly. In analogy to the en-face method mentioned above [10], Blatter et al. [16] were able to calculate absolute flow values from Doppler OCT tomograms without any additional measurements of the vessel’s en-face orientation. A different approach to making the flow measurement independent of additional measurements of the en-face angle was adopted by Trasischker et al [17]: they reported first results with a triple-beam system, which allows measuring the absolute flow velocity without any additional information on the vessel’s orientation – the system’s drawback, however, is the high complexity of the alignment procedure.

In this paper, we describe a dual beam system incorporating a fundus camera-based retinal vessel analyzer, which allows an exact determination of the vessel diameters concomitantly with the OCT measurements. The particular feature of our system is that the detection plane can be oriented both horizontally and vertically, allowing the absolute blood flow velocity of all retinal vessels exiting or entering the eye to be measured. This setup offers the possibility to measure the total retinal blood flow reliably and promises a high potential for the study of flow abnormalities in patients with ocular diseases.

2. Methods

2.1 Dual beam Doppler Fourier-domain OCT

The measurements were performed with a dual beam Doppler FD-OCT system, based on a setup published previously [14, 18]. The system uses two beams with different polarization states and wave vectors k _i (i = 1,2), passing through an interferometer. The beams in the interferometer’s sample arm are focused onto the specimen (i.e. the retina) with an angle Δα between each other. Using two beams eliminates the single-beam setups’ dependence on the unknown angle γ, as long as γ ≈90°, which is the case when measuring vessels in the posterior pole of the eye (see Fig. 1 ).

Fig. 1.

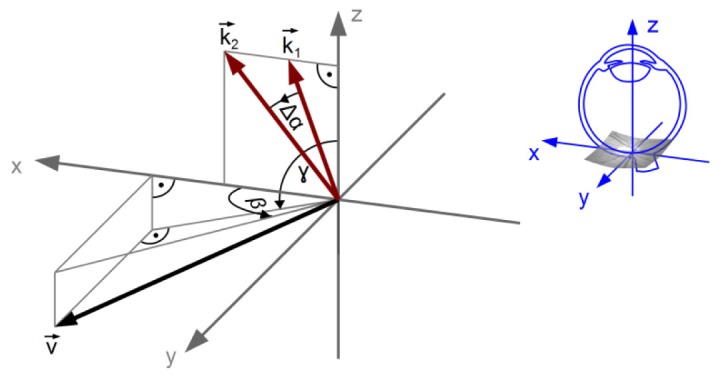
Schematic image of the vessel’s velocity vector v, the beam’s wave vectors k ₁ and k ₂ and the angles Δα, β and γ

With two identical spectrometers, the spectra of the two channels are detected as a function of frequency. Where the beams fall onto moving red blood cells (RBCs), their phase Φ _i is Doppler-shifted, resulting in a phase shift of ΔΦ _i = 2τ k _i·v _i, in which τ is the camera’s line rate and v _i is the RBCs’ velocity. This phase shift is obtained, in the experiment presented, from adjacent A-scans by Fourier-transforming the detected signal – thus giving the complex depth information – and then extracting the phase information. As derived from Riva’s equations [19] by Werkmeister [14], the absolute flow velocity can be given as

$$v=\Delta \Phi \cdot \frac{{\lambda }_0}{4\pi n\tau \cdot \cos \beta \cdot \Delta \alpha },$$ (1)

where ΔΦ = ΔΦ ₁ – ΔΦ ₂ is the phase difference between the two beams, λ ₀ = 838.8 nm is the light source’s central wavelength and n = 1.37 is the refractive index of blood at 840 nm [20]. The camera’s line rate τ was set to 27 µs for vessels with diameters above 65 µm and to 82 µs for smaller vessels. β is the angle of the vessel’s velocity vector to the plane spanned by k ₁ and k ₂. The beam separation at the pupil is 2.34 mm; however, the angle between the beams Δα depends not only on the beam separation but also on the eye length and the ametropia values (e.g. with an eye length of 24.2 mm from the physiological model [21] and no ametropia, Δα = 5.5°). For our calculations, the value was adapted to account for each subject’s eye length and ametropia (see section 2.4). As can be seen from Eq. (1), vessels perpendicular to the detection plane (β = 90°) cannot be measured with only a certain detection plane.

2.2 Experimental setup

The setup operates at a central wavelength of 838.8 nm and a spectral bandwidth (FWHM) of 54.0 nm. The power of the two probe beams on the cornea was measured to be 700 µW, which is below the limits of the safety norm EN 60825-1 [22].

As mentioned above, the instrument is based on a previously published setup [14], in which both beams use the same reference arm. However, several modifications were added (Fig. 2 ): first, the OCT-setup was integrated into a Dynamic Vessel Analyzer (DVA, Imedos Systems UG, Jena, Germany). This system comprises a modified fundus camera (FF450plus; Carl Zeiss Meditec AG, Jena, Germany) and a special measuring CCD camera with hard- and software units of the DVA for vessel analysis. The OCT beams are coupled into the DVA using a hot mirror (HM, Edmund Optics, NT64-471), which lets the DVA’s lighting pass unimpeded while redirecting the infrared OCT beams into the beam path. This combination has two advantages, namely that the DVA’s fundus view enables precise positioning of the OCT beams on the ocular fundus and that the DVA-software permits determining the vessel diameters with high accuracy [23] within the OCT measurement session.

Fig. 2.

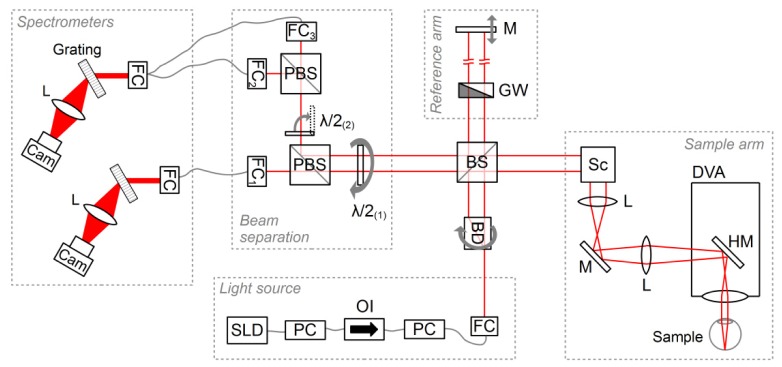
Experimental setup with superluminescent diode (SLD), polarization controllers (PC), optical isolator (OI), fiber couplers (FC_i), beam displacer (BD), polarizing and non-polarizing beam splitters (PBS and BS, respectively), half-wave plates (λ/2), lenses (L), line cameras (Cam), grey wedge (GW), mirrors (M), hot mirror (HM), scanner (Sc) and Dynamic Vessel Analyzer (DVA)

Moreover, the new setup’s beam displacer (BD, Thorlabs, BD27) was mounted in a motorized rotation stage (Thorlabs, PRM1/MZ8) with a servo controller (Thorlabs, TDC001), allowing it to be rotated by 90° at the push of a button. At a rotational position of 0°, the beam is split into two beams aligned vertically (i.e. in the x-z-plane in Fig. 1); at 90°, the two beams are aligned horizontally (which corresponds to the y-z-plane in Fig. 1). This is a major improvement, as it allows the measurement of all the vessels’ flow velocities: without the possibility of rotating the beams, vessels with an orientation perpendicular to the detection plane would not be measurable. The rotation does not require a realignment of the system; the only additional change necessary is the rotation of two half-wave plates: the rotation of the beams’ polarization due to the turning of the BD is compensated by a 90° rotation of a half-wave plate (λ/2₍₁₎, Thorlabs, AHWP05M-980) right before the point where the beams are separated spatially by a polarizing beam splitter (PBS, Thorlabs PBS252) and coupled into their respective spectrometers using fiber couplers (FC, OZ Optics, HPUCO-23-840-S-6.2AS): the ordinary beam is passed into FC₁. Depending on whether the extraordinary beam is above or beside the ordinary one, the former is either deflected from an additional PBS to enter FC₂, or passes an additional half-wave plate (λ/2₍₂₎) which is flipped into the beam path via a motorized filter flipper (Thorlabs, MFF001/M) to be transmitted straight through the PBS onto FC₃. Depending on whether FC₂ or FC₃ are in use, the corresponding fiber is manually attached to the spectrometer’s fiber coupler.

2.3 Measurement technique

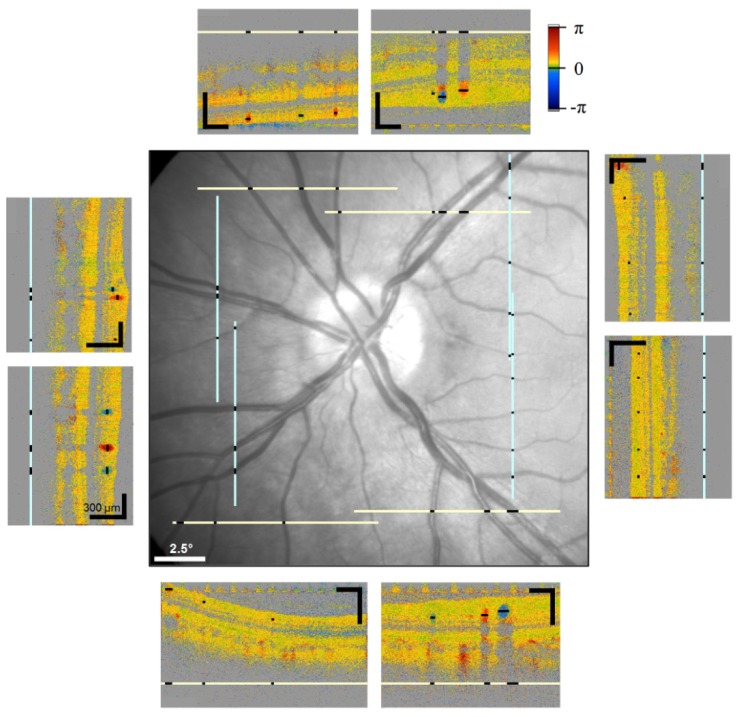
To determine the total blood flow in the eye, OCT measurements were performed with a rectangular scanning pattern around the ONH, as shown in Fig. 3 : scans were performed superior, inferior, nasally and temporally of the ONH: at each position, two shorter scans rather than one wide one were performed. This segmentation of the scanning pattern was adopted to avoid errors due aberrations in the focus overlap of the beams. The positions of the eight scans are given exemplarily for one subject by the horizontal and vertical lines in Fig. 3. The circumjacent images in Fig. 3 show a corresponding phase image for each of the scanning positions in pseudocolours: the phase shifts, which are due to the movements of blood in the vessels, are clearly visible in red or blue on the yellowish (i.e. non-moving) background.

Fig. 3.

Scanning pattern around the ONH; scanning positions denoted by lines in the fundus image (center); corresponding OCT phase images for each scanning position (small circumjacent images; black scale bars correspond to 300µm)

Scanning in a closed shape (in this case a rectangle) around the ONH ensures that the mean velocity v _mean of all vessels entering and exciting a subject’s eye is encompassed.

For the measurements superior and inferior to the ONH (where all velocity vectors point roughly in vertical direction), the beams were aligned vertically (BD at 0°) and scanned horizontally; for the measurements in nasal and temporal positions (velocities mainly horizontal), the beams entered the eye with a horizontal displacement and were scanned vertically, as illustrated in Fig. 4 . In each case, both beams were focused onto the same spot on the retina, which was monitored by overlapping the vessel positions in both channels and by visual inspection of the beams on the fundus image.

Fig. 4.

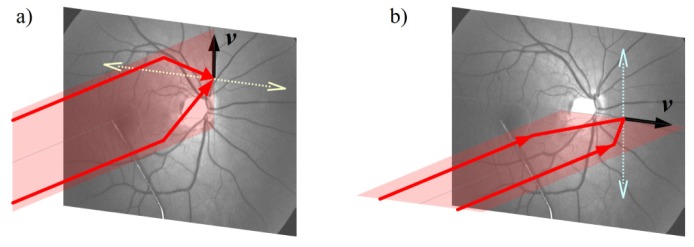
Beam alignment for superior/inferior vessels, which are scanned horizontally (a) and for nasal/temporal vessels, which are scanned vertically (b)

2.4 Image acquisition and data processing

At each position, two stacks of 60 B-scans with 3000 lines each were recorded. With a line rate of 27 µs, this leads to a measurement time of around 5 seconds, so that several pulse periods were recorded. The oversampling factor (OF) of phase tomograms is defined as OF = w∙N/D, where w is the spot size, N the number of sampling points and d the geometric width the tomogram. With a spot size of 18.7 µm, an OF of 14 was obtained.

Concomitantly with the OCT measurements, the diameters of the measured vessels were determined with the DVA. The DVA’s fundus camera and the accompanying analyzing software are calibrated to give absolute values in µm only for the Gullstrand eye model [21, 24]. Thus, diverging eye-lengths and ametropia values of the subjects’ eyes had to be corrected for. The corrective factors were determined by measuring the axial eye length and the axial refraction for each subject and correcting the results for each eye-fundus camera system.

Since the DVA measurements are less reliable for very small vessels, vessel diameters below 65 µm were measured in the OCT images and determined by comparison with the DVA results from larger vessels: 30 B-scans with 1000 lines at a line period of 82µs were recorded at all positions with vessels which were too small to be measured by the DVA (i.e. < 65 µm). The vessels’ axial diameter in pixels (z-direction in Fig. 1), which is only determined by the bandwidth of the OCT light source, the refractive index of the medium, and the recording spectrometer, was measured in each of the OCT images and averaged for all images. By comparing the number of pixels with that of a vessel large enough to have been measured with the DVA, underestimation of the diameters was avoided (see Discussion) and the values could be equated to values in µm. This method allowed determining the diameters of vessels down to about 30 µm.

The phase images were bulk motion corrected using a histogram based method originally proposed by Makita et al. [25] and adapted by Schmoll et al. [26] and Werkmeister et al. [18].

Phase values calculated with a Fourier transformation lie in the range of [-π,π]. In some larger vessels (especially in arteries), phase wrapping occurred, resulting in a seeming reversal of the flow where the values would exceed the range of [-π,π]. These regions were unwrapped by adding or subtracting 2π. Pixels with amplitude values below an empirically set threshold were fitted according to a parabolic flow profile, although parabolic profiles were not generally assumed. The average phase shift within each vessel was then calculated for each B-scan and each detection channel separately. Thereafter, the phase difference ΔΦ = ΔΦ ₁ – ΔΦ ₂ between the two channels was calculated for each B-scan and averaged for the whole stack. The angle β was determined from the fundus image recorded with the DVA’s camera. The angle Δα was determined for each subject by solving the matrix equation of the lens system with the subject’s eye length and ametropia values. The resulting values for Δα lay between 5.20° and 5.40°. Using Eq. (1) and inserting a vessel’s mean phase shift ΔΦ_mean, the mean flow velocity v _mean in each vessel was determined.

With both the mean velocity from the OCT and the vessel diameter from the DVA, the vessel’s blood flow Q can be calculated:

$$Q=\frac{v_{\text{mean}}{D}^2\pi }{4}.$$ (2)

2.5 In vivo measurements

The study protocol was approved by the Ethics Committee of the Medical University of Vienna and complied with the standards of the Declaration of Helsinki. A total of four healthy subjects aged between 20 and 30 years participated in the study. All subjects were informed about the nature of the study and gave their written consent to participate. Furthermore, all subjects passed an ophthalmic screening examination, including slit lamp biomicroscopy and indirect funduscopy. Inclusion criteria were normal ophthalmic findings and ametropia of less than 3 diopters.

The subjects’ pupils were dilated with one drop of a mydriatic (5 mg/mL, Mydriaticum Agepha eyedrops; AGEPHA GmbH, Austria) to allow the DVA’s fundus illumination to enter the pupil. Measurements were started after a resting period of at least 15 minutes. The OCT beams were positioned on the fundus by reference to the live image obtained with the DVA. As described above, the OCT beams were scanned in a rectangle within one to two disc diameters around the optic disc. At every scanning position, two measurements of the mean velocity v _mean were performed using the OCT, and the measured fundus region was recorded using the DVA. The recording allows the evaluation of the recorded vessels’ diameters to be postponed to after the measurement session, thus speeding up the procedure.

As each separate OCT-measurement only takes around five seconds, the fixation abilities of the subjects onto the system’s internal fixation target did not have to be exceptionally high.

3. Results

Two typical timelines (phase shift in each channel and phase shift difference over time) are given in Fig. 5 : for the artery (left), the pulse periods are clearly visible; the pulsations in the veins are usually very small or not visible at all. As explained in [27], dual beam measurements have the advantage that eye movements relative to the beams result in equal phase shifts in both channels and thus cancel each other out in the resulting phase shift difference.

Fig. 5.

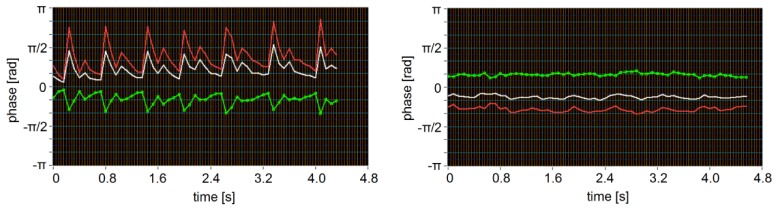
Timeline for an artery (left) and a vein (right); the red and white lines represent the phase shifts of the two beams, the green line denotes the resulting phase shift difference between them.

The total venous and arterial flow for each of the measured subjects is given in Table 1 . A possible reason for deviations between the arterial and venous flow might be that the focus overlap of the measurement beams on the retina was not optimal. Generally, however, the law of mass conservation was well fulfilled - the mean deviation of the arterial from the venous flow was 7.4%.

Table 1. Number of vessels with diameters above and below 65 µm, respectively; total venous flow Q_V, total arterial flow Q_A, and their percentage deviation Δ Q for each subject.

Subject #	# ves > 65 µm	# ves < 65 µm	QA [µl/min]	QV [µl/min]	ΔQ
1	14	4	38.2	35.4	7.4%
2	14	8	29.7	32.5	8.8%
3	11	8	37.2	37.6	1.1%
4	10	4	37.3	42.4	12.2%

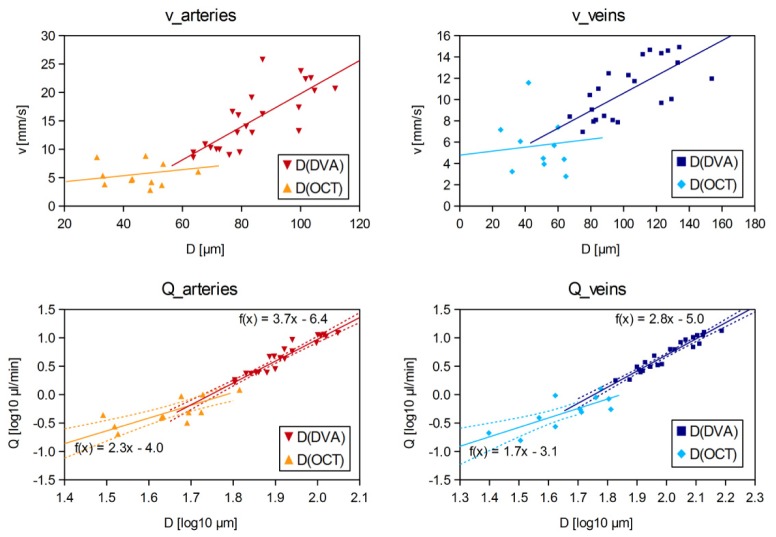
Figure 6 depicts the dependence of blood flow velocity on vessel diameter and a linear correlation analysis of flow and diameter (log-log plot). As mentioned in section 2.4, the DVA was used to determine vessel diameters above 65 µm, while smaller vessel diameters were determined from the OCT-images. The two methods’ results are represented by darker and brighter data points in Fig. 6, respectively. Determining the size of larger vessels from the OCT images in the same fashion as those of the small ones results in the same values as those measured by the DVA, which corroborates the validity of the diameter determination method.

Fig. 6.

Top: blood flow velocity v as a function of vessel diameter D for arteries (left) and veins (right). Bottom: log-log plot of blood flow Q over vessel diameter D for arteries (left) and veins (right); dotted lines give the 95% confidence interval. Vessel diameters were determined with OCT for vessels < 65 µm and with DVA for the larger ones.

Several earlier papers studied the difference in blood flow when dividing the vessels into temporal and nasal ones by an imaginary line through the optic disc. In accordance with these earlier studies [28–30], the blood flow in the temporal part of the retina was found to be much higher than in the nasal part (see Table 2 ). Riva et al. [28] attributed this to the larger area of the temporal retina.

Table 2. Arterial and venous blood flow (Q_A, Q_V) in the temporal (temp) and the nasal (nas) part of the retina for each subject individually; mean values and standard deviations for all subjects.

Subject	QA(temp) [µl/min]	QV(temp) [µl/min]	QA(nas) [µl/min]	QV(nas) [µl/min]
1	23.3	26.0	15.3	9.3
2	19.9	22.5	9.7	10.0
3	25.8	18.2	11.4	15.4
4	23.5	32.9	13.7	9.5
Mean ± SD	23.2 ± 2.4	24.9 ± 6.2	15.2 ± 3.3	11.1 ± 2.9

4. Discussion

A critical parameter regarding blood flow determination is the vessel diameter, as it enters quadratically into the calculation. One possibility is to determine the diameter from the OCT phase images: the maximal depth range z _max of the OCT is only dependent on the spectrometer’s wavelength resolution δλ, the central wavelength λ _c, and the medium’s index of refraction n, as$z_{\text{max}}={\lambda }_c^2/(4n\text{δ}\lambda )$ [31]. Thus, a pixel in depth direction can be equated to a certain length in real space. The spectrometer used in this study gives an image resolution of 1.3 µm per pixel. The actual axial resolution of the system, however, is limited by the physical resolution $\delta z=2\ln (2)\cdot {\lambda }_0^2/(\pi \cdot \Delta \lambda )=5.8\text{µm}$. The flow profile in a vessel is approximately parabolic, resulting in a very low velocity at the boarder of the vessel. At some point, the phase value no longer exceeds the noise and is thus no longer distinguishable from the background. Moreover, blood is very absorptive, resulting in shadowing effects behind the vessel, obscuring the rear vessel boundary. Consequently, the vessel diameter will usually be underestimated if extracted from the OCT images. To avoid using the OCT images, many earlier studies (e.g [28, 29, 32–34]) used fundus photography to determine the vessel diameter. Another possibility is measuring the vessel diameter with a DVA, as was done in several studies (e.g [30, 35, 36]); this method gives significantly more exact results [37]. The latter method was chosen in the study presented here; a comparison of the diameters extracted from the OCT images with the more reliable DVA values gave an average underestimation of 14% (cf. Figure 7 ).

Fig. 7.

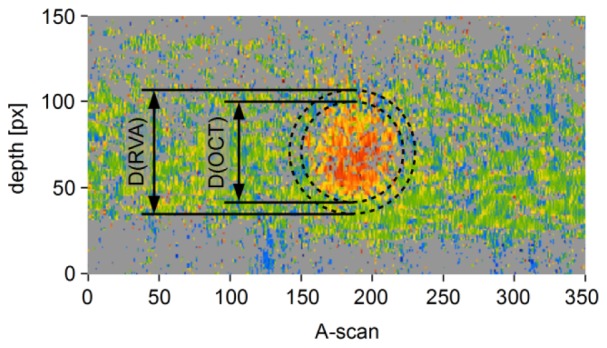
Underestimated vessel diameter as determined from the OCT image (inner circle) compared to more accurate diameter measured by the DVA (outer circle)

In the study presented in this paper, the DVA was implemented into the OCT setup, which makes it unnecessary to move the subjects from one instrument to another and allows measuring both the blood flow and the diameter of a vessel within a much smaller time frame. Only the diameters of vessels which were too small to be measured by the DVA were determined from OCT images; low line rates and small scan regions ensured maximal reliability. The smooth transition between the data points of the two methods indicates that they complement one another.

As was to be expected, velocity and vessel diameter were dependent on each other: the measured velocities decreased with falling diameters (see Fig. 6, top). However, although the velocity values were found to be linearly dependent on the vessel diameters above approx. 60 µm (cf. Grunwald et al. [33], Garhöfer et al. [30]), they diverged noticeably from the linear dependence for lower diameters, as can be clearly seen in Fig. 6. This divergence may be explained by the change in the viscosity of blood depending on the vessel diameter, as described by the Fåhræus-Lindqvist effect for glass capillaries [38] and in several studies in vivo as discussed in the review by Secomb et al. [39]. A divergence from the linear relationship would also explain why the regression line and the 95% confidence interval in the velocity-diameter graphs did not include the point (0,0) in the study by Garhöfer et al. [30], which took only vessels with diameters above 60 µm into account.

For all four subjects, the mean arterial flow was 35.7 ± 4.1 µl/min, and the mean venous flow was 36.0 ± 4.5 µl/min. Several studies have already attempted to quantify the total retinal blood flow. Overall, the results presented here are in the same range as those obtained by earlier studies: Riva et al. [28] used bidirectional laser Doppler velocimetry (LDV) to measure the vessels’ maximum velocity v _max, which they assumed to be 1.6 v _mean. By extrapolating their measured values for all vessels (including those too small to be evaluated), they obtained flow values of 33 ± 9.6 µl/min for all arteries and 34 ± 6.3 µl/min for all veins in n = 12 eyes of healthy subjects. Using a slightly different LDV setup [32] and a conversion factor v _max/v _mean = 2 (assumption of a parabolic flow profile [40]), Feke et al. [29] reported a higher flow value of 80 ± 12 µl/min for n = 6 subjects. The LDV measurements by Grunwald et al. (once again with v _max/v _mean = 1.6) resulted in extrapolated blood flow values of 38.1 ± 6.2 µl/min for all vessels (n = 12) [33] and 38.5 ± 4.7 µl/min (n = 16) [34]. All previously mentioned studies determined the vessel diameter from fundus photographs. Garcia et al. [41] used a commercially available bidirectional LDV to measure velocity and vessel diameter, yielding flows of 64.9 ± 12.8 µl/min (n = 5). LDV flow values published by our group were 34.1 ± 7.6 µl/min [36], 43 ± 16 µl/min [35] and 44.0 ± 13.3 µl/min [30] using a DVA to obtain the diameters. The first to measure total retinal blood flow using single-beam FD-OCT were Wang et al. [6], who measured 52.90 ± 2.75 and 45.23 ± 3.18 µl/min in two eyes and, in subsequent studies, 45.6 ± 3.8 µl/min (n = 10) [42] and 47.6 ± 5.4 µl/min (n = 20) [43].

As was anticipated from earlier studies, the retinal blood flow in the temporal part of the retina was found to be much higher than in the nasal part, which might be attributed to the larger area of the temporal retina [28].

In accordance with Murray’s law [44], log-log regression coefficient between blood flow and vessel diameter in the veins with diameters above 65 µm was close to 3, i.e. the blood flow scales with the cube of the radius. The value for the arteries was slightly higher (3.7 for the arteries with diameters above 65 µm); this may be explained by the higher velocities and pulsatile flow in the arteries. Once again, the values are within the range of literature values: e.g. Riva et al. [28] reported a coefficient of 2.76 ± 0.16 for arteries and 2.84 ± 0.12 for veins, Grunwald et al. [33] found a value of 2.78 and Garcia et al. [41] gave a value of 3.35 ± 0.23. To confirm the exact values, a higher number of data points would be necessary; nevertheless, the trend is clearly visible already with our relatively small sample number.

The setup of this study allowed measuring the flow in very small vessels (down to about 30 µm), an option that was not available to many earlier studies. It was thus possible for us to confirm that the flow in retinal vessels with a diameter of 60 µm is approximately 1 µl/min; this value was to be expected for arteries according to the data given by Riva et al. [28], who measured arteries down to 39 µm. Regarding the value for veins, both Riva et al. [28] and Garhöfer et al. [30] only reported measured data for veins with diameters above 60 µm, but extrapolated flow values of approximately 1 µl/min for smaller veins.

5. Conclusion

This paper presents the results of a new OCT system with integrated Dynamic Vessel Analyzer and rotatable beams. Using this system, it was possible to measure the total retinal blood flow in the human eye, taking into account also very small vessels (down to about 30 µm): the mean arterial flow measured was 35.7 ± 4.1 µl/min, the mean venous flow was 36.0 ± 4.5 µl/min. The log-log regression coefficient between blood flow and vessel diameter showed good agreement with Murray’s law. Overall, the results seem promising and the system offers a high potential for examining retinal blood flow abnormalities in patients with ocular diseases.