Dual sensitivity of inferior colliculus neurons to ITD in the envelopes of high-frequency sounds: experimental and modeling study

Abstract

Human listeners are sensitive to interaural time differences (ITDs) in the envelopes of sounds, which can serve as a cue for sound localization. Many high-frequency neurons in the mammalian inferior colliculus (IC) are sensitive to envelope-ITDs of sinusoidally amplitude-modulated (SAM) sounds. Typically, envelope-ITD-sensitive IC neurons exhibit either peak-type sensitivity, discharging maximally at the same delay across frequencies, or trough-type sensitivity, discharging minimally at the same delay across frequencies, consistent with responses observed at the primary site of binaural interaction in the medial and lateral superior olives (MSO and LSO), respectively. However, some high-frequency IC neurons exhibit dual types of envelope-ITD sensitivity in their responses to SAM tones, that is, they exhibit peak-type sensitivity at some modulation frequencies and trough-type sensitivity at other frequencies. Here we show that high-frequency IC neurons in the unanesthetized rabbit can also exhibit dual types of envelope-ITD sensitivity in their responses to SAM noise. Such complex responses to SAM stimuli could be achieved by convergent inputs from MSO and LSO onto single IC neurons. We test this hypothesis by implementing a physiologically explicit, computational model of the binaural pathway. Specifically, we examined envelope-ITD sensitivity of a simple model IC neuron that receives convergent inputs from MSO and LSO model neurons. We show that dual envelope-ITD sensitivity emerges in the IC when convergent MSO and LSO inputs are differentially tuned for modulation frequency.

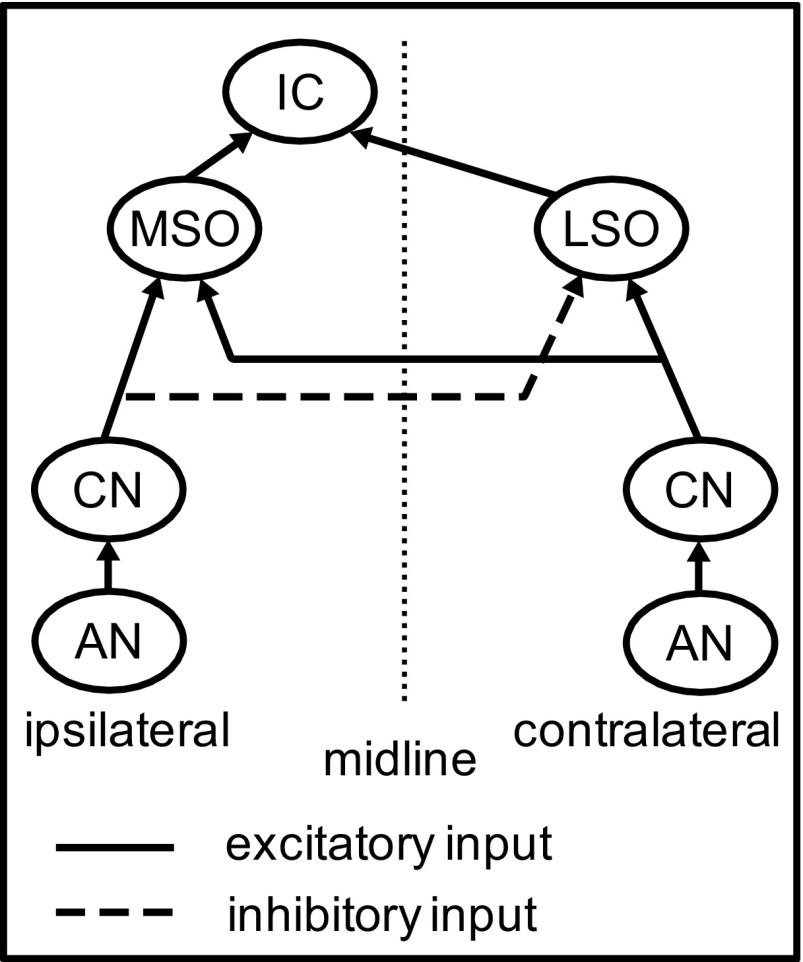
psychophysical studies have shown that human listeners can detect interaural time differences (ITDs) conveyed via the envelopes of high-frequency sounds (Bernstein and Trahiotis 1994, 2002; Henning 1974; Klumpp and Eady 1956; McFadden and Pasanen 1976; Nuetzel and Hafter 1976). Physiologically, the superior olivary complex (SOC) is considered to be the primary site for encoding ITDs in the ascending auditory pathway. Both principal nuclei of the SOC, the medial superior olive (MSO) and the lateral superior olive (LSO), contain high-frequency neurons that are sensitive to the envelope-ITD of sinusoidally amplitude-modulated (SAM) tones, although they appear to encode ITD in different ways.

MSO neurons receive predominantly excitatory inputs from both ears (Batra et al. 1997; Caird and Klinke 1983; Goldberg and Brown 1968; Langford 1984; Yin and Chan 1990), resulting in peak discharge rate when neural activities from both sides arrive coincidentally. These neurons are called “peak type” because their ITD tuning functions align at their peaks for sounds of different frequencies. In contrast, most LSO neurons receive excitatory input from the ipsilateral ear and inhibitory input from the contralateral ear (Batra et al. 1997; Boudreau and Tsuchitani 1968; Caird and Klinke 1983; Finlayson and Caspary 1989; Joris 1996; Joris and Yin 1995; Sanes 1990; Tollin and Yin 2005). Because of this excitation-inhibition (EI) interaction, coincidental arrival of binaural inputs produces maximal cancellation and therefore minimum discharge rate. These cells are said to be “trough type” because their ITD tuning functions align at the trough for different modulation frequencies.

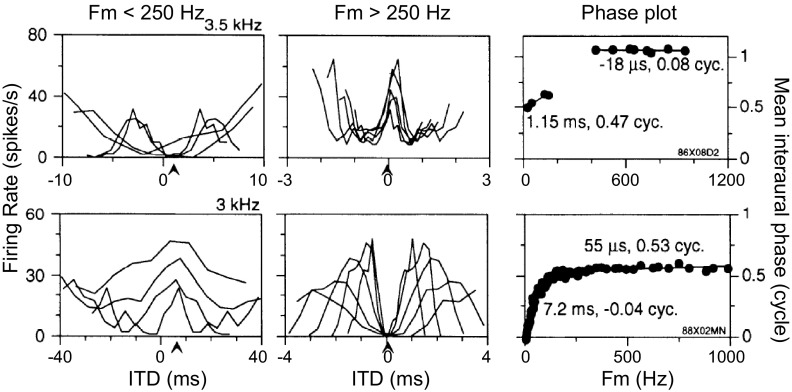
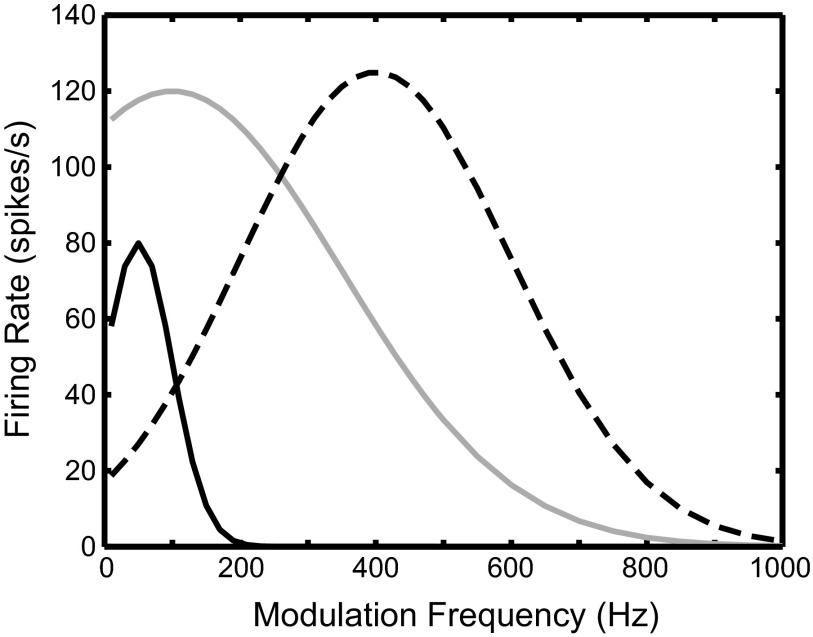
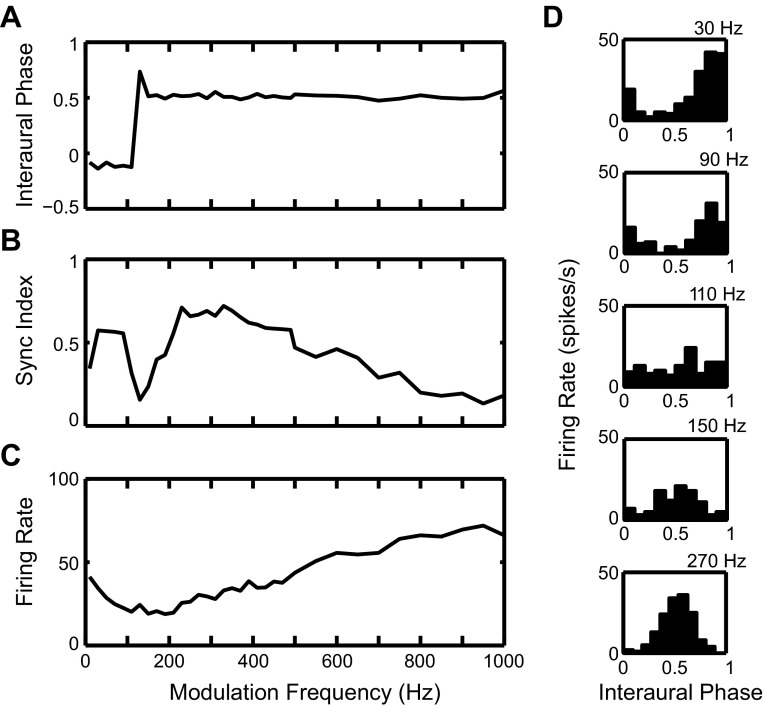
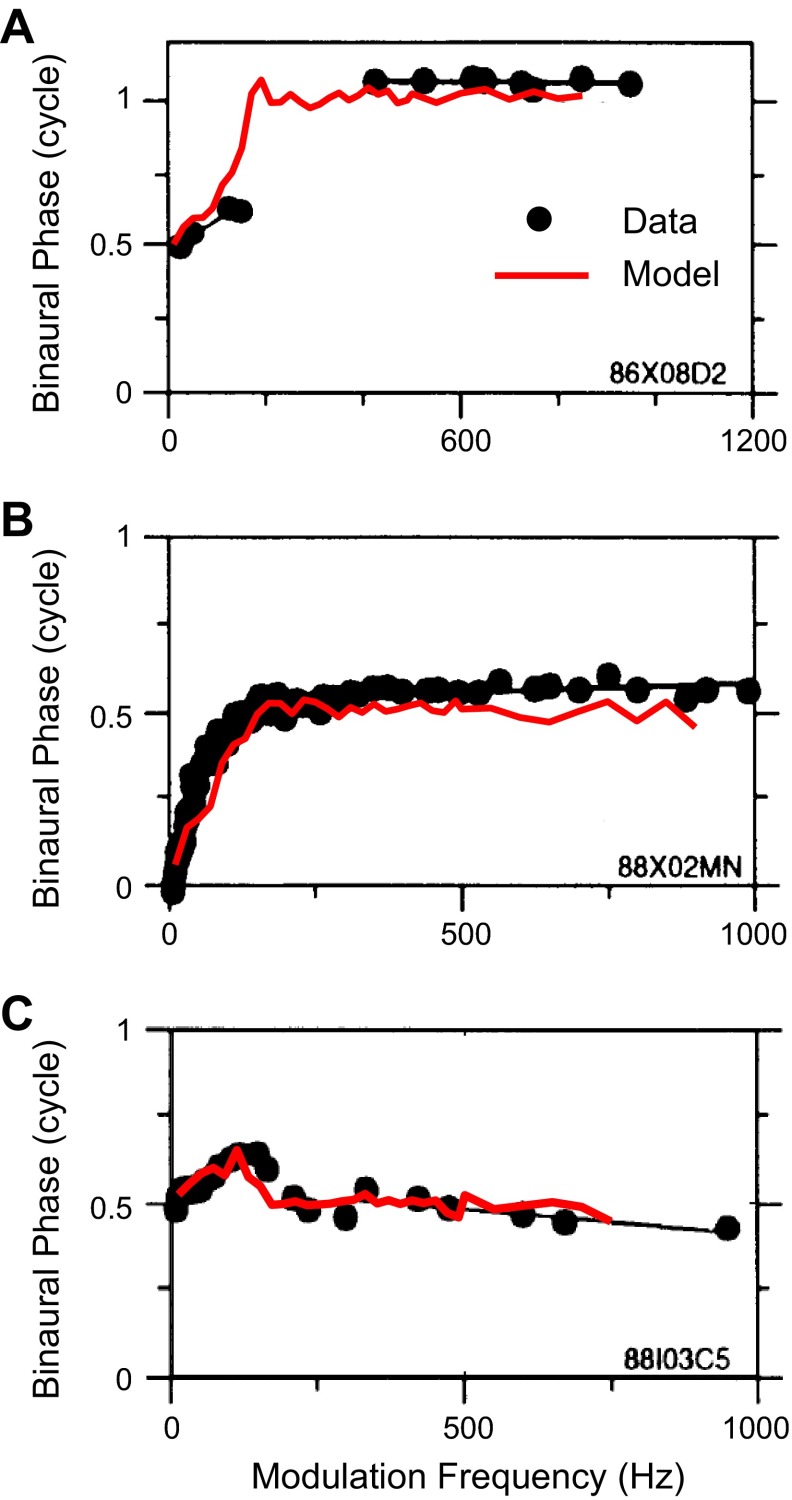
The SOC transmits the encoded envelope-ITD information to the next major nucleus in the auditory pathway, the inferior colliculus (IC), either via direct excitatory projections or via intervening inhibitory neurons such as those of the dorsal nucleus of the lateral lemniscus (DNLL). Many high-frequency neurons in the IC are sensitive to envelope-ITDs of SAM tones (Batra et al. 1989, 1993; Griffin et al. 2005; Yin et al. 1984) and also to ITDs in the cochlear-generated (CG) envelopes of broadband noise (Devore and Delgutte 2010; Joris 2003). In many cases, the ITD-tuning characteristics of IC neurons are similar to those of SOC neurons; thus the responses of these neurons can be explained by a single input from an SOC neuron with similar ITD sensitivity. However, some IC neurons exhibit emergent properties in their responses to envelope-ITD that have not been observed in the SOC. To describe neural sensitivity to envelope-ITD, the mean interaural phase of the neural responses is often plotted as a function of the modulation frequency (f_m) (Batra et al. 1993, 1997; Yin and Kuwada 1983; Yin et al. 1984). For simple coincidence detectors, there is a linear relationship between phase and f_m. The slope of the linear fit, termed the characteristic delay (CD), corresponds to the envelope-ITD at which the rate-ITD curves align. The phase intercept for zero f_m, termed the characteristic phase (CP), is 0 cycle for peak-type neurons and 0.5 cycle for trough-type neurons. One type of IC neuron with emergent ITD sensitivity shows two linear segments with different slopes (CDs) in their phase plot, with a half-cycle change in CP between the two segments (Batra et al. 1993). We refer to these IC cells as dual-CP neurons. Some of the dual-CP neurons show trough-type responses at low f_m and peak-type responses at high f_m (Fig. 1, top), while others show the opposite pattern: peak-type responses at low f_m and trough-type responses at high f_m (Fig. 1, bottom). The transition between peak-type and trough-type responses tends to occur for f_m between 150 and 250 Hz, and a drop in firing rate typically occurs in the transition region in the examples shown by Batra et al. (1993). The phase plots of these dual-CP neurons are suggestive of convergent inputs from the MSO and the LSO onto single high-frequency IC neurons.

Fig. 1.

Experimental data for 2 high-frequency inferior colliculus (IC) neurons showing dual characteristic delays (CDs) in response to binaural sinusoidally amplitude-modified (SAM) tones. Each row represents 1 IC neuron. Left and center: rate-interaural time difference (ITD) functions for modulation frequency (f_m) < 250 Hz (left) and > 250 Hz (center). Each curve represents a rate-ITD function for a single f_m. Note that the peaks are lined up for peak-type responses (bottom left and top center); the troughs are lined up for trough-type responses (top left and bottom center). Right: plot of the interaural phase as a function of f_m (phase plot). Note the 2 linear segments in the phase plot. One linear segment is for f_m < 250 Hz; another linear segment (with a different CP) is for f_m > 250 Hz. [Figure from Batra et al. (1993) with permission.]

In a combined experimental and modeling study of dual ITD sensitivity in IC, we first extend the experimental results of Batra et al. (1993) by showing that some neurons in the IC of unanesthetized rabbit exhibit the dual type of ITD sensitivity to amplitude-modulated broadband noise. By independently manipulating the interaural correlation of the waveform fine structure and the modulation of the envelope, we reveal distinct types of sensitivity to the ITD in the slower, externally imposed amplitude envelope (ITD_AM) versus the ITD in the faster envelope induced by cochlear filtering of the noise waveform (ITD_CG). The responses of these IC neurons are also suggestive of convergent inputs from the MSO and the LSO. Anatomical tracer studies have demonstrated convergence of projections from MSO and LSO onto the IC at the level of fibro-dendritic laminae (Loftus et al. 2004) and also onto highly local neighborhoods of physiologically characterized IC neurons (Loftus et al. 2010), making it likely that convergence actually occurs onto the same IC cell.

We developed a computational model of the binaural circuits up through the IC to test whether a convergence of inputs from LSO and MSO is adequate to explain the dual types of envelope-ITD sensitivity (peak type and trough type) of high-frequency IC neurons for both SAM tones and broadband noises. Using either existing models of SOC neurons or quantitative descriptions of available experimental data for the MSO and the LSO, we show that the IC model is able to reproduce the complex responses observed in the IC, including both the f_m dependence of the responses to SAM tones and the dual types of envelope-ITD sensitivity seen in the response to broadband noise.

METHODS

We first present the methods for the in vivo electrophysiology experiments. The details of the computational modeling are then presented.

In Vivo Electrophysiology

Surgical preparation.

Female Dutch Belted rabbits were prepared for chronic in vivo electrophysiology as described by Devore and Delgutte (2010). Briefly, under aseptic conditions, a stainless steel recording chamber and brass head post were affixed to the skull with dental acrylic and stainless steel screws. Custom ear mold impressions were made with vinyl polysiloxane (Reprosil). After a 1-wk recovery period, animals were gradually accustomed to head restraint and subsequently underwent a second aseptic surgical procedure in which an ∼3-mm craniotomy was made inside the recording chamber (coordinates from bregma: −10.5 mm AP and 3 mm ML). All procedures were approved by the animal care and use committees of both the Massachusetts Eye and Ear Infirmary and the Massachusetts Institute of Technology.

Experimental procedures.

Sound stimuli were generated by a 24-bit digital-to-analog converter (National Instruments NIDAC 4461) at a sampling rate of 50 kHz. Stimuli were digitally filtered to compensate for the transfer function of the acoustic assemblies, which consisted of a pair of Beyer-Dynamic (DT-48) speakers attached to sound tubes running through the custom-fitted ear molds. A probe-tube microphone (Etymotic ER-7C) measured acoustic pressure in the ear canal at the end of the sound delivery tube. At the start of each recording session, we determined the system transfer function in each ear with a broadband chirp stimulus and generated digital equalization filters over the range of 0.1–22.5 kHz.

Single neurons were isolated with epoxy-insulated tungsten electrodes (A-M Systems) inserted through a 25-gauge guide tube and advanced with a remote-controlled hydraulic micropositioner (David Kopf Instruments 650). The neural signal was amplified, band-pass filtered (0.3–3 kHz), and fed to a software spike detector triggering on level crossings. Animals were monitored on a closed-circuit video system throughout recording sessions. During the final recording session, recording sites were marked by electrolytic lesions (10-μA direct current for 30–45 s); subsequent histological examination verified the lesion sites to be within the IC.

Characterization of ITD sensitivity.

When a single neuron was well isolated, its characteristic frequency (CF) was determined with an automatic tracking procedure (Kiang and Moxon 1974) and the threshold for contralateral broadband noise was determined by measuring responses as a function of level. We then characterized ITD sensitivity, using three types of broadband noise stimuli. The first type comprised unmodulated broadband noises with the same waveforms at the two ears, so that their waveforms were interaurally correlated (unmod_corr). The second type comprised uncorrelated broadband noises, created with a Gramm-Schmidt orthogonalization procedure (Culling et al. 2001), that were amplitude modulated at the same frequency and depth at both ears (mod_uncorr). The third type comprised broadband noises with both correlated fine structure and the same amplitude modulation at both ears (mod_corr). The modulation depth was always 100%, and f_m was typically 100 Hz, although 40 Hz was used for some neurons.

For each of the three stimulus conditions, ITD sensitivity was assessed by measuring neural responses as a function of ITD applied to the whole waveform of the noises. We assessed ITD sensitivity over the range of ±2 ms in 0.2-ms steps for unmod_corr stimuli, ±20 ms in 2-ms steps for 40-Hz modulated stimuli, and ±10 ms in 1-ms steps for 100-Hz modulated stimuli. Noise stimuli were 200 ms in duration and were presented at a rate of 2/s at 15–20 dB above the unit's threshold. In all experiments, ITD sensitivity was first characterized for the unmod_corr stimuli. Only high-CF (>1,500 Hz) neurons exhibiting ITD sensitivity to the unmod_corr stimulus were further studied using the mod_uncorr and/or mod_corr stimuli in random order. For characterization of ITD sensitivity, ITD was randomly varied from trial to trial until 10 repeats were obtained at each ITD.

Data analysis.

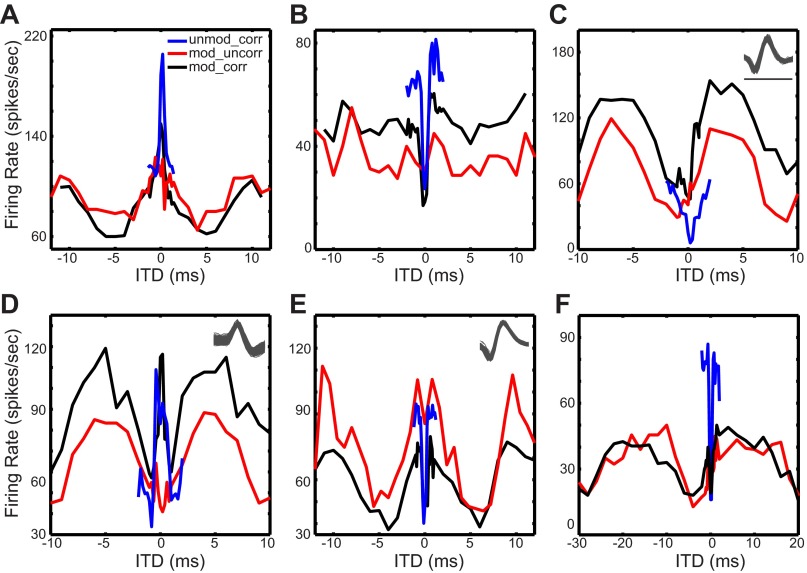
To ensure that we included responses from only single units, as opposed to multiunit responses, analysis was restricted to recording sites in which the spike amplitude and waveshape were stable and exceeded the noise floor by at least three standard deviations. Figure 5, C–E, insets, show representative spike waveforms from three IC neurons.

Fig. 5.

Neural sensitivity to ITD. Average firing rate as a function of ITD for the 3 broadband noise stimulus conditions: unmodulated noise with correlated fine structure (unmod_corr, blue lines), modulated noise with correlated fine structure (mod_corr, black lines), and modulated noise with uncorrelated fine structure (mod_uncorr, red lines). The unit characteristic frequencies (CFs, in kHz) are 3.79 (A), 3.0 (B), 2.39 (C), 3.66 (D), 1.7 (E), and 6.88 (F). The f_m of the SAM noise was 100 Hz except for the data in F, which were obtained with a SAM frequency of 40 Hz. Unit quality is illustrated by superimposed waveforms of >500 spikes recorded in response to the mod_corr stimulus for the units shown in C–E. Scale bar in C is 1 ms; all spike waveforms are plotted on the same timescale.

For each noise type, we computed a rate-ITD function by first counting the spikes over the 200-ms stimulus duration and averaging across all trials for each ITD. Rate-ITD curves were smoothed by a three-point digital filter with weights (1/6, 2/3, 1/6). ITD sensitivity to the unmod_corr stimuli was classified as peak type, trough type, or biphasic/intermediate with the classification scheme of Devore and Delgutte (2010).

Modeling Procedures

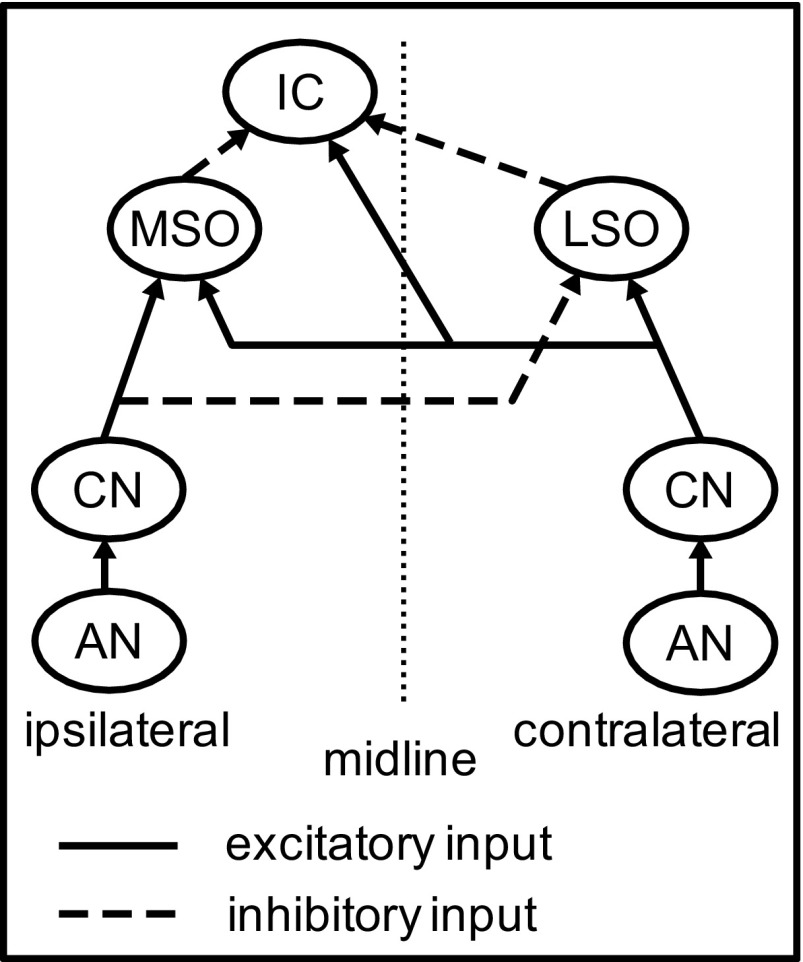
The IC model developed in the present study consists of four stages, as shown in Fig. 2. The first stage represents auditory nerve (AN) responses to SAM tones and broadband noises. The second stage represents the cochlear nucleus (CN), which is modeled here as a simple relay, as is the medial nucleus of the trapezoid body (MNTB). The third stage models the responses of high-frequency MSO and LSO neurons to binaural SAM tones and noises. The MSO and LSO models were either Hodgkin-Huxley (HH)-type models developed in previous studies (Colburn et al. 2009; Wang and Colburn 2012) or phenomenological models that directly simulate the experimentally measured discharge rates of MSO and LSO neurons in response to binaural SAM tones. The fourth stage models the responses of an IC cell with convergent input from MSO and LSO. In all simulations, the stimulus duration was the same as in the experimental data, i.e., 5 s for SAM tone stimuli and 200 ms for broadband noise stimuli.

Fig. 2.

Diagram of the IC model with excitatory inputs from the medial (MSO) and lateral (LSO) superior olive. The cochlear nucleus (CN) is modeled as simple relay. [For the phenomenological MSO and LSO models, the response patterns of MSO and LSO inputs are specified computationally without explicitly describing the inputs to these MSO and LSO neurons from the auditory nerve (AN) or the CN.]

AN models.

Two types of AN models were used: a simplified AN model based on Poisson processes and a detailed AN model with realistic cochlear processing (Zilany et al. 2009). The simplified AN model was used to simulate IC responses to binaural SAM tones, and the detailed AN model was used to simulate responses to binaural broadband noises. The simplified AN model lacks an explicit description of cochlear processing, and thus is not suitable for simulating responses to noise. Spikes generated by the AN models directly drive synaptic inputs to the MSO and LSO models since the CN and the MNTB are modeled as simple relays.

The simplified AN model is based on a point-process AN description similar to those used in previous modeling studies (Colburn et al. 2009; Zhou et al. 2005) except that there is no refractoriness in the simplified model (i.e., it is approximated as a Poisson process). The instantaneous firing rate of the Poisson process for a single AN fiber in response to SAM tones is characterized by four parameters: the modulation frequency f_m, the average firing rate R_avg, the synchronization index SI to the modulation, and the average response phase φ. The rate function is periodic, with a period T, equal to the inverse of the modulation frequency f_m. The parameters SI and φ determine the temporal aspects of the AN spike trains. The unit for φ is cycles, and its value was always 0.5 in the AN model.

To generate spikes, we first determined the expected number of spikes for each modulation cycle by multiplying the average firing rate R_avg by the modulation period T. If the expected number of spikes was not an integer, it was rounded either up or down (independently for each cycle) with a random number generator. Then the spike times t_k within each cycle were drawn repeatedly from a Gaussian distribution with mean Tφ and standard deviation T/(2F) until the expected number of spikes was generated. The synchrony index SI is determined by the value of the parameter F, which corresponds to the inverse of the coefficient of variation of the distribution of spike jitters. Specifically, SI can be calculated by inverting the formula F = π/($\sqrt{2\ln (1/\text{SI})}$). For cases when the Gaussian sample t_k fell outside of the period (t_k < 0 or t_k > T), the model constrained the event time to be within the current period by replacing t_k with its circular residue ${t\prime }_{\mathrm{k,}}^{}$ i.e., ${t\prime }_k^{}$ = t_k mod T whenever t_k > T and ${t\prime }_k^{}$ = t_k mod T + T for the case that t_k < 0. The spike times were generated by applying the above procedure for each period until enough spikes were generated for the whole duration of the stimulus, i.e., the overall number of spikes matched the theoretical total spike count 5 × R_avg for a 5-s stimulus duration.

Multiple model AN fibers were used to provide synaptic inputs to the MSO and LSO models on each side. AN fibers on the same side have the same values for the four parameters of the rate function. AN fibers from the two sides also share their input parameters except that f_m is 1 Hz lower on one side than the other side. The difference in f_m produces binaural modulation beats and gives rise to an interaural phase difference that traverses the full cycle at a rate equal to the 1-Hz beat frequency.

For simulating responses to binaural broadband noises, a more detailed AN model, developed by Zilany et al. (2009), was used to provide synaptic inputs to the MSO and LSO models. This AN model incorporates detailed descriptions of cochlear processing including frequency tuning, the cochlear amplifier, inner hair cell (IHC) transduction, the transmission at IHC-AN synapses, and refractoriness in AN fibers. These explicit descriptions of cochlear processing, which are lacking in the simplified AN model, are used to simulate AN responses to broadband noises. In the present study, the CF of the AN model was always 6,000 Hz and the stimulus level was fixed at 60 dB SPL for each ear.

MSO and LSO models.

Two types of models were used for the high-CF MSO and LSO neurons: HH models and phenomenological models with Poisson time-varying rate functions chosen to simulate experimental data. The HH-type models were implemented with NEURON (Hines and Carnevale 1997), a broad-purpose neuron simulation environment. For both types of MSO and LSO models, MATLAB (MathWorks, Natick, MA) was used to initialize the model parameters before each simulation and to analyze the results after each simulation.

HH-TYPE MSO AND LSO MODELS.

The HH-type LSO cell model was the same as in a previous study of LSO responses to monaural SAM tones (Wang and Colburn 2012). It is a single-compartment model with three ion channels in the membrane: a sodium channel, a high-threshold potassium channel (KHT), and a “leak” channel. The biophysical parameters of this model, including the passive membrane properties and the mathematical characterization of the ion channels, were as described by Wang and Colburn (2012). The LSO model receives 20 excitatory AN inputs from the ipsilateral side and 20 inhibitory inputs from the contralateral side.

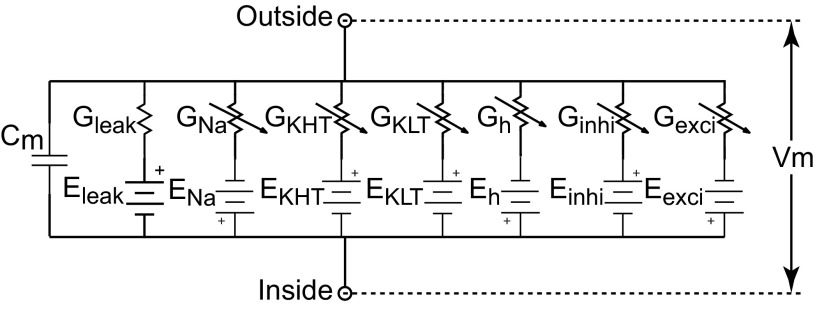
The HH-type MSO model was the same single-compartment model used previously to predict responses of MSO neurons to bilateral electrical stimulation through cochlear implants (Colburn et al. 2009). The model contained all the ion channels used in the LSO model and two additional ion channels: the h-current (I_h) channel and the low-threshold potassium channel (KLT) (Fig. 3). Parameter values for these channels were the same as used by Rothman and Manis (2003a, 2003b) to describe their experimental measurements of bushy cell membrane potentials in the ventral CN. The I_h channel was included in the MSO model to depolarize the resting potential so that the KLT channel would be partially activated at rest. This resting activation of the KLT channel gives rise to faster membrane time constants near resting potential and therefore better phase locking at high f_m. The MSO model receives 10 excitatory AN inputs from each side. Table 1 summarizes the parameters for the HH-type MSO and LSO models.

Fig. 3.

Circuit diagram for the Hodgkin-Huxley (HH)-type model for the MSO with 5 explicit channels in addition to the synaptic channels: a leak channel, a sodium channel (Na), a low-threshold potassium channel (KLT), a high-threshold potassium channel (KHT), and an h current (I_h) channel. The two synaptic channels, G_exci and G_inhi, represent excitatory and inhibitory synaptic inputs. The diagram for the HH-type LSO model is similar to the MSO model except that the LSO model contains no KLT channel and no I_h channel. The membrane parameters for the MSO and LSO models are summarized in Table 1. C_m, membrane capacitance; V_m, membrane potential.

Table 1.

Default parameters for HH-type LSO model and single-compartment MSO model

	Cm	gleak	gNa	gKHT	gKLT	gh	τE	τE_rise	τI	τI_rise	No. of ANs on each side
LSO model	31.4 pF	31.4 nS	8,000 nS	1,200 nS	0 nS	0 nS	2 ms	0.2 ms	5 ms	0.5 ms	20
MSO model	12 pF	2 nS	1,000 nS	150 nS	200 nS	20 nS	0.1 ms	0.01 ms	N/A	N/A	10

HH, Hodgkin-Huxley; LSO, lateral superior olive; MSO, medial superior olive; AN, auditory nerve; N/A, not applicable. See text for parameter definitions.

The HH-type MSO and LSO models used here were developed previously to describe MSO and LSO responses to other types of stimuli. In the present study, the membrane descriptions of these models, including the passive properties and characterization of the ion channels, are the same as in the original studies; however, the model for AN inputs, which was designed to describe AN responses to binaural high-frequency waveforms, differed from that in the original studies.

The HH-type MSO and LSO models receive inputs from either the simplified or the detailed AN model. Unless otherwise noted, the interaural delay between the AN inputs on the two sides was zero for both MSO and LSO models. Each spike generated by the AN model elicits an excitatory or inhibitory postsynaptic conductance (PSC), and the total excitatory (resp. inhibitory) synaptic conductance waveform is the superposition of all the excitatory (resp. inhibitory) PSCs occurring during the stimulus. Each PSC was simulated as the difference of two exponentials (rising and falling components), and the excitatory and inhibitory peak conductances (G_E and G_I, respectively) were specified separately. Values of G_E and G_I were varied to explore effects of the relative strengths of the AN inputs to MSO and LSO. Specifically, each excitatory PSC was expressed as

$$g_{\text{e}}(t)=\frac{G_{\text{E}}}{G_{\text{norm}}}\left[\exp (-t/{\tau }_{\text{E}})-\exp (-t/{\tau }_{\text{E\_rise}})\right]$$

where τ_{E_rise} and τ_E refer to the rise and decay time constants for excitation, respectively. The normalization factor to ensure the peak conductance is G_E is given by G_norm = exp(−t_p/τ_E) − exp(−t_p/τ_{E_rise}), where the peak latency

$$t_{\text{p}}=\frac{{\tau }_{\text{E\_rise}}\hspace{0.17em}\times \hspace{0.17em}{\tau }_{\text{E}}}{{\tau }_{\text{E}}-{\tau }_{\text{E\_rise}}}\hspace{0.17em}\ln \hspace{0.17em}\frac{{\tau }_{\text{E}}}{{\tau }_{\text{E\_rise}}}$$

with τ_E > τ_{E_rise}. Inhibition is given in the same form with corresponding parameters τ_{I_rise}, τ_I, and G_I. The reversal potential was 0 mV for excitatory synapses and −70 mV for inhibitory synapses. The resting potential was −63.6 mV for the MSO model and −64.9 mV for the LSO model. Note that Table 1 shows faster time constants for the MSO and slower time constants for the LSO.

PHENOMENOLOGICAL MSO AND LSO MODELS.

The second type of models for MSO and LSO neurons is phenomenological point-process models with rate functions based on experimental data from the MSO and the LSO in response to SAM tones with f_m chosen to create binaural beats (Joris 1996; Yin and Chan 1990). These models were only used to simulate the IC responses to SAM tones, and no AN inputs were generated explicitly in these models. For each f_m, the spike patterns for the MSO and LSO models were generated by the same method as for the simplified AN model, with the key difference that the instantaneous firing rate was phase locked to the 1-Hz binaural beat frequency rather than to f_m. For the MSO model, the synchronization SI to the beat frequency was fixed at 0.25 and the interaural phase φ was fixed at 0 for all f_m, as appropriate for a peak-type neuron. For the LSO model, SI was fixed at 0.33 and φ was fixed at 0.5 for all f_m, as appropriate for a trough-type neuron. These values are based on the average SI and φ measured experimentally in MSO and LSO neurons (Joris 1996). The distinguishing feature of these models is the binaural rate-f_m function representing the average firing rate over the entire stimulus duration in response to binaural SAM tones. Specifically, three synthetic functions were used as the binaural rate-f_m function for the MSO model, and the same three functions were also used for the LSO model (Fig. 4). These synthetic functions were chosen to approximate the range of binaural rate-f_m functions observed experimentally in MSO and LSO neurons (Joris 1996; Yin and Chan 1990).

Fig. 4.

Synthetic binaural rate-f_m functions of the phenomenological models. Each curve was used for both the MSO model and the LSO model. Different curves represent different shapes of the binaural rate-f_m function observed empirically in the MSO and the LSO: sharp low pass (black solid curve), broad low pass (gray curve), and band pass (dashed curve). The firing rate plotted here is computed as the average firing rate over the whole duration of the SAM tone stimulus (5 s). The synchronization index (SI) is fixed at 0.25 for the MSO and at 0.33 for the LSO for all f_m.

Unless otherwise noted, the internal interaural delays for the MSO and the LSO models were zero, which gave rise to a constant interaural phase as a function of f_m. In a few cases, nonzero internal interaural delays were introduced to reproduce the f_m-dependent phase curves observed in the experimental data. In these cases, the interaural phase of the MSO and the LSO model responses was varied linearly with f_m, with a slope equal to desired interaural delay.

IC model.

The IC model is a leaky integrate-and-fire (LIF) model that only contains a leak channel with constant resistance and the excitatory synaptic conductances derived from the spike inputs from the MSO and the LSO models. The membrane potential V_m of the IC model fluctuates as the input spikes arrive. Whenever V_m reaches a threshold V_th, an output spike is generated by transiently setting V_m to 0 mV. After each output spike, V_m is reset to the resting potential V_rest and held constant at V_rest for a duration T_ref to simulate the absolute refractory period. The spikes generated from the MSO and LSO models drive the IC model via the same synaptic model as described for the AN to SOC synapses, but with different parameters. Two variants of the IC model were developed; in one version the inputs from the SOC are excitatory, while they are inhibitory in the other version. For both variants, only one MSO input and one LSO input were used to drive the IC model. The model parameters for both model versions are summarized in Table 2.

Table 2.

Default parameters for IC model

		MSO-IC Synapse					LSO-IC Synapse
Cm	gleak	τE	τE_rise	τI	τI_rise	No. of inputs	τE	τE_rise	τI	τI_rise	No. of inputs
31.4 pF	31.4 nS	1 ms	0.1 ms	5 ms	0.5 ms	1	1 ms	0.1 ms	5 ms	0.5 ms	1

IC, inferior colliculus. See text for parameter definitions.

RESULTS

Physiological Evidence for Dual ITD Sensitivity in IC with Broadband Noise

We characterized the envelope-ITD sensitivity of 30 high-frequency neurons (mean CF: 4,098 ± 1,728 Hz) in the IC of unanesthetized rabbits (n = 3). These data were collected as part of a larger study of spatial tuning for a large sample (n = 791) of IC neurons (Devore and Delgutte 2010). In that study, we showed that high-frequency IC neurons (CF > 1,850 Hz) typically exhibit sensitivity to ITD in the CG envelope of broadband noise stimuli (ITD_CG), while low-frequency IC neurons are sensitive to ITD in the noise waveform fine structure (Devore and Delgutte 2010). Each of the 30 neurons in the present study was classified as ITD_CG sensitive according to prior criteria (Devore and Delgutte 2010).

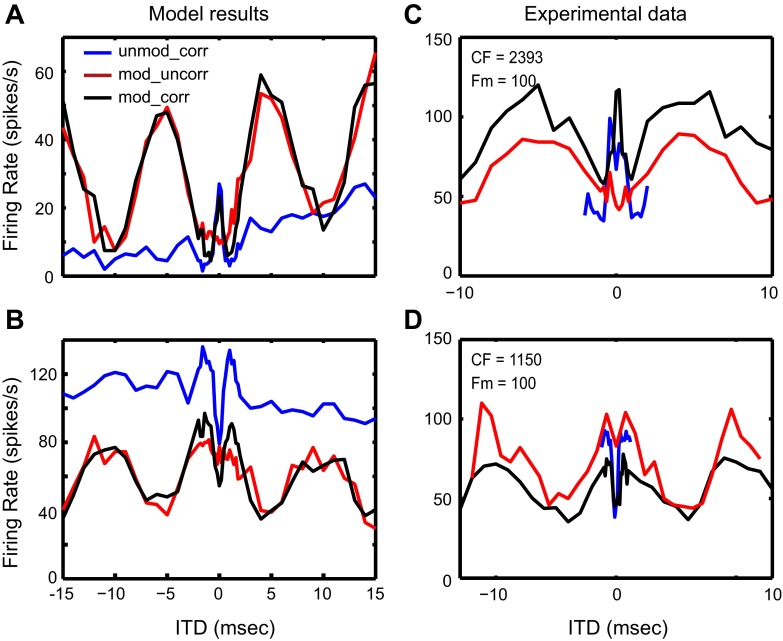
Our goal was to further characterize the ITD sensitivity of these high-frequency ITD_CG-sensitive neurons in the presence of an externally imposed SAM envelope. Figure 5 shows the response of six ITD_CG-sensitive neurons to three different types of broadband noise stimuli (see methods). The rate-ITD curves in response to binaurally identical noise waveforms with no amplitude modulation (unmod_corr, Fig. 5) typically exhibit either a single peak (Fig. 5, A and D) or a single trough (Fig. 5, B, C, E, and F), as expected for neurons that are ITD_CG sensitive (Devore and Delgutte 2010; Joris 2003). We next assessed ITD sensitivity to the externally imposed AM envelope (ITD_AM) by measuring the response to interaurally uncorrelated broadband noise with 100-Hz SAM (mod_uncorr, Fig. 5). Five of the six neurons in Fig. 5 (excluding Fig. 5B) exhibit cyclic variations in firing rate at the period of the externally imposed SAM. In contrast, the neuron in Fig. 5B shows no evidence for ITD_AM sensitivity, as evidenced by the flat mod_uncorr ITD curve. The sharp peak or trough resulting from ITD_CG sensitivity is not observed in the mod_uncorr condition because, for uncorrelated inputs, the envelopes generated by cochlear filtering will also be uncorrelated and thus there can be no ITD sensitivity to CG envelopes (Joris 2003). Overall, we observed ITD_AM sensitivity with mod_uncorr stimuli in 90% (27/30) of the ITD_CG-sensitive neurons.

There was a great diversity in the type of ITD sensitivity to each stimulus among our sample of units exhibiting both ITD_CG and ITD_AM sensitivity. In some neurons, the type of ITD_CG sensitivity was similar to that for ITD_AM. For example, the neuron in Fig. 5A responds to ITD_CG with a single peak centered around 0 ms (unmod_corr). The response to ITD_AM in the 100-Hz AM envelope (mod_uncorr) shows similar sensitivity, with a peak occurring around 0 ms ITD. Similarly, the neuron in Fig. 5C shows trough-type sensitivity to both ITD_CG and ITD_AM. However, in the majority of neurons, the sensitivity to ITD_CG differed from that observed in response to ITD_AM (Fig. 5, D–F). For example, the unit in Fig. 5D exhibits peak-type ITD_CG sensitivity but trough-type ITD_AM sensitivity, while the unit in Fig. 5E exhibits a prominent trough in response to ITD_CG but appears peaklike in response to ITD_AM. Finally, the unit in Fig. 5F exhibits trough-type sensitivity to ITD_CG, but this trough is located on the rising slope of the ITD tuning curve to the mod_uncorr stimulus, indicating a different type of sensitivity to the two types of envelope. In all cases (Fig. 5, A–F), the ITD tuning curve for the mod_corr stimulus was approximately the superposition of the response to ITD_CG and ITD_AM. The responses of the neurons in Fig. 5, D–F, are reminiscent of dual-CP neurons observed in the IC by Batra et al. (1993) in response to SAM tones and are also suggestive of convergent inputs from MSO and LSO.

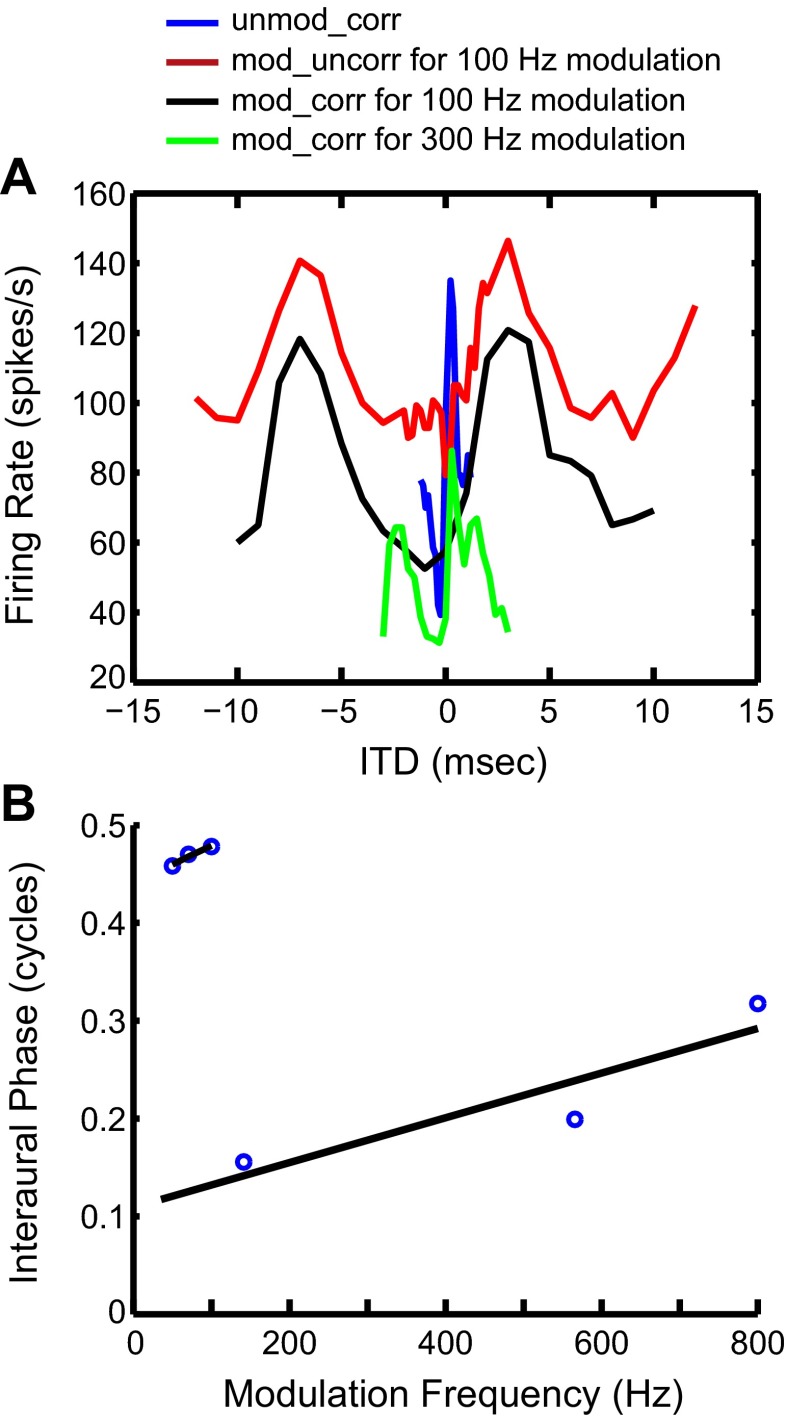
In one neuron (Fig. 6), we tested ITD sensitivity using binaural SAM tones in addition to the three broadband noise stimuli. With noise stimuli, this neuron shows trough-type sensitivity to ITD_AM and intermediate-type (biphasic) sensitivity to ITD_CG (Fig. 6A). With SAM tones, the phase plot of this neuron shows two linear segments (Fig. 6B). The low-f_m segment has a CP close to 0.5, characteristic of a trough-type response. The high-f_m segment has a CP around 0.1, which is significantly different from zero and therefore corresponds to an intermediate-type response. Thus the dual ITD sensitivity observed with noise stimuli is qualitatively consistent with the dual sensitivity observed with SAM tones in this neuron.

Fig. 6.

Responses of a single IC neuron to both SAM tones and broadband noises. A: rate-ITD functions for binaural broadband noises. Different colors represent different stimulus conditions, as indicated in key. The peak in the blue curve is not visible in the 100 Hz modulation case because in that case the ITD step is too large to allow the peak to appear. B: phase plot of this IC neuron in response to binaural SAM tones with 1-Hz difference in f_m between the 2 ears (binaural beat). Two black lines are linear fits for low f_m region and high f_m region.

Because most neurons in our sample were only tested at one f_m, their sensitivity to ITD_AM could not be quantitatively determined from a phase plot. Rather, we characterized the types of ITD sensitivity by defining at what phase of the ITD_AM curve—peak, trough, or slope—the main feature of the ITD_CG response appeared. For example, if a peak-type ITD_CG response appears in the trough of the ITD_AM curve, we classify the delay interaction as peak-trough. This method effectively assumes that the neuron's CD is small relative to the period of the low-frequency modulations, so that the response phase at f_m differs little from the CP. Table 3 lists the number of units falling into the different response classes. Overall, dual ITD sensitivity was observed in 14 of the 27 neurons (52%) sensitive to both ITD_CG and ITD_AM. Dual ITD sensitivity is thus common with broadband noise stimuli. Table 3 further shows that neurons with trough-type ITD_AM sensitivity and peak-type ITD_CG sensitivity were more common than the opposite pattern.

Table 3.

Breakdown of phase interactions for envelope-sensitive IC neurons

	Phase of AM Envelope Rate-ITD Curve at Which CG Envelope Feature Appears
Type of CG ITD Tuning	Peak	Slope	Trough	Total
Peak	5	1	7	13
Intermediate	0	2	2	4
Trough	2	2	6	10
Total	7	5	15	27

ITD, interaural time difference; CG, cochlear generated; AM, amplitude modulated.

We next use computational models to explicitly test whether convergent inputs from peak-type (MSO) and trough-type (LSO) inputs onto single IC neurons can generate the diversity in response profiles observed with noise stimuli in our sample of neurons as well as with SAM tones in the study of Batra et al. (1993).

Modeling IC Responses to Binaural SAM Tones

Results with HH-type MSO and LSO models.

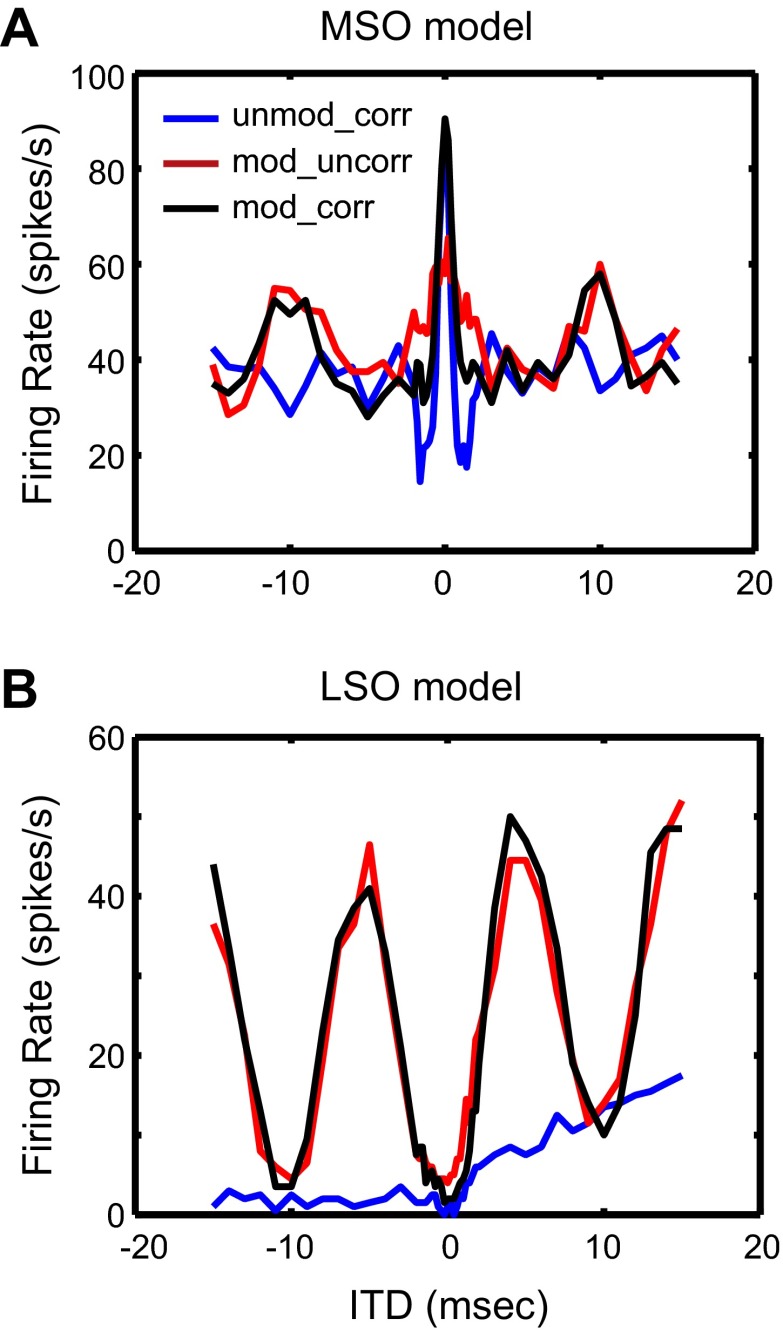
The IC model with convergent inputs from the MSO and the LSO is first used to simulate IC data for SAM tones. This section presents simulation results for inputs from existing HH-type MSO and LSO models. The parameters for the passive membrane properties and the ion channels in the MSO and LSO models were the same as in the original studies, i.e., Colburn et al. (2009) for the MSO and Wang and Colburn (2012) for the LSO. The average firing rate of the AN model R_avg was 150 spikes/s and the synchronization index SI was 0.7, as is typical for physiological measurements from the AN (Joris and Yin 1992, 1998). Typical responses of the MSO and LSO models to binaural SAM tones are shown as a function of f_m in Fig. 7. Figure 7A shows the average firing rate for both models, while Fig. 7B shows the corresponding SI with respect to the beat frequency. By construction, the mean interaural response phase was 0 at all f_m for the MSO model and 0.5 for the LSO model (not shown).

Fig. 7.

Responses of the HH-type MSO and LSO models to binaural SAM tones. A: binaural rate-f_m functions. B: binaural sync-f_m functions. Dashed lines show the output of the MSO model, and solid lines show the output of the LSO model. The membrane parameters for these models are given in Table 1, and the synaptic parameters are given here: for the AN to LSO synapse: str_E = 1 nS, str_I = 1.6 nS, τ_E = 2 ms, τ_{E_rise} = 0.2 ms, τ_I = 5 ms, τ_{I_rise} = 0.5 ms, N_E = N_I = 20; for the AN to MSO synapse: str_E = 15 nS, τ_E = 0.1 ms, τ_{E_rise} = 0.01 ms, N_E = 10.

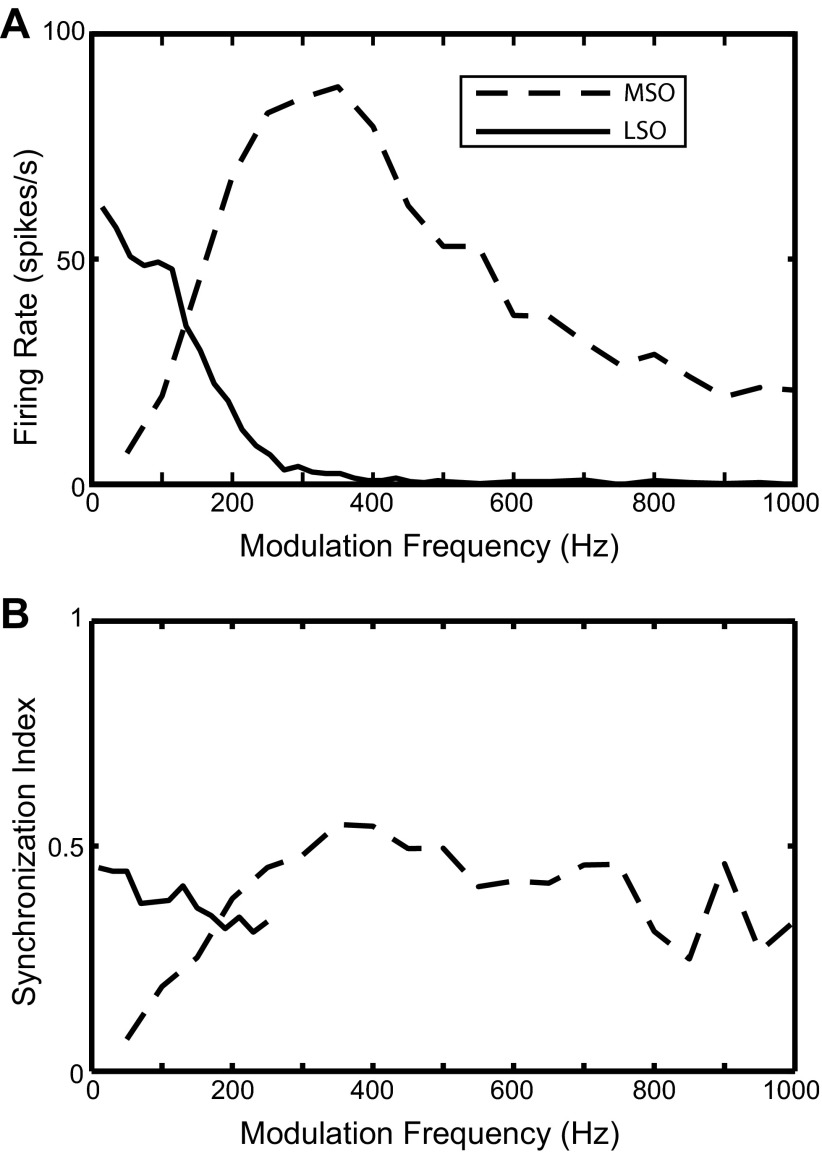
For the MSO model, the simulated binaural rate-f_m function has a band-pass shape with a maximum at 350 Hz and steep cutoffs on both sides. The corresponding binaural sync-f_m function gradually increases with f_m up to 350 Hz and then plateaus around 0.5. To investigate the underlying mechanism for the band-pass characteristic of the rate-f_m function, the MSO model was tested with constant current injections. The result shows that the MSO model only produces one spike at the stimulus onset in response to current steps up to 5 nA (not shown). This onset-type response is not caused by either the KLT channel or the I_h channel, since removing these channels did not significantly affect the response of the MSO model to current injections. Instead, the onset response might be created by the interaction between the sodium and potassium channels (both KHT and KLT). When the KLT channel was eliminated and both the Na and KHT conductances were increased by a factor of 8, the MSO model produced sustained response to current injections and the rate-f_m function became flatter than in the standard MSO model. These results suggest that the intrinsic properties in the MSO model are likely the main mechanism underlying the onset response to current injections and the band-pass tuning in the firing rate.

For the LSO model, the simulated binaural rate-f_m function is low pass, with essentially no response above 400 Hz (Fig. 7A). The SI is close to 0.5 at low f_m and decays with increasing f_m until it becomes statistically insignificant above 250 Hz (Fig. 7B). The low-pass characteristic of the rate-f_m function in the LSO model was produced without a KLT channel. Adding KLT channels did not significantly affect the low-pass profile of the binaural rate-f_m function in most cases, although when the KLT channel conductance was strong the rate-f_m function sometimes exhibited a high-pass segment at low f_m, producing a band-pass f_m tuning in the firing rate (results not shown). These results suggest that the KLT channel is not necessary to produce the low-pass feature in the LSO responses to binaural SAM tones. On the other hand, for SAM tones presented monaurally to the ipsilateral ear, the rate-f_m functions are also typically low pass but there is more variability across LSO neurons than in the binaural condition. In the monaural condition, KLT channels were shown likely to be the main mechanism underlying the low-pass f_m tuning in the firing rate of LSO cells (Wang and Colburn 2012). These contrasting results suggest that the low-pass character of the rate-f_m function in response to binaural and monaural SAM tones may be produced by different mechanisms. A likely explanation for the low-pass character of the binaural response is the interaction between ipsilateral excitation and contralateral inhibition received by the LSO. At low f_m, both the excitatory and the inhibitory synaptic conductances are phase locked to the modulation. Therefore, when the excitation and inhibition are out of phase, the excitation is only slightly suppressed by the inhibition. At higher f_m, the inhibition is no longer phase locked to the modulation because of its long time constant. This unmodulated inhibition suppresses the excitation more effectively than phase-locked inhibition, thus giving rise to a decreasing firing rate as f_m increases.

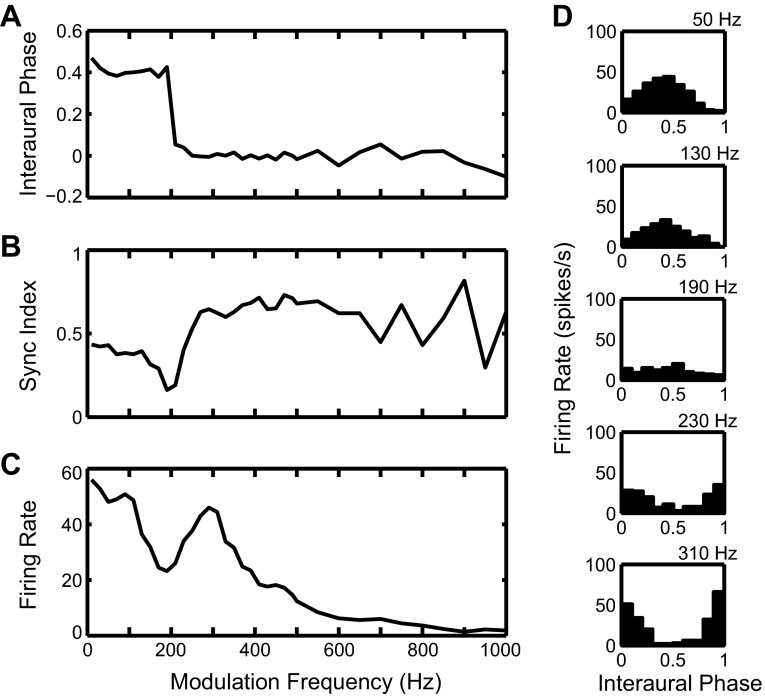
The responses of the MSO and LSO models shown in Fig. 7 were used as excitatory inputs to the IC cell model. Figure 8 addresses the temporal structure of the IC responses. Figure 8, A–C, show measures of temporal structure as a function of frequency, and Fig. 8D shows period histograms with respect to the binaural beat frequency. At low f_m (50 and 130 Hz), the period histograms show a single peak around 0.5 cycle, suggesting a dominance of the trough-type input from LSO. At high f_m (230 and 310 Hz), the peak of the period histograms shifts to 0 cycle, suggesting a dominance of the peak-type input from MSO. At an intermediate frequency (190 Hz), the period histogram is nearly flat and shows a decreased firing rate compared with responses at lower and higher f_m.

Fig. 8.

Responses of the leaky integrate-and-fire (LIF) IC cell model with inputs from HH-type MSO and LSO models. A: interaural phase as a function of f_m (phase plot). B: binaural sync-f_m function. C: binaural rate-f_m function. D: period histogram for 5 f_m. The synaptic parameters for the IC model shown in Fig. 3 are given here: for the MSO to IC synapse: str_E = 17.5 nS, τ_E = 1 ms, τ_{E_rise} = 0.1 ms; for the LSO to IC synapse: str_E = 18.25 nS, τ_E = 1 ms, τ_{E_rise} = 0.1 ms.

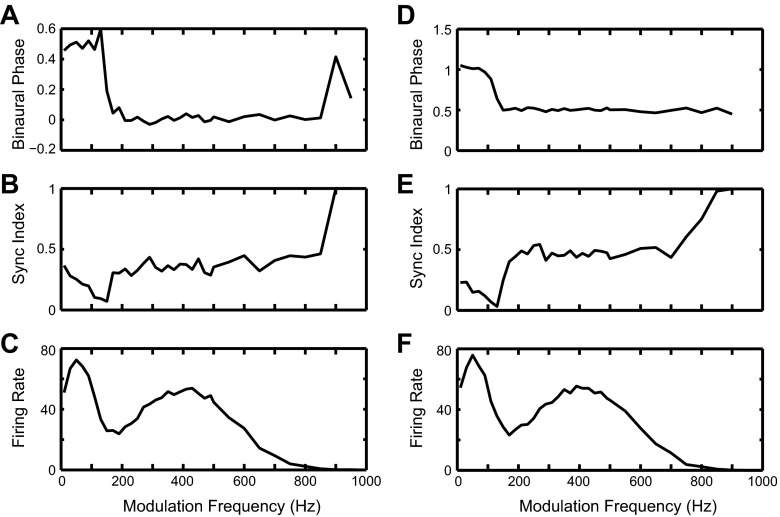
The mean interaural response phase (Fig. 8A) shows a sharp transition from 0.5 to 0 for f_m around 200 Hz. Both the average firing rate (Fig. 8C) and the synchronization index to the beat frequency (Fig. 8B) show a dip at the frequency of this phase transition, with elevated response on both sides of the dip. Together, these results indicate a transition from trough-type to peak-type response, similar to those seen in the experimental IC data (Fig. 1, top).

The results in Fig. 8 suggest that the IC model with convergent inputs from MSO and LSO can reproduce the trough-type to peak-type transition seen in some IC neurons. The key features of the model are the band-pass firing rate profile for the MSO and the low-pass profile for the LSO. At low f_m, the IC model shows the trough-type response inherited from its LSO input. As f_m increases, the LSO input rate decreases and the MSO input starts to dominate. The IC model then switches to the peak-type response inherited from its MSO input at high f_m. Near the transition frequency, the IC model receives weak inputs that are out of phase, resulting in a low firing rate and a flat period histogram. Note, however, that, although this IC model captures the half-cycle phase transition, it does not reproduce the large CD at low f_m (>1 ms) observed in some experimental data (Fig. 1, top). This issue is discussed in the following sections.

The IC model structure of Fig. 2 reproduces the IC responses with trough-type to peak-type transition. Some IC neurons show peak-type responses at low f_m and trough-type responses at high f_m (Fig. 1, bottom). In principle, a band-pass LSO input combined with a low-pass MSO input could reproduce the peak-type to trough-type transition. The HH-type LSO model used here was able to produce a band pass-shaped binaural rate-f_m function when it included a KLT channel (results not shown). The HH-type MSO model, however, never gave rise to a binaural low-pass f_m tuning in the firing rate for any of the parameters explored. To reproduce the peak-type to trough-type transition based on low-pass MSO input and band-pass LSO input, the structure of the IC model shown in Fig. 2 was modified. In the modified IC model structure (Fig. 9), the MSO and LSO inputs become inhibitory, and an additional excitatory monaural input (assumed to be from the contralateral CN) was added in order to induce discharges in the IC cell model. While Fig. 9 shows direct inhibitory projections from MSO and LSO to the IC, it is anatomically more likely that one or both of these projections would be implemented via an inhibitory interneuron that is assumed to act as a simple relay (see discussion). The same MSO and LSO inputs based on HH-type models as in Fig. 7 were used in the modified IC model, but now these inputs produced inhibitory PSCs in the IC cell model, and the synaptic strengths and time constants were also different from those used in the standard IC model in Fig. 2 (see Table 2). The additional monaural excitatory input in the modified IC model was the same AN input that was used to drive MSO and LSO models (R_avg = 150 spikes/s, SI = 0.7, φ = 0.5).

Fig. 9.

Diagram of the modified IC model with convergent inhibitory input from the MSO and the LSO and an additional excitatory CN input. Descriptions for the AN, CN, MSO, and LSO modules in the modified model are the same as the model in Fig. 2.

Figure 10 shows the responses of the modified IC model to SAM tones in the same format used for the original model in Fig. 8. The period histograms (Fig. 10D) show a peak near 0 cycle at low f_m (30 and 90 Hz), a peak near 0.5 cycle at high f_m (150 and 270 Hz), and a flat shape with decreased firing at 110 Hz. The phase curve (Fig. 10A) shows a sharp transition from a little less than 0 to 0.5 for f_m around 120 Hz. The synchronization to the binaural beat (Fig. 10B) is substantial for f_m above and below the phase transition, with a dip near the transition. The model also shows a broad trough in firing rate around the transition similar to the experimental data (Fig. 10C). These results suggest that the combination of a low-pass LSO input and a band-pass MSO input can also account for the peak-type to trough-type transition observed in some IC neurons, if these inputs are inhibitory and combined with another excitatory input.

Fig. 10.

Responses of the modified IC cell model in Fig. 9 with HH-type MSO and LSO models. Same format as Fig. 8. A: interaural phase as a function of f_m (phase plot). B: binaural sync-f_m function. C: binaural rate-f_m function. D: period histogram for 5 f_m. The synaptic parameters for the IC model shown in Fig. 9 are given here: for the MSO to IC synapse: str_I = 0.5 μS, τ_I = 5 ms, τ_{I_rise} = 0.5 ms; for the LSO to IC synapse: str_I = 0.5 μS, τ_I = 5 ms, τ_{I_rise} = 0.5 ms; for the CN to IC synapse: str_E = 20 nS, τ_E = 1 ms, τ_{E_rise} = 0.1 ms.

Results with phenomenological MSO and LSO models.

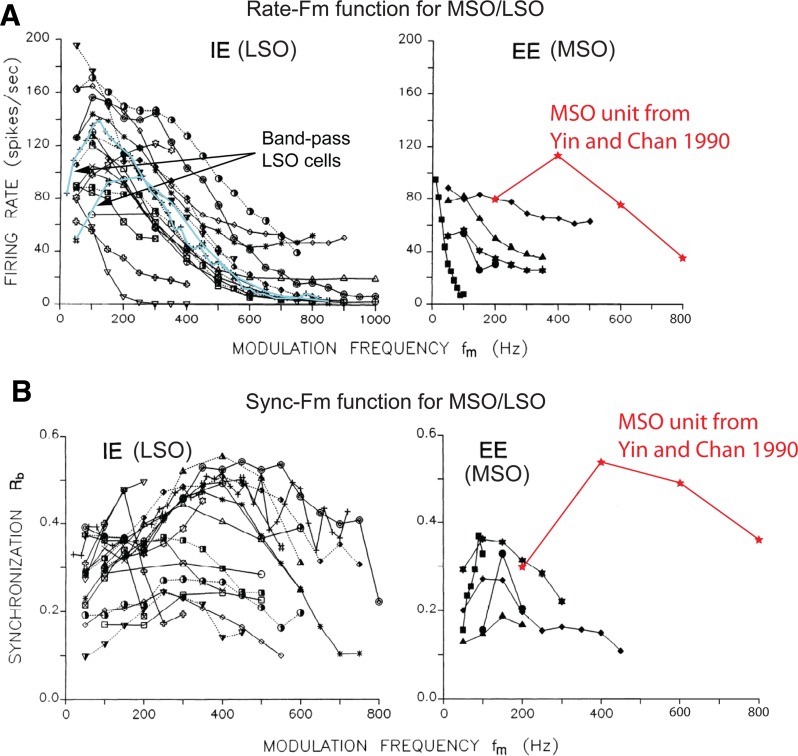
The HH-type LSO model gives rise to both low pass- and band pass-shaped binaural rate-f_m functions. In contrast, only band pass-shaped binaural rate-f_m functions were obtained with the MSO model. To test the validity of these constraints, the available data for the MSO and LSO are compared to model simulations. Joris (1996) reported binaural SAM tone responses for 21 high-frequency LSO units (CF > 2 kHz) and five MSO units (CF > 5 kHz). The majority of his LSO neurons exhibited prominent low-pass character in their binaural rate-f_m functions. A few LSO neurons, however, showed band pass-shaped binaural rate-f_m functions (Fig. 11A, left). The binaural sync-f_m functions for the LSO units (Fig. 11B, left) were more heterogeneous than the rate-f_m functions. Most of the SI values were between 0.2 and 0.5, and the dependence on f_m was rather shallow. Experimental data from the MSO in response to binaural SAM tones are much more limited. The firing rates in the five MSO cells from Joris (1996), shown in Fig. 11A, right, all decay as f_m increases, i.e., the functions are low pass. The amplitude and steepness of the rate decay vary among these five MSO cells. Yin and Chan (1990) reported the SAM tone response for another high-frequency MSO unit (red curves in Fig. 11, CF = 15 kHz). This unit showed band-pass characteristics in both firing rate and SI, with a peak at 400 Hz.

Fig. 11.

Experimental data for the MSO and the LSO in response to binaural SAM tones. A: binaural rate-f_m functions for the LSO (left) and the MSO (right). Each curve represents 1 neuron in the MSO or LSO. Examples of band-pass LSO neurons are highlighted with light blue curves (left). B: binaural sync-f_m functions for the LSO (left) and the MSO (right). Each curve represents 1 neuron in the MSO or the LSO. [Figure adapted from Joris (1996) with permission; data for additional MSO unit (red curves) from Yin and Chan (1990).]

The responses of the HH-type MSO and LSO models (Fig. 7) are consistent with the experimental data in some respects. The binaural rate-f_m function of the LSO model (Fig. 7A) captures the predominant low-pass trend seen in Fig. 11A, left. The band-pass feature in the binaural rate-f_m function of the MSO model is similar to the MSO unit in Yin and Chan (1990) but not to the five units in Joris (1996). The SI values of the model responses and the experimental data are also in the same range. Despite this agreement, the fact remains that some features of the experimental data are not captured by these HH-type models, most notably the fact that all MSO cells in Joris (1996) show a low-pass instead of a band-pass characteristic in their binaural rate-f_m function.

To test our IC model using MSO and LSO inputs that represent the full range of the experimental data, phenomenological MSO and LSO models (Fig. 4) were used as inputs to the basic IC model of Fig. 2. Three synthetic binaural rate-f_m functions were generated to cover the range of observations from both the MSO and the LSO: sharp low-pass (black solid curve in Fig. 4), broad low-pass (gray curve in Fig. 4) and band-pass (dashed curve, Fig. 4). For all three possible binaural rate-f_m functions, the binaural sync-f_m function was a constant at 0.25 for the MSO model and at 0.33 for the LSO model. Each MSO binaural rate-f_m function was paired with each LSO binaural rate-f_m function. Each pair of binaural rate-f_m functions was used to generate convergent MSO and LSO inputs to the IC model with the original model structure in Fig. 2.

Among the nine possible pairs of inputs, only two pairs of MSO and LSO inputs reproduced the key features of the data from dual-CP neurons, that is, a half-cycle phase transition and a trough in the firing rate at the transition frequency. The first pair comprises the band-pass MSO input (Fig. 4) and the sharp low-pass LSO input (Fig. 4), which gave rise to IC responses with a trough-type to peak-type transition (Fig. 12, A–C). The second pair comprises the sharp low-pass MSO input (Fig. 4) and the band-pass LSO input (Fig. 4), which produced IC responses with a peak-type to trough-type transition (Fig. 12, D–F). The results in Fig. 12, D–F, suggest that the peak-type to trough-type transition could also be explained by convergent excitatory inputs from the MSO and the LSO, as an alternative to the convergent inhibitory input mechanism used in the modified IC model (Fig. 9). When the IC model responses using other pairs of inputs were examined, the phase plots showed a half-cycle phase transition in some cases, but the corresponding IC firing rate did not show a dip in the transition region (results not shown). These results suggest that only when MSO and LSO inputs are tuned to well-separated f_m regions with minimum overlap can they explain the responses of those dual-CP IC neurons that show a dip in their firing rate at the transition frequency. Although all the examples of dual-CP neurons shown by Batra et al. (1993) featured a dip in firing rate at the phase transition, there may exist neurons with little or no dip. Reponses of such neurons could be explained by other pairs of MSO and LSO inputs, e.g., combination of broad low-pass and band-pass inputs.

Fig. 12.

Responses of the IC cell model with inputs from phenomenological MSO and LSO models. A–C: same format as Fig. 8, A–C. The binaural rate-f_m function is band pass for the MSO (Fig. 4, dashed curve) and sharp low pass for the LSO (Fig. 4, black solid curve). For the MSO to IC synapse: str_E = 18 nS, τ_E = 1 ms, τ_{E_rise} = 0.1 ms; for the LSO to IC synapse: str_E = 20 nS, τ_Ee = 1 ms, τ_{E_rise} = 0.1 ms. D–F: same format as Fig. 8, A–C. The binaural rate-f_m function is sharp low pass for the MSO (Fig. 4, black solid curve) and band pass for the LSO (Fig. 4, dashed curve), opposite to the combination used in A–C. For the MSO to IC synapse: str_E = 19 nS, τ_E = 1 ms, τ_{E_rise} = 0.1 ms; for the LSO to IC synapse: str_E = 18 nS, τ_E = 1 ms, τ_{E_rise} = 0.1 ms.

Both neurons in Fig. 1 show a rising slope in their phase plots at low f_m, a feature that was not reproduced by the IC model. This slope corresponds to a nonzero CD of the IC neuron. Because the interaural delays for the MSO and LSO models used so far were always fixed at zero, it is not surprising that the IC model responses do not exhibit the rising slope at low f_m. Figure 13 shows that the nonzero CD in the experimental IC data can be reproduced by introducing nonzero internal interaural delays in the SOC inputs. The experimental phase plots from Fig. 1 are replotted in Fig. 13, A and B, to facilitate comparison. Superimposed upon the data are the phase plots generated by the IC model with convergent inputs from the same pairs of phenomenological MSO and LSO models used in Fig. 12, except that nonzero interaural delays were introduced for the sharp low-pass MSO and LSO inputs. (The interaural delays for the band-pass MSO and LSO inputs were still zero.) For both neurons in Fig. 13, A and B, the IC model not only reproduces the half-cycle phase transition described above but also captures the rising slope at low f_m in the phase plot.

Fig. 13.

Measured and simulated phase plots for 3 high-frequency intermediate-type IC neurons. Black dots represent experimental data. Black lines are the linear fit for the experimental data at low f_m and high f_m. Red curve represents the simulated phase plot of the IC model. A: empirical phase plot is the same as that shown in Fig. 1 (top right). The inputs to the IC model are the same as in Fig. 12, A–C, except that an interaural delay of 1 ms is included in the LSO input. B: empirical phase plot is the same as that shown in Fig. 1 (bottom right). The inputs to the IC model are the same as in Fig. 12, A–C, except that an interaural delay of 3 ms is included in the MSO input. C: empirical phase plot is for a high-frequency IC neuron with nonlinear phase plot [adapted from Batra et al. 1993 with permission]. To simulate this phase plot, the IC model receives 2 LSO inputs. The binaural rate-f_m function is sharp low pass for one LSO input (black solid curve in Fig. 4) and band pass for the other LSO input (dashed curve in Fig. 4). The interaural delay was 2 ms for the low-pass LSO input and 0 for the band-pass LSO input. Note the curvature in both empirical and simulated phase plots at low f_m (<250 Hz). For the low-pass LSO input to the IC: str_E = 18 nS, τ_E = 1 ms, τ_{E_rise} = 0.1 ms; for the band-pass LSO input to the IC: str_E = 15 nS, τ_E = 1 ms, τ_{E_rise} = 0.1 ms.

Besides IC neurons with dual CPs, high-frequency IC neurons can exhibit other types of nonlinear phase plots in response to envelope-ITDs (Batra et al. 1993). Some neurons show peak-type or trough-type responses at high modulation frequencies and more complex nonlinear patterns at low modulation frequencies (e.g., Fig. 13C). A version of the IC model with convergent inputs from two phenomenological LSO models can reproduce the phase plot in Fig. 13C if the two LSO inputs have different binaural rate-f_m functions and also different CDs (Fig. 13C). In this case, the binaural rate-f_m function for one LSO input was sharp low pass and the function for the other LSO input was band pass. The low-pass LSO input had a 2-ms CD, which caused the interaural phase of the IC to deviate from 0.5 at low f_m. The band-pass input had a zero CD, which gave rise to a constant interaural phase of 0.5. This band-pass LSO input caused the interaural phase of the IC to recover back to 0.5 when this input became dominant at high f_m. This result shows that the IC model structure with convergent inputs can account for nonlinear phase plots in the IC other than those with dual CPs.

Modeling IC Responses to Binaural Broadband Noises

The IC model was also used to simulate the dual types of ITD sensitivity observed in response to binaural noises (Fig. 5, D and E; the same data are replotted in Fig. 15, C and D). For these simulations, the simplified AN model was replaced by a detailed AN model (Zilany et al. 2009) to provide realistic simulations of AN responses to noise. Only HH-type MSO and LSO models were used for these simulations. The membrane descriptions of the MSO, LSO, and IC as well as the synaptic parameters for the AN-MSO and AN-LSO synapses were the same as used in modeling response to binaural SAM tones. The only model parameters that had to be changed to reproduce the IC data for broadband noises were the synaptic strengths for the MSO-IC and LSO-IC synapses (see discussion).

Fig. 15.

A and B: rate-ITD functions of the IC model with inputs from HH-type MSO and LSO models in response to broadband noises. A: IC model responses with convergent excitatory inputs from the MSO and the LSO models (same structure as Fig. 2). The synaptic parameters for this IC model are given here: for the MSO to IC synapse: str_E = 18 nS, τ_E = 1 ms, τ_{E_rise} = 0.1 ms; for the LSO to IC synapse: str_E = 19 nS, τ_E = 1 ms, τ_{E_rise} = 0.1 ms. B: IC model responses with convergent inhibitory inputs from the MSO and the LSO models and an additional excitatory CN input (same structure as Fig. 9). The synaptic parameters for this IC model are given here: for the MSO to IC synapse: str_I = 10 nS, τ_I = 5 ms, τ_{I_rise} = 0.5 ms; for the LSO to IC synapse: str_I = 100 nS, τ_I = 5 ms, τ_{I_rise} = 0.5 ms; for the CN to IC synapse: str_E = 20 nS, τ_E = 1 ms, τ_{E_rise} = 0.1 ms. C and D: experimental data for the IC in responses to broadband noises. C: same as Fig. 5D. D: same as Fig. 5E.

Responses of the MSO and LSO models to broadband noises are shown in Fig. 14. The MSO model ITD tuning function shows a large peak in firing rate at zero ITD in response to ITD_CG and small modulations in firing rate in response to ITD_AM (Fig. 14A). The low firing rates and weak sensitivity to ITD_AM in the MSO model are consistent with the f_m (100 Hz) being below the peak of the band-pass response of the MSO model to SAM tones (Fig. 7). In contrast, the LSO model response exhibits strong modulations in firing rate as a function of the ITD_AM and a weak trough-type sensitivity to ITD_CG. The strong sensitivity to AM envelope ITDs is consistent with the low-pass response of the LSO model to binaural SAM tones, which gives rise to a high firing rate at 100 Hz (Fig. 7). The low firing rate in response to ITD_CG is probably due to the strong contralateral inhibition suppressing the ipsilateral excitation nearly completely for ITDs near zero. The slow increasing trend in the response to ITD_CG for positive ITDs results from an onset response due to the delay of the inhibition relative to excitation for positive ITDs, i.e., it represents sensitivity to onset ITD rather than envelope ITD.

Fig. 14.

Rate-ITD functions of the HH-type MSO and LSO models to binaural broadband noises. A: MSO model. B: LSO model. Different colors represent different stimulus conditions (same as Fig. 5). The membrane parameters for these models are given in Table 1, and the synaptic parameters are given here: for the AN to MSO synapse: str_E = 15 nS, τ_E = 0.1 ms, τ_{E_rise} = 0.01 ms, N_E = 10; for the AN to LSO synapse: str_E = 1 nS, str_I = 1.6 nS, τ_E = 2 ms, τ_{E_rise} = 0.2 ms, τ_I = 5 ms, τ_{I_rise} = 0.5 ms, N_E = N_I = 20.

When MSO and LSO responses in Fig. 14 are used to drive the original IC model via excitatory synapses (Fig. 2), the IC model shows a peak-type response to ITD_CG and a trough-type response to ITD_AM (Fig. 15A), comparable to the experimental data in Fig. 15C. To reproduce the opposite response pattern with peak-type response to ITD_AM and trough-type response to ITD_CG that is also observed, although less frequently, in the experimental data (Fig. 15D), the modified IC model (Fig. 9) with convergent inhibitory inputs from the MSO and the LSO was used. The resulting IC model responses (Fig. 15B) qualitatively capture the dual types of ITD sensitivity in the IC neuron shown in Fig. 15D. Although the general shapes of the curves in Fig. 15 are similar between the experimental data and the model results, the relative heights of the three curves in the model do not match the neural data. Additional inputs to the IC, such as a monaural inhibitory input, may produce different DC shifts in the three curves and lead to improved matches with the experimental data.

The simulation results for broadband noises presented above were made at a fixed sound level (60 dB SPL), consistent with the experimental IC data, which were also obtained at a single sound level for each neuron. To investigate how sound level affects IC responses, the sound level of the broadband noise was varied, with all parameters of the IC model kept fixed. For both the MSO and the LSO models, the ITD sensitivity to CG envelopes was not significantly affected by sound level; however, the modulation of the firing rate caused by ITD_AM was strongest at intermediate levels (60–70 dB) for both the MSO and LSO models. The weak ITD_AM sensitivity at low levels is probably due to the low overall firing rate of the input and the concomitant small changes in the firing rate when ITD changes. High sound levels also give rise to weak envelope-ITD sensitivity because saturation at the hair cell synapse decreases the modulation depth of the inputs. The effects of sound level on the IC model response were similar to those on the MSO and LSO models, since the responses of the IC model closely resemble the superposition of the MSO and LSO model responses.

DISCUSSION

The experimental and computational modeling results presented here address interaural sensitivity to the temporal structure of the envelopes of high-frequency waveforms. Specifically, attention was focused on previously published complex responses of IC neurons to SAM tone stimuli (e.g., Batra et al. 1993) and new data on IC neuron responses to broadband noise waveforms. Results show that a relatively straightforward conceptual structure is consistent with almost all aspects of these data.

As shown by the empirical and computational results presented above, the responses to broadband noise in neurons with dual-type ITD sensitivity are consistent with the responses of these neurons to SAM tones as a function of f_m. While the dual types of envelope-ITD sensitivity observed by Batra et al. (1993) were separately evoked by SAM tones of different frequencies, our results with SAM broadband noise show that the two types of sensitivity can be simultaneously observed with the same stimulus. Using convergent inputs from the MSO and the LSO, the IC model reproduced the complex forms of ITD sensitivity observed in the data for both SAM tones and broadband noises. For the IC model to reproduce responses to SAM tones, it was critical that the firing rates of the MSO and the LSO inputs be tuned to different f_m regions with minimal overlap, i.e., one had to be sharply low pass and the other one had to be band pass. The same IC model could reproduce the IC data for broadband noises, although different synaptic strengths for the SOC to IC synapses were required. In the following sections, these basic conclusions are discussed in more detail, first for the responses to SAM tones and then for the response to broadband noises.

IC Responses to SAM Tones

Comparison with previous IC models with convergent inputs from SOC.

Using a physiologically based computational model of the IC, we showed that convergent inputs from the MSO and the LSO onto single IC neurons are sufficient to create the nonlinear phase plots observed in dual-CP IC neurons in response to SAM tones. The key assumptions in this model are that each IC cell receives independent inputs from SOC neurons with different types of ITD sensitivity (i.e., peak and trough) and different binaural f_m tuning. An IC model based on similar assumptions was developed previously to explain the complex phase plots of low-frequency IC neurons sensitive to ITD in the temporal fine structure (Shackleton et al. 2000). In that model, the inputs to the IC cell are either from two MSO cells or from one MSO cell and one LSO cell and the two input cells typically have different CFs. Because of the different frequency tuning between the two inputs, the response of the IC cell transitions from being dominated by the lower-CF input at low frequencies to being dominated by the higher-CF input at high frequencies.

The present IC model is similar to the model of Shackleton et al. (2000) in that both models use two SOC cells with different frequency and ITD tuning to provide convergent input to the IC; however, the two models differ in the origin of the frequency tuning in the input SOC cells. The different frequency tunings for the MSO and LSO cells of Shackleton et al. (2000) directly result from the different CFs of their low-frequency AN fiber inputs, which in turn reflects different sites of innervation along the cochlea. The discharge rates of most high-frequency AN fibers, however, do not show a systematic dependence on f_m over the range investigated (Joris and Yin 1992, 1998). Therefore, in our model, the different f_m tunings in the binaural rate-f_m function of high-frequency MSO and LSO cells are not inherited from the AN inputs. Instead, for the MSO model, intrinsic membrane properties, i.e., the interaction between sodium and potassium channels, appear to be the main mechanism for the band-pass characteristic in the binaural rate-f_m function. For the LSO model, the interaction between the faster ipsilateral excitation and the slower contralateral inhibition seems to be the main factor underlying the low pass-shaped binaural rate-f_m function.

The two mechanisms for producing different frequency tuning are not mutually exclusive, that is, the CFs of the MSO input and the LSO input could also be mismatched for some high-frequency IC neurons and this CF mismatch could contribute to the nonlinear phase plot of dual-CP neurons. When the CFs of the MSO and LSO inputs are mismatched, the CF of at least one of these inputs must be different from the carrier frequency of the SAM tone stimuli. To test the possible effect of CF on the responses of the MSO and LSO models, the detailed AN model (Zilany et al. 2009) was used to provide inputs to the MSO and LSO models, and the responses to binaural SAM tones were obtained when CF of the AN input to the MSO or LSO model was systematically varied around the fixed carrier frequency of the SAM tone. Results showed that changing the CF of the AN fibers could, in some cases, slightly sharpen the f_m tuning in the MSO and the LSO model. As a result, MSO and LSO models with different CFs allowed the IC model to produce slightly improved matches with the experimental data compared with the case when MSO and LSO models with the same CF were used to drive the IC model. However, in general a CF mismatch between the MSO and LSO inputs did not appear to be sufficient by itself to create the different f_m tuning in the firing rates of the MSO and LSO inputs.

Alternative mechanisms for creating nonlinear phase plots.

In addition to convergent inputs from SOC discussed above, other mechanisms have been proposed to account for nonlinear phase plots in low-CF SOC neurons. Batra et al. (1997) suggested that additional monaural excitatory and inhibitory inputs with different delays may converge onto coincidence detector cells in the SOC and influence ITD tuning. They developed a model to show that such connections can account for certain types of nonlinearities in the phase plots. It is not clear, however, whether their model can reproduce the dual CPs observed in high-CF IC neurons. Batra et al. (1997) further suggested that phase plots in the SOC and the IC show different kinds of nonlinearities, and, in particular, phase plots with multiple linear segments have only been observed in the IC. Therefore, mechanisms like the one proposed by Batra et al. (1997) that operate at the site of primary binaural interaction using monaural inputs would not be expected to explain the emergent nonlinearities in the IC, including phase plots with dual CPs.

Bonham and Lewis (1999), on the other hand, showed that a simple coincidence detector with CF-mismatched AN inputs can produce a curvature in the phase plot for pure-tone stimuli. Day and Semple (2011) also showed that a model MSO cell with CF-mismatched AN inputs can reproduce the nonlinear phase plots observed in MSO neurons for low-frequency pure tones. The key factor in these two models is the frequency-dependent cochlear delay mismatch induced by the mismatch in the CFs of the AN inputs from the two sides. This mismatch in cochlear delay, however, is likely to be very small for high-CF AN fibers, which have smaller group delays than low-CF AN fibers. In addition, the function relating the group delay to cochlear place is downward convex, meaning that the same CF mismatch (in octaves) will produce a smaller delay mismatch in the high-CF region than in the low-CF region (Joris et al. 2006; Recio-Spinoso et al. 2005). Therefore, the mechanism based on mismatched CFs is unlikely to produce sufficient differences in group delays to account for the nonlinear phase plots of high-CF IC neurons.

Convergent inhibitory inputs from SOC to IC.

We found that convergent inhibitory inputs from peak-type and trough-type neuron models can explain the peak-type to trough-type transition observed in some IC neurons. The connection structure in Fig. 9 was assumed because the binaural rate-f_m functions of the HH-type MSO and LSO models were band pass and low pass, respectively, making it impossible to create a peak-type to trough-type transition with purely excitatory inputs. However, direct inhibitory projections from the MSO and the LSO to the IC as assumed in Fig. 9 are undoubtedly an oversimplification of actual neural connections. Most MSO cells contain excitatory neurotransmitters (Kumoi et al. 1993; Oliver et al. 1995), and the contralateral projection from the LSO to the IC is also excitatory (Oliver et al. 1995). Thus the direct inhibitory projections as shown in Fig. 9 are probably physiologically unrealistic. A more likely neural connectivity is that the MSO and the LSO influence the IC response via inhibitory interneurons that could be located either in the DNLL or in the IC itself. The DNLL contains primarily GABAergic neurons that receive inputs from MSO and LSO and project to the IC (Adams and Mugnaini 1984; Helfert and Aschoff 1997). The IC contains many inhibitory interneurons that could influence the responses of principal IC neurons via local circuits (Gonzalez-Hernandez et al. 1996). Although the actual neural connections may differ from cell to cell, the critical feature to obtain a peak-type to trough-type transition is the conversion of excitatory MSO and LSO inputs into inhibitory inputs.

One way to create the peak-type to trough-type transition without using inhibition is to combine a low-pass MSO input and a band-pass LSO input in a single IC cell as shown with the phenomenological MSO and LSO models (Fig. 12, D–F). This mechanism is appealing for its simplicity. Although most of the LSO cells studied by Joris (1996) showed a low-pass characteristic in their binaural rate-f_m functions, a few did show band-pass binaural rate-f_m function. In addition, all MSO cells in Joris (1996) had low-pass binaural rate-f_m functions. So it is possible that some IC neurons generate a peak-type to trough-type transition via convergent input from a band-pass LSO cell and a low-pass MSO cell.

Limitation of the HH-type MSO model.

Our HH-type MSO model predicts band-pass shapes for binaural rate-f_m function, consistent with one MSO cell in Yin and Chan (1990), but it does not reproduce the low pass-shaped binaural rate-f_m functions observed by Joris (1996) in all of his MSO cells. To rule out the possibility that the limited range of model responses is due to the particular characteristics of our MSO model, we also tested a multicompartment MSO model developed by Mathews et al. (2010). The parameters of this model were adjusted to generate realistic rate-ITD tuning functions for low-frequency pure tones (Brughera et al. 2013). The simplified AN model (based on Poisson processes describing responses to SAM tones) was used to drive the compartmental MSO model. Although the structure and parameters of the two MSO models differed, the multicompartment model also predicted band-pass binaural rate-f_m functions. This is not unexpected because both MSO models tested show phasic responses to current injections, i.e., they fire just one spike at the onset. Phasic cell models typically respond poorly to low-frequency inputs (Gai et al. 2010), therefore giving rise to band-pass binaural f_m tuning in the firing rate. The low-pass binaural rate-f_m functions seen in the majority of available MSO data (Fig. 11A, right) are somewhat unexpected and may be due to certain intrinsic properties in the MSO cell that are not captured by the HH-type MSO models or to additional inputs from lower nuclei. In any case, more data are needed to confirm the prevalence of low-pass f_m tuning in high-frequency MSO cells and to elucidate the mechanism underlying the low pass-shaped binaural rate-f_m function.

Large internal delay for SOC input to IC.

To account for the nonlinear phase plot of the IC neuron in Fig. 13C, a 2-ms CD was required for the low-pass LSO input that controlled the behavior of the IC model neuron at low f_m. Other dual-CP neurons in the IC also show large CDs at low f_m (Fig. 1). The CDs measured from MSO and LSO in response to SAM tones were always lower than 1 ms (Joris 1996), but only a small number of neurons have been studied, so it is possible that units with large CDs do exist in the MSO and LSO but have not been sampled yet. Alternatively, such long delays could be generated at sites farther up the auditory pathway than the SOC, such as the DNLL and the IC. For example, an IC neuron with a monaural input from one side and another monaural input from the other side could give rise to long delays (larger than 2 ms) if one monaural input has longer synaptic delays than the other input. If this IC neuron also receives an input from the MSO or the LSO that is tuned to higher f_m, this neuron might exhibit intermediate-type responses or dual types of ITD sensitivity with long delays at low f_m.

IC Responses to Broadband Noises

Relationship with IC responses to SAM tones.

The IC model presented here suggests that convergent inputs from the MSO and the LSO can account for the dual types of envelope-ITD sensitivity in the IC in response to either SAM tones or broadband noises. One of the IC neurons studied with broadband noise was also examined with binaural SAM tones (Fig. 6). With SAM tone stimulation, this neuron showed a trough-type response to low f_m and intermediate-type response to high f_m (Fig. 6B). This pattern is consistent with the trough-type ITD sensitivity to slower AM envelopes and the intermediate-type ITD sensitivity to faster CG envelopes (Fig. 6A) obtained with broadband noise stimuli. These very limited data provide direct evidence that the dual types of envelope-ITD sensitivity observed with SAM tones and broadband noises could be due to a common mechanism.

The IC models used to reproduce the SAM tone data and the broadband noise data, respectively, shared the same membrane properties for the MSO, LSO, and IC and the same parameters for the AN-MSO and AN-LSO synapses. The only model parameters that had to be changed to reproduce both sets of IC data were the synaptic strengths for the MSO-IC and LSO-IC synapses. Specifically, for the IC model with excitatory inputs from the MSO and the LSO used to reproduce trough-type to peak-type transitions (Fig. 2), the synaptic strengths of the SOC inputs to the IC were increased by a few percent to account for the noise data; for the IC model with inhibitory inputs from the MSO and the LSO used to reproduce peak-type to trough-type transitions (Fig. 9), the synaptic strengths of the SOC inputs to the IC had to be decreased by at least a factor of five. This parameter difference between the IC models used with SAM tones and broadband noises might be due to the different sound levels used in the two sets of experiments. To explore this hypothesis, the detailed AN model was used as input to the SOC models with SAM tone stimulation so that the sound level could be varied; however, varying the sound level did not lead to a unified IC model with common parameters (results not shown). It is possible that a broader parameter space of the membrane description of the MSO, LSO, and IC neurons has to be explored to reproduce the two sets of IC data using a unified IC model. Alternatively, stimulation with broadband noise might recruit additional inputs to the IC that are not activated by narrowband stimulation with SAM tones and not explicitly included in the IC model structure.

Other response patterns in IC responses to SAM noise.

Besides IC neurons with dual types of ITD sensitivity (Fig. 5, D and E), other IC neurons exhibit complex patterns in responses to ITD_AM and ITD_CG. For example, some neurons are sensitive to ITD_CG but not ITD_AM (Fig. 5B). The lack of ITD_AM sensitivity in these neurons could be due to the low firing rate of the SOC input in response to the slow envelopes (f_m = 40 or 100 Hz) used in the experiments. Some MSO and LSO neurons show band-pass characteristics in their binaural rate-f_m functions (Fig. 11), providing a possible basis for low firing rates at low f_m. Yet another type of IC neuron shows intermediate-type responses to ITD_CG (Fig. 6). The biphasic rate-ITD functions of these neurons may come from a combination of peak-type and trough-type inputs with slightly different interaural delays. Finally, some IC neurons are sensitive to ITD_AM, but neither the peak nor the trough in their rate-ITD tuning curve occurs at zero ITD (Fig. 5F). Their responses to AM envelopes may be explained by long interaural delays from SOC inputs or by binaural interactions occurring de novo in the DNLL or IC, as discussed above for IC responses to SAM tones. In summary, the responses of essentially every IC neuron in our sample could potentially be explained by simple combinations of SOC inputs to the same IC cell model.

Relative delay between MSO and LSO inputs.

As discussed above, the inhibitory inputs to the IC in the model structure of Fig. 9 are presumed to come from inhibitory interneurons in the DNLL or the IC even though the simulations ignored the effect of these intervening synapses. In particular, the additional delay in the inhibitory inputs relative to the direct inputs from the SOC was not included. To investigate the effect of delays in the inhibition on the IC responses, one of the inhibitory inputs in the modified IC model (Fig. 9) was delayed relative to the other input (up to 50 ms), creating a relative time shift between the MSO and the LSO inputs. The IC model responses to SAM tones and SAM noises were not significantly affected by the delay in the inhibition (results not shown). This is because, for SAM tones, the MSO and LSO models are tuned to different f_m, with the MSO being band pass and the LSO being low pass. Therefore, in the f_m range where one input is dominant over the other input, a relative delay between the two inputs does not significantly change the IC response. Furthermore, even in the f_m region where both the MSO and LSO inputs are activated, because the delay created by the inhibitory interneurons is much smaller than the binaural beat period (1 s), this delay is not sufficient to greatly affect the IC responses. In the SAM noise cases, consistent with the different f_m tuning in response to SAM tones, each SOC input (MSO or LSO) is primarily driven by one type of envelope-ITD. Specifically, the MSO response is strongly modulated by ITD in the faster CG envelope while the LSO response is strongly modulated by ITD in the slower AM envelope (cf. Fig. 14). As a result, the IC model response is dominated by one of the two SOC inputs and is not greatly sensitive to the time shift between the MSO and LSO inputs.

Functional significance of neurons with dual types of envelope-ITD sensitivity.

Neurons with dual types of sensitivity were quite common among IC neurons that were sensitive to ITD_CG and ITD_AM of broadband noise, forming roughly one-half of the sample. While Batra et al. (1993) did not specify the incidence of dual-CP neurons with SAM tone stimulation, it is clear from the examples shown that different types of ITD sensitivity to low and high f_m are common in their data. If, as our modeling suggests, such dual types of sensitivity to envelope-ITD are created via convergent inputs from MSO and LSO, an obvious question is, what is the functional significance of such convergence?

For neurons with dual ITD sensitivity, the sensitivity occurring at higher f_ms is likely to be the most functionally relevant because the changes in interaural phase within the natural range of ITDs for low f_ms are too small to significantly modulate the neurons' firing rates. This is shown in the example neurons in Fig. 5, where the variations in firing rate within the ±300-μs natural range of ITDs for the rabbit are much greater for the unmod_corr stimulus (which contains CG envelope ITDs) than for the mod_uncorr stimulus (which has imposed AM). When both ITD_CG and ITD_AM are present in the mod_corr stimulus, the sensitivity within the natural ITD range resembles that for CG envelope only, with the effect of the imposed AM being mainly that of raising or lowering the overall firing rate. Thus ITD sensitivity to the low f_ms tested is very weak within the natural range and unlikely to be functionally significant in most situations.

What then is the function of the SOC input tuned to low f_ms that gives rise to ITD_AM tuning in the model? In cases when ITD sensitivity to low frequencies is trough type and sensitivity to high frequencies is peak type, the low-frequency input is thought to come from LSO. While LSO neurons are sensitive to envelope ITDs, they are also sensitive to interaural level differences (ILDs) via an EI interaction (Batra et al. 1997; Boudreau and Tsuchitani 1968; Caird and Klinke 1983; Finlayson and Caspary 1989, Joris 1996; Joris and Yin 1995; Sanes 1990; Tollin and Yin 2005). As suggested by Batra et al. (1993), high-CF IC neurons with trough-type ITD sensitivity at low f_ms and peak-type sensitivity at high frequencies are therefore likely to be sensitive to both ILD and envelope ITDs within the natural range. Such neurons, which were common in our sample, might play a role in the integration of directional information from ILD and envelope ITD, which are the two main acoustic cues for azimuthal localization at high frequencies. A specific functional role for neurons with peak-type to trough-type transitions is harder to define, as the ITD sensitivity to low-frequency AM, presumably inherited from the peak-type MSO input, would be too weak in most circumstances. Interestingly, such neurons were uncommon in our sample.

In reverberant environments, the ITD sensitivity of high-frequency IC neurons to CG envelope of broadband noise is severely degraded (Devore and Delgutte 2010). In such cases, neurons with trough-type to peak-type transitions would still be sensitive to ILD via their trough-type LSO input. Perceptual and physiological data suggest that ILD is a relatively robust cue in reverberation (Devore and Delgutte 2010; Rakerd et al. 2006). Similar situations would occur in multisource environments, where the spatial separation of two noise sources causes a decorrelation of the ear input signals and their envelopes. This decorrelation in turn leads to major changes in firing rate of IC neurons sensitive to ITD in CG envelopes (Day et al. 2012). If these neurons have dual ITD sensitivity, they could provide a cue to the spatial separation of sound sources via the changes in firing rate resulting from decorrelation, while also preserving directional information through the ILD sensitivity inherited from their putative LSO input. In short, IC neurons with dual ITD sensitivity would be expected to convey information about the complex, dynamic changes in binaural cues occurring in multisource and reverberant environments. Whether the decoding stages further up the auditory pathway can make use of such information remains to be determined.

Conclusion

In summary, we have shown that the dual types of envelope-ITD sensitivity observed in some high-CF IC neurons can be accounted for by a relatively simple IC model. The convergent inputs from MSO and LSO with different binaural f_m tuning in firing rate are sufficient to explain the transition between peak-type and trough-type responses in the IC in response to SAM tones. The same neural mechanism can also explain the combination of peak-type and trough-type responses to broadband noises with both ITD_CG and ITD_AM. Similar mechanisms based on convergent inputs from the SOC have been shown to underlie complex phase plots in low-CF IC neurons (Shackleton et al. 2000), consistent with the contention that the binaural mechanisms are similar between the low- and high-frequency regions (Colburn and Esquissaud 1976).

GRANTS

This work was supported by National Institute on Deafness and Other Communication Disorders Grants 5R01 DC-00100 (H. S. Colburn), R01 DC-002258 (B. Delgutte), P30 DC-004463 (Boston University), and P30 DC-005209 (Massachusetts Eye and Ear Infirmary). S. Devore was partly supported by training grant T32 DC-000038 and by a Helen Carr Peake fellowship from MIT.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: L.W., S.D., B.D., and H.S.C. conception and design of research; L.W. and S.D. performed experiments; L.W., S.D., and H.S.C. analyzed data; L.W., S.D., B.D., and H.S.C. interpreted results of experiments; L.W. and S.D. prepared figures; L.W. drafted manuscript; L.W., S.D., B.D., and H.S.C. edited and revised manuscript; L.W., S.D., B.D., and H.S.C. approved final version of manuscript.