Learning Classification Models from Multiple Experts

Abstract

Building classification models from clinical data using machine learning methods often relies on labeling of patient examples by human experts. Standard machine learning framework assumes the labels are assigned by a homogeneous process. However, in reality the labels may come from multiple experts and it may be difficult to obtain a set of class labels everybody agrees on; it is not uncommon that different experts have different subjective opinions on how a specific patient example should be classified. In this work we propose and study a new multi-expert learning framework that assumes the class labels are provided by multiple experts and that these experts may differ in their class label assessments. The framework explicitly models different sources of disagreements and lets us naturally combine labels from different human experts to obtain: (1) a consensus classification model representing the model the group of experts converge to, as well as, and (2) individual expert models. We test the proposed framework by building a model for the problem of detection of the Heparin Induced Thrombocytopenia (HIT) where examples are labeled by three experts. We show that our framework is superior to multiple baselines (including standard machine learning framework in which expert differences are ignored) and that our framework leads to both improved consensus and individual expert models.

1. Introduction

The availability of patient data in Electronic Health Records (EHR) gives us a unique opportunity to study different aspects of patient care, and obtain better insights into different diseases, their dynamics and treatments. The knowledge and models obtained from such studies have a great potential in health care quality improvement and health care cost reduction. Machine learning and data mining methods and algorithms play an important role in this process.

The main focus of this paper is on the problem of building (learning) classification models from clinical data and expert defined class labels. Briefly, the goal is to learn a classification model f : x → y that helps us to map a patient instance x to a binary class label y, representing, for example, the presence or absence of an adverse condition, or the diagnosis of a specific disease. Such models, once they are learned can be used in patient monitoring, or disease and adverse event detection.

The standard machine learning framework assumes the class labels are assigned to instances by a uniform labeling process. However, in the majority of practical settings the labels come from multiple experts. Briefly, the class labels are either acquired (1) during the patient management process and represent the decision of the human expert that is recorded in the EHR (say diagnosis), or (2) retrospectively during a separate annotation process based on past patient data. In the first case, there may be different physicians that manage different patients, hence the class labels naturally originate from multiple experts. Whilst in the second (retrospective) case, the class label can in principle be provided by one expert, the constraints on how much time a physician can spend on patient annotation process often requires to distribute the load among multiple experts.

Accepting the fact that labels are provided by multiple experts, the complication is that different experts may have different subjective opinion about the same patient case. The differences may be due to experts’ knowledge, subjective preferences and utilities, and expertise level. This may lead to disagreements in their labels, and variation in the patient case labeling due to these disagreements. However, we would like to note that while we do not expect all experts to agree on all labels, we also do not expect the expert's label assessment to be random; the labels provided by different experts are closely related by the condition (diagnosis, an adverse event) they represent.

Given that the labels are provided by multiple experts, two interesting research questions arise. The first question is whether there is a model that would represent well the labels the group of experts would assign to each patient case. We refer to such a group model as to the (group) consensus model. The second question is whether it is possible to learn such a consensus model purely from label assessments of individual experts, that is, without access to any consensus/meta labels, and this as efficiently as possible.

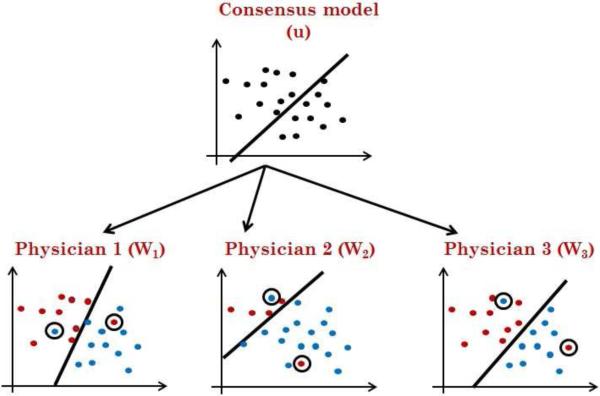
To address the above issues, we propose a new multi-expert learning framework that starts from data labeled by multiple experts and builds: (1) a consensus model representing the classification model the experts collectively converge to, and (2) individual expert models representing the class label decisions exhibited by individual experts. Figure 1 shows the relations between these two components: the experts’ specific models and the consensus model. We would like to emphasize again that our framework builds the consensus model without access to any consensus/meta labels.

Figure 1.

The consensus model and its relation to individual expert models.

To represent relations among the consensus and expert models, our framework considers different sources of disagreement that may arise when multiple experts label a case and explicitly represents them in the combined multi-expert model. In particular our framework assumes the following sources for expert disagreements:

• Differences in the risks annotators associate with each class label as signment: diagnosing a patient as not having a disease when the patient has disease, carries a cost due to, for example, a missed opportunity to treat the patient, or longer patient discomfort and suffering. A similar, but different cost is caused by incorrectly diagnosing a patient. The differences in the expert-specific utilities (or costs) may easily explain differences in their label assessments. Hence our goal is to develop a learning framework that seeks a model consensus, and that, at the same time, permits experts who have different utility biases.

• Differences in the knowledge (or model) experts use to label examples: while diagnoses provided by different experts may be often consistent, the knowledge they have and features they consider when making the disease decision may differ, potentially leading to differences in labeling. It is not rare when two expert physicians disagree on a complex patient case due to differences firmly embedded in their knowledge and understanding of the disease. These differences are best characterized as differences in their knowledge or model they used to diagnose the patient.

• Differences in time annotators spend when labeling each case: different experts may spend different amount of time and care to analyze the same case and its subtleties. This may lead to labeling inconsistency even within the expert's own model.

We experiment with and test our multi-expert framework on the Heparin Induced Thrombocytopenia (HIT) [23] problem where our goal is to build a predictive model that can, as accurately as possible, assess the risk of the patient developing the HIT condition and predict HIT alerts. We have obtained the HIT alert annotations from three different experts in clinical pharmacy. In addition we have also acquired a meta-annotation from the fourth (senior) expert who in addition to patient cases have seen the annotations and assessments given by other three experts. We show that our framework outperforms other machine learning frameworks (1) when it predicts a consensus label for future (test) patients, and (2) when it predicts individual future expert labels.

2. Background

The problem of learning accurate classification models from clinical data that are labeled by human experts with respect to some condition of interest is important for many applications such as diagnosis, adverse event detection, monitoring and alerting, the design of recommender systems, etc.

Standard classification learning framework assumes the training data set $D={\left\{(x_i,y_i)\right\}}_{i=1}^n$ consists of n data examples, where x_i is a d-dimensional feature vector and y_i is a corresponding binary class label. The objective is to learn a classification function: f : x → y that generalizes well to future data.

The key assumption for learning the classification function f in the standard framework is that examples in the training data D are independent and generated by the same (identical) process, hence there are no differences in the label assignment process. However, in practice, especially in medicine, the labels are provided by different humans. Consequently, they may vary and are subject to various sources of subjective bias and variations. We develop and study a new multi-expert classification learning framework for which labels are provided by multiple experts, and that accounts for differences in subjective assessments of these experts when learning the classification function.

Briefly, we have m different experts who assign labels to examples. Let $D^k={\left\{({\mathbf{x}}_i^k,y_i^k)\right\}}_{i=1}^{n_k}$ denotes training data specific for the expert k, such that ${\mathbf{x}}_i^k$ is a d-dimensional input example and $y_i^k$ is binary label assigned by expert k. Given the data from multiple experts, our main goal is to learn the classification mapping: f : x → y that would generalize well to future examples and would represent a good consensus model for all these experts. In addition, we can learn the expert specific classification functions g_k : x → y^k for all k = 1, · · ·, m that predicts as accurately as possible the label assignment for that expert. The learning of f is a difficult problem because (1) the experts’ knowledge and reliability could vary, and (2) each expert can have different preferences (or utilities) for different labels, leading to different biases towards negative or positive class. Therefore, even if two experts have the same relative understanding of a patient case their assigned labels may be different. Under these conditions, we aim to combine the subjective labels from different experts to learn a good consensus model.

2.1. Related work

Methodologically our multi-expert framework builds upon models and results in two research areas: multi-task learning and learning-from-crowds, and combines them to achieve the above goals.

The multi-task learning framework [9, 27] is applied when we want to learn models for multiple related (correlated) tasks. This framework is used when one wants to learn more efficiently the model by borrowing the data, or model components from a related task. More specifically, we can view each expert and his/her labels as defining a separate classification task. The multi-task learning framework then ties these separate but related tasks together, which lets us use examples labeled by all experts to learn better individual expert models. Our approach is motivated and builds upon the multi-task framework proposed by Evgeniou et al. [9] that ties individual task models using a shared task model. However, we go beyond this framework by considering and modeling the reliability and biases of the different experts.

The learning-from-crowds framework [17, 18] is used to infer consensus on class labels from labels provided jointly by multiple annotators (experts). The existing methods developed for the problem range from the simple majority approach to more complex consensus models representing the reliability of different experts. In general the methods developed try to either (1) derive a consensus of multiple experts on the label of individual examples, or (2) build a model that defines the consensus for multiple experts and can be applied to future examples. We will review these in the following.

The simplest and most commonly used approach for defining the label consensus on individual examples is the majority voting. Briefly, the consensus on the labels for an example is the label assigned by the majority of reviewers. The main limitation of the majority voting approach is that it assumes all experts are equally reliable. The second limitation is that although the approach defines the consensus on labels for existing examples, it does not directly define a consensus model that can be used to predict consensus labels for future examples; although one may use the labels obtained from majority voting to train a model in a separate step.

Improvements and refinements of learning a consensus label or model take into account and explicitly model some of the sources of annotator disagreements. Sheng et al. [17] and Snow et al. [18] showed the benefits of obtaining labels from multiple non-experts and unreliable annotators. Dawid and Skene [8] proposed a learning framework in which biases and skills of annotators were modeled using a confusion matrix. This work was later generalized and extended in [25], [24], and [26] by modeling difficulty of examples. Finally, Raykar et al. [14] used an expectation-maximization (EM) algorithm to iteratively learn the reliability of annotators. The initial reliability estimates were obtained using the majority vote.

The current state-of-the-art learning methods with multiple human annotators are the works of Raykar et al. [14], Welinder et al. [24], and Yan et al. [26]. Among these, only Raykar et al. [14] uses a framework similar to the one we use in this paper; that is, it assumes (1) not all examples are labeled by all experts, (2) the objective is to construct a good classification model. However, the model differs from our approach in how it models the skills and biases of the human annotators. Also the authors in [14] show that their approach improves over simple baselines only when the number of annotators is large (more than 40). This is practical when the labeling task is easy so crowd-sourcing services like Amazon Mechanical Turk can be utilized. However, it is not practical in domains in which the annotation is time consuming. In real world or scientific domains that involve uncertainty, including medicine, it is infeasible to assume the same patient case is labeled in parallel by many different experts. Indeed the most common cases is when every patient instance is labeled by just one expert.

The remaining state-of-the-art learning from crowds methods, i.e. the works of Welinder et al. [24] and Yan et al. [26], are optimized for different settings than ours. Welinder et al. [24] assumes that there is no feature vector available for the cases; it only learns expert specific models g_ks, and it does not attempt to learn a consensus model f. On the other hand, Yan et al. [26] assumes that each example is labeled by all experts in parallel. As noted earlier, this is unrealistic, and most of the time each example is labeled only by one expert. The approach we propose in this paper overcomes these limitations and is flexible in that it can learn the models when there is one or more labels per example. In addition, our approach differs from the work of Yan et al. [26] in how we parameterize and optimize our model.

3. Methodology

We aim to combine data labeled by multiple experts and build (1) a unified consensus classification model f for these experts and (2) expert-specific models g_k, for all k = 1, · · · , m that can be applied to future data. Figure 2 illustrates the idea of our framework with linear classification models. Briefly, let us assume a linear consensus model f with parameters (weights) u and b from which linear expert-specific models g_ks with parameters w_k and b_k are generated. Given the consensus model, the consensus label on example x is positive if u^Tx + b ≥ 0, otherwise it is negative. Similarly, the expert model g_k for expert k assigns a positive label to example x if ${\mathbf{w}}_k^{\mathsf{T}}\mathbf{x}+b_k\ge 0$, otherwise the label is negative. To simplify the notation in the rest of the paper, we include the bias term b for the consensus model in the weights vector u, the biases b_k in w_ks, and extend the input vector x with constant 1.

Figure 2.

The experts’ specific linear models w_k are generated from the consensus linear model u. The circles show instances that are mislabeled with respect to individual expert's models and are used to define the model self consistency.

The consensus and expert models in our framework and their labels are linked together using two reliability parameters:

1. α_k: the self-consistency parameter that characterizes how reliable the labeling of expert k is; it is the amount of consistency of expert k within his/her own model w_k.

2. β_k: the consensus-consistency parameter that models how consistent the model of expert k is with respect to the underlying consensus model u. This parameter models the differences in the knowledge or expertise of the experts.

We assume, all deviations of the expert specific models from the consensus model are adequately modeled by these expert-specific reliability parameters. In the following we present the details of the overall model and how reliability parameters are incorporated into the objective function.

3.1. Multiple Experts Support Vector Machines (ME-SVM)

Our objective is to learn the parameters u of the consensus model and parameters w_k for all expert-specific models from the data. We combine this objective with the objective of learning the expert specific reliability parameters α_k and β_k. We have expressed the learning problem in terms of the objective function based on the max-margin classification framework [16, 19] which is used, for example, by Support Vector Machines. However, due to its complexity we motivate and explain its components using an auxiliary probabilistic graphical model that we later modify to obtain the final max-margin objective function.

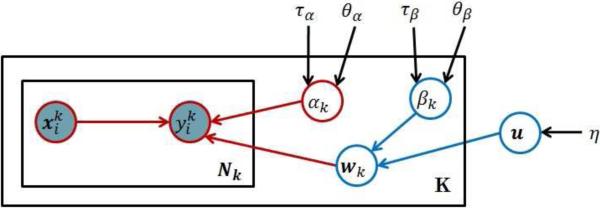
Figure 3 shows the probabilistic graphical model representation [5, 13] that refines the high level description presented in Figure 2. Briefly, the consensus model u is defined by a Gaussian distribution with zero mean and precision parameter η as:

$$p(\mathbf{u}\mid 0_d,\eta )=\mathcal{N}(0_d,{\eta }^{-1}{\mathbf{I}}_d)$$ (1)

where I_d is the identity matrix of size d, and 0_d is a vector of size d with all elements equal to 0. The expert-specific models are generated from a consensus model u. Every expert k has his/her own specific model w_k that is a noise corrupted version of the consensus model u; that is, we assume that expert k, w_k, is generated from a Gaussian distribution with mean u and an expert-specific precision β_k:

$$p({\mathbf{w}}_k\mid \mathbf{u},{\beta }_k)=\mathcal{N}(\mathbf{u},{\beta }_k^{-1}{\mathbf{I}}_d),$$

The precision parameter β_k for the expert k determines how much w_k differs from the consensus model. Briefly, for a small β_k, the model w_k tends to be very different from the consensus model u, while for a large β_k the models will be very similar. Hence, β_k represents the consistency of the reviewer specific model w_k with the consensus model u, or, in short, consensus-consistency.

Figure 3.

Graphical representation of the auxiliary probabilistic model that is related to our objective function. The circles in the graph represent random variables. Shaded circles are observed variables, regular (unshaded) circles denote hidden (or unobserved) random variables. The rectangles denote plates that represent structure replications, that is, there are k different expert models w_k, and each is used to generate labels for N_k examples. Parameters not enclosed in circles (e.g. η) denote the hyperparameters of the model.

The parameters of the expert model w_k relate examples (and their features) x to labels. We assume this relation is captured by the regression model:

$$p(y_i^k\mid {\mathbf{x}}_i^k,{\mathbf{w}}_k,{\alpha }_k)=\mathcal{N}({\mathbf{w}}_k^{\mathsf{T}}{\mathbf{x}}_i^k,{\alpha }_k^{-1}),$$

where α_k is the precision (inverse variance) and models the noise that may corrupt expert's label. Hence α_k defines the self-consistency of expert k. Please also note that although $y_i^k$ is binary, similarly to [9] and [27], we model the label prediction and related noise using the Gaussian distribution. This is equivalent to using the squared error loss as the classification loss.

We treat the self-consistency and consensus-consistency parameters α_k and β_k as random variables, and model their priors using Gamma distributions. More specifically, we define:

$$\begin{array}{cc}\hfill p({\beta }_k\mid {\theta }_{\beta },{\tau }_{\beta })=& \mathcal{G}({\theta }_{\beta },{\tau }_{\beta }),\hfill \\ \hfill p({\alpha }_k\mid {\theta }_{\alpha },{\tau }_{\alpha })=& \mathcal{G}({\theta }_{\alpha },{\tau }_{\alpha }),\hfill \end{array}$$ (2)

where hyperparameters θ_βk and τ_βk represent the shape and the inverse scale parameter of the Gamma distribution representing β_k. Similarly, θ_αk and τ_αk are the shape and the inverse scale parameter of the distribution representing α_k.

Using the above probabilistic model we seek to learn the parameters of the consensus u and expert-specific models W from data. Similarly to Raykar at al [14] we optimize the parameters of the model by maximizing the posterior probability p(u, W, α, β|X, y, ξ), where ξ is the collection of hyperparameters η, θ_βk, τ_βk, θ_αk, τ_αk. The posterior probability can be rewritten as follows:

$$p(\mathbf{u},W,,\alpha ,\beta \mid X,\mathbf{y},\xi )\propto p(\mathbf{u}\mid 0_d,\eta )\left(\prod _{k=1}^{m}p({\beta }_k\mid {\theta }_{\beta },{\tau }_{\beta })p({\alpha }_k\mid {\theta }_{\alpha },{\tau }_{\alpha })p({\mathbf{w}}_k\mid \mathbf{u},{\beta }_k)\prod _{i=1}^{n_k}p(y_i^k\mid {\mathbf{x}}_i^k,{\alpha }_k,{\mathbf{w}}_k)\right)$$ (3)

where $X=[{\mathbf{x}}_1^1;\dots ;{\mathbf{x}}_{n_1}^1;\dots ;{\mathbf{x}}_1^m;\dots ;{\mathbf{x}}_{n_m}^m]$ is the matrix of examples labeled by all the experts, and $\mathbf{y}=[y_1^1;\dots ;y_{n_1}^1;\dots ;y_m^1;\dots ;y_{n_m}^m]$ are their corresponding labels. Similarly, X^k and y^k are the examples and their labels from expert k. Direct optimization (maximization) of the above function is difficult due to the complexities caused by the multiplication of many terms. A common optimization trick to simplify the objective function is to replace the original complex objective function with the logarithm of that function. This conversion reduces the multiplication to summation [5]. Logarithm function is a monotonic function and leads to the same optimization solution as the original problem. Negative logarithm is usually used to cancel many negative signs produced by the logarithm of exponential distributions. This changes the maximization to minimization. We follow the same practice and take the negative logarithm of the above expression to obtain the following problem (see Appendix A for the details of the derivation):

$$\begin{array}{cc}\hfill \underset{\mathbf{u},\mathbf{w},\alpha ,\beta }{\min }\frac{\eta }{2}{\Vert \mathbf{u}\Vert }^2+& \frac{1}{2}\sum _{k=1}^m{\alpha }_k\sum _{i=1}^{n_k}{\Vert y_i^k-{\mathbf{w}}_k^{\mathsf{T}}{\mathbf{x}}_i^k\Vert }^2\hfill \\ \hfill +& \frac{1}{2}\sum _{k=1}^m{\beta }_k{\Vert {\mathbf{w}}_k-\mathbf{u}\Vert }^2\hfill \\ \hfill +& \sum (-\ln \left({\beta }_k\right)-n_k\ln \left({\alpha }_k\right))\hfill \\ \hfill +& \sum (-({\theta }_{{\beta }_k}-1)\ln \left({\beta }_k\right)+{\tau }_{{\beta }_k}{\beta }_k)\hfill \\ \hfill +& \sum (-({\theta }_{{\alpha }_k}-1)\ln \left({\alpha }_k\right)+{\tau }_{{\alpha }_k}{\alpha }_k)\hfill \end{array}$$ (4)

Although we can solve the objective function in Equation 4 directly, we replace the squared error function in Equation 4 with the hinge loss² for two reasons: (1) the hinge loss function is a tighter surrogate for the zero-one (error) loss used for classification than the squared error loss[15], (2) the hinge loss function leads to the sparse kernel solution[5]. Sparse solution means that the decision boundary depends on a smaller number of training examples. Sparse solutions are more desirable specially when the models are extended to non-linear case where the similarity of the unseen examples needs to be evaluated with respect to the training examples on which the decision boundary is dependent. By replacing the squared errors with the hinge loss we obtain the following objective function:

$$\begin{array}{cc}\hfill \underset{\mathbf{u},\mathbf{w},\alpha ,\beta }{\min }\frac{\eta }{2}{\Vert \mathbf{u}\Vert }^2+& \frac{1}{2}\sum _{k=1}^m{\alpha }_k\sum _{i=1}^{n_k}\max \left(0,1-y_i^k{\mathbf{w}}_k^{\mathsf{T}}{\mathbf{x}}_i^k)\right)\hfill \\ \hfill +& \frac{1}{2}\sum _{k=1}^m{\beta }_k{\Vert {\mathbf{w}}_k-\mathbf{u}\Vert }^2\hfill \\ \hfill +& \sum (-\ln \left({\beta }_k\right)-n_k\ln \left({\alpha }_k\right))\hfill \\ \hfill +& \sum (-({\theta }_{{\beta }_k}-1)\ln \left({\beta }_k\right)+{\tau }_{{\beta }_k}{\beta }_k)\hfill \\ \hfill +& \sum (-({\theta }_{{\alpha }_k}-1)\ln \left({\alpha }_k\right)+{\tau }_{{\alpha }_k}{\alpha }_k)\hfill \end{array}$$ (5)

We minimize the above objective function with respect to the consensus model u, the expert specific model w_k, and expert specific reliability parameters α_k and β_k.

3.2. Optimization

We need to optimize the objective function in Equation 5 with regard to parameters of the consensus model u, the expert-specific models w_k, and expert-specific parameters α_k and β_k.

Similarly to the SVM, the hinge loss term: max $(0,1-y_i^k{\mathbf{w}}_k^{\mathsf{T}}{\mathbf{x}}_i^k)$ in Equation 5 can be replaced by a constrained optimization problem with a new parameter ${∊}_i^k$. Briefly, from the optimization theory, the following two equations are equivalent [6]:

$$\underset{{\mathbf{w}}_k}{\min }\max (0,1-y_i^k{\mathbf{w}}_k^{\mathsf{T}}{\mathbf{x}}_i^k)$$

and

$$\underset{{∊}_i^k,{\mathbf{w}}_k}{\min }{∊}_i^{k}s.t.y_i^k{\mathbf{w}}_k^{\mathsf{T}}{\mathbf{x}}_i^k>1-{∊}_i^k$$

Now replacing the hinge loss terms in Equation 5, we obtain the equivalent optimization problem:

$$\begin{array}{cc}\hfill \underset{\mathbf{u},\mathbf{w},∊,\alpha ,\beta }{\min }\frac{\eta }{2}{\Vert \mathbf{u}\Vert }^2+& \frac{1}{2}\sum _{k=1}^m{\alpha }_k\sum _{i=1}^{n_k}{∊}_i^k\hfill \\ \hfill +& \frac{1}{2}\sum _{k=1}^n{\beta }_k{\Vert {\mathbf{w}}_k-\mathbf{u}\Vert }^2\hfill \\ \hfill +& \sum (-\ln \left({\beta }_k\right)-n_k\ln \left({\alpha }_k\right))\hfill \\ \hfill +& \sum (-({\theta }_{{\beta }_k}-1)\ln \left({\beta }_k\right)+{\tau }_{{\beta }_k}{\beta }_k)\hfill \\ \hfill +& \sum (-({\theta }_{{\alpha }_k}-1)\ln \left({\alpha }_k\right)+{\tau }_{{\alpha }_k}{\alpha }_k)\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& y_i^k{\mathbf{w}}_k^{\mathsf{T}}{\mathbf{x}}_i^k\ge 1-{∊}_i^k,k=1\dots m,i=1\dots n_k\hfill \\ \hfill & {∊}_i^k\ge 0,k=1\dots m,i=1\dots n_k\hfill \end{array}$$ (6)

where ε denote the new set of ${∊}_i^k$ parameters.

We optimize the above objective function using the alternating optimization approach [4]. Alternating optimization splits the objective function into two (or more) easier subproblems, each depends only on a subset of (hidden/learning) variables. After initializing the variables, it iterates over optimizing each set by fixing the other set until there is no change of values of all the variables. For our problem, diving the learning variables into two subsets, {α, β} and {u, w} makes each subproblem easier, as we describe below. After initializing the first set of variables, i.e. α_k = 1 and β_k = 1, we iterate by performing the following two steps in our alternating optimization apparoach:

• Learning u and w_k: In order to learn the consensus model u and expert specific model w_k, we consider the reliability parameters α_k and β_k as constants. This will lead to an SVM form optimization to obtain u and w_k. Notice that ${∊}_i^k$ is also learned as part of SVM optimization.

• Learning α_k and β_k: By fixing u, w_k for all experts, and ε, we can minimize the objective function in Equation 6 by computing the derivative with respect to α and β. This results in the following closed form solutions for α_k and β_k:

  $${\alpha }_k=\frac{2(n_k+{\theta }_{{\alpha }_k}+1)}{{\sum }_{y_i^k=1}{∊}_i^k+2{\tau }_{{\alpha }_k}}$$ (7)

  $${\beta }_k=\frac{2{\theta }_{{\beta }_k}}{{\Vert {\mathbf{w}}_k-\mathbf{u}\Vert }^2+2{\tau }_{{\beta }_k}}.$$ (8)

  Notice that ${∊}_i^k$ is the amount of violation of label constraint for example ${\mathbf{x}}_i^k$ (i.e. the i^th example labeled by expert k) thus ${\sum }_{i=1}{∊}_i^k$ is the summation of all labeling violations for model of expert k. This implies that α_k is inversely proportional to the amount of misclassification of examples by expert k according to its specific model w_k. As a result, α_k represents the consistency of the labels provided by expert k with his/her own model. β_k is inversely related to the difference of the model of expert k (i.e. w_k) with the consensus model u. Thus it is the consistency of the model learned for expert k from the consensus model u.

4. Experimental evaluation

We test the performance of our methods on clinical data obtained from EHRs for post-surgical cardiac patients and the problem of monitoring and detection of the Heparin Induced Thrombocytopenia (HIT) [23, 22]. HIT is an adverse immune reaction that may develop if the patient is treated for a longer time with heparin, the most common anticoagulation treatment. If the condition is not detected and treated promptly it may lead to further complications, such as thrombosis, and even to patient's death. An important clinical problem is the monitoring and detection of patients who are at risk of developing the condition. Alerting when this condition becomes likely prevents the aggravation of the condition and appropriate countermeasures (discontinuation of the heparin treatment or switch to an alternative anticoagulation treatment) may be taken. In this work, we investigate the possibility of building a detector from patient data and human expert assessment of patient cases with respect to HIT and the need to raise the HIT alert. This corresponds to the problem of learning a classification model from data where expert's alert or no-alert assessments define class labels.

4.1. Data

The data used in the experiments were extracted from over 4, 486 electronic health records (EHRs) in Post-surgical Cardiac Patient (PCP) database [11, 20, 12]. The initial data consisted of over 51, 000 unlabeled patient-state instances obtained by segmenting each EHR record in time with 24-hours period. Out of these we have selected 377 patient instances using a stratified sampling approach that were labeled by clinical pharmacists who attend and manage patients with HIT. Since the chance of observing HIT is relatively low, the stratified sampling was used to increase the chance of observing patients with positive labels. Briefly, a subset of strata covered expert-defined patterns in the EHR associated with the HIT or its management, such as, the order of the HPF4 lab test used to confirm the condition [22]. We asked three clinical pharmacists to provide us with labels showing if the patient is at the risk of HIT and if they would agree to raise an alert on HIT if the patient was encountered prospectively. The assessments were conducted using a web-based graphical interface (called PATRIA) we have developed to review EHRs of patients in the PCP database and their instances. All three pharmacists worked independently and labeled all 377 instances. After the first round of expert labeling (with three experts) we asked a (senior) expert on HIT condition to label the data, but this time, the expert in addition to information in the EHR also had access to the labels of the other three experts. This process led to 88 positive and 289 negative labels. We used the judgement and labels provided by this expert as consensus labels.

We note that alternative ways of defining consensus labels in the study would be possible. For example, one could ask the senior expert to label the cases independent of labels of other reviewers and consider expert's labels as surrogates for the consensus labels. Similarly one can ask all three experts to meet and resolve the cases they disagree on. However, these alternative designs come with the different limitations. First, not seeing the labels of other reviewers the senior expert would make a judgment on the labels on her own and hence it would be hard to speak about consensus labels. Second, the meeting of the experts and the resolution of the differences on every case in the study in person would be hard to arrange and time consuming to undertake. Hence, we see the option of using senior expert's opinion to break the ties as a reasonable alternative that (1) takes into account labels from all experts, and, (2) resolves them without arranging a special meeting of all experts involved.

In addition, we would like to emphasize that the labels provided by the (senior) expert were only used to evaluate the quality of the different consensus models. That is, we we did not use the labels provided by that expert when training the different consensus models, and only applied them in the evaluation phase.

4.2. Temporal feature extraction

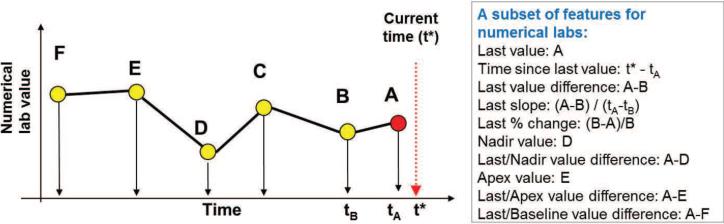
The EHR consists of complex multivariate time series data that reflect sequences of lab values, medication administrations, procedures performed, etc. In order to use these for building HIT prediction models, a small set of temporal features representing well the patient state with respect to HIT for any time t is needed. However, finding a good set of temporal features is an extremely challenging task [10, 2, 7, 3, 1]. Briefly, the clinical time series, are sampled at irregular times, have missing values, and their length may vary depending on the time elapsed since the patient was admitted to the hospital. All these make the problem of summarizing the information in the time series hard. In this work, we address the above issues by representing the patient state at any (segmentation) time t using a subset of pre-defined temporal feature mappings proposed by Hauskrecht et al [11, 20, 12] (Table 1 in Appendix B) that let us convert patient's information known at time t to a fixed length feature vector. The feature mappings define temporal features such as last observed platelet count value, most recent platelet count trend, or, the length of time the patient is on medication, etc. Figure 4 illustrates a subset of 10 feature mappings (out of 14) that we applied to summarize time series for numeric lab tests. We used feature mappings for five clinical variables useful for the detection of HIT: Platelet counts, Hemoglobin levels, White Blood Cell Counts, Heparin administration record, Major heart procedure. The full list of features generated for these variables is listed in Table 1 in Appendix B. Briefly, temporal features for numeric lab tests: Platelet counts, Hemoglobin levels and White Blood Cell Counts used feature mappings illustrated in Figure 4 plus additional features representing the presence of last two values, and pending test. The heparin features summarize if the patient is currently on the heparin or not, and the timing of the administration, such as the time elapsed since the medication was started, and the time since last change in its administration. The heart procedure features summarize whether the procedure was performed or not and the time elapsed since the last and first procedure. The feature mappings when applied to EHR data let us map each patient instance to a vector of 50 features. These features were then used to learn the models in all subsequent experiments. The alert labels assigned to patient instances by experts were used as class labels.

Figure 4.

The figure illustrates a subset of 10 temporal features used for mapping time-series for numerical lab tests.

4.3. Experimental Set-up

To demonstrate the benefits of our multi-expert learning framework we used patient instances labeled by four experts as outlined above. The labeled data were randomly split into the training and test sets, such that 2/3 of examples were used for training examples and 1/3 for testing. We trained all models in the experimental section on the training set and evaluated on the test set. We used the Area Under the ROC Curve (AUC) on the test set as the main statistic for all comparisons. We repeated train/test split 100 times and report the average and 95% confidence interval. We compare the following algorithms:

• SVM-baseline: This is a model obtained by training a linear SVM classifier that considers examples and their labels and ignores any expert information. We use the model as a baseline.

• Majority: This model selects the label in the training data using the majority vote and learns a linear SVM classifier on examples with the majority label. This model is useful only when multiple experts label the same patient instance. Notice that SVM and Majority performs exactly the same if each example is labeled by one and only one expert.

• Raykar: This is the algorithm and model developed by Raykar et. al. [14]. We used the same setting as discussed in [14].

• ME-SVM: This is the new method we propose in this paper. We set the parameters η = τ_α = τ_β = 1, θ_α = θ_β = 1.

• SE-SVM: Senior-Expert-SVM (SE-SVM) is the SVM model trained using the consensus labels provided by our senior pharmacist. Note that this method does not derive a consensus model from labels given by multiple experts; instead, it ’cheats’ and learns consensus model directly from consensus labels. This model and its results are used for comparison purposes only and serve as the reference point.

We investigate two aspects of the proposed ME-SVM method:

1. The performance of the consensus model on the test data when it is evaluated on the labels provided by the senior expert on HIT.

2. The performance of the expert-specific model w_k for expert k when it is evaluated on the examples labeled by that expert.

4.4. Results and Discussion

4.4.1. Learning consensus model

The cost of labeling examples in medical domain is typically very high, so in practice we may have a very limited number of training data. Therefore, it is important to have a model that can efficiently learn from a small number of training examples. We investigate how different methods perform when the size of training data varies. For this experiment we randomly sample examples from the training set to feed the models and evaluate them on the test set. We simulated and tested two different ways of labeling the examples used for learning the model: (1) every example was given to just one expert, and every expert labeled the same number of examples, and (2) every example was given to all experts, that is, every example was labeled three times. The results are shown in Figure 5. The x-axis shows the total number of cases labeled by the experts. The left and right plots respectively show the results when labeling options 1 and 2 are used.

Figure 5.

Effect of the number of training examples on the quality of the model when: (Left) every example is labeled by just one expert; (Right) every example is labeled by all three experts

First notice that our method that explicitly models experts’ differences and their reliabilities consistently outperforms other consensus methods in both strategies, especially when the number of training examples is small. This is particularly important when labels are not recorded in the EHRs and must be obtained via a separate post-processing step, which can turn out to be rather time-consuming and requires additional expert effort. In contrast to our method the majority voting does not model the reliability of different experts and blindly considers the consensus label as the majority vote of labels provided by different experts. The SVM method is a simple average of reviewer specific models and does not consider the reliability of different experts in the combination. The Raykar method, although modeling the reliabilities of different experts, assumes that the experts have access to the label generated by the consensus model and report a perturbed version of the consensus label. This is not realistic because it is not clear why the expert perturb the labels if they have access to consensus model. In contrary, our method assumes that different experts aim to use a model similar to consensus model to label the cases however their model differs from the label of the consensus model because of their differences in the domain knowledge, expertise and utility functions. Thus, our method uses a more intuitive way and realistic approach to model the label generating process.

Second, by comparing the two strategies for labeling patient instances we see that option 1, where each reviewer labels different patient instances, is better (in terms of the total labeling effort) than option 2 where all reviewers label the same instances. This shows that the diversity in patient examples seen by the framework helps and our consensus model is improving faster, which is what we intuitively expect.

Finally, note that our method performs very similarly to the SE-SVM – the model that ’cheats’ and is trained directly on the consensus labels given by the senior pharmacist. This verifies that our framework is effective in finding a good consensus model without having access to the consensus labels. .

4.4.2. Modeling individual experts

One important and unique feature of our framework when compared to other multi-expert learning frameworks is that it models explicitly the individual experts’ models w_k, not just the consensus model u. In this section, we study the benefit of the framework for learning the expert specific models by analyzing how the model for any of the experts can benefit from labels provided by other experts. In other words we investigate the question: Can we learn an expert model better by borrowing the knowledge and labels from other experts? We compared the expert specific models learned by our framework with the following baselines:

• SVM: We trained a separate SVM model for each expert using patient instances labeled only by that expert. We use this model as a baseline.

• Majority*: This is the Majority model described in the previous section. However, since Majority model does not give expert specific models, we use the consensus model learned by the Majority method in order to predict the labels of each expert.

• Raykar*: This is the model developed by Raykar et. al. [14], as described in the previous section. Similarly to Majority, Raykar's model does not learn expert specific models. Hence, we use the consensus model it learns to predict labels of individual experts.

• ME-SVM: This is the new method we propose in this paper, that generates expert specific models as part of its framework.

Similarly to Section 4.4.1, we assume two different ways of labeling the examples: (1) every example was given to just one expert, and every expert labeled the same number of examples, and (2) every example was given to all experts, that is every example was labeled three times.

We are interested in learning individual prediction models for three different experts. If we have a budget to label some number of patient instances, say, 240, and give 80 instances to each expert, then we have can learn an individual expert model from: (1) all 240 examples by borrowing from the instances labeled by the other experts, or (2) only its own 80 examples. The hypothesis is that learning from data and labels given by all three experts collectively is better than learning each of them individually. The hypothesis is also closely related to the goal of multi-task learning, where the idea is to use knowledge, models or data available for one task to help learning of models for related domains.

The results for this experiment are summarized in Figure 6, where x-axis is the number of training examples fed to the models and y-axis shows how well the models can predict individual experts’ labels in terms of the AUC score. The first (upper) line of sub-figures shows results when each expert labels a different set of patient instances, whereas the second (lower) line of sub-figures shows results when instances are always labeled by all three experts. The results show that our ME-SVM method outperforms the SVM trained on experts’ own labels only. This confirms that learning from three experts collectively helps to learn expert-specific models better than learning from each expert individually and that our framework enables such learning. In addition, the results of Majority* and Raykar* methods show that using their consensus models to predict expert specific labels is not as effective and that their performance falls bellow our framework that relies on expert specific models.

Figure 6.

Learning of expert-specific models. The figure shows the results for three expert specific models generated by the ME-SVM and the standard SVM methods, and compares them to models generated by the Majority* and Raykar* methods. First line: different examples are given to different experts; Second line: the same examples are given to all experts.

4.4.3. Self-consistency and consensus-consistency

As we described in Section 3, we model self-consistency and consensus-consistency with parameters α_k and β_k. α_k measures how consistent the labeling of expert k is with his/her own model and β_k measures how consistent the model of expert k is with respect to the consensus model. The optimization problem we proposed in Equation 6 aims to learn not just the parameters u and w_k of the consensus and experts’ models, but also the parameters α_k and β_k, and this without having access to the labels from the senior expert.

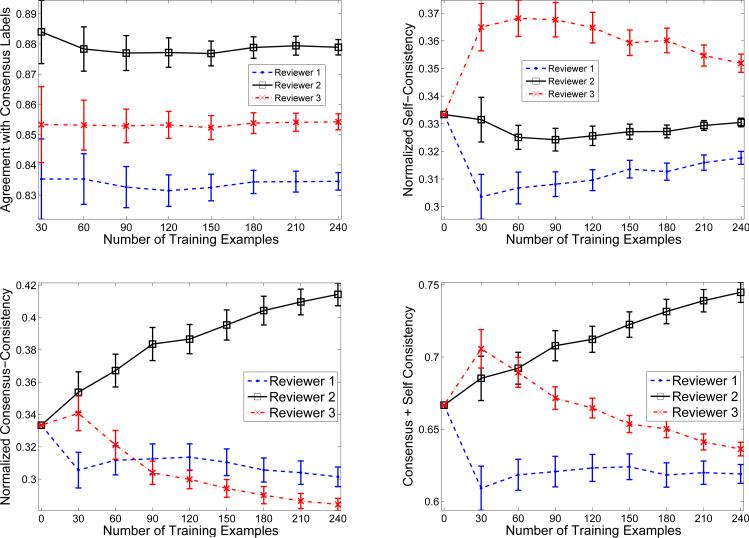
In this section, we attempt to study and interpret the values of the reliability parameters as they are learned by our framework and compare them to empirical agreements in between the senior (defining the consensus) and other experts. Figure 7(a) shows the agreements of labels provided by the three experts with labels given by the senior expert, which we assumed gives the consensus labels. From this figure we see that Expert 2 agrees with the consensus labels the most, followed by Expert 3 and then Expert 1. The agreement is measured in terms of the absolute agreement, and reflects the proportion of instances for which the two labels agree.

Figure 7.

(left-top) Agreement of experts with labels given by the senior expert; (right-top) Learned self-consistency parameters for Experts 1-3; (left-bottom) Learned consensus-consistency parameters for Experts 1-3; (right-bottom) Cumulative self and consensus consistencies for Expert 1-3

Figures 7(b) and 7(c) show the values of the reliability parameters α and β, respectively. The x-axis in these figures shows how many training patient instances per reviewer are fed to the model. Normalized Self-Consistency in Figure 7(b) is the normalized value of α_k in Equation 6. Normalized Consensus-Consistency in Figure 7(c) is the normalized inverse value of Euclidean distance between an expert specific model and consensus model: 1/∥w_k – u∥, which is proportional to β_k in Equation 6. In Figure 7(d) we add the two consistency measures in an attempt to measure the overall consistency in between the senior expert (consensus) and other experts.

As we can see, at the beginning when there is no training data all experts are assumed to be the same (much like the majority voting approach). However, as the learning progresses with more training examples available, the consistency measures are updated and their values define the contribution of each expert to the learning of consensus model: the higher the value the larger the contribution. Figure 7(b) shows that expert 3 is the best in terms of self-consistency given the linear model, followed by expert 2 and then expert 1. This means expert 3 is very consistent with his model, that is, he likely gives the same labels to similar examples. Figure 7(c) shows that expert 2 is the best in terms of consensus-consistency, followed by expert 3 and then expert 1. This means that although expert 2 is not very consistent with respect to his own linear model his model appears to converge closer to the consensus model. In other words, expert 2 is the closest to the expected consensus in terms of the expertise but deviates with some labels from his own linear model than expert 3 does³.

Figure 7(d) shows the summation of the two consistency measures. By comparing Figure 7(a) and Figure 7(d) we observe that the overall consistency mimics well the agreements in between the expert defining the consensus and other experts, especially when the number of patient instances labeled and used to train our model increases. This is encouraging, since the parameters defining the consistency measures are learned by our framework only from the labels of the three experts and hence the framework never sees the consensus labels.

5. Conclusion

The construction of predictive classification models from clinical data often relies on labels reflecting subjective human assessment of the condition of interest. In such a case, differences among experts may arise leading to potential disagreements on the class label that is assigned to the same patient case. In this work, we have developed and investigated a new approach to combine class-label information obtained from multiple experts and learn a common (consensus) classification model. We have shown empirically that our method outperforms other state-ofthe-art methods when building such a model. In addition to learning a common classification model, our method also learns expert specific models. This addition provides us with an opportunity to understand the human experts’ differences and their causes which can be helpful, for example, in education and training, or in resolving disagreements in the patient assessment and patient care.

Paper highlights.

• Learning of classification models when labels are provided by multiple experts

• A new multi-expert learning approach that gives: (a) consensus, and (b) experts’ models

• Tests the approach on clinical data with three expert reviewers and one meta-reviewer

• The results show the improved learning of the consensus model

• The results show the improved learning of individual expert models

Appendix A: Taking the negative logarithm of the posterior in Equation 3

In this appendix, we give a more detailed derivation of Equation 4 from 3:

$$p(\mathbf{u},W,,\alpha ,\beta \mid X,\mathbf{y},\xi )\propto p(\mathbf{u}\mid 0_d,\eta )\left(\prod _{k=1}^{m}p({\beta }_k\mid {\theta }_{\beta },{\tau }_{\beta })p({\alpha }_k\mid {\theta }_{\alpha },{\tau }_{\alpha })p({\mathbf{w}}_k\mid \mathbf{u},{\beta }_k)\prod _{i=1}^{n_k}p(y_i^k\mid {\mathbf{x}}_i^k,{\alpha }_k,{\mathbf{w}}_k)\right)=\mathcal{N}(\mathbf{u}\mid 0,{\beta }_{\mathbf{k}}^{-1}{\mathbf{I}}_{\mathbf{d}})\left(\prod _{\mathbf{k}=1}^{\mathbf{m}}\mathcal{G}({\beta }_{\mathbf{k}}\mid {\theta }_{\beta },{\tau }_{\beta })\mathcal{G}({\alpha }_{\mathbf{k}}\mid {\theta }_{\alpha },{\tau }_{\alpha })\mathcal{N}({\mathbf{w}}_{\mathbf{k}}\mid \mathbf{u},{\beta }_{\mathbf{k}})\mathcal{N}({\mathbf{w}}_{\mathbf{k}}\mid \mathbf{u},{\beta }_{\mathbf{k}})\prod _{\mathbf{i}=1}^{{\mathbf{n}}_{\mathbf{k}}}\mathcal{N}({\mathbf{y}}_{\mathbf{i}}^{\mathbf{k}}\mid {\mathbf{w}}_{\mathbf{k}}^{\mathsf{T}}{\mathbf{x}}_{\mathbf{i}}^{\mathbf{k}},{\alpha }_{\mathbf{k}})\right)=\frac{{\beta }_k}{\sqrt{2\pi }}{e}^{-\frac{\eta {\Vert \mathbf{u}\Vert }^2}{2}}\times \left(\prod _{k=1}^m\frac{1}{\Gamma \left({\theta }_{\beta }\right)}{\tau }_{\beta }^{{\theta }_{\beta }}{\beta }_k^{{\theta }_{\beta -1}}{e}^{-{\tau }_{\beta }{\beta }_k}\frac{1}{\Gamma \left({\theta }_{\alpha }\right)}{\tau }_{\alpha }^{{\theta }_{\alpha }}{\alpha }_k^{{\theta }_{\alpha }-1}{e}^{-{\tau }_{\alpha }}{\alpha }_k\frac{{\beta }_k}{\sqrt{2\pi }}{e}^{-\frac{{\beta }_k{\Vert {\mathbf{w}}_k-\mathbf{u}\Vert }^2}{2}}\prod _{i=1}^{n_k}\frac{{\alpha }_k}{\sqrt{2\pi }}{e}^{-\frac{{\alpha }_k{\Vert y_i^k-{\mathbf{w}}_k^{\mathsf{T}}{\mathbf{x}}_i^k\Vert }^2}{2}}\right)$$

Getting the negative logarithm of the last statement, we will have:

$$-\log \left(\eta \right)-log\left(\sqrt{2\pi }\right)+\frac{1}{2}\eta {\Vert \mathbf{u}\Vert }^2+\sum _{k=1}^m\left(\log \left(\Gamma \left({\theta }_{\beta }\right)\right)-{\theta }_{\beta }\log \left({\tau }_{\beta }\right)-({\theta }_{\beta }-1)\log \left({\beta }_k\right)+{\tau }_{\beta }{\beta }_k+\log \left(\Gamma \left({\theta }_{\alpha }\right)\right)={\theta }_{\alpha }\log \left({\tau }_{\alpha }\right)-({\theta }_{\alpha }-1)\log \left({\alpha }_k\right)+{\tau }_{\alpha }{\alpha }_k-\log \left({\beta }_k\right)+\log \left(\sqrt{2\pi }\right)+\frac{1}{2}{\beta }_k{\Vert {\mathbf{w}}_k-\mathbf{u}\Vert }^2+\sum _{i=1}^{n_k}-\log \left({\alpha }_k\right)+\log \left(\sqrt{2\pi }\right)+\frac{1}{2}{\alpha }_k{\Vert y_i^k-{\mathbf{w}}_k^{\mathsf{T}}{\mathbf{x}}_i^k\Vert }^2\right)$$

Removing the constants terms (i.e. those related to η, θ_α, τ_α, θ_β and τ_β, we will have:

$$\frac{1}{2}\eta {\Vert \mathbf{u}\Vert }^2+\sum _{k=1}^m\left(-({\theta }_{\beta }-1)\log \left({\beta }_k\right)+{\tau }_{\beta }{\beta }_k-({\theta }_{\alpha }-1)\log \left({\alpha }_k\right)+{\tau }_{\alpha }{\alpha }_k-\log \left({\beta }_k\right)+\frac{1}{2}{\beta }_k{{{\Vert }_{\mathbf{w}}}_k-\mathbf{u}\Vert }^2+\sum _{i=1}^{n_k}-\log \left({\alpha }_k\right)+\frac{1}{2}{\alpha }_k{y_i^k-{\mathbf{w}}_k^{\mathsf{T}}{\mathbf{x}}_i^k\Vert }^2\right)$$

Rearranging the terms in the above equation, we obtain Equation 4.

Appendix B: Features used for constructing the predictive models

Table 1.

Features used for constructing the predictive models. The features were extracted from time series data in electronic health records using methods from Hauskrecht et al [11, 20, 12]

Clinical variables	Features
Platelet count (PLT)	1 2 3 4 5 6 7 8 9 10 11 12 13 14	last PLT value measurement time elapsed since last PLT measurement pending PLT result known PLT value result indicator known trend PLT results PLT difference for last two measurements PLT slope for last two measurements PLT % drop for last two measurements nadir HGB value PLT difference for last and nadir values apex PLT value PLT difference for last and apex values PLT difference for last and baseline values overall PLT slope
Hemoglobin (HGB)	15 16 17 18 19 20 21 22 23 24 25 26 27 28	last HGB value measurement time elapsed since last HGB measurement pending HGB result known HGB value result indicator known trend HGB results HGB difference for last two measurements HGB slope for last two measurements HGB % drop for last two measurements nadir HGB value HGB difference for last and nadir values apex HGB value HGB difference for last and apex values HGB difference for last and baseline values overall HGB slope
White Blood Cell count (WBC)	29 30 31 32 33 34 35 36 37 38 39 40 41 42	last WBC value measurement time elapsed since last WBC measurement pending WBC result known WBC value result indicator known trend WBC results WBC difference for last two measurements WBC slope for last two measurements WBC % drop for last two measurements nadir WBC value WBC difference for last and nadir values apex WBC value WBC difference for last and apex values WBC difference for last and baseline values overall WBC slope
Heparin	43 44 45 46	Patient on Heparin Time elapsed since last administration of Heparin Time elapsed since first administration of Heparin Time elapsed since last change in Heparin administration
Major heart proce-dure	47 48 49 50	Patient had a major heart procedure in past 24 hours Patient had a major heart procedure during the stay Time elapsed since last major heart procedure Time elapsed since first major heart procedure