Dynamic Nuclear Polarization of ¹⁷O: Direct Polarization

Abstract

Dynamic nuclear polarization of ¹⁷O was studied using four different polarizing agents – the biradical TOTAPOL, and the monoradicals trityl and SA-BDPA, as well as a mixture of the latter two. Field profiles, DNP mechanisms and enhancements were measured to better understand and optimize directly polarizing this low-gamma quadrupolar nucleus using both mono- and bi-radical polarizing agents. Enhancements were recorded < 88 K and were > 100 using the trityl (OX063) radical and < 10 with the other polarizing agents. The > 10,000 fold savings in acquisition time enabled a series of biologically relevant small molecules to be studied with small sample sizes and the measurement of various quadrupolar parameters. The results are discussed with comparison to room temperature studies and GIPAW quantum chemical calculations. These experimental results illustrate the strength of high field DNP and the importance of radical selection for studying low-gamma nuclei.

1. Introduction

Over the past few decades a number of new methods and technologies have been developed to boost sensitivity and resolution in solid-state NMR experiments, for example Hartmann-Hahn cross polarization¹, magic-angle spinning (MAS)^{2, 3}, innovative methods for decoupling^4–7, and high magnetic fields (≥ 16.4 T). These improvements have in turn enabled structural studies of peptides⁸ membrane^9–12 and amyloid proteins^13–17 which would not be possible using conventional solution-state NMR or diffraction methods. Thus, it is now routine to examine ¹³C, ¹⁵N and ³¹ P spectra, and, to measure distances and torsion angles that lead to molecular structures. More recently the ability to extensively ²H label proteins together with back exchange of the amide NH’s and the availability of probes that spin at ω_r/2π≥ 65 kHz, have made detection of ¹H MAS spectra possible.^18–21

In contrast, NMR studies of oxygen, the other copious element in biological systems, has progressed slowly due to its low natural abundance (0.037%) and small gyromagnetic ratio (−5.774 × 10⁷ MHz T⁻¹) which leads to inherently low sensitivity. In particular, these two factors result in a sensitivity reduction of ~15 when compared to ¹³C.²² In addition, ¹⁷O is a quadrupolar nucleus (I=5/2, Q = −2.558 fm²) and the spectra exhibit a significant broadening due to the interaction between the quadrupole moment and the asymmetric electric field gradient in the chemical environments in proteins and nucleic acids.²³ Despite these technical difficulties ¹⁷O is an appealing species to study since, like nitrogen, it is directly involved in hydrogen bonds, and therefore the chemical shifts are exquisitely sensitive to the chemical environment.^24–26 Furthermore, also like nitrogen, it possesses a large chemical shift range (~1000 ppm), and in addition an interesting quadrupolar interaction.^{27, 28} It is therefore important to develop the spectroscopic techniques that allow observation of ¹⁷O with high sensitivity.

In the past, modest sensitivity gains for studying ¹⁷O NMR were achieved by using isotopic enrichment and applying population transfer techniques.^{29, 30} It is also possible to remove the 2^nd order quadrupolar interaction in order to obtain simplified isotropic spectra. This requires advanced techniques including special instrumentation, for example double rotation (DOR) and dynamic-angle spinning (DAS)^{31, 32}, or special spectroscopic techniques such as multiple-quantum magic angle spinning (MQMAS)³³ and satellite-transition magic angle spinning (STMAS)³⁴. However, when the quadrupole coupling is large (> 5 MHz), as is often found for oxygen environments in proteins and nucleic acids, the excitation efficiency of these approaches drops dramatically; in the case of MQMAS spectra to about ~5%.^{35, 36} Thus, although there are a number of exciting MQMAS studies of ¹⁷O labeled biological samples, the experimental results are clearly limited by signal-to-noise, hence requiring long acquisition times.^37–46

Dynamic nuclear polarization (DNP) has been shown to provide immense gains in NMR sensitivity.^47–50 This is accomplished by transferring the large electron spin polarization of unpaired electrons to nuclei via microwave irradiation of the electron-nuclear transitions. For efficient DNP, samples are cooled to cryogenic temperatures (<110 K) where increased electron and nuclear spin-lattice relaxation times (T_1I) can assist in a more efficient electron-nuclear spin transfer mechanism. For several compelling reasons including reduced ¹H spin-lattice relaxation, improved sensitivity from employing cross polarizing and a large database of nitroxide radicals, optimal for ¹H CE, ¹H is often the nucleus of choice for polarization at cryogenic temperatures using a biradical polarizing agent such as TOTAPOL⁵¹, or other TEMPO biradical variants.^52–56 Subsequent to polarization of ¹H, a cross-polarization step is used to observe other low-gamma nuclei (e.g., ¹³C,¹⁵N, etc.).^{47, 49, 57–61} This method (i.e., indirect polarization, e⁻ → ¹H → X, where X is an NMR active nucleus, such as ¹³C, ¹⁵N, ¹⁷O,³¹ P, etc.) has been successfully applied to membrane proteins, peptides, amyloid fibrils, pharmaceuticals, and surfaces, resulting in an enhancement of NMR signal intensity (ε) between 30-and 180-fold.^{9, 47, 49, 57, 58, 62–76} Many of these studies focused on I=1/2 nuclei (e.g., ¹³C,³¹P,²⁹ Si, etc.) and reports regarding quadrupolar nuclei have been scarce.^77–81 An alternative to indirect polarization, is polarizing an NMR active nucleus (X) directly from an electron spin source, e⁻ → X, (i.e. direct polarization).^{62, 77, 82–87} This approach is of interest for many chemical systems that cross-polarize by high-ı nuclei (e.g., ¹H or¹⁹ F) poorly, found within chemical environments where high-ı nuclei are absent or may be of assistance in spectral editing between protonated and non-protonated chemical environments.

Recently, we illustrated the extension of this approach to ¹⁷O using indirect polarization via ¹H DNP.⁷⁸ During that study we determined that the optimized radical for ¹H (i.e., nitroxide-based biradical) performed poorly when polarizing ¹⁷O directly.^{88, 89} Similar observations were observed with the biradical bTbk when studying ¹⁷O DNP in two synthetic minerals, Periclase (MgO, Cubic-Fm3m) and Brucite (Mg(OH)₂, Trigonal-P3m1).⁸² Herein, we report an extensive study for efficient direct polarization of ¹⁷O using a series of polarizing agents dissolved in a water/glycerol model system. Utilizing enhancements greater than 100, we also show applications of ¹⁷O DNP, which are presented in conjunction with quantum chemical calculations – further extending the ability to use DNP to address problems involving low-gamma quadrupolar systems. The reduction in acquisition time for ¹⁷O will likely provide a new approach that can be extended to studies in other chemical systems.

2. Theory

2.1. Polarization mechanisms for DNP

Since DNP mechanisms involve the transfer of spin polarization from electrons to nuclei, an exogenous polarizing agent is generally added to the medium containing the solute. Polarizing agents typically are persistent organic mono- or bi-radicals (e.g., trityl (OX063), SA-BDPA, TOTAPOL, etc.), or more recently high-spin metal complexes.⁹⁰ In the case of ¹⁷O, a theoretical enhancement of over 4,800, determined by the ratio of the gyromagnetic ratios (i.e., ı_e/ı_17O), is possible.

At high magnetic fields and temperatures close to liquid N₂ there are two dominant mechanisms that mediate electron–nuclear polarization transfer: (1) the cross-effect (CE) and (2) the solid-effect (SE), and both mechanisms require irradiation of the sample with microwaves of appropriate frequency. In the following we will briefly outline the salient features of each.

The cross-effect is a three-spin process between two electrons and a nuclear spin that are dipolar coupled.^91–96 The difference between the Larmor frequencies of the two electron spins, determined by their g-values and g-anisotropies (ω_0S1,ω_0S2) must approximate the nuclear Larmor frequency (ω_0I) for maximum efficiency:

$${\omega }_{0I}=|{\omega }_{0S_1}-{\omega }_{0S_2}|$$ (1)

For this condition to be met the inhomogeneous breadth (Δ) of the radical’s EPR spectrum is required to be larger than the nuclear Larmor frequency, while the homogeneous component (δ)may be smaller than the nuclear Larmor frequency.

$$\mathrm{\Delta }>{\omega }_{0I}>\delta$$ (2)

The solid-effect is a two-spin process whereby microwave irradiation is applied at the electron-nuclear zero- or double-quantum frequency.⁹⁷

$${\omega }_{mw}={\omega }_{0S}\pm {\omega }_{0I}$$ (3)

Due to partial mixing of the nuclear spin states by non-secular electron-nuclear dipolar coupling, these “forbidden” transitions become partially allowed, albeit with a transition moment that is typically 2–3 orders of magnitude smaller than that of the single-quantum EPR transition. Because the zero- and double-quantum transition lead to nuclear enhancements of opposite signs, the homogeneous (δ) and inhomogeneous (Δ) EPR linewidths have to be smaller than the Larmor frequency of the nucleus to be polarized in order to avoid overlap and therefore cancellation of positive and negative enhancements:

$${\omega }_{0I}>\delta ,\mathrm{\Delta }$$ (4)

Therefore the SE is the dominant mechanism when polarizing agents with narrow linewidths relative to the nuclear Larmor frequency are used.

2.2. NMR parameters

Since ¹⁷O is a quadrupolar nucleus, a coupling between the inherent quadrupole moment and the electric field gradient generated by its surroundings results in a quadrupolar interaction. This coupling will manifest in the observed spectrum and be accompanied by a characteristic shape based on the local symmetry at the ¹⁷O site. In solids such as the case for ¹⁷O, vide infra, the magnetic field Zeeman Field, B_o) is significantly larger than the quadrupolar interaction. This condition allows us to treat the interaction as a perturbation on B_o, where only the first- and second-order quadrupole interactions are of concern. Hence, the spectra in solids of half-integer quadrupolar nuclei exhibit are governed by the quadrupole Hamiltonian

$${Ĥ}_Q=\sum _k{\mathit{I}}_k{\mathit{Q}}_k{\mathit{I}}_k$$ (5)

where the quadrupole coupling tensor Q_k may be expressed in terms of the electric field gradient tensor V_k at the k_th nuclear site

$${\mathit{Q}}_k=\frac{e{Q}_k}{2I_k(2I_k-1)ħ}{\mathit{V}}_k.$$ (6)

Here Î is the nuclear spin operator, V is the electric field gradient at the quadrupolar nucleus, e is the electric charge, ħ is defined as usual, and Q_k is the quadrupole moment. Taking V_k,zz = eq_k we obtain an expression for the first order frequency

$${{\omega }_{Qk}}^{(1)}=\frac{3e^2{q}_k{Q}_k}{4I_k(2I_k-1)ħ}$$ (7)

The asymmetry is conventionally defined as η_k = (Vk,xx − V_{k, yy})/V_k,zz and leads to the form for the Hamiltonian in the principal axis system where V is diagonal with components |V_zz|≥|V_yy|≥|V_xx|.

$${Ĥ}_{Qk}={\omega }_{Qk}\left\{\right(I_{kz}^2-\frac{1}{3}{\mathit{I}}_k^2)+\frac{\eta }{3}(I_{kx}^2-I_{ky}^2\left)\right\}$$ (8)

Although the central transition (m_I = −1/2 <−> +1/2) is not affected by the first-order quadrupole interaction $({\omega }_{Qk}^{(1)})$), its lineshape is influenced by a second-order interaction $({\omega }_{Qk}^2)$ that scales quadratically with the magnitude of the first-order interaction and inversely with the nuclear Zeeman frequency (ω_0I)^97–99: ${\omega }_{Qk}^{(2)}={({\omega }_{Qk}^{(1)})}^2/{\omega }_{0I}$

The nuclear quadrupole interaction is described by a coupling constant, C_Q, C_Qk = (eQV_zzk /ħ) that typically ranges between 0 and 12 MHz for ¹⁷O and an asymmetry parameter, η, which can assume values between 0 and 1.^{28, 100–102} A more comprehensive explanation of the quadrupolar interaction for solids can be found elsewhere.^{98, 103–105}

The chemical shift anisotropy can also influence the appearance of the spectrum, especially under non-spinning conditions and at higher magnetic fields for powdered samples. Although its magnitude is negligible relative to the quadrupole broadening at 5 T for the ¹⁷O environments studied here, these parameters should be considered when analyzing higher field spectra.

3. Materials and Methods

3.1. Sample preparation

Samples were prepared using mixtures of d₈-glycerol (60 vol. %), D₂O (30 vol. %) and H₂O (10 vol. %). The H₂O was labeled with oxygen-17 (H₂ ¹⁷O – 35%) and was purchased from Cambridge Isotope Laboratories (Andover, MA). Each sample contained 40 mM electron spins homogeneously dispersed at 298 K. The liquid samples were packed into 4 mm o.d. sapphire rotors using between 40 and 60 µL of sample. Samples were prepared with radical concentrations of 20 mM in the case of TOTAPOL and 40 mM of trityl (OX063) and SA-BDPA, respectively. Additionally, an equimolar mixture (i.e., 20 mM trityl and 20 mM SA-BDPA) was prepared. For the experiments shown in section 4.5, 40 mM trityl was dissolved together with ¹³C- ¹⁷O-urea¹⁰⁶ (~20% ¹⁷O) or ¹⁷O-phenol (~30% ¹⁷O) purchased from Cambridge Isotope Laboratories (Andover, MA) with a concentration of 2.0 and 0.65 M, respectively in a mixture of d₈-glycerol/D₂O/H₂O (60/30/10 vol.-%), where H₂O was used in natural abundance (0.037%). A third sample containing 40 mM trityl was prepared following the protocol at the beginning of the section to allow for H₂ ¹⁷O NMR analysis. Field profiles were acquired using a mixture of 60/40 (v/v) d₈-glycerol/H₂ ¹⁷O (35% - ¹⁷O – H₂O) and 40 mM electrons. Please note the ¹⁷O background due to natural abundance H₂O (for urea and phenol samples) or hardware (i.e., sapphire-rotor and/or stator materials) can be neglected in comparison to the signals arising from the isotopically enriched analytes for this study, although care should be considered when dealing with alternative materials (e.g., Macor, Al₂O₃, ZrO₂), during MAS at higher magnetic fields and / or low ¹⁷O enrichments.

3.2. Dynamic nuclear polarization nuclear magnetic resonance

Dynamic nuclear polarization NMR experiments were performed using a home-built spectrometer equipped with a 5 T (¹H, 212 MHz) wide bore magnet (courtesy of Dr. D. J. Ruben, FBML, MIT) and a 140 GHz gyrotron with ≤ 15 W of microwave output. ¹⁷O spectra were recorded using a home-built cryogenic double resonance (¹H and ¹⁷O) DNP NMR probe equipped with a 4 mm Kel-F stator (Revolution NMR, Fort Collins, CO). Microwaves were guided to the DNP probe via a circular corrugated, overmoded waveguide to reduce mode conversion and ohmic losses.¹⁰⁷ At the probe entrance, the waveguide tapers to a fundamental mode, from which microwaves are launched towards the sample.^{108, 109} Experimental temperatures for all data were maintained below 88 K. Direct ¹⁷O polarization experiments were acquired with continuous microwave irradiation, while applying a Hahn-echo sequence on ¹⁷O (ω₁/2π = 180 kHz, solid (85 K)) using CW or TPPM⁴ proton decoupling (ω₁/2π > 71 kHz). Recycle delays were determined via a saturation recovery sequence which accomplishes saturation using the phase cycling scheme described by Daviso et al.¹¹⁰ Polarization buildup (T_B) and spin-lattice relaxation (T_1I) times between 4.0 and 6.0 seconds were measured; recycle delays were chosen as T_B/T_1I × 1.3.¹¹¹ Directly polarized ¹⁷O detected DNP field-profiles were performed by sweeping the main NMR field using a superconducting sweep coil (± 0.1 T) between 4.961 and 4.996 T (211.7 and 212.3 MHz, ¹H nuclear Larmor frequency). All spectra were referenced with neat water (15 % - H₂ ¹⁷O) to 0 ppm at 298 K. Simulations of ¹⁷O NMR central transition line shapes were performed using SPINEVOLUTION¹¹² and WSOLIDS¹¹³. The SPINEVOLUTION software package was used to fit the ¹⁷O central-transition lineshape by adjusting the C_Q, η and δ_iso. Input files are available within the software package and were adjusted to incorporate the experimental conditions used during acquisition, and varying the apodization. WSOLIDS was also used to simulate the ¹⁷O central transition lineshape for the non-spinning data to assist in evaluating the experimental uncertainty. Quadrupolar parameters from GIPAW calculations were simulated without further modification within WSOLIDS. To confirm even excitation for these rather broad ¹⁷O spectra (i.e., ~100 kHz), on-signals were further investigated using a solid (quadrupolar) echo¹¹⁴ as well as employing the frequency-stepped¹¹⁵ or variable offset cumulative spectra (VOCS)¹¹⁶ method.

3.3. Quantum Chemical Calculations

Electric field gradient and chemical shielding calculations for crystalline ice¹¹⁷, urea¹¹⁸ and phenol¹¹⁹ were performed using a gauge-including projector-augmented wave (GIPAW) density functional theoretical method implemented within CASTEP¹²⁰. The Perdew-Burke-Ernzerhof (PBE) functionals are used in the generalized gradient approximation (GGA) for the exchange-correlation energy^{121, 122} and ultrasoft pseudopotentials.¹²³ All calculations were performed using the fine accuracy basis set and a maximum plane-wave energy of 550 eV in order to calculate both chemical shieldings and electric field gradients.^{124, 125} The Monkhorst-Pack grid had a maximum density of up to 4 × 4 × 4 k points. All calculated chemical shieldings (σ_cal) were referenced with respect to (σ_ref) 255.0 ppm (Table S1–S3) using ¹H optimized (within CASTEP) crystal structures.¹²⁶

4. Results and Discussion

4.1. Polarizing Agents

Three polarizing agents were studied for direct detection of ¹⁷O, incorporated in a water/glycerol glass-forming cryoprotectant. These water soluble radicals (Figure 1) include TOTAPOL⁵¹, SA-BDPA¹²⁷ and the OX063 version of trityl.¹²⁸

Figure 1.

Molecular structures for (a) TOTAPOL (bi-radical), (b) SA-BDPA (mono-radical) and (c) trityl-OX063 (mono-radical) polarizing agents capable of directly polarizing ¹⁷O.

The EPR spectrum of the biradical TOTAPOL introduced by Song et al.⁵¹, largely resembles that of the monomeric TEMPO radical precursor and displays a large g-anisotropy resulting in a asymmetric inhomogeneous spectrum with Δ≥ 600 MHz at 5 T. SA-BDPA and trityl are both monomeric radicals and exhibit narrow, approximately symmetric EPR spectra with inhomogeneous linewidths on the order of 28 and 50 MHz, respectively.¹²⁷ We have shown that cross-effect DNP of ¹H followed by cross polarization is the optimal approach thus far in studying a variety of biological systems.^{9, 59, 63, 64, 66, 67, 78, 94, 129, 130}

With the advent of higher powered microwave devices and the use of paramagnetic metal centers, the solid-effect is also of interest, providing significant enhancements can be obtained at elevated fields.¹³¹ To better understand these radicals and the dominant DNP mechanism for direct ¹⁷O polarization we studied ¹⁷O detected field profiles and enhancements.

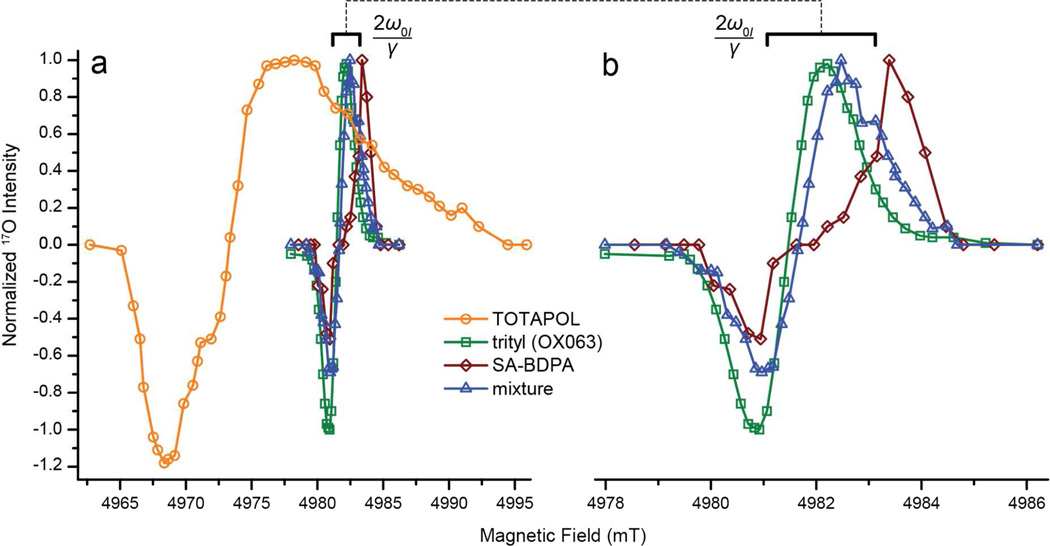
4.2. Field profiles

Since direct polarization of ¹⁷O is in its naissance we must carefully study both the radical and field profile in order to determine the dominant DNP mechanism for this low-γ nucleus with a nuclear Larmor frequency approximately 1/7^th that of ¹H (~28.8 MHz at 5.0 T). Field profiles for each polarizing agent are shown in Figure 2. The DNP field profile obtained using TOTAPOL closely resembles the profile when ¹H’s are polarized under similar conditions, exhibiting a slight upfield shift of the DNP maximum (4.9789 T).⁵¹ It is important to note that the maximum negative enhancement (4.9691 T) using the biradical TOTAPOL is actually ~20 % higher than the maximum positive enhancement. The negative lobe of the field profile is also narrower (i.e., sharper) for ¹⁷O than when studying the indirect field profile (i.e., ¹H).⁷⁸ Similar, effects have been seen for directly detected DNP of low-γ nuclei and the polarizing agent TOTAPOL^{77, 85} and bTbk⁸², as a more favorable enhancement is found at the field of maximum negative enhancement. We would like to point out that significant quadrupolar interaction leads to enhanced nuclear relaxation and a broad NMR spectrum that may affect the CE performance. Furthermore, the experiments in this study are performed on static samples since quadrupolar effects are too strong to be efficiently averaged by magic angle spinning, MAS (see Supp. Info. Figs. S5 and S6) whereas above mentioned experiments on low-γ nuclei have been carried out under MAS conditions.

Figure 2.

(a) ¹⁷O detected field profiles for (circle, orange) TOTAPOL (96 scans / point), (square, green) trityl (8 scans / point), (diamond, red) SA-BDPA (384 scans / point) and (triangle, blue) SA-BDPA-trityl mixture (16 scans / point). (b) Expanded region for the three narrow-line radical field profiles. Sample composition for field profiles was 60/40 (v/v) d₈-glycerol/H₂ ¹⁷O (35%- ¹⁷O-H₂O) with 40 mM electrons.

In contrast to TOTAPOL, SA-BDPA has a narrow ¹⁷O field-profile with nearly symmetric positive and negative maxima at 4.9833 and 4.9806 T, respectively. The decreased breadth of the profile is directly related to the significantly narrower EPR spectrum of SA-BDPA with respect to TOTAPOL. This narrow width occurs due to a small inhomogeneity caused by hyperfine coupling to intramolecular ¹H, while the g-tensor anisotropy is vanishing.¹²⁷ Furthermore the isolated positive and negative enhancement peaks are separated by 68 ± 7 MHz in the EPR domain with a flat plateau in the center, indicative of a dominant solid-effect polarization mechanism. However, we note that this separation is significantly larger than the expected separation by 2ω_0I = 57.4 MHz. The reason for that discrepancy is unclear. It might be caused in part or whole by the relatively low signal enhancement and therefore large error in the extrema of the field profile. At the same time the quadrupolar properties might lead to a slightly different SE matching condition, vide infra. In any case, the large separation clearly rules out CE as the DNP mechanism. Trityl exhibits a similar narrow field profile, with symmetric positive (4.9820 T) and negative (4.9808 T) enhancement lobes. The trityl field profile is similar to those of other low-γ nuclei studied (²H and ¹³C).^{77, 86} The large ratio of the inhomogeneous breadth, Δ ≈ 50 MHz, of the near symmetric EPR spectrum of trityl and the nuclear Larmor frequency, ω_0I = 29 MHz (at 5 T), leads to a highly symmetric and unstructured field profile dominated by the CE (see Eq. 2). This is in contrast to other studies of ¹³ C DNP using trityl, where Δ ≈ ω_0I and SE played an equally important role as DNP mechanism besides CE.⁸⁶

The field position of the negative enhancement from trityl and/or SA-BDPA is useful because a slight adjustment in field from the maximum of TOTAPOL for ¹H (4.9798 T) enables one to reach the position for maximum negative DNP enhancement of low-γ nuclei (e.g., ²H, ¹³C and ¹⁷O) at 4.9808 T. This permits the direct polarization of ¹⁷O or other low-γ nuclei using trityl and their indirect polarization via ¹H using TOTAPOL without further adjustment of the external magnetic field.

4.3. Enhancements

To evaluate the efficiency of polarization transfer and enhancements, a series of samples were studied, each using a concentration of 40 mM electron spins of the three polarizing agents. Saturation recovery experiments were performed to determine the effective T_B for direct oxygen detection using SA-BDPA, TOTAPOL, and trityl. Common issues surrounding direct detection for many spins other than ¹H are the long buildup and relaxation times, and the drastic increases in these parameters associated with a decrease in temperature. The combination of the presence of the paramagnetic species in solution, the system being in a disordered state, and oxygen bearing quadrupolar properties (i.e., quadrupolar relaxation) promotes efficient longitudinal relaxation. This enables the use of reasonable recycle delays, comparable to those applied for ¹H. DNP buildup times were measured for each sample; T_B of 5.2, 4.2 and 5.0 seconds were determined for SA-BDPA, TOTAPOL, and trityl, respectively (Table 1).

Table 1.

¹⁷O enhancements and build-up times for direct polarization of oxygen in a 60/30/10 (v/v) d₈-glycerol/D₂O/H₂ ¹⁷O (35%- ¹⁷O-H₂O) with 40 mM electrons and sample temperature of 85 K.

Radical	DNP Mechanism	ε	TB (s)c	T1S (ms)
SA-BDPA	SE	3 ± 0.6	5.2	28.986
TOTAPOL	CE	7 (−8)a ± 1	4.2	~0.3132
Trityl (OX063)	CE	115 ± 11	5.0	1.486
Mixture	CE	40 ± 6	5.7	1.4/3.6b86

All enhancements were acquired at the field position of maximum positive value with and without microwaves.

^(a)17O DNP enhancement for the biradical, TOTAPOL is non-symmetric, the value you parenthesis is the negative enhancement. The value in parentheses is the enhancement determined at the maximum negative point with and without microwaves.

^(b)Values for trityl and SA-BDPA components, respectively.

^(c)Nuclear spin-lattice relaxation times (T_1I) were measured independently (microwaves off) and found to be within experimental error to the DNP build-up relaxation times (T_B).

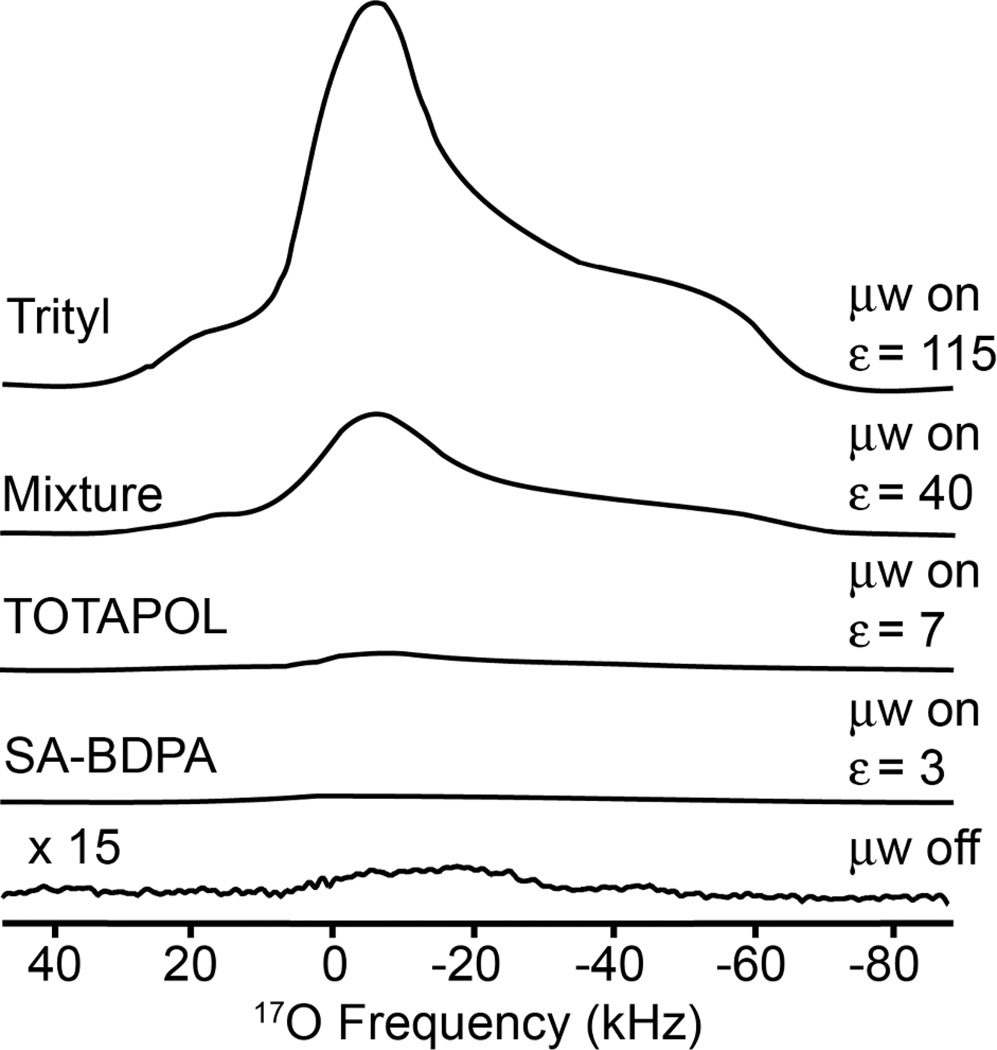
By maintaining identical sample conditions for SA-BDPA, TOTAPOL, and trityl samples and adjusting only the polarizing agent, the absolute enhancements were determined to be ε = 3, 7 and 115, respectively (Table 1, Figure 3). The gain in sensitivity is further increased due to the larger Boltzmann factor at T = 85 K, adding gains of approximately 3.5 (ε^† = 10, 25 and 400, respectively).

Figure 3.

Direct polarization of ¹⁷O in 60/30/10 (v/v) d₈-glycerol/D₂O/H₂ ¹⁷O using 35% labeled ¹⁷O water and 40 mM electrons, using 9 W of microwave power. Radicals are arranged from highest enhancement to lowest, with trityl (16 scans, ~2 minutes), mixture (64 scans, ~8 minutes), TOTAPOL (608 scans, ~60 minutes) and SA-BDPA (1,664 scans and ~180 minutes), and, the microwaves off x15 (6,646 scans, ~12 hours) spectrum from the trityl sample. NB: Enhancements and uncertainties in Table 1 were determined by acquiring an on/off signal on the same sample; the bottom trace in the figure is the off spectrum for the trityl radical and is included here for reference purposes.

The I = 5/2 ¹⁷O nucleus poses several differences compared to the typically I = 1/2 system (e.g., ¹H, ¹³C, ²⁹Si, ³¹ P etc.) such as six energy levels (i.e., ±1/2, ±3/2 and ±5/2) and multiple allowed transitions. Furthermore, quadrupolar nuclei in the solid-state experience a significant dispersion of resonance frequencies unless they are situated in a cubic (isotropic) environment. For covalently bound ¹⁷O, this dispersion covers a range of up to 9 MHz independent of the external magnetic field strength. Therefore, the matching conditions for the CE and SE in principle are altered to represent the effective Larmor frequency rather than just the Zeeman frequency. This translates the dispersion in the nuclear frequency domain into a dispersion in the matching condition between nuclear spin frequencies and the required irradiation frequency of electron spins, as well as the shape of the DNP field profiles. However, the central transition (m_I = −1/2 → +1/2) is an exception to this dispersion. The residual second-order broadening of ~90 kHz (for ¹⁷O in a frozen glass environment at 5 T) can be neglected with respect to the magnitude of the EPR line widths of at least several tens of MHz, and naively, one tends to simply utilize the matching conditions Eqs. (1) and (3).

Nevertheless, several reasons argue against this simplification. The eigenframes of all nuclear m_I states are significantly tilted with respect to the external magnetic field axis absent the fortuitous case of co-linearity between the EFG tensor and the external magnetic field (i.e., the external magnetic field vector is oriented along one of the canonical orientation of the EFG). This tilting leads to significant mixing of the nuclear states. The states are coupled by the non-secular quadrupole interaction components, which are on the order of a few MHz. These couplings are typically much larger than those leading to the electron-nuclear double- and zero-quantum coherences invoked during SE DNP and will therefore affect the state mixing which is a prerequisite for SE. Additional coherences are introduced, which couple the central transition states (i.e., |m_I| = 1/2) to those with |m_I| > 1/2. Although these transitions are generally off-resonant under SE matching, fast oscillations to these states might compete with the SE transfer and allow for additional nuclear relaxation pathways (vide infra). For the CE, the situation is slightly more complicated because two types of coherences are involved: electron-electron and electron-nuclear dipole coupling between one of the electron spins and the nuclear spin polarized. The former typically is larger than the quadrupole interaction if biradicals are used as polarizing agents (e.g., ~25 MHz for TOTAPOL); whereas it approaches the coupling if intermolecular couplings are involved in the case of monoradicals. The electron-nuclear dipole coupling again is expected to be smaller than the nuclear quadrupolar interaction, however, it might also be of similar order since the polarization pathway is less clear than in the SE case. Furthermore, the direct impact of electron-electron and electron-nuclear coupling is not completely understood for the CE, therefore, effects that quadrupolar nuclei impose on the CE efficiency are not clear.

Besides the effect of the quadrupole coupling, non-coherent relaxation processes will affect the DNP transfer. The nuclear quadrupolar interaction leads to very efficient spin-lattice relaxation; competing directly with build-up of enhanced polarization by DNP. Corzilius et al.¹³³ have introduced a DNP equilibrium constant K_DNP which is calculated from the enhancement factor and takes into account the DNP rate constant k_DNP, and the nuclear spin-lattice relaxation time constant T_1I:

$$K_{\mathrm{D}\mathrm{N}\mathrm{P}}=k_{\mathrm{D}\mathrm{N}\mathrm{P}}{T}_{1I}=\frac{({\epsilon }_{\infty }-1)}{(\frac{P_S^{\infty }}{P_{I,\text{eq}}}-{\epsilon }_{\infty })}\approx \frac{({\epsilon }_{\infty }-1)}{({\epsilon }_{\text{max}}-{\epsilon }_{\infty })}\approx \frac{{\epsilon }_{\infty }}{{\epsilon }_{\text{max}}}\text{for}1-{\epsilon }_{\infty }-{\epsilon }_{\text{max}}$$ (9)

$P_S^{\infty }$ and P_I,eq describe the residual electron polarization after infinite polarization time and the nuclear polarization in thermal equilibrium, respectively; ε_max is the thermodynamically maximum achievable enhancement: ε_max = γ_s/γ_I; and ε_∞ is the enhancement (ε) after infinite polarization time. For the first approximation in Eq. (9) it is assumed that the effective electron polarization is not depleted during DNP transfer, which is the case when electron longitudinal relaxation is fast. With this equation we can estimate the effect of fast quadrupolar relaxation on the experimentally observed enhancement. Under this assumption, we find that K_DNP≪1, so that ε_max must be much larger than ε_∞. Therefore, we can finally replace ε_max − ε_∞ with ε_max, and ε_∞ −1 with ε_∞. In this case, the observed enhancement scales linearly with T_1I. We note that T_1I only accounts for spin-lattice relaxation including paramagnetic relaxation enhancement (PRE); DNP effects that shorten the experimentally observed time constant have to be excluded. For the SE this is trivial, since DNP is only active when the electron-nuclear spin system is irradiated with the appropriate microwave frequency. In this case, the DNP buildup rate constant and the spin-lattice relaxation rate constant additively form the observed overall buildup rate constant 1/T_B:

$$\frac{1}{T_B}=k_{\mathrm{D}\mathrm{N}\mathrm{P}}+\frac{1}{T_{1I}}$$ (10)

The CE, however, is always active, because the driving coherences are introduced by the electron-electron coupling, which cannot be switched off; DNP is always active, however, in thermal equilibrium no net polarization transfer occurs because the rates for positive and negative enhancement of nuclear polarization are equal. In this case, net polarization transfer is achieved by disturbing the thermal equilibrium polarization of one of the electron spins by microwave irradiation induced saturation and the resulting change in one of the DNP rate constants. Therefore, a disentanglement of rate constants according to Eq. (10) is not possible.

The observed buildup time constants in Table 1 clearly show a rather uniform distribution with an average of 5.0 s and a small maximum deviation of only 0.8 s. This deviation lies well within the error of the experiments, especially given the small absolute signals when small enhancements are encountered. This leads us to the conclusion that all T_B’s are limited by short T_1I, and that k_DNP is rather small in all cases. Despite this theoretically unfavorable situation, trityl allows for a significant enhancement of 115, which results in more than a factor of 13,000 reduction of acquisition time. TOTAPOL, on the other hand yields only ε = 7. The discrepancy between trityl and TOTAPOL is explained by the dramatically different EPR lineshapes. While trityl has a Gaussian-like lineshape with Δ = 50 MHz, the overall breadth of the TOTAPOL powder lineshape due to the g-anisotropy is ~600 MHz at 5 T. Therefore, the trityl spectrum concentrates the electrons in a more narrow spectral region for efficient ¹⁷O CE matching with ω_{0 ¹⁷O} ~29 MHz. This demonstrates the potential of radicals with a narrow EPR line as effective polarizing agents for CE DNP of low-γ nuclei. We reported similar observations when directly polarizing ²H.⁷⁷

SA-BDPA yields a rather small enhancement ε=3. We attribute this to the fact that the SE is active in this case, and also be affected by a large quadrupole coupling. Even though a reduction of T_B with respect to T_1I is expected for the SE we have observed T_B ≈ T_1I within the experimental error for all samples, including SA-BDPA. According to Eq. (10) this leads us to conclude that k_DNP − 1/T_1I and is in line with the very small observed enhancement. Another potential problem is the depletion of the electron spin polarization by off-resonant saturation of the EPR resonance. The combination of extremely long T_1S = 29 ms and small resonance offset of ω_0I = 29 MHz is supposed to significantly reduce the electron spin polarization available for transfer to nuclear spins by off-resonance irradiation of the EPR transition.¹³¹

It would seem that nuclear relaxation is a significant factor in obtaining effective DNP gains as both ²H (ω_0I = 32.5 MHz, I=1) and ¹⁷O (ω_0I = 28.7 MHz, I=5/2) are quadrupolar and their respective nuclear Larmor frequencies are similar.² H detection on identical samples exhibited an enhancement >500 with a T_B of 70 s, whereas ¹⁷O direct detection was ε=115 and T_B of 5 s. If ¹⁷O T_1I relaxation rates could be reduced, we surmise that the enhancements would increase.

Further enhancements could be gained from magic-angle spinning at a moderate frequency (figure S6). Rotating the sample has several effects that lead to improved DNP efficiency: including a reduction of certain anisotropies and an increase in the efficiency of polarizing by allowing the microwaves to average over the full surface of the rotor. Our group and others have noted gains in enhancement when studying system under MAS conditions.⁵⁹ We will report on non-spinning and MAS experiments at higher fields in a future publication.

4.4. Mixture

In theory, the CE mechanism is most efficient when two narrow EPR lines are separated by the nuclear Larmor frequency while an appropriate coupling allows for transfer of polarization between the two lines.^{95, 96} The concept has first been demonstrated by Hu et al. by mixing the narrow-line radical trityl with the nitroxide radical TEMPO.⁹¹ Irradiation on resonance with the center of the trityl EPR transition resulted in a four-fold increase of enhancement compared to the use of TEMPO as a polarizing agent alone. Therefore a mixture of SA-BDPA and trityl OX063 might allow for cross effect, where the SA-BDPA resonance is irradiated with microwaves and polarization is transferred to a dipolar coupled nucleus during an electron-electron cross-relaxation flip-flop between SA-BDPA and trityl, this approach was illustrated to work extremely well in the case of direct ¹³C DNP NMR.⁸⁶ In an attempt to improve the enhancement of SA-BDPA, a mixture of 20 mM SA-BDPA and 20 mM trityl in a water/glycerol glass was acquired. The field profile is shown in Figure 2b; the profile indicates a cross-effect mechanism with a broadened inhomogeneous linewidth and a positive maximum (4.982 T). The overall enhancement improved to 40 from 3 (Figure 3). Note that the maximum positive enhancement position coincides with the EPR resonance field of SA-BDPA together with the asymmetry between the positive and negative maxima indicates that the CE is active between SA-BDPA and trityl. The asymmetry was reported by Hu et al.⁹¹ and is caused in part by different longitudinal relaxation properties of the radicals involved. In particular, SA-BDPA has a T_1S that is significantly longer than that of trityl.¹²⁷ Subsequently, irradiation at the EPR resonance of SA-BDPA leads to a very effective spin saturation, and polarization can be efficiently replenished by fast-relaxing trityl in a cross-relaxation process. Irradiation of the trityl spin on the other hand, would be less efficient due to faster T_1I relaxation, while cross-relaxation would saturate the slowly relaxing SA-BDPA, effectively quenching the CE.

4.5. Structurally relevant oxygen environments

The ability to polarize 17O directly and indirectly (through ¹H) has enabled this challenging nucleus to be used within a variety of 1D and 2D experiments as a probe for local oxygen environments, which vary within organics, proteins, sugars, surfaces, and oxides. Three common functional groups providing a unique oxygen environment can be envisioned for aiding in structural elucidation of various chemical systems. First, water (H₂O) plays an important role in hydrogen bonding, transport and surface chemistry. Second, carbonyl (C=O), a double-bonded oxygen, is integral to protein structure, folding and function. Third, hydroxyl (-OH) moiety is often associated with hydration-dehydration reactions, hydrogen bonding, and layered hydroxides. To illustrate the widespread ability of DNP on oxygen environments, ¹⁷O spectra of three small molecules are discussed below using direct polarization ¹⁷O DNP NMR, room temperature NMR experiments on the crystalline solid (without DNP), and quantum chemical calculations for crystalline water, urea and phenol using GIPAW.

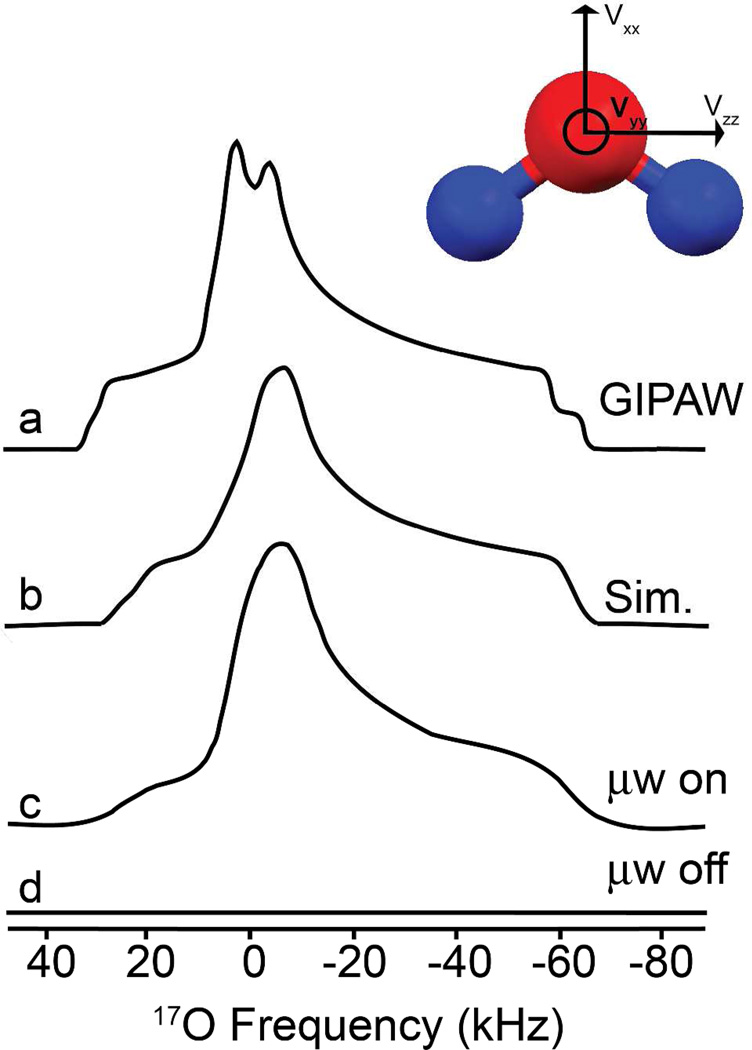
DNP of water environments was recently illustrated using the indirect polarization method via DNP of ¹H followed by cross-polarization.⁷⁸ As water is frozen a variety of arrangements can occur (e.g., Ice-Ih, Ice-XI, etc.) depending on temperature, isotopic content (¹H :² H), freezing rate and pressure.¹³⁴ The frozen solution studied is comprised of a cryoprotecting solvent in an amorphous state, whereby crystal packing is inhibited. Nevertheless, with the significant gains offered by DNP, the quadrupolar NMR parameters can still be determined. A moderate quadrupole coupling constant of 6.8 MHz in magnitude was obtained by spectral simulation of the central transition. The asymmetry parameter and isotropic chemical shift were 0.95 and 0 ppm, respectively, agree well with literature studies of frozen water.^{135, 136} An ordered ice crystal structure¹¹⁷, which apparently occurs at cryogenic temperatures, was calculated using GIPAW in order to evaluate the calculated oxygen NMR properties, crystal structure, and DNP NMR experimental data. The two crystallographic oxygen sites contained quadrupolar coupling constants of −6.632 and −7.034 MHz with asymmetry parameters of 0.91 and 0.88. The averages of these two sites agree well with the experimentally determined parameters above (Figure 4 and Table 2).

Figure 4.

¹⁷O DNP NMR spectrum of water using direct polarization from trityl. a) Simulation using GIPAW calculated parameters for crystal structure, b) simulation of quadrupolar lineshape, c) experiment on-signal for amorphous sample (64 scans, ~7 minutes) and d) experiment off-signal (6646 scans, ~12 hours). Sample conditions: 60/30/10 (v/v) d₈-glycerol/D₂O/H₂ ¹⁷O using 35% labeled ¹⁷O water and 40 mM trityl.

Table 2.

Experimental (DNP and non-DNP) and calculated ¹⁷O NMR parameters for model oxygen environments

Molecule	CQ (MHz)	η	δiso (ppm)	Ω (ppm)	κ
Water (DNP)	6.8 (2)	0.95 (5)	0 (150)	n.d.	n.d.
Water (exp.)i	6.43	0.935	n.d.	n.d.	n.d.
Water (exp.)ii	6.66	0.935	0	n.d.	n.d.
Water (GIPAW)*	−6.833	0.90	−68.24	35.59	−0.40
Urea (DNP)	7.5 (3)	0.5 (2)	150 (150)	n.d.	n.d.
Urea (exp.)iii	7.24	0.92	108	280	−0.857
Urea (GIPAW)	7.576	0.96	172.37	262.98	−0.82
Phenol (DNP)	8.3 (3)	0.95 (5)	100 (150)	n.d.	n.d.
Phenol (exp.) iv	8.3 (1)	0.95 (5)	80 (5)	n.d.	n.d.
Phenol (GIPAW)*	−8.686	0.84	81.61	71.12	0.53

ⁱ- Ba et al.¹³⁶;

ⁱⁱ- Spiess et al.¹³⁵;

ⁱⁱⁱ- Dong et al.¹⁰⁶;

^iv- ¹⁷O MAS NMR data acquired at 17.4 T (see Figure S4);

^*-Where multiple crystallographic oxygen sites existed the averages of these are presented within the table (please refer to supporting information Tables S1 to S3). Experimental uncertainties are given in parenthesis. The Herzfeld-Berger¹⁴¹ convention is used to describe the chemical shift anisotropy, with the span (Ω) and skew (κ) defined as, Ω = (δ₁₁ − δ₃₃) and κ = 3(δ₂₂−δ_iso)/ Ω, respectively.

Practically all high-field DNP based studies on biological proteins involve a cryoprotecting matrix with approximately 40 % water. This potentially creates a challenge when studying oxygen environments within solutes that need to be dispersed within water as the labeled oxygen sites may compete with the high molarity of the natural abundance oxygen in water (i.e., 55 M oxygen). To illustrate both the major boost in sensitivity of DNP on oxygen and to provide evidence that natural abundant background oxygen is not an issue, organic based carbonyl and hydroxyl small molecules were studied using 3–4 mgs of ≤30 % labeled ¹⁷O. The small sample volume and low enrichments are important aspects for validating DNP as ¹⁷O labeling is at present costly and limited concentration within biological solids.¹³⁷

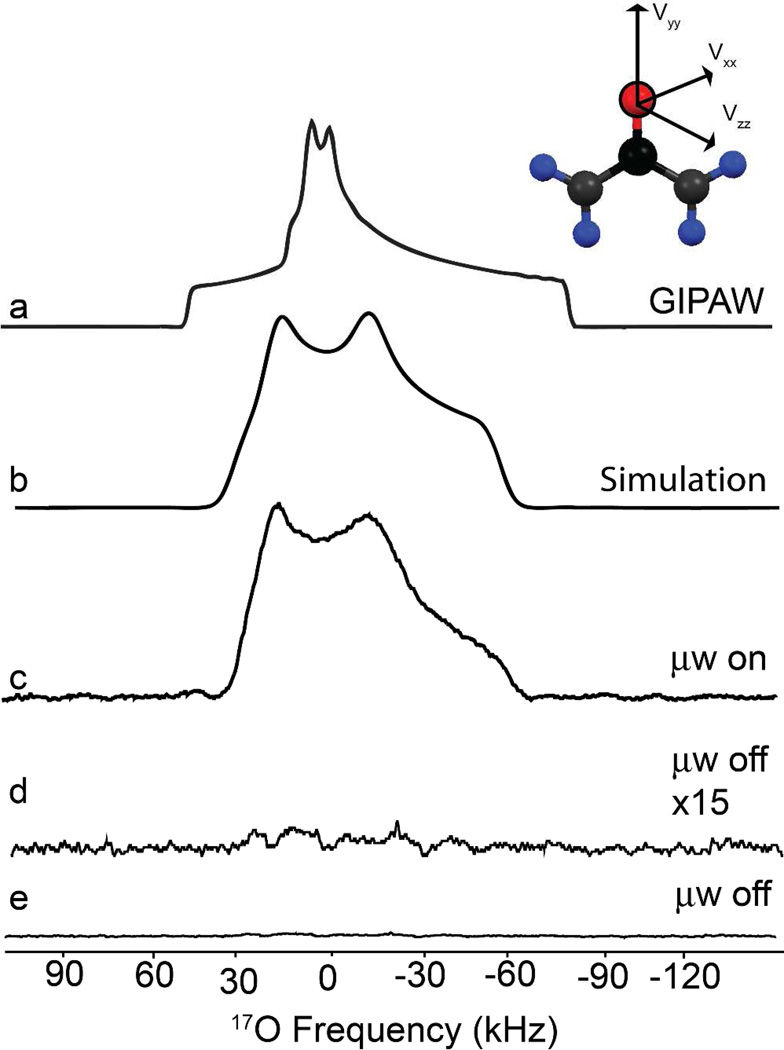
The central transition ¹⁷O DNP NMR spectrum of urea, (NH₂)₂C= ¹⁷O, a representative C=O is shown in Figure 5 with and without microwave radiation. Determining the exact ¹⁷O DNP enhancement is difficult due to the poor S/N ratio from the collected off spectrum, nonetheless the enhancement is ≥ 80. The quadrupolar coupling parameters (C_Q = 7.5 MHz and η= 0.5) and isotropic chemical shift (δ_iso = 150 ppm) were obtained by spectral simulation (fig. 5b) of the ¹⁷O central transition (fig. 5c). The off spectrum was acquired for six days (144 hours) under identical conditions with little success, thus limiting our ability to quantify ε. Thus, without DNP this experiment would have been impossible due to the small gyromagnetic ratio, sample volume, and large quadrupolar coupling.

Figure 5.

¹⁷O DNP NMR spectrum of ¹⁷O labeled urea (4 mgs) in 60/30/10 (v/v) d₈-glycerol/D₂O/H₂O and 40 mM trityl using direct polarization. a) Simulation using GIPAW calculated parameters, b) simulation of quadrupolar lineshape, c) experiment on-signal (~ 8 hours), d) experiment off-signal scaled by 15 and e) experiment off-signal (~ 144 hours).

The quadrupolar coupling determined experimentally by DNP and calculated using GIPAW agree quite well with the experimental (non-DNP) solid-state NMR data acquired on crystalline urea¹⁰⁶ (Table 2). One parameter, however, is poorly represented, which is the asymmetry parameter of the cryoprotected small molecule (Figure 5). We experimentally observed η~0.5, while in the crystalline sample, η ~1 due to the C_2v point group symmetry of urea which is the same as for water. Previous studies of crystalline urea by Dong et al.¹⁰⁶ illustrated the importance of incorporating the long-range structure for accurate Gaussian-based calculations in order to calculate the asymmetry parameter properly. With gas-phase based calculations they illustrated that the asymmetry parameter changes from 0.6 to 0.9 as they constructed the surrounding environment around a single urea molecule, indicating that the hydrogen bonding arrangement is important in determining η. Urea solubilized in the cryoprotectant lacks the local environment of the crystalline phase and hence affects the packing, hydrogen bonding, and the effective EFG. Therefore we attribute this change with the EFG to a “solvent effect” that should be considered when studying small molecules with large chemical shieldings or quadrupolar coupling constants as different asymmetry parameters may be observed.^{138, 139}

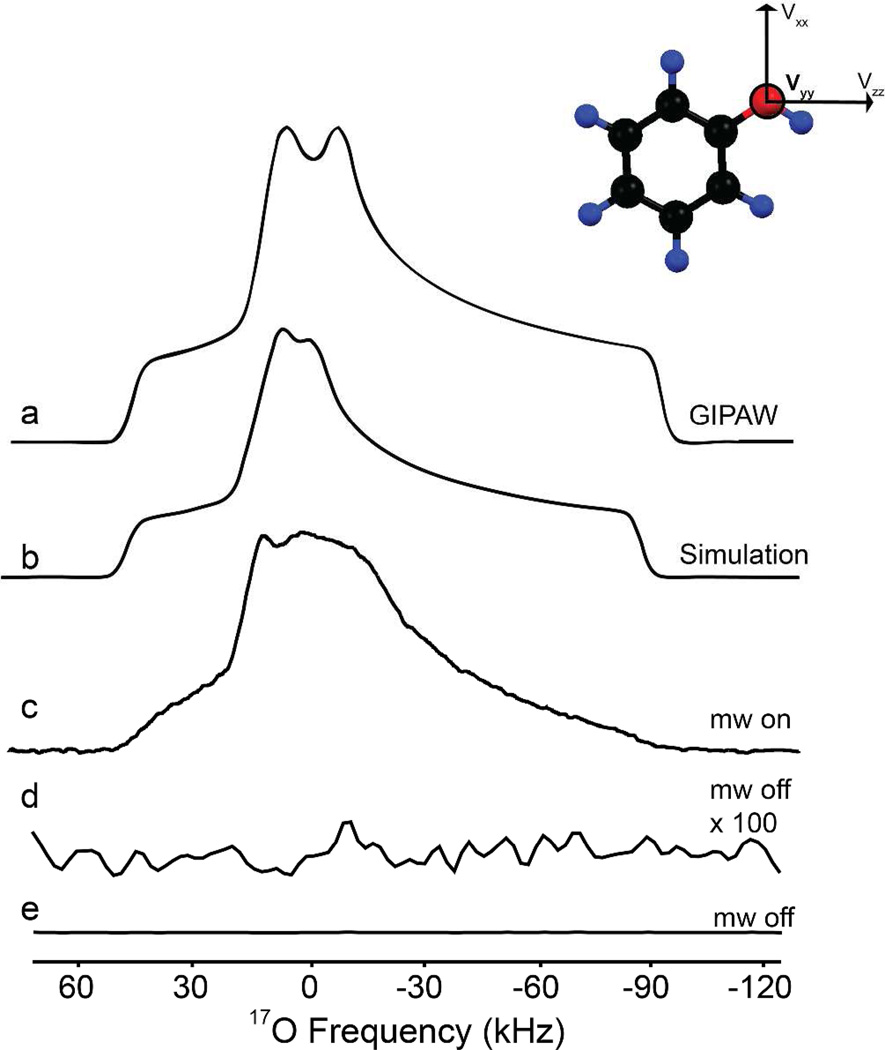
Phenol, a hydroxyl containing aromatic ring is often associated with tyrosine-like residues and provided ε > 100 as shown in Figure 6. As in the case of urea the off signal (acquired for six days) and the on signal (acquired for ~18 hours) exhibited no interference from the oxygen present in the cryoprotectant (or rotor). The lineshape spans over 4,500 ppm (> 130 kHz) with an associated distribution of sites (disordered, glass like structure) causing further broadening of the central region similar to H₂O). The experimental ¹⁷O NMR parameters were determined in a fashion similar to that described above with a quadrupolar coupling constant of 8.3 MHz, asymmetry parameter of 0.88 and isotropic chemical shift of 100 ppm. GIPAW calculations and NMR experiments of the crystalline solid (non-DNP) at higher magnetic fields (Table 2, Figure S4) agree well with experimental parameters as well as other phenolic-like systems studied previously.^{100, 140}

Figure 6.

¹⁷O DNP NMR spectrum of ¹⁷O labeled phenol (3 mgs) in 60/30/10 (v/v) d₈-glycerol/D₂O/H₂O and 40 mM trityl using direct polarization. a) Simulation using GIPAW calculated parameters, b) simulation of quadrupolar lineshape, c) experiment on-signal (~ 18 hours), d) experiment off-signal scaled by 100 and e) experiment off-signal (~ 144 hours).

Three distinct oxygen environments (i.e., water, carbonyl and hydroxyl) using trityl as a polarizing agent lead to enhancements > 80. The ability to fit NMR parameters, in particular quadrupolar couplings, which are in reasonable agreement with experimental data acquired at room temperature illustrates the strength of this method for sensitivity gains. The experimentally determined ¹⁷O quadrupolar coupling constants from DNP agree well with those obtained from the room temperature NMR data of the crystalline solids (non-DNP) and are reproduced well by the GIPAW based calculations (Figure S1–S3, Tables S1–S3). Although care is advised when recording spectra of quadrupolar and / or highly polarizable nuclei at low temperatures and in a cryoprotecting solvent as both the asymmetry parameter and chemical shielding parameters (i.e., η, δ_iso, Ω and κ) are known to be highly sensitive to local chemical environments. DNP is an ideal tool for studying microcrystalline environments which will have limited solvent and temperature effects, enabling the potential to combine DNP with NMR crystallography methods¹⁴² for studying difficult NMR nuclei in other chemical systems.

5. Conclusion

The direct DNP of ¹⁷O has been demonstrated on typical oxygen environments relevant to the study of molecular biology. The array of radicals available is vast, however the three most prominent, currently used polarizing agents illustrate the ability to polarize ¹⁷O directly without the need of protons. This enables a method to study oxygen environments that lack presence of ¹H for CP. Although all radicals discussed provide gains over conventional room temperature NMR, trityl yields the greatest enhancements, while the system offers experimentally convenient relaxation times at cryogenic temperatures. The gains in sensitivity for this spectroscopically difficult quadrupolar nucleus provide significant savings in acquisition time. This provides new opportunities for studying ¹⁷O by NMR, enabling extension to multidimensional studies or studies of small sample sizes with isotropic labeling. As DNP moves towards higher magnetic fields and higher frequency spinning this technique should prove promising in the study of biological, medical and material applications.