Skip to main content
PMC home page
The Journal of Physiology logoLink to The Journal of Physiology
. 2013 Nov 18;592(Pt 2):313–324. doi: 10.1113/jphysiol.2013.261099

Branching patterns emerge in a mathematical model of the dynamics of lung development

Yina Guo 1,✉, Ting-Hsuan Chen 2, Xingjuan Zeng 1, David Warburton 3, Kristina I Boström 4, Chih-Ming Ho 5, Xin Zhao 1, Alan Garfinkel 4,6
PMCID: PMC3922496  PMID: 24247979

Abstract

Recent experimental work has described an elegant pattern of branching in the development of the lung. Multiple forms of branching have been identified, including side branching and tip bifurcation. A particularly interesting feature is the phenomenon of ‘orthogonal rotation of the branching plane’. The lung must fill 3D space with the essentially 2D phenomenon of branching. It accomplishes this by rotating the branching plane by 90° with each generation. The mechanisms underlying this rotation are not understood. In general, the programmes that underlie branching have been hypothetically attributed to genetic ‘subroutines’ under the control of a ‘global master routine’ to invoke particular subroutines at the proper time and location, but the mechanisms of these routines are not known. Here, we demonstrate that fundamental mechanisms, the reaction and diffusion of biochemical morphogens, can create these patterns. We used a partial differential equation model that postulates three morphogens, which we identify with specific molecules in lung development. We found that cascades of branching events, including side branching, tip splitting and orthogonal rotation of the branching plane, all emerge immediately from the model, without further assumptions. In addition, we found that one branching mode can be easily switched to another, by increasing or decreasing the values of key parameters. This shows how a ‘global master routine’ could work by the alteration of a single parameter. Being able to simulate cascades of branching events is necessary to understand the critical features of branching, such as orthogonal rotation of the branching plane between successive generations, and branching mode switch during lung development. Thus, our model provides a paradigm for how genes could possibly act to produce these spatial structures. Our low-dimensional model gives a qualitative understanding of how generic physiological mechanisms can produce branching phenomena, and how the system can switch from one branching pattern to another using low-dimensional ‘control knobs’. The model provides a number of testable predictions, some of which have already been observed (though not explained) in experimental work.

Key points

  • The development of the lung is a highly stereotypical process, including the structured deployment of three distinct modes of branching: first side branching and then tip splitting with and without 90° rotation of the branching plane.

  • These modes are supposedly under genetic control, but it is not clear how genes could act to produce these spatial patterns.

  • Here, we show that cascades of branching events emerge naturally; the branching cascade can be explained by a relatively simple mathematical model, whose equations model the reaction and diffusion of chemical morphogens.

  • Our low-dimensional model gives a qualitative understanding of how generic physiological mechanisms can produce branching phenomena, and how the system can switch from one branching pattern to another using low-dimensional ‘control knobs’.

  • The model makes a number of experimental predictions, and explains several phenomena that have been observed but whose mechanisms were unknown.

Introduction

Recent experimental work has described an elegant pattern of branching in the morphogenesis of the lung (Metzger et al. 2008). Three forms of branching have been identified: domain, orthogonal, and planar. In the development of the lung, these occur in sequence: first, domain (or side) branching creates the primary stalks; then, orthogonal branching fills the 3D space with tip bifurcations in planes that rotate 90 deg from one generation to the next; finally, planar branching (tip splitting without orthogonal rotation) completes the architecture. To understand the mechanisms that create this sequence, the branching program has been hypothetically attributed to four modular ‘subroutines’: a ‘bifurcator’, a ‘rotator’, a ‘domain specifier’ and a ‘periodicity generator’. These subroutines may be coupled together but function independently, organized by a ‘global master routine’ that invokes particular subroutines at the proper times and locations (Metzger et al. 2008; Warburton, 2008).

These routines are postulated to be under genetic controls, but it is far from clear how genes could possibly act to create these spatial phenomena. At a certain point in lung development, there is a switch from side to tip branching, presumably under genetic control. But how could a gene act to achieve such a switch? There is a periodicity generator, but what sorts of mechanisms could that generator act through to bring about the periodicity? How can a gene carry out orthogonal rotation of the branching plane?

Here we show how these patterns and subroutines can emerge from the reaction and diffusion of chemical morphogens, as modelled by a single set of partial differential equations (PDEs). The paradigm for this type of modelling was the revolutionary paper of Turing (1952). Turing's original paper postulated abstract and unknown ‘activator’ and ‘inhibitor’ morphogens, arguing that ‘a system of chemical substances, called morphogens, reacting together and diffusing through a tissue, is adequate to account the main phenomena of morphogenesis’ (Turing, 1952). Turing's original model produced simple patterns of spots or stripes. Later, more complex models were developed to generate more complex patterns, such as branching patterns in two dimensions (Meinhardt, 1976).

Despite of the attractiveness of Turing's paradigm, for a long time, biological applications were limited by the difficulty of identifying those postulated morphogens. However, Sonic hedgehog (SHH), a member of a family of putative signalling molecules, was implicated as a morphogen as early as 1993 (Echelard et al. 1993; Riddle et al. 1993). In 2001, Vincent and Perrimon said “The existence of morphogens in vertebrates has been controversial”. However, they concluded “One suspect is now shown to fit the bill” (Vincent & Perrimon, 2001). The suspect was Squint, a member of the transforming growth factor-β (TGF-β) superfamily (Chen & Schier, 2001). Many other additional morphogens have been identified, including a number that are active in lung morphogenesis, such as FGF10, BMP4, SSH, Sprty2 and MGP (Bellusci et al. 1996, 1997; Weaver et al. 2000; Mailleux et al. 2001; Gilbert & Rannels, 2004; Yao et al. 2007; Lazarus et al. 2011). While we know that these morphogens are active in lung morphogenesis, it is not clear how they interact with each to produce the observed spatial patterns.

Here we used a set of PDEs, with three reacting and diffusing chemical morphogens and a fourth variable to record cell differentiation. We found that cascades of branching events, including side branching, tip branching and orthogonal rotation of the branching plane, all emerge from the model. Specifically, in two-dimensional simulations, we were able to reproduce side branching and tip bifurcation. When we extended the simulation into three dimensions, orthogonal rotation of branching plane, in both side branching and tip bifurcation, emerged naturally from the interaction of morphogens. In addition, one branching mode can be easily switched to another by increasing or decreasing the values of key parameters.

We found that relatively simple mechanisms underlying the branching phenomena can be grasped by studying the model. For example, one factor that drives orthogonal rotation of the branching plane is the presence of high levels of inhibitor in the previous branching plane, due to the pooled secretion from the previous branches. This pooled inhibition drives the next generation of branching into the perpendicular plane, where it is subjected to the least inhibition.

The dynamics and interactions among those chemical morphogens, represented by the PDE model, provides a generic template for how genetic routines could possibly act in order to produce those observed spatial structures. The key parameters that switch spatial patterns suggest how the ‘global master routine’ could work by the alteration of a single parameter. These serve as ‘control knobs’ through which specific biochemical changes can act to produce a variety of spatial patterns, providing a paradigm for the experimental biologist, suggesting how specific genes might act, and generating a variety of experiments and testable predictions.

Other models of lung development

Since Meinhardt's 1976 paper, there have been several other mathematical models that study lung branching phenomena. The model of Menshykau et al. (2012) is based on the reaction and diffusion of FGF10 and SHH as well as the SHH receptor patched (Ptc). Celliere et al. (2012) then add FGF9 to the model. Their model, like ours, uses a Turing-style approach to reproduce the mutant effect that ‘reduction in FGF10 expression not only reduces the number of branches but increases the distance between branching points by 50%.’ However, their model is not a model of morphogenetic growth, but rather, a model of periodic spots appearing surrounding the lung bud. Thus, it is not a model for what Clement et al. (2012a) call ‘shape emergence’ or morphological growth, which is the goal of our model. Menshykau et al. also show that side branching and tip bifurcation can be differentially produced by choosing different growth speeds of the lung bud. In their model, the growth of the lung bud is not caused by the morphogens, but is implemented by a command that the cylinder-shaped lung bud grow as a function of time. Later, in their approach to kidney branching (Menshykau & Iber, 2013), they developed a model in which “growth was prescribed to be normal to the boundary and proportional to the local level of signaling”. Using this prescribed motion of the mesenchymal boundary, they show that branching of the ureteric bud results from expansion of the mesenchyme. However, the relation is only stipulated; in our model, outgrowth of the lung epithelium is a causal response to the morphogen FGF10.

Another approach to lung development modelling is that of Hirashima et al. (2009), a reaction–diffusion model of several morphogens interacting. They show that different branching modes can be controlled by external geometry: the bud develops one FGF10 peak at the tip when the boundary is ‘near’ the tip of the stalk, and two FGF10 peaks when the boundary is ‘near’ the two sides of the stalk, that is, when the boundary has high curvature. However, it is not a growth model. Clement et al. observed that the ‘model does not implement growth, so the link between patterning and shape remains missing.’ Because it is not a growth model, it can only treat one generation.

Clement et al. (2012a,2012b) also approach branching morphogenesis through diffusion-based mechanisms. They correctly address the importance of ‘shape emergence’. Their model considered two factors during lung development, the spatial diffusion of FGF10, and the epithelial growth response to an FGF10 gradient. Their simulations showed that side branching could be distinguished from tip splitting by choosing different growth functions. The fundamental dynamics in the Clement et al. papers is that growth of the epithelium is stipulated to be a sigmoidal function of the gradient of FGF10. But again, because it is a stipulated function, the causal factors that create this relation are left unclear.

Thus, these papers either have fundamental molecular mechanisms but no morphological growth (Hirashima et al. 2009; Celliere et al. 2012; Menshykau et al. 2012) or shaped growth but no fundamental mechanisms driving it (Clement et al. 2012a,b2012b). The PDE model in our paper includes morphological growth as a causal response to fundamental mechanisms, a differential equation rather than a stipulated function. Therefore, cascades of branching events can naturally emerge from our model or others of this kind.

Methods

Mathematical model

Our mathematical model is a reaction–diffusion partial differential equation (PDE) for branching morphogenesis. Based on the work of Meinhardt (1976), the model postulates four quantities, which are concentrations continuously distributed over space. The first three are concentrations of chemical morphogens: an activator A, an inhibitor H, and a ‘substrate’ chemical S, while the last, Y, is a marker for cell differentiation.

The identities of the morphogens can be hypothesized. A detailed argument for these identifications is carried out in the Discussion. Briefly, we suggest that the substrate S is FGF10. We propose several candidate pairs for activator and inhibitor; the most likely is that activator A is BMP4 and inhibitor H is MGP. Their approximate spatial distributions are shown in Fig. 1.

Figure 1.

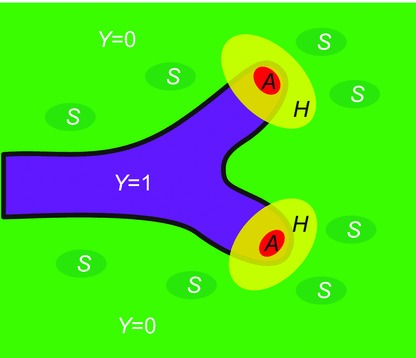
Figure 1

Open in a new tab

Schematic of the model Airway is represented by sites at which Y = 1. Substrate S is distributed over the domain surrounding the airway, while A and H become concentrated at the growing tips.

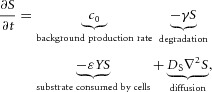
The equations of the model are:

graphic file with name tjp0592-0313-mu1.jpg
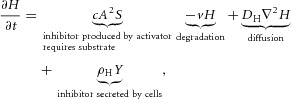graphic file with name tjp0592-0313-mu2.jpg
graphic file with name tjp0592-0313-mu3.jpg
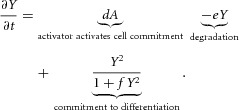graphic file with name tjp0592-0313-mu4.jpg

The model assumes that activator, inhibitor and substrate are all diffusible substances. DA, DH, and DS are the diffusion coefficients of activator, inhibitor, and substrate, respectively. Activator A is up-regulated by itself in autocatalytic reaction kinetics at rate c (this is the 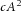Inline graphic part of the first term in the ‘A-equation’; Garfinkel et al. 2004). This autocatalytic process is augmented by substrate S, which is represented by the term 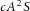Inline graphic. The production of activator A is inhibited by inhibitor H, which is modelled by placing the H term in the denominator (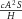Inline graphic in the A-equation). A is also secreted by differentiated cells Y at a rate ρA (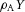Inline graphic in A-equation). The production of inhibitor H is increased by activator A, again requiring substrate S (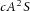Inline graphic in H-equation). H is also produced by differentiated cells Y at a rate ρH (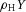Inline graphic in H-equation). Substrate S is produced at a rate c0, and is consumed by differentiated cells Y at a rate ε. The fact that substrate is consumed by cells in a stoichiometric reaction is modelled by the product term 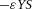Inline graphic in the S-equation. Cell commitment Y is created by high concentrations of activator A (the +dA term in the Y-equation) in an irreversible on–off switch: cell commitment (Y = 1 means a committed cell) is irreversibly activated when the concentration of activator A grows over a certain threshold, as formulated by the sigmoidal term in the Y-equation. A, H, Y and S are all subject to first-order degradation, at rates μ, ν, e, and γ, respectively.

Anatomy and physiology

In this model, tissue growth takes place inside a fixed 3D volume that represents the region that will be occupied by the lung epithelium. At the beginning of the simulation, almost all sites in the volume are set to Y = 0, meaning that the site does not contain an epithelially committed cell, but a small region is set to Y = 1, representing the initial lung stalk. Then, growth takes place by sites in the 3D volume converting from Y = 0 to Y = 1, in the presence of high concentrations of activator (the +dA term in the Y-equation). Tissue is represented by sites at which Y = 1.

Numerical simulation

Our models were numerically simulated using a forward Euler method with no-flux boundary conditions. The spatial domain was discretized into a uniform grid with space step Inline graphic. The domain size for 1D, 2D and 3D simulations were 128, 128 × 128, and 128 × 128 × 64 respectively. For the diffusion operator, we used a second-order two-point Laplacian in 1D simulation, a four-point Laplacian in 2D and a six-point Laplacian in 3D. The initial conditions were as follows. At the beginning of the simulation, activator, inhibitor and substrate are uniformly distributed in space. Activator and inhibitor have very small values: A = 0.001, H = 0.01, while substrate has a high value: S = 1.0. For the initial condition of Y, almost all sites in the volume (2D or 3D) are set to Y = 0, except for a small region near the left edge of the simulation boundary, which is rectangular in 2D and a rectangular solid in 3D.

Programs were written in CUDA for GPU implementation. 2D contour plots were done in Mathematica. We used Opendx to render our 3D simulation results. All codes were run on a platform with a CPU from Intel (Model: Intel Core i7–2600), GPU from NVIDIA (Model: NVIDIA GTX580), and 8GB memory. All codes will be supplied upon request.

We also considered a two-variable reduction of the model using only A and H because, in the full model, the variables S and Y drive the stalk forward while the dynamics of A and H are responsible for local dynamics transverse to the direction of growth. The two-variable model was obtained by setting Y and S equal to constants.

Results

Domain (or side) branching

Lung development begins with side branches emerging in rows around the circumference of the parent branch. The parent branch elongates and new side branches bud off, in the process called ‘domain branching’ (Metzger et al. 2008).

Y-Stalk elongation (Fig. 2A)

In our model, Y-stalk growth begins with the formation of peaks of activator, due to the positive feedback of A on itself. The activator peak then causes that micro-region to become committed to differentiated cells Y (via the +dA term in the Y-equation). However, Y cells consume S (the –εYS term in the S-equation), which is needed for new growth. The gradient of S is the main driver of activator migration, so the newly formed activator peak will migrate in the direction of high S concentration, which is away from the present stalk where S has been depleted. Also, inhibitor H is produced in response to the activator peak and diffuses. The stalk elongates because the H that diffuses to the side serves as lateral inhibition which results in filamentary elongation of the Y stalk rather than isotropic or circular expansion.

Insertion of new activator peaks

As the Y-stalk elongates (Fig. 2A), new activator peaks arise, always directly behind the leading activator peak. This phenomenon is also seen in actual lung development: as the lung stalk elongates, new buds emerge, always immediately behind the leading bud (Weaver et al. 2000; Metzger et al. 2008; Fig. 2B). The mechanism is that activator A gives rise to inhibitor H, which inhibits new activator peaks in the immediate neighborhood of established activator peaks. The elongating Y-stalk then gives rise to a new activator peak behind the leading activator peak when the leading peak has migrated far enough away that it no longer inhibits peak formation.

Figure 2.

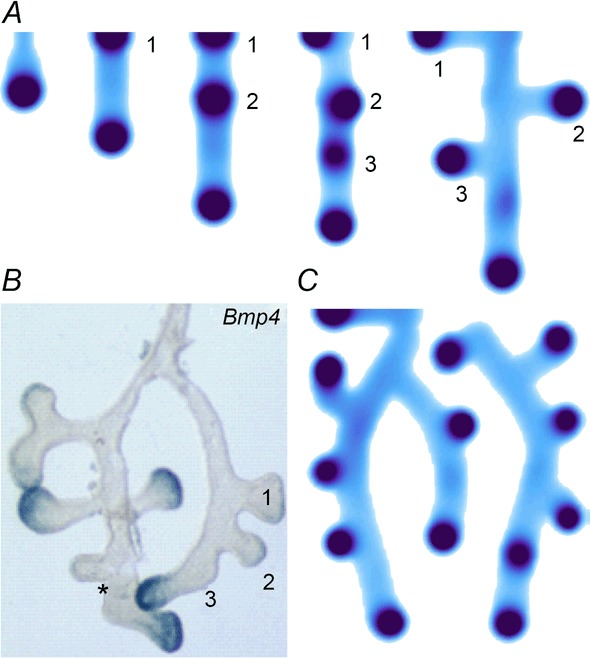
Figure 2

Open in a new tab

Periodic insertion of new activator peaks along the growing Y-stalk A, each new activator peak emerges directly behind the leading activator peak. The sequence of emergence is marked 1, 2 and 3. Side branches then grow out of the activator peaks. B, in lung development, daughter branches bud off from the main stalk in the same sequence. Branches marked 1 and 2 formed in that order, and a new branch 3 is forming. The asterisk denotes the primary bud (Weaver et al. 1999, 2000). Note also that the branching is biased to one side. C, similar biased side branching is seen in a simulation of two closely spaced trunks. 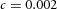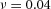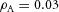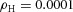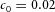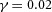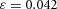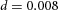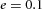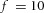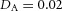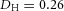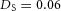Parameters: Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic.

Formation of side branches

Along the Y-stalk, side branches emerge perpendicularly when the attraction of the substrate overcomes the lateral inhibition (Fig. 2A). Each activator peak on the Y-stalk gives rise to a side branch as that activator peak expands into regions of high substrate S far away from the main Y-stalk, where Y cells have depleted S. The budding branch secretes inhibitor H, which prevents the next branch from forming on the same side of the stalk, thus producing an alternating side branch pattern. Alternating branches are occasionally seen in the real lung, but a much more frequent occurrence is side branching biased to one side of the stalk. We were able to reproduce this biased branching by simulating two stalks growing in parallel (Fig. 2C). Side branching in each stalk occurred preferentially on the side away from the other stalk, suggesting that a mechanism like the depletion of substrate in between the stalks could drive side branching to be away from the other stalk.

Periodicity generator in side branching

As new activator peaks emerge, they form at a fixed distance from the previous peak (Fig. 2A). These spatial intervals are controlled by several factors, including (1) substrate availability surrounding the Y-stalk, (2) the inhibitory range of each activator peak.

When we decreased substrate availability, by decreasing the S production rate c0, the spatial interval between side branches increased (Fig. 3A). However, this only occurs when the reduction exceeds a certain threshold (in this case 60%). Given our hypothesis that S is FGF10, this finding agrees with the observation that only substantial reductions of FGF10 produce the hypomorphic phenotype (Mailleux et al. 2001; Ramasamy et al. 2007).

Figure 3.

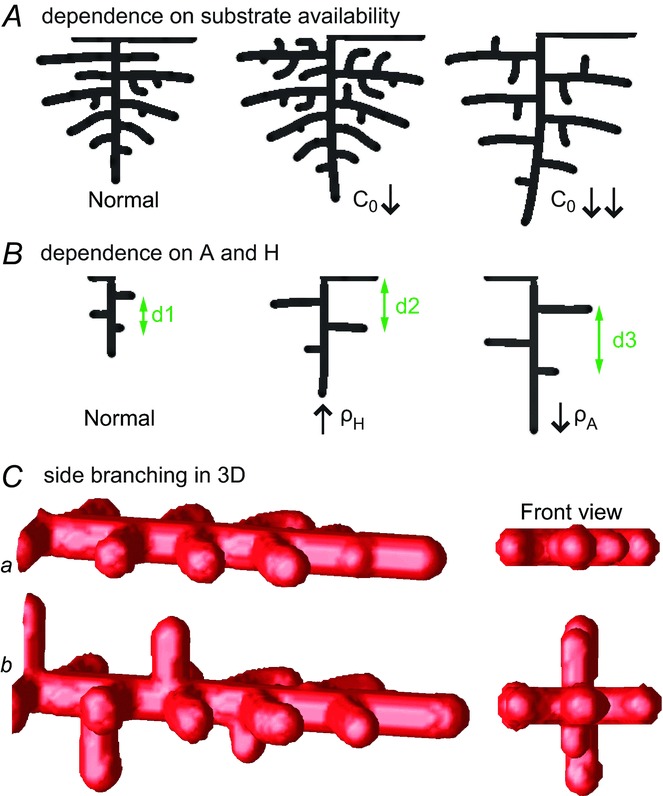
Figure 3

Open in a new tab

Domain branching: spatial intervals and orthogonal rotation of the branching plane A, decreases in the net production rate of substrate S (via the parameter c0) decreased the spatial frequency, but only when c0 decreased beyond a certain threshold. Values for c0 were 0.02 (left), 0.015 (middle) and 0.008 (right). B, increasing the inhibition between activator peaks, by either up-regulating the secretion of inhibitor H by Y cells (ρH increased from 0.000025 to 0.0001) or down-regulating the secretion of activator A by Y cells (ρA decreased from 0.025 to 0.0008), enlarges the spatial intervals between activator peaks. Ca, in 3D simulation, the Y-stalk developed its first generation of side branches in the horizontal plane. Cb, at a later stage, a secondary row of branches emerged perpendicularly to the previous horizontal plane. 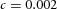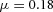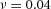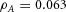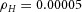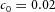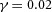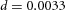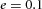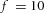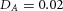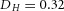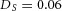(Parameters:Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic.)

Additionally, the spatial interval between side branches also depends on the inhibitory range of each activator peak: if we up-regulate the secretion of inhibitor H by Y cells or down-regulate the secretion of activator A by Y cells, the inhibition range of each activator peak enlarges, leading to a longer spatial interval between side branches (Fig. 3B).

Orthogonal rotation of the branching plane in domain branching

The model also explains the phenomenon of orthogonal rotation of the branching plane. In lung development, a row of domain branching first occurs in one plane, say, the lateral–medial plane, and the next row of branches forms in an orthogonal plane, such as the antero–posterior plane (Metzger et al. 2008).

Simulation of our PDE model in 3D shows that a row of side branches first extends in the horizontal plane, and then another secondary row forms in the vertical plane (Fig. 3C). Two symmetry-breaking events are involved in this orthogonal change of branching plane (Fig. 3C, front view): the first symmetry-breaking extends the 1D Y-stalk to an array of side branches in the 2D horizontal plane; the second symmetry-breaking creates a second row of protrusions in the plane perpendicular to the previous 2D plane, producing orthogonal rotation of the side branching planes.

Orthogonal rotation is created by two mechanisms. The first is the spread of pooled inhibition: when side branches extend, say, into the horizontal plane, high levels of inhibitor H secreted by the branches then pool into that plane. Consequently, the next branching event must be into an orthogonal plane, because it is driven to be as far as possible from the zone of high inhibition. The second mechanism is the search for substrate: substrate S has been depleted in the horizontal plane, and branching always extends into regions of high gradients in S. This also drives branching into the perpendicular plane.

Tip bifurcation

In lung development, after domain branching, the dynamics switches to a new mode: instead of side branching, branches bifurcate at their tips, and the stalk splits into two daughter stalks (Fig. 4A).

Figure 4.

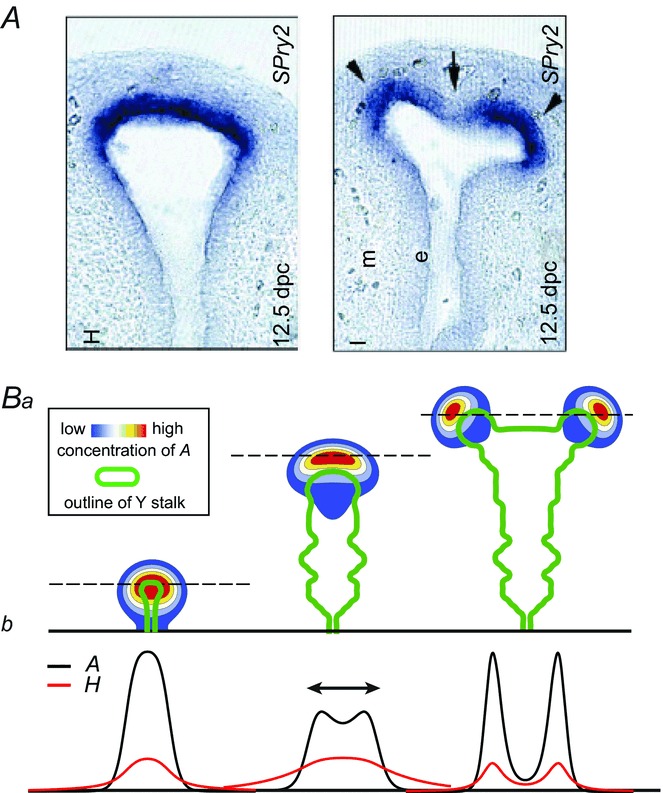
Figure 4

Open in a new tab

Tip bifurcation A, in the development of mouse lung airway, the parent stalk splits into two daughter stalks following the widening of the tip of the parent stalk (Mailleux et al. 2001). Ba, in the model, the first activator peak emerges at the end of the tip and migrates upward (left). While moving upward, the peak expands transversely to the direction of growth (middle). However, the inhibitor peak, which is still lingering (due to the time lag between activator and inhibitor), acts as a knife to cut the activator peak into two daughter peaks (right). (The contours represent activator activity: red denotes high activity, blue denotes low activity. The continuous green line denotes the outline of the Y-stalk.) Bb, activator distribution (red) and inhibitor profile (black), taken along the dashed transects in the upper panel. 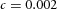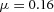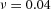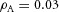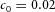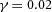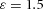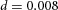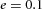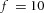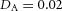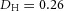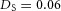Parameters:Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic.).

‘Bifurcator’ in tip splitting (Fig. 4B)

The dynamical process that gives rise to tip bifurcation begins with the expansion of the activator profile in the direction transverse to growth, as it seeks fresh substrate, which has been depleted locally (Fig. 4Ba). The activator peak gives rise to a delayed inhibitor peak, and the lingering inhibitor peak then acts as a knife to force the activator peak to split into two (Fig. 4Bb).

Periodicity

In tip bifurcation, the spatial interval between bifurcation events is controlled by the distance that the leading activator peak propagates before the next tip splitting. The principal factor that controls this length is the rate at which the tip expands transverse to the direction of movement. Since the expansion of the tip is always in the direction of fresh substrate S, it is the rate at which Y consumes S that determines how much S remains in the stalk. When that consumption rate is high, there is very little S left in the stalk, and the tip expands faster in the transverse direction, leading to a shorter spatial interval between branch events. Our model confirmed these observations: as we increased ε, the consumption rate of S by Y, the distance between tip splittings grew shorter (Fig. 5).

Figure 5.

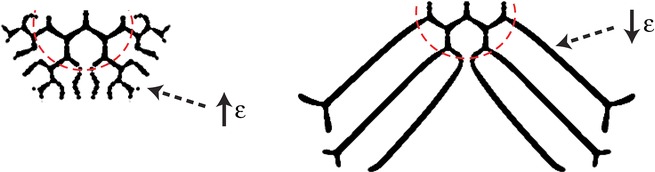
Figure 5

Open in a new tab

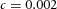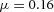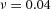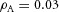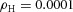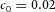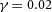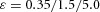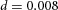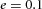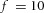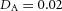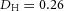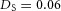Y-stalk segment length regulation Left, when ε was increased (from 1.5 to 5.0), the spatial interval between sequential branching events decreased. Right, when ε was decreased from 1.5 to 0.35, the spatial interval between branches increased. Parameters: Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic.

Orthogonal rotation of branching plane in tip bifurcation

In tip bifurcation in the lung, the plane defined by the pair of daughter branches rotates orthogonally from one generation to the next, thereby producing a 3D space-filling structure (Metzger et al. 2008). In our PDE model, orthogonal rotation of the branching plane emerges naturally (Fig. 6A). Note that, tip branching occurs first in the left–right plane, then in the up–down plane, and then in the front–back plane (Fig. 6B). In the end-on view, the first two generations formed four granddaughters arranged in a rosette (Fig. 6Ca), similarly to what is seen in the lung (Fig. 6Cb).

Figure 6.

Figure 6

Open in a new tab

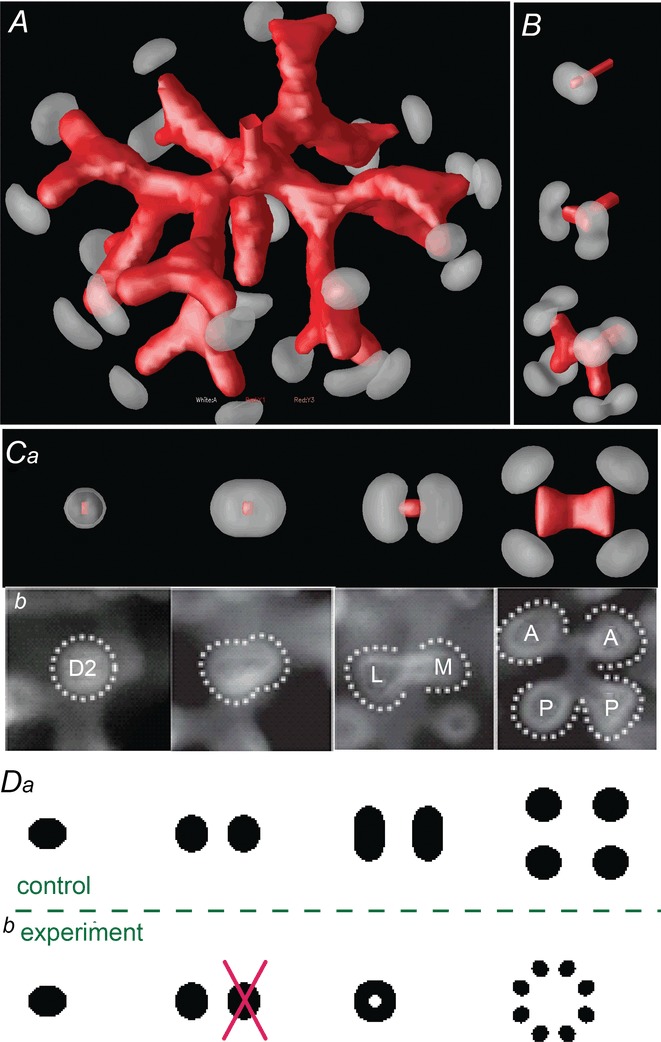
Orthogonal bifurcation A, orthogonal rotation between branching planes emerges naturally in the 3D simulation. Airway is shown in red (where Y ≅ 1); the grey areas represent high activator concentration (A > 1.5). Parameters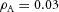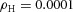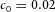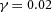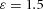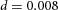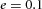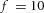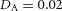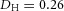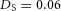: Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic. B, the first and second generations of orthogonal branching. Ca, in the model, branching occurs first horizontally and then vertically, forming four granddaughters arranged in a ‘rosette’ in an end-on view. Cb, in actual lung airway development, a similar rosette process is also observed (L, lateral; M, medial; A, anterior; P, posterior; Metzger et al. 2008). D, numerical experiment using the reduced 2-variable model. Da, an initial activator rectangle first elongates and splits into two daughters horizontally. In the next round, each of the two daughters bifurcates vertically. Db, we eliminated the right daughter in the first generation. Without the contribution of this inhibitor source, the remaining daughter failed to bifurcate vertically as before, instead spreading out radially. 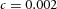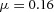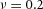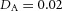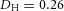Parameters:Inline graphic, Inline graphic, Inline graphic,Inline graphic, Inline graphic.

The causes of orthogonal rotation are the same as in side branching, namely, the avoidance of pooled inhibition and the search for fresh substrate. The region of high pooled inhibitor H between the two daughter branches prohibits the next round of branching from occurring in the same plane, and drives the next generation to branch as far away as possible from the previous plane, namely, along the perpendicular axis. The search for fresh substrate also drives the next generation of tip bifurcation in the perpendicular direction, away from the present plane where substrate has been depleted.

To confirm this ‘pooled inhibition’ hypothesis, we did an experiment using the reduced two-variable model. This model describes the local dynamics at the growing tip between activator A and inhibitor H. From a disk-shaped initial condition, the activator peak first elongates and then splits in the horizontal plane. At the next round, the daughters elongate and bifurcate in the vertical plane (Fig. 6Da), consistent with the observation of orthogonal branching in the full model (Fig. 6B). In our experiment, we deleted one of the two daughters after the first generation of splitting (Fig. 6Db). Lacking pooled inhibition, the subsequent splitting lost its orthogonality, instead spreading out radially (Fig. 6Db, right).

The idea that pooled inhibition is a potential mechanism for orthogonal rotation is also supported by considering how much inhibitor H actually lingers in the previous branching plane, and is present when the next generation of branching is forming (Fig. 7A).

Figure 7.

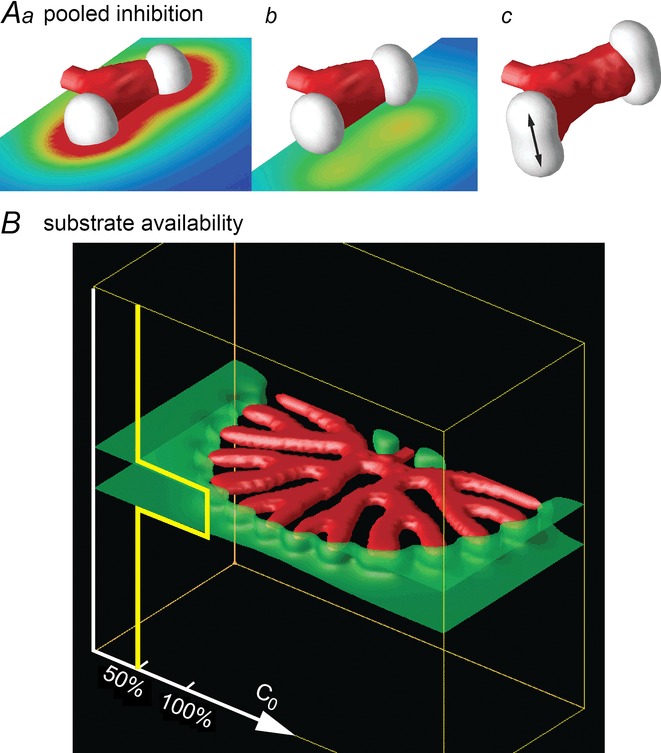
Figure 7

Open in a new tab

Pooled inhibition, substrate availability and planar bifurcationA, pooled inhibition. Aa, one generation of branching has occurred, in the horizontal plane. Superimposed on the branching, we show a horizontal cutting plane bisecting the branched structure, and show the distribution of inhibitor H in that plane (blue = low, red = high). Note high levels of pooled inhibition. The next splitting should therefore be driven in the direction perpendicular to the horizontal plane. Ab, by contrast, another horizontal cutting plane, below the plane of branching, shows much lower values of H. Ac, the next generation has begun to split in the vertical plane (arrow), perpendicular to the plane of pooled inhibition. B, planar bifurcation. Tip bifurcation in 3D loses the orthogonal rotation property and forms planar branching when the substrate has restricted availability. In a 3D simulation, when the value of the substrate production rate, c0, was set to half its value outside the layer marked by the green planes, tip bifurcation could not expand in the vertical direction, and orthogonal rotation was lost.

Another, perhaps more important mechanism that impairs orthogonal rotation is a loss of available substrate S in the region surrounding the stalk. When we restricted substrate availability outside the current branching plane, rotation was abolished (Fig. 7B). These results suggest that the ‘rotator’ that reorients the bifurcation plane by 90 deg could work either through pooled inhibition or the availability of substrate, or both.

Late in the branching programme, at the periphery of the lung, branching tips bifurcate in the same plane, in contrast to orthogonal branching. This phenomenon is called ‘planar bifurcation’ (Metzger et al. 2008). The fact that we could reproduce planar branching by restricting substrate availability is in agreement with the findings of Lazarus et al. (2011), who argued that the vasculature supplied a factor, probably FGF10 ( = substrate S) that controls orthogonal rotation. If the peripheral lung had less access to vasculature, that would explain the prevalence of planar branching in the periphery.

Mode switching from domain branching to tip bifurcation

In early lung development, domain branching happens first and sets up the central scaffold of the lung (Metzger et al. 2008; Affolter et al. 2009). Then orthogonal tip bifurcation fills the interior space of the lung.

Using our model, we found that this mode switching can be controlled by a single parameter. When we gradually increased ε (the consumption rate of substrate S by Y) beyond a critical value, side branching automatically turned into tip bifurcation (Fig. 8). When ε is in the range for tip bifurcation, further increases in ε decreased the spatial interval between bifurcation events.

Figure 8.

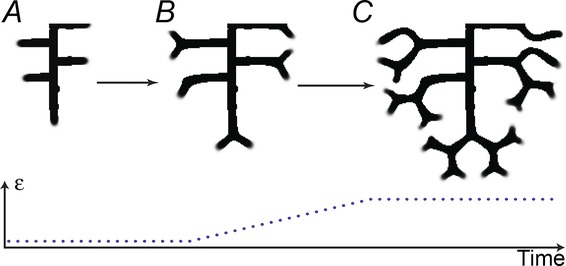
Figure 8

Open in a new tab

Mode switching: from side branching to tip bifurcation A, when the consumption rate of S by Y (parameter ε) was low, side branches formed perpendicular to the main stalk. B, when we increased ε, side branches bifurcated at their tips. C, final pattern exhibits mode switching from domain branching to tip bifurcation. (Here we gradually increased ε from 0.03 to 1.5.)

Another phenomenon that we observed in tip bifurcation, but not in domain branching, is that no additional activator peaks emerged behind the leading activator peak. This is because the high consumption of S by Y leaves too little S to produce more activator peaks in the established stalk.

Discussion

Our model explains how the branching patterns observed in the lung could emerge from a single PDE describing the reactions and diffusions of chemical morphogens. It also explains how the system can switch from one pattern to another as key parameters are varied.

Tip bifurcation

Tip splitting is created by the time lag between activator and inhibitor (Fig. 4B). When the activator peak expands in the transverse direction, due to the attraction of fresh substrate, there is still high inhibitor activity lingering in the centre. This forces the leading activator peak to split into two.

Periodicity generator

In tip bifurcation, the periodicity generator determines how far down the stalk the activator peak can propagate before it bifurcates. Several factors can change this distance. For example, when we increased ε, the spatial interval between tip bifurcations decreased (Fig. 5). The reason is that increased ε creates a greater gradient of S from the stalk to the surrounding tissue. In domain branching, similarly, several factors can alter the distance between side branches. For example, when the availability of substrate S around the stalk decreased, by decreasing the S production rate c0, branches occurred at longer spatial intervals (Fig. 3A). And when we elevated the inhibitory range of each activator peak, by up-regulating ρH or down-regulating ρA, the spatial interval between side branches increased (Fig. 3B).

Orthogonal rotation

In both domain branching and tip bifurcation, orthogonal rotation emerges from the reaction–diffusion dynamics due to two causes, namely, the avoidance of pooled inhibition and the search for fresh substrate. The only time that the branching plane does not rotate is when rotation is frustrated by the absence of pooled inhibition and/or the lack of substrate. The substrate requirement would explain the observation that in lung development, planar tip bifurcation is only seen in the periphery of the lung (Metzger et al. 2008). It also explains the observation that vascular ablation impairs the orthogonal rotation of airway branches, producing a flatter lung. The mechanism by which vascular ablation impairs branch plane rotation has been described as ‘perfusion-independent’ and attributed to factors secreted by the vasculature, resulting in a perturbation of ‘the unique spatial expression pattern of the key branching mediator FGF10’ (Lazarus et al. 2011). Since FGF10 is our candidate for substrate S (see below), these observations are consistent with our model.

Physiological realism of the model

Our model postulates four quantities: activator A, inhibitor H, substrate S and commitment Y. What do these quantities correspond to in reality? The activator carries out autocatalysis, and induces commitment (Y = 1). The inhibitor acts to prevent an autocatalytic explosion of the activator. Both activator and inhibitor depend on a substrate, which may come from other cell types nearby, as has been suggested (Lazarus et al. 2011). Using the functional definitions of each morphogen as a template, we can propose potential candidates for the morphogens.

Substrate S

Epithelial–mesenchymal interactions are critical for the branching morphogenesis of lung airway. For example, FGF10 is expressed in the mesenchyme of lung, directing the elongation of the lung bud (Weaver et al. 2000; Metzger et al. 2008). In our model, substrate S is consumed by Y cells, producing S patterns that are spatially complementary to the Y-stalks. Also, the gradient of substrate in our model guides the migration of activator peaks, laying down committed Y cells, and thus elongating the Y-stalk. This is precisely the role attributed to FGF10 (Weaver et al. 2000). Based on the similarity of the spatial pattern, and also on the functional definition of substrate in our model, we propose FGF10 as a candidate for the substrate S. This hypothesis is consistent with the observation that Spry2 plays a critical role in the periodicity generator in domain branching. Spry2 is an inhibitor of FGF10 signalling. Thus, the Spry2 null mutant will have more FGF10 activity, that is, more S in the tissue surrounding the stalk, hence will have more frequent branching (Metzger et al. 2008; Warburton, 2008).

Activator–inhibitor pairs

In our model, activator and inhibitor exhibit the following dynamics: (1) both concentrate at the tip of the growing stalk, (2) activator has a positive feedback on its own production, (3) activator promotes commitment of cells, (4) activator produces inhibitor, and inhibitor inhibits the production of activator, and (5) both activator and inhibitor require the substrate for their production. Based on these five principles, we propose several potential activator-inhibitor pairs.

One likely set of candidates would be BMP4 as activator, MGP as inhibitor and FGF10 as substrate.

BMP4

BMP4 has many features that qualify it as a potential activator morphogen in our model. Its expression is spatially localized to the terminal epithelial buds and rises at the tips of new branches (Weaver et al. 2000; Mailleux et al. 2001). BMP4 has an auto-stimulatory positive feedback on itself in lung development (Bellusci et al. 1996). Exogenous BMP4 in organ culture significantly increased the number of terminal branches and enhanced epithelial cell proliferation (Bragg et al. 2001; Shi et al. 2001). Other papers also suggest that BMP4 plays a critical role in lung development. For example Bellusci et al. (1996) report “BMP4 misexpression leads to a dramatic effect on lung development. In particular, transgenic lungs are smaller than normal, are about half the wet weight and have fewer, greatly distended, epithelial terminal buds separated by abundant mesenchyme.”

Therefore, our reading of the literature is that BMP4 plays a significant role in branching, and that it increases branching in a manner consistent with our postulate that BMP4 is an activator for the lung epithelium.

MGP

MGP is a well-known inhibitor of BMPs (Yao et al. 2007). MGP inhibits BMP4 in the lung (Gilbert & Rannels, 2004; Yao et al. 2011). BMP4 induces expression of MGP (Yao et al. 2007; Shao et al. 2009). The expression of BMP4 is positively stimulated by FGF10 (Lebeche et al. 1999; Weaver et al. 2000). MGP expression occurs predominantly near the epithelial tips of distal buds (Gilbert & Rannels, 2004).

Therefore, we propose that BMP4 and MGP act as an activator–inhibitor pair, with FGF10 playing the role of substrate.

In an explant lung culture system, down-regulating expression of MGP by treatment with anti-MGP antibodies greatly reduced terminal lung bud counts (Gilbert & Rannels, 2004). This is consistent with the role played by the inhibitor in our model. In the reaction–diffusion dynamics, the inhibitor is necessary for branching; indeed, the inhibitor creates branching, because it is the inhibition that sculpts the activator peak into two. Therefore, less inhibitor can also result in less branching. Other candidate inhibitors of BMP4 could include Gremlin (Shi et al. 2001) and Noggin (Chuang & McMahon, 2003). There may also be other candidate triads of activator–inhibitor–substrate, such as SHH–Ptc1–FGF10 or SHH–Hip1–FGF10 (Chuang & McMahon, 2003).

Spatiotemporal parameters

The PDE model we used here is an idealized description. We can, however, make some estimates of the real-world spatial and temporal scales of key parameters. The development literature (for example, Fig. 1b in Metzger et al. 2008) gives real-world space and time scales to our simulation. One tip splitting generation in the embryonic mouse lung takes ∼1 day. The real-world spatial extent corresponding to our simulations of three to four generations is about 0.8 mm  × 0.8 mm. If we use these numbers to scale our simulations, we can then make reality checks on our model: do the parameters, translated into real-world numbers, make sense? For example, we calculated the diffusion coefficient of activator A and the degradation rate of inhibitor H. In the model, the value of the diffusion coefficient of A, DA, is 0.02 L2/T, where L and T are the space and time units of the model. In the simulation the spatial extent is 18 L, so, taking 18 L = 0.8 mm gives us L = 45 μm. Similarly, in the model, one generation of tip slitting takes about 115 T, so setting 115 T = 1 day gives us T = 750 s. Therefore, the real-world value of DA, 0.02 L2/T, corresponds to 0.054 × 10−8 cm2 s–1. This value is within experimentally determined values: Kicheva et al. (2007) estimated the value of the effective diffusion coefficient of Dpp (a BMP homologue) in tissue to be (0.1 ± 0.05) × 10−8 cm2 s–1, which agrees with our estimates.

Another number that is important for the interpretation of our results is the real-world degradation rate of inhibitor. In the simulation (for example, in Fig. 3), the degradation rate of inhibitor is ν = 0.04/T, which corresponds to 0.5 × 10−4 s−1. Kicheva et al. (2007) estimate the Dpp degradation rate as (2.52 × 10−4) ± (1.29 × 10−4) s−1 corresponding to a half-life of about 45 min. In previous work (Garfinkel et al. 2004), we estimated the degradation rate of MGP to be of the same order of magnitude as BMP (which is comparable to Dpp), so our estimate is comparable to real-world values.

Generic mechanisms for genetic processes

The activator–inhibitor–substrate model we used is a highly stylized picture of how an activation process and an inhibitory process, interacting with a substrate chemical, can produce the phenomena observed in lung branching. The development of the real lung is certainly much more complex, involving multiple tissue types such as epithelium and mesenchyme. Our model is of a single cell type, which we take to be epithelium, while the mesenchyme in our model is stylized as the source for the substrate FGF10.

A further limitation of our model is that it deals strictly with reacting and diffusing chemical morphogens, thus ignoring, for example, the critical role of mechanical factors in lung development (Oster et al. 1983; Warburton et al. 2010). However, it has been suggested that even some cases of mechanically induced morphogenesis can be seen abstractly as local activation and lateral inhibition (Oster, 1988), which would make them amenable to this model.

The absence of mechanical forces in our model may account for several limitations of the model. For example, our present model does not incorporate mechanisms that could lead to the formation of hollow tubes. The biological literature suggests that the mechanism behind tubulogenesis may depend on fluid pressure and fluid–mechanical interactions. Lubarsky & Krasnow (2003) say that “liquid secretion is an essential step in tube formation and expansion”. So our current biochemical model will ultimately have to be extended to include mechanical factors. However, we do note that even mechanical factors may act through biochemical morphogens. Warburton et al. (2010) note that, when increasing intraluminal pressure, “the rate of bud extension increases about twofold whilst inter-bud distance is halved. These effects depend on FGF10–FGFR2b–Sprouty signalling.”

The absence of fluid or mechanical effects may also explain another limitation of our model, that it does not include a reduction in branch diameter as development proceeds from one generation to the next. Lubkin & Murray (1995) treated the epithelium as a viscous fluid with surface tension. They predicted that branch size will be inversely related to the pressure difference between the external medium (and native mesenchyme) and the lumen.

Another simplification in our model is that the growth of the lung bud is modelled as the invasion of epithelium into existing mesenchyme. In fact, in the developing lung, both epithelium and mesenchyme expand together, against fluid pressures. Relating our biochemical model to the mechanical and fluid dynamical factors in lung development is the goal of future research.

However, the advantage of a highly generic model like ours is that it tells us how a set of genes could conceivably act to produce the observed phenomena. Metzger et al. suggest that “it will be particularly important to identify genes that underlie the periodicity generator, domain specifier, bifurcator and rotator”. Our model provides specific mechanisms for generating, for example, domain branching, tip splitting and orthogonal rotation, suggesting pathways through which any genetic programme could act to produce the observed phenomena.

For example, the hypothesized ‘master routine’ must command a switch from domain branching to tip branching. In our model, a gradual up-regulation of key parameter ε would provide a control knob through which genetic changes can produce this phenotypic change. Similarly, other phenomena like orthogonal rotation of the branching plane and tip bifurcation can also be effected in our model by low-dimensional control knobs, offering templates for how genes might act.

Glossary

PDE

partial differential equation

Competing interests

None declared.

Author contributions

The experiments in this paper were numerical simulations, performed at Nankai University and at the University of California, Los Angeles. Y.G., A.G., T.-H.C., X.J.Z., X.Z. and C.M.H. contributed to the conception and design of the experiments. Y.G., X.J.Z. and A.G. collected the data. Y.G., D.W., K.I.B., X.Z. and A.G. contributed to the analysis and interpretation of data. Y.G., T.-H.C. and A.G. drafted the paper, and Y.G. and A.G. revised the paper. All authors contributed to the writing of the paper, and read and approved the final version of the manuscript.

Funding

We are pleased to acknowledge support from the U.S. National Institutes of Health (NIH) (Grant Nos. HL30568, HL81397), the National Natural Science Foundation of China (NSFC; Grant Nos. 61327802, 61273341), The National High Technology Research and Development Program (‘863’ Program) of China (Grant No. 2013AA041102), and The Research Fund for Doctoral Program of Higher Education of China (Grant No. 2011003111032).

References

  1. Affolter M, Zeller R, Caussinus E. Tissue remodelling through branching morphogenesis. Nat Rev Mol Cell Biol. 2009;10:831–842. doi: 10.1038/nrm2797. [DOI] [PubMed] [Google Scholar]
  2. Bellusci S, Furuta Y, Rush MG, Henderson R, Winnier G, Hogan BL. Involvement of Sonic hedgehog (Shh) in mouse embryonic lung growth and morphogenesis. Development. 1997;124:53–63. doi: 10.1242/dev.124.1.53. [DOI] [PubMed] [Google Scholar]
  3. Bellusci S, Henderson R, Winnier G, Oikawa T, Hogan BL. Evidence from normal expression and targeted misexpression that bone morphogenetic protein (Bmp-4) plays a role in mouse embryonic lung morphogenesis. Development. 1996;122:1693–1702. doi: 10.1242/dev.122.6.1693. [DOI] [PubMed] [Google Scholar]
  4. Bragg AD, Moses HL, Serra R. Signaling to the epithelium is not sufficient to mediate all of the effects of transforming growth factor beta and bone morphogenetic protein 4 on murine embryonic lung development. Mech Dev. 2001;109:13–26. doi: 10.1016/s0925-4773(01)00508-1. [DOI] [PubMed] [Google Scholar]
  5. Celliere G, Menshykau D, Iber D. Simulations demonstrate a simple network to be sufficient to control branch point selection, smooth muscle and vasculature formation during lung branching morphogenesis. Biol Open. 2012;1:775–788. doi: 10.1242/bio.20121339. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Chen Y, Schier AF. The zebrafish Nodal signal Squint functions as a morphogen. Nature. 2001;411:607–610. doi: 10.1038/35079121. [DOI] [PubMed] [Google Scholar]
  7. Chuang PT, McMahon AP. Branching morphogenesis of the lung: new molecular insights into an old problem. Trends Cell Biol. 2003;13:86–91. doi: 10.1016/s0962-8924(02)00031-4. [DOI] [PubMed] [Google Scholar]
  8. Clement R, Blanc P, Mauroy B, Sapin V, Douady S. Shape self-regulation in early lung morphogenesis. PLoS One. 2012a;7:e36925. doi: 10.1371/journal.pone.0036925. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Clement R, Douady S, Mauroy B. Branching geometry induced by lung self-regulated growth. Phys Biol. 2012b;9:066006. doi: 10.1088/1478-3975/9/6/066006. [DOI] [PubMed] [Google Scholar]
  10. Echelard Y, Epstein DJ, St-Jacques B, Shen L, Mohler J, McMahon JA, McMahon AP. Sonic hedgehog, a member of a family of putative signalling molecules, is implicated in the regulation of CNS polarity. Cell. 1993;75:1417–1430. doi: 10.1016/0092-8674(93)90627-3. [DOI] [PubMed] [Google Scholar]
  11. Garfinkel A, Tintut Y, Petrasek D, Bostrom K, Demer LL. Pattern formation by vascular mesenchymal cells. Proc Natl Acad Sci U S A. 2004;101:9247–9250. doi: 10.1073/pnas.0308436101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Gilbert KA, Rannels SR. Matrix GLA protein modulates branching morphogenesis in fetal rat lung. Am J Physiol Lung Cell Mol Physiol. 2004;286:L1179–L1187. doi: 10.1152/ajplung.00188.2003. [DOI] [PubMed] [Google Scholar]
  13. Hirashima T, Iwasa Y, Morishita Y. Mechanisms for split localization of Fgf10 expression in early lung development. Dev Dyn. 2009;238:2813–2822. doi: 10.1002/dvdy.22108. [DOI] [PubMed] [Google Scholar]
  14. Kicheva A, Pantazis P, Bollenbach T, Kalaidzidis Y, Bittig T, Julicher F, Gonzalez-Gaitan M. Kinetics of morphogen gradient formation. Science. 2007;315:521–525. doi: 10.1126/science.1135774. [DOI] [PubMed] [Google Scholar]
  15. Lazarus A, Del-Moral PM, Ilovich O, Mishani E, Warburton D, Keshet E. A perfusion-independent role of blood vessels in determining branching stereotypy of lung airways. Development. 2011;138:2359–2368. doi: 10.1242/dev.060723. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Lebeche D, Malpel S, Cardoso WV. Fibroblast growth factor interactions in the developing lung. Mech Dev. 1999;86:125–136. doi: 10.1016/s0925-4773(99)00124-0. [DOI] [PubMed] [Google Scholar]
  17. Lubarsky B, Krasnow MA. Tube morphogenesis: making and shaping biological tubes. Cell. 2003;112:19–28. doi: 10.1016/s0092-8674(02)01283-7. [DOI] [PubMed] [Google Scholar]
  18. Lubkin SR, Murray JD. A mechanism for early branching in lung morphogenesis. J Math Biol. 1995;34:77–94. doi: 10.1007/BF00180137. [DOI] [PubMed] [Google Scholar]
  19. Mailleux AA, Tefft D, Ndiaye D, Itoh N, Thiery JP, Warburton D, Bellusci S. Evidence that SPROUTY2 functions as an inhibitor of mouse embryonic lung growth and morphogenesis. Mech Dev. 2001;102:81–94. doi: 10.1016/s0925-4773(01)00286-6. [DOI] [PubMed] [Google Scholar]
  20. Meinhardt H. Morphogenesis of lines and nets. Differentiation. 1976;6:117–123. doi: 10.1111/j.1432-0436.1976.tb01478.x. [DOI] [PubMed] [Google Scholar]
  21. Menshykau D, Iber D. Kidney branching morphogenesis under the control of a ligand-receptor-based Turing mechanism. Physical Biology. 2013;10:046003. doi: 10.1088/1478-3975/10/4/046003. [DOI] [PubMed] [Google Scholar]
  22. Menshykau D, Kraemer C, Iber D. Branch mode selection during early lung development. PLoS Comput Biol. 2012;8:e1002377. doi: 10.1371/journal.pcbi.1002377. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Metzger RJ, Klein OD, Martin GR, Krasnow MA. The branching programme of mouse lung development. Nature. 2008;453:745–750. doi: 10.1038/nature07005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Oster GF. Lateral inhibition models of developmental processes. Mathematical Biosciences. 1988;90:265–286. [Google Scholar]
  25. Oster GF, Murray JD, Harris A. Mechanical aspects of mesenchymal morphogenesis. J Embryol Exp Morphol. 1983;78:83–125. [PubMed] [Google Scholar]
  26. Ramasamy SK, Mailleux AA, Gupte VV, Mata F, Sala FG, Veltmaat JM, Del Moral PM, De Langhe S, Parsa S, Kelly LK, Kelly R, Shia W, Keshet E, Minoo P, Warburton D, Bellusci S. Fgf10 dosage is critical for the amplification of epithelial cell progenitors and for the formation of multiple mesenchymal lineages during lung development. Dev Biol. 2007;307:237–247. doi: 10.1016/j.ydbio.2007.04.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Riddle RD, Johnson RL, Laufer E, Tabin C. Sonic hedgehog mediates the polarizing activity of the ZPA. Cell. 1993;75:1401–1416. doi: 10.1016/0092-8674(93)90626-2. [DOI] [PubMed] [Google Scholar]
  28. Shao ES, Lin L, Yao Y, Bostrom KI. Expression of vascular endothelial growth factor is coordinately regulated by the activin-like kinase receptors 1 and 5 in endothelial cells. Blood. 2009;114:2197–2206. doi: 10.1182/blood-2009-01-199166. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Shi W, Zhao J, Anderson KD, Warburton D. Gremlin negatively modulates BMP-4 induction of embryonic mouse lung branching morphogenesis. Am J Physiol Lung Cell Mol Physiol. 2001;280:L1030–L1039. doi: 10.1152/ajplung.2001.280.5.L1030. [DOI] [PubMed] [Google Scholar]
  30. Turing A. The chemical basis of morphogenesis. Philosophical Transactions of the Royal Society (London) 1952;237:37–72. [Google Scholar]
  31. Vincent S, Perrimon N. Developmental biology. Fishing for morphogens. Nature. 2001;411:533–536. doi: 10.1038/35079214. [DOI] [PubMed] [Google Scholar]
  32. Warburton D. Developmental biology: order in the lung. Nature. 2008;453:733–735. doi: 10.1038/453733a. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Warburton D, El-Hashash A, Carraro G, Tiozzo C, Sala F, Rogers O, De Langhe S, Kemp PJ, Riccardi D, Torday J, Bellusci S, Shi W, Lubkin SR, Jesudason E. Lung organogenesis. Curr Top Dev Biol. 2010;90:73–158. doi: 10.1016/S0070-2153(10)90003-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Weaver M, Dunn NR, Hogan BL. Bmp4 and Fgf10 play opposing roles during lung bud morphogenesis. Development. 2000;127:2695–2704. doi: 10.1242/dev.127.12.2695. [DOI] [PubMed] [Google Scholar]
  35. Weaver M, Yingling JM, Dunn NR, Bellusci S, Hogan BL. Bmp signalling regulates proximal-distal differentiation of endoderm in mouse lung development. Development. 1999;126:4005–4015. doi: 10.1242/dev.126.18.4005. [DOI] [PubMed] [Google Scholar]
  36. Yao Y, Jumabay M, Wang A, Bostrom KI. Matrix Gla protein deficiency causes arteriovenous malformations in mice. J Clin Invest. 2011;121:2993–3004. doi: 10.1172/JCI57567. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Yao Y, Nowak S, Yochelis A, Garfinkel A, Bostrom KI. Matrix GLA protein, an inhibitory morphogen in pulmonary vascular development. J Biol Chem. 2007 doi: 10.1074/jbc.M704297200. [DOI] [PubMed] [Google Scholar]

Articles from The Journal of Physiology are provided here courtesy of The Physiological Society

RESOURCES