Sequence analysis of chromatin immunoprecipitation data for transcription factors

Abstract

Chromatin immunoprecipitation (ChIP) experiments allow the location of transcription factors to be determined across the genome. Subsequent analysis of the sequences of the identified regions allows binding to be localized at a higher resolution than can be achieved by current high-throughput experiments without sequence analysis, and may provide important insight into the regulatory programs enacted by the protein of interest. In this chapter we review the tools, workflow, and common pitfalls of such analyses, and recommend strategies for effective motif discovery from these data.

1. Introduction

The regulatory programs enacted by transcription factors in response to developmental or environmental cues depend on specific interactions between these proteins and the genes whose expression they regulate. This specificity is provided, in large part, by short DNA sequences that are recognized and bound by transcription factors, thereby localizing them to their targets (1). In general, different transcription factors recognize different binding sites. The varying sequence specificities of these regulators, and the genomic location of the sites they bind, form a regulatory code whose decipherment has been an important area of research in molecular biology for over 40 years (2, 3).

There are a number of challenges that must be overcome in order to decipher this code. The interactions of transcription factors with DNA are transient, making detection difficult. In addition, it is clear that in vivo binding events vary extensively in their function; the same protein bound at different sites or at the same site under different conditions may activate, repress or have no effect on transcription, depending on which other proteins bind with it (4). For these reasons, a combination of condition-specific experimental data and computational analysis are critical for understanding transcriptional regulation.

One experimental technique that has provided significant insight into the regulatory code of eukaryotes is chromatin immunoprecipitation (ChIP). In a ChIP experiment, the transient interactions between proteins and DNA are stabilized by chemically cross-linking in vivo. After subsequent isolation and fragmentation of the cross-linked chromatin, protein-bound DNA fragments are immunoprecipitated using an antibody specific to the transcription factor of interest. Coupling this procedure to a high throughput readout technique like microarrays (ChIP-chip) or massively parallel sequencing (ChIP-seq) allows the location of transcription factors to be experimentally profiled on a genome-wide basis (5, 6).

ChIP data provide a starting point for many types of analysis of transcription. In this chapter, we will focus on computational techniques that use these data to understand how a transcription factor is localized to its targets in a profiled tissue or cell type. This can involve identifying the sequences that are recognized and bound by the protein itself, or sites bound by other proteins it cooperates with to control gene expression. Since high-throughput ChIP experiments may have significant experimental noise, identifying sequences that have a strong statistical association with ChIP-enriched regions can provide additional confidence in the quality of the data and increase the resolution at which binding sites can be localized.

A variety of approaches have been proposed to represent the specificity of protein-DNA interactions, and the resulting models are commonly referred to as sequence motifs (7). The most intuitive representation of a sequence motif is the consensus sequence. A consensus sequence describes the binding site preference of a protein as a string of nucleotides. Sites where a range of nucleotides are accommodated are denoted using ambiguity codes. For example, the specificity of the Lrp regulatory protein from E. coli can be described as YAGHAWATTWTDCTR (8). However, consensus sequences fail to capture the fact that transcription factors generally have a range of affinities for target sequences. An alternative model that conveys the range of affinities is the frequency matrix. Frequency matrices describe the binding site preference of a protein as a set of position-specific multinomial distributions over the four nucleotides A, C, G, and T. When an estimate of nucleotide frequencies is available for regions that are not bound by the transcription factor, frequency matrix motifs can be converted to ‘log-odds’ matrices by taking the log of each entry and then subtracting the log of the background frequency for the appropriate nucleotide.

Log-odds matrix motif models have a link to underlying biophysical parameters like binding free energy (9, 10). For the purposes of analyzing ChIP data, biophysically-based models often have the advantage of allowing more realistic modeling of transcription factor-DNA interaction. Because binding interactions are transient, a particular binding site is occupied in only a fraction of cells across the population. We refer to this fraction as the occupancy, θ. Consider a transcription factor present in the nucleus at a free concentration [P]. This protein can bind to a particular unbound site, U, of length N to form a bound complex, B.

$$P+U\leftrightarrow B$$

The association constant K_a, which is a measure of the protein’s affinity for the site, is given by $K_a=\frac{[B]}{\left[U\right]\left[P\right]}$. The occupancy of the site is related to this association constant and the transcription factor concentration according to $\theta =\frac{K_a[P]}{1+K_a[P]}$. Now assume that the free energy of protein binding to any site is given by a simple sum of nucleotide contributions at each position i. Because the association constant is related to the free energy by K_a = exp(−ΔG/RT), we can re-write the expression for occupancy to take on a convenient logistic form:

$$\theta =\frac{1}{1+\exp \left(-\log \left[P\right]+\sum _i\sum _j{g}_{i,j}{n}_{i,j}\right)}$$ (1)

Where the g_i,j correspond to the position specific free energy contributions (scaled by 1/RT) of each nucleotide (indexed by j=1…4) and the n_i,j are a matrix of 4N binary variables indicating the presence or absence of nucleotide j at site i. We now derive a simple relationship between a standard sequence motif and the position-specific free energy contribution of each nucleotide. Let p_i,j be the posterior probability of observing nucleotide j at position i in a genomic site, given that the site is bound in vivo. These probabilities correspond to the entries in the motif frequency matrix and are given by:

$$p_{i,j}=\frac{P(\mathit{bound}\mid n_{i,j}=1)P(n_{i,j}=1)}{\sum _{n}P(\mathit{bound}\mid n_{i,j}=1)P(n_{i,j}=1)}$$ (2)

where P(n_i,j=1) denotes the prior probability of observing nucleotide j (i.e., its background frequency). If we now assume that the protein concentration is very low, then from Equations (1) and (2), a site’s occupancy is approximated by $\theta \approx \exp \left(\log \left[P\right]-\sum _i\sum _j{g}_{i,j}{n}_{i,j}\right)$. We define an occupancy estimate which ignores the contribution of nucleotide m at position k as ${\theta }^{\backslash k,m}=\exp \left(\log \left[P\right]-\sum _i\sum _j{g}_{i,j}{n}_{i,j}+g_{k,m}\right)$. Then, Equation (2) reduces to:

$$\begin{array}{lll}{p}_{i,j}& =& \frac{\left[\sum _{S\backslash i}{\theta }_S^{\backslash i,j}P\left(S\right)\right]\exp (g_{i,j})P\left(n_{i,j}=1\right)}{\left[\sum _{S\backslash i}{\theta }_S^{\backslash i,j}P\left(S\right)\right]\sum _j\exp (g_{i,j})P\left(n_{i,j}=1\right)}\\ & =& \frac{\exp (g_{i,j})P\left(n_{i,j}=1\right)}{\sum _j\exp (g_{i,j})P\left(n_{i,j}=1\right)}\end{array}$$ (3)

In Equation (3), the sum over S\i (which cancels out) denotes a summation over all possible binding site sequences holding position i constant. Taking the logarithm of Equation 3 and rearranging gives:

$$\begin{array}{l}\log p_{i,j}-\log P\left(n_{i,j}=1\right)=g_{i,j}-\log \sum _j\exp \left(g_{i,j}\right)P\left(n_{i,j}=1\right)\\ =g_{i,j}-\log Z_i\end{array}$$ (4)

The entries of a log-odds matrix (the left hand side of Equation (4)) can be interpreted as the scaled relative free energy contributions of those nucleotides to the binding reaction.

In a high-throughput ChIP experiment where there is both positive and negative information about binding occupancy, it is possible to use this information to exploit the relationship of the biophysical and probabilistic approaches to learn accurate and interpretable binding specificity estimates. The simple logistic equation (1) relates occupancy, which has been measured in the ChIP experiment, to energies, and thus, as we showed above, sequence motifs. Given a set of bound and unbound example binding sites, fitting a motif model can be accomplished by simply training a logistic regression classifier to distinguish the two classes (11). Similar biophysically-based approaches, making different simplifying assumptions, have been explored in the context of ChIP-chip data analysis and have been proven to be effective (see Chapters 9 and 10 and refs. (12, 13)).

Fitting appropriate motif models to the ChIP data does not end the analysis. Most de novo motif discovery algorithms produce multiple motif hypotheses, and it is often advantageous to generate hypotheses using several different techniques. These motifs must be assessed for statistical significance, ranked, and clustered to reduce redundancy. Once a core set of non-redundant motifs has been identified, it is useful to be able to map them back to the genome to identify putative binding sites at high resolution. In this chapter we discuss tools and techniques for obtaining transcription factor binding specificity estimates from ChIP-chip and ChIP-seq data and for performing the downstream analyses that allows sequence information to be used to maximum effect alongside ChIP data.

2. Software

A wide variety of software packages exist to analyze ChIP data and perform motif discovery and an exhaustive overview of the various options is outside the scope of this chapter. Instead we offer several suggestions which may be used as starting points for these types of analyses. For identifying bound regions from a ChIP-chip experiment, the ChIPOTle (14), TiMAT (15), COCAS (16), and JBD (17) tools are all suitable for analysis of modern tiled microarray data. For ChIP-seq data, the MACS (18) and USeq (19) packages are publicly available, have demonstrated good performance, and allow for sophisticated statistical analyses of sequence reads. Dozens of motif discovery algorithms have been described in the literature and are publicly available for use including the Weeder (20), AlignACE (21), MEME (22), and MDScan (23) algorithms. These tools have been integrated into an online motif discovery package, WebMOTIFS (24). Suites of tools for motif analysis have also been developed including cisGenome (see also Chapter 22) (25), the MEME suite (26), and TAMO (27). The performance of select methods is discussed in Chapter 8 using the Motif Tool Assessment Platform (MTAP).

3. Methods

The process of identifying biologically meaningful sequence motifs from a ChIP-chip or ChIP-seq experiment and mapping them back to the genome involves several steps. The overall workflow is summarized in the flow chart of Fig. 11.1.

Figure 1. Typical sequence motif analysis workflow for ChIP data.

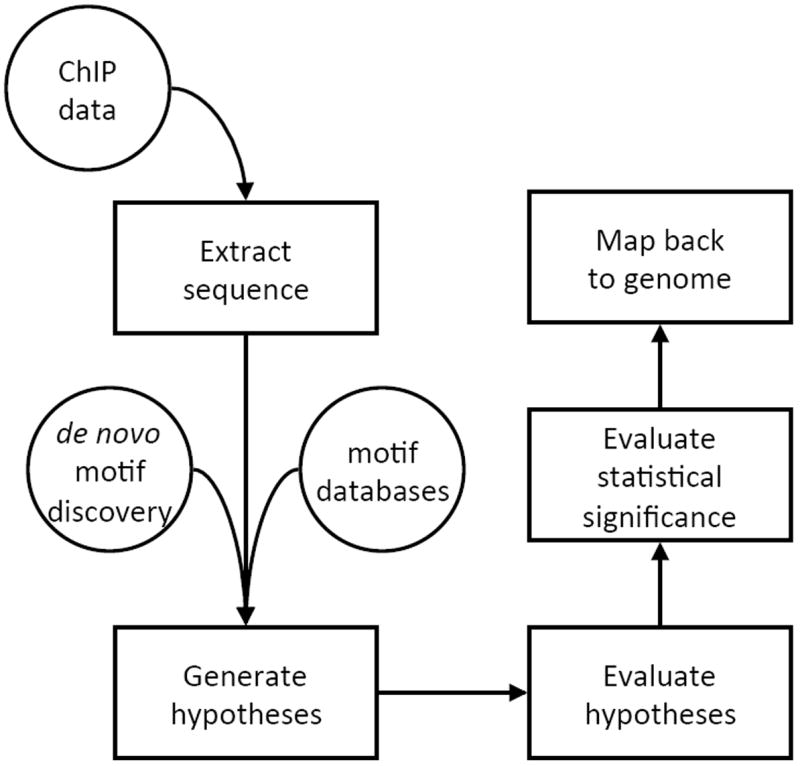
After identification of bound regions from the experiment, motif hypotheses are generated using de novo motif discovery algorithms or assembled from databases. Hypothesis quality is measured against the binding data using a quality score and statistical significance testing is performed. Motifs may then be mapped back to the genome to improve the resolution of binding site identification.

3.1. Sequence extraction

Motif analysis of high-throughput ChIP data begins by first identifying and extracting the DNA sequence of bound regions detected in the experiment. Most software packages used to analyze ChIP data will output the genomic coordinates of regions identified as bound in the experiment. For ChIP-chip, binding sites for the immunoprecipitated protein can be located several hundred bp away from the center of the peak identified by the ChIP analysis software. Data from ChIP-seq experiments is at significantly higher resolution, and the majority of bound regions identified by software packages have a putative binding site within a 300bp window of the peak center as shown in Fig.11.2 for PPARγ ChIP seq data (28). Even for ChIP-seq data, however, when the goals of a motif analysis include identification of binding sites corresponding to other transcription factors that may cooperate with the immunoprecipitated protein to enact a regulatory program, extending the sequences may allow these binding sites to be better captured. Of course, extending sequences also serves to decrease the signal-to-noise ratio in the data, and makes motif discovery more challenging. Fig. 11.3 shows how the probability of observing a binding site in bound and randomly selected unbound regions changes as sequence length increases for the dataset of Fig. 11.2. At relatively small sequence sizes, sensitivity is improved by increasing the size window since binding sites that are offset from the peak center are excluded when the length is too small. However, the probability of randomly observing a binding site in unbound sequence also increases. For the ChIP-seq data in Fig. 11.3, a sequence window size of approximately 250bp adequately balances sensitivity and specificity considerations.

Figure 2. Representative distribution of distances between ChIP-seq peaks and binding site matches.

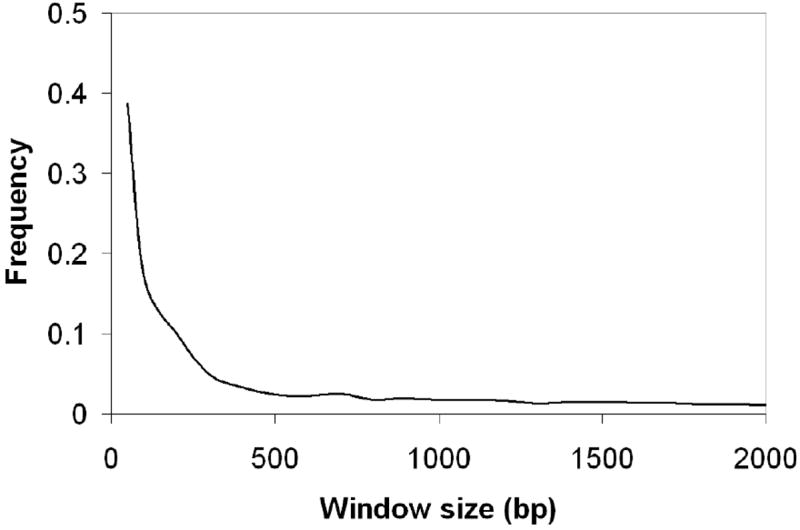
Genomic regions identified as bound by PPARγ in the study of Nielsen et. al were scanned for peroxisome proliferator response elements (PPREs) and the distribution of distances between the peak center and the closest PPRE is shown. The majority of bound regions have a PPRE within 250bp of the peak center.

Figure 3. Fraction of bound and unbound regions with a motif match as a function of region size.

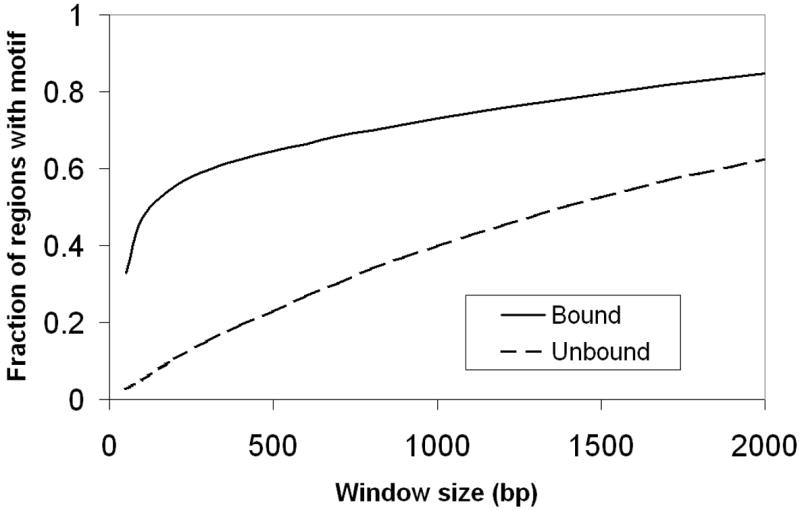
For the PPARγ ChIP data of Nielsen et al. increasing the size window around the ChIP peak centers increases the fraction of bound regions containing a PPRE. However, the fraction of randomly selected unbound regions that contain a PPRE also increases.

3.2. Hypothesis generation

Once the sequences to be analyzed have been identified and extracted, the data can be mined for sequence motifs that may represent the binding specificity of the immunoprecipitated protein. This hypothesis generation step is often performed using one or more de novo motif discovery algorithms (29). These computer programs attempt to learn a representation of the protein’s binding specificity directly from the sequence data in an unbiased manner, and may be especially useful for immunoprecipitated proteins with unknown binding specificity and with no close homologs with known binding specificities. As the relative performance of particular algorithms has been shown to vary significantly from dataset to dataset (see ref. (30)), it is recommended that when de novo motif discovery is used as the primary hypothesis generation tool in an analysis two or more different programs be employed. It has been previously demonstrated that this can significantly improve the chances of identifying a motif consistent with the protein’s true binding specificity (31). An alternate approach for generating hypotheses is to mine public or commercial databases for previously described DNA sequence motifs. When the DNA binding domain family of the protein is known, hypotheses can be limited to motifs corresponding to transcription factors from that family (32, 33). A more comprehensive approach is to compile all motifs corresponding to transcription factors represented in a particular species or class and to treat these as motif hypotheses. For the PPARγ data set introduced in section 3.2, we tested the large set of 101 DNA-binding domain derived motifs reported in (33) to see which motif best represented the binding specificity of this transcription factor. To better make use of the sequence information at PPARγ-bound regions, we fit each motif to the binding data using an Expectation maximization motif discovery approach (see Chapter 6). The resulting motifs were subsequently evaluated for quality (see section 3.3).

3.3. Hypothesis evaluation

The hypotheses that have been assembled, either by de novo motif discovery or by other methods, must be evaluated to determine which does the best job of representing the transcription factor’s binding specificity. This involves calculating a score for each motif that measures its quality. Although most de novo motif discovery algorithms have built-in scoring methods for evaluating and ranking motifs, these scores are usually not directly comparable between different programs. Furthermore, for ChIP-chip and ChIP-seq data, it is natural, and generally desirable, to make use of the negative information in unbound regions from the experiment when evaluating different motif hypotheses (34); many de novo algorithms do not make use of this information. One particularly simple and useful scoring scheme is to calculate a p-value based on the hypergeometric distribution associated with each motif’s occurrence in bound sequences relative to its occurrence in a pooled set of bound and unbound sequences from the experiment. Although the hypergeometric enrichment calculation produces a p-value, we will see in the next section that this statistic is not a reliable estimate of significance, and should be treated like any other type of score. Alternatively, to avoid the difficulties associated with defining a match threshold for position weight matrix motif models, motif hypotheses can be ranked by evaluating the area under the receiver-operating characteristic curve for a motif-based classifier used to distinguish bound and unbound sequences. For the set of hypotheses generated from the PPARγ ChIP-seq data in section 3.3, we used a similar approach, evaluating each motif’s ability to correctly classify held out bound and unbound sequences. In Figure 4 we show the distribution of mean 5-fold cross-validation errors for the 101 hypotheses. The motif with the lowest mean error, tgaCCTyTgNCCy, is an excellent match to the peroxisome proliferator response element bound by this transcription factor in vivo (35).

Figure 4. Distribution of motif scores for PPARγ ChIP-seq data.

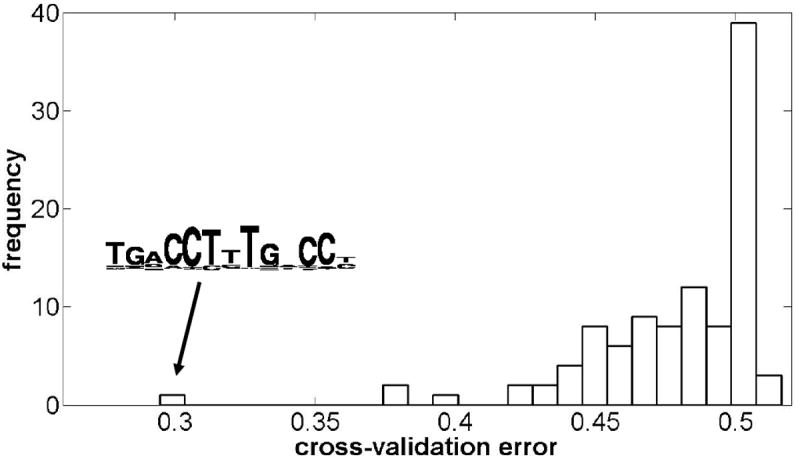
A diverse set of 101 motif hypotheses were evaluated by assessing their ability to discriminate bound and unbound sequences. The resulting distribution of mean 5-fold cross validation errors is shown. The motif with the lowest cross-validation error matches the previously reported PPARγ binding specificity.

3.4. Evaluating the statistical significance of motifs

High-scoring motifs may represent biologically meaningful transcription factor binding sites present in the immunoprecipitated regions identified by the experiment. To confidently link a particular motif to the binding data, however, it is necessary to estimate the level of statistical significance of the motif’s score. Overfitting is a danger associated with any hypothesis generation scheme, like de novo motif discovery, that involves fitting a model to sequence data. Although even simple models can overfit the data, as model complexity increases (for example by increasing the number of nucleotide positions in a position weight matrix model), overfitting becomes an increasingly serious problem. p-values are frequently used to evaluate the statistical significance of a motif. For motif analyses, the definition of a p-value is the probability of obtaining the same quality/score or higher for the motif when it is not bound by the transcription factor studied. A practical strategy for evaluating this probability is to estimate the null distribution using random sampling. The basic idea is as follows: the bound and unbound labels of the pooled set of sequences from the experiment are randomly permuted, the randomly sampled ‘bound’ set is used to fit a motif model, and this model is then scored. Repeating this process many times allows the distribution of scores under the null hypothesis to be estimated. By comparing the scores of interesting motif hypotheses to this distribution, an empirical p-value for each motif can be obtained. When more than one hypothesis has been tested, it is important to account for this by performing a multiple test correction. There are several methods of performing multiple hypothesis correction including step-down False Discovery Rate (FDR) methods and Bonferroni correction (36). We tested the statistical significance of the top-ranked motif from our analysis in section 3.4 using this randomization strategy. After permuting bound and unbound labels in the PPARγ ChIP-seq data, we then fit the motif to this randomized data by EM. The ability of the resulting motif to classify “bound” and “unbound” sequences was assessed. Repeating this process 25 times we observed a mean cross-validation error of 0.49 with a standard deviation of 0.01. By comparison, on the actual data the mean cross-validation error of the top-ranked motif was 0.27, indicating that this motif is quite likely to have biological relevance.

3.5. Mapping motifs back to the genome

The resolution of ChIP-chip and ChIP-seq experiments has improved tremendously, but unfortunately it is still does not exceed a level of approximately 200bp. For this reason, it is often of interest to identify putative in vivo transcription factor binding sites at higher resolution by mapping motifs back to the genome. Another important consideration is the noise in the data. Also, weakly bound regions with low ChIP enrichment may be biologically relevant. However, lowering the detection threshold may result in an unacceptably high level of false positives. Identification of motif matches allows sequence information to be used to adjust the confidence level associated with putatively bound regions detected in the experiment. The main challenge associated with identifying potential transcription factor binding sites using a sequence motif is in deciding what constitutes good enough agreement with the motif to be counted as a putative match. For matrix models, each genomic site can be scored using the matrix and a match threshold defined and used to identify putative binding sites. In the past, we have found that an empirically reasonable threshold to use is 0.6 times the maximum possible score of a log-odds matrix (29). However, more statistically principled methods for identifying motif matches can certainly be applied. It is always possible to associate an empirical p-value for a match score by evaluating the genome-wide distribution of scores for that motif. Alternatively, given a reasonable background model of nucleotide frequency in relevant genomic regions, a p-value can be obtained by calculating the log probability of the sequence under the motif and background models. We can then make the standard assumption that their ratio will be approximately chi-square distributed with degrees of freedom equal to the difference in degrees of freedom between the motif and background models. Of course, even when such p-values can be calculated, their relationship to the underlying biological reality is still unclear and the motif match threshold selection problem has simply been converted into a p-value threshold selection problem. For this reason, we recommend a data driven approach for picking a match threshold that takes advantage of the information the ChIP experiment has provided. By treating a motif as a feature that discriminates bound and unbound sequences in the experiment, reasonable criteria for selecting a match threshold naturally emerge. A threshold can be selected to keep FDR below some desired level, to minimize classification error, or to maximize sensitivity subject to a reasonable penalty on false positives. We define a true positive (TP) as a bound region in the ChIP experiment with a match to the motif, a false negative (FN) as a bound region with no match, a true negative (TN) as an unbound region with no match, and a false positive (FP) as an unbound region with a motif match. Figure 5 shows how, on PPARγ bound regions and an equally sized set of unbound regions, sensitivity (TP/(TP+FN)) and specificity (TN/(TN+FP)) change as the match threshold is increased for the PPARγ motif. For these data, a match threshold selected to maximize sensitivity while keeping the FDR below 20% recovers 56% of the bound sequences.

Figure 5. Data-driven motif match threshold selection.

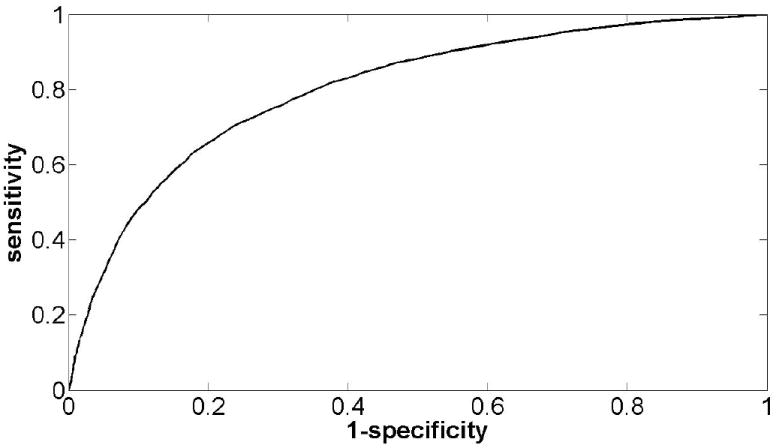
Shown is a sensitivity vs. specificity curve for the PPARγ motif used as a classifier of bound and unbound sequences. A threshold selected to maximize sensitivity while keeping the false-discovery rate below 20% recovers 56% of the bound sequences.